Главная
Лекция
9 (продолжение). Задачи для самостоятельного
решения
Содержание
Расчеты на устойчивость в сложных случаях
Продольный
изгиб
Задача 1.
Какой
из двух стержней одинаковой длины, условия закрепления и нагружения
которых также одинаковы, является более гибким – стержень квадратного или
круглого сечения с равной площадью? Ответ: гибкость второго на 2,3 % больше.
Задача 2.
Критическая
нагрузка на стержень с шарнирно-опертыми концами равна 200 кН.
Во сколько раз увеличится критическая нагрузка при увеличения площади поперечного сечения в 2 раза, если
стержень имеет: а) квадратное сечение, б) круглое, в) кольцевое с 
Е=200 ГПа, 
Указание: При 
применять формулу 
МПа. Ответ: а) 3,48 раза, б) 3,55 раза, в)
1,86 раза.
Задача 3.
Шарнирно
– опертый стержень I
№14 сжимается силой F=500
кН. Вычислить и сравнить коэффициенты запаса
прочности Ппц и устойчивости Пу, если Е=200 Гпа, 
.
Ответ: Ппц=3,83, Пу=1,65.
Задача 4.
Шарнирно-опертый
стержень круглого сечения сжимается силой F=50 кН. Длина
стержня l=1 м, материал – дюраль, 
запас устойчивости [Пу]=2.
Найти массу стержня. Установить также, во сколько раз увеличится масса стержня,
если заменить дюраль на сталь, сохранив прежнюю длину и запас устойчивости,
принимая 
Ответ: 
Задача 5.
Определить
минимальную величину сжимающей силы, при которой шарнирно-опертая по концам
стальная труба с наружным диаметром 
внутренним 
и длиной l=4
м потеряет устойчивость. Чему равны при этом напряжения в трубе? Ответ: Fкр=208
кН, 
Задача 6.
Как изменится эйлерова критическая сила, если одновременно увеличить диаметр круглой стойки в 2 раза и длину в 4 раза?
Задача 7.
Конструктивный
элемент представляет собой шарнирно опертый по концам круглый стержень диаметра
d=4 см и длины l=1 м. По проекту он должен быть изготовлен из стали Ст20,
имеющий предел пропорциональности 
Ввиду отсутствия данного материала его
изготовили из легированной стали 12ХНЗА с 
На сколько за счет
этого повысится запас устойчивости элемента при той же самой сжимающей силе?
Задача 8.
Стойка
проектируется из двух равнобоких уголковых профилей. Как следует соединить их между собой, чтобы
получить наибольшую несущую способность составной стойки?
Задача 9.
Стержень шатуна кривошипно-шатунного механизма проверяют на устойчивость от осевой сжимающей силы, причем в плоскости движения шатуна концы его считают шарнирно опертыми, а в плоскости, нормальной к плоскости движения – жестко заделанными. При каком соотношении между осевыми моментами инерции сечения шатуна обеспечивается его равноустойчивость в указанных плоскостях?
Задача 10.
Две деревянные стойки одинаковой длины и веса отличаются только формой поперечного сечения (у одной сечение круглое, а у другой - квадратное). У какой стойки несущая способность выше?
Задача 11.
Стойка имеет прямоугольное сечение 10х40 см. Как следует закрепить ее по концам, чтобы обеспечить равноустойчивость в главных плоскостях?
Задача 12.
Круглая стальная стойка гибкостью λ=100 выдерживает сжимающую силу F=100 кН при запасе устойчивости Пу=2. Во сколько раз можно увеличить сжимающую силу, уменьшив длину стойки в 2 раза и сохранив прежний коэффициент запаса устойчивости?
Задача 13.
Конструктивный элемент квадратного сечения подвергается действию сжимающей силы. В первоначальном варианте его планировалось изготовить из титана и закрепить по схеме консольного стержня. В последующем нагрузку потребовалось увеличить в 4 раза. Укажите возможные варианты достижения поставленной цели, не связанные с изменением геометрических размеров стержня. Формулу Эйлера считать применимой.
Задача 14.
Учитывая, что потеря устойчивости происходит в упругой стадии, установите, какому из двух, совершенно одинаковых по форме и размерам стержней, изготовленных из разных материалов, соответствует меньшая критическая сила.
|
|
Материал стержней |
|||||
|
Вариант |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
алюминий |
титан |
бетон |
медь |
чугун |
бетон |
|
2 |
чугун |
медь |
сосна |
дюраль |
бетон |
алюминий |
Задача 15.
Пользуясь
таблицей значений коэффициента снижения допускаемого напряжения, определить
наибольшую допускаемую величину сжимающей нагрузки на стойку двутаврового
поперечного сечения (двутавр № 24а) из Ст. 3 при основном допускаемом напряжении [σ] =160 МПа. Длина стойки
Решение.
Двутавр № 24а по сортаменту имеет S = 47,7 см2 и iтin = 
.
Из таблицы значений φ
— коэффициента снижения допускаемого напряжения при продольном
изгибе—путем линейной интерполяции находим: φ
= 0,574. Допускаемое усилие равно [F]=φ∙[σ]∙S=0,574∙160∙106∙47,7∙10-4=438 кН.
Задача 16.
Как изменится критическая сила, определяемая по формуле Эйлера, если все размеры прямоугольного сечения стержня увеличатся в 2 раза?
Ответ: Fcr увеличится в 16 раз.
Задача 17.
Как изменится критическая сила, определяемая по формуле Эйлера, если длина стержня увеличится в 2 раза?
Ответ: Fcr уменьшится в 4 раза.
Задача 18.
Как изменится критическая сила, определяемая по формуле Эйлера, если размер h (высота) прямоугольного поперечного сечения (см. рис.) увеличить в 2 раза?
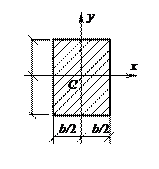
Ответ: Fcr увеличится в 2 раза.
Задача 19.
Определить критическую силу и критическое напряжение для чугунной стойки диаметром d = 30 см и длиной l =4,5 м. Оба конца стойки шарнирно оперты.
Ответ: λ=60; σcr=242 Мпа; Fcr=17097 кН.
Задача 20.
Определить критическую силу и критическое напряжение для центрально сжатой стальной стойки двутаврового сечения (двутавр № 33) длиной l =4 м. Нижний конец стойки защемлен, верхний – шарнирно оперт.
Ответ: λ=100,35; σcr=201,8 Мпа (по формуле Эйлера); Fcr=1085 кН.
Задача 21.
Определить критическую силу и критическое напряжение для сжатой вдоль оси пустотелой дюралюминиевой трубы длиной 2 м. Наружный диаметр трубы d = 10 см, внутренний диаметр d1 = 8 см. Нижний конец трубы защемлен, верхний конец – свободен. Принять модуль продольной упругости дюралюминия E=7∙104 Мпа.
Ответ: λ=125; σcr=44,2 Мпа; Fcr=125 кН.
Задача 22.
Двутавровая балка № 24 длиной l = 6 м заделана обоими концами в двух жестких стенах при температуре 20о С. В процессе эксплуатации помещения балка нагревается. Определить температуру t нагрева балки, при которой наступит ее продольный изгиб (потеря устойчивости).
Ответ: t = 72о С.
Задача 23.
Определить допускаемую нагрузку сжатого стержня из стали С245, имеющего прямоугольное сечение 4х6 см. Концы стержня закреплены шарнирно. Длина стержня l = 80 см, а γс=1.
Ответ: Nadm = 443,35 кН.
Задача 24.
Определить
величину допускаемой нагрузки на деревянную стойку высотой 5 м и сечением 18
22 см. Концы стойки закреплены шарнирно. Материал стойки –
сосна с RС = 14 МПа.
Ответ: Nadm = 187,4 кН.
Задача 25.
Определить величину допускаемой нагрузки на деревянную стойку круглого поперечного сечения с радиусом r =10 см и высотой 3м. Материал стойки – сосна с RС = 14 МПа. Один конец стойки жестко защемлен, а другой – свободен.
Ответ: Nadm = 111 кН.
Задача 26.
Определить допускаемую Nadm и критическую Fcr нагрузку для сжатого стержня из двутавра № 30. Длина стержня – 6 м. Один конец его жестко заделан, а другой – шарнирно закреплен. Материал – сталь с Ry=240 Мпа, а γc=1.
Ответ: Nadm = 287 кН; Fcr = 388 кН.
Задача 27.
Определить допускаемую продольную силу для чугунной стойки (чугун СЧ 15) диаметром 30 см и длиной 4,5 м. Оба конца стойки соединены с опорами шарнирно, γc=1.
Ответ: Nadm = 4974 кН.
Задача 28.
Определить допустимую нагрузку Nadm центрально сжатого столба высотой 5 м. Нижний конец столба заделан в фундамент, верхний конец – свободен. Поперечное сечение – прямоугольное с размерами 51×64 см. При расчете принять R = 2 МПа, mд = 1.
Ответ: А = 0,326 м2; φ=0,738; Nadm = 482 кН.
Задача 29.
Подобрать диаметр сплошного стержня из стали С285. Стержень сжат продольной силой N = 20 кН. Концы стержня закреплены шарнирно. Длина стержня l = 100 см, а коэффициент условий работы γc=1.
Ответ: d = 2,288 см.
Задача 30.
Стальной
стержень с шарнирно опертыми концами подвергается центральному сжатию силой F. Определить размер
сечения, до которого расчет на устойчивость при заданной длине l можно вести по формуле Эйлера, и найти
допускаемую нагрузку в следующих условиях: а) круглое сечение, l=1,2
м, d=30
мм; б) двутавровое сечение № 16, l=1,7 м. Дано: Е=200
ГПа, 
Ответ:
а) 
Задача 31.
Концы
сжатого стержня в одной плоскости защемлены, а в перпендикулярной к ней
плоскости шарнирно оперты. Определить размеры прямоугольного сечения стержня, равноустойчивого в указанных плоскостях, если 
=10
кН.
Ответ:
20х40 мм.
Задача 32.
Концы
шатуна двигателя в плоскости движения закреплены шарнирно, а в перпендикулярной
к ней плоскости защемлены. Расчетное сжимающие усилие, возни кающиеся при максимальном
давлении газов, равно 175 кН, длина шатуна l=1
м. определить из расчета на устойчивость размеры сечения шатуна в двух случаях:
а) сечение сплошное, круглое диаметром d; б) сечение трубчатое с отношением 
Найти
также отношение весов для сплошного и трубчатого
стержней. Дано: Е=200 ГПа, 
Ответ:
d=50
мм, 
Задача 33.
Шарнирно
опертый стержень круглого сечения сжимается силой F=50 кН. Длина
стержня l=1 м, материал – дюраль, 
т/м3,
Ед=70 ГПа, запас
устойчивости 
Найти массу стержня. Установить также, во
сколько раз увеличиться масса стержня, если заменить дюраль на сталь, сохранив
прежнюю длину и запас устойчивости, принимая 
т/м3, Ест=200 ГПа.
Ответ:
Задача 34.
Шарнирно
опертый стержень двутаврового сечения № 14 сжимается силой F=500 кН. Вычислить и сравнить коэффициенты запаса прочности 
и устойчивости 
,
если Е=200 ГПа, 
Ответ:
Задача 35.
Определить
минимальную величину сжимающей силы, при которой шарнирно опертая по концам
стальная труба с наружным диаметром 
внутренним 
и длиной l=4
м потеряет устойчивость. Чему равны при этом напряжения в трубе?
Ответ:
Fкр=208
кН,
Задача 36.
Размеры
сечений прокатных профилей периодически пересматриваются с целью более
экономного использование материала. Так, например, стандарт на швеллеры,
установленный в 1939 г (ОСТ 10017-39), был заменен в 1956г., а затем в 1972 г.
новым стандартом (ГОСТ 8240-72). На примере сравнивания двух сжатых гибких
стоек, одна из которых изготовлена из двух швеллеров № 30б (ОСТ 10017-39), а
другая – из двух швеллеров № 30 (ГОСТ 8240-72) определить, какой экономический
эффект получен в результате улучшения сечения. В качестве характеристики
экономичности принять отношение критической силы к единице массы стойки. длины и условия закрепления
концов обеих стоек одинаковы. Швеллеры расположены так, что обеспечивается
условие равноустойчивости стойки относительно главных
центральных осей. справочные данные для швеллера № 30б (ОСТ 10017-39): масса 1
м длины профиля m=39,16
кг, площадь сечения А=49,6 см2, моменты
инерции Iх=6498
см4.
Ответ:
Стойка, изготовленная из швеллера № 30
(ГОСТ 8240-72), на 10% экономичнее стойки изготовленной из швеллера № 30б (ОСТ
10017-39).
Задача 37.
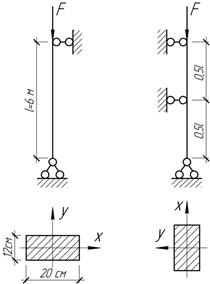
Определить
величины допускаемой сжимающей силы и допускаемого напряжения для деревянной
стойки прямоугольного сечения 12х20 см, если Е=10 ГПа,
Ответ:
[F]=73,1
кН, 
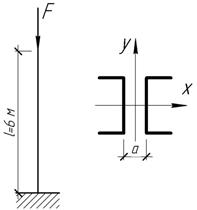
Задача 38.
Сечение
консольной стойки состоит из двух швеллеров №30, расставленных так, что
центральные моменты инерции сечения относительно главных осей координат.
Определить наибольшую величину допускаемой нагрузки и наименьшую необходимую
величину расстояния а, если [σ]=160
МПа.
Ответ:
[F]=778
кН, 
Задача 39.
Определить
коэффициент запаса устойчивости винта домкрата грузоподъемностью 100 кН,
изготовленного из стали Сталь 5.
Внутренний диаметр винта 
Максимальная высота подъема 500 мм. Указание.
При 
больше 
применять формулу 
МПа.
Ответ:
Задача 40.
Дюралевая
труба сжимается с силой F=7,6
кН. Определить диаметр d трубы, если отношение d/t=25, Е=70 ГПа, 
Ответ:
d=30
мм.
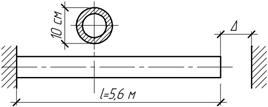
Задача 41.
Подкос
АВ представляет собой шарнирно опертый по концам круглый стержень, изготовленный
из дерева. Подобрать сечение подкоса, если допускаемое напряжение 
Ответ:
d=25
см.
Задача 42.
Считая
указанное на рисунке положение наиболее опасным, подобрать сечение шатуна, если Е=200 ГПа, 
Ответ:
d=60
мм.
Задача 43.
Стальной
стержень трубчатого сечения (
)
подвергается нагреву. При каком повышении температуры он потеряет устойчивость,
если Δ=1,5 мм, 
Ответ:
Δt=100,4
0С.
Задача 44.
Стойка состоит из четырех уголков 100х100х10, скрепленных планками. Оба конца стойки шарнирно-оперты, ее длина 6 м, она сжата силой 1 МН. Определить размер стороны а поперечного сечения, если [σ]=160 МПа.
Ответ: а=21,9 см.
Задача 45.
Сечение консольной стойки состоит из двух швеллеров № 30, расставленных так, что центральные моменты инерции сечения относительно главных осей одинаковы. определить наибольшую величину допускаемой нагрузки и наименьшую необходимую величину расстояния а, если [σ]=160 МПа.
Ответ:
[F]=778 кН,
Задача 46.
Укажите след плоскости, в которой будет выпучиваться стержень заданной формы поперечного сечения при потере устойчивости.
Задача 47.
Какой из пяти стержней одинакового сечения, выполненных из одного материала, наиболее устойчив?
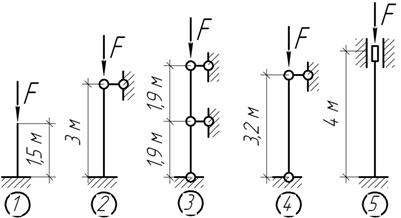
Задача 48.
Повысится ли несущая способность круглого стержня, если левое сечение закрепить от перемещения вдоль оси у?
Задача 49.
Имеются две круглые стальные стойки. Какая из них работает с большим коэффициентом запаса устойчивости?
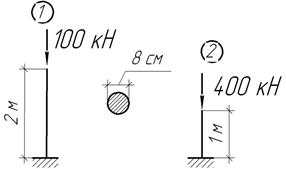
Задача 50.
Жесткий
брус СВ поддерживается двумя стальными подкосами
квадратного сечения 10х10 см. При какой длине l подкосов
система потеряет устойчивость в упругой стадии работы материала?
Ответ:
l=5
м.
Задача 51.
Определить
из условия устойчивости стойки допускаемое повышение ее температуры, если Е =200 ГПа, 
Во сколько раз изменится результат решения,
если принять, что балка абсолютно жесткая?
Ответ:
[Δt]=1040,
уменьшится в 10,1 раза.
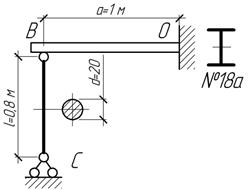
Задача 52.
Определить
допустимое значение погонной нагрузки из условия устойчивости стальной стойки
СД, если Проверить прочность балки при найденном [q], полагая [σ]=160 МПа. Указание.
При определении усилия в стойке ее сжатием пренебречь.
Ответ:
[q]=121
кН/м, 
(
)
Задача 53.
Определить
допустимое значение погонной нагрузки из условия устойчивости стальной стойки
СД, если Проверить прочность балки при найденном [q], полагая [σ]=160 МПа. Нижний конец
стойки шарнирно закреплен. Указание. При определении усилия в стойке ее сжатием
пренебречь.
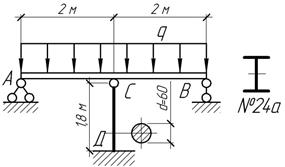
Ответ:
[q]=77,5
кН/м, 
Задача 54.
На рис.
показано колесо сеялки. Диаметр обода колеса D =1,22 м; диаметр ступицы D1=60 мм;
диаметр спицы круглого сечения d=
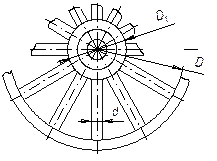
Ответ: Критическая сила Fкр = 22,6 кН; критическое напряжение σcr= 200 МПа.
Задача 55.
Определить
величину критического усилия и критического напряжения - для стойки
прямоугольного поперечного сечения 12х20 см2
длиной
Ответ:
145 кH;
6,04 МПа.
Задача 56.
Стержень
круглого поперечного сечения (см. рис.) длиной l =1 м
сжимается осевой силой F
= 50 кН. Диаметр стержня d =
Ответ: Фактический коэффициент запаса устойчивости пу = 3,54.
Задача 57.
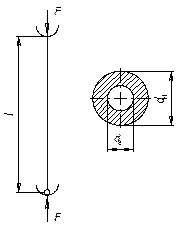
Проверить
устойчивость полой стальной штанги механизма газораспределения двигателя (см.
рис.) длиной l =
Ответ: Устойчивость штанги гарантирована, поскольку nу
=2,59>[ nу].
Задача 58.
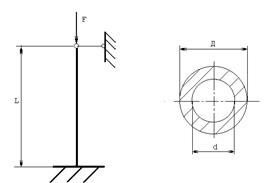
Определить критическую силу для стальной стойки трубчатого сечения, если его L=3м , Д=20см , d/Д=0,7 .
Задача 59.
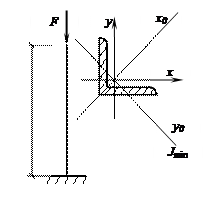
Определить критическую нагрузку для стержня из равнобокого уголка 100×100×10 мм.
Модуль упругости стали уголка принять E=2∙105 Мпа. Длина консольного стержня l = 1,5 м (см. рис.).
Ответ: λ=152; Fкр =162,35 кН; λ=152.
Задача 60.
Определить величину допускаемой нагрузки на деревянную стойку высотой 5 м и сечением 18×22 см. Концы стойки закреплены шарнирно. Материал стойки – сосна с RС = 14 МПа. Стойка ослаблена отверстиями диаметром 4 см (см. рис.).
Ответ: Nadm = 187,4 кН.
Задача 61.
Определить критическую Fcr и допускаемую Nadm нагрузку для стержня из равнобокого уголка 100×100×10 мм. Материал стержня – сталь С245. Длина стержня l = 1,5 м (см. рис.), а γc=1.
Ответ: Fcr = 162,35 кН; λ= 152; Nadm = 126,82 кН.
Задача 62.
Двутавр с двумя защемлёнными концами теряет устойчивость при повышении температуры на 800 С. Как следует изменить концевые условия, чтобы повысить безопасный температурный перепад до 1000 С?
Задача 63.
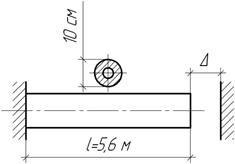
Стальной
стержень трубчатого сечения (
)
подвергается нагреву. При каком повышении температуры он потеряет устойчивость,
если 
Ответ: Δt=100,4 0С.
Задача 64.
Круглый стержень постоянного сечения А находится под действием всестороннего постоянного давления р. При этих условиях, очевидно, на стержень действует продольная сжимающая сила F, равная F=pA. Не может ли это сила при достаточной величине давления вызвать потерю устойчивости стержня?
Задача 65.
Прямой деревянный стержень постоянного поперечного сечения погружается одним концом в воду. На уровне воды стержень защемлен. Может ли этот стержень при достаточно большой длине l потерять устойчивость под действием выталкивающих архимедовых сил?
Задача 66.
Труба, защемленная нижним концом, заполняется через верхнее отверстие жидкостью с удельным весом γ. Может ли такая труба при заполнении потерять устойчивость по Эйлеру?
Задача 67.
Толстостенная прямая труба заполнена несжимаемой жидкостью. В верхнее отверстие трубки без трения вставлена пробка. Трубка и пробка закреплены шарнирно. Когда к пробке прикладывается сила F, жидкость сжимается, но в трубке продольная сжимающая сила отсутствует. Может ли трубка при этих условиях потерять устойчивость по Эйлеру?
Задача 68.
Через трубу, шарнирно закрепленную по концам, прогоняется жидкость удельного веса γ. Покажите, что при некотором значении скорости жидкости V труба теряет устойчивость, подобно тому, как теряет устойчивость стержень по Эйлеру.
Задача 69.
1) Определить
значения критических сил для абсолютно жесткого стержня, показанного на рис.1.
Жесткости верхней и нижней упругих связей (пружин) равны k.
2) Определить критическую силу для абсолютно жесткого стержня, показанного на рис.2.
3) Определить при помощи энергетического метода критическую силу для абсолютно жесткого стержня, показанного на рис. 2. Жесткость упругой связи равна k.
4) Определить энергетическим методом значения критических сил для абсолютно жесткого стержня, показанного на рис. 1. Жесткости верхней и нижней упругих связей (пружин) равны k.
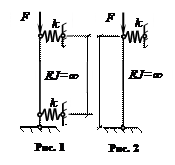
Ответ
к условию 1: Fcr,1
= kl/2; Fcr,2
=
.
Ответ к условию 2: Fcr = kl.
Ответ к условию 3: Fcr = kl.
Ответ
к условию 4: Fcr,1
= kl/2; Fcr,2
=.
Задача 70.
Определить критическую силу для абсолютно жесткой системы, показанной на рисунке.
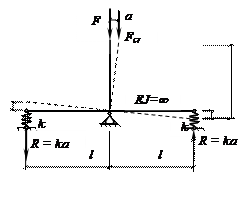
Ответ:
Fcr = 2kl.
Задача 71.
Определить значения критических сил в системе, представленной на рис. 1. Элементы системы – абсолютно жесткие. Жесткость связей равна k.
Определить критическую силу в системе, представленной на рис. 2. Элементы системы – бесконечно жесткие. Жесткость упругой связи равна k.
Определить критическую силу в системе, представленной на рис. 3. Элементы системы – бесконечно жесткие. Жесткость упругой связи равна k.
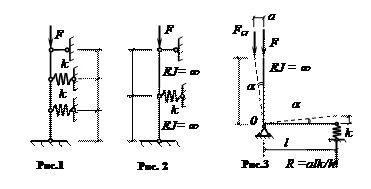
Ответ к рис.1: Fcr,1 = kl/3; Fcr,2 = kl.
Ответ к рис.2: Fcr = kl/2.
Ответ к рис.3: Fcr = kl2/h.
Задача 72.
Определить энергетическим методом критическую силу в системе, представленной на рис. 3. Элементы системы – бесконечно жесткие. Жесткость упругой связи равна k.
Определить энергетическим методом критическую силу в системе, представленной на рис. 2. Элементы системы – бесконечно жесткие. Жесткость упругой связи равна k.
Ответ к рис.3: Fcr = kl2/h.
Ответ к рис.2: Fcr = kl/2.
Задача 73.
Определить энергетическим методом критическую силу для сжатого прямого стержня, один конец которого жестко заделан, а другой свободен. Длина стержня – l. Жесткость на изгиб в обоих направлениях поперечного сечения равна EI.
У к а з а н и е
Уравнение криволинейной формы равновесия рассчитываемого стержня взять из табл. 2.
Ответ:
Задача 74.
Два бесконечно жестких стержня связаны между собой шарниром (см. рис.) и оперты на упругие пружины, жесткость которых равна k. Определить критическое значение сжимающей силы с применением формулы для потенциальной энергии
Ответ: Fcr,1 = 0,38kl ; Fcr,2 = 2,63kl.
Расчеты на устойчивость в сложных
случаях
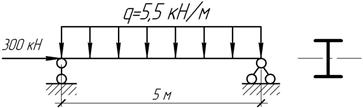
Задача 1.
Шарнирно
опертая по концам стальная труба с наружным диаметром 
толщиной стенки t=2 мм, длиной l=175
см сжата силой, приложенной с эксцентриситетом е=2,5 мм. Определить допускаемую
величину сжимающей силы, если 
Ответ:
[F]=30
кН.
Задача 2.
Определить
наибольший прогиб и наибольшее напряжение в стальной балке, имеющей начальное
искривление, если l=2 м.
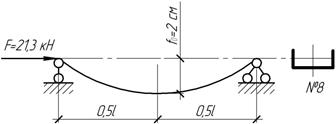
Ответ:
f=3
см, 
Задача 3.
Определить
наибольший прогиб и наибольшее сжимающее напряжение в балке для двух случаев:
а) без учета собственного веса балки, б) с учетом собственного веса балки 
м3.
Ответ:
а) f=1,8
мм; σ=26,1 МПа; б) f=4,2 мм; σ=43,9
МПа.
Задача 4.
Определить
наибольший прогиб и наибольшее сжимающее напряжение в балке.
Ответ:
f=4,91
мм; σ=146,2 МПа.
Задача 5.
Определить
наибольший прогиб и наибольшее сжимающее напряжение, а так же коэффициент
запаса прочности 
по отношению к пределу текучести 
и запаса устойчивости
,
с которыми работает балка.
Ответ:
f=0,303
см; σ=124 МПа; 
Задача 6.
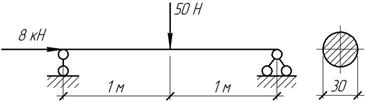
Подобрать
сечение двутавровой балки, если [σ]=160
МПа, нормативный запас прочности [n]=1,7.
Для предотвращения бокового выпучивания балка разделена связями пополам.
Ответ:
Двутавр № 24.
Задача 7.
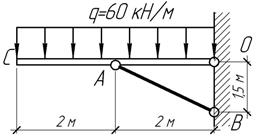
Поперечное
сечение балки ОВ составлено из двух неравнобоких уголков 80х50х6 мм,
соединенных большими полками вплотную и сваренных. Проверить прочность и
устойчивость балки в предположении, что узел В не
может перемещаться в направлении, перпендикулярном к плоскости чертежа, если [σ]=160
МПа, [n]=1,6.
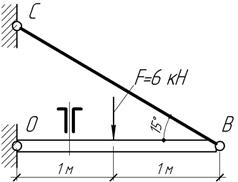
Ответ:
Сжимающее усилие в балке s=11,2
кН<[Fу]=126,4
кН; 
(растяжение).
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
