Главная
Лекция 9 (продолжение). Примеры решения по устойчивости сжатых стержней
Подбор сечения составных колонн из условия устойчивости
Пример 1.
Для составной
колонны, состоящей из четырех неравнобоких уголков, схема закрепления которой
показана на рис. а, требуется:
подобрать номер уголка, определить расстояние ![]() и
и ![]() , выбрать размеры соединительных планок и
вычислить коэффициент запаса устойчивости колонны, полагая Р=1000
кН,
, выбрать размеры соединительных планок и
вычислить коэффициент запаса устойчивости колонны, полагая Р=1000
кН, ![]() ,
,![]() , материал Ст.3.
, материал Ст.3.

Решение.
1) Подбор
номера прокатного профиля
Подбор поперечного сечения производят из условия устойчивости колонны относительно главной центральной оси с минимальным моментом инерции площади сечения. Для заданной колонны такой осью является ось Х (рис. г), так как относительно другой главной оси Y, момент инерции может быть изменен путем раздвижения или сближения ветвей колонны.
В случае если составные профили сечения могут раздвигаться относительно обоих главных центральных осей, минимально необходимый момент инерции сечения определяют по формуле Эйлера для критической силы, добавив в нее нормативное для данного материала значение коэффициента запаса устойчивости:
 ,
,
где Р – действующая нагрузка на стержень.
По вычисленной величине Imin, с учетом количества профилей, выбирают из сортамента необходимый номер профиля, и затем проводят проверку устойчивости колонны.
Минимально необходимую площадь поперечного сечения определяют из условия устойчивости колонны:
![]() ,
,
где ![]() - коэффициент
продольного изгиба, уменьшающий допускаемое напряжение в стойке при расчете на
устойчивость.
- коэффициент
продольного изгиба, уменьшающий допускаемое напряжение в стойке при расчете на
устойчивость.
В расчетной
формуле одновременно два неизвестных: А и ![]() . Поэтому, расчет ведем методом проб.
. Поэтому, расчет ведем методом проб.
Первый цикл
расчета. Задаем коэффициент ![]() =0,5. Находим требуемую площадь поперечного сечения колонны.
=0,5. Находим требуемую площадь поперечного сечения колонны.
![]()
На долю одного уголка придется
125/4=31,25 см2
По таблицам
сортамента неравнобоких уголков (ГОСТ 8510–86) выбираем уголок № 18/11, у
которого ![]() ,
,![]() ,
, ![]() ,
, ![]() (обозначение осей и
размеров даны на рис. б).
(обозначение осей и
размеров даны на рис. б).
Вычисляем момент инерции уголка относительно оси х (рис. г):
![]()
Находим наименьший радиус инерции поперечного сечения колонны:
![]()
Вычисляем гибкость
![]() ,
,
где ![]() коэффициент приведения
длины зависящий от формы закрепления.
коэффициент приведения
длины зависящий от формы закрепления.
По таблице
снижения коэффициентов снижения допускаемого напряжения (справочные
данные), находим коэффициент ![]() :
:
![]() .
.
Проверяем прочность колонны
![]()
Перенапряжение составляет
![]()
Что не
допустимо. Второй цикл расчета. Принимаем значение коэффициента![]()
Находим требуемую площадь
![]()
На долю одного уголка придется
152,44/4=38,11см2
По таблицам
сортамента берем уголок №20/12,5, у которого ![]() ,
, ![]() ,
,![]() ,
, ![]() .
.
Вычисляем момент и радиус инерции уголка относительно оси x:
![]() .
.
![]() .
.
Тогда ![]() .
.
По таблице
коэффициентов снижения допускаемого напряжения (справочные
данные) с помощью линейной интерполяции находим коэффициент ![]() :
:
![]()
|
|
130 |
140 |
134 |
|
|
0,40 |
0,36 |
0,384 |
Проверяем прочность колонны
![]() .
.
Перенапряжение составляет
![]()
При небольшом
пере- и недонапряжении (в пределах 10-20%) удобнее варьировать номером профиля.
Возьмем уголок с большей площадью №20/12,5, у которого![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Находим
![]()
![]() .
.
Гибкость колонны
![]()
По таблице
коэффициентов снижения допускаемого напряжения с помощью линейной интерполяции
находим ![]()
![]()
|
|
130 |
140 |
135 |
|
|
0,40 |
0,36 |
0,38 |
Проверяем прочность колонны
![]()
Недонапряжение составляет
![]()
С более подходящей площадью поперечного сечения уголка в сортаменте нет. Поэтому окончательно принимаем уголок 200х125х14 мм, хотя при этом стойка работает с недонапряжением более 5%.
2)
Определение расстояния между ветвями и соединительными планками колонны.
Подсчет числа соединительных планок.
Чтобы стойка была одинаково устойчива в главных плоскостях инерции, необходимо выполнить условие
![]()
Т.е.

Расстояние ![]() между соединительными
планками определяется из условий, что
гибкость отдельной ветви между соединительными планками не должна превосходить
гибкость колонны в целом:
между соединительными
планками определяется из условий, что
гибкость отдельной ветви между соединительными планками не должна превосходить
гибкость колонны в целом:
![]() .
.
Участок колонны между планками условно считаем шарнирно опертым. Тогда получим
![]()
Где ![]() минимальный радиус инерции уголка, берется из сортамента.
минимальный радиус инерции уголка, берется из сортамента.
Подсчитаем число пролетов между планками в колонне:
![]()
Принимаем по 3 планки с каждой стороны стойки. В нижнем сечении она не нужна из-за жесткой заделки.
3) Выбор
размеров соединительных планок.
Размеры соединительных планок принимают из следующих общепринятых конструктивных соотношений:
![]()
![]()
![]() ,
,
где В - длина планки, в - ширина полки уголка, Н – высота планки,
![]() - толщина планки, d - толщина полки уголка.
- толщина планки, d - толщина полки уголка.
![]()
![]()
![]()
4)
Вычисление коэффициента запаса устойчивости колонны.
Поскольку
гибкость колонны![]() при вычислении критического напряжения воспользуемся формулой
Эйлера:
при вычислении критического напряжения воспользуемся формулой
Эйлера:
![]()
Находим коэффициент запаса устойчивости
![]() ,
,
где 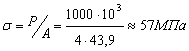 - нормальное напряжение сжатия колонны.
- нормальное напряжение сжатия колонны.
Для стальных
стержней строительных конструкций ![]() ,для
деревянных
,для
деревянных ![]() , чугунных
, чугунных ![]() , для элементов машиностроительных конструкций
, для элементов машиностроительных конструкций ![]() .
.
Пример 2.
Для стальной
составной колонны, защемленной нижним концом
и состоящей из двух
двутавров, расположенных на
расстоянии С
= 4 см, определить размеры поперечного сечения, если сжимающая нагрузка F = 500 кН, длина колонны l = 3 м, основное
допускаемое напряжение для материала колонны ![]() =150 МПа (см. рис.1).
=150 МПа (см. рис.1).

Рис.1
Рис.2
Решение.
Первая попытка. Принимаем ![]() = 0,5. По формуле проектировочного расчета получим:
= 0,5. По формуле проектировочного расчета получим:
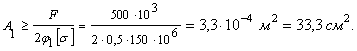
По сортаменту
ГОСТ 8239 – 89 принимаем двутавр № 24,
для которого А1
= 34,8 см2, ![]() = 9,97 см,
= 9,97 см, ![]() = 2,37 см, b1 = 11,5 см.
= 2,37 см, b1 = 11,5 см.
Для
определения действительного значения
коэффициента ![]() необходимо рассчитать гибкость
необходимо рассчитать гибкость ![]() , зависящую от минимального радиуса инерции imin. Для определения imin
вычислим главные радиусы инерции и выберем из них наименьший (рис.2):
, зависящую от минимального радиуса инерции imin. Для определения imin
вычислим главные радиусы инерции и выберем из них наименьший (рис.2):
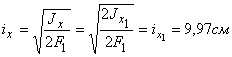 .
.
Таким
образом, видим, что ![]() из сортамента.
из сортамента.

Сравнивая значения ![]() и
и ![]() видим, что imin = iy = 8,10 см = 8,10×10-2м.
видим, что imin = iy = 8,10 см = 8,10×10-2м.
Тогда вычислим гибкость: ![]()
По таблице
коэффициентов ![]() для стали Ст.3, используя метод линейной интерполяции, вычисляем
для стали Ст.3, используя метод линейной интерполяции, вычисляем ![]() при
при ![]() = 74:
= 74: ![]() ,
,
где ![]() = 0,81 при
= 0,81 при ![]() = 70;
= 70; ![]() = 0,75 при
= 0,75 при
![]() = 80.
= 80.
Определяем:
![]()
Принимаем: ![]()
Вторая попытка. Вычисляем площадь поперечного сечения:

По сортаменту
подбираем двутавр № 20, для которого
А2 =
26,8 см2; ![]() = 8,28 см,
= 8,28 см, ![]() = 2,07 см, , b2 = 10 см.
= 2,07 см, , b2 = 10 см.
Минимальный
радиус инерции:

Гибкость
колонны: ![]()
Вычисляем коэффициент ![]() при
при ![]() = 823:
= 823: ![]()
![]()
Принимаем:
![]()
Третья попытка. Вычисляем площадь поперечного сечения:
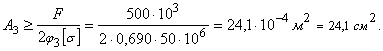
По сортаменту
подбираем двутавр № 18а, для которого
А2 =
25,4 см2; ![]() = 7,51 см,
= 7,51 см, ![]() 2,12 см, b3 = 10 см.
2,12 см, b3 = 10 см.
Минимальный
радиус инерции:

Гибкость
колонны: ![]()
Уточняем
коэффициент ![]() при
при ![]() = 82,1:
= 82,1:
![]()
Тогда
![]()
Делаем еще
одну попытку, вычислив ![]() по формуле:
по формуле:
![]()
Четвертая попытка. Вычисляем площадь
поперечного сечения:

По сортаменту
подбираем двутавр № 18, для которого
А2 =
23,4 см2; ![]() 7,42 см,
7,42 см, ![]() 1,88 см, b4 = 9 см.
1,88 см, b4 = 9 см.
Минимальный
радиус инерции
![]()
Гибкость
колонны: ![]()
Коэффициент ![]() при
при ![]() = 88,6 равен:
= 88,6 равен: ![]()
Тогда
![]()
Вычисляем
рабочее напряжение:

Допускаемое
напряжение на устойчивость:
![]()
Перенапряжение
составляет:

Окончательно
принимаем для сечения колонны двутавр №18. Совместная работа составной колонны
из двух ветвей (двух двутавров) будет обеспечена лишь при надежном соединении с
помощью планок, приваренных к ним. Расстояния ![]() (рис. 3) между
соединительными планками должны быть выбраны так, чтобы отдельная ветвь не
выпучилась в плоскости наименьшей жесткости. Это условие будет обеспечено, если
гибкость отдельной ветви на длине
(рис. 3) между
соединительными планками должны быть выбраны так, чтобы отдельная ветвь не
выпучилась в плоскости наименьшей жесткости. Это условие будет обеспечено, если
гибкость отдельной ветви на длине ![]() будет не больше
гибкости всей колонны. Для практических расчетов гибкость отдельной ветви на
участках между планками принимают
будет не больше
гибкости всей колонны. Для практических расчетов гибкость отдельной ветви на
участках между планками принимают ![]() .
.
Для двутавра
№18 минимальный радиус инерции ![]() . Тогда
. Тогда ![]() м.
м.
В этом случае
длина колонны l = 3 м разделится планками
на четыре участка
(т = 4).
Из конструктивных соображений получим длину
планки (см. рис. 3):
![]()
Принимаем
высоту планки:
![]()
Толщину
планки tп возьмем
равной толщине полки двутавра t. В
нашем случае из
сортамента
![]() .
.
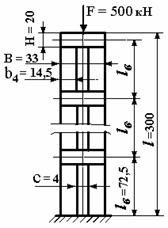
Рис.3
С учетом
способа закрепления концов колонны и высоты планок Н = 20 см окончательно принимаем длину ветви при числе
участков т = 4:

Расчет
окончен.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов