Главная

Во всем предыдущем изложении мы определяли поперечные размеры стержней из условий прочности. Однако разрушение стержня может произойти не только потому, что будет нарушена прочность, но и оттого, что стержень не сохранит той формы, которая ему придана конструктором; при этом изменится и характер напряженного состояния в стержне.

Наиболее типичным примером является работа стержня, сжатого силами Р. До сих пор для проверки прочности мы имели условие

Это условие предполагает, что стержень все время, вплоть до разрушения работает на осевое сжатие. Уже простейший опыт показывает, что далеко не всегда возможно разрушить стержень путем доведения напряжений сжатия до предела текучести или до предела прочности материала.

Если мы подвергнем продольному сжатию тонкую деревянную линейку, то она может сломаться, изогнувшись; перед изломом сжимающие силы, при которых произойдет разрушение линейки, будут значительно меньше тех, которые вызвали бы при простом сжатии напряжение, равное пределу прочности материала. Разрушение линейки произойдет потому, что она не сможет сохранить приданную ей форму прямолинейного, сжатого стержня, а искривится, что вызовет появление изгибающих моментов от сжимающих сил Р и, стало быть, добавочные напряжения от изгиба; линейка потеряет устойчивость.

Поэтому для надежной работы конструкции мало, чтобы она была прочна; надо, чтобы все ее элементы были устойчивы: они должны при действии нагрузок деформироваться в таких пределах, чтобы характер их работы оставался неизменным. Поэтому в целом ряде случаев, в частности, для сжатых стержней, помимо проверки на прочность, необходима и проверка на устойчивость. Для осуществления этой проверки надо ближе ознакомиться с условиями, при которых устойчивость прямолинейной формы сжатого стержня нарушается.

Под устойчивостью понимают способность систем сохранять их состояние равновесия или движения во времени под действием малых возмущений. Под неустойчивостью понимают способность систем при действии весьма малых возмущений получать большие перемещения.

Наглядной иллюстрацией устойчивого состояния равновесия служит поведение тяжёлого шарика на гладкой поверхности (рис. 9.1).

а) б) в)

Рис. 9.1

Если слегка отклонить шарик от состояния равновесия I, как показано пунктиром, и предоставить его самому себе, то в случае а) шарик начнёт колебаться около нижнего положения I и вернётся к нему; в б) он остаётся безразличным, а в случае в) он начнёт сразу же удаляться от положения I.

Приведённый пример отождествляет понятие устойчивого состояния шарика со свойством возмущённого (отклонённого) состояния II возвращаться к исходному I.

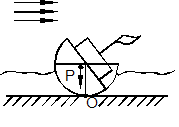
История науки знает различные определения понятия устойчивости. Одним из первых было определение, данное Л.Эйлером в 1749г. в связи с практически важным вопросом того времени – вопросом устойчивости кораблей Российского флота: «тела равновесное положение будет устойчиво, ежели оное тело, будучи несколько наклонено, опять справится» (рис. 9.2).

Термин устойчивость был введён в науку впервые Л.Эйлером. Применительно к упругим системам определение Эйлера можно сформулировать следующим образом: равновесие упругой системы при заданных внешних силах считается устойчивым в смысле Эйлера, если после статического приложения и последующего снятия малой возмущающей силы система возвращается к своему исходному состоянию (рис. 9.3). В противном случае исходное состояние равновесия системы считается неустойчивым.

а) Исходное состояние

б) Возмущённое состояние

с восстанавливающим моментом

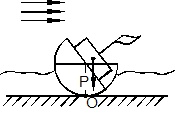
в) Возмущённое состояние

с опрокидывающим моментом

Рис. 9.2

а) б) в) г)

Рис. 9.3

Минимальное значение силы P, при котором система впервые не возвращается к исходному состоянию, называется бифуркационным. При этом значении нагрузки происходит нарушение единственности решения задачи, т.к. наряду с исходной прямолинейной формой равновесия стержня существует отклонённая форма.

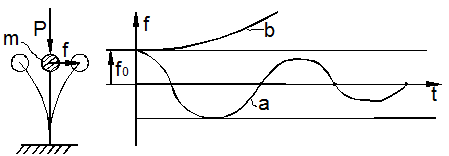
Другим, более общим, определением устойчивости состояния равновесия является определение Лагранжа: исходное состояние равновесия упругой системы устойчиво, если после отклонения её от этого состояния она, предоставленная самой себе, стремится вернуться к нему, совершая малые колебания, затухающие со временем при наличии сил внешнего и внутреннего сопротивления (рис. 9.4,а).

С увеличением сжимающей силы частота собственных колебаний системы стремится к нулю, а затем движение становится апериодически неустойчивым (рис. 9.4,б).

Для консервативных внешних сил критическая нагрузка находится из условия равенства нулю частоты собственных колебаний и совпадает с эйлеровой нагрузкой.

а) б)

Рис. 9.4

Если система (сжатый стержень) испытывает пластические деформации, то при любом малом возмущении он изгибается и затем при снятии возмущения не возвращается в своё исходное состояние (рис. 9.2, г). Получается, что по Эйлеру всякое равновесное состояние сжатой системы за пределом упругости – неустойчивое. Такое допущение с практической точки зрения является абсурдным. В.Г.Зубчаниновым предложено частное определение устойчивости сжатой системы за пределом упругости: состояние равновесия упругопластической системы является устойчивым, если она после статического приложения и последующего снятия малой возмущающей силы стремится вернуться в своё исходное состояние, пребывая в его малой окрестности.

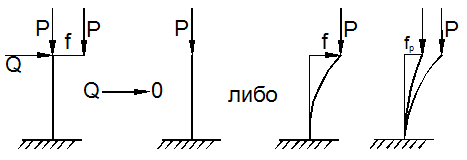
Из приведённых выше трёх определений по существу вытекает одинаковый метод исследования элементов конструкций на устойчивость – метод проб на устойчивость путём возмущения исходного состояния равновесия при достигнутом уровне нагружения. Этот метод обладает тем недостатком, что не рассматривает процесс нагружения, с помощью которого был достигнут данный уровень внешних сил, а также тем, что ограничивает область анализа устойчивости лишь малой окрестностью точки бифуркации (рис. 9.5).

Что произойдёт за точкой бифуркации при дальнейшем нагружении системы? На этот вопрос метод проб ответа не даёт. Судить об устойчивости или неустойчивости конструкции без исследования послебифуркационного поведения невозможно.

Так, для стержней (см. рис. 9.5, кривая 1) после бифуркации перемещения растут настолько быстро, что предельное значение нагрузки практически не отличается от бифуркационного.

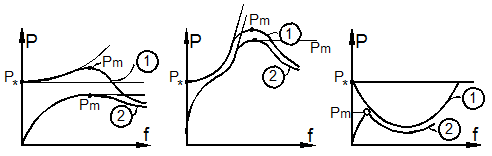
Рис. 9.5

При достижении предельного значения прогибы катастрофически нарастают и для их развития не требуется увеличивать сжимающую нагрузку. Такое поведение стержней предопределило успех бифуркационной теории Эйлера при расчёте стержней и стержневых систем на устойчивость. Для пластин после бифуркации вначале также наблюдается быстрый рост прогибов в некоторой окрестности исходного состояния (рис. 9.5, кривая 1).

Тонкие пластины и панели образуют выпучины, которые становятся явно заметными. В послебифуркационной стадии прогибы продолжают увеличиваться по мере увеличения нагрузки, но пластина остаётся в малой окрестности своего исходного плоского состояния, пока не достигнуто предельное значение нагрузки .

У оболочек после бифуркации наблюдается резкое падение сжимающей нагрузки и потому они весьма чувствительны к начальным несовершенствам (рис. 9.5, кривая 1).

В основе современной концепции устойчивости, её методологии лежит исследование процессов нагружения конструкций и их элементов. Процесс нагружения упругой или упругопластической системы считается неустойчивым, если сколь угодно малому продолжению этого процесса отвечают катастрофическое развитие перемещений и деформаций. Катастрофа наступает в предельных точках, называемых точками бифуркации Пуанкаре. Соответствующие нагрузки называют пределами устойчивости или критическими нагрузками. В предельных точках

Условие (9.1) принимается за критерий неустойчивости при квазистатическом нагружении упругопластических систем.

На практике все реальные элементы имеют начальные несовершенства (технологические прогибы, эксцентриситет приложения нагрузки и др.).

Такие элементы начинают выпучиваться (изгибаться) с самого начала нагружения (рис. 9.6,а).

Неустойчивость реальных элементов наступает в предельных точках точно так же, как и у идеальных систем с устойчивым докритическим выпучиванием (рис. 9.5, кривые 2).

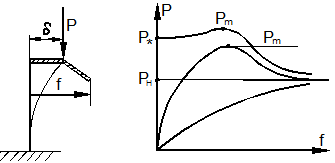
а) б)

Рис. 9.6

В связи с этим все малые начальные несовершенства отнесём к возмущениям. Это естественно, ибо когда смотрим на инженерную конструкцию (например, мостовую ферму со сжатыми элементами), мы представляем её геометрически и статически совершенной (идеальной).

На процесс выпучивания системы с начальными несовершенствами мы будем смотреть как на возмущённый процесс по отношению к послебифуркационнному процессу идеальной системы. Однако если возмущающие факторы чрезмерно велики, то задачи устойчивости может и не быть (см. рис.9.6,б).

Здесь изображено поведение сжатого стержня при выпучивании за пределом упругости. Если возмущающий эксцентриситет меньше некоторого числа , то при некоторой предельной нагрузке (предел устойчивости) произойдёт потеря устойчивости. Если достаточно велико (), то задачи устойчивости не возникает, в этом случае имеет место продольный изгиб. В обоих случаях кривые стремятся по мере роста прогиба к некоторой нагрузке , разделяющей указанные задачи и называемой нагрузкой надёжности устойчивых состояний.

Для стержней и пластин пределы устойчивости в возмущённом и невозмущённом состояниях близки друг к другу. Поэтому предел устойчивости для идеальных элементов следует принять за расчётные критические нагрузки. Для стержней, как мы уже отмечали, предел устойчивости близок к нагрузке бифуркации, что существенно облегчает задачу их расчёта на устойчивость.

У пластин в пределах упругости бифуркационные нагрузки значительно меньше предела устойчивости и потому задача расчёта на устойчивость сводится, в конечном счёте, к решению нелинейной задачи выпучивания.

У оболочек предел устойчивости весьма чувствителен к начальным несовершенствам (рис. 9.7). Поэтому здесь существенное значение приобретает знание среднестатического значения начальных несовершенств .

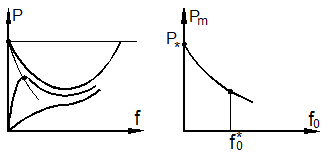
Рис. 9.7

Ещё одним важным обстоятельством при формировании концепции устойчивости является учёт ползучести материалов. В связи с этим процесс нагружения разделяется на два этапа: мгновенный процесс нагружения и этап процесса ползучести во времени при постоянной внешней нагрузке. На втором этапе процесс протекает во времени, значительно большем, чем требуется для процесса нагружения до заданного уровня.

Здесь возможны два варианта постановки задачи устойчивости. Первый относится к случаю ограниченной ползучести материала, второй – неограниченной.

Рассмотрим первый случай. На рис. 9.8,а кривая 1 относится к первому этапу нагружения, кривая 2 – ко второму после полной выборки ограниченной ползучести. Через обозначен предел устойчивости при мгновенном нагружении, через - предел устойчивости при длительном нагружении после выборки ползучести. Он называется пределом длительной устойчивости.

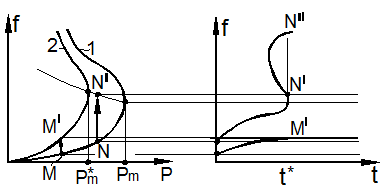
а) б)

Рис. 9.8

Рассмотрим точку М на кривой 1, для которой . В результате ограниченной ползучести (см. рис. 9.8,б) она переходит в точку . Такой процесс выпучивания на втором этапе – устойчив, поскольку он ограничен по перемещениям. Пусть теперь (точка N на кривой 1 (рис. 9.8,а)). Несмотря на ограниченную ползучесть материала, выпучивание элемента будет происходить до достижения мерой перемещения f некоторого значения (точка на штрихпунктирной кривой пределов устойчивости), после чего происходит выщёлкивание элемента конструкции (рис. 9.8,б, отрезок ), которое называют иногда локальной катастрофой, представляющую собой во времени разрывную динамическую бифуркацию.

В случае ограниченной ползучести оказывается возможным найти длительный предел устойчивости - такой, что при можно быть уверенным в том, что система останется устойчивой и будет пребывать в малой окрестности исходного состояния равновесия.

Рассмотрим теперь процесс выпучивания элемента материала, обладающего неограниченной ползучестью (рис. 9.9).

В этом случае кривая 1 (рис. 9.9) по-прежнему относится к мгновенному нагружению и на её основании можно найти предел устойчивости . Однако на втором этапе для любого процесс является неустойчивым (рис. 9.9,б). При достижении точки N^/ происходит локальная катастрофа по истечении некоторого промежутка времени, называемого критическим временем.

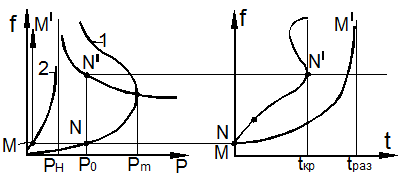
а) б)

Рис. 9.9

В этот момент имеет место условие:

а перемещение f достигает некоторого предельного конечного значения . При и заданном постоянном происходит динамический хлопок, называемый иногда локальной динамической катастрофой или бифуркацией. Если то потери устойчивости не происходит. Элемент испытывает продольный изгиб (рис. 9.9,а, линия 2). Процесс выпучивания приводит при к разрушению элемента конструкции. Время назовём временем разрушения или жизни элемента при продольном нагружении в условиях ползучести.

Таким образом, при учёте ползучести материалов, следует руководствоваться двумя критериями неустойчивости (9.1), (9.2). Может случиться так, что конструкция, устойчивая на первом этапе, т.е. без учёта свойств материалов во времени, окажется неустойчивой на втором длительном этапе функционирования.

Модельные задачи и методы исследования устойчивости упругих систем

1. Метод Эйлера. Рассмотрим простую модельную задачу, которая поможет выяснить все особенности потери устойчивости. Пусть абсолютно жёсткий стержень (стойка) шарнирно опёрт на нижнем конце и закреплён с помощью упругой горизонтальной пружины на верхнем (рис. 9.10,а). Эта пружина отражает упругие свойства системы при поперечном отклонении. Реакцию пружины R представим соотношением:

где f - горизонтальное перемещение верхнего конца стойки. Если перемещение f мало, то нелинейными членами можно пренебречь и принять . В противном случае задача принимает геометрически нелинейный характер.

Нагрузим стойку вертикальной силой P. Если подействовать на жёсткий стержень поперечной малой возмущающей силой q, то он отклонится на некоторый малый угол . Теперь снимем эту силу статически. Если стойка вернётся при заданном значении силы P в исходное состояние, то она устойчива в смысле Эйлера, если не вернётся, то неустойчива. Пусть имеет место второй случай. Составим уравнение равновесия стойки:

где - реакция упругой пружины.

Из (9.4) следует уравнение

откуда либо f=0 (устойчивость), либо (неустойчивость). Пусть . Тогда в нуль обратится круглая скобка, что позволяет найти критическую силу

Полученное значение силы , при котором система впервые не возвратилась к исходному состоянию, называется бифуркационной нагрузкой Эйлера. При этом значении силы происходит нарушение единственности решения задачи (f=0), т.е. бифуркация или ветвление решения. Вопрос о том, как будет вести себя стойка при остаётся открытым.

2. Метод Лагранжа. В основу этого метода положено динамическое определение устойчивости состояния равновесия Лагранжа. Для отклонённого состояния стойки, пользуясь принципом Даламбера, имеем (рис. 9.10,б):

где R=kf - упругая реактивная сила, - сила инерции, - прогиб, - ускорение, m – масса груза на конце стойки.

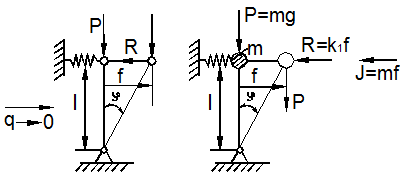
а) б)

Рис. 9.10

Из (9.6) находим уравнение колебаний системы с сосредоточенной массой m:

Полагая , получим характеристическое уравнение:

где

Если , то

где - круговая частота колебаний, - начальная фаза, A – амплитуда колебаний. Движение носит периодический характер и потому устойчиво. Если учесть внешнее и внутреннее сопротивление системы, то решение будет иметь вид

где - параметр, определяющий сопротивление движений. Колебания с ростом времени t затухнут, и система вернётся в своё исходное состояние. Следовательно, исходное состояние равновесия устойчиво.

Если , то k – действительное число. Решение принимает вид:

и носит апериодический, т.е. неустойчивый характер. При имеем . При происходит переход от устойчивого периодического движения стойки к неустойчивому апериодическому. Это происходит при критической силе

Таким образом, динамический метод Лагранжа приводит к тому же результату, что и метод Эйлера.

3. Метод Кармана (начальных несовершенств). Т.Карман первым рассмотрел процесс продольного изгиба стойки с начальными несовершенствами как задачу устойчивости и трактовал предельную нагрузку не как исчерпания несущей способности системы, а как предел устойчивости. Однако такая точка зрения долгое время (вплоть до наших дней) не находила поддержки. Применим метод Кармана к стойке на рис. 9.11,а.

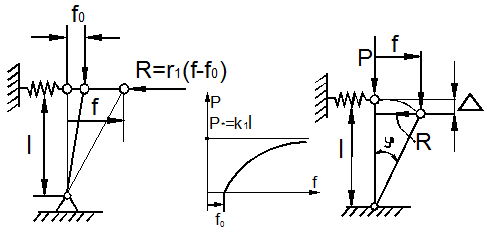
а) б) в)

Рис. 9.11

Стойка имеет отклонение от вертикали на некоторый угол и сжимается силой P. При P>0 стойка отклонится от вертикали на угол . Уравнение равновесия в некоторый момент процесса продольного нагружения стойки имеет вид

где . Из (9.12) следует:

Дифференцируя по f или по P соответственно, находим:

откуда при следует Согласно изложенной концепции значение силы является пределом устойчивости и совпадает с эйлеровой силой.

4. Энергетический метод С.П. Тимошенко. При отклонении системы на угол от положения равновесия (рис. 9.11,в), верхний конец стержня опускается на величину . Сила P совершает работу . Перемещение

где прогиб

Работа силы P на перемещение принимает вид

Упругая внутренняя реактивная сила R=kf совершает работу, называемую потенциальной энергией деформации:

Величина

носит название полной потенциальной энергии системы, связанной с потерей устойчивости. Если П>0 (P<kl), то энергии П достаточно для возвращения стержня в исходное состояние, т.е. его состояние равновесия устойчиво. Если П<0 (P>kl), то энергии деформации недостаточно для возвращения стержня в исходное состояние равновесия, т.е. он находится в неустойчивом состоянии равновесия. Граничное значение энергии П=0 является критерием для определения критической силы P=kl. Таким образом, энергетический метод приводит к критической нагрузке, равной нагрузке Эйлера для данной модели.

5. Метод Койтера исследования нелинейного послебифуркационного процесса выпучивания (нагружения). Пусть реакция в упругой пружине (рис. 9.13):

т.е. зависимость носит нелинейный характер.

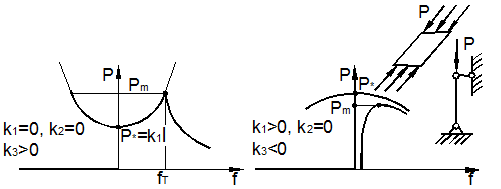
а) б)

Рис. 9.13

Тогда уравнение равновесия (9.3) примет вид

откуда либо f=0, либо , и тогда равно нулю выражение в квадратной скобке. Второе условие приводит к соотношению, которое позволяет установить зависимость между силой P и перемещением f в процессе нагружения элемента:

Если , то имеем кривые зависимости с симметричной бифуркацией (рис. 9.13,а). Предположим, что с развитием выпучивания и увеличением перемещения f в пружине при возникают пластические деформации. Тогда вместо (9.3) при имеем:

откуда

и с ростом f нагрузка P будет падать (рис. 9.13,а).

В реальных системах переход к пластической стадии деформирования осуществляется на графике P от f плавно с экстремальной предельной точкой.

Если , то согласно (9.17) имеем симметричную неустойчивую бифуркацию, характерную для сжатых неупругих стержней и пластины (рис. 9.13,б).

Пусть теперь

Тогда, согласно (9.12), имеем:

откуда при получаем:

При зависимость (9.19) имеет несимметричный вид (рис. 9.14,а). Прогибы f после бифуркации растут при падающей нагрузке. Такая точка бифуркации называется неустойчивой. Она характерна для упругих оболочек.

Если , то бифуркация будет также несимметричной (рис. 9.14,б).

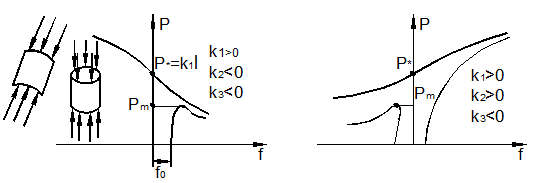
а) б)

Рис. 9.14

Задача Эйлера об устойчивости сжатого стержня

Познакомившись с концепцией устойчивости и модельными задачами, мы можем теперь перейти к рассмотрению задач устойчивости упруго сжатого стержня (рис. 9.15).

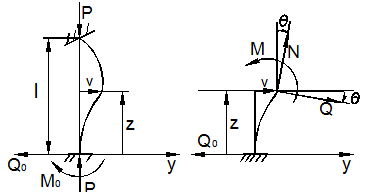
а) б)

Рис. 9.15

Считаем стержень идеально прямым и сжатым центрально приложенными силами P (рис. 9.15,а). Следуя методу Эйлера, будем считать исходное состояние равновесия упругого стержня устойчивым, если после статического приложения и снятия возмущающей силы при постоянных внешних сжимающих силах P стержень возвращается к своей исходной прямолинейной форме равновесия. В противном случае состояние равновесия считаем неустойчивым.

Допустим, что стержень остался в изогнутом состоянии (рис. 9.15,б). Отсечём часть стержня на расстоянии z от начала координат, считая угол поворота сечения малой величиной, и составим уравнения равновесия:

Изгибающий момент в поперечном сечении, согласно (6.9), равен:

Приравнивая выражения моментов (9.20), (9.21), находим:

Дифференцируя (9.22) по z, получим:

дифференцируя (9.23) по z, приходим к уравнению изогнутой оси потерявшего устойчивость стержня четвёртого порядка:

Введём обозначение:

Тогда уравнения (9.22), (9.24) можно записать в виде

Общее решение уравнения (9.26) имеет вид:

В него входят четыре произвольные постоянные .

Общее решение уравнения (9.27):

В него входят четыре произвольные постоянные

Производные:

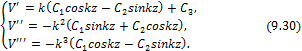
Используя (9.30), из (9.21), (9.23) находим:

Постоянные находятся из граничных условий. Для шарнирно закреплённого по концам стержня при z=0 и z=l имеем условия:

Для стержня, защемлённого при z=0 и свободного от закрепления при z=l, должны выполняться условия:

при z=0,

при z=l.

Если на незакреплённом конце при z=l действуют внешние момент m и поперечная сила R, то

M=m, Q=R.

При любом закреплении концов стержня мы имеем четыре граничных условия (по два на каждом краю), которые при подстановке в них выражений (9.28), (9.29) приводят к системе четырёх однородных алгебраических уравнений вида:

или

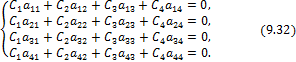
Система уравнений (9.32) имеет отличные от нуля решения только при условии, что её определитель:

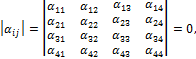
откуда, после его раскрытия, находим некоторое числовое значение kl:

где - некоторое число. Возводя обе части полученного равенства в квадрат и используя обозначение (9.25), получаем формулу для критического значения силы (нагрузки бифуркации) Эйлера:

где - приведённая длина стержня, - коэффициент приведения длины стержня к длине шарнирно опёртого по концам стержня.

Можно сказать, что – число, показывающее, во сколько следует увеличить длину шарнирно-опертого стержня, чтобы критическая сила для него равнялась критической силе стержня длиной в рассматриваемых условиях закрепления.

Понятие о приведенной длине было впервые введено профессором Петербургского института инженеров путей сообщения Ф. Ясинским.

Соответствующее критическое напряжение Эйлера:

где

гибкость стержня,

- радиус инерции площади поперечного сечения.

Формула (9.33) для критической силы сжатой колонны была получена Эйлером в 1744г. а для сжатого шарнирно опёртого стержня - в 1757г. Во времена Эйлера (1707 – 1783) главными конструкционными материалами были камень и древесина. Их слабое сопротивление нагрузкам заставляло инженеров создавать массивные конструкции и сооружения, для которых вопросы устойчивости не имели первостепенного значения. Поэтому теория устойчивости Эйлера долгое время не находила практического применения. Только с введением стали в проектирование инженерных конструкций с гибкими элементами, вопросы устойчивости получили большое практическое значение.

Устойчивость сжатого стержня с шарнирно закреплёнными краями

Л.Эйлер рассмотрел задачу с шарнирно опёртыми краями, т.е. с граничными условиями:

при

Удовлетворяя решение (9.29) четырём условиям (9.36), получим систему четырёх уравнений относительно неизвестных постоянных

откуда получаем

Если , то V=0. Если , то и откуда следует где n=1,2,3,… Следовательно

откуда эйлерова бифуркационная нагрузка:

Минимальная бифуркационная сила имеет место при n=1, т.е. при изгибе стержня по одной полуволне:

При n>1 выпучивание возможно, если в точках смены знаков кривизны и прогибов установить дополнительные опоры (рис. 9.16). В этом случае .

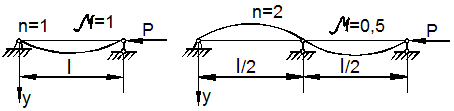
Рис. 9.16

Устойчивость стержней с иными видами закрепления

Рассмотрим задачи о продольном изгибе сжатых стержней с иными видами закрепления их краёв. На рис. 9.17 представлены различные случаи закрепления краёв стержня. Случаи а) и б) уже рассмотрены нами в 9.4. Обратимся к другим случаям на рис. 9.17:

а) Колонна с защемлённым нижним и свободным верхним краями (рис. 9.17, в). Пусть при z=0 стержень жёстко защемлён, а при z=l - свободен от закрепления.

Граничные условия имеют вид

при z=0,

при

Удовлетворяя решение (9.29) граничным условиям (9.39) получим:

откуда находим

Это условие может быть выполнено, если Мы получим

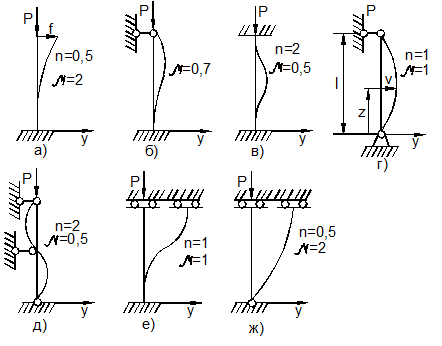
Рис. 9.17

В этом случае стержень остаётся в исходном прямолинейном состоянии равновесия, т.е. устойчив. Если coskl=0, то это приводит к значениям . Критическая сила с учётом равна:

Её наименьшее значение отвечает n=0, т.е.

Уравнение изогнутой оси стержня при найденных значениях постоянных :

Сравнивая (9.40) с (9.33) находим

Эту задачу можно решить несколько иначе, воспользовавшись решением (9.28) уравнения (9.26) второго порядка. Для рассматриваемой задачи где f- прогиб незакреплённого края при z=l .Тогда, согласно (9.28), имеем:

Удовлетворяя это решение граничным условиям:

получаем

откуда следует: Это условие удовлетворяется, если положить

Тогда

Следовательно, оба решения приводят к одной критической силе Эйлера (9.40).

б) Стержень с шарнирно опёртым и жёстко защемлённым краями. В этом случае граничные условия имеют вид

Подстановка общего решения (9.29) в (9.41) приводит к системе уравнений:

откуда находим а также систему двух уравнений:

Приравнивая к нулю определитель этой системы, находим уравнение

tgkl=kl,

откуда получаем его наименьший корень: kl =4,493 (рис. 9.18).

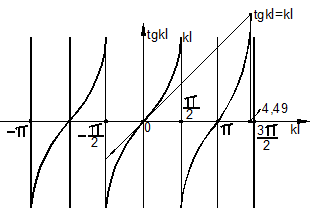
Рис. 9.18

С учётом находим критическое значение силы Эйлера:

Сравнивая (9.42) с (9.33), получаем . Уравнение изогнутой оси имеет вид:

в) Сжатый стержень с двумя жёстко защемлёнными краями

Граничные условия имеют вид:

Удовлетворяя решение (9.29) граничным условиям (9.43), получим систему уравнений:

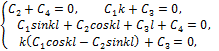
откуда находим: и систему двух уравнений:

Приравнивая к нулю определитель этой системы двух уравнений, получим соотношение:

, которое будет выполнено, если

либо .

Первое приводит к и критической силе Эйлера при n=1:

Второе условие приводит к наименьшему значению и критической силе Эйлера:

большей, чем значение, которое даёт формула (9.44). Таким образом, наименьшей критической силой для жёстко защемлённого по обоим концам стержня является (9.44), для которой . Уравнение изогнутой оси в этом случае описывается уравнением:

г) Влияние упругого защемления на устойчивость сжатой колонны.

Рассмотрим сжатую стойку (колонну), нижний конец которой при z=0 упруго защемлён (рис. 9.19). Мысленно рассечём узел и заменим упругую связь пружиной. Граничные условиями задачи будут:

Поскольку момент m заранее неизвестен, то следует дополнить условие совместности деформирования стержня и балки в узле при z=0. Это дополнительное граничное условие имеет вид

где угол найден из решения задачи об изгибе балки с помощью формулы Мора.

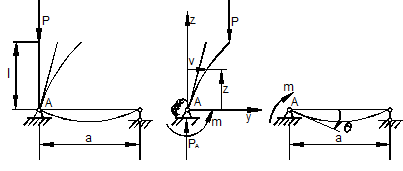
а) б)

Рис. 9.19

Удовлетворяя теперь решение (9.24) граничным условиям, находим:

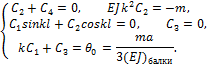
Решая полученную систему уравнений, находим:

откуда следует:

Если стержень жёстко защемлён при z = 0, то

что с учётом

приводит к выражению критической силы Эйлера:

Пусть . Тогда и наименьшее значение корня этого трансцендентного уравнения С учётом получаем выражение критической силы для упругозащемлённого стержня при частных соотношениях геометрических параметров:

что в 1,74 раза меньше критической нагрузки при жёстком защемлении. Таким образом, упругое защемление концов стержня снижает критическое значение сжимающей силы.

На практике, однако, почти никогда не встречаются в чистом виде те закрепления концов стержня, которые мы имеем на наших расчетных схемах.

Вместо шаровых опор обычно применяются цилиндрические шарниры. Подобные стержни следует считать шарнирно-опертыми при выпучивании их в плоскости, перпендикулярной к оси шарниров; при искривлении же в плоскости этих осей концы стержней следует считать защемленными (с учетом оговорок, приведенных ниже для защемленных концов).

В конструкциях очень часто встречаются сжатые стержни, концы которых приклепаны или приварены к другим элементам, часто еще с добавлением в месте прикрепления фасонных листов. Такое закрепление, однако, трудно считать защемлением, так как части конструкции, к которым прикреплены эти стержни, не являются абсолютно жесткими.

Между тем, достаточно возможности уже небольшого поворота опорного сечения в защемлении, чтобы оно оказалось в условиях, очень близких к шарнирному опиранию. Поэтому на практике недопустимо рассчитывать такие стержни, как стойки с абсолютно защемленными концами. Лишь в тех случаях, Когда имеет место очень надежное защемление концов, допускается небольшое (процентов на 10—20) уменьшение свободной длины стержня.

Наконец, на практике встречаются стержни, опирающиеся на соседние элементы по всей плоскости опорных поперечных сечений. Сюда относятся деревянные стойки, отдельно стоящие металлические колонны, притянутые болтами к фундаменту, и т. д. При тщательном конструировании опорного башмака и соединения его с фундаментом можно считать эти стержни имеющими защемленный конец. Сюда же относятся мощные колонны с цилиндрическим шарниром при расчете их на выпучивание в плоскости оси шарнира. Обычно же трудно рассчитывать на надежное и равномерное прилегание плоского концевого сечения сжатого стержня к опоре. Поэтому грузоподъемность таких стоек обычно мало превышает грузоподъемность стержней с шарнирно-опертыми концами.

Значения критических нагрузок могут быть получены в виде формул типа эйлеровой и для стержней переменного сечения, а также при действии нескольких сжимающих сил.

Пределы применимости формулы Эйлера

Формулы Эйлера (9.33), (9.34) получены в предположении упругого поведения материала, т.е. при условии:

где - предел пропорциональности.

При из (9.45) получаем предельное значение гибкости:

разделяющей области упругой () и неупругой () потерь устойчивости стержня. Для малоуглеродистой стали получаем:

Для алюминиевого сплава Д16Т (дюраль) , находим: .

На практике часто элементы конструкций оказываются недостаточно гибкими и . В этих случаях формула Эйлера даёт неверные, завышенные, результаты. Впервые это обнаружил Ходкинсон (Англия) в своих опытах по продольному изгибу сжатых колонн в 1840г. Формула Эйлера подтверждалась для гибких стержней и обнаруживала значительные отклонения для коротких стержней.

Е. Ламарль (Бельгия) в 1845г. первым установил границу применимости формулы Эйлера. Он предложил для стержней малой гибкости принять критическое напряжение , равным пределу текучести . В дальнейшем теория устойчивости Эйлера подверглась проверке в опытах И. Боушингера (1887г.), Л. Тетмайера и М. Консидера (1890-1896гг.)

В 1889г. Ф. Энгессер (Германия) предложил вычислить критическое напряжение по формуле Эйлера с заменой модуля упругости E на касательный модуль ,

Напряжение, вычисляемое по формуле (9.47), называют критическим касательно-модульным напряжением Ф. Энгессера. Соответствующая формула для касательно-модульной нагрузки имеет вид:

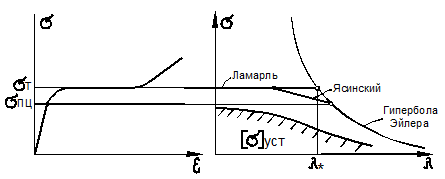
Для построения диаграммы критических напряжений формулу (9.48) следует записать в виде:

Обрабатывая диаграмму сжатия , можно найти зависимость . Тогда для каждого правая часть в (9.49) вычисляется и поэтому становится известной гибкость .

На рис. 9.20 представлены диаграммы сжатия и критических напряжений.

а) б)

Рис. 9.20

В 1895г. Л. Тетмайер и Ф. Ясинский на основе анализа экспериментальных данных предложили для вычисления критических напряжений эмпирическую линейную формулу

где - наибольшее значение гибкости для которой ещё можно считать

Полагая в (9.50) и получаем:

откуда находим формулу для выражения коэффициентов:

На основании (9.51) ниже составлена таблица значений коэффициентов a,b для некоторых материалов.

Таблица 9.1. Таблица значений коэффициентов а, b для некоторых материалов

Материал	МПа	МПа	МПа	МПа			a МПА	b МПа
Сталь мало- углеродистая	2	200	240	-	100	40	266,7	2/3
Сплав Д16Т (дюраль)	0,75	200	-	400	62	0	400	3,33
Сталь 30ХГСА (хромансил)	2,1	750	-	1100	52,6	0	1100	6,65
Сталь 45	2	260	300	-	87	30	321	0,7
Дерево (сосна)	0,1	10	-	20	70	0	30	0,2

Джонсон для материалов с площадкой текучести предложил для критического напряжения параболическую формулу:

Постоянные А, В определяются из условий при при Используя эти условия, находим:

После подстановки этих значений А, В в (9.52) получаем:

Как видно, для построения диаграммы критических напряжений достаточно знать всего две механические характеристики материала .

Формулу (9.53) можно записать в виде

где

эмпирический модуль Джонсона. Для его вычисления необходимо знать лишь и . Формула (9.54) записана в форме (9.47). Поэтому на модуль (9.55) можно смотреть как на приближённую аппроксимацию касательного модуля

Практический инженерный метод расчёта на устойчивость Ф. Ясинского

Теоретическое решение, полученное Эйлером, оказалось применимым на практике лишь для очень ограниченной категории стержней, а именно, тонких и длинных, с большой гибкостью. Между тем, в конструкциях очень часто встречаются стержни с малой гибкостью. Попытки использовать формулу Эйлера для вычисления критических напряжений и проверки устойчивости при малых гибкостях вели иногда к весьма серьезным катастрофам, да и опыты над сжатием стержней показывают, что при критических напряжениях, больших предела пропорциональности, действительные критические силы значительно ниже определенных по формуле Эйлера.

Таким образом, надо найти способ вычисления критических напряжений и для тех случаев, когда они превышают предел пропорциональности материалов, например, для стержней из мягкой стали при гибкостях от 0 до 100.

Необходимо сразу же отметить, что в настоящее время важнейшим источником для установления критических напряжений за пределом пропорциональности, т.е. при малых и средних гибкостях, являются результаты экспериментов. Имеются попытки и теоретического решения этой задачи, но они скорее указывают путь к дальнейшим исследованиям, чем дают основания для практических расчетов.

Прежде всего надо выделить стержни с малой гибкостью, от 0 примерно до 30—40; у них длина сравнительно невелика по отношению к размерам поперечного сечения. Например, для стержня круглого сечения гибкости 20 соответствует отношение длины к диаметру, равное 5. Для таких стержней трудно говорить о явлении потери устойчивости прямолинейной формы всего стержня в целом в том смысле, как это имеет место для тонких и длинных стержней.

Эти короткие стержни будут выходить из строя главным образом за счет того, что напряжения сжатия в них будут достигать предела текучести (при пластичном материале) или предела прочности (при хрупких материалах). Поэтому для коротких стержней, до гибкости примерно 30-40, критические напряжения «будут равны, или немного ниже (за счет наблюдающегося все же некоторого искривления оси стержня), соответственно или (сталь), или (чугун, дерево).

Таким образом, мы имеем два предельных случая работы сжатых стержней: короткие стержни, которые теряют грузоподъемность в основном за счет разрушения материала от сжатия, и длинные, для которых потеря грузоподъемности вызывается нарушением устойчивости прямолинейной формы стержня. Количественное изменение соотношения длины и поперечных размеров стержня меняет и весь характер явления разрушения. Общим остается лишь внезапность наступления критического состояния в смысле внезапного резкого возрастания деформаций.

В сжатых стержнях большой гибкости, для которых применима формула Эйлера, после достижения силой Р критического значения обычно наблюдается резкий рост деформаций. До этого момента прогибы, как правило, растут с ростом нагрузки, но остаются незначительными. Теоретически можно было бы ожидать, что до критической силы стержень будет оставаться прямым; однако ряд неизбежных на практике обстоятельств — начальная кривизна стержня, некоторый эксцентриситет приложения нагрузки, местные перенапряжения, неоднородность материала — вызывают небольшие прогибы и при сжимающих силах, меньших критических.

Подобный же характер имеет и зависимость укорочений от напряжения при сжатии коротких стержней; мы имеет ту же внезапность роста деформаций при определенной величине напряжений (когда ).

Нам остается теперь рассмотреть поведение сжатых стержней при средних величинах гибкости, например для стальных стержней при гибкостях от 40 до 100; с подобными значениями гибкостей инженер чаще всего встречается на практике.

По характеру разрушения эти стержни приближаются к категории тонких и длинных стержней; они теряют свою прямолинейную форму и разрушаются при явлениях значительного бокового выпучивания. При опытах для них можно отметить наличие ясно выраженной критической силы в «эйлеровом» смысле; критические напряжения получаются выше предела пропорциональности и ниже предела текучести для пластичных и предела прочности для хрупких материалов.

Однако потеря прямолинейной формы и понижение критических напряжений по сравнению с короткими стержнями для этих стержней «средней» гибкости связаны с такими же явлениями нарушения прочности материала, какие вызывают потерю грузоподъемности в коротких стержнях. Здесь комбинируются и влияние длины, понижающее величину критических напряжений, и влияние значительного роста деформаций материала при напряжениях за пределом пропорциональности.

Экспериментальное определение критических сил для сжатых стержней производилось неоднократно как у нас, так и заграницей. Особенно обширный опытный материал собрал проф. Ф. Ясинский, составивший таблицу критических («ломающих») напряжений в. зависимости от гибкости для целого ряда материалов и положивший начало современным методам расчета сжатых стержней на устойчивость.

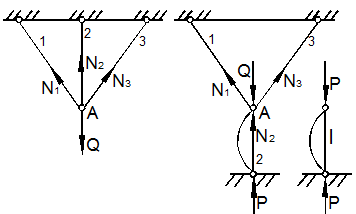
Рассмотрим две простейшие стержневые системы (рис. 9.21).

Узел А в обоих примерах испытывает одинаковое по модулю воздействие реактивных сил. Однако условия работы среднего стержня 2 будут различны. В схеме на рис. 9.21,а все стержни работают на растяжение, и мы должны потребовать выполнения условия прочности для растягивающих напряжений:

а) б)

Рис. 9.21

Во втором случае на рис. 9.21,б средний стержень 2 работает на сжатие, а два других - на растяжение, и мы кроме условия прочности на растяжение должны обеспечить условие прочности на сжатие:

Однако этого недостаточно, т.к. сжатый стержень может потерять устойчивость. Поэтому мы должны потребовать выполнения условия устойчивости:

Ф. Ясинский ввёл понятие коэффициента продольного изгиба (снижения основного допускаемого напряжения):

и записал условие устойчивости в виде

или

где - называют расчётным напряжением.

Поначалу Ф. Ясинский считал Тогда:

Для имеет место формула Эйлера и условие для предельной гибкости:

откуда следует

Тогда для коэффициента продольного изгиба получаем:

Следовательно, коэффициент изменяется в зависимости от по закону гиперболы.

Для воспользуемся формулой касательного модуля либо её аппроксимацией в форме Джонсона:

для коэффициента получаем формулу

из которой видно, что изменяется по закону параболы.

На рис. 9.22 представлен график от для стали 3 В этом случае В последствии в СНиПе было уточнено отношение коэффициентов запаса , и расчёт стал производиться по формуле (9.56):

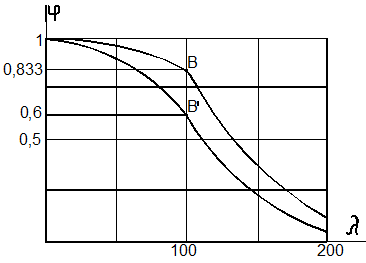
Рис. 9.22

Для стали обычно . Коэффициент запаса на устойчивость для принимается постоянным: . При Точка В, в которой , снижается до значения

что отмечено на рис. 9.22 в точке В.

Для стержней из дерева в СНиПе рекомендуется формула

Для сосны

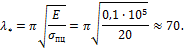
Для коэффициента продольного изгиба составлены таблицы. Ниже приведена такая таблица для ряда материалов (табл. 9.2).

Различают три типа расчёта на устойчивость: проверочный, определение допускаемой силы и проектный расчёт. При проверочном расчёте известны действующая сила Р, размеры стержня l,F, допускаемое напряжение на сжатие , способ закрепления стержня, т.е. коэффициент . Вычисляется гибкость стержня и по таблице коэффициентов для данного материала находится сам коэффициент . При этом допускается линейная интерполяция , если она не кратна десяти. Затем производится проверка выполнения расчётной формулы (9.57) на устойчивость:

При проектном расчёте заданы сила Р, длина стержня l, коэффициент приведения длины . Неизвестными остаются площадь сечения F и коэффициент продольного изгиба . Поэтому расчёт может быть выполнен только методом последовательных приближений в таком порядке: задаются каким либо значением коэффициента , например ; рассчитывают по нему требуемую площадь . Затем рассчитывается момент инерции , радиус инерции , уточняется площадь , вычисляется гибкость и по таблице находится соответствующий коэффициент . После этого рассчитывается расчётное напряжение:

Если разница между расчётным и допускаемым напряжением более 5%, то рассматривается второе приближение с новым значением коэффициента:

и расчёт повторяется в указанном выше порядке до тех пор пока разница между и станет не более .

Таблица 9.2. Коэффициенты продольного изгиба

	Сталь 3,4	Сталь 5	Сталь 15ХСНД	Сплав Д16Т	Чугун	Железобетон	Дерево (сосна)
0	1	1	1	1	1	1	1
10	0,99	0,98	0,98	1	0,96	1	0,99
20	0,97	0,95	0,95	1	0,91	1	0,99
30	0,95	0,92	0,93	0,84	0,81	1	0,93
40	0,92	0,89	0,90	0,70	0,69	1	0,87
50	0,89	0,86	0,83	0,57	0,57	1	0,80
60	0,86	0,82	0,78	0,46	0,44	0,83	0,71
70	0,81	0,76	0,71	0,35	0,34	0,73	0,61
80	0,75	0,70	0,63	0,27	0,26	0,64	0,49
90	0,69	0,62	0,54	0,21	0,20	0,57	0,38
100	0,60	0,51	0,45	0,17	0,16	0,52	0,31
110	0,52	0,43	0,39	0,14	-	-	0,25
120	0,45	0,38	0,33	0,12	-	-	0,22
130	0,40	0,32	0,29	0,10	-	-	0,18
140	0,36	0,28	0,26	0,087	-	-	0,16
150	0,32	0,26	0,23	0,076	-	-	0,14
160	0,29	0,24	0,21	-	-	-	0,12
170	0,26	0,21	0,19	-	-	-	0,11
180	0,23	0,19	0,17	-	-	-	0,10
190	0,21	0,17	0,15	-	-	-	0,09
200	0,19	0,16	0,13	-	-	-	0,08

При сжатии стержень изгибается в направлении наименьшей жесткости, его гибкость тем больше, чем меньше радиус инерции сечения. Отсюда вытекают следующие требования, которым должно удовлетворять сечение стержня, работающего на продольный изгиб:

1) стержень должен обладать одинаковой жесткостью по всем направлениям. Для этого моменты инерции, а следовательно, и радиусы инерции сечения относительно главных осей должны быть равны. Если же условия закрепления концов стержня в обеих главных плоскостях неодинаковы, как, например, шатун двигателя, то для получения одинаковой жесткости моменты инерции сечения относительно главных осей должны быть подобраны соответственно различными;

2) момент, а следовательно, и радиус инерции сечения при данной величине его площади должен быть возможно большим. Для этого элементы сечения должны быть удалены, возможно, дальше от его центра тяжести.

Указанным требованиям полностью удовлетворяют пустотелые стержни круглого и квадратного сечений. Стенки пустотелых стержней нельзя делать слишком тонкими, т. к. они могут потерять устойчивость, покрывшись волнистыми складками.

Для повышения устойчивости стенок принимают продольные ребра жесткости или поперечные распорки (диафрагмы), помещаемые на определенных расстояниях.

По степени рациональности известные сечения можно распределить следующим образом: трубчатое сечение, коробчатое, двутавровое, состоящее из швеллеров, квадратное, круглое, прямоугольное.

Пример 1.

Стальной стержень длиной l=4м двутаврового сечения №18, шарнирно закреплённый на одном и жёстко на другом краях, сжимается силами P. Требуется определить допускаемое и критическое значения силы P, если

Решение.

Из сортамента стального проката для двутавра №18 находим F = 23,4 см², Коэффициент приведения длины Ясинского для данного типа закрепления , гибкость стержня

Так как то критическая сила может быть определена по формуле Эйлера:

По таблице коэффициентов после интерполяции находим Вычисляем допускаемое значение внешней силы:

Коэффициент запаса на устойчивость

Если принять длину l=2 м, то В этом случае для определения критической силы использовать формулу Эйлера нельзя. Воспользуемся формулой Джонсона:

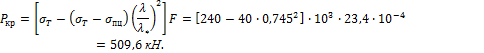
Допустимая нагрузка:

Коэффициент запаса

Если воспользоваться формулой Ясинского, то

Коэффициент запаса:

Пример 2.

Подобрать размеры круглого поперечного сечения стержня длиной l=3м из дерева (сосна), нагруженного силой P=100 кН, если Один конец стержня жёстко защемлён, а другой свободен от закрепления

Решение.

Условия устойчивости записываем в виде

Подбор диаметра D сечения производим методом последовательных приближений.

Первое приближение. Принимаем . Тогда:

Так как то

Подбор диаметра ведём с точностью до целого см. Для найденного диаметра D = 13см находим:

Находим гибкость По таблице коэффициентов с учётом интерполирования находим

Вычисляем:

Сравнивая с , видим, что в стержне будет перенапряжение в или на 429%. Поэтому следует рассмотреть второе приближение.

Второе приближение. Задаёмся новым значением:

Находим

Диаметр Далее после округления размера диаметра до целых значений см вычисляем:

По таблице находим и рассчитываем:

Перенапряжение составляет т.е. 83%. Поэтому необходимо рассмотреть третье приближение.

Третье приближение. Принимаем

Вычисляем:

Находим диаметр

Округляем диаметр до целых значений см и получаем D₃ = 20см. Корректируем новую площадь:

Вычисляем:

По таблице 9.2 для находим с учётом интерполяции Расчётное сопротивление:

Недонапряжение т.е. 7,7%.

На этом расчёт можно прекратить и принять размер диаметра D = 20 см.

Пример 3.

Определить допускаемую нагрузку для стойки из швеллеров №10 (Ст.3) (рис.9.22.1) расчётное сопротивление при растяжении R=220 МПа, Е=210⁵МПа. Расстояние а между швеллерами выбрать из условия равноустойчивости.

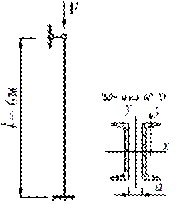
Рис.9.22.1

Решение.

Равноустойчивость стойки будет обеспечена при равенстве моментов инерции относительно осей х и у. Момент инерции относительно оси х не зависит от расстояния между швеллерами и определяется на основе табличных данных (ГОСТ 8239-89) J_x=174 см⁴, J_у=20,4 см⁴, А=10,9 см², z_o=1,44 см:

Момент инерции относительно оси у

Условие равноустойчивости , тогда

откуда а = 2,63см.

Определяем допускаемую нагрузку

F_adm= RA

Гибкость стойки

где см (равно i_х одного швеллера!).

По таблице 9.2 определяем:

Тогда допускаемая нагрузка

Определяем коэффициент запаса устойчивости

Так как гибкость стойки больше предельной для Ст.3 () ,то F_cr определяем по формуле Эйлера

откуда

Задача Энгессера об устойчивости сжатого стержня из нелинейно - упругого материала

В 1889 г. Ф. Энгессер (Германия) предложил расширить область применения формулы Эйлера путём введения вместо упругого модуля E переменного касательного модуля :

Формула (9.58) носит название формулы Энгессера для касательно- модульной нагрузки. Ошибка Энгессера состояла в том, что он не учёл за пределом упругости различие законов нагрузки и разгрузки, потому получил формулу бифуркационной нагрузки для нелинейно - упругого тела. Свою ошибку он понял в 1895 году после критического замечания Ф. Ясинского. При изгибе стержня под действием продольной силы Р возникает дополнительная деформация продольного волокна АВ на расстоянии y (рис. 9.24,б), равная:

Так как то имеем:

Согласно рис. 9.23,в в произвольной точке M диаграммы нелинейно-упругого тела догрузка и разгрузка происходят по одному и тому же закону:

Изгибающий момент M, возникающий в результате выпучивания стержня:

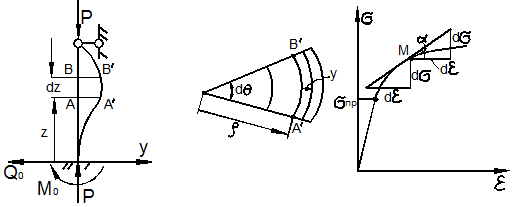
а) б) в)

Рис. 9.23

Подставляя вместо его выражение (9.59), находим:

С другой стороны, из условия равновесия отсечённой части стержня имеем:

Приравняв моменты, получаем:

Дифференцируя дважды, получаем:

или

где

Уравнение (9.60) в точности совпадает с (9.27) для упругого стержня. Отличие задачи состоит лишь в том, что выражение (9.61) для иное, чем (9.26) в линейно-упругом случае.

Общее решение уравнения (9.60) имеет вид

Дальнейший ход решения конкретных задач ничем не отличается от задачи Эйлера. Из (9.55) находим формулу (9.58) Энгессера:

Для бифуркационного значения напряжения по Энгессеру имеем:

откуда

Задавая значение из (9.64), вычисляем гибкость и строим диаграмму критических, а точнее бифуркационных значений напряжений (рис. 9.24).

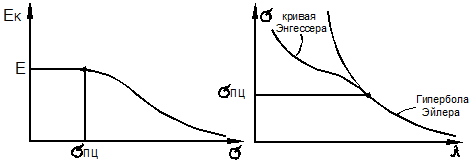
а) б)

Рис. 9.24

Устойчивость сжатого стержня за пределом упругости. Формула Кармана

Теория устойчивости сжатого стержня за пределом упругости окончательно была построена Т. Карманом (Германия) в 1910 году. Он учёл, что нагрузка на вогнутой стороне стержня и разгрузка на выпуклой стороне при выпучивании происходят по различным законам (рис. 9.25):

- при догрузке

- при разгрузке

Нейтральная ось дополнительных деформаций не совпадает с центральной осью, как при упругом изгибе, и определяется координатой . Поэтому представим их в виде:

Эп. Эп.

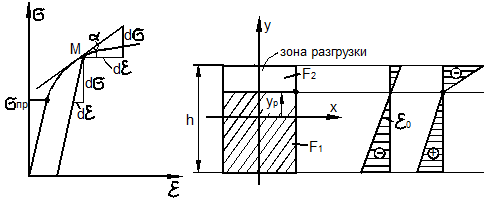
Рис. 9.25 Рис. 9.26

Величина даёт границу зон пластической догрузки и упругой разгрузки с площадями и соответственно. На границе раздела зон имеем:

откуда следует:

Следовательно, выражение (9.65) можно записать в виде

Вычислим с учётом (9.65) дополнительные нормальную силу dN и момент M, возникающие при выпучивании стержня по методу проб Эйлера – Кармана – Зубчанинова:

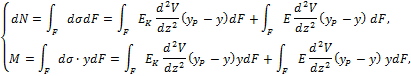
откуда находим

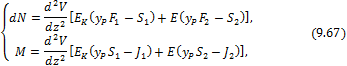
где

Так как

то, исключая , соотношения (9.67) приведём к виду:

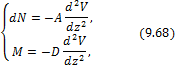
где

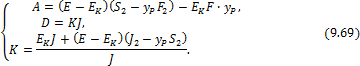
Величина К называется приведённым модулем Кармана–Ильюшина. С другой стороны, из уравнений равновесия отсечённой части стержня (рис. 9.16,б) имеем:

Сравнивая (6.66), (9.70), получим:

Дифференцируя дважды уравнение (9.72), находим:

Применяя к исследованию устойчивости стержня метод проб, будем считать dP = 0 при сколь угодно малом выпучивании стержня. Тогда из (9.68), (9.71) следует уравнение

из которого можно найти границу раздела зон . При этом изгибная жёсткость D=kJ также будет постоянной величиной. Дифференциальное уравнение (9.73) может быть записано в виде:

где

Таким образом, задача о потере устойчивости за пределом упругости свелась к решению уравнения (9.75), которое совпадает с уравнением (9.27) для упругой задачи Эйлера. Отличие задач заключается в различии выражений (9.27) и (9.76) для величины . Поэтому формула для нагрузки бифуркации за пределом упругости может быть получена из формулы Эйлера (9.33) простой заменой модуля Е на приведённый модуль К:

Формула (9.77) определяет бифуркационную нагрузку Кармана. Её также называют приведенно-модульной нагрузкой. Формула для бифуркационного значения напряжения имеет вид:-

Так как К зависит от , то построение диаграммы бифуркационных значений напряжений производится так же, как и для задачи Энгессера. Формула (9.75) представляется в виде:

Задавая , вычисляют , а затем гибкость и строят диаграмму . Вычислим приведённый модуль K для некоторых частных случаев поперечного сечения.

а) Рассмотрим случай идеализированного двутавра (рис. 9.27,а). Геометрические характеристики сечения:

Уравнение (9.74) принимает вид

откуда находим границу раздела зон:

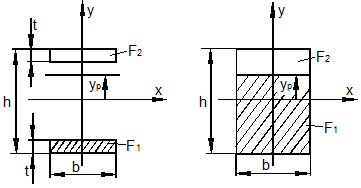
а) б)

Рис. 9.27

Согласно соотношению (9.69) получим:

б) В случае прямоугольного сечения (рис. 9.27,б)

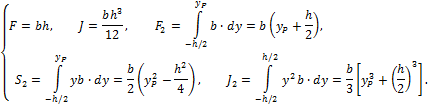
Уравнение (9.74) принимает вид

откуда находим границу раздела зон:

Приведённый модуль K, согласно (9.69), равен:

Из (9.74), (9.80) видно, что приведённый модуль явно зависит от . Поэтому при построении диаграммы критических (бифуркационных) напряжений сначала строятся зависимости и K от . На основании диаграммы сжатия (рис. 9.28,а) находится касательный модуль как функция напряжения , а затем по формулам (9.69), либо (9.80), (9.81) вычисляется приведённый модуль K. После этого по формуле (9.79) строится диаграмма критических напряжений .

Приведём более простой вывод формулы Кармана для приведенно-модульной критической силы. Обозначим радиус кривизны нейтрального слоя буквой r в отличие от радиуса оси стержня. Расстояние от нейтрального слоя до текущего волокна , а перемещение точек этого слоя .

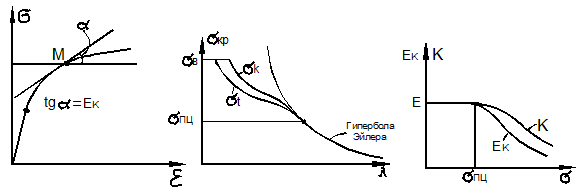
а) б) в)

Рис. 9.28

Тогда дополнительные напряжения:

где принято

Дополнительные нормальная сила и изгибающий момент:

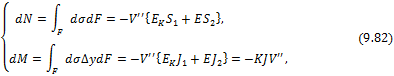
где

статические моменты и моменты инерции площадей F₁, F₂ для зон пластической догрузки и упругой разгрузки; – момент инерции всей фигуры относительно нейтральной оси,

приведённый модуль Кармана. Из уравнения равновесия отсечённой части потерявшего устойчивость стержня имеем:

Сравнивая с (9.82), получаем дифференциальные уравнения:

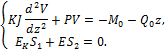
После двукратного дифференцирования первого уравнения получаем:

где

Для случая идеализированного двутавра (рис. 9.27,а) второе уравнение (9.84) с учётом:

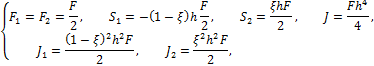
принимает вид

откуда

Следовательно,

Аналогично можно получить выражение приведённого модуля для стержней прямоугольного сечения.

Т. Карман не только создал теорию приведённого модуля, но и проверил её тщательно поставленными экспериментами. Опытные значения пределов устойчивости легли между кривыми, рассчитанными по теории приведённого модуля и теории продольного выпучивания сжатых стержней для эксцентриситета прилагаемых сжимающих сил, равно 0,005h где h – толщина прямоугольного поперечного сечения стержня.

Исследования Энгессера, Кармана, Ясинского по созданию теории устойчивости сжатых стержней за пределом упругости оставили глубокий след в истории её развития.

Устойчивость стержня в процессе нагружения за пределом упругости. Концепция Шенли

В 1946 году американский учёный Ф. Шенли пришёл к мысли о том, что теория приведённого модуля Кармана отвечает лишь частной теории стержня. Он показал на модельной задаче, что в процессе нагружения стержень начнёт изгибаться при касательно-модульной нагрузке Энгессера с разгрузкой на выпуклой стороне (рис. 9.29). При приближении сжимающей силы к приведённо-модульному значению прогиб f устремляется к бесконечности. Если учесть при этом возможность появления вторичных пластических деформаций на выпуклой стороне от растяжения, то приведенно-модульная нагрузка не будет достигнута и неустойчивость наступит в предельной точке при нагрузке называемой пределом устойчивости.

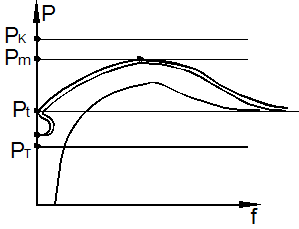
Рис. 9.29

В.Г. Зубчаниновым в 1969 г. было показано, что если при некотором значении силы , меньшем касательно-модульного значения , но большем значения соответствующего переходу стержня в пластическое состояние, стержень начнёт изгибаться под действием малой поперечной нагрузки q, действие которой прекращается раньше, чем сжимающая сила Р достигает значения , то изгиб стержня ликвидируется, если q достаточно мало, либо изгиб не ликвидируется, но стремится уменьшиться, если q недостаточно мало. В дальнейшем кривая процесса близка к процессу продолжающегося нагружения в смысле Шенли. Этим было доказано, что касательно-модульная нагрузка Энгессера – Шенли не является опасной для потери устойчивости, т.е. не является критической нагрузкой.

Ф. Шенли показал, что в процессе нагружения идеально прямого стержня он начинает изгибаться при достижении сжимающей силой касательно-модульной нагрузки. В этот момент происходит нарушение единственности процесса деформирования, исключающее понятие неустойчивости, т.к. за этой бифуркацией решения не следует катастрофического развития перемещений, деформаций и напряжений. Неустойчивость наступает в предельной точке, называемой точкой бифуркаии Пуанкаре. Соответствующую нагрузку, мы называем пределом устойчивости. Нельзя путать эту нагрузку с нагрузкой исчерпания несущей способности конструкции вследствие образования пластических шарниров. Процесс выпучивания после достижения силой P значения предела устойчивости называем послекритическим. Нагрузка P при увеличивающихся перемещениях падает до нагрузки, которую мы назвали нагрузкой надёжности устойчивых состояний :

где - предельное значение касательного модуля на диаграмме сжатия.

На рисунках 9.30 – 9.31 приведены диаграммы сжатия для сплава дюралюминия Д16Т и стали 3 и диаграмма их критических напряжений. В таблицах даны результаты обработки этих диаграмм.

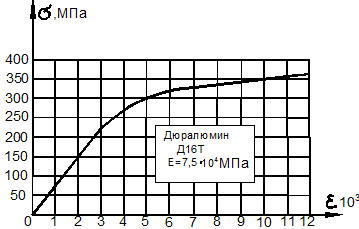
а) диаграмма сжатия для дюралюмина Д16Т.

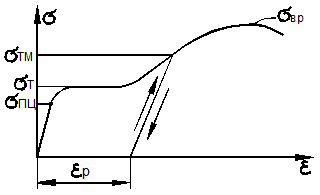
б) диаграмма сжатия стали Ст.3.

Рис. 9.30

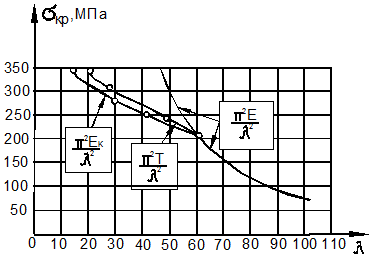
а) диаграмма «критическое напряжение – гибкость»

для дюралюмина Д16Т.

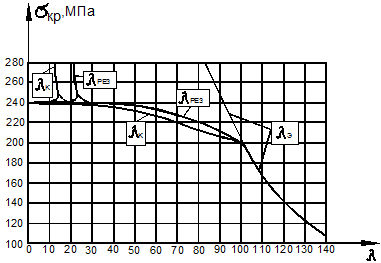
б) диаграмма «критическое напряжение – гибкость» для стали Ст. 3.

Рис. 9.31

Таблица 9.3. Расчётные параметры для дюралюмина Д16Т

МПа

2,67

3,0

3,5

4,0

4,5

200

220

246

264

278

290

308

320

332

340

345

356

364

7,50

5,96

4,34

3,72

2,55

2,05

1,50

1,17

0,97

0,82

7,50

6,65

5,50

4,97

3,81

3.22

2,50

2,03

1,72

1,48

60,5

54,7

47,0

43,0

36,8

33,0

28,3

25,0

22,6

20,8

20,6

20,2

20,0

60,5

51,6

37,5

30,2

26,5

18,9

15,4

15,3

15,1

14,9

Таблица 9.4. Расчётные параметры для стали Ст. 3

кг/см²

0,95

1,0

1,1

1,2

1,3

1,4

1,5

1,6

1,8 – 4,0

4,5

2000

2100

2200

2280

2340

2380

2390

2400

2410

2420

2470

2575

2685

2800

2,10

1,42

0,99

0,67

0,46

0,26

0,13

0,06

0,02

0,04

0,05

2,10

1,72

1,39

1,05

0,85

0,54

0,33

0,19

0,07

0,13

0,15

102

67,6

47,5

24,5

23,6

102

81,8

66,6

32,7

23,1

15,7

9,1

12,7

14,2

13,8

13,6

13,5

Устойчивость стержней как элементов конструкций

Стержни являются, как правило, элементами различных стержневых конструкций. На рис. 9.32 изображена простейшая статически неопределимая система, в которую входит сжатый силой Р стержень. В докритическом состоянии (рис. 9.32,б) имеем известную зависимость:

где - сближение концов стержня, f - прогиб балки.

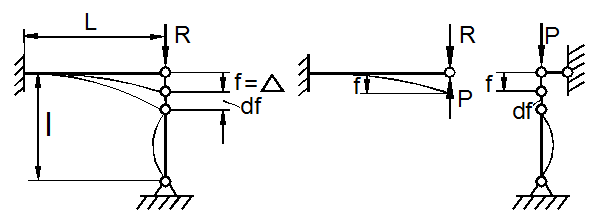
а) б)

Рис. 9.32

В результате потери устойчивости при R=const произойдёт дополнительное сближение концов стержня , которое можно выразить через изменение сил путём дифференцирования (9.83):

где

разгружающая жёсткость конструкции.

Из (9.83) следует, что при потере устойчивости стержня dP<0, т.е. передаваемая на стержень нагрузка P уменьшится. Такая конструкция для рассматриваемого стержня называется разгружающей конструкцией.

Изменим конструкцию (рис. 9.33).

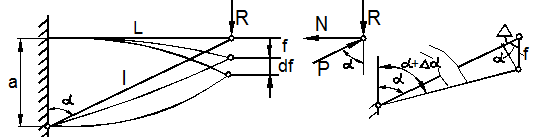
а) б)

Рис. 9.33

В докритическом состоянии имеем (рис. 9.33,а):

где прогиб балки f связан со сближением концов стержня зависимостью (рис. 9.33,б):

Кроме того имеем очевидное соотношение:

Допустим, что произошла потеря устойчивости стержня при R = const, и он получил дополнительное сближение своих концов, а балка получила дополнительный прогиб (рис. 9.33,а). Дифференцируя (9.89) – (9.91), получим:

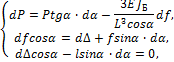
откуда следует:

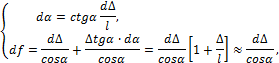
где

Если k<0, то dP>0. Такая конструкция для данного стержня называется догружающей. Если k>0, то dP<0, и мы имеем разгружающую систему.

На рис. 9.34,а приведена статически неопределимая стержневая конструкция, нагруженная в узле А силой Q.

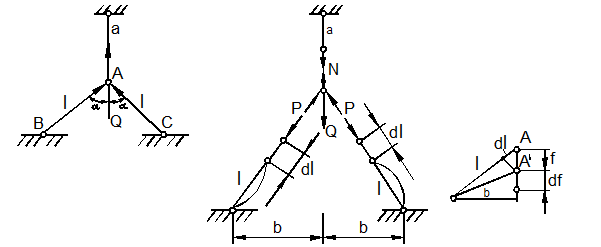
а) б) в)

Рис. 9.34

Наклонные стержни конструкции с длинами l сжаты силами Р за пределом упругости, а вертикальный стержень длины a растянут усилием N в пределах упругости. Уравнение равновесия узла А (рис. 9.34,б) имеет вид

В результате деформации конструкции узел А перемещается вниз на величину , равную удлинению вертикального стержня:

Из рис. 9.34, в следует соотношение между удлинением стержня и перемещением узла А конструкции:

Полученное соотношение представляет собой уравнение совместности деформаций и стержневой системы. Из рис. 9.34,в находим другое геометрическое соотношение:

Допустим, что при некотором критическом значении силы произошли потери устойчивости сжатых наклонных стержней в смысле Эйлера . В результате узел получил перемещение df, а у стержней АВ и АС концы сблизятся на расстояние dl. С учётом (9.92) – (9.95), получаем систему уравнений:

откуда после исключения находим:

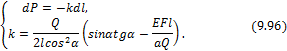
Из (9.91) следует, что при малых при заданных Q, EF, l/a жёсткость k может быть меньше нуля, а dP>0. В этом случае стержни при потере устойчивости догружаются. При достаточно больших можно получить k>0, dP<0. В этом случае стержни при потере устойчивости будут разгружаться. Если k=0,

то стержни потеряют устойчивость в соответствии с теорией приведённого модуля Кармана.

Таким образом, рассмотренная конструкция может быть как догружающей, так и разгружающей. Догружающее либо разгружающее действие конструкции на стержень оказывает существенное влияние на величину нагрузки бифуркации. Запишем первое уравнение (9.67) для границы раздела зон в развёрнутом виде:

Граница раздела зон заключена в пределах:

Пусть (см. рис. 9.27, 9.28). В этом случае все сечения полностью перейдут в упругое состояние.

Геометрические характеристики поперечного сечения стержня:

Из (9.97) получаем:

Следовательно, этот случай реализуется в разгружающей системе. Жёсткость D, согласно (9.66), (9.67), (9.94), равна D=EJ. Решение уравнения (9.71) приводит к эйлеровой нагрузке (9.33).

Пусть теперь . В этом случае все сечения находятся в пластическом состоянии, так что

Из (9.97) следует:

Следовательно, этот случай реализуется в догружающих системах. Жёсткость D, согласно (9.68), (9.69), равна . Решение уравнения (9.73) приводит к касательно-модульной нагрузке Энгессера – Шенли (9.48).

При dP=0 имеем задачу Кармана, когда . Бифуркационная нагрузка определяется приведенно-модульным значением (9.75). На рис. 9.35 приведены границы распределения пластических и упругих зон деформирования в продольном разрезе стержня. Таким образом, нагрузка бифуркации при работе стержня за пределом упругости в догружающих системах лежит в интервале

а при работе в разгружающих системах – в интервале:

где - нагрузка бифуркации для предельно жёсткой разгружающей системы (рис. 9.36).

После бифуркации примерная зависимость между сжимающей силой P и прогибом f изображена на рис. 9.36,а. Для интервала бифуркационных нагрузок (9.100) увеличение прогибов требует увеличения нагрузки P в догружающих системах. Поэтому соответствующие этим нагрузкам точки бифуркации называются устойчивыми или докритическими. При нагрузках бифуркации из интервала (9.96) увеличение прогибов происходит при падающей нагрузке P. Соответствующие точки бифуркации для изолированного стержня называются неустойчивыми (послекритическими).

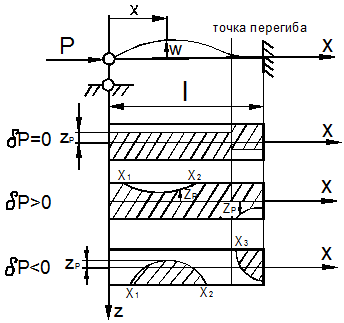
а)

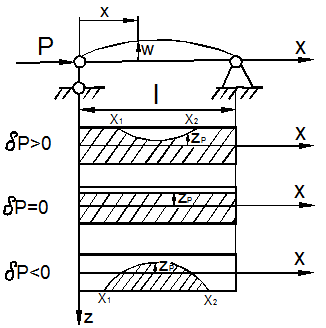
б)

Рис. 9.35

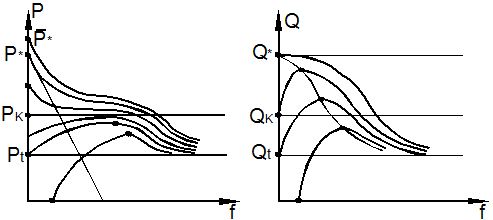
а) б)

Рис. 9.36

Однако при работе этого же стержня в разгружающей системе увеличение прогибов требует увеличения внешней нагрузки Q (рис. 9.36, б). Благодаря поддерживающему влиянию конструкции, стержню не грозит опасность катастрофического выпучивания. Поэтому все нагрузки бифуркации из интервала оказываются устойчивыми, т.к. для них dQ/df>0 Это означает, что если удержать стержень от выпучивания при касательно-модульной нагрузке с помощью какой-либо временной поддерживающей связи (рис. 9.37,а) и нагрузить силой из интервала , а затем снять временную связь, то стержень сохранит свое устойчивое состояние.

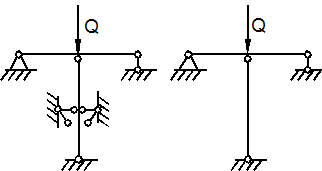
а) б)

Рис. 9.37

Отмеченное исключительное свойство пластически сжатого стержня, работающего в разгружающей системе, может быть использовано для повышения его устойчивости. Для этого следует применить систему временных поддерживающих связей, от которых впоследствии можно освободиться. Вместо дополнительных поддерживающих связей можно применить иной метод – метод упругопластической тренировки, предложенной В.Г. Зубчаниновым. Согласно ему стержень подвергается сжатию до заданной нагрузки в заводских условиях на специальном стенде с поддерживающими связями, а затем разгружается (рис. 9.37). Элемент поступает на сборку конструкции. После тренировки зависимость между критическим напряжением и гибкостью становится иной, что отражает эффект использования временных поддерживающих систем и наличие целого спектра нагрузок бифуркации, которые естественно зависят от достигнутого пластического состояния и жёсткости стержня в момент выпучивания (рис. 9.38).

Эффект увеличения критических нагрузок в разгружающих системах должен учитываться при расчёте составных элементов конструкций (слоистые стержни, плиты, подкреплённые рёбрами жёсткости и др.).

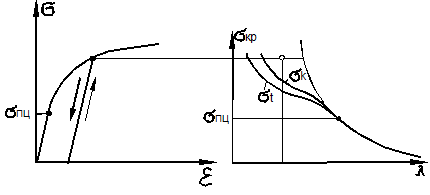
а) б)

Рис. 9.38

На рис. 9.39 приведены результаты расчёта, выполненные для случая, когда стержень изготовлен из дюраля. Кривые 1, 2, 3 на рис. 9.39 соответствуют теории касательного модуля, приведенно–модульной теории и теории Эйлера для упругого стержня. Кривая 4 соответствует разработанной нами теории устойчивости разгружающих конструкций.

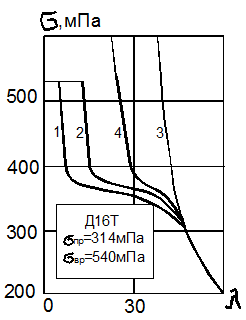
Рис. 9.39

Продольно-поперечный изгиб упругого стержня

Рассмотрим упругий стержень постоянного поперечного сечения, сжатый силами P (рис. 9.40,а). Отсечём от стержня часть его длиной z (рис. 9.40,б). Уравнения его равновесия имеют вид

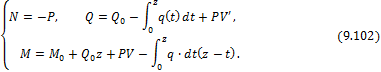
С другой стороны, изгибающий момент в поперечном сечении выражается через кривизну по формуле (9.21):

Приравнивая отмеченные выше выражения моментов (9.102), (9.103) получим:

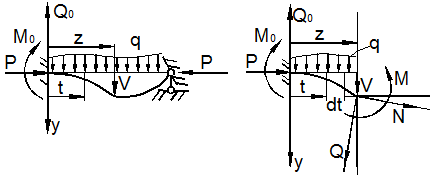
а) б)

Рис. 9.40

Дифференцируя полученное уравнение два раза по z, последовательно находим:

Введём обозначение

Тогда уравнение (9.104) примет вид

Общее решение (9.100) имеет вид

где для q=const частное решение имеет вид

Удовлетворяя решение (9.106) граничным условиям шарнирного опирания балки:

приходим к системе уравнений

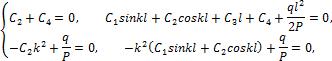
откуда находим постоянные интегрирования:

В результате общее решение задачи (9.101) принимает вид

При z=l/2 получаем максимальное значение прогиба:

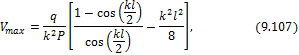
где или

При из (9.107) следует, что а

Если на балку действует только поперечная нагрузка q(z), то P=0 (). Обозначим прогиб от поперечной нагрузки через . Тогда из (9.105) следует:

Уравнение (9.105) на основании (9.108) принимает вид:

В уравнении (9.104) прогиб можно трактовать так же, как начальный технологический прогиб. Для изгибающего момента имеем выражение:

Рассмотрим снова случай шарнирного опирания стержня по краям. Тогда при z=0 имеем:

Представим общее решение уравнения (9.107) и начальный прогиб (либо прогиб от поперечной нагрузки) в виде рядов Фурье:

Подставляя в (9.107) вместо V, эти выражения, находим уравнение:

которое удовлетворится, если все фигурные скобки обращаются в нуль.

Это приводит к формуле:

где

эйлеровы нагрузки бифуркации.

Прогиб в середине стержня при z=l/2 равен:

При , согласно (9.110), имеем т.е. неограниченно увеличиваются перемещения от изгиба по одной полуволне. Все же другие формы остаются ограниченными. Следовательно, выпучивание шарнирно опёртого стержня по одной полуволне есть главная форма изгиба. Среди множества искривлений оси стержня можно учитывать лишь начальный прогиб по одной полуволне синусоиды. Это весьма важный для практических расчётов качественный результат, который следует учитывать при расчётах на устойчивость элементов конструкций.

Максимальный прогиб может быть приближённо принят равным:

Согласно принятому критерию устойчивости сила

должна быть принята за предел устойчивости или критическую, так как при

Аналогичный результат можно получить для иных видов закрепления концов стержня.

Выпучивание сжатой колонны при внецентренном сжатии

Пусть стержень-колонна сжимается внецентренно силой P, жёстко закреплена внизу при z=0 и свободна от закрепления вверху при z=l (рис. 9.41,а). Для решения задачи используем уравнение (9.22):

Из рис. 9.41, а получаем:

Подставляя эти значения в (9.110), находим:

или, после деления на EJ,

общее решение уравнения (9.107) имеет вид

Граничные условия задачи:

при z=0,

V=f при z=l. (9.114)

Удовлетворяя решение (9.113) условиям (9.114), получаем:

откуда находим:

Решение (9.113), с учётом найденных коэффициентов, принимает вид:

Из (9.115) при z=l получаем значение максимального прогиба:

При из (9.116) получаем .

График зависимости P от f приведён на рис. 9.41, б.

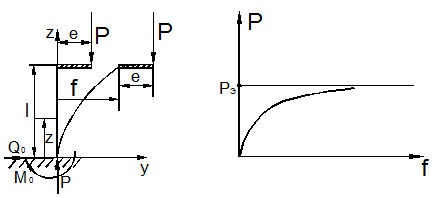
а) б)

Рис. 9.41

Значение соответствует критической нагрузке Эйлера:

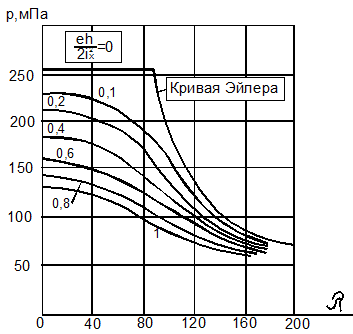
Рис. 9.42

Максимальное нормальное напряжение в изгибаемой колонне находим по формуле:

которую называют формулой секанса для .

Так как , то формулу (9.117) запишем в виде:

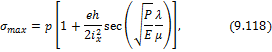
где p=P/F - параметр внешней нагрузки, имеющий размерность напряжения.

Назовём предельным упругим состоянием такое, при котором в стержне в опасной точке впервые достигается предел текучести, т.е. . Тогда, согласно (9.113), соответствующий параметр внешней нагрузки

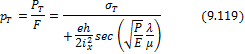
Если форма и размеры сечения известны, то известны F, h, . Методом проб и ошибок можно построить зависимости от гибкости для различных значений (рис. 9.42).

Устойчивость стержня, сжатого следящей силой

Рассмотрим задачу о сжатии следящей силой, т.е. силой, которая при выпучивании стержня поворачивается так, что остаётся касательной к изогнутой оси на конце стойки (рис. 9.43). Такая сила может быть создана реактивной струёй ракеты.

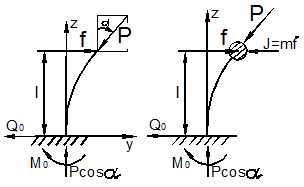
а) б)

Рис. 9.43

Ввиду малости прогибов считаем, что горизонтальная и вертикальная составляющие следящей силы:

Общее решение задачи представлено выражением (9.29). Граничные условия задачи имеют вид

при z=0;

при z=l, (9.120)

где

Удовлетворяя решение (9.29) граничным условиям (9.120), получим:

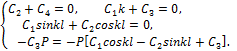
Исключая постоянные , находим:

Определитель этой системы:

Следовательно, система уравнений (9.116) не имеет отличных от нуля решений и потому

Таким образом, по методу Эйлера сжатый следящей силой стержень не имеет искривлённых форм равновесия. Эту задачу впервые рассмотрел А.Пфлюгер (Германия) в 1950 г. и пришёл к выводу, что сжатый следящей силой стержень всегда устойчив.

Такой вывод оказался неверным, т.к. метод Эйлера и его понятие устойчивости не являются общими и относятся только к задачам с консервативными внешними силами.

В данной задаче потеря устойчивости проявляется не в переходе системы в смежное равновесное состояние в смысле Эйлера, а в переходе её в режим движения. Поэтому для исследования устойчивости со следящей неконсервативной силой следует применить динамический метод Лагранжа. Предположим, что на конце стержня сосредоточена масса m (рис. 9.43,б). Тогда при её движении вместе со стержнем возникает сила инерции , где точки над f означают дифференцирование по времени. Для решения задачи воспользуемся принципом Даламбера и уравнением (9.105), которое в силу q=0 принимает вид:

где прогиб есть функция z и времени t, т.е. V=V(z,t) Для решения задачи воспользуемся методом разделения переменных Фурье, полагая:

Подставляя (9.123) в (9.122), получим:

Общее решение (9.124) имеет вид:

Граничные условия задачи:

при z=0,

при

Удовлетворяя решение (9.120) граничным условиям (9.121), получим граничные условия для:

при z=0

при

Первые три условия очевидны. Последнее поясним подробнее. После подстановки (9.123) в четвёртое условие (9.126) имеем:

откуда, разделяя переменные, получим:

где - постоянная величина.

Следовательно,

Полагая в (9.128) находим

для действительных значений и

для мнимых ( - действительных) значений .

Подставляя (9.125) в граничные условия (9.127), находим:

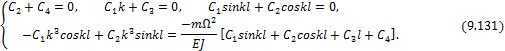
Исключая из (9.131) найдём

Приравнивая определитель системы (9.132) к нулю, получим:

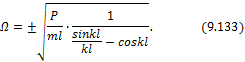
Пока выражение под радикалом в (9.128) положительно (tgk>kl), оба значения действительны и имеет место устойчивый периодический процесс движения (9.130).

Случай

отвечает и переходу от устойчивого движения к неустойчивому. Корень уравнения (9.133) нами уже вычислялся:он равен kl=4,493, откуда получаем критическое значение следящей силы:

при которой сжатый стержень получит динамическую бифуркацию. При этой силе колебательный процесс становится неустойчивым. Примером такого беспорядочного процесса могут служить катастрофы при запуске баллистических ракет.

Задача А.Р. Ржаницына об устойчивости сжатого стержня в условиях ограниченной ползучести

Все материалы обладают тремя основными свойствами – упругости, пластичности и вязкости. При длительной эксплуатации конструкции, которая содержит сжатый силами Р стержень, может проявиться свойство вязкости материала в виде его ползучести либо релаксации напряжений.. Эти явления при ограниченной ползучести (для таких материалов, как бетон, полимеры,композиты) описываются законом Кельвина:

где - время релаксации, E – модуль продольной упругости, H- длительный модуль упругости, и - скорости напряжений и деформаций.

Рассмотрим шарнирно опёртый стержень, сжатый силами P (рис. 9.45).

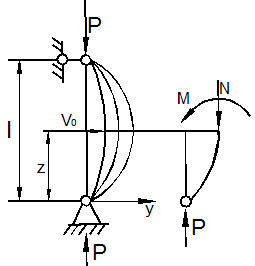
Рис. 9.45

Из условий равновесия отсечённой части стержня имеем N=-P, Q=0, M=PV. Деформация и её скорость при изгибе стержня:

Умножая (9.135) на ydF, интегрируя по площади стержня и используя (9.136), получаем:

где

Подставляя в (9.132) выражения , находим:

Примем для прогиба V и его скорости выражения

Тогда из (9.138) получаем:

где

бифуркационнные нагрузки Л. Эйлера и А.Р. Ржаницына.

Обозначим:

Тогда уравнение (9.139) преобразуется к виду

Разделяя переменные и интегрируя, получаем:

или, после потенцирования,

Постоянную C находим из начального условия при

В результате получаем:

Если - прогиб по методу проб Эйлера на устойчивость, то выражение (9.142) даёт закон поведения прогиба после снятия возмущающей поперечной силы. Возможны три состояния процесса изгиба стержня во времени t. При коэффициент , и из (9.143) следует, что при прогиб , т.е. стержень устойчив, т.к. возвращается со временем к своей начальной прямолинейной форме (рис. 9.45).

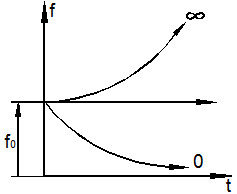
Рис. 9.46

При имеем , и при прогиб , т.е. стержень неустойчив. При имеем и решение уравнения (9.137) . Стержень остаётся в безразличном состоянии на границе между устойчивым и неустойчивым состояниями процесса выпучивания.

Таким образом, мы обнаруживаем что при сжатый стержень обладает свойством длительной устойчивости, т.к. после снятия возмущения остаётся пребывать в малой окрестности исходного невозмущенного состояния при

Реальные стержни обладают начальными несовершенствами своей прямолинейной геометрической формы. Пусть – начальный технологический прогиб оси стержня. Будем смотреть на него как на малый возмущающий фактор. Тогда кривизна изогнутой оси стержня в процессе его деформирования:

а относительные деформации и напряжения:

Умножим вновь (9.122) на ydF и, интегрируя, получим уравнение

Полагая в (9.144):

и учитывая обозначение (9.141), приходим к уравнению

Решение уравнения (9.140) имеет вид

Начальным условием при t=0для решения (9.146) является статическое решение (9.106) задачи о выпучивании упругого стержня с начальным прогибом:

Удовлетворяя решение (9.141) этому условию, получим:

и общее решение:

При имеем и поэтому из (9.147) при получаем, что прогиб f ограничен и стремится к значению (рис. 9.46):

При имеем и поэтому из (9.141) при получаем

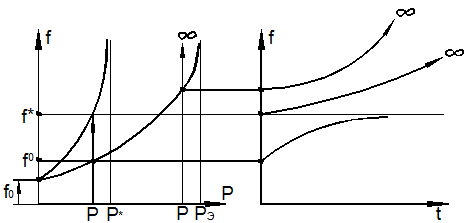
Рис. 9.46

Процесс выпучивания во времени неограничен и, следовательно, неустойчив (рис. 9.47).

При коэффициент , и из уравнения (9.140) получаем:

При нагрузке впервые процесс выпучивания стержня из материала с ограниченной ползучестью становится неустойчивым. Поэтому названа длительной критической нагрузкой А.Р. Ржаницына.

Устойчивость упругого стержня в условиях неограниченной ползучести

Ползучесть некоторых полимерных материалов в установившейся стадии является нелинейной и описывается при вязкоупругих деформациях законом:

Тогда постановка задачи об устойчивости на бесконечном интервале времени не имеет смысла. При ограниченной ползучести задача об устойчивости сжатого стержня имеет смысл, в соответствии с концепцией устойчивости, если сжимающая нагрузка P больше нагрузки надёжности устойчивых состояний. В противном случае стержень может разрушиться от чрезмерного продольного изгиба вследствие развивающихся деформаций ползучести. Инженерной задачей является определение критического времени, в течение которого стержень способен воспринимать внешнюю нагрузку.

Рассмотрим стержень идеализированного двутаврового поперечного сечения (рис. 9.48), шарнирно опёртый по краям и сжатый силами P.

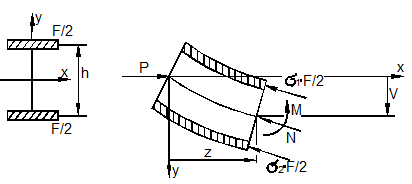
Рис. 9.47

Пусть l - длина стержня, площадь каждой полки составляет F/2, и их размеры малы по сравнению с высотой сечения h, так что можно считать напряжения в каждой полке распределены равномерно. Площадью тонкой стенки пренебрегаем. Определяем момент инерции поперечного сечения:

Уравнение равновесия части стержня, отсечённого на расстоянии z от края (рис. 9.47), записываем в виде:

где и - напряжения в полках соответственно на вогнутой и выпуклой сторонах; P – сжимающая сила; V – прогиб в сечении.

Деформация в стержне:

В частности, для полок двутавра получаем:

Вычитая деформации друг из друга, находим дифференциальное уравнение изогнутой оси стержня:

Введём безразмерные прогиб и осевую координату:

Тогда уравнения равновесия (9.149), (9.151) примут вид

где - среднее напряжение в поперечном сечении стержня.

Из уравнений (9.152) найдём:

Дифференцируя (9.152), (9.153) по t, получим:

Подставив (9.154), (9.155) в (9.148), найдём для каждой из полок:

Подставив (9.157) в (9.156) и приняв n=3, найдём:

Примем для определения прогиба выражение:

Разложив нелинейный член в (9.158) в ряд Фурье по синусам и приравняв нулю коэффициент при получим:

Здесь

Разделив переменные и проинтегрировав (9.160) от до получим:

Здесь безразмерный мгновенный прогиб, определяемый из решения упругой задачи:

Выражение (9.161) характеризует время, необходимое для достижения заданного прогиба при данном мгновенном прогибе . Критическая ситуация, характеризуемая исчерпанием несущей способности стержня и быстрым нарастанием прогибов, наступает при некотором критическом времени , когда В этом случае из (9.156) следует:

Если то , т.е. наступает мгновенная потеря устойчивости. При критическое время увеличивается. На рис. 9.48 а,б приведены зависимости безразмерного прогиба от времени t для и критического времени от безразмерного параметра нагрузки . В расчётах было принято

При прогибы стержня неограниченно увеличиваются.

При линейной неограниченной ползучести (n=1) вместо уравнения (9.158) получаем:

Приняв прогиб в той же форме (9.159), имеем:

а после интегрирования:

Следовательно, при , т.е. бесконечно большой прогиб реализуется в течение бесконечно большого времени, иными словами, в условиях неограниченной ползучести конечного, отличного от нуля предела длительной устойчивости не существует.

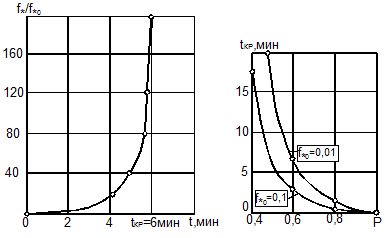
а) б)

Рис. 9.48

Устойчивость плоской формы изгиба балок

Балка, изогнутая в своей плоскости, может потерять устойчивость своей плоской формы изгиба при некотором критическом значении внешней нагрузки и выпучиться в сторону (рис. 9.51). При этом поперечное сечение балки повернётся, т.е. балка будет испытывать изгиб с кручением.

Рассмотрим свободно опёртую балку длиной l, изгибаемую по концам моментом m (рис. 9.51,а). В докритическом состоянии дифференциальное уравнение изогнутой оси имеет вид:

Интегрируя дважды, получим:

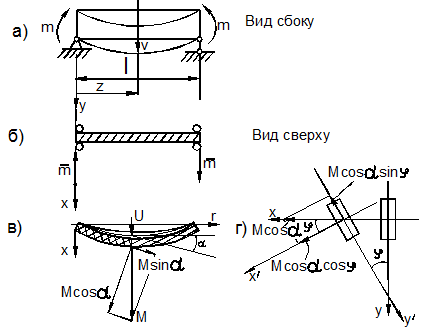
Рис. 9.49

Так как при z=0, прогиб V=0, то и потому

Максимальное значение прогиба:

На рис. 9.50 показан график зависимости от значений момента m.

Кружочек отвечает моменту появления пластических деформаций (пределу пропорциональности ), сплошной кружочек – предельному моменту , при котором происходит образование пластического шарнира и исчерпание несущей способности балки, тонкая линия соответствует упругопластическому поведению балки.

Если сечение балки узкое (высокое), как у полосы или двутавра (рис. 9.47), то при некотором критическом значении изгибающего момента произойдет бифуркация решения, и балка получит боковое выпучивание с закручиванием.

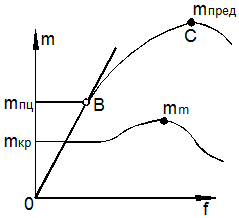
Рис. 9.50

Пусть угол характеризует наклон изогнутой оси балки в плоскости x-z при боковом отклонении, а - угол закручивания в некотором произвольном сечении z. Представим момент M=m в сечении в виде вектора по правилу правого винта (буравчика). Тогда, проецируя на оси , отнесённые к сечению (рис. 9.51,г), получим:

Следовательно, дифференциальные уравнения изгиба и кручения принимают вид

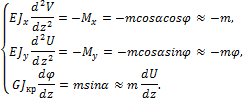
где учтена малость величин

Для прямоугольника:

Первое уравнение совпадает с (9.162) и описывает докритический изгиб после точки бифуркации A.

Дифференцируя третье уравнение по z и исключая с помощью второго уравнения производную , получаем:

где

Общее решение уравнения (9.163) имеет вид

Удовлетворяя (9.165) граничным условиям:

при z=0. Z=l,

получим

Если положим в (9.166) , то получим тривиальное решение, при котором балка не получает бокового выпучивания. Если то откуда и, согласно (9.159), находим:

Более трудным оказывается решение задач о плоской форме изгиба при поперечном изгибе. Так, для консольной балки, нагруженной поперечной силой, имеем:

При изгибе шарнирно опёртой балки длиной l силой Р, приложенной посередине пролёта, имеем:

а при действии распределённой нагрузки q:

Энергетический метод определения критических нагрузок

Энергетический метод представляет собой один из способов определения критических нагрузок. Пусть согласно методу проб Эйлера сжатый силами P стержень не вернулся в исходное состояние равновесия (рис. 9.51).

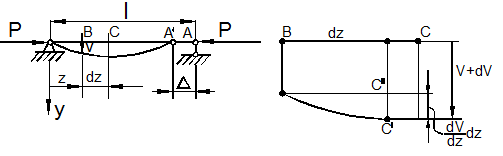
а) б)

Рис. 9.51

При этом подвижная шарнирная опора переместится на величину так, что сила P совершит работу , а стержень выпучится (изогнётся). Энергия изгиба:

Учитывая, что получим:

Рассмотрим элемент стержня . Этот элемент к моменту потери устойчивости уже сжат, и при упругом изгибе его длина не меняется. После изгиба элемент BC займёт положение . Поэтому укорочение стержня BC по направлению z будет:

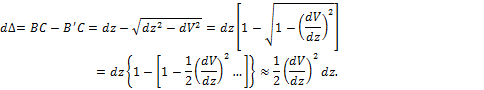
Сближение концов стержня при потере устойчивости:

Работа, совершаемая силой P, определится соотношением:

Приравнивая выражение (9.167), (9.168), получим:

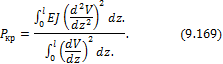
Если точная функция прогибов стержня известна, то значение критической силы находится просто. Для шарнирно опёртого стержня что даёт известную формулу:

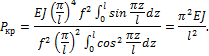
В общем случае функция прогибов V неизвестна, и её задают приближённо. Пусть, например, в той же задаче V=fz(l-z).

Тогда

Как видно, при приближённом задании прогиба, удовлетворяющем граничным условиям, критическое значение силы больше, чем при точном задании прогиба.

Можно показать в общем случае, что по сравнению со всеми функциями прогиба V(z), удовлетворяющим граничным условиям, истинная функция прогиба даёт минимальное значение .

Пример 4.

Найти критическую силу для сжатой колонны (рис. 9.52).

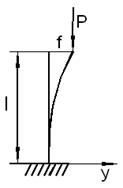
Рис. 9.52

Граничные условия для данной задачи имеют вид:

при z=0.

Примем для прогиба выражение:

удовлетворяющее граничным условиям. Сохраним в (9.170) два члена ряда:

После подстановки выражения прогиба (9.171) в (9.164) и интегрирования, получим:

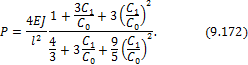
Если выражение прогиба положим , т.е. сохраним только один член, то найдём минимальное значение силы Р, равное:

что даёт погрешность по отношению к точному значению равную 21,6%.

При двух значениях постоянных минимальное значение P найдём, дифференцируя (3) по и приравнивая выражение к нулю:

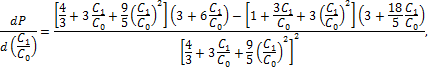
или

откуда

Наименьшее значение критической силы даёт первый корень:

что отличается от точного решения только на 0,92 %.

Расчет сжато-изогнутого стержня по деформированному состоянию

В разделе «Сложное сопротивление» рассматривался расчет жестких стержней, подверженных внецентренному растяжению-сжатию. Расчет этих стержней велся по недеформированному состоянию, т.е. при определении внутренних усилий не учитывалось искривление оси стержня. Для гибких стержней необходимо учитывать влияние деформаций изгиба на внутренние усилия. Такой расчет носит название расчета по деформированному состоянию.

При расчете по деформированному состоянию изгибающий момент вызывается не только поперечной нагрузкой, но и сжимающей силой. Будем рассматривать стержень, подверженный действию поперечной, примерно симметричной относительно середины пролета нагрузки, действующей в плоскости симметрии поперечного сечения, и сжимающей силы F. В этом случае наибольший прогиб имеет место посередине пролета. Максимальное нормальное напряжение в опасном сечении стержня определяется по формуле

где – изгибающий момент в опасном сечении, вызванный действием только поперечной нагрузки (при отсутствии сжимающей силы); – прогиб посередине пролета, вызванный только поперечной нагрузкой; – значение критической нагрузки, вызывающей потерю устойчивости стержня в плоскости действия поперечной нагрузки, W – момент сопротивления сечения стержня относительно той оси, которая будет нейтральной при изгибе от поперечной нагрузки.

В формуле (9.173) два первых слагаемых определяют наибольшее напряжение в стержне при расчете по недеформированному состоянию, третье слагаемое показывает вклад сжимающей силы в напряжения от изгиба. Видно, что зависимость напряжения от сжимающей нагрузки нелинейная, поэтому проверку прочности стержня нельзя производить расчетом по допускаемым напряжениям. Проверку прочности гибких сжато-изогнутых стержней необходимо вести расчетом по предельному состоянию, обеспечивая запас прочности не по напряжениям, а по нагрузке. В этом случае условие прочности имеет вид:

где n – нормируемый коэффициент запаса прочности материала.

Проверка жесткости гибкого сжато-изогнутого стержня расчетом по деформированному состоянию производится по формуле

В формуле (9.174) – коэффициент запаса по прогибам, обычно принимаемый равным коэффициенту запаса прочности n.

Кроме проверки прочности и жесткости по условиям (9.174), (9.175) необходимо проверить условие устойчивости гибкого стержня и обеспечить невозможность потери устойчивости стержня в плоскости наименьшей жесткости, обычно перпендикулярной плоскости действия поперечной нагрузки.

Пример расчета гибкого сжато-изогнутого стержня

Стержень, показанный на рис. 9.53, сжимается силой F =300 кН и изгибается поперечной нагрузкой q = 5 кН/м. Сечение стержня состоит из двух швеллеров, выполненных из стали С235 с . Требуется подобрать номер швеллера так, чтобы удовлетворялись условия прочности и жесткости по деформированному состоянию, а также условие устойчивости в плоскости наименьшей жесткости. Допускаемый прогиб примем равным l/200.

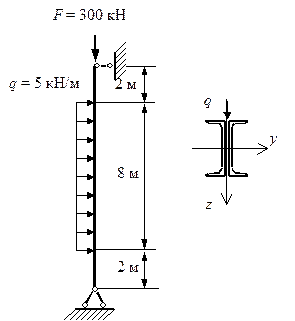
Рис.9.53

Решение.

Построим эпюру изгибающих моментов от поперечной нагрузки (рис. 9.54, а) и подберем сечение расчетом по недеформированному состоянию без учета продольной силы.

Откуда

Выберем из сортамента прокатной стали швеллер № 27, у которого , и проверим прочность с учетом продольной силы:

Увеличим размер швеллера. Для швеллера № 30 с такими характеристиками: условие прочности по недеформированному состоянию выполняется:

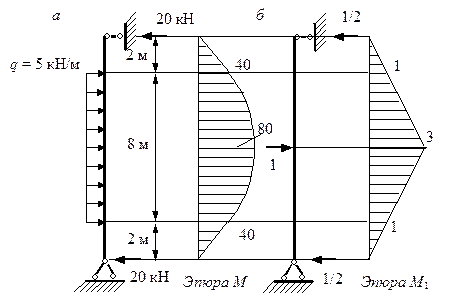
Рис.9.54

Проверим прочность по деформированному состоянию. Найдем максимальный прогиб в середине пролета, перемножая эпюры М от поперечной нагрузки и М₁ от единичной силы (рис. 9.54, б).

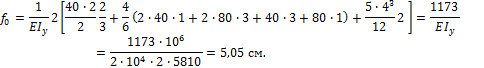
Чтобы найти критическую силу, найдем гибкость стержня в плоскости изгиба, где жесткость максимальна.

Гибкость стержня для стали С235, поэтому определяем критическую силу по формуле Эйлера.

Принимая коэффициент запаса прочности n = 1,5, проверим прочность по условию прочности по деформированному состоянию (9.174).

Поскольку условие прочности по деформированному состоянию для швеллера № 30 не выполняется, проверим прочность по условию (9.174) для швеллера № 33, у которого .

Поскольку , определяем критическую силу по формуле Ясинского.

Тогда условие прочности (9.174)

выполняется.

Проверим жесткость стержня расчетом по деформированному состоянию по формуле (9.175). Примем и допускаемый прогиб . Тогда условие жесткости

выполняется.

Осталось удовлетворить третьему условию – условию устойчивости в плоскости наименьшей жесткости. Найдем минимальный радиус инерции сечения из двух швеллеров:

Если швеллеры расположены вплотную друг к другу, то Тогда

и . Гибкость стержней больше, чем 200, не допускается. Для сечения из двух швеллеров можно уменьшить гибкость, не увеличивая размер швеллера. Для этого следует раздвинуть швеллеры. Величину а нужно подобрать так, чтобы гибкость стержня была меньше 200 и условие устойчивости выполнялось. В рассматриваемом примере такой величиной будет a=5,38 см, которой соответствует расстояние между стенками швеллеров (5,38-2,59)2=5,60 см. Для стержня с таким сечением

Этой гибкости соответствует , и условие устойчивости

выполняется. Таким образом, всем условиям (прочности, жесткости и устойчивости) удовлетворяет сечение из двух швеллеров № 33, расстояние между стенками которых равно 5,60 см.

Вопросы для самопроверки

- Дайте определение понятия критическое состояние системы?

- Опишите явление потери устойчивости.

- Что происходит со сжатым стержнем при потере устойчивости прямолинейной формы равновесия?

- Чем опасна потеря устойчивости?

- Причины потери устойчивости.

- Что понимается под устойчивым и неустойчивым равновесием?

- Какая механическая система называется устойчивой и неустойчивой?

- Приведите примеры устойчивых и неустойчивых объектов.

- Что означает выражение «сжатый стержень потерял устойчивость»?

- Какие брусья следует рассчитывать на устойчивость?

- Какая сила называется критической?

- Какая геометрическая характеристика определяет величину критической силы, сжимающей упругий стержень?

- От какой физической константы материала зависит критическое значение сжимающей силы?

- Почему в реальных конструкциях сжимающие стержень силы должны быть меньше критических?

- Почему нельзя допускать потерю устойчивости элементов конструкций?

- Какое ослабление стержня считают местным?

- Почему местные ослабления не учитывают в расчетах на устойчивость?

- Как влияют условия закрепления стержня на величину критической силы?

- Что понимается под запасом устойчивости?

- Как записывается формула Эйлера?

- Получите выражение критической силы по Эйлеру для центрально сжатых стержней?

- Охарактеризуйте влияние способа закрепления концов стержня на величину критической силы?

- Получите выражение для критических напряжений по Эйлеру?

- В каких случаях формула Эйлера дает ошибочный результат и почему?

- Объясните формулу Эйлера и предел ее применимости.

- Почему в формулу Эйлера вводится минимальный момент инерции I_min?

- Почему существуют ограничения в применении формулы Эйлера? В чем они заключаются?

- Если сжатый стержень ошибочно рассчитан по формуле Эйлера в области ее неприменимости, опасна ли эта ошибка или она приведет к перерасходу материала на изготовление стержня?

- Как рассчитывается стержень на продольный изгиб, если гибкость стержня такова, что формула Эйлера не применима?

- Запишите формулу Эйлера с учетом условий закрепления стержня.

- В чем разница в понятиях "Эйлерова сила" и "критическая сила", вычисляемая по формуле Эйлера?

- Сформулируйте условие применимости формулы Эйлера.

- По какой зависимости определяют критические напряжения в случае, если напряжения превышают предел пропорциональности?

- Какой величиной ограничивается предел применимости формулы Эйлера?

- Какие зоны имеет графическая зависимость критических напряжений от гибкости стержней?

- Почему при подсчёте критических напряжений в формулу подставляют значения площади без учёта местных ослаблений сечения?

- Что учитывает коэффициент продольного изгиба?

- В чём разница в понятиях – Эйлерова сила и критическая сила, вычисляемая по формуле Эйлера?

- При каких условиях можно использовать формулу Эйлера для расчета критической силы?

- Напишите формулу Эйлера для расчета критической силы и назовите входящие величины и их единицы измерения?

- Как находятся критические напряжения для стержней средней и малой гибкости?

- Какой вид имеет график опасных напряжений для центрально-сжатых стержней?

- Что выражает собой коэффициент продольного изгиба , от каких параметров он зависит и как используется при расчете стержней на устойчивость?

- В чем заключается условие устойчивости сжатого стержня?

- Что называют гибкостью стержня, какой смысл заложен в этом названии? Назовите категории стержней в зависимости от гибкости?

- В каой плоскости изогнется стойка при потере устойчивости?

- От каких параметров стержня зависит предельная гибкость?

- В чем заключается расчет сжатого стержня на устойчивость?

- Напишите условие устойчивости. Чем отличается допускаемая сжимающая сила от критической?

- Как влияет закрепление концов стержня на критическое значение силы?

- Что представляет собой коэффициент запаса устойчивости?

- Как подбирают размеры сечения при заданном коэффициенте запаса устойчивости?

- Как подбирают размеры сечения при нормативном значении коэффициента запаса устойчивости?

- Какие формы сечения более рациональны для гибких сжатых стержней?

- Критические напряжения.

- Порядок расчёта сжатых стержней на устойчивость.

- Что такое приведенная длина стержня? От чего она зависит?

- Что такое гибкость стержня?

- Как определяется гибкость стержня?

- Вычислите гибкость стерня круглого поперечного сечения диаметром d=6 см. Длина стержня l=120 см, концы закреплены шарнирно?

- Как определяется приведенная гибкость для составных стержней из швеллеров?

- Как определяется приведенная гибкость для составных стержней из уголков?

- Как определяется длина ветви (расстояние между соединительными планками)?

- Какие эмпирические формулы используются, если гибкость стержня меньше предельной величины?

- Какое влияние на поведение сжатой стойки оказывает эксцентриситет сжимающей силы и начальное ее искривление?

- Как определяется допускаемое напряжение при продольном изгибе, если формулой Эйлера воспользоваться нельзя?

- От каких факторов зависит коэффициент уменьшения допускаемого напряжения ?

- Как определяется напряжение при продольно-поперечном изгибе?

- Рациональное расположение сечений для предотвращения потери устойчивости.

- Запишите формулу Ясинского.

- Когда применяется зависимость Ясинского?

- Какие стержни называются стержнями большой, средней и малой гибкости?

- Могут ли быть такие случаи, когда сжатый стержень не будет терять устойчивость?

- Нарисуйте график зависимости

- Опишите в общем виде схему расчета сжатых стержней с помощью коэффициента уменьшения допускаемого напряжения.

- Какие случаи загружения называют продольно-поперечным изгибом?

- В чем сложность расчета на продольно-поперечный изгиб?

- Можно ли применять принцип независимости действия сил при продольно-поперечном изгибе?

- Как зависят прогибы при продольно-поперечном изгибе от сжимающей силы и Эйлеровой силы?

- Приведите формулу Перри и охарактеризуйте ее использование в расчетах?

- Опишите принцип расчета стержней при продольно-поперечном изгибе?

- Как определяют наибольшие нормальные напряжения при продольно- поперечном изгибе?

- Почему расчёт на устойчивость всегда предшествует расчёту на продольно-поперечный изгиб?

- Почему при определении коэффициента запаса при продольно-поперечном изгибе его следует рассчитывать по допускаемым нагрузкам, а не по допускаемым напряжениям?

- Явление потери устойчивости заключается в . . .

- В основе вывода формулы Эйлера положено дифференциальное уравнение . . .

- С увеличением жёсткости EI поперечного сечения критическая сила …

- С увеличением длины стержня критическая сила . . .

- Коэффициент приведения длины зависит от . . .

- Формула Тетмайера-Ясинского применяется для стержней, имеющих гибкость . . .

- Использование формулы Эйлера вне пределов её применимости приводит . . .

- Предельная гибкость зависит только от . . .

- При определении критических напряжений в формулу подставляют площадь . . .

- Коэффициент φ продольного изгиба представляет собой . . .

- Для определения величины коэффициента поперечного изгиба необходимо знать … и … стержня.

- При продольно-поперечном изгибе в сечении действуют не только изгибающие моменты от поперечных сил, но и моменты, вызываемые . . .

- При продольно-поперечном изгибе наибольшее нормальное напряжение в стержне определяется по формуле . . .

- Оценка коэффициента запаса при продольно-поперечном изгибе проводится не по допускаемым напряжениям, а по допускаемым . . .

- Какими должны быть возмущения при исследовании устойчивости сиситемы: малыми или большими? Достаточно ли при этом ограничиваться всего одним возмущением? Что является критерием устойчивости состояния равновесия системы?

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00