Главная
Лекция 17. Балка
на упругом основании
Содержание
Дифференциальное уравнение оси изогнутой
балки, лежащей на сплошном упругом основании
Анализ общего решения дифференциального
уравнения изгиба балки на упругом основании
Расчет бесконечно длинной балки,
нагруженной сосредоточенной силой
Расчет балки бесконечной длины, нагруженной
системой сосредоточенных сил
Расчет коротких балок на упругом основании.
Функции Крылова
Расчет шпалы рельсового пути, как короткой
балки на упругом основании
Дифференциальное уравнение оси изогнутой балки, лежащей на сплошном упругом основании
В инженерной практике часто встречаются балочные элементы конструкций, лежащие на сплошном упругом основании. К таким конструкциям могут быть отнесены шпалы железнодорожного пути, ленточные фундаменты зданий, фундаменты плотин, опирающиеся на грунты, разного рода трубопроводы, уложенные на грунт или внутрь его и др. Кроме того, к таким конструкциям относятся также и рельсы, у которых число опор бесконечно велико, а расстояние между ними мало по сравнению с длиной.
В машиностроении и различных других областях техники для многих конструкций в эксплуатационном режиме, находящихся в условиях сплошного контакта с другими изделиями, можно применить расчетную схему балки на упругом основании.
При расчетах таких элементов
предполагается, что грунт обладает упругими свойствами и его деформация
пропорциональна приложенной нагрузке. Кроме этой основной предпосылки, при
расчете балок на упругом основании принимаются и другие допущения:
- трение между основанием и
балкой отсутствует;
- между опорной поверхностью
балки и основанием имеется неразрывная связь, вследствие чего в основании могут
возникнуть растягивающие усилия;
- упругое основание по всей длине балки однородно и ширина
постели балки постоянная;
Расчет балки на упругом основании в строгой постановке сводится к решению контактной задачи между конструкцией и основанием. Сложность решения контактных задач в строгой постановке общеизвестна. Поэтому для решения инженерных задач, связанных с расчетом балки применяются приближенные подходы, суть которых заключается в следующем.
Предварительно устанавливается зависимость между реактивным отпором и осадкой поверхности основания. Одной из наиболее распространенных гипотез является гипотеза о пропорциональной зависимости между реакцией и осадкой - гипотеза Винклеровского основания.
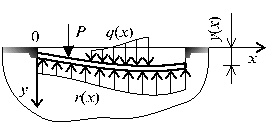
Рис.
17.1
На рис.17.1 показана деформация балки от внешней нагрузки, распределенной по произвольному закону. Реакция со стороны основания в произвольной точке, при соблюдении условий проскальзывания на контактной поверхности между подошвой балки и основанием, принимается пропорциональной прогибу:
где r(x) -
реакция основания, приходящаяся на единицу длины балки, (Н/м); y(x) - просадка основания; 
; b - ширина подошвы балки; k1 - коэффициент,
характеризующий жесткость основания и называемый коэффициентом податливости основания
или коэффициентом постели, [Па/м].
Этот коэффициент представляет собой отпор основания, приходящийся на 1 м2 площади при просадке, равной единице. Знак минус в выражении (17.1) означает, что реакция противоположна направлению просадки.
Значения коэффициента постели k1 для некоторых грунтовых и скальных оснований приведены в таблице 17.1.
Балка, лежащая на сплошном упругом основании,
представляет собой статически неопределимую систему, так как одного условия
равновесия – равенства внешней нагрузки всей общей реакции основания –
недостаточно для установления закона распределения этой реакции по длине балки
и для определения усилий в сечениях. Интенсивность реакции в каждой точке
связана с прогибом балки, поэтому для решения задачи необходимо найти уравнение
изогнутой оси балки, затем по этому уравнению определить закон распределения
реактивных сил.
Таким образом, со стороны основания на балку действует сплошная распределенная нагрузка интенсивностью r(x). Суммарная интенсивность распределенной нагрузки, приложенной к балке при произвольном значении x определяется:
где q(x) - приложенная к балке, заданная распределенная нагрузка (например, вес погонной длины балки).
Таблица 17.1. Значения коэффициента постели k1 для различных грунтов
|
№ |
Материал основания |
k1, МПа/м |
|
1 |
Песок свеженасыпанны Глина мокрая, размягченная |
1-5 |
|
2 |
Грунты средней плотности: песок слежавшийся; гравий насыпной; глина влажная |
5-50 |
|
3 |
Грунты плотные: песок и гравий,
плотно слежавшийся; глина малой влажности |
50-100 |
|
4 |
Грунты весьма плотные: грунт песчано-глинистый, искусственно
уплотненный; глина твердая; |
100-200 |
|
5 |
Известняк, песчаник, мерзлота |
200-1000 |
|
6 |
Твердая скала |
10000-15000 |
Дифференциальное уравнение изгиба упругой балки в данном случае принимает вид:
или после подстановки (17.2) в (17.3) получим:
Физический смысл модели, приводящий к уравнению (17.4), может быть различен. Так, если основание принимать в виде упругого полупространства, взамен модели Винклеровского основания, из приближенных решений контактных задач, то коэффициент k имеет вид:
где Eo - модуль деформации грунта основания; m - коэффициент Пуассона.
В случае балки постоянного сечения интегрирование уравнения (17.4) не представляет особых затруднений. Вводится обозначение:
где β - называется коэффициентом относительной жесткости основания, [1/м].
Тогда дифференциальное уравнение (17.4) принимает вид:
Решение уравнения (17.5) можно получить общими методами решения дифференциальных уравнений с постоянными коэффициентами, и оно имеет следующую структуру:
где Сj - произвольные постоянные, j = 1, 2, 3, 4; yj (x) - частное линейно - независимое решение соответствующего (17.5) однородного уравнения
y*(x) - частное решение неоднородного уравнения (17.5), зависящее от характера внешней нагрузки q(x).
Частное решение однородного уравнения (17.7)
представляется в виде 
, подставляя которое в (17.7), получим
характеристическое уравнение
Используя формулы Муавра для корней из комплексных чисел найдем четыре корня уравнения (17.8):
где i - мнимая единица (i = 
).
Следовательно, решение вида (17.6) будет таким
Произвольные постоянные С1, С2, С3 и С4 находятся из граничных условий для конкретной задачи, как и при расчете обычной балки.
Анализ общего решения дифференциального уравнения изгиба балки на упругом основании
Как нетрудно видеть из (17.9), общее решение включает выражения для затухающей и возрастающей гармоник или, иными словами, для двух затухающих гармоник, одна из которых затухает по направлению к правому концу балки, а другая - к левому. Затухание здесь довольно быстрое. Чтобы установить его степень, увеличим x на π/β. Тогда получим
Анализируя полученный результат, приходим к
выводу, что первое слагаемое получило множитель 
, а второе слагаемое 
. Таким образом, при переходе к следующей
полуволне значение первого слагаемого (17.10) уменьшаются в 23,14 раза, а
второго слагаемого -
увеличивается во столько же раз.
В случае длинной балки члены уравнения,
содержащие множитель 
, для правого ее конца становятся очень
большими. Так как в действительности там деформации и внутренние силы имеют
конечную величину, то коэффициенты С3
и С4 при членах, содержащих множитель , должны быть очень малыми и для достаточно
длинной балки практически обращаться в нуль. В этом случае общее решение
упрощается и получает вид
На расстоянии трех полуволн 
от
левого конца балки члены общего решения с постоянными интегрирования С1 и
С2 практически исчезнут.
Поэтому балку длиной 
можно
считать бесконечно длинной. Точнее ее можно рассчитывать, как бесконечно
длинную, поскольку уже в середине ее влияние концевых граничных условий будет сказываться очень мало. Практически принимают, что если 
, то балка принимается бесконечно длинной (бесконечно длинная балка).
К общему решению (17.9) надо добавить частное
решение 
, зависящее от нагрузки 
. Если нагрузка представляет
собой алгебраический полином от x, то
частное решение можно найти в виде полинома той же степени методом неопределенных
коэффициентов. В частности, для линейной функции вида 
(рис.17.2), частное решение уравнения (17.5)
имеет вид
Рис.
17.2
При отсутствии приложенной к балке нагрузки, т.е. при q = 0, момент и поперечная сила на них равны нулю; этому вполне удовлетворяет частное решение (17.12) и добавлять к нему общее решение не требуется. Следовательно, (17.12) будет полным решением, и балка не будет изгибаться. Очевидно, что внутренние силы в ней везде равны нулю.
Рис.
17.3
Если балка имеет на концах какие-либо закрепления, например опоры (рис.17.3), то в ней появляются изгибающие моменты и кривизна оси, которые можно определить общим методом нахождения произвольных постоянных общего решения по граничным условиям.
Расчет бесконечно длинной балки, нагруженной сосредоточенной силой
Рассмотрим балку бесконечной длины,
простирающуюся в области 
, нагруженную в сечении с абсциссой x сосредоточенной силой P (рис.17.4). Дифференциальное уравнение
изогнутой оси балки записывается аналогично (17.4):
где δ(x) - единичная функция Дирака.
Общее решение (17.13) записывается аналогично (17.9). Произвольные постоянные С1, С2, С3 и С4 определяются из граничных условий задачи:
при
при x=0, 
; 
C учетом (17.14) следует, что
Рис.
17.4
Из первого из условий (17.15) получим:
или
Следовательно, решение (17.13) запишется в виде:
Из (17.19) легко установить, что
C учетом второго условия (17.15) можно записать, что
откуда окончательно получим:
Подставляя (17.22) в (17.19), получим окончательную формулу по определению прогибов балки на упругом основании при действии сосредоточенной силы P в следующем виде:
Последовательно определяем выражение изгибающего момента и поперечной силы:
Если в выражениях (17.23)¸(17.25) принять Р = 1 кН, то эпюры y (0), Mz(0) и Qy(0) можно трактовать, как линии влияния, соответственно, деформаций, изгибающих моментов и поперечных сил для сечения балки х = 0. Соответствующие эпюры приведены на рис.17.4.
Обратим внимание на тот
факт, что согласно (17.25) наибольший изгибающий момент 
, возникающий под силой P при заданной жесткости балки EIz , в
большей степени зависит от жесткости основания k, т.к. коэффициент относительной жесткости основания β
зависит от соотношения k и EIz .
Например, в случае, если балка лежит на жестком основании (k
), то 
; и, наоборот, в
случае, если балка лежит на мягком основании (k
), то 
. Простым подтверждением этого явления может
служить то, что железнодорожные рельсы, уложенные на жесткое основание, могут
безболезненно выдерживать довольно значительные поездные нагрузки. В то же
время, те же рельсы, уложенные на слабое основание, либо, если рельс
"провисает" (т.е. пространство между шпалами содержит пустоты), могут
разрушиться при значительно меньших нагрузках.
Расчет балки бесконечной длины, нагруженной системой сосредоточенных сил
Рассмотрим решение следующей задачи. Предположим, что на балку бесконечной длины в точках с абсциссами xj (j = 1, 2,..., N) приложена система сосредоточенных сил P1, P2, P3,...,Pn (рис.17.5).
Рис.
17.5
Рассматривая решение поставленной задачи, на примере рельса верхнего строения пути в качестве балки, лежащей на сплошном упругом основании при действии системы сосредоточенных грузов P1, P2, P3, ... , Pn , передающихся на путь от подвижного состава.
Железнодорожный путь должен отвечать требованиям прочности, жесткости и устойчивости при воздействии на него подвижного состава.
Напряжения и деформации, возникающие в
опасных сечениях конструкции верхнего строения пути должны удовлетворять
условиям прочности и жесткости,
т.е.
где 
, ymax - соответственно,
максимально возможное значение напряжений и прогибов конструкции в опасных
сечениях; 
, 
- предельно допустимые величины напряжений
и прогибов.
В данном случае формулы по определению прогибов, изгибающих моментов и поперечных сил в сечениях с координатами xn (n = 1, 2, ... , N) на основании теоремы о независимости действия внешних сил в упругих системах и теоремы о взаимности можно записать в виде
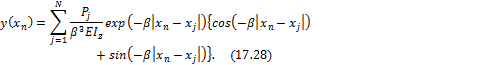
Последовательно определяем выражение изгибающего момента и поперечной силы:
По максимальному значению момента, вычисляемому по (17.29):
в опасном поперечном сечении рельса в опасных точках вычисляется максимальное значение нормальных напряжений:
где Wz - момент сопротивления поперечного сечения рельса пути.
Прочность рельса пути считается обеспеченной, если выполняется условие
где R - расчетное сопротивление материала конструкции инвентарного верхнего строения пути.
Основные геометрические характеристики стандартных рельсов приведены в таблице 17.2.
Таблица 17.2. Основные геометрические характеристики стандартных рельсов
|
Геометрические характеристики |
Тип рельсов |
|||||
|
Р38 |
Р43 |
Р50 |
Р65 |
Р75 |
||
|
ГОСТ |
||||||
|
3542-47 |
7173-54 |
7174-75 |
8161-75 |
16210-77 |
||
|
Моменты инерции, 10-8 м4 |
Jz Jy |
1222,5 209,3 |
1489,0 260,0 |
2011,0 375,0 |
3548,0 569,0 |
4490,0 661,0 |
|
Масса пог.м, кг |
q |
38,4 |
44,7 |
51,7 |
64,7 |
74,4 |
|
Моменты сопротивления относительно осей, 10-6 м3 |
Wzниз Wzгол Wyпод |
182,0 180,3 36,7 |
208,3 217,3 45,6 |
248,0 286,0 57,1 |
358,0 435,0 76,3 |
509,0 432,0 88,0 |
|
Основные размеры сечения рельса, мм |
H bпод hгол bгол 𝛿 |
135,0 114,0 40,0 68,0 13,0 |
140,0 114,0 42,0 70,0 14,5 |
152,0 132,0 42,0 71,9 16,0 |
180,0 150,0 45,0 75,0 18,0 |
192,0 160,0 48,5 75,0 20,0 |
|
Площадь сечения, 10-4 м2 |
A |
49,1 |
57,0 |
65,9 |
82,6 |
95,1 |
Расчет элементов верхнего строения железнодорожного пути как балки бесконечной длины на упругом основании
Пусть требуется определить прогибы и внутренние усилия в элементах железнодорожного пути. Характеристика пути: рельсы типа Р43; шпалы сосновые: длина шпалы 2,7 м, ширина 0,25 м; балласт песчаный с коэффициентом постели k1 = 50 МПа (см. табл.17.1), площадь подкладки ω= 4,64∙10-2 м2 ; локомотив -тепловоз серии ТЭЗ с нагрузками от колес на рельс (105 + 105 + 105 + 105 + 105 + 105) кН с расстояниями между колесами (2,1 + 2,1 + 4,4 + 2,1 + 2,1) м (рис.17.6).
Рис.
17.6
Решение:
1. Определение
прогибов и внутренних усилий
Последовательно вычисляем или находим по таблицам все необходимые геометрические и жесткостные расчетные характеристики для заданной системы:
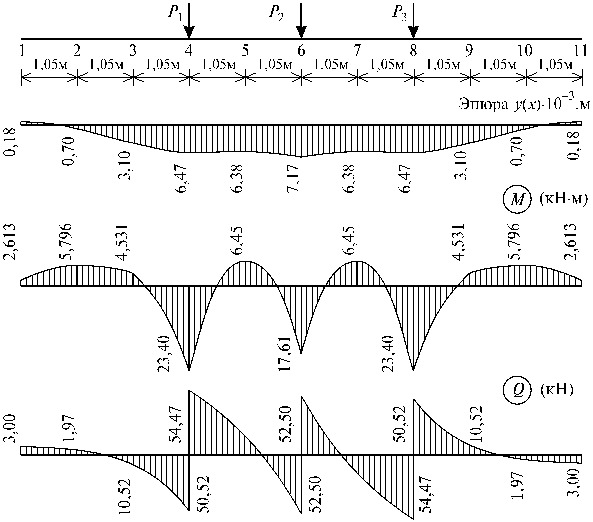
Рис.
17.7
Iz = 1,489∙10-5 м4; Wz = 2,083∙10-4 м3; (см. табл.17.2)
EIz = 2,1∙1011∙1,489∙10-5 = 3,127∙106 Нм2;
k = k1∙b = 50∙106∙0,14 = 7,0∙106 Па.
Площадь полушпалы Ω = l×b/2 = 2,7×0,25/2 = 0,3375 м2.
Определим 
м. Таким образом, в расчете будем учитывать
нагрузки лишь от трех колес локомотива.
Разбиваем балку на участки в точках 1, 2,..., 11. На балку действует система сосредоточенных грузов Р1 = Р2 = Р3 = 105 кН, приложенных в сечениях 4, 6 и 8 системы (рис.17.7, а).
Расчеты будем вести в табличной форме (см. табл.17.4 - 17.6), по формулам (17.28)¸(17.30), для чего в каждом сечении определяется параметр βx. По этому параметру в табл.17.3 находятся соответствующие значения специальных функций от действия отдельно каждой из нагрузок. Остальное ясно из таблиц 17.4 - 17.6.
Таблица 17.3
|
βx |
|
|
|
|
0,0 |
1,0000 |
1,0000 |
1,0000 |
|
0,1 |
0,9907 |
0,8100 |
0,9003 |
|
0,2 |
0,9651 |
0,6398 |
0,8024 |
|
0,3 |
0,9267 |
0,4888 |
0,7077 |
|
0,4 |
0,8784 |
0,3564 |
0,6174 |
|
0,5 |
0,8231 |
0,2415 |
0,5323 |
|
0,6 |
0,7628 |
0,1431 |
0,4530 |
|
0,7 |
0,6997 |
0,0599 |
0,3708 |
|
p/4 |
0,6448 |
0,0000 |
0,3224 |
|
0,8 |
0,6354 |
-0,0093 |
0,3131 |
|
0,9 |
0,5712 |
-0,0657 |
0,2527 |
|
1,0 |
0,5083 |
0,1108 |
0,1988 |
|
1,1 |
0,4476 |
-0,1457 |
0,1510 |
|
1,2 |
0,3899 |
0,1716 |
0,1091 |
|
1,3 |
0,3355 |
-0,1897 |
0,0729 |
|
1,4 |
0,2849 |
-0,2011 |
0,0419 |
|
1,5 |
0,2384 |
-0,2068 |
0,0158 |
|
p/2 |
0,2079 |
-0,2079 |
0,0000 |
|
1,6 |
0,1959 |
-0,2077 |
-0,0059 |
|
1,7 |
0,1576 |
-0,2047 |
-0,0235 |
|
1,8 |
0,1234 |
-0,1985 |
-0,0376 |
|
1,9 |
0,0932 |
-0,1899 |
-0,0484 |
|
2,0 |
0,0667 |
-0,1794 |
-0,0563 |
|
2,1 |
0,0439 |
-0,1675 |
-0,0618 |
|
2,2 |
0,0244 |
-0,1548 |
-0,0652 |
|
2,3 |
0,0080 |
-0,1416 |
-0,0668 |
|
3π/4 |
0,0000 |
-0,1340 |
-0,0670 |
|
2,4 |
-0,0056 |
-0,1282 |
-0,0669 |
|
2,5 |
-0,0166 |
0,1149 |
-0,0658 |
|
2,6 |
-0,0254 |
-0,1019 |
-0,0636 |
|
2,7 |
-0,0320 |
-0,0895 |
-0,0608 |
|
2,8 |
-0,0369 |
-0,0777 |
-0,0573 |
|
2,9 |
0,0403 |
-0,0666 |
-0,0534 |
|
3,0 |
-0,04226 |
-0,05632 |
-0,04929 |
|
3,1 |
-0,04314 |
-0,04688 |
-0,04501 |
|
π |
-0,04321 |
-0,04321 |
-0,04321 |
|
3π/2 |
-0,00898 |
0,00898 |
0,0000 |
|
2π |
0,00187 |
0,00187 |
0,00187 |
Таблица 17.4
|
№ сеч. |
Расстояние x до сечения от нагрузки, м (в скобках значение аргумента βx |
Значения функции ηi в соответствующих точках от действия нагрузки |
|
10-3 м |
||||
|
P1 |
P2 |
P3 |
P1 |
P2 |
P3 |
|||
|
1 |
-3,15 (2,7) |
-5,25 (4,5) |
-7,35 (6,3) |
-0,0334 |
-0,0123 |
0,0019 |
-0,0438 |
-0,2845 |
|
2 |
-2,10 (1,8) |
-4,20 (3,6) |
-6,30 (5,4) |
0,1181 |
-0,0357 |
-0,0003 |
0,0821 |
0,5323 |
|
3 |
-1,05 (0,9) |
-3,15 (2,7) |
-5,25 (4,5) |
0,5659 |
-0,0334 |
-0,0123 |
0,5202 |
3,3738 |
|
4 |
0,00 (0,0) |
-2,10 (1,8) |
-4,20 (3,6) |
1,0000 |
0,1181 |
-0,0357 |
1,0823 |
7,0194 |
|
5 |
1,05 (0,9) |
-1,05 (0,9) |
-3,15 (2,7) |
0,5659 |
0,5659 |
-0,0334 |
1,0985 |
7,1240 |
|
6 |
2,10 (1,8) |
0,00 (0,0) |
-2,10 (1,8) |
0,1181 |
1,0000 |
0,1181 |
1,2363 |
8,0177 |
|
7 |
3,15 (2,7) |
1,05 (0,9) |
-1,05 (0,9) |
-0,0334 |
0,5659 |
0,5659 |
1,0985 |
7,1240 |
|
8 |
4,20 (3,6) |
2,10 (1,8) |
0,00 (0,0) |
-0,0357 |
0,1181 |
1,0000 |
1,0824 |
7,0194 |
|
9 |
5,25 (4,5) |
3,15 (2,7) |
1,05 (0,9) |
-0,0123 |
-0,0334 |
0,5659 |
0,5202 |
3,3737 |
|
10 |
6,30 (5,4) |
4,20 (3,6) |
2,10 (1,8) |
-0,0003 |
-0,0357 |
0,1181 |
0,0821 |
0,5323 |
|
11 |
7,35 (6,0) |
5,25 (4,5) |
3,15 (2,7) |
0,0019 |
-0,0123 |
-0,0334 |
-0,0438 |
-0,2845 |
Таблица 17.5
|
№ сеч. |
Расстояние x до сечения от нагрузки, м (в скобках значение аргумента βx |
Значения функции ψi в соответствующих точках от действия нагрузки |
|
кНм |
||||
|
P1 |
P2 |
P3 |
P1 |
P2 |
P3 |
|||
|
1 |
-3,15 (2,7) |
-5,25 (4,5) |
-7,35 (6,3) |
-0,0865 |
0,0087 |
0,0016 |
-0,0762 |
-2,312 |
|
2 |
-2,10 (1,8) |
-4,20 (3,6) |
-6,30 (5,4) |
-0,1972 |
-0,0108 |
0,0061 |
-0,2020 |
-6,130 |
|
3 |
-1,05 (0,9) |
-3,15 (2,7) |
-5,25 (4,5) |
-0,0699 |
-0,0865 |
0,0087 |
-0,1477 |
-4,481 |
|
4 |
0,00 (0,0) |
-2,10 (1,8) |
-4,20 (3,6) |
1,0000 |
-0,1972 |
-0,0108 |
0,7919 |
24,031 |
|
5 |
1,05 (0,9) |
-1,05 (0,9) |
-3,15 (2,7) |
-0,0699 |
-0,0699 |
-0,0865 |
-0,2263 |
-6,866 |
|
6 |
2,10 (1,8) |
0,00 (0,0) |
-2,10 (1,8) |
-0,1972 |
1,0000 |
-0,1972 |
0,6054 |
18,374 |
|
7 |
3,15 (2,7) |
1,05 (0,9) |
-1,05 (0,9) |
-0,0865 |
-0,0699 |
-0,0699 |
-0,2262 |
-6,866 |
|
8 |
4,20 (3,6) |
2,10 (1,8) |
0,00 (0,0) |
-0,0108 |
-0,1972 |
1,0000 |
0,7919 |
24,031 |
|
9 |
5,25 (4,5) |
3,15 (2,7) |
1,05 (0,9) |
-0,0087 |
-0,0865 |
-0,0699 |
-0,1477 |
-4,481 |
|
10 |
6,30 (5,4) |
4,20 (3,6) |
2,10 (1,8) |
0,0061 |
-0,0108 |
-0,1972 |
-0,2020 |
-6,130 |
|
11 |
7,35 (6,0) |
5,25 (4,5) |
3,15 (2,7) |
0,0016 |
-0,0087 |
-0,0865 |
-0,0762 |
-2,312 |
Таблица 17.6
|
№ сеч. |
Расстояние x до сечения от нагрузки, м (в скобках значение аргумента βx |
Значения функции ψi в соответствующих точках от действия нагрузки |
|
кН |
||||
|
P1 |
P2 |
P3 |
P1 |
P2 |
P3 |
|||
|
1 |
-3,15 (2,7) |
-5,25 (4,5) |
-7,35 (6,3) |
0,0599 |
0,0018 |
-0,0017 |
0,0600 |
3,151 |
|
2 |
-2,10 (1,8) |
-4,20 (3,6) |
-6,30 (5,4) |
0,0395 |
0,0233 |
-0,0029 |
0,0599 |
3,148 |
|
3 |
-1,05 (0,9) |
-3,15 (2,7) |
-5,25 (4,5) |
-0,2480 |
0,0599 |
0,0018 |
-0,1863 |
-9,779 |
|
4 |
0,00 (0,0) |
-2,10 (1,8) |
-4,20 (3,6) |
-1,0000 |
0,0395 |
0,0233 |
-0,9371 |
-49,199 |
|
4' |
0,00 (0,0) |
-2,10 (1,8) |
-4,20 (3,6) |
1,0000 |
0,0395 |
0,0233 |
1,0628 |
55,797 |
|
5 |
1,05 (0,9) |
-1,05 (0,9) |
-3,15 (2,7) |
0,2480 |
-0,2480 |
0,0599 |
0,0599 |
3,1448 |
|
6 |
2,10 (1,8) |
0,00 (0,0) |
-2,10 (1,8) |
-0,0395 |
-1,0000 |
0,0395 |
-1,0000 |
-52,500 |
|
6' |
2,10 (1,8) |
0,00 (0,0) |
-2,10 (1,8) |
-0,0395 |
1,0000 |
0,0395 |
1,0000 |
52,500 |
|
7 |
3,15 (2,7) |
1,05 (0,9) |
-1,05 (0,9) |
-0,0599 |
0,2480 |
-0,2480 |
-0,0599 |
-3,1448 |
|
8 |
4,20 (3,6) |
2,10 (1,8) |
0,00 (0,0) |
-0,0233 |
-0,0395 |
-1,0000 |
-1,0628 |
-55,797 |
|
8’ |
4,20 (3,6) |
2,10 (1,8) |
0,00 (0,0) |
-0,0233 |
-0,0395 |
1,0000 |
0,9371 |
49,199 |
|
9 |
5,25 (4,5) |
3,15 (2,7) |
1,05 (0,9) |
-0,0018 |
-0,0599 |
0,2480 |
0,1863 |
9,779 |
|
10 |
6,30 (5,4) |
4,20 (3,6) |
2,10 (1,8) |
0,0029 |
-0,0233 |
-0,0395 |
-00599 |
-3,148 |
|
11 |
7,35 (6,0) |
5,25 (4,5) |
3,15 (2,7) |
0,0017 |
-0,0018 |
-0,0599 |
-0,0600 |
-3,151 |
По этим результатам построены эпюры прогибов, изгибающих моментов и поперечных сил (см. рис.17.7, б, в, г).
2. Определение напряжений в элементах
верхнего строения пути
Напряжения от изгиба в подошве рельса:
Значения напряжений на шпале под подкладкой и на баласте под шпалой будут соответственно равны:
Расчет коротких балок на упругом основании. Функции Крылова
Рис.
17.8
Значительно более сложным оказывается решение для коротких балок, когда требуется учесть условия на обоих концах балки. К таким балкам относится, например, рельсовый путь на шпалах (рис.17.8). Для коротких балок нельзя использовать решения, полученные для балок бесконечной длины и требуется исходить из общего интеграла (17.9), содержащего четыре произвольные постоянные интегрирования. Для решения обычно пользуются нормальными фундаментальными функциями уравнения (17.5). Эти функции называемые функциями Крылова, являются решениями однородного уравнения (17.5) и удовлетворяют специальным условиям при x = 0.
Cоставим следующую таблицу, в которой сведены начальные значения функций Крылова и их производных:
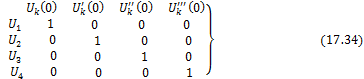
Так как во всех клетках этой таблицы стоят нули, лишь на главной диагонали единицы, то система частных решений Uk , называется системой с единичной матрицей. Эти решения суть:
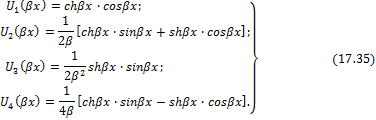
Следует отметить, что производные функций Крылова (17.35) выражаются снова через те же функции, причем:
Таким образом, общий интеграл уравнения (17.9) может быть представлен через функции Крылова:
Постоянные интегрирования C1 , C2 , C3 , C4 имеют здесь совершенно определенный смысл. Действительно, если положить x = 0, и воспользоваться свойством (17.34) введенных функций, получим:
Таким
образом:
Формула (17.39) представляет общий интеграл уравнения (17.5). Постоянные интегрирования имеют здесь простой смысл: это начальные (при x = 0) значения искомой функции и ее производные. Поэтому, метод интегрирования дифференциальных уравнений, основанный на формуле (17.39), и широко применяемый в строительной механике, называется методом начальных параметров.
Согласно метода начальных параметров, балка разбивается на участки. Подставив (17.38) в (17.39), получим функцию прогибов на I участке балки:
Пользуясь приведенными в (17.36) правилами
дифференцирования от функций прогибов (17.40) переходим к углам поворота 
и
далее по формулам (17.25), (17.26) к внутренним усилиям на I участке:
Функцию 
продолжаем на второй и последующие участки.
Приращения 
этой
функции будут зависеть от приращений внутренних сил 
, 
и интенсивности нагрузки на границах
между участками 
. Добавляя эти приращения к функции прогибов,
углов поворота, изгибающих моментов и поперечных сил, получим универсальные
формулы:
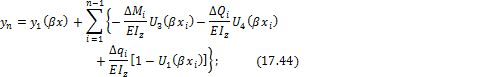
здесь для краткости обозначено 
; 
-
абсцисса i-ой границы между участками.
Как и в обычной балке, в начале координат часть начальных параметров бывает известна, а остальные определяются из граничных условий, формируемых для противоположного конца стержня.
С целью облегчения вычислений при выполнении практических расчетов балок на упругом основании в таблице 17.7 приводятся значения тригонометрических, гиперболических функций и функций Крылова при заданном аргументе.
Таблица 17.7
|
βz |
sinβz |
cosβz |
shβz |
chβz |
|
βU2(βz) |
β2U3(βz) |
β3U4(βz) |
|
0,0 |
0,0000 |
1,0000 |
0,0000 |
1,0000 |
1,0000 |
0,0000 |
0,0000 |
0,0000 |
|
0,1 |
0,0998 |
0,9950 |
0,1002 |
1,0050 |
0,9999 |
0,1000 |
0,0050 |
0,0002 |
|
0,2 |
0,1987 |
0,9801 |
0,2013 |
1,0201 |
0,9998 |
0,1999 |
0,0200 |
0,0024 |
|
0,3 |
0,2955 |
0,9553 |
0,3045 |
1,0453 |
0,9986 |
0,2999 |
0,0450 |
0,0045 |
|
0,4 |
0,3894 |
0,9210 |
0,4108 |
1,0811 |
0,9957 |
0,3997 |
0,0800 |
0,0107 |
|
0,5 |
0,4794 |
0,8776 |
0,5211 |
1,1276 |
0,9896 |
0,4989 |
0,1249 |
0,0208 |
|
0,6 |
0,5646 |
0,8253 |
0,6367 |
1,1855 |
0,9784 |
0,5974 |
0,1797 |
0,0360 |
|
0,7 |
0,6442 |
0,7648 |
0,7586 |
1,2552 |
0,9600 |
0,6944 |
0,2443 |
0,0571 |
|
π/4 |
0,7071 |
0,7071 |
0,8687 |
1,3246 |
0,9366 |
0,7754 |
0,3071 |
0,0806 |
|
0,8 |
0,7173 |
0,6967 |
0,8881 |
1,3374 |
0,9318 |
0,7890 |
0,3185 |
0,0851 |
|
0,9 |
0,7833 |
0,6216 |
1,0265 |
1,4331 |
0,8908 |
0,8803 |
0,4020 |
0,1211 |
|
1,0 |
0,8415 |
0,5403 |
1,1752 |
1,5431 |
0,8337 |
0,9667 |
0,4944 |
0,1659 |
|
1,1 |
0,8912 |
0,4536 |
1,3356 |
1,6685 |
0,7568 |
1,0464 |
0,5951 |
0,2203 |
|
1,2 |
0,9320 |
0,3624 |
1,5095 |
1,8107 |
0,6562 |
1,1173 |
0,7034 |
0,2851 |
|
1,3 |
0,9636 |
0,2675 |
1,6984 |
1,9709 |
0,5272 |
1,1767 |
0,8183 |
0,3612 |
|
1,4 |
0,9854 |
0,1700 |
1,9043 |
2,1509 |
0,3656 |
1,2216 |
0,9382 |
0,4489 |
|
1,5 |
0,9975 |
0,0707 |
2,1293 |
2,3524 |
0,1663 |
1,2485 |
1,0620 |
0,5490 |
|
π/2 |
1,0000 |
0,0000 |
2,3013 |
2,5092 |
0,0000 |
1,2546 |
1,1507 |
0,6273 |
|
1,6 |
0,9996 |
-0,0292 |
2,3756 |
2,5775 |
-0,0753 |
1,2536 |
1,1873 |
0,6615 |
|
1,7 |
0,9917 |
-0,1288 |
2,6456 |
2,8283 |
-0,3643 |
1,2320 |
1,3118 |
0,7864 |
|
1,8 |
0,9738 |
-0,2272 |
2,9422 |
3,1075 |
-0,7060 |
1,1788 |
1,4326 |
0,9236 |
|
1,9 |
0,9463 |
-0,3233 |
3,2682 |
3,4174 |
-1,1049 |
1,0886 |
1,5463 |
1,0726 |
|
2,0 |
0,9093 |
-0,4161 |
3,6269 |
3,7622 |
-1,5655 |
0,9559 |
1,6420 |
1,2320 |
|
2,1 |
0,8632 |
-0,5048 |
4,0219 |
4,1443 |
-2,0920 |
0,7736 |
1,7359 |
1,4019 |
|
2,2 |
0,8084 |
-0,5885 |
4,4571 |
4,5679 |
-2,6882 |
0,5348 |
1,8016 |
1,5789 |
|
2,3 |
0,7457 |
-0,6663 |
4,9370 |
5,0372 |
-3,3563 |
0,2334 |
1,8408 |
1,7614 |
|
3π/4 |
0,7071 |
-0,7071 |
5,2280 |
5,3228 |
-3,7634 |
0,0335 |
1,8484 |
1,8651 |
|
2,4 |
0,6754 |
-0,7374 |
5,4662 |
5,5569 |
-4,0976 |
-0,1388 |
1,8459 |
1,9460 |
|
2,5 |
0,5985 |
-0,8011 |
6,0502 |
6,1323 |
-4,9126 |
-0,5883 |
1,8105 |
2,1292 |
|
2,6 |
0,5155 |
-0,8569 |
6,6947 |
6,7690 |
-5,8003 |
-1,1236 |
1,7256 |
2,3065 |
|
2,7 |
0,4274 |
-0,9041 |
7,4063 |
7,4735 |
-6,7568 |
-1,7509 |
1,5827 |
2,4725 |
|
2,8 |
0,3390 |
-0,9422 |
8,1919 |
8,2527 |
-7,7757 |
-2,4604 |
1,3885 |
2,6290 |
|
2,9 |
0,2392 |
-0,9710 |
9,0596 |
9,1146 |
-8,8503 |
-3,3083 |
1,0835 |
2,7443 |
|
3,0 |
0,1411 |
-0,9900 |
10,0179 |
10,0677 |
-9,9670 |
-4,2486 |
0,7068 |
2,8346 |
|
3,1 |
0,0416 |
-0,9991 |
11,0765 |
11,1215 |
-11,1114 |
-5,3019 |
0,2304 |
2,8822 |
|
π |
0,0000 |
-1,0000 |
11,5487 |
11,5920 |
-11,5920 |
-5,7960 |
0,0000 |
2,8872 |
Расчет шпалы рельсового пути, как короткой балки на упругом основании
Пусть требуется определить прогибы и внутренние усилия в железобетонных шпалах E = 3,05∙1010 Н/м2, длиной 2l = 2,7 м, с размерами поперечного сечения b × h = 0,25×0,18 м2, лежащей на балластном слое щебня k1 = 75 МПа (см. табл.17.1), нагруженной двумя силами P = 210 кН каждый, приложенных на расстоянии a = 0,54 м от ее концов (рис.17.8).
Решение:
1. Расчет начальных параметров
Последовательно вычисляем все необходимые геометрические и жесткостные расчетные характеристики для заданной системы:
Поместим начало системы координат xy в центре тяжести левого крайнего сечения шпалы. Граничные условия задачи в начальном сечении при x = 0 запишем в виде:
Согласно (17.40)¸(17.43) запишем функции прогибов, углов поворота и внутренних усилий для I участка (0≤x≤a):
Составим соответствующие выражения для
II участка (
), учтя,
что на границе участков I и II, т.е. при x = a и имеем скачок
функции поперечной силы на величину 
:
Для определения y0 и φ0, используем
симметричный характер нагружения балки относительно
среднего сечения x = l, где имеем:
φ(l) = 0; Q(l) = 0.
Составим следующую систему уравнений:
Cогласно (17.54) и (17.55), учитывая, что
βl= 1,06×1,35 » 1,5; β(l-a) = 1,06×(1,35 - 0,54) = 0,9,
с учетом данных таблицы 17.7, получим:
После ряда преобразований приходим к системе:
корни которой принимают значения:
В качестве условия проверки правильности вычисления значений начальных параметров, подставим их значения в (17.54) и (17.55), получим:
Следовательно, величины y0 и φ0 определены верно.
2. Определение прогибов, углов поворота и внутренних усилий
Разобьем балку на 10 участков. Используем симметрию задачи, поэтому будем рассматривать только половину балки, т.е. сечения 0, 1, 2, 2’, 3, 4, 5 (см. рис.17.9, а). Расчеты будем вести в табличной форме (см. табл.17.8). Поэтому, согласно (17.52), запишем выражения прогибов, углов поворота и внутренних усилий для I и II участков:
Участок I.
Сечение 0, x = 0:
y0 = 8,68∙10-3 м; φ0 = -2,5∙10-4 рад; M0 = 0; Q0 = 0.
Cечение 1, x = 0,27 м.
Cечение 2, x = 0,54 м.
Участок II.
Cечение 2’, x = 0,54 м.
Cечение 3, x = 0,81 м.
Сечение 4, x = 1,08 м.
Сечение 5, x = 1,35 м.
Результаты расчетов внесены в таблицу 17.8 и по этим значениям построены эпюры прогибов, углов поворота, изгибающих моментов и поперечных сил (см. рис.17.9, б, в, г).
Таблица 17.8
|
№ сеч. |
x |
βx |
β(x-a) |
U1 |
U2 |
U3 |
U4 |
y, 10-2
м |
φ, 10-3 рад |
M, кНм |
Q, кН |
|
0 |
0 |
0 |
- |
1,000 |
0,000 |
0,000 |
0,000 |
8,680 |
-0,250 |
0,000 |
0,000 |
|
1 |
0,27 |
0,3 |
- |
0,999 |
0,299 |
0,045 |
0,004 |
8,597 |
-0,251 |
6,50 |
45,82 |
|
2 |
0,54 |
0,6 |
- |
0,978 |
0,597 |
0,179 |
0,036 |
8,352 |
-1,570 |
25,87 |
90,90 |
|
2’ |
0,54 |
0,6 |
0 |
0,978 |
0,597 |
0,179 |
0,036 |
8,352 |
-1,570 |
25,87 |
-119,1 |
|
3 |
0,81 |
0,9 |
0,3 |
0,891 |
0,880 |
0,402 |
0,121 |
7,738 |
-2,413 |
1,71 |
-76,33 |
|
4 |
1,08 |
1,2 |
0,6 |
0,656 |
1,117 |
0,703 |
0,285 |
7,143 |
-1,938 |
-17,67 |
-36,98 |
|
5 |
1,35 |
1,5 |
0,9 |
0,166 |
1,249 |
1,062 |
0,549 |
6,904 |
0,000 |
-22,85 |
-0,04 |
Рис.
17.9
Вопросы для самопроверки
- Раскройте суть гипотезы Винклеровского основания.
- Поясните физический смысл коэффициента постели.
- Дайте определение относительно коротких и балок бесконечной длины
- Подчеркните отличительные особенности между дифференциальными уравнениями изгиба обычных балок и балок на упругом основании.
- Какими свойствами должны обладать функции Крылова.
- Сформулируйте условия достаточной жесткости и прочности конструкций на упругом основании.
- Что понимается под термином «балка на упругом основании»?
- Сформулируйте предпосылки, на которых построен расчет балок на упругом основании?
- Напишите общее выражение для интенсивности нагрузки балки на упругом основании и сформулируйте смысл параметров, входящих в это выражение?
- Получите дифференциальные уравнения для прогибов и изгибающих моментов балки на упругом основании?
- Напишите уравнение для изгибающих моментов балки на упругом основании по методу начальных параметров?
- Опишите технику написания выражения для М балки на упругом основании по методу начальных параметров?
- Приведите дифференциальные соотношения между функциональными коэффициентами А, В, С, D.
- Получите выражения для Q, р, р' путем дифференцирования выражения для М.
- Какие начальные параметры входят в уравнения балки на упругом основании и как они находятся?
- Опишите технику решения задач балки на упругом основании по методу начальных параметров?
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
