Главная

Лекция 19. Изгиб и кручение тонкостенных стержней

Содержание

Общие положения и основные особенности расчета

Секториальная площадь

Секториальные характеристики и их определение

Общий случай нагружения тонкостенного стержня. Бимомент

Расчет тонкостенного стержня открытого профиля

Кручение тонкостенных стержней открытого профиля

Кручение тонкостенных стержней замкнутого профиля

Вопросы для самопроверки

Общие положения и основные особенности расчета

В настоящее время в машиностроении, авиации, строительстве, железнодорожном транспорте все больше используются конструкции, выполненные из тонкостенных и штампованных профилей или просто из тонколистовой стали. Эти конструкции обеспечивают высокую жесткость и прочность при сравнительно небольшом весе, поэтому их применение в технике является весьма экономичным. На железнодорожном транспорте это элементы тележек, стенок локомотивов, вагонов и многих других конструкций.

Специфика расчета этих конструкций на прочность породила особую расчетную схему - схему тонкостенного стержня.

Основным признаком тонкостенного стержня является характерное отношение его геометрических размеров. В поперечном сечении одно из измерений (толщина) существенно меньше другого - срединной длины контура s. Последняя в свою очередь намного меньше, чем длина стержня l (рис.19.1).

Длина контура для тонкостенного стержня, представленного на рис.19.1:

s=h+2b.

Следовательно, характерные размеры тонкостенных стержней открытого профиля взаимосвязаны и меняются в пределах l/s≥10 и s>>δ.

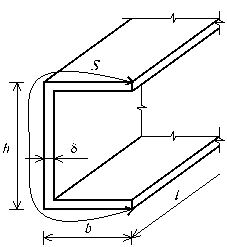
Рис. 19.1

Основные положения теории тонкостенных стержней были даны С.П. Тимошенко. Полное и общее развитие эта теория получила в трудах В.З. Власова и потому обычно называется теорией Власова.

Тонкостенный стержень, как расчетная схема, сохраняет в себе основные свойства обыкновенного стержня и формулы сопротивления материалов, связанные с растяжением (сжатием), изгибом и кручением бруса, остаются в основном справедливыми.

Вместе с тем, тонкостенный стержень в силу геометрических соотношений обнаруживает свойства, существенно отличающие его от стержней сплошного сечения. При некоторых видах загружения не соблюдается гипотеза плоских сечений, происходит так называемая депланация сечения за счет неравномерной деформации стержня вдоль его оси. Иными словами, не соблюдается принцип Сен-Венана - глубина «проникновения» краевых особенностей вдоль оси существенно больше, чем в сплошном стержне.

Вообще говоря, сравнительная оценка нормальных и касательных напряжений σ и τ в поперечных сечениях бруса при переходе от сплошного сечения к тонкостенному профилю существенно меняется, и этот вопрос требует особого изучения.

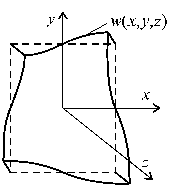
Рис. 19.2

При кручении тонкостенных стержней и вообще стержней с некруглым поперечным сплошным сечением, поперечные сечения плоские до деформации, искривляются по некоторой поверхности w(x, y, z) (рис.19.2), что называется депланацией сечения. По характеру формирования депланаций сечения по длине стержня, следует различать два типа кручения стержней: свободное и стесненное.

Если депланация во всех поперечных сечениях одинакова по длине стержня или иначе w(x, y, z) = w(x, y), т.е. она является постоянной и не зависит от z, то такое кручение называется свободным. При переменных депланациях по длине стержня, кручение называется стесненным.

При свободном кручении в поперечных сечениях стержня возникают только касательные напряжения, а при стесненном кручении, наряду с касательными возникают и нормальные напряжения. Эффект от неравномерной депланации сечения по его длине наиболее существенен для стержней открытого профиля.

Заметим, что порядок вычисления напряжений и перемещений в тонкостенном стержне закрытого профиля при свободном кручении принципиально ничем не отличается от метода расчета обычных стержней. Поэтому, здесь этому вопросу специальное внимание не уделяется.

Секториальная площадь

В дополнение к уже известным геометрическим характеристикам сечений (A - площадь поперечного сечения; S_x, S_v - статические моменты сечения; I_x, I_v, I_xy - осевые и центробежный моменты инерции) введем ряд новых. Эти характеристики свойственны только тонкостенным стержням и определяются на основе понятия секториальной площади.

Рассмотрим срединную линию контура поперечного сечения (рис.19.3). Срединная линия - это геометрическое место точек поперечного сечения, равноудаленно расположенных от контурных линий. Выберем на срединной линии начало 0 отсчета дуги s и из заданного полюса Р. Проведем два луча к концам элементарного отрезка ds. Удвоенную площадь треугольника PAB обозначают через dω.

Очевидно, что

где r - расстояние от полюса Р до касательной к линии контура в точке А.

Интеграл

называется секториальной площадью. Таким образом, секториальная площадь представляет собой удвоенную площадь, очерчиваемую радиус-вектором РА при движении т. А по контуру от начала отсчета 0 до некоторого значения дуги s. Если радиус-вектор вращается по часовой стрелке, приращение площади dω имеет знак плюс, против часовой стрелки - минус.

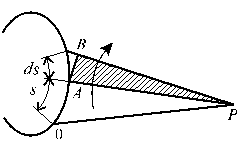
Рис. 19.3

Точка Р называется секториальным полюсом.

При заданном полюсе и заданном начале отсчета в каждом конкретном случае может быть построена эпюра секториальной площади.

Рис. 19.4

В качестве примера построим эпюру секториальной площади для контура, приведенного на рис.19.4, а. Выбираем в качестве полюса точку P, а за начало отсчета принимаем точку 0 (рис.19.4, а).

Рассмотрим участок 0-3. На этом участке 0 ≤ s ≤ a. Вектор r вращается по часовой стрелке, следовательно эпюра ω имеет знак плюс:

На участке 3-4, 0 ≤ s ≤ a, вектор r вращается против часовой стрелки, то есть приращение площади будет отрицательным:

На участке 0-2, 0 ≤ s ≤ a, вектор r вращается против часовой стрелки, то есть приращение площади будет отрицательным:

На участке 2-1, 0 ≤ s ≤ a, вектор r вращается по часовой стрелке, то есть приращение площади будет положительным:

Эпюра секториальной площади ω приведена на рис.19.4, б.

Отметим, что при переносе полюса секториальная площадь меняется на величины, линейно зависящие от координат x и y, т.е.:

где и - секториальная площадь относительно нового Р₀ и старого полюса Р', соответственно; x_c, y_c, x₀, y₀ - координаты центра изгиба и начала отсчета, соответственно.

Секториальные характеристики и их определение

Наряду с общепринятыми, для тонкостенных стержней вводятся дополнительные характеристики поперечных сечений.

Секториально статический момент поперечного сечения:

Секториально линейные моменты площади поперечного сечения:

Секториальный момент инерции поперечного сечения:

Окончательные выражения секториальных характеристик, исходя из предположения, что толщина тонкостенного сечения по всему контуру постоянна и равна d.

При поперечном изгибе или кручении всегда существует такая точка, относительно которой момент от касательных сил, возникающих в поперечном сечении, равен нулю. Эта точка называется центром изгиба или кручения. Для сечений, имеющих две оси симметрии, центр изгиба или центр кручения совпадают с центром тяжести.

Положение центра изгиба (или кручения) не зависит от действующих на стержень сил, а зависит только от формы и размеров поперечного сечения тонкостенного стержня.

При стесненном кручении центр кручения, а также начало отсчета секториальной площади не могут быть выбраны произвольно. Эти точки должны быть выбраны так, чтобы секториально линейные моменты, а также секториально статический момент были равны нулю, т.е.:

Выполнение условий первых двух условий из (19.4) зависит только от выбора координат полюса. Выполнение же третьего из условий (19.4) зависит от выбора начала отсчета 0.

Эпюра , построенная при полюсе, в качестве которого взят центр изгиба, и удовлетворяющая третьему уравнению (15.4), носит название эпюры главной секториальной площади.

Положение центра изгиба и секториальные характеристики сечения на практике определяются в следующей последовательности.

Сначала выбирается положение полюса Р и строится эпюра секториальной площади ω¢ относительно полюса.

Далее определяются величины и относительно полюса P и вычисляются координаты центра изгиба по формулам:

Определяется секториальная площадь относительно центра изгиба по формуле (19.3) и вычисляется секториaльно стaтический момент поперечного сечения по формуле:

как площадь эпюры , умноженную на δ.

Далее определяется постоянная D из третьего условия (19.4) по формуле:

и строится эпюра главной секториальной площади:

Секториальные геометрические характеристики прокатных двутавров и швеллеров приведены в табл.19.1 и 19.2, значения моментов инерции при чистом кручении прокатных уголков приведены в табл.19.3 и 19.4., а формулы координат центра изгиба и секториальных моментов инерции некоторых металлических профилей – в табл.19.5.

Таблица 19.1

		Секториальные геометрические характеристики прокатных двутавров (ОСТ 10016-39)
Номер профиля	Секториальный момент инерции , см^6	Секториальная площадь для крайней точки профиля , см^2	Секториальный момент сопротивления , см^4	Момент инерции при чистом кручении , см^4	Изгибно-крутильная характеристика , см^-1
10	644,3	15,25	42,26	2,873	0,04122
12	1353	20,10	67,33	4,243	0,03457
14	2560	25,54	100,23	5,911	0,02966
16	4879	32,25	151,30	8,406	0,02562
18	8219	38,90	211,28	11,37	0,02295
20а	13121	46,15	284,31	14,81	0,02074
20б	13857	47,05	284,50	17,85	0,02215
22а	22773	55,91	407,33	20,32	0,01844
22б	23930	56,90	420,55	24,08	0,01958
24а	33799	64,48	524,15	25,57	0,01698
24б	35426	65,57	540,25	30,12	0,01800
27а	52987	76,68	690,99	31,93	0,01515
27б	55414	77,92	711,21	37,60	0,01608
30а	76704	88,38	867,93	38,83	0,01389
30б	80114	89,75	892,60	45,78	0,01475
30с	83612	91,13	917,50	55,23	0,01587
33а	107160	100,69	1064,3	46,19	0,01281
33б	111780	102,21	1093,6	54,49	0,01363
33с	116520	103,73	1123,3	65,74	0,01466
36а	154820	115,19	1344,0	56,85	0,01183
36б	161210	116,85	1379,6	66,72	0,01256
36с	167760	118,51	1415,6	79,99	0,01348
40а	228900	134,13	1706,6	68,75	0,01070
40б	237950	136,00	1749,6	80,68	0,01137
40с	247210	137,85	1793,3	96,55	0,01220
45а	376630	159,75	2357,6	95,31	0,009819
45б	390770	161,96	2414,4	111,3	0,01041
45с	405220	163,96	2471,5	131,8	0,01113
50а	611990	187,10	3270,9	131,2	0,009038
50б	633900	189,44	3346,2	150,3	0,009504
50с	656270	191,79	3421,8	174,9	0,01007
55а	906350	216,79	4180,8	159,9	0,008198
55б	937220	219,36	4272,5	182,7	0,008617
55с	968720	221,94	4364,8	211,5	0,009119
60а	1349900	251,22	5373,4	195,5	0,007427
60б	1393200	254,04	5484,2	221,9	0,007790
60с	1437300	256,86	5595,7	255,3	0,008226

Примечание: При вычислении α приняты G = 8∙10⁴ МПа, E = 2,1∙10⁵ МПа

Таблица 19.2

					Секториальные геометрические характеристики прокатных швеллеров (ОСТ 10016-39)
Номер профиля	Координаты центра изгиба , см	Секториальный момент инерции , см^6	Секториальные площади		Секториальные моменты сопротивления		Момент инерции при чистом кручении , см^4	Изгибно-крутильная характеристика , см^-1
			, см^2	, см^2	, см^4	, см^4
5	1,08	24,91	2,70	4,26	9,22	5,85	1,350	0,14370
6,5	1,15	64,88	3,86	6,36	16,80	10,21	1,497	0,09375
8	1,22	141,8	5,15	8,75	27,57	16,20	1,940	0,07219
10	1,34	254,8	7,19	12,71	49,35	27,92	2,727	0,05411
12	1,48	768,3	9,54	17,31	80,51	44,39	3,634	0,04245
14а	1,58	1512	12,03	22,63	125,74	66,85	4,815	0,03483
14б	1,39	1711	11,46	23,85	149,32	71,75	6,248	0,03730
16а	1,68	2760	14,74	28,63	187,23	96,40	6,306	0,02950
16б	1,48	3099	14,03	30,09	220,87	103,00	8,227	0,03180
18а	1,83	4745	17,68	35,32	268,41	134,34	8,128	0,02555
18б	1,57	5292	16,83	37.02	314,50	142,95	10,50	0,02749
20а	1,94	7698	21,27	42,46	361,95	181,28	9,84	0,02207
20б	1,73	8560	20,24	44,45	422,87	192,57	12,50	0,02359
22а	2,07	11593	24,84	49,60	466,69	233,73	11,66	0,01958
22б	1,86	12863	23,63	51,88	544,42	247,95	14,60	0,02079
24а	2,10	15326	27,48	55,21	557,74	277,59	13,21	0,01812
24б	1,88	17007	26,10	57,75	651,56	394,50	16,47	0,01921
24с	1,67	18640	24,91	60,09	748,35	310,21	21,31	0,02087
27а	2,14	24337	31,85	66,46	764,11	366,19	16,25	0,01505
27б	1,91	26883	30,23	69,39	889,34	387,42	20,34	0,01698
27с	1,70	29355	28,82	72,10	1018,6	407,14	26,34	0,01848
30а	2,26	36645	37,21	76,54	984,87	478,78	20,39	0,01456
30б	2,03	40436	35,23	79,98	1147,8	505,61	25,01	0,01535
30с	1,80	44104	33,59	83,06	1313,0	530,97	31,75	0,01656
33а	2,25	53630	41,39	88,54	1271,7	594,43	24,29	0,01326
33б	2,02	57844	39,27	92,27	1473,2	626,93	29,92	0,01404
33с	1,80	62890	37,44	95,69	1679,8	657,23	38,04	0,01518
36а	2,47	92,189	49,50	104,55	1862,2	881,77	38,91	0,01268
36б	2,24	100430	47,30	108,51	2123,4	925,54	46,56	0,01329
36с	2,02	108420	45,36	112,18	2390,2	966,48	57,18	0,01417
40а	2,43	148100	55,78	121,67	2655,1	1217,2	59,74	0,01240
40б	2,21	160100	53,51	125,86	2991,7	1272,1	70,78	0,01298
40с	2,00	171870	51,51	129,80	3336,4	1324,0	85,72	0,01378

Примечание: При вычислении α приняты G = 8∙10⁴ МПа, E = 2,1∙10⁵ МПа

Таблица 19.3

	Значения моментов инерции при чистом кручении прокатных равнобоких уголков (ОСТ 10014-39)
Размеры, мм		, см^4	Размеры, мм		, см^4
b	d		b	d
20	3	0,03330	100	8	3,277
	4	0,07680		10	6,333
25	3	0,04230		12	10,83
	4	0,09813		14	17,01
30	4	0,1195		16	25,12
	5	0,2292	120	10	7,667
35	4	0,1408		12	13,13
	5	0,2708		14	20,67
40	4	0,1621		16	30,58
	5	0,3125		18	43,16
	6	0,6328	130	10	8,333
45	4	0,1835		12	14,28
	5	0,3542		14	22,49
	6	0,6048		16	33,31
50	5	0,3958	150	12	16,59
	6	0,6768		14	26,15
60	5	0,4792		16	38,78
	6	0,8208		18	54,82
	8	1,911		20	74,67
65	6	0,8928	180	14	31,64
	8	2,082		16	46,97
	10	4,000		18	66,48
75	6	1,037	200	16	52,43
	8	2,423		18	74,26
	10	4,667		20	101,3
	12	7,949		24	173,2
80	6	1,109		30	333,0
	8	2,594	220	16	57,89
	10	5,000		20	112,0
90	8	2,935		24	191,7
	10	5,667		28	301,5
	12	9,667	230	24	200,9
	14	15,18

Таблица 19.4

		Значения моментов инерции при чистом кручении прокатных неравнобоких уголков (ОСТ 10014-39)
Размеры, мм			, см^4	Размеры, мм			, см^4
B	b	d		B	b	d
30	20	3	0,04230	100	75	12	9,389
		4	0,09813	120	80	8	3,277
35	20	4	0,1088			10	6,333
		5	0,2080			12	10,83
45	30	4	0,1515	130	90	8	3,618
		6	0,4968			10	7,000
60	40	5	0,3958			12	11,98
		6	0,6768			14	18,84
		8	1,570	150	100	10	8,000
75	50	5	0,5000			12	13,71
		6	0,8568			14	21,58
		8	1,997			16	31,95
		10	3,833	180	120	12	16,59
80	55	6	0,9288			14	26,15
		8	2,167			16	38,78
		10	4,167	200	120	12	17,74
90	60	6	1,037			14	27,98
		8	2,423			16	41,51
		10	4,667	200	150	12	19,47
100	75	8	2,850			16	45,60
		10	5,500			18	64,54
						20	88,00

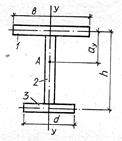
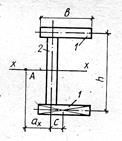
Таблица 19.5. Формулы для вычисления координат центра изгиба и секториальных

моментов инерции некоторых металлических профилей

Сечение	Координата центра изгиба	Секториальный момент инерции
	Центр изгиба находится в пересечении осей профиля	0

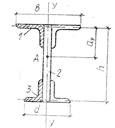
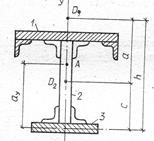
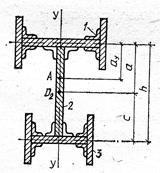
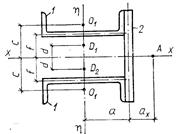
Примечания: A - центр изгиба профиля; D₁, D₂, D₃ - центры изгиба отдельных элементов профиля; 1, 2, 3 – номера элементов, составляющих профиль; , - осевые моменты инерции всего сечения относительно указанных на чертеже осей; , , , , , - осевые моменты инерции отдельных элементов профиля относительно указанных на чертеже осей: первый индекс – номер элемента, второй – ось; , , - секториальные моменты инерции отдельных элементов относительно собственных центров изгиба.

Общий случай нагружения тонкостенного стержня. Бимомент

В общем случае нагружения осевые перемещения сечения тонкостенного бруса можно представить в виде следующего выражения:

где , и характеризуют: смещение по продольной оси z; поворот сечения как жесткого целого относительно координатных осей x и y; γ - удельный угол закручивания относительно продольной оси z, ω - эпюра главной секториальной площади.

Нормальные напряжения в сечении, согласно закону Гука, в данном случае определяются согласно выражения:

С учетом последнего выражения, формулы по определению внутренних силовых факторов от нормальных напряжений σ, примут вид:

Здесь через обозначена новая силовая характеристика, называемая бимоментом, размерность которой будет кНм².

В результате совместного рассмотрения (19.9) и (19.10) выражение нормальных напряжений можно представить в следующем виде:

Первые три слагаемых уже известные нам величины нормальных напряжений из курса «Сопротивления материалов», являются результатом действия продольной силы и изгибающих моментов. Что же касается четвертого слагаемого, то оно характеризует изменения, вносимые в линейные законы распределения напряжений, депланацией сечения, силовой мерой которой является бимомент.

Заметим, что бимомент является самоуравновешенным фактором и по методу сечений не может быть определен. Следовательно, задача в общем случае нагружения тонкостенного стержня является статически неопределимой. Например, если нагрузить стержень двутаврового сечения четырьмя равными силами Р (рис.19.5), бимомент в торцевом сечении будет равен:

где - значение секториальной площади для точки приложения силы P_i, т.е.:

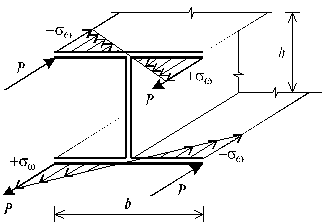
Рис. 19.5

В этом случае, очевидно, что и продольная сила N, и изгибающие моменты M_x , M_y равны нулю.

Касательные напряжения в поперечном сечении стержня в общем случае нагружения слагаются из касательных напряжений поперечного изгиба, простого (свободного) кручения, и наконец, из вторичных касательных напряжений, возникающих за счет стесненного кручения:

Следовательно, в общем случае нагружения в поперечных сечениях тонкостенного стержня возникают следующие внутренние усилия: Q_x, Q_y- поперечные силы, от касательных напряжений , ; M_x, M_y -изгибающие моменты, от нормальных напряжений ; M_z - крутящий момент свободного кручения от касательных напряжений ; - бимомент от действующих нормальных напряжений , вследствии изгиба элементов тонкостенного стержня; - изгибно- крутящий момент от дополнительных касательных напряжений .

Формулы для вычисления перечисленных факторов даны в таблице 19.6, где приняты следующие обозначения: u, v - перемещения линий центров изгиба сечений в направлении координатных осей x и y; - соответственно, статические моменты относительно координатных осей и секториально статический момент отсеченной части сечения, расположенной по одну сторону от расчетной точки.

Все эти величины легко определяются, если известна функция . Последняя может быть найдена из условия равенства суммы крутящих моментов стесненного и свободного кручения полному крутящему моменту:

Подставляя в (19.14) значения и из табл. 19.1, получим:

Дифференцируя (15.15) по z, имеем:

или

где - изгибно-крутильная характеристика поперечного сечения стержня; - распределенный крутящий момент.

Таблица 19.6

Силовой фактор	Усилие	Напряжение
Поперечная сила Qx, Qy
Изгибающий момент Mx, My
Крутящий момент при свободном кручении тонкостенного стержня постоянной толщины стенки δ, Mz
Крутящий момент при стесненном кручении тонкостенного стержня постоянной толщины стенки δ,
Бимомент

Рис. 19.6

Рассмотрим случай кручения, когда на свободном конце тонкостенного стержня, защемленного с другим концом, действует крутящий момент (рис.19.6). В этом случае имеем:

интеграл которого записывается:

Откуда имеем:

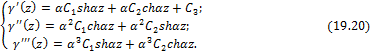
Для определения C₁, C₂, C₃ и C₄ с учетом граничных условий:

при z = 0, и ;

при z = l, и

получим:

Учитывая выражения произвольных постоянных (19.22) из (19.19) и (19.20), будем иметь:

Здесь shx и chx - гиперболический синус и гиперболический косинус, соответственно, аргумента x:

В заключении, учитывая (19.23) и выражения усилий из таблицы 19.1, окончательно получим:

Заметим, что существует полная аналогия в основных зависимостях теории стесненного кручения стержней открытого и замкнутого профилей. Основные расчетные зависимости теории расчета стержней замкнутого профиля можно получить, путем замены в приведенных выше зависимостях для расчета стержней открытого профиля, уже известных нам секториальных координат и секториальных геометрических характеристик сечений , и т.д., на обобщенные величины , и т.д., для замкнутого профиля.

При этом, главная обобщенная секториальная координата , для замкнутого профиля (рис.19.7), определяется:

где - секториальная координата, вычисляемая по аналогии теории стержня открытого профиля; r - длина перпендикуляра, опущенного из полюса А, взятого внутри контура, на касательную к контуру; - параметр, условно называемый «средним радиусом» замкнутого контура; - удвоенная площадь, охваченная срединной линией контура s; - приведенная длина дуги данной точки контура.

Рис. 19.7

Главный обобщенный секториальный момент сечения и секториальный статический момент для замкнутого контура определяются по формулам:

где

Расчет тонкостенного стержня открытого профиля

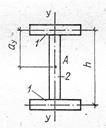
Для тонкостенного стержня открытого профиля, изображенного на рис.19.8, а, при следующих исходных данных: H = 12,5∙10^-2 м; B = 19∙10^-2 м; l = 2 м; = 1∙10^-2 м; P = 1 кН; E  = 2∙10⁵ МПа; G = 8∙10⁴ МПа, требуется:

1. Определить площадь, положение центра тяжести, главные центральные моменты инерции поперечного сечения;

2. Найти положение центра изгиба;

3. Определить момент инерции при чистом кручении I_кр и секториальные характеристики сечения;

4. Вычислить изгибно-крутильную характеристику ;

5. Построить эпюры поперечной силы Q_x, изгибающего момента M_y, момента чистого кручения M_z, изгибно-крутящего момента , бимомента ;

6. Построить эпюры нормальных напряжений , и их суммарную эпюру.

Решение:

1. Определение площади, положения центра тяжести и главных центральных моментов инерции

Вычислим расчетные размеры сечения стержня (рис.19.8, б, в), приняв в дальнейших расчетах:

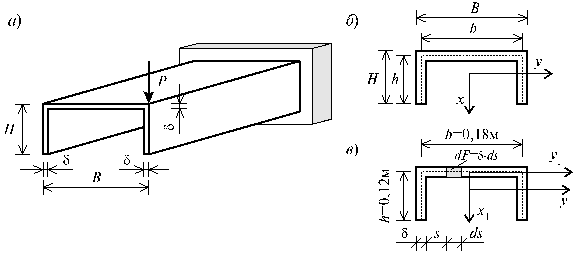
Рис. 19.8

Тогда

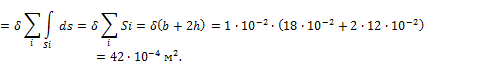
В выбранной системе координат x₁y₁, определим положение центра тяжести сечения: y_c = 0; .

Для этого построим эпюру координат x₁ (рис.19.9, а) и вычислим статический момент сечения относительно оси y₁:

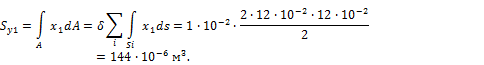
Тогда координата центра тяжести сечения будет равна:

Для вычисления главных центральных моментов инерции предварительно построим эпюру координат x и y (рис.19.9, б, в). С применением этих эпюр, определяются:

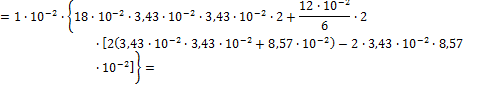
2. Определение положения центра изгиба

Вначале построим эпюру секториальных координат площади , в характерных точках (1, 2, 3, 4) профиля, выбрав произвольный полюс в точке B (рис.19.9, г):

Рис. 19.9

Координаты центра изгиба вычисляем по формулам (19.5).

Используя эпюры и y и применяя правило Верещагина, вычисляем секториально линейный статический момент:

Тогда координата центра изгиба по вертикальной оси принимает значение:

Координата центра изгиба по горизонтальной оси вычисляется

Так как эпюра x симметрична, а эпюра обратно симметрична относительно x, то по правилу Верещагина секториально-линейный статический момент равен нулю, т.е.:

Cледовательно, y_А = 0 и поэтому центр изгиба лежит на оси x.

Вычислим постоянную D, предварительно построив эпюру секториальных площадей (рис.19.9, д).

При этом полюс расположим в центре изгиба (т. А). За начало отсчета возьмем точку 3 (произвольно):

Постоянную D вычисляется по формуле (19.6):

Далее вычисляем секториально статический момент , как произведение площади эпюры на d :

В этом случае величина постоянной D будет равна:

Далее, используя зависимость (19.7), вычисляем секториальные координаты характерных точек профиля:

По полученным координатам строим эпюру (рис.19.9, е).

3. Определить момент инерции при чистом кручении и секториальные характеристики сечения

Для корытообразного профиля поперечного сечения бруса (рис. 19.8, б), имеем:

Cекториальный момент инерции I_w вычисляем по эпюре ω (рис.19.9, е):

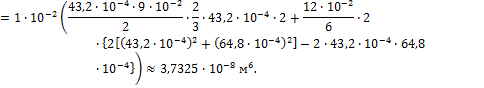
4. Определение изгибно- крутильной характеристики α

Изгибно-крутильную характеристику α вычисляем по формуле:

5. Построение эпюр поперечной силы Q_x, изгибающего момента M_y , момента чистого кручения M_z, изгибно-крутящего момента М_w и бимомента В_w

В рассматриваемом примере:

;  chαl= 6,7690;  α× chαl= 1,3×6,7690 = 8,7997 м^-1.

Тогда, согласно (19.25), получим:

Предварительно разбив тонкостенный брус по длине на 5 равных частей, для этих сечений численные значения величин Q_x , M_y , M_z , и приведены в таблице 19.7.

По результатам табл. 19.7 строим эпюры Q_x , M_y , M_z , и (рис.19.10). При этом в случае действия на брус сосредоточенной силы, во всех сечениях выполняется следующее условие: .

Таблица 19.7

z, м	αz	shαz	chαz	Qx, Н	My, Нм	Mz, Нм	, Нм	, Нм^2
0,00	0,00	0,0000	1,0000	1000	0	80,97	14,03	0
0,40	0,52	0,5438	1,1383	1000	400	79,03	15,97	5,87
0,80	1,04	1,2379	1,5913	1000	500	72,67	22,33	13,37
1,20	1,56	2,2743	2,4845	1000	1200	60,14	34,86	24,50
1,60	2,08	3,9398	4,0647	1000	1600	37,96	57,04	42,56
2,00	2,60	6,6947	6,7690	1000	2000	0,00	95,01	72,32

6. Построить эпюры нормальных напряжений, и их суммарную эпюру

Нормальные напряжения зависят от внутренних силовых факторов M_y и согласно выражения (19.11). Опасным сечением является сечение в заделке, так как в нем действуют наибольшие по величине M_y и (рис.19.10, в, д). Нормальные напряжения от изгиба (рис.19.11, а) определяем по формуле:

В точке 1: x₁ = 8,57∙10^-2 м, = -303,8∙8,57∙10^-2 = -26 Мпа.

В точке 2: x₁ = -3,43∙10^-2 м, = -303,8∙(-3,43∙10^-2) = 11,94 МПа.

В точке 3: x₁ = -3,43∙10^-2 м, = -303,8∙(-3,43∙10^-2) = 11,94 МПа.

В точке 4: x₁ = 8,57∙10^-2 м, = -303,8∙8,57∙10^-2 = -26 МПа.

По найденным данным строим эпюру (рис.19.11, а).

Рис. 19.10 Рис. 19.11

Нормальные напряжения в точках профиля от действия бимомента вычисляем по формуле:

В точке 1:

В точке 2:

В точке 3:

В точке 4:

По полученным данным строим эпюру . Суммарные нормальные напряжения в опасном сечении тонкостенного стержня от совместного действия изгиба и стесненного кручения вычислим путем сложения эпюр и по формуле: .

В точке 1: σ₁ = -26 - 1,55 = -38,55 МПа.

В точке 2: σ₂ = 11,94 + 8,37 = 20,31 МПа.

В точке 3: σ₃ = 11,94 - 8,37 = 3,57 МПа.

В точке 4: σ₄ = -26 + 12,55 = -13,45 МПа.

Суммарная эпюра нормальных напряжений σ приведена на рис.19.11, в.

Кручение тонкостенных стержней открытого профиля

В машиностроении, авиастроении и вообще в технике широко применяются тонкостенные стержни с замкнутыми (рис. 19.12, а) и открытыми профилями (рис. 19.12, б) поперечных сечений. Поэтому расчеты на кручение таких тонкостенных стержней имеет большое практическое значение.

Рис. 19.12

Характерной геометрической особенностью тонкостенных стержней является то, что их толщина существенно (на порядок и более) меньше других геометрических размеров (длиной срединной линии контура поперечного сечения и длины стержня).

Характер распределения напряжений по толщине тонкостенного стержня открытого профиля близок к равномерному (рис. 19.12, б), а замкнутого профиля меняется по линейному закону, как это показано на рис. 19.12, а. Откуда следует, что напряжения в поперечных сечениях открытого профиля практически не изменятся, если профиль сечения распрямить. Иначе говоря, напряжения в криволинейном открытом профиле будут примерно такими же, как и в прямом.

Касательные напряжения и угол закручивания в таком стержне будут:

где δ - толщина профиля; s - длина контура профиля; l - длина стержня.

Рис. 19.13

В случае, если тонкостенный незамкнутый профиль является составным (рис. 19.13) и не может быть развернут в вытянутый прямоугольник, воспользовавшись почленной аналогией, легко определить выражения напряжений на i-ом произвольном участке:

где M_к(i) - доля крутящего момента, соответствующего i-му участку:

где j - угловое перемещение, единое для всех участков:

Изложенный подход к определению напряжений является приближенным, так как он не позволяет определить напряжения в зонах сопряжения элементов поперечного сечения профиля, которые являются зонами концентрации напряжений.

Кручение тонкостенных стержней замкнутого профиля

Наиболее целесообразными при кручении являются тонкостенные стержни замкнутого профиля. Геометрическое место точек, равноотстоящих от внешнего и внутреннего контуров поперечного сечения, называется средней линией сечения (рис.19.14).

Рис.19.14

Наибольшее касательное напряжение в поперечном сечении стержня определяется по формуле

где А_ср – площадь сплошного сечения, ограниченного средней линией сечения; t_min – минимальная толщина стенки в сечении; Т – внутренний крутящий момент в сечении.

Формула

позволяет вычислить угол закручивания стержня длиной l. Интегрирование производится по длине s контура сечения.

Если тонкостенный стержень имеет постоянную толщину стенки t, тогда формула

принимает вид

где S – длина контура сечения, отсчитываемая вдоль средней линии сечения.

Пример 1.

Определить наибольшее касательное напряжение и угол закручивания стержня с трубчатым прямоугольным поперечным сечением, если внешний крутящий момент М = 2 кНм, длина стержня l = 1 м (рис.19.15, а), а модуль сдвига материала стержня G = 8∙10⁴ МПа.

Рис.19.15

Решение.

По рис. 19.15, б находим А_ср = 4∙6 = 24 см², t_min = 1 см. Формула дает

Угол закручивания φ в сечении, где приложен внешний крутящий момент М, определяем по формуле :

Пример 2.

Определить наибольшее касательное напряжение и угол закручивания φ трубчатого сечения (рис. 19.16), если внешний крутящий момент М = 2 кНм действует на участке длиной l = 1 м, а модуль сдвига материала трубчатого стержня G = 8∙10⁴ МПа.

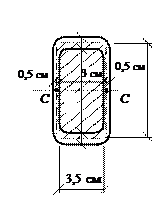
Рис.19.16

Решение.

По рис. 19.14 находим t_min = 0,5 см, А_ср = 6∙3,5 = 21 см², тогда формула дает

Максимальное касательное напряжение будет в середине длинной стороны (точка С) поперечного сечения, имеющей минимальную толщину t_min = 0,5 см.

По формуле определяем угол закручивания сечения на длине стержня в 1 м:

Пример 3.

Определить наибольшее касательное напряжение и угол закручивания участка стержня кольцевого трубчатого сечения, показанного на рис.19.17, если внутренний крутящий момент Т = 0,2 кНм действует на участке стержня длиной l = 1 м, модуль сдвига материала стержня G = 8∙10⁴ МПа, а d = 2 см, D =3 см.

Рис.19.17

Задачу решить двумя способами:

1) поперечное сечение рассматривать как тонкостенный замкнутый профиль и определить максимальное касательное напряжение и угол закручивания в пределах участка длиной 1 м;

2) поперечное сечение рассматривать как кольцевое поперечное сечение и определить угол закручивания и касательное напряжение в точке С сечения, используя формулы и .

Ответ: φ₁ = 0,041 рад; = 40,76 МПа;

φ₂ = 0,039 рад; = 39,2 МПа

Пример 4.

Пусть задан тонкостенный стержень (рис. 19.18, а) при действии самоуравновешивающих крутящих моментов на двух противоположных концах.

Требуется:

1. Определить выражения максимальных напряжений и углов закручивания в случаях, когда стержень имеет открытый (рис. 19.18, б) и замкнутый (рис. 19.18, в) профиль;

2. Сопоставить вычисленные значения напряжений и углов закручивания для двух различных профилей тонкостенного стержня.

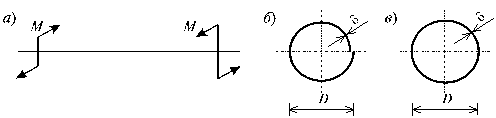
Рис. 19.18

Решение.

1. Определение выражения максимальных напряжений и углов закручивания в случаях, когда стержень имеет открытый и замкнутый профиль. Для стержня с открытым профилем (рис.19.18, б), согласно (19.26), получим:

Для стержня замкнутого профиля (рис.19.18, в), имеем:

2. Сопоставить вычисленные значения напряжений и углов закручивания для двух различных профилей тонкостенного стержня. Для наглядности составим отношения выражений напряжений и углов закручивания, т.е.:

Откуда следует, что отношение напряжений имеет величину порядка D/δ, а отношение углов закручивания - порядка (D/δ)². Так как для тонкостенных стержней D>>δ, следовательно, стержень с замкнутым профилем является существенно более прочным и жестким, нежели стержень с открытым профилем при идентичных исходных данных.

Заметим, что этот вывод является общим для тонкостенных стержней независимо от формы сечений.

Вопросы для самопроверки

1. Дайте определение тонкостенного стержня как геометрической фигуры.

2. Что называется депланацией сечения?

3. Дайте пояснение, что такое свободное и стесненное кручение соответственно.

4. Дайте определение серединной линии поперечного сечения тонкостенного стержня.

5. Дайте определение понятия секторальной площади.

6. Какая точка называется секторальным полюсом.

7. Сформулируйте понятие секториально статический момент сечения, секториально линейный момент площади поперечного сечения и секториальный момент инерции поперечного сечения тонкостенного стержня.

8. Дайте пояснение понятия главной секториальной площади.

9. Дайте пояснение понятия бимомента.

10. Сформулируйте выражения перемещения, нормальные и касательные напряжения, возникающие при общем характере нагружения тонкостенного стержня.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00