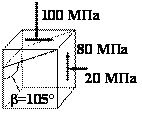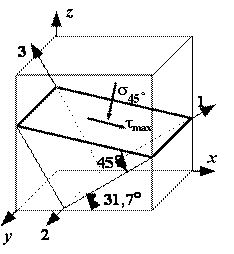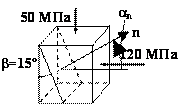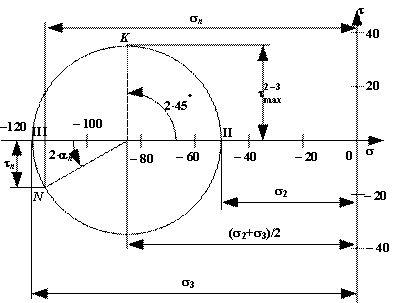Главная
Лекция 3 (продолжение). Примеры решения по теории напряженного состояния
Пример 1.
Стальной кубик (рис.1)
находится под действием сил, создающих плоское напряженное состояние (одно из
трех главных напряжений равно нулю). Требуется найти:
1) главные напряжения и
направление главных площадок;
2) максимальные
касательные напряжения, равные наибольшей полуразности главных напряжений;
3) главные деформации 
, 
, 
;
4) эквивалентное
напряжение 
по четвертой
(энергетической) теории прочности;
5) относительное изменение объема;
6)
удельную потенциальную энергию деформации.
Исходные
данные: 
= 90 МПа, 
= 80 MПa, 
= 50 МПа.
Рис.1
Решение.
При выполнении этой задачи необходимо руководствоваться следующим правилом знаков для нормальных и касательных напряжений: растягивающее нормальное напряжение положительно, а сжимающее - отрицательно. Касательное напряжение по боковой грани призмы положительно, если изображающий его вектор стремится вращать призму по часовой стрелке относительно любой точки, лежащей на внутренней нормали этой грани.
Расставим
знаки в исходных данных в соответствии с направлением напряжений на рис.1.
Получим: 
= 90 МПа, 
= - 80 MПa,
= - 50 МПа, 
= 50 МПа.
1. Найдем главные напряжения
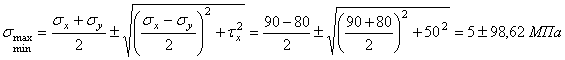(1)
Главные
напряжения обозначают 
, 
и 
; при этом индексы расставляют так, чтобы выполнялось
неравенство
.
(2)
В задаче рассматривается плоское напряженное состояние, т.е. одно из трех главных напряжений равно нулю, поэтому из формулы (1) и правила (2) следует:
МПа,
, 
МПа.
Направление главных площадок относительно площадок, показанных на рис.1, определяется по следующей формуле:
.
, 
.
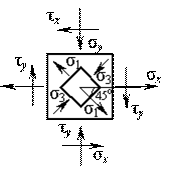
Рис.2
Отрицательный угол
откладывается по
часовой стрелке от площадки с большим нормальным напряжением (в данном случае ) (рис.2). Можно также пользоваться правилом: для определения
положения главной площадки с напряжением 
необходимо площадку с большим (в алгебраическом смысле) нормальным напряжением повернуть на
угол в направлении, в
котором вектор касательного напряжения, действующего по этой же площадке,
стремится вращать элементарный параллелепипед относительно его центра.
2. Найдем максимальные касательные напряжения
МПа.
3. Найдем
главные деформации 
, 
и 
из обобщенного закона
Гука;
4. Найдем эквивалентное напряжение
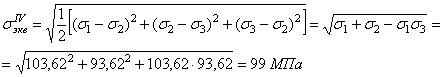
5. Найдем относительное изменение объема
.
6. Найдем удельную потенциальную энергию деформации
.
В данной задаче .
Пример 2.
Подобрать диаметр стержня круглого сечения (см. рис.) из условия, что наибольшее касательное напряжение в нем не должно превышать 100 МПа. Найти также величину нормального напряжения в точке К сечения mn, если F = 8 кН.
Решение.
1. Строим эпюру продольной силы и устанавливаем:
Nmax = NAB
= 2F, NBC
= F.
2. Определяем
диаметр стержня. Из условия прочности по касательным напряжениям 
или
,
откуда 
.
3. Определяем нормальное напряжение в точке К сечения mn (уч. ВС)
МПа.
Пример 3.
Тензометр, имеющий коэффициент увеличения k = 1000 и базу s = 20 мм, установлен на стальном образце сечением 20х7 мм под углом 45° к его оси (см. рис.). Определить показание тензометра при нагружении образца силой F = 40 кН. Принять Е = 200 ГПа, n = 0,3.
Решение.
Деформация в направлении базы тензометра равна
.
(а)
С другой стороны,
.
(б)
Приравнивая (а) и (б), находим
.
Пример 4.
Найти
аналитически и графически величины и направления главных напряжений,
действующих в плоском элементе (см. рис.), на гранях которого заданы
напряжения: = 20 МПа, = -60 МПа, 
= -80 МПа.
Решение.
1. Аналитический метод. Величины главных напряжений
,
,
следовательно,
МПа; 
; 
МПа.
Направление главной оси 1 
; 
.
2. Графический метод. Для графического
решения задачи необходимо по заданным напряжениям построить круговую диаграмму
Мора. Отложив по оси абсцисс отрезки, изображающие в выбранном масштабе
нормальные напряжения, ОА = , ОВ = и разделив отрезок АВ пополам, найдем центр круга С, абсцисса
которого 
. Далее отложим из точки А
отрезок Ах = , а из точки В в противоположном направлении отрезок Вy = 
. Замечая, что 
, найдем радиус круга 
. Окружность, описанная этим радиусом, отсекает на оси
абсцисс отрезки 
и 
. Нетрудно установить, что 
, а 
, как вписанный. Следовательно, линия 3х графически определяет направление оси (оси 1), а линия 3y – оси 
(оси 3).
Пример 5.
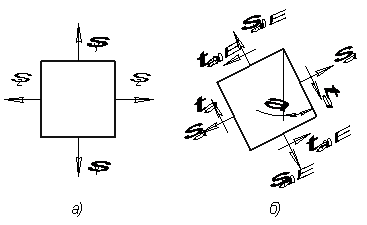
На плоское
напряженное состояние чистого сдвига с напряжением 
= 10 МПа накладывается
двухосное сжатие с напряжениями, равными 10 МПа. Каково будет результирующее
напряженное состояние?
Решение.
Задачу решаем
графически. По двум точкам х и y строим
круговую диаграмму (рис. б), из которой находим главные напряжения 
, 
МПа, т.е.
результирующее напряженное состояние является одноосным сжатием (рис. в).
Пример 6.
В пластине,
изготовленной из хрупкого материала, от некоторой нагрузки возникают
пропорциональные ей напряжения (рис. а).
Условно принимая, что прочность материала зависит только от наибольшего
растягивающего напряжения, определить, во сколько раз должна возрасти нагрузка,
чтобы в пластине появилась трещина, если предел прочности материала на
растяжение равен 
МПа. Под каким углом к оси х будет наклонена трещина?
Решение.
Вычисляем наибольшее главное напряжение
МПа.
Ориентация оси
1 
, откуда 
. Трещина, будучи перпендикулярной к
наибольшему растягивающему напряжению , направлена под углом 
к оси х.
Находим запас
прочности 
.
Пример 7.
Вычислить
величины главных напряжений, действующих по граням элемента, если известно, что
после приложения этих напряжений приращения показаний тензометров А и В составили соответственно: 
= 9,9 мм, 
= 3,1 мм. Тензометр А установлен под
углом 
= 30° к
направлению напряжения , а тензометр В
перпендикулярно к тензометру А. Базы
тензометров одинаковы и равны s = 20 мм, коэффициент увеличения k = 1000. Модуль упругости
материала пластины Е = 80 ГПа,
коэффициент Пуассона n = 0,35.
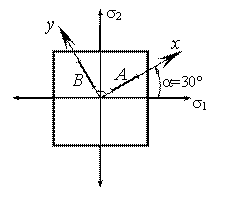
Решение.
Относительные удлинения в направлении тензометров А и В равны
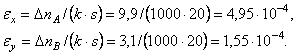
Пользуясь законом Гука в обратной форме, находим напряжения
Для вычисления главных напряжений имеем следующую систему:
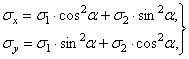
решая которую, найдем 
= 60 МПа, 
= 20 МПа.
Пример 8.
Между
параллельными неподвижными абсолютно жесткими плитами плотно вставлен стальной
параллелепипед со сторонами а = 4 см, b = 2 см, l = 6 см. Вычислить
коэффициент Пуассона материала бруса, если известно, что при сжатии силами F = 100 кН давление последнего на
плиты составляет 
= 37,5 МПа. Определить
также укорочение бруса 
, пренебрегая силами трения, если модуль упругости Е = 200 ГПа.
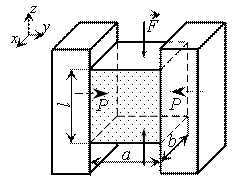
Решение.
Напряжения,
действующие на гранях параллелепипеда,
равны 
; 
МПа; 
МПа.
Так как плиты являются абсолютно жесткими, то ребро, перпендикулярное к ним, не деформируется, т.е.
,
откуда 
= 37,5/125 = 0,3.
По закону Гука находим укорочение бруса:
мкм.
Пример 9.
По двум
граням стального параллелепипеда должны действовать две заданные силы Fx = 400 и Fy = -600 кН.
Спрашивается, какую силу необходимо приложить к грани, перпендикулярной оси z, чтобы объем бруса
остался неизменным, если дано a = b
= 5 см, с = 10 см.
Решение.
Так как объем не меняется, то
,
откуда 
.
Но 
, 
, 
.
Cледовательно, 
.
Отсюда 
кН.
Таким образом, к грани, перпендикулярной оси z, необходимо приложить растягивающую силу Fz = 100 кН.
Пример 10.
Резиновый брус
квадратного сечения 4х4 см, жестко закрепленный обоими концами на участке
длиной а, подвергается действию
равномерно распределенного давления = 4 МПа (см. рис.).
Определить перемещение сечения mn,
если Е = 8 МПа, n =
0,5; а
= 8 см.
Решение.
1. Раскрытие статической неопределимости. Данная
система является однажды статически неопределимой, поэтому в дополнение к
уравнению статики
, RA - RB = 0, RA
= RB = R;
необходимо составить уравнение
совместности деформаций 
. При вычислении следует учесть, что на
нагруженном участке бруса напряженное состояние является объемным, а на
остальной части – линейным.
Поэтому 
.
Но 
; 
; 
.
Следовательно,
, откуда 
.
2. Определение искомого перемещения. Перемещение сечения mn определяется как укорочение участка бруса, заключенного между сечением mn и заделкой В,
см
и направлено вправо. Эпюра
продольных перемещений для всего бруса приведена на
рис. б.
Пример 11.
Проверить прочность конструкции, если в опасной точке
имеет место указанное на рисунке напряженное
состояние.
Дано: 
= 150 МПа, 
= 600 МПа, [П] = 5.
Решение.
1. Определение главных напряжений. Напряженное состояние в точке
является плоским, поэтому
,
откуда = 10 МПа, = -60 МПа. Следовательно, величины главных напряжений
равны = 10 МПа, = 0, = -60 МПа.
2. Проверка прочности конструкции. Здесь возможны два
подхода
или 
.
Эквивалентное напряжение вычисляем по гипотезе О.Мора, так как материал
хрупкий и неодинаково работает на растяжение и сжатие:
МПа.
Допускаемое напряжение [
] = /[П] = 150/5 = 30 МПа.
Следуя первому подходу, сравниваем 
и []. Так как = 25 МПа < [] = 30 МПа, то прочность конструкции обеспечена.
Согласно второму подходу находим фактический коэффициент
запаса прочности 
.
Как видим, П = 6 > [П] = 5,
т.е. прочность конструкции обеспечена.
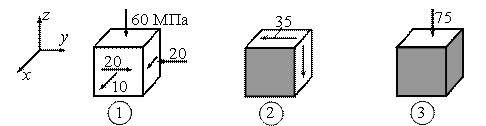
Пример 12.
Какое из трех приведенных напряженных состояний является
более опасным (см. рис.)? Дано: 
.
Решение.
Для сравнения напряженных состояний находим эквивалентные напряжения. Материал является пластичным и одинаково работает на растяжение и сжатие, поэтому воспользуемся 3-й гипотезой прочности.
Точка 1. Напряженное состояние является объемным, причем одно из главных напряжений уже известно. Для определения двух других главных напряжений воспользуемся формулами для плоского напряженного состояния. Имеем
= 20 МПа, = -30 МПа.
Следовательно, = 20 МПа, = -30 МПа, = -60 МПа.
Эквивалентное напряжение
.
Точка
2. Напряженное состояние является чистым сдвигом, поэтому 
МПа, , 
МПа.
Эквивалентное напряжение
.
Точка
3. Напряженное состояние является линейным (одноосное сжатие), поэтому 
, = -75 МПа.
Эквивалентное напряжение
.
Так как 
, то наиболее опасным является напряженное состояние в точке
1.
Пример 13.
На стальной стержень действуют две осевые силы F и = 20° к
поперечному, а также и 
, если
поперечное сечение — круглое, диаметром d =
Решение.
Разобьем
стержень на два участка и найдем внутренние силы N1=F=200 кН, a N2=-F=-200 кН. Нормальные напряжения в поперечных сечениях 
МПа, а 
МПа (рис. б).
Напряженное состояние линейное, для первого элемента – растяжение, для второго
– сжатие. Напряжения в I наклонном сечении:
нормальное 
МПа;
касательное 
МПа.
Во II наклонном сечении 
МПа, 
МПа (см. рис. в). Максимальные (в алгебраическом
смысле) напряжения в I сечении 
МПа, во II сечении 
. Максимальные касательные напряжения: 
МПа (= -45°); 
МПа (= 45°).
Пример 14.
Элемент,
вырезанный (мысленно) из детали, испытывает по граням напряжения 
= 120 МПа и =60 МПа (см. рис. а). Определить нормальные и касательные
напряжения по граням элемента, вырезанного в повернутом на угол =20° положении.
Решение.
Напряженное состояние — плоское, так как 
. Используем зависимости для 
и 
учитываем, что в
исходных площадках 
.
Поэтому 
МПа;
МПа.
Для
определения применяем свойство суммы нормальных напряжений 
. Отсюда
= 120 + 60 + 112,9 = 67,1
МПа, касательные напряжения в соответствии с законом парности 
МПа (см. рис. б).
Пример 15.
Для
элементарного объема (см. рис. а), находящегося под действием сил, создающих
плоское напряженное состояние, требуется вычислить:
1) главные напряжения и положение главных
площадок;
2) максимальные касательные напряжения, если =40 МПа=400 кг/см2, =20 МПа=200 кг/см2, = 10 МПа=100 кг/см2.
Решение.
1. Вычисляем
главные напряжения по формуле:
= 441 кг/см2 = 44,1 Мпа; 
= 159 кг/см2 = 1,59 МПа.
Учитывая, что
между главными напряжениями существует зависимость 
, получим 
44,1 МПа; 
1,59 МПа; 
= 0.
Положение главных площадок определяем по формуле:
;
= –22,5º.
Знак перед 
принимают согласно
правилу (рис. б).
Учитывая, что
положительный угол отсчитывается от оси против часовой стрелки, а отрицательный
– по часовой стрелке, откладываем от направления напряжения углы =–22,5º и 
и,
проведя оси, строим на этих осях главные площадки и показываем главные напряжения
(рис. а).
При этом 
направлено в тот
квадрант, где касательные напряжения и сходятся к ребру.
2. Вычислим
максимальные касательные напряжения по формуле:
Пример 16.
Стальной кубик (см. рис.) находится под действием сил, создающих плоское напряженное состояние.
Требуется найти:
1)
относительные деформации 
, 
и 
;
2)
относительное изменение объема;
3) удельную
потенциальную энергию деформации, если 
=50 МПа=500 кг/см2, 
= 40 МПа = 400 кг/см2, 
= 20 МПа = 200 кг/см2.
Модуль продольной
упругости 
кг/см2, модуль сдвига 
кг/см2.
Решение.
1. Рассчитаем
относительные деформации , и . Примем
для стали коэффициент
Пуассона 
= 0,3. Учтем, что, согласно рисунку, = +500 кг/см2, = -400
кг/см2, 
=0, = –200 кг/см2, =+200 кг/см2, кг/см2, кг/см2.
Тогда получим, используя формулу обобщенного закона Гука:
;
;
.
2. Вычислим
относительное изменение объема по формуле
или
.
3. Вычислим
удельную потенциальную энергию деформации для двухосного напряженного состояния
(=0) по формуле:
Пример 17.
Для напряженного состояния изображенного на рисунке определить:
1) главные напряжения и положение главных площадок;
2) максимальные касательные напряжения;
3)
относительные деформации , , ;
4) относительное изменение объёма;
5) полную
удельную потенциальную энергию деформации, если дано = 20 МПа,
= 40 МПа, = 30 МПа.
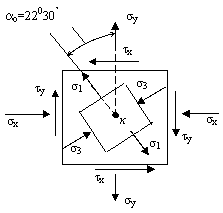
Решение.
В соответствии
с рисунком имеем:
= -20 МПа, = 40 МПа, = - 30 МПа, = 30 МПа.
1. Находим
главные напряжения:
Направление
главных площадок:
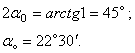
Этот угол
откладываем от вертикали (алгебраически большее из главных напряжений) против
часовой стрелки и получаем направление , направление перпендикулярно ему
(см. рис.).
2. Находим
максимальные касательные напряжения, которые будут действовать на площадках, наклонённых
под углом 45º к главным площадкам:
3. Находим
относительные деформации:
4. Находим
относительное изменение объёма:
5. Находим полную
удельную потенциальную энергию деформаций:
Пример 18.
Дано 
кН/см2, 
кН/см2, 
кН/см2 (рис. а).
Найти главные напряжения 
, направления главных
площадок и максимальное касательное напряжение 
.
Решение.
Напомним правила знаков для нормальных и
касательных напряжений.
Нормальное
напряжение, соответствующее растяжению, считается положительным, а сжатию –
отрицательным.
Касательное
напряжение считается положительным, если одновременно выполняются (или одновременно не выполняются)
следующие два условия:
- направление
напряжения совпадает с положительным направлением соответствующей координатной
оси;
- внешняя
нормаль к площадке, на которой оно возникает, направлена в ту же сторону, что и
другая, соответствующая, координатная ось.
1. Определяем
главные напряжения, возникающие на
трех главных площадках, проходящих
через рассматриваемую точку твердого тела.
Для плоского
напряженного состояния одно из главных напряжений, возникающее на площадке с
нормалью x, равно нулю.
Вычисляем значения двух других главных напряжений:
кН/см2;
кН/см2.
Учитывая, что
, окончательно имеем:
кН/см2, , 
кН/см2.
2. Делаем
проверку (
):
или 
,
то есть верно.
3. Находим
положение главных площадок.
Углы 
и 
, определяющие положение двух взаимно перпендикулярных
площадок, на которых возникают главные
напряжения и 
, определяются из формулы
.
Отсюда: 
и 
.
Напомним, что
угол считается положительным, если он
отсчитывается от оси z против хода часовой стрелки.
Найденные
углы (см. рис. б) определяют и
направления «действия» главных напряжений и .
4. Определяем наибольшее касательное напряжение, возникающее в рассматриваемой точке тела:
кН/см2.
Оно
«действует» на площадке, которая наклонена под углом 450 к первой и
третьей главным площадкам.
Пример 19.
Для
напряженного состояния, изображенного на рис. а, определить аналитически и при помощи круга Мора напряжения 
и 
возникающие на
площадке, расположенной под углом 
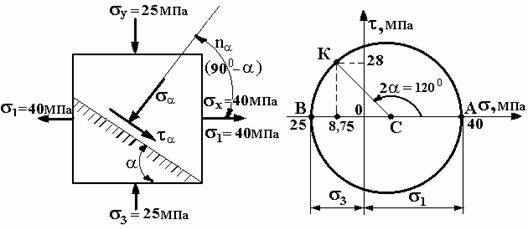
а)
б)
Решение.
В заданном
напряженном состоянии, учитывая, что , получим: 
Нормальные напряжения вычисляем
по формуле:
, где 
- угол между
большим главным напряжением и нормалью к
площадке .
Этот угол положительный, т.к. отсчитывается против часовой стрелки. Тогда получим:
.
Касательные напряжения заданной площадке:
Показываем на
схеме (рис. а) 
и 
с учетом их знаков.
Причем для определения направления касательного напряжения воспользуемся схемой,
представленной на рис. в.
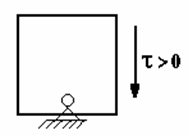
в)
Решим эту
задачу при помощи круга Мора (рис. б).
На оси 
откладываем величины
главных напряжений, 
и (точки А и В). На отрезке АВ, как на диаметре, строим круг Мора.
Из центра круга
Мора (точка С) проводим радиус СК под
углом 
к направлению оси . Координаты точки К пересечения радиуса с кругом
Мора и есть напряжения на площадке: 
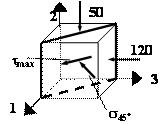
Пример 20.
Стальной кубик
находится под действием сил, создающих плоское напряженное состояние (рис. а). Определить величины и направление
главных нормальных напряжений и экстремальные
касательные напряжения аналитически и при
помощи круга Мора, если 
, 
а) б)
Решение.
Определяем
главные напряжения по формуле:
Определяем
положение главных площадок:
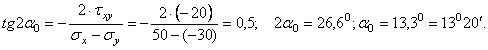
Поворачиваем
кубик против часовой стрелки на угол 
отсчитывая его от большего напряжения . На главной площадке под углом 
действует напряжение 
а на
ортогональной . Вектор на площадке с большим
нормальным напряжением = 50 МПа показывает направление поворота кубика. Определяем
величину максимального касательного напряжения по формуле:
.
Строим круг
Мора (рис. б). В координатных осях 
в выбранном масштабе
наносим точки А и
В. Координаты точки А соответствуют напряжениям, действующим на вертикальной
грани кубика, а координаты точки В-напряжениям
на его горизонтальной грани. На отрезке
АВ, являющемся диаметром круга Мора
строим круг. Находим полюс круга Мора Р (проводя для этого горизонталь
через точку А, либо вертикаль через точку В). На окружности
отмечаем точки 1 (соответствующую
площадке с напряжением 
), 2 (площадке с напряжением ), 3 (площадке с напряжением ) и 4 (площадке с напряжением 
). Лучи, соединяющие эти точки с полюсом Р,
перпендикулярны площадкам, по которым
действуют соответствующие напряжения. Измерением (в принятом масштабе) абсцисс
точек 1 и 2 и ординат точек 3 и 4 определяем, соответственно, величины:
На рис. б показан угол между главной площадкой,
по которой действует напряжение 
, и площадкой по которой действует напряжение 
.
Измерением
устанавливаем 
Пример 21.
В опасной точке упруго деформированной конструкции выделен бесконечно малый элемент, по граням которого действуют нормальные и касательные напряжения (см. рис.1).
а) материал –
сталь 
= 160 МПа, 
= 0,28, 
МПа.
б) материал –
чугун; 
МПа, 
МПа.
Рис.1
Вычислить:
1. величины главных напряжений и их направление аналитически и при помощи диаграммы Мора;
2. максимальные касательные напряжения и положение площадок, по которым они действуют;
3. определить деформацию по трем главным направлениям и объемную деформацию элемента;
4. проверить прочность конструкции по II, III и IV теориям и оценить результаты; вычислить эквивалентные напряжения;
5. показать площадки разрушения (по желанию);
Решение.
1. Вычисление величин главных напряжений и их
направление аналитически и с помощью кругов Мора.
а) вычисление аналитическим способом
Для нахождения главных напряжений применяем формулы для плоского напряженного состояния:
Так как вдоль оси y нормальные
напряжения не действуют, то = 0.
Тогда подставляя в выражение значения, получаем:
МПа;
Тогда в силу
того, что 
получаем: 
МПа, МПа, 
МПа.
Теперь определяем расположение главных площадок:
Углы 
и 
отсчитываются от наибольшего нормального напряжения, в данном случае от (
, т.к. 
и 
): угол указывает на
наибольшее главное напряжение и откладывается по
часовой стрелке (т.к. < 0), угол указывает на главное напряжение
на смежной площадке и откладывается против
часовой стрелки (т.к. > 0). Показываем расположение главных площадок в
элементе (рис.2).
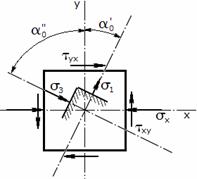
Рис.2
б) вычисление с помощью кругов Мора
В осях и отмечаем две точки 
и 
, в нашем случае Dx(-60;-40)
и Dy(0;40)
(рис. 3).
Проводим
прямую DxDy,
и из точки пересечения прямой с осью (т. C) радиусом DxC проводим окружность. Точки пересечения окружности с осью
(т. A и B) дают значения главных напряжений
(т. A 
, т. B 
).
Из точки наибольшего нормального напряжения (т. Dy) проводим
прямую, параллельную оси – получаем полюс
(т. M), соединяя
полюс M с т. A и т. B, получаем направление главных
напряжений (луч MA
указывает направление , MB
– , относительно оси y), углы между лучами и
осью дают углы и .
Рис.3
2. Определение максимальных касательных напряжений и положения площадок, по которым они действуют
Максимальные касательные напряжения действуют по площадкам, наклоненным под углом 45° к главным площадкам (рис. 4), и по величине равны:
МПа.
С помощью кругов Мора максимальное касательное напряжение определяется точкой пересечения окружности и перпендикуляра, проведенного из ее центра (рис.3).
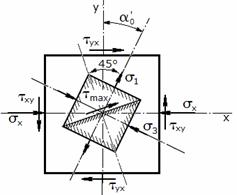
Рис.4
3. Определение деформаций по трем главным
направлениям и объемной деформации
Деформации по главным направлениям по закону Гука равны:
Подставляя значения главных напряжений, получаем:
Объемная деформация примерно равна сумме линейных деформаций по главным направлениям (с точностью величин второго порядка этих деформаций):
4. Проверка прочности конструкции по II, III, V и оценка результатов
а) по II теории (для хрупких материалов)
II теория прочности – теория наибольших линейных деформаций, разрушение элемента, находящегося в сложном напряженном состоянии, наступит тогда, когда наибольшая линейная деформация достигнет величины, при которой в случае простого растяжения-сжатия наступает разрушение:
в нашем случае:
Эквивалентное напряжение меньше допускаемого.
б) по III теории (для пластичных материалов)
III теория прочности – теория наибольших касательных напряжений, текучесть материала наступит тогда, когда наибольшие касательные напряжения превысят допустимые.
в нашем случае:
МПа.
Эквивалентное напряжение меньше допускаемого.
в) по V теории (для хрупких и пластичных материалов)
V теория прочности – теория Мора основана на том, что прочность материала в общем случае напряженного состояния зависит главным образом от величины и знака наибольшего и наименьшего напряжений:
Коэффициент k – отношение допускаемых напряжений при растяжении и при сжатии:
– для стали: 
и k = 1;
– для
чугуна: 
= 28..80 МПа и 
= 120..150 МПа, берем = 28 МПа
и = 120 МПа, тогда k = 0,233;
Определяем эквивалентные напряжения:
– для стали:
;
– для чугуна:
Эквивалентные напряжения в обоих случаях меньше допускаемого.
5. Площадки разрушения
По III теории прочности для пластичных материалов разрушение нагруженного элемента происходит под действием максимального касательного напряжения и в его плоскости действия. Расположение площадки разрушения по III теории представлено на рис. 5.
Рис.5
Пример 22. Исследование
плоского напряженного состояния по заданным напряжениям на произвольных
площадках. Проверка прочности
Элемент, выделенный из тела, находится в плоском напряженном состоянии (рис.1). По граням элемента заданы нормальные и касательные напряжения, значения которых приведены на рисунке.
Рис.1
Материал
элемента – сталь с такими характеристиками: предел текучести 
МПа; модуль Юнга 
МПа; коэффициент Пуассона 
; модуль сдвига 
МПа; нормируемый коэффициент запаса прочности 
.
Требуется:
1) найти
нормальное, касательное и полное напряжения на наклонной площадке, заданной
углом 
105° (см.
рис. 1);
2) определить величины главных напряжений и положение главных площадок;
3) найти наибольшее касательное напряжение и положение площадки, по которой оно действует;
4) оценить прочность материала в точке и показать вероятное направление плоскости сдвига или отрыва (опасной площадки);
5) найти
величины относительных продольных деформаций в исходной системе координат 
и по главным
направлениям; вычислить относительную объемную
деформацию.
Примечание. Пп. 1–3 следует выполнить двумя способами: аналитическим и графическим.
Решение.
Изобразим
элемент в виде плоского рисунка, на котором должна быть указана система
координат (см. рис. 2). Введенная система координат позволяет присвоить
напряжениям обозначения: 
МПа, 
МПа, 
МПа.
На рисунке следует показать также наклонную площадку, указать штриховкой ее внутреннюю сторону, задать внешнюю нормаль к площадке.
Рис.2
Аналитический способ исследования
напряженного состояния
Определение напряжений на наклонной площадке. Напряжения, действующие на наклонной площадке (см. рис. 2), находим по формулам
(1)
и 
.
(2)
В этих
формулах положение площадки задает угол 
между нормалью n к площадке и осью 
. Этот угол нельзя путать с углом 
, указанным на рис. 1.
Можно
отсчитывать угол не от оси , а от оси z, но тогда в формулах
(1) и (2) напряжения , 
надо поменять местами
и напряжение 
заменить напряжением 
. Надо выбирать более удобный способ.
Используем
угол между n и осью , отсчитывая его от оси к нормали n: 
(см. рис. 2).
Значение угла положительное, так как угол отсчитывается против часовой стрелки.
Согласно формулам (1) и (2)
,
Получившееся
нормальное напряжение 
отрицательно, значит,
оно направлено к площадке (сжимающее). Касательное напряжение 
положительно, это
значит, что оно обходит площадку по часовой стрелке.
Используем
теперь угол между нормалью n и осью 
, отсчитывая его от z к n: 
.
Формулы (1) и (2) записываем в измененном виде:
Абсолютная величина полного напряжения (или просто полное напряжение)
Вычисленные напряжения показаны на рис. 3.
Рис.3
Определение
главных напряжений и главных направлений. Согласно 
главные напряжения
.
После вычисления главные напряжения следует пронумеровать согласно убыванию. Чтобы не путать напряжения до и после нумерации, специально используются для этих напряжений разные обозначения. Главные напряжения, пронумерованные согласно их величине,
, 
, 
.
Найдем
положение главных площадок. Сказанное о способах вычисления напряжений по
наклонной площадке относится и к способам вычисления положения главных
площадок. Здесь мы вычислим углы 
, 
, определяющие положения главных площадок, одним способом:
будем отсчитывать эти углы от направления оси . Углы являются решениями уравнения 
:
,
то есть
Получены два
значения угла, которые отвечают площадкам с напряжениями , (рис. 4).
Выясним, какому из этих напряжений соответствует угол . Для этого определим по формуле 
знак второй
производной 
при
:
.
Рис.4
Знак
отрицательный, следовательно, по этой площадке действует бoльшее из найденных главных напряжений – напряжение . Теперь можно в соответствии с нумерацией главных напряжений
пронумеровать и углы: 
, 
.
Определение
максимального касательного напряжения. Касательное напряжение,
максимальное среди касательных напряжений на площадках, перпендикулярных
плоскости 
(рис. 5),
определяется формулой :
МПа.
Рис.5
В
рассматриваемом примере главные напряжения 
, 
, поэтому касательное напряжение 
является максимальным
среди касательных напряжений для всей совокупности площадок, проходящих через
заданную точку: 
.
Нормальные напряжения на той же площадке даются формулой:
МПа.
Графический способ исследования напряженного
состояния
Круг напряжений Мора является средством вычисления. При выполнении задачи его необходимо построить в крупном масштабе на миллиметровке, используя заточенный карандаш. Чем точнее выполнены построения, тем точнее будет получен результат.
Строим круг
напряжений Мора (рис. 6). Изображаем систему координат 
с одинаковым масштабом
по вертикальной и горизонтальной осям. Отмечаем на координатной
плоскости две точки X, 
,
соответствующие заданным площадкам с нормалями 
.
Координатами точек 
, 
являются нормальные и
касательные напряжения на заданных площадках. Соединяем точки отрезком, который
представляет собой диаметр круга Мора. Точка О пересечения диаметра с осью – центр круга. Проводим окружность.
Рис.6
Точкам I, III пересечения круга с горизонтальной
осью соответствуют главные площадки 1, 3. Горизонтальные координаты этих точек
(измеренные в масштабе) являются главными напряжениями: 
МПа, 
МПа.
Углы 
, 
, определяют положения главных площадок. Отмеченные на
рисунке углы дают удвоенные значения , . По рисунку сразу видно, какому главному напряжению
соответствует каждое значение угла. Графически найденные значения: 
, 
. Графический способ дает возможность проверить аналитическое
решение, поэтому в расчетной работе следует рядом с кругом напряжений на
отдельном рисунке показать положения главных площадок и напряжения на них.
Площадке, по
которой действует максимальное касательное напряжение, соответствует точка 
круга. Координаты
точки дают значения 
МПа, 
МПа.
Найдем с
помощью круга напряжений напряжения на наклонной площадке. Построим на круге
точку 
, соответствующую наклонной площадке. Для этого отложим от
радиуса OX (соответствующего
оси x) против часовой стрелки угол 
, либо от радиуса ОZ (соответствующего оси z) в том же направлении угол . Координаты точки дают напряжения на
наклонной площадке: 
, 
.
Полное
представление о напряженном состоянии дают три круга напряжений. Точки каждого
круга соответствуют площадкам, которые перпендикулярны одной из главных
площадок. Круги строятся по главным напряжениям. Обычно изображение
напряженного состояния в виде трех кругов Мора используется в качестве
иллюстрации, а не в качестве способа вычисления, поэтому данный рисунок можно
выполнить в меньшем масштабе и не обязательно на миллиметровке. Все три круга
напряжений для рассматриваемого напряженного состояния показаны на рис. 7.
Построенный на рис. 6 круг напряжений соответствует площадкам,
перпендикулярным плоскости чертежа (перпендикулярным второй главной площадке). Из рис. 7 видно, что максимальное касательное напряжение определяется по бoльшему кругу.
Рис.7
Проверка
прочности. Главные напряжения , , уже известны
(вычислены выше).
Начать решение вопроса нужно с выбора соответствующей материалу теории прочности. По условию задачи материал – сталь (пластичный материал), поэтому используем третью и четвертую теории прочности.
Согласно третьей теории прочности эквивалентное напряжение
.
Сравнение 
с пределом текучести 
показывает, что
материал работает упруго. Действительно,
.
Но условие прочности не выполнено:
.
Это означает, что не обеспечен нормативный коэффициент запаса прочности. Конструкцию, имеющую точку с такими напряжениями, эксплуатировать запрещается. Действительный (фактический) коэффициент запаса
меньше
нормативного .
Согласно четвертой теории прочности
МПа.
Условие прочности не выполнено и согласно четвертой теории. Однако фактический коэффициент запаса оказывается другим:
.
Положения опасных площадок согласно третьей и четвертой теориям приведены на рис. 8 и рис.9.
Рис.8 Рис.9
По площадке, показанной жирной линией на рис. 8, действует максимальное касательное напряжение. Эта площадка перпендикулярна к площадке 2 и наклонена под углом в 45° к площадкам 1 и 3. Площадка, показанная жирной линией на рис. 9, соответствует четвертой теории прочности. Она равно наклонена ко всем трем главным площадкам.
Специально обратим внимание на способ изображения опасных площадок: эти площадки показаны с привязкой к исходному элементу. Так необходимо сделать и при оформлении задачи.
Положение исходного элемента по отношению к конструкции, из которой вырезан элемент, известно. Примененный способ изображения опасных площадок позволяет указать эти площадки непосредственно на конструкции.
Определение деформаций в точке. Следует начать с выяснения, работает ли материал в упругой области. Вычисленное выше эквивалентное напряжение оказалось меньше предела текучести. Это означает, что уровень напряжений соответствует упругой стадии деформирования и можно использовать обобщенный закон Гука.
Если уровень напряжений соответствует неупругой стадии деформирования, то закон Гука определяет только упругую часть полных деформаций. В задаче при этой ситуации нужно вычислить только упругую составляющую деформации, отметив это примечанием в тексте.
Линейные
деформации в направлении осей 
,
,
.
Угловая деформация
.
Знак минус
означает, что угол уменьшается. Две другие угловые деформации отсутствуют: 
, так как равны нулю соответствующие касательные напряжения.
Линейные деформации вдоль главных направлений 1, 2, 3
Относительная объемная деформация
.
Рис. 10 и
рис.11 разъясняют результаты вычислений. Условно исходные длины ребер элемента
считаются равными единице. При этом линейные относительные деформации в
направлении этих ребер равны абсолютным изменениям длин. В исходном
недеформированном состоянии грани элемента параллельны координатным плоскостям
системы координат . В результате деформации тела элемент перемещается как
жесткое целое и деформируется. На рис. 10 жирной линией изображен деформированный
элемент.
Рис.10
Недеформированный элемент показан штриховой линией. Перемещение элемента как жесткого целого не изображено. Этот элемент получает угловые и линейные деформации.
Деформированный элемент, грани которого в исходном недеформированном состоянии были параллельны главным площадкам, показан на рис. 11. Этот элемент получает только линейные деформации.
Рис.11
Пример 23. Исследование
плоского напряженного состояния по заданным напряжениям на главных площадках.
Проверка прочности
На гранях
элементарного параллелепипеда заданы главные напряжения (рис.1). Материал
элемента – чугун c
характеристиками 
МПа, 
МПа, 
МПа, 
. Нормативный коэффициент запаса прочности 
.
Рис.1
Требуется:
1) найти
нормальное , касательное и полное 
напряжения на
наклонной площадке, заданной углом и изображенной на
рис. 1;
2) найти величины наибольшего касательного напряжения и соответствующего ему нормального напряжения, показать положение площадки, на которой эти напряжения действуют;
3) проверить прочность материала; найти действительный коэффициент запаса прочности.
Решение.
Заданный
элемент ограничен главными площадками, поэтому сразу пронумеруем главные
напряжения по убыванию (
, 
МПа, 
МПа) и изобразим на рисунке главные оси (рис. 2).
Рис.2
Определение напряжений. Напряжения на наклонной площадке вычисляются так же, как в примере 16. Единственное отличие состоит в том, что можно использовать частный случай
(3)
общих формул
(1) и (2). Положение наклонной площадки будем задавать углом , отсчитываемым от оси 3 к нормали n.
Значение 
положительно, так как
угол отсчитывается против часовой стрелки.
Согласно (3)
Модуль полного напряжения
МПа.
Примененная
формула для касательного напряжения справедлива для
площадок, перпендикулярных плоскости чертежа. Максимальное для таких площадок
касательное напряжение
МПа.
Соответствующее нормальное напряжение
МПа.
Подсчитанное
выше значение касательного напряжения 
не самое большое из
всех возможных значений. Это значение является максимумом для касательных
напряжений по площадкам, перпендикулярным плоскости чертежа. Площадка, на
которой действует , расположена под углом 45° к главным
площадкам 2, 3 (рис. 3).
Рис.3
Максимальное касательное напряжение (максимум вычисляется для всех возможных площадок, проведенных через точку) и соответствующее ему нормальное напряжение
МПа,
МПа
всегда
действуют на площадке, перпендикулярной второй главной площадке и повернутой на
угол в 45°
к первой и третьей главным площадкам (рис. 4). Заметим особо, что теперь,
в отличие от результата в примере №16, 
.
Рис.4
Круг
напряжений для заданного плоского напряженного состояния показан на
рис. 5. Координаты точки дают значение
напряжений на площадке с нормалью n. Площадке с соответствует точка круга.
Рис.5
На рис. 6
показаны все три круга напряжений. Видно, что площадке с наибольшим по модулю
касательным напряжением соответствует точка,
лежащая на бoльшем
круге напряжений.
Рис.6
Проверка прочности. По условию задачи материал элемента хрупкий. При проверке прочности используем теории прочности, относящиеся к хрупким материалам.
Расчетное напряжение, соответствующее первой теории прочности
.
Видим, что первая теория прочности не годится для оценки прочности, так как она выдает в рассматриваемой ситуации неправдоподобный результат: при любом уровне напряжений прочность обеспечена.
Расчетное напряжение, соответствующее второй теории прочности,
Прочность обеспечена с фактическим коэффициентом запаса
,
большем
нормативного ().
Расчетное напряжение, соответствующее теории прочности Мора,
Прочность обеспечена. Фактический коэффициент запаса
.
Опасная плоскость показана на рис. 7 жирной линией. Она перпендикулярна первому главному направлению.
Рис.7
Если
напряженное состояние достигнет критического уровня (для этого все напряжения
надо увеличить в 
раз), то по указанной
плоскости произойдет разрушение.
Расчет длинной тонкостенной трубы,
подверженной действию внутреннего давления, продольной силы и крутящего момента
Основные формулы
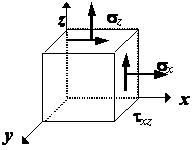
Рассматривается
длинная прямолинейная цилиндрическая тонкостенная труба (рис. 1) с 
, 
. Труба нагружена внутренним
давлением 
, по ее торцам приложены силы 
и крутящие моменты 
.
Рис.1
Напряжения в трубе будем обозначать, используя местную декартову систему координат x, y, z (см. рис. 1): ось x параллельна оси трубы, ось z направлена по касательной к срединной линии поперечного сечения, осью y служит продолжение радиуса R.
Сила вызывает в поперечном
сечении трубы продольное усилие 
и создает нормальное
напряжение (рис. 2)
.
Здесь 
– значение площади
поперечного сечения тонкостенной трубы.
Рис.2
Внутреннее
давление вызывает растяжение трубы в кольцевом направлении (рис. 3), чему
соответствует напряжение в продольных сечениях
трубы:
.
Напряжения положительны при 
. Случай 
отвечает давлению, приложенному
к наружной поверхности.
Крутящий момент создает касательные напряжения в поперечном сечении трубы (рис. 4):
.
Рис.4
Направление
касательного напряжения совпадает с
направлением крутящего момента .
Остальные напряжения либо в точности равны нулю, либо малы:
, 
.
Напряженное состояние элементарного параллелепипеда, вырезанного из трубы (рис. 5), является плоским. Анализ напряженного состояния выполняется так же, как в примере №16.
Пример 24.
Труба с
радиусом сечения 
м
толщиной 
см загружена продольной
растягивающей силой 
кН, внутренним давлением 
МПа и крутящим моментом 
. Материал трубы – чугун с такими характеристиками: 
МПа, МПа, 
. Нормативный коэффициент запаса прочности .
Требуется:
1) найти напряжения на гранях элемента, выделенного из трубы;
2) найти главные напряжения и положения главных площадок;
3) проверить прочность и определить действительный коэффициент запаса прочности;
4) показать направление трещины, возникающей при повышении уровня напряженного состояния до критического.
Решение.
Начать решение задачи нужно с изображения трубы и действующих на нее сил. Рядом со стрелками указываются абсолютные значения сил. Знаки учитываются соответствующим направлением стрелок.
Проверим
применимость к данной задаче формул для вычисления напряжений в тонкостенной
трубе. Так как 
, то труба является тонкостенной. Следовательно,
вышеприведенные формулы применимы.
Нормальное
напряжение от продольного растяжения силой 
положительно.
Нормальное
напряжение, вызванное внутренним давлением 
,
МПа
также положительно.
Касательное
напряжение, вызванное моментом 
, по модулю равно
.
Принимая во
внимание направление крутящего момента (см. рис. 1) и учитывая правило
знаков для касательного напряжения при плоском напряженном состоянии, получаем 
.
Изобразите найденное напряженное состояние точки трубы в виде плоского рисунка, учтя при этом правила знаков для напряжений.
Для последующей проверки прочности вычислим главные напряжения:
Главные напряжения, пронумерованные должным образом,
, 
, 
.
Тангенс угла наклона главной площадки
.
Отсюда два главных угла
.
Соответствие
угла 
главным площадкам (1
или 2) устанавливается так же, как в примере №16. Главные направления 1 и 2
показаны на рис.6. Проверку вычисленных значений главных напряжений и главных
направлений можно выполнить графически, построив круг напряжений Мора.
Построение круга напряжений описано при решении примера №16.
Рис.6
Материал является хрупким (чугун), поэтому с целью проверки прочности используем вторую теорию прочности или теорию прочности Мора.
Согласно второй теории прочности
,
значит, прочность обеспечена.
Вычислим действительный коэффициент запаса прочности:
.
Вероятная
плоскость отрыва (трещины) перпендикулярна первому главному направлению, то есть наклонена к продольной оси трубы под углом 
. Она показана на рис. 2, где ось – продольная ось
трубы. Направление вероятной плоскости отрыва на рисунке привязано к оси
конструкции, значит, может быть показано и на самой конструкции.
Согласно пятой теории прочности (теории Мора)
,
то есть прочность также обеспечена.
Вычислим фактический коэффициент запаса прочности:
.
Онлайн-калькулятор "Расчет по различным теориям прочности"
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
