Главная

Тестовые вопросы по теме «Определение перемещений в статически определимых балках»

- Какие перемещения получают поперечные сечения балок при изгибе?

1. линейные;

2. угловые;

3. линейные и угловые.

- Как изменится прогиб балки, если изгибающий момент уменьшить в три раза?

1. уменьшится в три раза;

2. уменьшится в шесть раз;

3. уменьшится в девять раз.

- Балки, изготовленные из стали и чугуна, имеющие одинаковые размеры и устройства опор, подвергаются действию одинаковых сил. Сравните величину максимальных прогибов этих балок?

1. у стальной балки прогиб больше;

2. у чугунной балки прогиб больше;

3. прогиб балок одинаковый.

- Определить наибольший прогиб в шарнирно опертой балке пролетом l=2 м, нагруженной посередине силой F=15 кН. Балка имеет квадратное сечение со стороной а=10 см. Модуль упругости материала балки Е=2∙10⁵ МПа.

1. f = 0,15 см;

2. f = 1,5 см;

3. f = 0,5 см;

4. f = 0,3 см.

- Определить наибольший прогиб в шарнирно опертой балке пролетом l=2 м, нагруженной посередине силой F=15 кН. Балка имеет круглое сечение D=10 см. Модуль упругости материала балки Е=2∙10⁵ МПа.

1. f = 0,26 см;

2. f = 2,6 см;

3. f = 0,026 см;

4. f = 26 см.

- Определить наибольший прогиб в шарнирно опертой балке пролетом l=2 м, нагруженной посередине силой F=15 кН. Сечение балки – двутавр №12. Модуль упругости материала балки Е=2∙10⁵ МПа.

1. f = 0,357 см;

2. f = 3,57 см;

3. f = 0,9 см;

4. f = 9 см.

- Определить максимальный прогиб консоли длиной l = 1 м, нагруженной на свободном конце силой F= 2 кН. Сечение консоли – квадрат со стороной а =15 см. Модуль упругости материала балки Е=10⁴ МПа.

1. f = 0,5 см;

2. f = 1,6 см;

3. f = 0,16 см;

4. f = 5 см.

- Определить максимальный прогиб консоли длиной l = 1 м, нагруженной на свободном конце силой F =2 кН. Сечение консоли – круг, D =10 см. Модуль упругости материала балки Е=10⁴ МПа.

1. f = 13,6 см;

2. f = 0,36 см;

3. f = 1,36 см;

4. f = 1,6 см.

- Определить прогиб посередине шарнирно опёртой балки, нагруженной равномерно распределённой нагрузкой q=4 кН/м. Сечение балки прямоугольник b=10 см, h=20 см, l=3 м, Е=10⁴ МПа.

1. f = 0,63 см;

2. f = 6,3 см;

3. f = 63 мм

4. Верны ответы 2 и 3.

- Определить прогиб посередине шарнирно опёртой балки, нагруженной равномерно распределённой нагрузкой q=4 кН/м. Сечение балки – круг D=10 см, l =3 м, Е=10⁴ МПа.

1. f = 8,6 см;

2. f = 86 мм;

3. f = 0,8 см;

4. Верны ответы 1 и 2.

- Определить прогиб посередине шарнирно опёртой балки, нагруженной равномерно распределённой нагрузкой q=4 кН/м. Сечение балки – кольцо dхD, α= 0,8, Е=10⁴ МПа, D=20 cм, l=3 м.

1. f = 0,91 см;

2. f = 0,7 см;

3. f = 9,1 мм;

4. Верны ответы 1 и 3.

- Определить максимальный прогиб консоли длиной l=1 м, нагруженной на конце силой F  =2 кН. Сечение консоли – двутавр №10. Модуль упругости материала Е=2∙10⁵ МПа.

1. f = 1,7 см;

2. f = 0,17 см;

3. f = 17 см;

4. f = 2,9 см.

- Формула максимального прогиба для консольной балки длиной l, нагруженной на конце силой F:

1. ;

2. ;

3. ;

4. .

- Формула максимального прогиба для шарнирно опёртой балки длиной l, нагруженной посредине силой F:

1. ;

2. ;

3. ;

4. .

- Укажите верную формулу для определения стрелы прогибов f шарнирно опёртой по краям балке длиной l при действии силы P в середине пролёта

1.

2.

3.

4.

- Укажите верную формулу для определения стрелы прогибов f консольной балки длиной l при действии силы P на конце

1.

2.

3.

4.

- Формула определения максимального прогиба для шарнирно опёртой балки длиной l, нагруженной равномерно распределённой нагрузкой q:

1. ;

2. ;

3. ;

4. .

- К балке приложены сила F и момент m. Подобрать поперечное сечение балки в форме прокатного двутавра из условия жесткости , если [f] =0,5 см, a= 1 м, E=2∙10¹¹ МПа и F=6 кН.

1. I N14; J_x=572 см⁴;

2. I N16; J_x=873 см⁴;

3. I N18; J_x=1290 см⁴;

4. I N20; J_x=1430 см⁴.

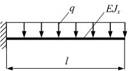
- Консольная балка длиной l нагружена равномерно распределенной нагрузкой интенсивности q. Жесткость поперечного сечения на изгиб EJ_x по всей длине постоянна. Прогиб свободного конца балки по абсолютной величине равен …

1.

2.

3.

4.

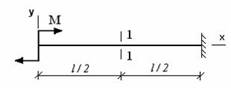
- φ – угол поворота, v – прогиб. Сечение 1-1 имеет перемещения…

1. v;

2. φ и v;

3. нет перемещений;

4. φ.

- φ - угол поворота, v - прогиб. Сечение 1-1 имеет перемещения...

1. v;

2. φ;

3. φ и v.

4. нет перемещений

- φ - угол поворота, v - прогиб. Сечение 1-1 имеет перемещения...

1. v

2. φ

3. φ и v

4. нет перемещений

- φ - угол поворота, v - прогиб. Сечение 1-1 имеет перемещения...

1. v

2. φ

3. φ и v

4. нет перемещений

- Максимальный прогиб возникает в сечении...

1. 2-2

2. 1-1

3. 3-3

4. 4-4

- Максимальный прогиб возникает в сечении...

1. 2-2

2. 1-1

3. 3-3

4. 4-4

- Максимальный угол поворота возникает в сечении...

1. 2-2

2. 1-1

3. 3-3

4. 4-4

- Максимальный угол поворота возникает в сечении...

1. 2-2

2. 1-1

3. 3-3

4. 4-4

- К балке постоянной жёсткости ЕJ_z в точке С приложена сила F. Величина прогиба в этом сечении V_c ,будет равна:

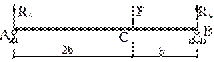
1.

2.

3.

4.

- Балка деформируется под действием силы Р. Сечение С балки имеет линейные U_c, V_c и угловое φ_С перемещения. Из-за малости можно пренебречь перемещением...

1. U_c и φ_С

2. φ_С

3. U_c

4. V_c

- На рисунке показана схема нагружения балки. Форма деформированной оси балки имеет вид...

1.

2.

3.

4.

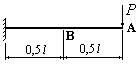
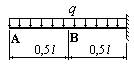
- В сколько раз прогиб в сечении А на конце изображенной на рисунке балки, больше, чем прогиб в сечении В посредине балки?

1. в 3 раза;

2. в 3,5 раза;

3. в 2,8 раза;

4. в 3,2 раза.

- В сколько раз угол поворота сечения А на конце изображенной на рисунке балки больше, чем угол поворота сечения В посредине балки?

1. в 1,225 раза;

2. в 1,143 раза;

3. в 1,159 раза;

4. в 1,137 раза.

- Прогиб среднего сечения шарнирно опертой балки (P, l, EI_x – известны) равен...

1. ;

2. ;

3. ;

4. .

- Чему равен угол поворота балки в сечении «С»?

1. ;

2. ;

3. .

- Чему равен угол поворота в среднем сечении балки?

1. ;

2. ;

3. .

- Чему равен угол поворота свободного конца балки?

1. ;

2. ;

3. .

- Чему равен прогиб свободного конца балки?

1. ;

2. ;

3. .

- Чему равен прогиб балки в сечении «С»?

1. ;

2. ;

3. .

- Чему равен прогиб свободного конца балки?

1. ;

2. ;

3. ;

- Чему равен угол поворота балки в сечении «С»?

1. ;

2. ;

3. .

4. верный ответ не приведен

- Чему равен угол поворота балки в сечении «С»?

1. ;

2. ;

3. .

4. верный ответ не приведен

- Если к однопролетной балке приложить силу F, то при EI_x=const угол поворота сечения над левой опорой по модулю |φ_A| равен:

1. ;

2. ;

3. ;

4. .

- Однопролетная балка нагружена силой F. Если EI_x=const, то угол поворота сечения, в котором приложена эта, равен:

1. ;

2. ;

3. ;

4.

- Если балка нагружена силой F, то прогиб сечения С (v_c) при EI_x=const равен:

1. ;

2. ;

3. ;

4. .

- Стальная балка (модуль продольной упругости Е=2∙10¹¹ Па) имеет длину l = 0,6 м и круговое поперечное сечение с диаметром d=60 мм. Если стрела прогиба f (наибольший прогиб) равна 2 мм, то интенсивность равномерно распределенной нагрузки q в кН/м равна:

1. 150;

2. 200;

3. 250;

4. 300.

- Если на правой части консольной балки находится равномерно распределенная нагрузка интенсивности q, то угол поворота сечения В (φ_В) по модулю при EI_x=const равен:

1. ;

2. ;

3. ;

4. .

- Если балка, имеющая промежуточный шарнир С, находится под воздействием силы F, то вертикальное перемещение этого шарнира равно:

1. ;

2. ;

3. ;

4.

- Если однопролетная балка длиной l=2 м имеет поперечное сечение в виде двутавра (I_x=1290 см⁴), то под действием силы F = 50 кН угол поворота сечения над левой опорой (φ_А) при модуле продольной упругости E=2∙10¹¹ Па по абсолютной величине равен:

1. 0,35º;

2. 0,32º;

3. 0,28º;

4. 0,25º.

- К балке приложены два момента m. Их допускаемое значение [m] из условия жесткости [f/l]=1/400 где f – наибольший прогиб, длина l=2 м, диаметр поперечного сечения d=0,1 м и модуль продольной упругости E=2∙10¹¹ Па, равно в кНм:

1. 21;

2. 28;

3. 35;

4. 42.

- Если половина балки находится под действием равномерно распределенной нагрузки интенсивностью q, то модуль угла поворота сечения, расположенного над левой опорой, равен:

1. ;

2. ;

3. ;

4. .

- Если сила F и прогиб под силой (v_c) известны, а также заданы размер b и модуль продольной упругости Е, то осевой момент инерции поперечного сечения I_x должен быть равен:

1. ;

2. ;

3. ;

4. .

- Если к средней части балки приложена равномерно распределенная нагрузка интенсивности q, то максимальный прогиб f (стрела прогиба) равен:

1. ;

2. ;

3. ;

4.

- Посередине балки приложен момент m=70кНм. Поперечное сечение – двутавр N22 (I_x=2550см⁴; W_x=232см³). Если модуль продольной упругости Е = 2 ∙10¹¹Па, то абсолютная величина угла поворота сечения, расположенного над опорой (левой или правой), равна в градусах?

1. 0,050;

2. 0,066;

3. 0,082;

4. 0,100.

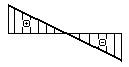
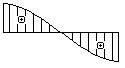
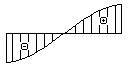
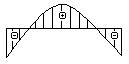
- Какая из эпюр углов поворота соответствует представленной на рисунке эпюре изменения прогибов?

1.

2.

3.

4.

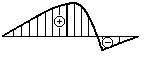
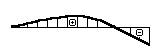
- Какая из эпюр прогибов соответствует представленной на рисунке эпюре изгибающих моментов?

1.

2.

3.

4.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00