Главная

Тестовые вопросы по теме «Изгиб. Построение эпюр изгибающего момента»

- Изгибающий момент считается положительным, если слева от сечения он направлен

1. По ходу часовой стрелки?

2. Против хода часовой стрелки?

- В поперечном сечении балки возникли изгибающий момент и поперечная сила. Укажите вид изгиба.

1. чистый изгиб;

2. поперечный изгиб.

- Как будет выглядеть эпюра изгибающих моментов, если на участок конструкции действует сосредоточенная сила?

1. квадратная парабола;

2. прямая линия, параллельная оси;

3. синусоида;

4. вообще отсутствует;

5. прямая наклонная линия.

- Укажите внутренние силовые факторы и напряжения, возникающие в поперечных сечениях балки при прямом поперечном изгибе в плоскости Оху

1. изгибающий момент M_z и нормальные напряжения по х;

2. поперечная сила Q_y, изгибающий момент M_z, нормальные напряжения по х и касательные напряжения ух;

3. изгибающие моменты М_y, M_z и нормальные напряжения по х;

4. поперечная сила Q_y, изгибающий момент M_z и нормальные напряжения по х.

- Положение нейтральной оси при изгибе балок с несимметричным относительно этой оси сечением зависит от …

1. знака изгибающего момента;

2. действующей на балку нагрузки;

3. положения центра тяжести;

4. момента инерции сечения.

- Какой из дифференциальных зависимостей необходимо воспользоваться, чтобы определить максимальный изгибающий момент?

1.

2.

3.

4.

- Наличие каких внутренних силовых факторов определяет возникновение чистого изгиба?

1.

2.

3.

4.

5.

- Что означает скачок на эпюре моментов?

1. изменение сечения;

2. наличие сосредоточенного момента;

3. приложение сосредоточенной силы.

- Знак изгибающего момента не зависит от внешних сил?

1. нет;

2. да;

3. при наличии сосредоточенного момента.

- В поперечном сечении балки возникли изгибающий момент и поперечная сила. Укажите вид изгиба?

1. чистый изгиб;

2. поперечный изгиб.

- Изменится ли величина и знак поперечной силы и изгибающего момента, если они будут вычислены по внешним силам, расположенным слева или справа от сечения?

1. изменится;

2. не изменится.

- Изгибающие моменты в сечении на расстояние z от концов балок выражены уравнениями: M₁=R_a∙z; M₂=M. Укажите какими линиями очерчены эпюры изгибающих моментов?

1. в обоих случаях наклонными прямыми линиями;

2. в первом случае – прямой, наклонной к оси, во второй – прямой, параллельной оси.

- Могут ли быть скачки на эпюре изгибающих моментов, если балка нагружена сосредоточенными силами и распределенной нагрузкой?

1. могут;

2. не могут.

- Чему равна поперечная сила в сечении бруса, в котором изгибающий момент достигает экстремальных значений?

1. Поперечная сила в этом сечении бруса равна нулю.

2. Поперечная сила в этом сечении бруса равна следующему значению Q=τA.

3. Поперечная сила тоже достигает экстремальных значений.

4. Поперечную силу в данном случае можно определить по формуле Журавского.

- Возникновением каких внутренних силовых факторов характеризуется прямой поперечный изгиб?

1. М_изг;

2. М_изг и Q;

3. Q;

4. нет правильного ответа.

- Возникновением каких внутренних силовых факторов характеризуется прямой чистый изгиб?

1. М_изг;

2. М_изг и Q;

3. Q;

4. нет правильного ответа.

- По какому закону меняется по длине оси бруса поперечная сила и изгибающий момент при отсутствии распределенной нагрузки?

1. Q=0, изгибающий момент имеет постоянное значение;

2. сила имеет постоянное значение, изгибающий момент меняется по линейному закону;

3. поперечная сила меняется по линейному закону, а изгибающий момент – по закону квадратной параболы.

- По какому закону меняется по длине оси бруса поперечная сила и изгибающий момент на участках бруса, на которых действует равномерно распределённая нагрузка?

1. Q=0, изгибающий момент имеет постоянное значение;

2. сила имеет постоянное значение, изгибающий момент меняется по линейному закону;

3. поперечная сила меняется по линейному закону, а изгибающий момент – по закону квадратной параболы.

- Чему равна поперечная сила в сечениях бруса, в которых изгибающий момент достигает экстремальных значений?

1. 0;

2. Q_max;

3. не зависит.

- Первая производная от изгибающего момента по длине балки равна:

1. поперечной силе;

2. изгибающему моменту;

3. интенсивности равномерно распределенной нагрузки.

- На участке балки, производная от момента по координате сечения dM/dz=0. Какой изгиб испытывает балка, если все силы лежат в главной плоскости инерции на этом участке?

1. плоский изгиб;

2. поперечный изгиб;

3. чистый изгиб;

4. нет правильного ответа.

- Вторая производная от изгибающего момента по длине балки равна:

1. поперечной силе;

2. изгибающему моменту;

3. интенсивности равномерно распределенной нагрузки.

- Первая производная от поперечной силы по длине балки равна:

1. поперечной силе;

2. изгибающему моменту;

3. интенсивности равномерно распределенной нагрузки.

- Дифференциальные зависимости при изгибе между поперечной силой и изгибающим моментом:

1. ;

2. ;

3. ;

4. .

- Для чего необходимо строить эпюру изгибающих моментов?

1. для определения наибольшего значения поперечной силы;

2. для определения опасного сечения балки;

3. для расчета касательных напряжений.

- Какая из эпюр, изображенных на рисунке, отображает изгибающие

моменты в сечениях бруса, нагруженного поперечной силой F?

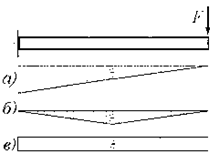
1. а;

2. б;

3. в;

4. ни одна из представленных эпюр.

- Определите правильно построенную эпюру изгибающих моментов

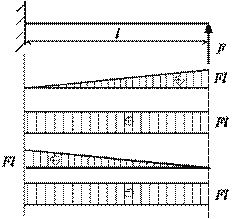
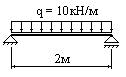
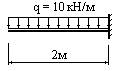
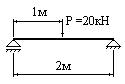
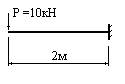
- В каком из изображенных случаев наибольший изгибающий момент равен 10 кНм?

1.

2.

3.

4.

- Дана эпюра изгибающих моментов. Которая из эпюр поперечных сил ей соответствует?

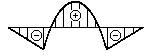
1.

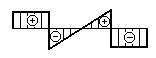
2.

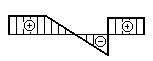
3.

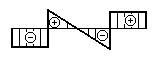
4.

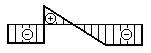
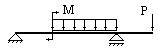
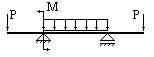
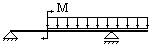
- Дана эпюра изгибающих моментов. Которая из балок ей соответствует?

1.

2.

3.

4.

- Какое из уравнений для изгибающего момента, возникающего в сечении x, написано верно?

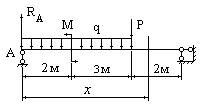
1.

2.

3.

4.

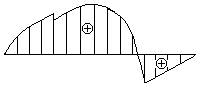
- Построить с помощью метода “характерных” сечений эпюру изгибающих моментов и определить, какой из приведенных ниже эпюр она соответствует?

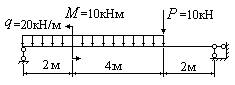
1.

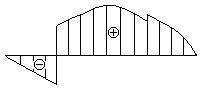
2.

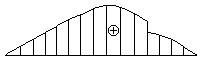
3.

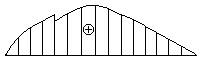
4.

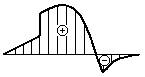
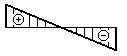
- Какая из эпюр изгибающих моментов соответствует наличию в изгибаемом элементе чистого изгиба?

1.

2.

3.

4.

- Что возникает на эпюре изгибающих моментов М в сечении, где приложена сосредоточенная сила F?

1. изменений нет;

2. эпюра моментов претерпевает скачок на величину F;

3. эпюра моментов становится линейной;

4. излом эпюры М на “острие” вектора .

- Что возникает на эпюре изгибающих моментов М в сечении, где приложена внешняя пара сил М_е?

1. изменений нет;

2. отмечается изменение угла наклона касательной к эпюре М;

3. скачок на величину М_е в сторону сжимаемого этой парой “волокна”;

4. скачок на величину М_е в сторону растягиваемого этой парой “волокна”.

- Если переходим с участка, на котором заканчивается действие равномерно распределённой нагрузки q, то на эпюре изгибающих моментов М:

1. происходит изменение угла наклона линейной эпюры;

2. криволинейная эпюра изменяет кривизну на противоположную;

3. эпюра М остаётся неизменной по характеру;

4. прежде криволинейная эпюра становится линейной.

- На участке, где имеется равномерно распределённая нагрузка и эпюра изгибающих моментов изменяется по квадратичной зависимости, то наличие экстремума (М_экстр.) обусловлено:

1. изменением знака функции М(х);

2. равенством нулю поперечной силы в пределах участка;

3. равенством нулю производной dQ/dx;

4. изменением характера функции М(х).

- Условием определения (в пределах участка) положения сечения, где М = М_экстр. является:

1. dQ/dx=0;

2. q=0;

3. Q=0;

4. скачок на эпюре М.

- Для расчётной схемы аналитическое выражение для изгибающего момента M_z:

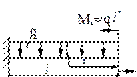
1.

2.

3.

4.

- Балка длиной l нагружена равномерно распределенной нагрузкой с интенсивностью q. Значение (по абсолютной величине) максимального изгибающего момента равно …

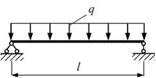
1.

2.

3.

4. .

- В сечении 1-1 имеют место внутренние силовые факторы…

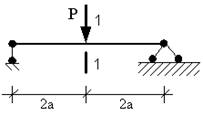
1. M=0; Q=0;

2. M≠0; Q≠0;

3. M≠0; Q=0;

4. M=0; Q≠0.

- Чему равны (по модулю) изгибающие моменты в сечениях А, В, С, D? (Сечения В и С находятся на ничтожно малых расстояниях от сечения, где приложена сила Р).

1. M_A=0, M_B=M_C=2P/3, M_D=Pa;

2. M_A=M_B=0, M_C=2Pa, M_D=Pa;

3. M_A=M_D=0, M_B=2Pa, M_C=Pa;

4. M_A=M_D=0; M_B=M_C=3Pa/4.

- Чему равны (по модулю) изгибающие моменты в сечениях А, В, С, D? (Сечения В и С находятся на ничтожно малых расстояниях от сечения, где приложен момент L).

1. M_A=0, M_B=M_C=L, M_D=2L;

2. M_A=M_D=0, M_B=3L/4, M_C=5L/4;

3. M_A=M_D=0, M_B=3L/4, M_C=L/4;

4. M_A=M_D=0, M_B=M_C=3L/4.

- Построить эпюры Q, M и определить Q_мax, M_мax.

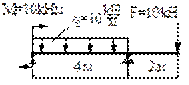
Q_мax [кH]: 1) 10; 2)35 3) 40; 4)55.

M_мax [кHм]: 1) 40; 2) 41,5; 3) 20; 4) 37,5.

- Построить эпюры Q, M и определить Q_мax, M_мax.

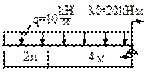
Q_мax [кH]: 1) 20; 2) 30; 3) 40; 4) 50.

M_мax [кHм]: 1) 20; 2) 30; 3) 40; 4) 50.

- Построить эпюры Q, M и определить Q_мax, M_мax.

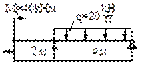
Q_мax [кH]: 1) 20; 2) 35; 3) 45; 4) 50.

M_мax [кHм]: 1) 52,5; 2) 63,5; 3) 40; 4) 42,5.

- Построить эпюры Q, M и определить Q_мax, M_мax.

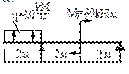
Q_мax [кH]: 1) 15; 2) 20; 3) 25; 4) 40.

M_мax [кHм]: 1) 10; 2) 20; 3) 30; 4) 40.

- Построить эпюры Q, M и определить Q_мax, M_мax.

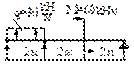
Q_мax [кH]: 1) 20; 2) 30; 3) 40; 4) 60.

M_мax [kHм]: 1) 20; 2) 30; 3) 40; 4) 60.

- Для расчётных схем а, б, в, г найдите соответствующие эпюры (д, е, ж, з) поперечных сил и эпюры (и, к, л, м) изгибающих моментов (длина балки – l).

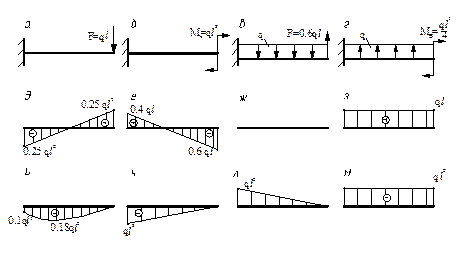
- Для расчётных схем а, б, в, г найдите соответствующие эпюры (д, е, ж, з) поперечных сил и эпюры (и, к, л, м) изгибающих моментов (длина каждого участка – l, М_е=ql²).

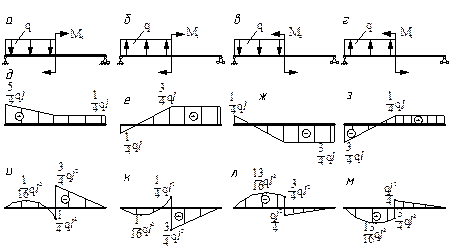
- В расчётной схеме выражение для изгибающего момента M_z:

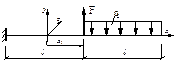
1. –ql(l/2+x)+Fx;

2. – qx²/2+Fx;

3. ql(l/2+x)- Fx;

4. ql(l/2+x)+Fx.

- В сечении 1-1 имеют место внутренние силовые факторы...

1. ;

2. ;

3. ;

4. .

- В сечении 1-1 имеют место внутренние силовые факторы...

1. ;

2. ;

3. ;

4. .

- В сечении 1-1 имеют место внутренние силовые факторы...

1. ;

2. ;

3. ;

4. .

- В сечении 1-1 имеют место внутренние силовые факторы...

1. ;

2. ;

3. ;

4. .

- В сечении 1-1 имеют место внутренние силовые факторы...

1.;

2. ;

3. ;

4. .

- В сечении 1-1 имеют место внутренние силовые факторы...

1. ;

2. ;

3. M=0, Q=0,

4. .

- В поперечном сечении балки при изгибе могут возникать внутренние силовые факторы: Q - поперечная сила и M - изгибающий момент. В сечении 1-1 балки, представленной на рисунке...

1. нет M и Q

2. есть только Q

3. есть M и Q

4. есть только M

- Укажите участок или участки, на которых происходит деформация поперечного изгиба?

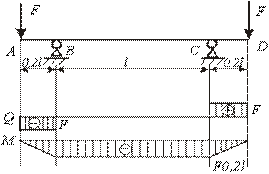
1. А-В;

2. В-С;

3. C-D;

4. A-D.

- Какие нагрузки, расположенные слева от сечения I-I балки, вызывают в нем положительный изгибающий момент?

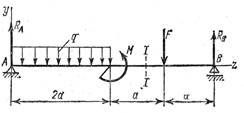
1. сила R_A;

2. распределенная нагрузка 2aq;

3. момент М.

- На рисунке изображена балка, нагруженная сосредоточенными силами. Определите, какая из приведенных на рисунке эпюр изгибающих моментов соответствует нагружению балки.

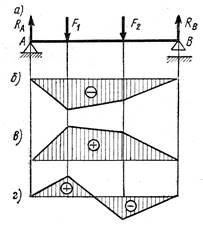
1. эпюра на рисунке (б);

2. эпюра на рисунке (в);

3. эпюра на рисунке (г).

- Выбрать участок чистого изгиба

1. 1 участок;

2. 2 участок;

3. 3 участок;

4. 4 участок.

- Выбрать участок чистого изгиба

1. 1 участок;

2. 2 участок;

3. 3 участок;

4. 4 участок.

- Выбрать формулу для расчета изгибающего момента в сечении 2-2

1. m₁+ F₁z₂ - F₂(z₂ – 2);

2. - m₁ - F₁z₂ - F₂z₂ – m₂;

3. - m₁+ F₁z₂ - F₂(z₂ – 2);

4. - m₁+ F₁z₂ - F₂(z₂ – 2) – F₃.

- Выбрать формулу для расчета изгибающего момента в сечении 3-3

1. F₁z₃ - m + F₂(z₃ - 3);

2. - F₁z₃ + m - F₂(z₃ - 6);

3. - F₁z₃ + m - F₂z₃ ;

4. F₁z₃ - m + F₂(z₃ - 6).

- Выбрать формулу для расчета изгибающего момента в сечении 3-3

1. F₁z₃ - m₁ + F₂(z₃ - 3 ) – F₃;

2. - F₁z_{3 -} m₁ - F₂(z₃ - 3 ) – F₃(z₃ - 6 );

3. F₁z₃ + m₁ + F₂(z₃ - 3 ) – F₃;

4. - F₁z₃ - m₁ + F₂(z₃ - 3 ) – F₃(z₃ - 6 ).

- Выбрать формулу для расчета изгибающего момента в сечении 3-3

1. F₁z₃ - F₂(z₃ - 2) – F₃(z₃ - 4);

2. - F₁z₃ + F₂(z₃ - 2) + F₃(z₃ - 4);

3. - F₁z₃ + F₂(z₃ – 2) + F₃(z₃ - 4) – m₁;

4. -F₂z₃ + F₂(z₃ - 2)+ F₃(z₃ - 4).

- Выбрать формулу для расчета изгибающего момента в сечении 3-3

1. m₁+ F₁z₃ - F₂(z₃ – 4) + m₂ ;

2. m₁+ F₁z₃ - F₂(z₃ – 4) + m₂ + F₃;

3. m₁+ F₁z₃ - F₂(z₃ – 4) + m₂ + F₃ (z₃-7);

4. m₁+ F₁z₃ - F₂(z₃ – 2) + m₂ .

- Определить величину изгибающего момента в точке Г, если F₁ = 10 кН; F₂ = 15 кН;

F₃ = 18 кН; m₁ =20 кНм; m₂ = 30 кНм

1. 59 кНм;

2. 39 кНм;

3. 179 кНм;

4. 76 кНм.

- Определить величину изгибающего момента в точке Г справа, если F₁ = 15 кН; F₂ = 22 кН; F₃ = 37 кН; m₁ = 25 кНм; m₂ = 45 кНм

1. 359 кНм;

2. 179 кНм;

3. 129 кНм;

4. 134 кНм.

- Определить величину изгибающего момента в точке Г, если m₁= 100 кНм; m₂ =50 кНм; F₁ = 10 кН; F₂= 18 кН; F₃ = 20 кН

1. 140 Нм;

2. 190 Нм;

3. 370 Нм;

4. 150 Нм.

- Определить величину изгибающего момента в точке Г, если F₁ = 22 кН; F₂ = 18 кН; F₃ = 36 кН; m = 36 кНм

1. 138 кНм;

2. 102 кНм;

3. 198 кНм;

4. 182 кНм.

- Определить величину изгибающего момента в точке Г слева, если F₁ = 10 кН; F₂ = 20 кН; F₃ = 28 кН; m₁ = 18 кНм; m₂ = 36 кНм; m₃ = 5 кНм

1. 54 кНм;

2. 98 кНм;

3. 62 кНм;

4. 90 кНм.

- Определить изгибающий момент в точке С

1. 42 кНм;

2. 67 кНм;

3. 55 кНм;

4. 76 кНм.

- Определить изгибающий момент в точке С

1. 10 кНм;

2. 15 кНм;

3. 25 кНм;

4. 195 кНм.

- Определить координату точки, в которой изгибающий момент достигает максимума

1. 4 м;

2. 4,5 м;

3. 5 м;

4. 6 м.

- Определить изгибающий момент в точке С (справа)

1. 47 кНм;

2. 102 кНм;

3. 126 кНм;

4. 149 кНм.

- Выбрать уравнения для расчета изгибающего момента на участке 2

1. ;

2. ;

3. ;

4. .

- Определить координату точки z, в которой изгибающий момент достигает максимума или минимума?

1. 2 м;

2. 3 м;

3. 4 м;

4. 5 м.

- Определить изгибающий момент в точке С (слева)

1. 8 кНм;

2. 30 кНм;

3. 64 кНм;

4. 104 кНм.

- Вычислить величину изгибающего момента в сечении С

1. 37,8 кНм;

2. 72 кНм;

3. 34,2 кНм;

4. 24 кНм.

- Вычислить величину изгибающего момента в сечении С

1. 6 кНм;

2. - 2 кНм;

3. 10 кНм;

4. 5 кНм.

- Вычислить величину изгибающего момента в сечении С

1. 6 кНм;

2. 5,2 кНм;

3. 10 кНм;

4. 15 кНм.

- Вычислить величину изгибающего момента в сечении D

1. 94,5 кНм;

2. 62, 5 кНм;

3. 74,5 кНм;

4. 109,5 кНм.

- Определить величину изгибающего момента в сечении С (справа)

1. 94,5 кНм;

2. 62,5 кНм;

3. 74,5 кНм;

4. 109,5 кНм.

- Указать правильную эпюру изгибающих моментов М.

1. 1;

2. 2;

3. 3.

- Указать правильную эпюру изгибающих моментов М.

1. 1;

2. 2;

3. 3.

- Указать правильную эпюру изгибающих моментов М.

1. 1;

2. 2;

3. 3.

- Указать правильную эпюру изгибающих моментов М.

1. 1;

2. 2;

3. 3.

- Указать правильную эпюру изгибающих моментов М.

1. 1;

2. 2;

3. 3.

- Указать правильную эпюру изгибающих моментов М.

1. 1;

2. 2;

3. 3.

- Указать правильную эпюру изгибающих моментов М.

1. 1;

2. 2;

3. 3.

- Указать правильную эпюру изгибающих моментов М.

1. 1;

2. 2;

3. 3.

- Из представленных эпюр выбрать эпюру изгибающихся моментов для балки

1. Б;

2. В;

3. Д;

4. Е.

- Из представленных эпюр выбрать эпюру изгибающих моментов для балки

1. А;

2. Г;

3. Д;

4. Е.

- Из представленных эпюр выбрать эпюру изгибающих моментов для балки

1. А;

2. Б;

3. В;

4. Е.

- Из представленных эпюр выбрать эпюру изгибающих моментов для балки

1. Б;

2. В;

3. Г;

4. Д.

- Из представленных эпюр выбрать эпюру изгибающих моментов для балки

1. А;

2. Б;

3. Д;

4. Е.

- Из представленных эпюр выбрать эпюру изгибающих моментов для балки

1. 1;

2. 2;

3. 4;

4. 6.

- Из представленных эпюр выбрать эпюру изгибающих моментов для балки

1. 1;

2. 4;

3. 5;

4. 6.

- Из представленных эпюр выбрать эпюру изгибающих моментов для балки

1. 2;

2. 3;

3. 4;

4. 6.

- Из представленных в вопросе эпюр выбрать эпюру изгибающих моментов для балки

1. 1;

2. 2;

3. 4;

4. 6.

- Из приведенных эпюр выбрать эпюру изгибающих моментов для балки

1. 2;

2. 3;

3. 4;

4. 6.

- Из приведенных эпюр выбрать эпюру изгибающих моментов для балки

1. 2;

2. 3;

3. 4;

4. 6.

- Если плоская рама находится под воздействием вертикальной равномерно распределенной нагрузки интенсивностью q, то наибольшая величина изгибающего момента (maxM_x) по модулю равна:

1. 1,5 qb²;

2. 2,0 qb²;

3. 2,5 qb²;

4. 3,0 qb².

- Наибольшая величина изгибающего момента (max M_x) для плоской рамы, нагруженной равномерно распределенной нагрузкой интенсивности q и сосредоточенной силой F=2qa равна:

1. 1,5 qa²;

2. 2,0 qa²;

3. 2,5 qa²;

4. 3,0 qa².

- Если рама находится под воздействием горизонтальной силы F, то наибольшая величина изгибающего момента (max M_x) по модулю равна:

1. Fb;

2. 1,5 Fb;

3. 2,0 Fb;

4. 3,0 Fb.

- Если один из двух участков балки находится под действием равномерно распределенной нагрузки интенсивности q, то максимальная величина изгибающего момента (max M_x) по модулю достигает величины:

1. ;

2. ;

3. ;

4. .

- Если на балку действуют две нагрузки, то по модулю изгибающий момент M_x в среднем сечении, вычисленный в кНм, равен:

1. 1;

2. 9;

3. 10;

4. 21.

- Если на балку действуют две силы, равные соответственно F₁=6 кН и F₂=10 кН, то модуль величины изгибающего момента в среднем сечении () в кНм равен:

1. 4;

2. 6;

3. 8;

4. 10.

- Если на балку действуют две нагрузки – q и m, то по модулю величина изгибающего момента M_x в сечении I-I в кНм равна:

1. 28;

2. 32;

3. 36;

4. 40.

- Если на балку действуют две нагрузки, то величина изгибающего момента M_x в среднем сечении (I-I) по модулю в кНм равна:

1. 6,5;

2. 12,0;

3. 13,5;

4. 15,0.

- Если на балку действуют три различные нагрузки, то модуль изгибающего момента M_x в сечении I-I в кНм равен:

1. 12;

2. 15;

3. 19;

4. 24.

- Если плоская рама нагружена горизонтальной силой F = 28 кН, то наибольшее значение изгибающего момента M_max по абсолютной величине в кНм равно:

1. 24;

2. 32;

3. 56;

4. 84.

- Если на балку действуют две нагрузки – равномерно распределенная и пара сил, то отношение модулей величин изгибающих моментов M_x в двух сечениях () равно:

1. 1,20;

2. 1,35;

3. 1,50;

4. 1,65.

- Если плоская рама испытывает действие горизонтальной равномерно распределенной нагрузки интенсивности q, то наибольшее значение изгибающего момента M_x по модулю в пределах вертикального участка ВС равно:

1. 2 qa²;

2. 1,5 qa²;

3. 1,2 qa²;

4. 1,0 qa².

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00