Главная

Тестовые вопросы по теме «Осевое растяжение-сжатие, определение внутренних усилий и деформаций»

- Какой из внутренних силовых факторов возникает при осевом растяжении и сжатии?

1. Изгибающий момент.

2. Поперечная сила.

3. Продольная сила.

4. Крутящий момент.

- Какое количество уравнений статики существует для линейных систем (стержней) при растяжении/сжатии?

1. одно (ΣF);

2. два (ΣF_x; ΣF_y);

3. три (ΣF_x; ΣF_y; ΣM);

4. шесть (ΣF_x; ΣF_y; ΣF_z; ΣM_x; ΣM_y; ΣM_кр);

5. нет правильных ответов.

- Поперечные сечения стержня при центральном растяжении и сжатии …

1. перестают быть плоскими и становятся вогнутыми;

2. перестают быть плоскими и становятся выпуклыми;

3. остаются плоскими и перемещаются поступательно вдоль оси стержня;

4. остаются плоскими и поворачиваются одно относительно другого.

- Абсолютное удлинение (укорочение) Δl при растяжении или сжатии силой Р прямо пропорционально …

1. длине стержня l;

2. модулю упругости материала стержня E;

3. приложенной силе Р;

4. площади поперечного сечения F;

- Укажите жесткость стержня при центральном растяжении (сжатии) и ее размерность

1. EJ, кН∙см²;

2. E/F, кН/см;

3. EF, кН;

4. EF, кН∙см.

- При деформации растяжения в сечениях бруса возникают только…

1. поперечные силы;

2. касательные силы;

3. продольные силы;

4. предельно допустимые силы.

- Как изменится абсолютное удлинение стержня, если площадь его поперечного сечения увеличить в два раза?

1. увеличится в 4 раза;

2. увеличится в 2 раза;

3. уменьшится в 2 раза;

4. уменьшится в 4 раза;

5. нет правильных ответов.

- Формула Герца устанавливает зависимость между…

1. напряжениями, свойствами материала и относительным удлинением бруса;

2. относительной поперечной и продольной деформациями;

3. критической силой, материалом, способом закрепления и геометрическими характеристиками бруса;

4. контактными напряжениями, нагрузкой, материалом и геометрическими характеристиками цилиндрических тел.

- Определите абсолютное удлинение ступенчатого стержня.

1.

2.

3.

- Укажите правильный вариант записи силового граничного условия.

1. N(0)=P,

2. N(0)=-P,

3. N(l)=0.

- Укажите правильный вариант записи силового граничного условия.

1. N(0)=0,

2. N(0)=-q,

3. N(0)=q.

- Укажите правильный вариант записи силового граничного условия.

1. N(0)=-P,

2. N(l)=P,

3. N(l)=0.

- Укажите правильный вариант записи силового граничного условия.

1. N(0)=-P,

2. N(l)=P,

3. N(l)=0.

- Чье имя носит коэффициент относительной поперечной деформации?

1. Матисса.

2. Мопассана.

3. Пуассона.

4. Сен-Венана.

- Укажите деформированное состояние стержня, нагруженного осевой силой, если его поперечные размеры увеличились?

1. стержень растянут;

2. стержень сжат.

- Какие внутренние усилия возникают при растяжении (сжатии)?

1. поперечная сила;

2. продольная сила.

- Что является характеристикой жесткости при растяжении?

1. модуль упругости первого рода;

2. модуль упругости второго рода.

- Что характеризует жесткость при растяжении (сжатии)?

1. модуль упругости второго рода;

2. модуль упругости первого рода;

3. коэффициент Пуассона.

- Что связывает поперечную и продольную деформацию при растяжении (сжатии)?

1. модуль упругости;

2. модуль сдвига;

3. коэффициент Пуассона.

- Что характеризует произведение ЕА при растяжении (сжатии)?

1. твердость материала;

2. жесткость материала;

3. жесткость стержня.

- Что называется жесткостью поперечного сечения при растяжении (сжатии)?

1. Жесткостью называется такое состояние материала, при котором деформации ниже допустимых величин.

2. Отношение s/e называется жесткостью поперечного сечения.

3. Произведение ЕV называется жесткостью поперечного сечения.

4. Произведение ЕА называется жесткостью поперечного сечения.

- Три вида задач из условия жесткости:

1. определение линейных размеров;

2. проверка на условие жесткости; определение размеров сечения; определение максимально допустимых размеров;

3. определение изменения объема конструкции.

- Выбор сечения из условия жесткости

1. сечение должно удовлетворять как условию прочности, так и жесткости;

2. сечение должно удовлетворять только условию прочности;

3. сечение должно удовлетворять только условию жесткости.

- При расчетах на жесткость получают:

1. гибкость стержня;

2. твердость материала;

3. линейные и угловые деформации.

- Растягиваемый стержень заменили другим, тех же размеров, с модулем Юнга в два раза большим. В каком из вариантов относительное удлинение останется прежним:

1. силу увеличили в 4 раза;

2. силу увеличили в 2 раза;

3. силу оставили неизменной;

4. силу уменьшили в 2 раза.

- Разделив абсолютное удлинение стержня на его относительное удлинение, что мы получим:

1. коэффициент Пуассона;

2. модуль Юнга;

3. первоначальную длину стержня;

4. нет правильного ответа.

- Условие жёсткости при растяжении – сжатии:

1. ;

2. ;

3. . ;

4. .

- Какие перемещения получают поперечные сечения стержня при растяжении–сжатии?

1. линейные;

2. угловые;

3. линейные и угловые.

- Отношение абсолютного удлинения к первоначальной длине бруса называется:

1. относительной продольной деформацией;

2. модулем упругости;

3. относительной поперечной деформацией;

4. полным удлинением.

- Указать выражение, соответствующее жёсткости сечения при растяжении–сжатии.

1. EJ;

2. EA;

3. GA;

4. GJ_p.

- Абсолютное удлинение выражается формулой:

1. ;

2. ;

3. ;

4. нет правильного ответа.

- Сколько внутренних силовых факторов возникает в поперечных сечениях прямого бруса при центральном растяжении (сжатии)?

1. два;

2. один;

3. отсутствуют;

- Если продольная сила N вызывает растяжение, то она считается:

1. положительной;

2. отрицательной;

3. нет правильного ответа.

- Относительное удлинение определяют по формуле:

1. ;

2. ;

3. ;

4. ;

5. .

- Что определяют модули упругости?

1. мягкость материала;

2. твёрдость материала;

3. жёсткость материала;

4. пластичность материала;

5. прочность материала.

- Физический смысл модулей упругости состоит в том, что они характеризуют:

1. отношение продольной относительной деформации к поперечной;

2. относительное удлинение в упругой области;

3. сопротивляемость металлов смещению атомов из положений равновесия в решётке;

4. скорость уменьшения напряжения по мере упругой деформации;

5. обратную пропорциональность между напряжением и упругой деформацией.

- Полная работа на пластическую деформацию равна:

1. ;

2. ;

3. ;

4. ;

5. .

- Что характеризует жесткость при растяжении (сжатии)?

1. модуль упругости второго рода,

2. модуль упругости первого рода,

3. коэффициент Пуассона.

- Что связывает поперечную и продольную деформацию при растяжении (сжатии)?

1. модуль упругости,

2. модуль сдвига,

3. коэффициент Пуассона.

- Что характеризует произведение ЕА при растяжении (сжатии)?

1. твердость материала,

2. жесткость материала,

3. жесткость стержня.

- Укажите деформированное состояние стержня, нагруженного осевой силой, если его поперечные размеры увеличились.

1. стержень растянут;

2. стержень сжат.

- Что характеризует модуль сдвига?

1. способность материала сопротивляться продольной деформации;

2. способность материала сопротивляться поперечной деформации;

3. способность материала сопротивляться ударным нагрузкам.

- Каково отличие модулей упругости, полученных испытаниями на растяжение и сжатие?

1. модуль упругости при сжатии меньше модуля упругости, полученного испытанием образца на растяжение;

2. модуль упругости при сжатии больше модуля упругости, полученного испытанием образца на растяжение;

3. отличий нет.

- К стержню квадратного поперечного сечения приложены одинаковые растягивающие силы. Если одновременно увеличить в 2 раза длину стержня и размер стороны, абсолютное удлинение стержня…

1. увеличится на 0,25l;

2. уменьшится в 2 раза;

3. увеличится в 2 раза;

4. уменьшится на 0,25l.

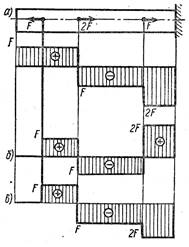
- Различаются ли внутренние силовые факторы в поперечных сечениях брусьев?

1. продольная сила для стержня на рисунке (а) в два раза больше;

2. продольные силы одинаковы.

- Какая из эпюр, приведенных на рисунке, соответствует заданной нагрузке стержня?

1. изображенная на рисунке (а);

2. изображенная на рисунке (б);

3. изображенная на рисунке (в).

- Для стержня изображенного на рисунке, эпюра нормальных сил N будет иметь вид....

1.2. 3. 4.

- Для стержня, схема которого изображена на рисунке, нормальное усилие N, действующее в сечении 1-1, будет...

1. растягивающим

2. равно нулю

3. растягивающим и сжимающим

4. сжимающим

- Для стержня, схема которого изображена на рисунке, нормальное усилие N, действующее в сечении 1-1, будет...

1. растягивающим

2. равно нулю

3. растягивающим и сжимающим

4. сжимающим

- Для стержня, схема которого изображена на рисунке, нормальное усилие N, действующее в сечении 1-1, будет...

1. растягивающим

2. равно нулю

3. растягивающим и сжимающим

4. сжимающим

- Растягиваемый стержень заменили другим, тех же размеров, с модулем Юнга в два раза большим. В каком из вариантов относительное удлинение останется прежним:

1. силу увеличили в 4 раза;

2. силу увеличили в 2 раза;

3. силу оставили неизменной;

4. силу уменьшили в 2 раза.

- При какой длине образца можно получить упругую деформацию сжатия 0,01 см, если σ_ПЦ =200 МПа, =10⁵ МПа?

1. 10 см;

2. 5 см;

3. 15 см.

- Определить модуль Юнга, если D = 2см, l = 2м, F = 8кН, ∆l = 0,5мм.

1. ≈ 2 ∙10⁵ МПа;

2. ≈1 ∙10⁵ МПа;

3. ≈10⁴ МПа;

4. 1,33∙10⁵ МПа.

- Проволока длиной l=10 м под действием растягивающей силы F=700 Н удлинилась на ∆l=11 мм. Определить модуль упругости Е, если A=3,1 мм².

1. Е=2,05∙10⁵ МПа;

2. Е=1∙10⁵ МПа;

3. Е=1,33∙10⁵ МПа.

- Две проволоки, одна стальная, другая медная, имеют одинаковую длину и нагружены одинаковыми растягивающими усилиями. Медная проволока имеет диаметр D=1мм. Чему равен диаметр стальной проволоки, если обе проволоки удлиняются на одинаковую величину. Принять Е_ст=2∙10⁵ МПа, Е_м=1∙10⁵ МПа

1. D≈0,9 мм;

2. D≈0,71 мм;

3. D≈1,9 мм;

4. D≈0,98 мм.

- Стальной брус квадратного сечения под действием нагрузки удлиняется в продольном направлении на величину ∆l=3,2∙10^–2 мм, а в поперечном направлении сжался на ∆h=0,03∙10^–2 мм. Найти коэффициент Пуассона μ, если l=30 см; h=1 см

1. μ=0,28;

2. μ=0,25;

3. μ=0,3;

4. μ=0,2.

- Проволока длиной l=10м под действием растягивающей силы F=800 Н удлинилась на ∆l=15 мм. Определить модуль упругости Е, если A=4 мм².

1. Е=2,05∙10⁵ МПа;

2. Е=1∙10⁵ МПа;

3. Е=1,33∙10⁵ МПа.

- Стальной образец диаметром D=20 мм и расчётной длиной l=200мм растянут на испытательной машине. Длина деформированного образца l₁=200,15мм. Определить растягивающее усилие, приняв модуль Е=2∙10⁵ МПа.

1. N=47,1кН;

2. N=36,2кН;

3. N=38кН;

4. N=76,2кН.

- При подвешивании некоторого груза к стальной проволоке (Е=2∙10⁵ МПа) длиной 3 м и диаметром 1,6 мм её удлинение оказалось равным 1,5 мм. Затем тот же груз был подвешен к медной проволоке длиной 1,8 м с диаметром 3,2 мм, и в этом случае удлинение получилось равным 0,39 мм. Определить модуль упругости медной проволоки.

1. Е=2,05∙10⁵ МПа;

2. Е=1,15∙10⁵ МПа;

3. Е=1,33∙10⁵ МПа.

- Чугунная колонна (Е=2∙10⁵ МПа) кольцевого поперечного сечения имеет наружный диаметр 30 см и толщину стенки 30 мм. Определить относительное укорочение колонны при нагрузке 600 кН, если высота колонны 4 м.

1. ε = 0,78;

2. ε = 1,95∙10^-4;

3. ε = 1,95∙10^-2;

4. ε = 0,95∙10^-2.

- Выбрать соответствующую эпюру продольных сил в поперечных сечениях бруса

1. А;

2. В;

3. С;

4. Соответствующей эпюры не представлено.

- Для бруса определить наибольшую продольную силу, возникшую в поперечном сечении

1. -16 кН;

2. -38 кН;

3. 70 кН;

4. -54 кН.

- Стальной стержень длиной 3 м нагружен силой 240 кН; форма поперечного сечения стержня - швеллер №10; модуль упругости материала Е=2∙10⁵ Мпа

Определить удлинение стержня АВ.

1. 3,5 мм;

2. 3,3 мм;

3. 12·10 ^{– 4} мм;

4. 12·10^-3 мм.

- Выбрать соответствующую эпюру продольных сил в поперечных сечениях бруса

1. А;

2. Б;

3. В;

4. Г.

- Для бруса определить наибольшую продольную силу, возникшую в поперечном сечении

1. 306 кН;

2. 70 кН;

3. 100 кН;

4. -30 кН.

- Выбрать соответствующую эпюру продольных сил в поперечных сечениях бруса

1. А;

2. Б;

3. В;

4. Г.

- Для бруса определить наибольшую продольную силу, возникшую в поперечном сечении

1. 190 кН;

2. 50 кН;

3. 85 кН;

4. 35 кН.

- Стальной стержень длиной 4 м нагружен силой 360 кН, форма поперечного сечения стержня - швеллер №8, модуль упругости материала Е=2∙10⁵ МПа.

Определить удлинение стержня АВ

1. Среди данных ответов верного нет;

2. 0,007 мм;

3. 0,2 мм;

4. 8 мм.

- Выбрать соответствующую эпюру продольных сил в поперечных сечениях бруса

1. А;

2. Б;

3. В;

4. Г.

- Для бруса определить наибольшую продольную силу, возникшую в поперечном сечении

1. 20 кН;

2. 90 кН;

3. 50 кН;

4. 70 кН.

- Выбрать соответствующую эпюру продольных сил в поперечных сечениях бруса

1. А;

2. Б;

3. В;

4. Г.

- Для бруса определить наибольшую продольную силу, возникшую в поперечном сечении

1. 30 кН;

2. 40 кН;

3. 70 кН;

4. 100 кН.

- Определить общее изменение длины бруса, если А=10 см², l=1 м, Е=2·10⁵ МПа, F = 20 кН.

1. ∆l = 0,3 мм;

2. ∆l = 0,45 мм;

3. ∆l = 0,58 мм;

4. ∆l = 4,5 мм.

- Определить изменение длины бруса. Если F=10 кН, A=2 см², Е=2∙10⁵ МПа, l=0,2 м

1. ∆l = –0,15 мм;

2. ∆l = –2 мм;

3. ∆l = –3 мм;

4. ∆l = 4,5 мм.

- Если F = 250 кН, А = 25 см² , l = 0,5 м, Е = 200 ГПа, а = 0,4 м, то изменение длины среднего участка (в мм) составит

1. 0,2

2. 0,3

3. 0,4

4. 0,5

- Ступенчатый брус при нагружении заданными силами укоротится на величину, кратную

1.

2.

3.

4.

- Считая перемещение влево положительным и полагая , определите перемещение сечения В

1.

2.

3.

4. 2

- Деформация, замеренная тензометром Т, равна ε = 1,5∙10^{-4 .} Какова величина силы F (в кН), если ЕА = 200 МН?

1. 60

2. 80

3. 100

4. 120

- К стержню приложено несколько осевых сил. Если F=50 кН, площадь поперечного сечения A=25см², l=0,4 м и модуль продольной упругости Е=2∙10¹¹ Па, то изменение длины среднего участка ∆l_cp в мм равно:

1. 0,04;

2. 0,06;

3. 0,08;

4. 0,10.

- Если к ступенчатому стержню, участки которого имеют площади поперечного сечения соответственно А и 3А, а модуль продольной упругости Е, приложены две осевые силы F и 2F, то длина всего стержня уменьшается на величину ∆l:

1. _;

2. _;

3. _;

4. _;

- Если ступенчатый стержень нагружен силами F и 3F, а А – параметр величины поперечного сечения, то перемещение сечения I–I λ₁ (перемещение вправо считается положительным) равно:

1. _;

2. _;

3. ;

4. _.

- Если на ступенчатый стержень действуют две осевые силы А и их величины известны, так же, как известны размер a, параметр величины площади поперечного сечения A, и модуль продольной упругости E, то сечение I-I приблизится к опоре В на величину λ₁, равную:

1. _;

2. _;

3. _;

4.

- Для стержня, схема которого изображена на рисунке, продольная сила N в сечении 2-2 будет…

1. равной нулю;

2. равномерно распределенной по сечению;

3. растягивающей;

4. сжимающей.

- Для стержня круглого поперечного сечения, схема которого изображена на рисунке, абсолютное удлинение ∆L равно…

1.

2.

3.

4. 0.

- Стержень нагружен системой сил. Модуль упругости материала Е, площадь поперечного сечения А, размер а, значение силы F заданы. Продольная деформация на участке СК равна …

1.

2.

3.

4.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00