Главная

Тестовые вопросы по теме «Расчет стержневых систем на осевое растяжение-сжатие»

 

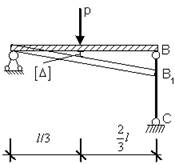
- Если стержень ВС одинаково работает на растяжение и сжатие, то проверку на жесткость проводят по условию…

6F4F684D4666B7180627DC73FD7012D3

1.

2.

3.

4.

 

- Если стержень ВС одинаково работает на растяжение и сжатие, то проверку прочности проводят по условию...

1. ;

2. ;

3. ;

4.

 

- Проверку на прочность стержня АВ, имеющего разные допускаемые напряжения на растяжение  и сжатие , проводят по формуле...

1. ;

2. ;

3. ;

4. .

 

- Пусть , - допускаемые изменения длины стержня ВС при растяжении и сжатии,  - абсолютное удлинение-укорочение стержня ВС. Тогда проверку на жесткость стержня ВС проводят по условию...

1. ;

2. ;

3. ;

4. .

 

- Проверку на прочность стержня ВС, имеющего разные допускаемые напряжения на растяжение  и сжатие проводят по формуле...

1.

2. ;

3. ;

4. .

 

- Проверку на прочность стержня АВ, имеющего разные допускаемые напряжения на растяжение  и сжатие , проводят по формуле...

1. ;

2. ;

3. ;

4. .

 

- Если стержень ВС одинаково работает на растяжение и сжатие, то проверку прочности проводят по условию...

1. ;

2.;

3. ;

4. .

 

- Если стержень ВС одинаково работает на растяжение и сжатие, то проверку на жесткость проводят по условию....

1.  

2. ;

3. ;

4..

 

- Однородная жесткая плита весом G= 20 кН нагружена силой F= 10 кН. Длина стержня АВ =4м; материал - сталь Е=2∙105 МПа; форма поперечного сечения - двутавр №10. Определить удлинение стержня АВ

1. 0,27 мм;

2. 0,4 мм;

3. 0,2 мм;   

4. 0,615 мм.

 

- Однородная жесткая плита весом G= 4 кН нагружена силой F= 2 кН. Длина стержня АВ = 6 м, материал - сталь Е=2∙105 Мпа, форма поперечного сечения - швеллер №6,5.

Определить удлинение стержня АВ

 

 

 

 

 

 

 

 

 

1. 0,03 мм;

2. 0,02 мм;

3. 0,12 мм;

4. 0,18 мм.    

 

- Однородная жесткая плита весом G= 10 кН нагружена силой F= 8 кН. Длина стержня  АВ= 3 м, материал - сталь Е=2∙105 МПа, форма поперечного сечения - двутавр № 10.

Определить удлинение стержня АВ.

1.  0, 023 мм;

2.  0,084 мм;   

3.  0,125 мм;

4.  0,84 мм.

 

- Если F = 30 кН, А1 = 5 см2 , l = 0,5 м, Е = 200 ГПа, то удлинение стержня 1 (в мм) составит

Подпись: l

1. 0,1    

2. 0,2    

3. 0,3    

4. 0,5

 

- Стержни кронштейна, изготовленные из одного материала с коэффициентом линейного расширения α нагреваются на ∆T  градусов. При этом вертикальное перемещение узла В составит, полагая .

Подпись: l

1. ;

2.  ;

3.  ;

4.  .

 

- Наибольшее напряжение в конструкции равно, полагая F/A=σ0

Подпись: l

1.             

2.                         

3.                          

4.

 

- Если предел текучести материала стержней равен σT, то при нагружении заданной силой F  запас прочности конструкции равен, полагая

1. 1,3n0

2. 1,4n0

3. 1,5n0

4. 1,6n0

 

- Тензометр Т, прикрепленный вдоль оси стержня 1, показывает деформацию ε1 = 4·10-4 . Чему равна величина силы F (в кН), если площадь поперечного сечения стержня А = 10 см2 ,и модуль Юнга Е= 200 ГПа?

1. 60

2. 70         

3. 80         

4. 90

 

- Если А1 = 10 см2 , А2 = 16 см2 , [σ] = 160 МПа, то грузоподъемность кронштейна G (в кН) равна

1. 160   

2. 172   

3. 181   

4. 190

 

- Если F = 200 кН,  = 200 МПа, А1 = 16 см2 ,  = 340 МПа, А2 = 10 см2, то фактический запас прочности конструкции равен

1. 1,5    

2. 1,6    

3. 1,7    

4. 1,8

 

- При нагружении заданной стержневой системы силой F отношение  удлинений  стержней 1 и 2 численно равно

1. 2,0    

2.            

3.  0,5     

4.

 

- Считая известными размеры а, l, ∆, площадь поперечного сечения A и модуль Юнга Е, определите монтажное усилие в  стержне 2 после сборки системы, полагая

Подпись: lПодпись: Δ

1. 0,1N0

2. 0,2N0

3. 0,3N0    

4. 0,4N0

 

- Для разгрузки вертикального стержня 1 дополнительно установлены стержни 2. Если все три стержня абсолютно одинаковы, то за счет установки наклонных стержней 2 разгрузка стержня 1 (в процентах) составит

1.  23

2.  28       

3.  33       

4.  43

 

- Жесткий брус ВД подвешивается на трех титановых стержнях, каждый из которых короче проектной длины на 0,1%. Если Е = 100 ГПа, то после сборки системы наибольшее монтажное напряжение составит (в МПа)

Подпись: 2lПодпись: lПодпись: l

1.  20       

2.  40      

3.  60       

4.  80

 

- Система состоит из трех одинаковых стальных стержней (Е = 200 ГПа, α= 12,5∙10-6). На сколько градусов нужно нагреть всю систему, чтобы наибольшее напряжение достигло величины 100 МПа?

1. 40°      

2. 50°     

3. 60°      

4. 80°

 

- При нагреве стержня 3 на ∆T градусов во всех стержнях системы возникли усилия. Какой температурный режим нужно создать для стержня 1, чтобы эти усилия исчезли?

Подпись: l

1. охладить на ∆T                 

2. нагреть на ∆T

 

- Определите наибольшее по модулю напряжение в системе, полагая F/A=σ0

Подпись: l

1.  

2.

3.

4.

 

- Если все стержни системы нагреть на одно и то же число ∆T  градусов, то при заданных величинах ЕА и α усилие в стержне 2 будет равно, полагая  

Подпись: 2lПодпись: l

1. 0               

2. N0        

3. 1,5N0       

4. 2N0

 

- Стержни 1 и 2 имеют одинаковую жесткость c=EA/l, причем стержень 1 изготовлен короче проектной длины на величину ∆. После сборки системы в стержне 1 возникнет монтажное усилие, равное

Подпись: lПодпись: Δ

1.                                           

2.                                     

3.                                     

4.  

 

- Стальной стержень помещен между двумя медными стержнями. Все три стержня жестко соединены по концам. Если αС =12,5·10-6, Ес = 200 ГПа, αМ = 16,5·10-6, Ем = 100 ГПа, то при нагревании системы на 50° в стальном стержне возникнут напряжения, равные (в МПа)

Подпись: tПодпись: tПодпись: t

1. 15     

2. 20     

3. 25     

4. 30

 

- Для разгрузки стержня 1 вводится дополнительный стержень 2 (показан пунктиром), совершенно аналогичный стержню 1. В результате напряжение в стержне 1 уменьшится на величину (в процентах)

Подпись: l

1. 15                                

2. 20         

3. 25         

4. 30

 

- При нагружении системы силой F относительная деформация стержня 1, замеренная тензометром, составила величину ε = 5·10-4. Если А = 15 см2, Е = 200 ГПа, то величина силы равна (в кН)

Подпись: 1,5lПодпись: l

1. 100     

2. 200    

3. 300     

4. 400

 

- Брус CD подвешен на трех стержнях. На какую величину ∆l1 в мм удлинится левый стержень, если сила F=30 кН, площадь поперечного сечения A=5 см2, длина l =0,5 м и модуль продольной упругости E=2∙1011 Па?

1.   0,1;     

2.   0,2;

3.   0,3;

4.   0,5.

 

- Для разгрузки вертикально стержня, нагруженного силой F, установлены два наклонных дополнительных стержня. Если все три стержня сделаны из одного материала, имеют одинаковую длину (l) и площадь поперечного сечения (А), то вертикальный стержень разгружается на … процентов.

1.   18%; 

2.   23%;

3.   28%; 

4.   33%.

 

- Недеформируемый брус АВ подвешен на трех стержнях, имеющих площади поперечного сечения соответственно 2А, 1,5А и А. Если приложить горизонтальную силу F, то наибольшее напряжение σмах станет равным:

1.  ;

2. 

3. 

4. 

 

- Если два стержня (CL и DK) удерживают в равновесии недеформируемый брус CD, а A – параметр величины поперечного сечения, то модуль наибольшего напряжения равен:

1. ;

2. ;

3.

4. .

 

- Стержень I поддерживает недеформируемый брус СD (рис I).  Для уменьшения напряжений (σ1) в этом стержне вводится дополнительный стержень II (рис. II) такого же поперечного сечения А. В результате напряжение в стержне I уменьшится на… процентов.

1.   20;     

2.   30;

3.   40;

4.   50.

 

- Если принять допускаемое напряжение [σ] = 160 МПа, то грузоподъемность кронштейна Q равна приближенно в кН:

1. 85;

2. 93;    

3. 100;

4. 108.

 

- Если сила F, параметр величины площади поперечного сечения А и предел текучести σT известны, то фактический коэффициент запаса прочности n равен:

1. ;

2. ;

3. ;

4. .

 

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

 

Теоретическая механика   Строительная механика

Прикладная механика  Детали машин  Теория машин и механизмов

 

 

 

00:00:00

 

Top.Mail.Ru