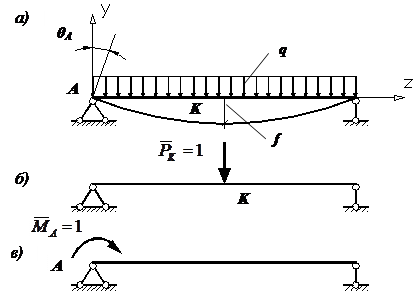
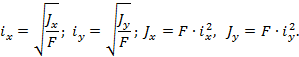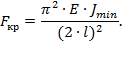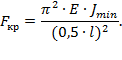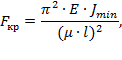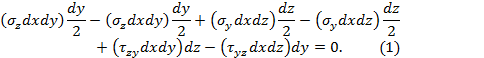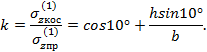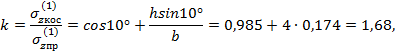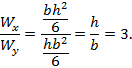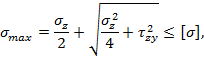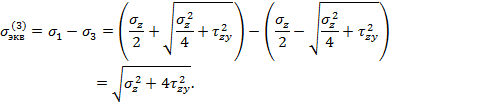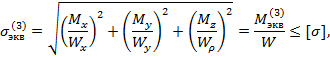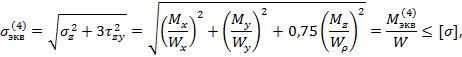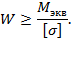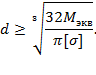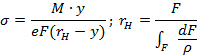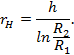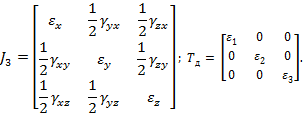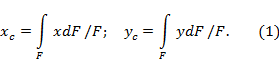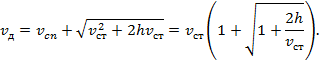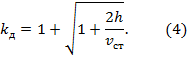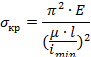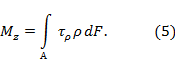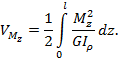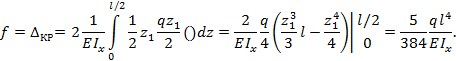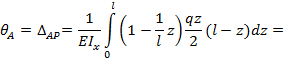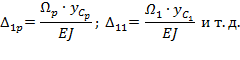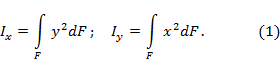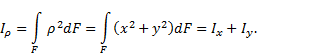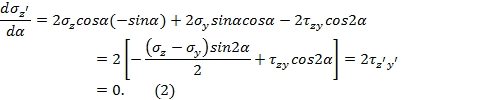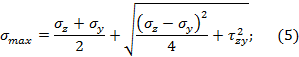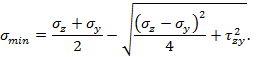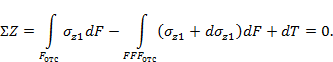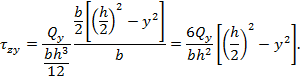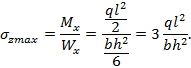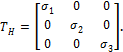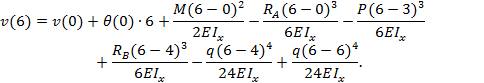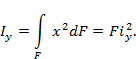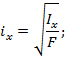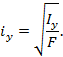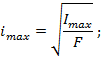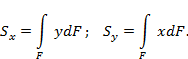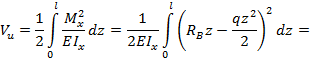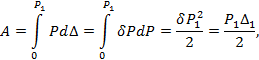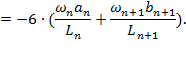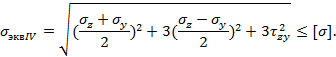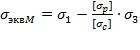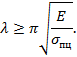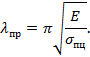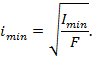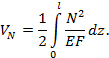Главная

Глоссарий

А

Абсолютная поперечная деформация стержня	определяется как разность поперечных размеров стержня до и после деформации.
Амплитуда колебаний	наибольшее смещение упругой системы от положения статического равновесия.
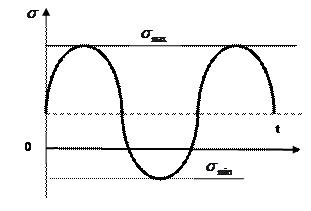
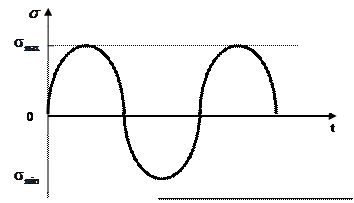
Амплитуда цикла напряжений	наибольшее числовое положительное значение переменной составляющей цикла напряжений, равная алгебраической полуразности максимального и минимального напряжения цикла
Аналогия гидродинамическая	Если отверстие трубы и скручиваемый стержень будут иметь одинаковый профиль, то линии тока совпадут с силовыми линиями. Благодаря этому, можно судить о распределении касательных напряжений в стержнях при кручении по распределению скоростей движения жидкости в трубе того же профиля.
Аналогия мембранная	Если тонкую пластинку с отверстием, совпадающим с профилем скручиваемого стержня, покрыть тонкой пленкой (мембраной), то под действием равномерно распределенной нагрузки пленка в отверстии провиснет, образуя поверхность, горизонтали которой располагаются аналогично силовым линиям при кручении. Эта дает возможность составить картину распределения касательных напряжений по расположению горизонталей поверхности мембраны.
Ассиметричный цикл	максимальное и минимальное напряжения не равные по абсолютной величине. При этом асимметричный цикл может быть знакопеременным или знакопостоянным.

Б

База испытаний	предварительно задаваемое наибольшее число циклов при испытании на усталость.
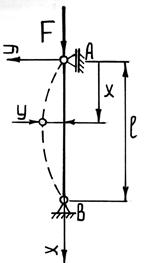
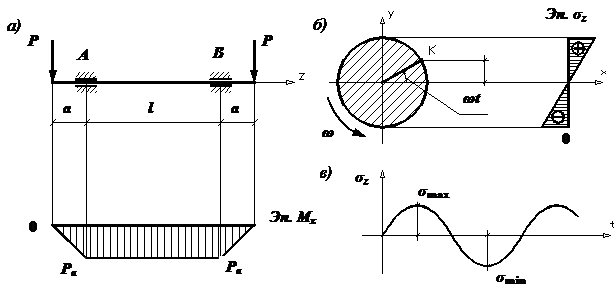
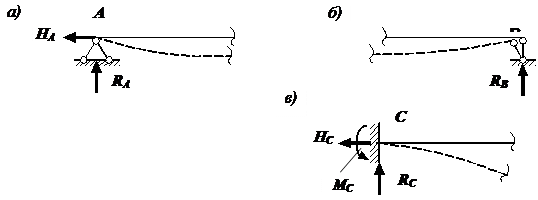
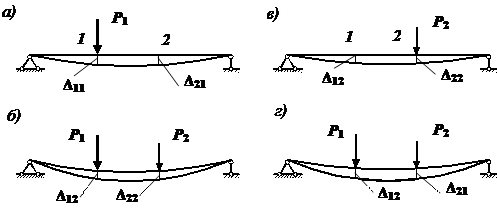
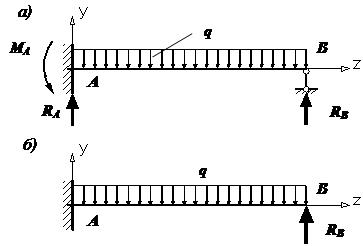
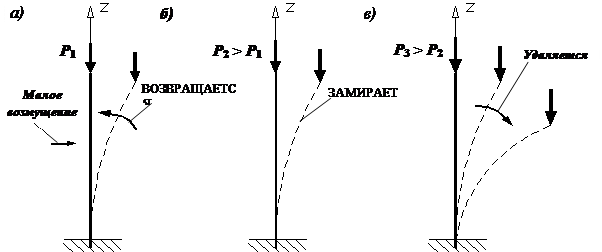
Балка	брус, нагруженный внешними силами, перпендикулярными его оси, и работающий главным образом на изгиб. В сопротивлении материалов рассматриваются три типа балок. Рис. 1. Типы балок: а – жестко защемленная балка (или консоль); б – простая балка (или шарнирно опертая балка); в – шарнирно опертая балка с консолями Расчетные схемы этих балок и их названия указаны на рис. 1. Консолью называют часть балки, расположенную по одну сторону от опоры. Расстояние между шарнирными опорами называется пролетом балки и обозначается l.
Брус	тело, два измерения которого малы по сравнению с третьим.

В

Вал	брус, нагруженный парами сил, лежащими в плоскости поперечного сечения, и работающий на кручение.
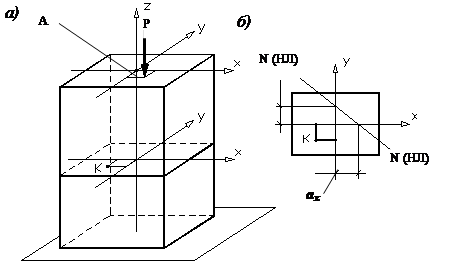
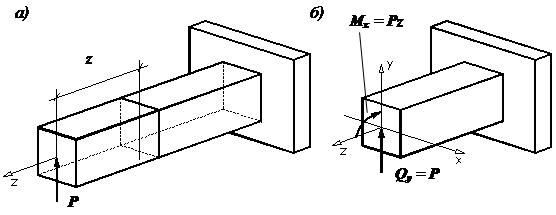
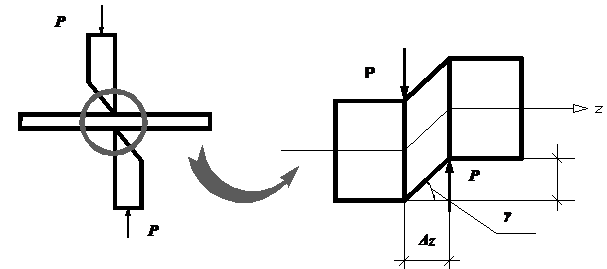
Внецентренное растяжение-сжатие	растяжение или сжатие стержня, при котором равнодействующая внутренних сил направлена по нормали к поперечному сечению, но не проходит через его центр тяжести или когда в поперечных сечениях стержня возникают только три силовых фактора: продольная сила N и два изгибающих момента Mx и My (рис.1). Рис.1. Внецентренное сжатие Будем считать, что стержень обладает большой жесткостью на изгиб. Это допущение мы будем использовать при вычислении изгибающих моментов от продольной силы P, пренебрегая прогибом стержня. Задача о внецентренном сжатии стержня (массивной колонны) впервые была рассмотрена Юнгом в 1802 г. Определим внутренние усилия и напряжения при внецентренном сжатии. Пусть сжимающая сила P приложена в некоторой точке A с координатами xp и yp в главных центральных осях инерции x и y (см. рис. 1, а). Тогда, с учетом принятого нами допущения, N=-P; ; . Точные значения изгибающих моментов определяются по формулам где v и u – прогибы рассматриваемого поперечного сечения стержня в направлении осей x и y соответственно. Принятое нами выше допущение о большой жесткости стержня на изгиб заключается в предположении, что v<<yp; u<<xp. Напряжения в произвольной точке K с координатами x и y равны: где, согласно принципу независимости действия сил, первое слагаемое представляет собой напряжение от сжатия, а второе и третье – от изгиба. Значения изгибающих моментов и координат исследуемой точки K подставляются в формулу (1) по абсолютному значению, а знак второго и третьего слагаемых определяется по физическому смыслу. N>0 – если сила растягивающая, Mx, My>0, если моменты "растягивают" сечение в I-ой четверти. Определим положение нейтральной линии. Преобразуем формулу (1), подставляя в нее значения изгибающих моментов: Обозначим координаты некоторой точки нулевой линии xN и yN. Подставим эти координаты в (2) вместо x и y соответственно, а также учтем, что напряжения в точках нейтральной линии равны нулю. После сокращения на P/F получим уравнение нейтральной линии: Таким образом, положение нулевой линии зависит от значений главных радиусов инерции поперечного сечения ix, iy и координат точки приложения нагрузки xp, yp и совершенно не зависит от величины силы P. Важно также отметить, что нейтральная линия и точка приложения нагрузки всегда расположены по разные стороны от центра тяжести поперечного сечения (см. рис. 1, б). Определим отрезки, отсекаемые нейтральной линией от осей координат. Эти отрезки, которые мы обозначим через ax и ay (см. рис. 1, б), легко найти из выражения (3). Если сначала в нем принять xN=0, yN=ay, а затем – yN=0, xN=ax, то мы легко найдем, что отрезки, отсекаемые нейтральной линией от осей координат, определяются по формулам Ядром сечения называется малая область вокруг центра тяжести поперечного сечения стержня. Она характеризуется тем, что всякая сжимающая сила, приложенная внутри этой области, вызывает во всех точках поперечного сечения (и соответственно во всем стержне) только напряжения сжатия. 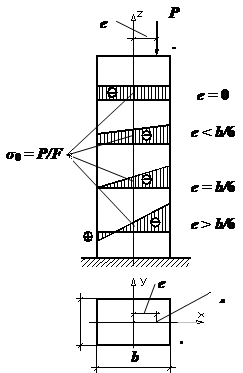Понятие о ядре сечения впервые ввел Бресс в 1854 г. Рассмотрим следующий пример. Пусть стержень имеет прямоугольное поперечное сечение с размерами b и h и одна из координат точки приложения нагрузки (точка A) равна нулю, например xP=0, yP=0 (рис. 2). Рис.2. Ядро сечения Тогда напряжения в крайних точках K и L поперечного сечения стержня будут определяться по формулам Из этих формул видно, что при е=0 во всех точках поперечного сечения, в том числе и в крайних точках K и L, будут возникать одинаковые сжимающие напряжения. При e < b/6 напряжения по-прежнему будут сжимающими, но будут изменяться по ширине сечения. При e = b/6 в точках K и L они будут равны: Если e > b/6, то нейтральная линия разделит поперечное сечение на две части. В одной из них напряжения будут сжимающими, а в другой – растягивающими. Для всех этих случаев (см. рис. 2) показаны эпюры напряжений. Таким образом, если мы не хотим, чтобы в поперечном сечении внецентренно сжатого стержня возникали растягивающие напряжения (а многие строительные материалы, как известно, очень плохо работают на растяжение), то эксцентриситет нагрузки не должен выходить за некоторую область вокруг центра тяжести этого сечения. 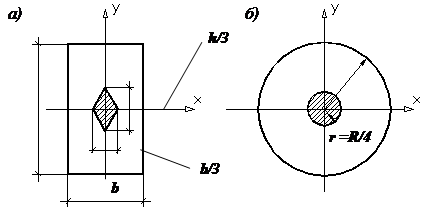Эту область и называют ядром сечения. Определим форму ядра сечения для прямоугольного и для круглого поперечных сечений стержня. Рис.3. Форма ядра для прямоугольного и круглого ядра сечения Для прямоугольника ядро сечения имеет форму ромба (рис. 3, а), а для круглого сплошного стержня – круга (рис. 3, б). Заметим, что для любого поперечного сечения форма ядра всегда представляет собой выпуклую фигуру.
Внешние силы	силы, действующие со стороны какого-либо тела или системы на рассматриваемое тело или систему. К внешним силам относятся не только активные силы (нагрузка), но и реакции связей или опор. Внешние силы, действующие на конструкцию, делятся на активные, которые принято называть нагрузками, и реактивные – реакции связей. По способу приложения нагрузки могут быть объемными (собственный вес, силы инерции), то есть действующими на каждый бесконечно малый элемент объема, и поверхностными. Поверхностные нагрузки делятся на сосредоточенные и распределенные. Нагрузки, распределенные по некоторой поверхности и действующие по направлению нормали к этой поверхности, характеризуются давлением, то есть отношением силы, действующей на элемент поверхности, к площади данного элемента. В Международной системе единиц (СИ) давление измеряется в паскалях, мегапаскалях (1 ПА = 1 Н/м^2; 1 МПа = 10^6 Па) и т.д., а в технической системе – в килограммах силы на квадратный миллиметр и т. д. (кгс/мм^2, кгс/см^2). В сопротивлении материалов часто рассматриваются поверхностные нагрузки, распределенные по длине элемента конструкции. Такие нагрузки характеризуются интенсивностью, обозначаемой обычно буквой q и выражаемой в ньютонах (килоньютонах) на метр (Н/м, кН/м) или в килограммах силы на метр (кгс/м) и т. д. Реальные нагрузки, действующие на конструкцию, не всегда могут быть сведены лишь к сосредоточенным и распределенным нагрузкам. Возможны и моментные воздействия, например, в виде сосредоточенных моментов. Последние выражаются в единицах силы, умноженных на единицу длины (кН∙м, кгс∙м и т.д.). Напомним, что термины «сосредоточенный момент», «пара», «плечо» были введены в 1804 г. французским ученым Луи Пуансо (Poinsot, 1777–1859 гг.). По характеру изменения во времени нагрузки бывают статические (нарастающие медленно от нуля до своего конечного значения и в дальнейшем не изменяющиеся) и динамические (изменяющиеся с течением времени свою величину и (или) точку приложения и при этом изменяющие их достаточно быстро).
Внутренние силы	силы взаимодействия между мысленно рассеченными частями материального тела. Иначе: силы упругости, силы сопротивления, усилия. Для нахождения величины и направления внутренних усилий мысленно рассекают стержень сечением, перпендикулярным продольной оси стержня, это позволит отбросить ненужный для расчета элемент конструкции (или часть этого элемента), заменить его силой, действие которой будет эквивалентно действию отброшенного элемента (его части). Для определения этой силы нужно использовать уравнения равновесия (уравнения статики).
Возмущающая сила	сила, действующая на упругое основание со стороны возбудителя, вызывающая вынужденные колебания системы.
Временное сопротивление (предел прочности)	максимальное напряжение (определенное без учета изменения площади поперечного сечения в процессе нагрузки) выдерживаемое материалом при растяжении. Для стали марки Ст3 временное сопротивление σв=370…470 МПа.
Выносливость	способность материалов сопротивляться разрушению при действии повторно-переменных напряжений.
Вынужденные колебания	движение упругой системы, происходящее под действием изменяющихся внешних сил, называемых возмущающими.
Вязкость	способность материала сопротивляться образованию пластических деформаций.

Г

Геометрически изменяемая система	такая система, элементы которой могут перемещаться под действием внешних сил без деформации (механизм).
Геометрически неизменяемая система	такая система, изменение формы которой возможно лишь в связи с деформациями ее элементов.
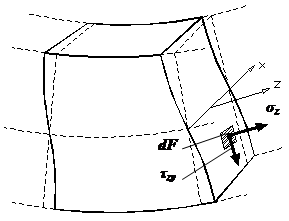
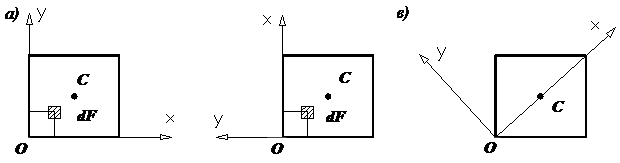
Геометрические характеристики сечений	числовые величины (параметры), определяющие размеры, форму, расположение поперечного сечения однородного по упругим свойствам деформируемого элемента конструкции (и, как следствие, характеризующие сопротивление элемента различным видам деформации). Площадь поперечного сечения ; статический момент относительно оси x или y равен произведению всей площади фигуры на расстояние от ее центра тяжести до этой оси. Размерность статических моментов площади м^3. Статические моменты площади могут быть положительны, отрицательны и равные нулю: координаты центра тяжести: осевой момент инерции относительно рассматриваемой оси – сумма произведений элементарных площадей dF на квадрат их расстояний до этой оси, взятая по всей площади сечения F. полярный момент инерции относительно данной точки – сумма произведений элементарных площадей dF на квадраты их расстояний () до этой точки, взятая по всей площади сечения F: ; центробежный момент инерции относительно осей координат – сумма произведений элементарных площадей dF на их расстояния до этих осей, взятая по всей площади сечения F: . Центробежный момент инерции имеют размерность м^4 и может быть положительным, отрицательным и равным нулю. Оси, относительно которых центробежный момент инерции равен нулю, называются главными центральными осями. Прямоугольник: Круг: Четверть круга: Моменты инерции относительно параллельных осей: . Моменты инерции при повороте осей: ; ; . Угол, определяющий положение главных осей: Моменты инерции относительно главных центральных осей инерции: Радиус инерции: Осевой момент сопротивления относительно рассматриваемой оси – величина равная моменту инерции относительно той же оси отнесенному к расстоянию до наиболее удаленной от этой оси точки: для прямоугольника: для круга: трубчатое сечение (кольцо): Полярный момент сопротивления: Для круга:
Гибкость стержня
Гипотезы прочности	Гипотезы, указывающие критерии эквивалентности различных напряженных состояний (НС), называют гипотезами прочности. Приведем и другие, используемые в учебниках по сопротивлению материалов, названия: теории предельных напряженных состояний, теории прочности и т. д. Как следует из изложенного, применение гипотез прочности избавляет нас от необходимости проведения огромного количества экспериментов. Тот или иной критерий эквивалентности может быть основой для практических расчетов на прочность лишь при условии, что для ряда частных случаев он проверен опытным путем и результаты эксперимента оказались достаточно близкими к результатам теоретического расчета. Будем называть два НС эквивалентными, если они одновременно переходят в предельные при увеличении соответствующих им главных напряжений в одно и то же число раз. Это означает, что коэффициенты запаса прочности для эквивалентных НС одинаковы. Остается решить вопрос, что же является критерием эквивалентности различных по характеру НС. Если решение этого вопроса каким-то образом найдено (его как раз и дают гипотезы прочности), тогда для расчета стержня на прочность в случае сложного НС его следует заменить на эквивалентное одноосное растяжение (сжатие) и сравнить соответствующее ему эквивалентное напряжение σэкв=f(σ1, σ2, σ3) с предельным (или допускаемым) напряжением для данного материала. Определение истинной причины разрушения материала является труднейшей задачей. Это обстоятельство не позволило до настоящего времени создать единую общую гипотезу прочности и повлекло за собой появление многих теорий, каждая из которых основывается на своей гипотезе о причине разрушения материала. Независимо от принятой гипотезы прочности условие прочности после определения эквивалентного напряжения представляется в виде одного из следующих неравенств: или, при заданном коэффициенте запаса,
Гипотеза прочности первая (гипотеза наибольших нормальных напряжений)	Первая гипотеза прочности основывается на предположении о том, что причиной разрушения материала являются наибольшие по абсолютному значению нормальные напряжения. Эту, самую простую и старую, гипотезу, предложенную еще Галилеем, называют гипотезой наибольших нормальных напряжений. Условие прочности по первой гипотезе прочности имеет вид: В случае, когда наибольшим по абсолютному значению будет сжимающее главное напряжение |σ3|, условие (1) записывается в виде: Существенный недостаток первой гипотезы виден из приведенных выше двух формул. Заключается он в том, что при определении эквивалентного напряжения совершенно не учитываются два других главных напряжения, оказывающих, естественно, большое влияние на прочность материала. Эта гипотеза подтверждается экспериментальными данными только для хрупкого материала и только при растяжении, когда главные напряжения σ2, σ3 значительно меньше, чем σ1. При всестороннем сжатии, например, цементного кубика она приводит к ошибочным результатам, поскольку кубик выдерживает напряжения, во много раз превышающие предел прочности при одноосном сжатии. В настоящее время эта гипотеза прочности не применяется и имеет лишь историческое значение.
Гипотеза прочности вторая (гипотеза наибольших линейных деформаций)	Отмеченные недостатки первой гипотезы прочности привели к появлению второй гипотезы прочности, предложенной Мариоттом и затем развитой Сен-Венаном. Согласно этой гипотезе, называемой гипотезой наибольших линейных деформаций, причиной разрушения являются наибольшие линейные деформации. Условие прочности по этой гипотезе записывается в виде: где μ – коэффициент Пуассона. Отметим следующее. Вторая гипотеза прочности предполагает, что для пластичных материалов закон Гука выполняется вплоть до предела текучести, а для хрупких – до предела прочности, что, конечно, является чересчур грубым допущением. Достоинством же этой гипотезы является то, что при вычислении эквивалентного напряжения она учитывает все три главных напряжения. С помощью этой гипотезы можно объяснить разрушение хрупких материалов при простом сжатии. Однако, как и первая гипотеза, вторая гипотеза прочности недостаточно подтверждается опытами и поэтому в настоящее время не применяется.
Гипотеза прочности третья (гипотеза наибольших касательных напряжений)	Согласно этой гипотезе, которую называют также гипотезой наибольших касательных напряжений, причиной разрушения материала являются наибольшие касательные напряжения. Линии Людерса, разрушение по наклонной плоскости образца из хрупкого материала, образование воронки при разрыве – все это указывает на большую роль, которую играют касательные напряжения. Согласно третьей гипотезе, максимальное касательное напряжение для заданного объемного НС и эквивалентного ему линейного НС одинаковы, то есть Напомним, что в случае объемного напряженного состояния наибольшее касательное напряжение определяется по формуле Эквивалентное напряжение при одноосном растяжении равно: С учетом формул (1) и (2), условие прочности по третьей гипотезе прочности принимает вид: Недостатком этой гипотезы является то, что она не учитывает второго главного напряжения σ2. Опыты показывают, что для пластичных материалов гипотеза наибольших касательных напряжений дает удовлетворительные результаты. Ошибка от пренебрежения влиянием σ2 не превышает обычно 10 – 15%. Третья гипотеза прочности впервые была высказана Кулоном. Критерий наибольших касательных напряжений был предложен им в 1773 г. Условие наступления пластического состояния впервые выдвинул в 1868 г. французский инженер Анри Эдуард Треска (Treska, 1814 – 1885 гг.). Затем это условие было математически сформулировано Сен-Венаном.
Гипотеза прочности четвертая (энергетическая)	Энергетическая гипотеза прочности строится на предположении о том, что количество удельной потенциальной энергии изменения формы, накопленной к моменту наступления предельного состояния материала, одинаково как при сложном напряженном состоянии, так и при простом одноосном растяжении. Необходимо обратить внимание на то, что в этой гипотезе речь идет не обо всей удельной потенциальной энергии деформации, а лишь о той ее части, которая накапливается за счет изменения формы кубика с ребром, равным единице. В общем случае полная удельная потенциальная энергия деформации может быть представлена как сумма энергий, связанных с изменением объема кубика и изменением его формы. Условие прочности по четвертой гипотезе прочности приведем без вывода: Очевидным достоинством этой теории является то, что эквивалентное напряжение определяется значениями всех трех главных напряжений. Энергетическая гипотеза прочности хорошо согласуется с опытными данными для пластичных материалов. Для них она приводит к несколько лучшим результатам, чем гипотеза наибольших касательных напряжений. Идею энергетического критерия прочности материала впервые предложил в 1856 г. английский ученый Джеймс Клерк Максвелл (Maxwell, 1831 – 1879 гг.). В 1885 г. ее развил итальянский ученый Эудженио Бельтрами (Beltrami, 1835 – 1900 гг.). В 1904 г. польский ученый Максимилиан Тытус Губер (Huber, 1872 – 1950 гг.) и в 1911 г. немецкий ученый Рихард Мизес (Mises, 1883 – 1953 гг.) завершили разработку этой теории прочности.
Гипотеза прочности Мора	Согласно этой гипотезе, которую в 1900 г. предложил немецкий ученый Отто Христиан Мор (Mohr, 1835–1918 гг.), два напряженных состояния равноопасны, если для соответствующих главных напряжений соблюдается соотношение: Тогда условие прочности по гипотезе прочности Мора имеет вид: (2) Из формулы (2) видно, что данная гипотеза прочности не учитывает влияния второго главного напряжения σ2. В (1) и (2) коэффициент v представляет собой отношение предельных напряжений, соответствующих одноосным растяжению и сжатию, то есть этот коэффициент равен: - для хрупких материалов - для пластичных v=1. Гипотеза прочности Мора может быть рекомендована для хрупких материалов. Для пластичных материалов она тождественна третьей гипотезе прочности.
Гипотеза плоских сечений (гипотеза Бернулли)	Многочисленные эксперименты показывают, что при растяжении стержня продольные и поперечные риски, нанесенные на его поверхности до деформации, остаются практически прямолинейными и взаимно перпендикулярными между собой и после деформации стержня. Изменяются лишь расстояния между ними. Причем между поперечными рисками расстояния увеличиваются, а между продольными – уменьшаются. Можно предположить, что и внутри стержня деформации имеют такой же характер, как и на его поверхности. Следовательно, поперечные сечения, плоские и нормальные к оси стержня до деформации, остаются плоскими и нормальными к его оси и после деформации. В этом и заключается смысл гипотезы плоских сечений, предложенной итальянским ученым Яковом Бернулли (Bernoulli, 1654 – 1705 гг.).
Главные моменты инерции сечения	Моменты инерции относительно главных осей инерции сечения. Обычно, говоря о главных моментах, подразумевают осевые моменты инерции относительно главных центральных осей инерции.
Главные напряжения	нормальные напряжения, действующие по главным площадкам.
Главные оси поперечного сечения	Оси, относительно которых центробежный момент инерции сечения обращается в нуль.
Главные площадки	три взаимно перпендикулярные площадки в окрестности исследуемой точки, на которых касательные напряжения равны нулю. На главных площадках нормальные напряжения принимают свои экстремальные значения Тензор напряжений для главных площадок:
Главные центральные оси инерции сечения	это оси, осевые моменты инерции относительно которых принимают свои экстремальные значения (максимум и минимум).

Д

Деформации пластические (остаточные)	Та часть деформации, которая не исчезает при разгрузке, называется пластической, а способность материала сохранять деформацию – пластичностью. Пластическая деформация называется также остаточной деформацией. Как правило, возникновение пластических деформаций связано с нарушением нормальной работы инженерной конструкции и поэтому их появление считается недопустимым. Если же мы хотим придать твердому телу желательную для различных целей форму, например, при прокатке, ковке, штамповке и т.п., то без возникновения пластической деформации нам не обойтись.
Деформации упругие	деформации тела, исчезающие после снятия внешних сил. Предположим, что тело не разрушилось под действием внешней нагрузки. Будем теперь уменьшать нагрузку до нуля. При этом, благодаря внутренним силам, будет уменьшаться и деформация тела. Способность материала восстанавливать первоначальные размеры и форму после снятия нагрузки называется упругостью. Та часть деформации, которая исчезает при разгрузке, называется упругой деформацией. Тело называется абсолютно упругим, если оно полностью восстанавливает свои размеры и форму после снятия нагрузки.
Деформация	Это изменение твердым телом своей первоначальной формы и размеров под действием приложенных к нему сил или температуры. Под действием внешней нагрузки любое реальное твердое тело изменяет свои первоначальные размеры и форму, или деформируется. Например, если Вы, наступите на обычный строительный кирпич, то под действием Вашего веса его высота уменьшится примерно на 1/20000 см. Именно деформация (пусть даже очень маленькая, как в приведенном выше примере) и позволяет твердому телу создать те внутренние силы, которые способны противодействовать внешней нагрузке и соответственно его разрушению. Когда мы к концу веревки подвешиваем груз, веревка удлиняется. Это удлинение, в свою очередь, приводит к возникновению внутри веревки результирующей внутренней силы, которая «тянет» камень вверх, удерживая его от падения (действие и противодействие, как известно, равны по величине и противоположны по направлению). Если внутренняя сила, обусловленная удлинением веревки, не сможет уравновесить вес груза, то веревка порвется. Важно осознать, что деформация конструкции вовсе не является каким-то дефектом (если она, конечно, не слишком велика с точки зрения цели, которой служит эта конструкция). Наоборот, деформация является тем важным свойством конструкции, без которого она не смогла бы противодействовать внешней нагрузке.
Деформация относительная при растяжении-сжатии
Деформация относительная поперечная	стержня определяется отношением абсолютной поперечной деформации к соответствующему первоначальному размеру . Относительная поперечная деформация при растяжении (сжатии) для изотропных материалов во всех направлениях одинакова:
Диаграмма растяжения	график зависимости между растягивающей силой F и удлинением рабочей части образца ∆l.
Динамическая нагрузка	нагрузка, характеризующаяся быстрым изменением во времени ее значения, направления или точки приложения и вызывающая в элементах конструкции или в деталях машин значительные силы инерции. К динамическим нагрузкам, несмотря на отсутствие значительных инерционных сил, можно отнести периодические многократно повторяющиеся (циклические) нагрузки, действующие на элементы конструкции. Такого рода нагружения характерны для большинства машиностроительных конструкций, таких, как оси, валы, штоки, пружины, шатуны и т. д.
Диаграмма предельных амплитуд (диаграмма Хейга)	Детали машин в процессе эксплуатации испытывают напряжения, изменяющиеся во времени по самым разнообразным циклам, характеризуемым коэффициентом асимметрии R. И для каждого такого цикла, в принципе, необходимо определить свой предел выносливости материала σR. В диапазоне от симметричного цикла до постоянного цикла (простого растяжения) укладывается бесконечное количество самых разнообразных циклов. Кроме того, опытное определение σR для каждого возможного цикла требует большого количества образцов и длительного времени испытаний. Поэтому в лабораторных условиях решить эту задачу практически невозможно. Вследствие перечисленных причин по ограниченному числу опытов строится так называемая диаграмма предельных амплитуд (рис. 1). 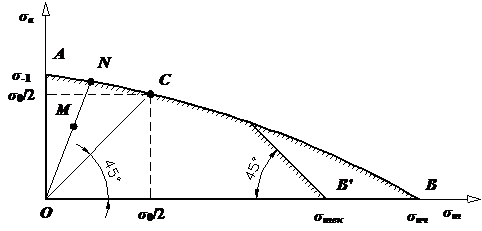Рис.1. Диаграмма предельных амплитуд Будем в дальнейшем называть предельным циклом такой цикл, у которого максимальное напряжение σmax равно пределу выносливости цикла σR. По оси ординат диаграммы (см. рис. 1) откладывают значение амплитудного напряжения σa, а по оси абсцисс – значение среднего напряжения σm предельного цикла. Каждая пара напряжений σa и σm определяет соответствующий предельный цикл, который изображается на диаграмме точкой. Точка A соответствует симметричному предельному циклу. Ее ордината – σa=σ-1, а абсцисса – σm=0. Точка B, имеющая координаты σa=0, σm=σпч, характеризует предельный постоянный цикл для хрупкого материала, а точка B’ с координатами σa=0, σm=σтек – предельный постоянный цикл для пластичного материала. Точка C отвечает предельному отнулевому циклу. Для нее σa=σm. Таким образом, кривая AСB характеризует предельные циклы для хрупких материалов, а кривая ACB’ – для пластичных. Точки, расположенные ниже этих кривых (внутри диаграммы), представляют собой безопасные циклы, то есть циклы, не приводящие к разрушению образца.
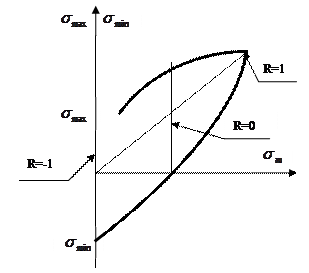
Диаграмма предельных напряжений (диаграмма Смита)	Диаграмма Смита строится, как минимум, по трем режимам нагружения (по трем точкам), для каждого из которых определяют предел выносливости. Первый режим (точка 1) – обычный симметричный цикл нагружения (R=-1, ); Второй режим (точка 2) – асимметричный цикл нагружения, как правило, отнулевой (R=0, ); Третий режим (точка 3) – простое статическое растяжение (R=1, ). Полученные точки соединяют плавной линией, ординаты точек которой соответствуют пределам выносливости материала при различных значениях коэффициента асимметрии цикла. Луч, проходящий под углом через начало координат диаграммы предельных напряжений, характеризует циклы с одинаковым коэффициентом асимметрии R:
Долговечность	состоит в способности конструкции сохранять необходимые для эксплуатации служебные свойства в течение заранее предусмотренного срока времени.
Допускаемое напряжение	максимальное значение напряжения, которое может быть допущено в опасном сечении для обеспечения безопасности и надежности работы, необходимых в условиях эксплуатации
Допущения в сопротивлении материалов	Структура реальных твердых тел настолько сложна, что они в своем естественном виде не могут стать предметом изучения в сопротивлении материалов. Твердые тела приходится идеализировать, то есть наделять их такими свойствами, которые, с одной стороны, достаточно точно передают основные характеристики реальных твердых тел, а с другой стороны, являются достаточно простыми для их представления в виде математических соотношений. Целью такой идеализации является получение определенных законов в виде уравнений, правильно описывающих основные свойства твердого тела. При построении теории расчета на прочность, жесткость и устойчивость принимаются допущения, относящиеся как к свойствам материалов, так и допущения, связанные с деформацией твердого тела. К первой группе допущений относятся следующие: 1) Считается, что материал твердого тела представляет собой сплошную среду, то есть полагают, что материал полностью заполняет весь объем тела, без каких-либо пустот. Это представление о твердом теле, как о сплошной среде, дает возможность применять при исследовании его напряженно-деформированного состояния методы дифференциального и интегрального исчислений, которые требуют непрерывности функции в каждой точке объема тела. 2) Материал считается однородным, то есть его физико-механические свойства являются одинаковыми во всех точках тела. 3) Материал считается изотропным, то есть его физико-механические свойства в каждой точке тела одинаковы во всех направлениях. Материал, не обладающий этим свойством, называется анизотропным. К анизотропным материалам, например, относится дерево. 4) Полагают, что материал является идеально упругим, то есть после снятия внешней нагрузки его деформация полностью исчезает. Вторая группа допущений связана с деформацией твердого тела: 1) Деформации считаются малыми. Отсюда следует, что при составлении уравнений равновесия, а также при определении внутренних сил можно не учитывать деформацию тела. Это допущение иногда называют принципом начальных размеров. 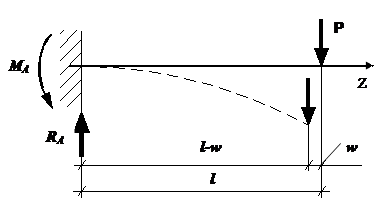Рис. 1. Принцип начальных размеров Рассмотрим, например, стержень, заделанный одними концом в стену и нагруженный на свободном конце сосредоточенной силой P (рис.1). Определим значение реактивного момента MA, возникающего в жесткой заделке. Для этого воспользуемся соответствующим уравнением равновесия, известного из теоретической механики: ΣMA=0; +MA-Pl=0. Отсюда легко можно найти, что MA=Pl. Но все ли здесь нами выполнено правильно? К сожалению, нет. Ведь прямолинейное положение стержня вовсе не является его положением равновесия. Под действием силы P стержень неизбежно изогнется. При этом точка приложения нагрузки сместится как по вертикали, так и по горизонтали. Если записать уравнение равновесия стержня для деформированного (изогнутого) состояния, то реактивный момент, возникающий в заделке, окажется равным: MA=P(l-w). Принимая в сопротивлении материалов упомянутое выше допущение о малости деформаций, мы полагаем, что перемещением w можно пренебречь по сравнению с длиной стержня l, то есть w<<l. Тогда, действительно, мы получим, что MA≈Pl. Однако необходимо помнить, что допущение о малости деформаций не всегда является справедливым. Заметим, что иногда принцип начальных размеров называют принципом отвердения, что не совсем верно. Принцип отвердения используется, например, при изучении поведения жидких тел. Если такая система находится в равновесии, то можно предположить, что она отвердела и сделалась неизменяемой. И тогда к ней можно будет применить уравнения равновесия твердого тела. 2) Полагают, что перемещения точек твердого тела пропорциональны внешним нагрузкам, вызывающим эти перемещения, то есть считается, что тело является линейно деформируемым. Необходимо отметить, что допущение о линейной деформируемости конструкции нельзя отождествлять с законом Гука, как это делается, к сожалению, в некоторых учебниках по сопротивлению материалов. Дело в том, что закон Гука устанавливает линейную зависимость между внутренними силами и деформациями, а не внешними силами и перемещениями. 3) Для линейно деформируемых конструкций справедлив принцип независимости действия сил (принцип суперпозиции). Этот принцип формулируется следующим образом: Результат действия группы сил не зависит от последовательности нагружения ими конструкции и равен сумме результатов действия каждой из этих сил в отдельности. В основе этого принципа лежит допущение о малости деформаций, а также предположение об обратимости процессов нагрузки и разгрузки конструкции.

Ж

Жесткость

Жесткостью называется способность конструкции сопротивляться образованию упругих деформаций, возникающих под действием внешних сил. Иногда деформация конструкции, отвечающей условию прочности, может воспрепятствовать нормальной ее эксплуатации. Пусть, например, прогиб нагруженного моста посредине составил 1/500 от длины его пролета l. При этом по нормам допускаемый прогиб не должен превышать l/800. В этом случае говорят, что мост является прочным, но жесткость его недостаточна.

З

Закон Гука при растяжении-сжатии	Для большинства материалов в пределах упругих деформаций между напряжением σ и продольной деформацией ε существует линейная зависимость σ=Eε. Напряжение пропорционально деформации – так формулируется в настоящее время закон Гука. Впервые этот закон был опубликован в виде анаграммы ceiiinosssttuv в 1676 г. английским ученым Робертом Гуком в его работе «Десяток изобретений, которые я намерен опубликовать». При правильной расстановке букв анаграмма читается следующим образом: «Ut tensio, sic vis». В переводе с латинского языка это означает: «Каково удлинение, такова и сила». Заметим, что к такому же заключению в 1680 г., независимо от Гука, пришел и французский ученый Эдме Мариотт (Mariotte, 1620 – 1684 гг.). Коэффициент пропорциональности E, стоящий в формуле σ=Eε, называется модулем продольной упругости или модулем Юнга – по имени английского ученого Томаса Юнга (Iounge, 1773–1829 гг.). Его значение для данного материала может быть установлено только опытным путем. В справочниках обычно приводится среднее значение модуля Юнга. Иногда модуль Юнга называют и «модулем упругости первого рода». Модуль Юнга является константой материала (например, для стали Е=2∙10^11 Па, для меди Е=1,2∙10^11 Па, для титана Е=1,2∙10^11 Па). Заметим, что существуют материалы (например, чугун), которые лишь с некоторым приближением можно считать подчиняющимися закону Гука. А такие материалы, как кожа и ткани, и вовсе ему не подчиняются. Необходимо также отметить, что материалы, которые подчиняются закону Гука, перестают ему следовать при достижении деформации (напряжения) определенного значения.
Закон Гука при сдвиге	Опытным путем установлено, что в пределах упругой сдвиговой деформации касательные напряжения пропорциональны углу сдвига: Данное соотношение представляет собой закон Гука при сдвиге. Коэффициент пропорциональности G в этой формуле называется модулем сдвига. Видно, что он измеряется в тех же единицах, что и касательное напряжение. Модуль сдвига G является физической постоянной для материала, характеризующей его жесткость при сдвиге. Значение модуля сдвига G может быть определено экспериментально.
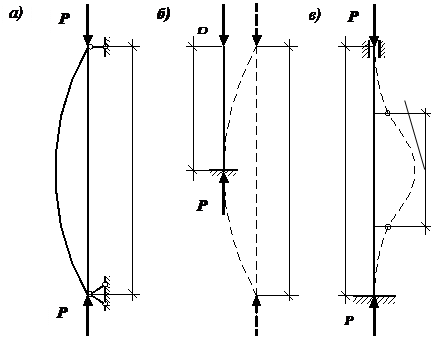
Зависимость критической силы от условий закрепления стержня	Формула Эйлера была получена нами для, так называемого, основного случая – в предположении шарнирного опирания стержня по концам. На практике встречаются и другие случаи закрепления стержня. При этом можно получить формулу для определения критической силы для каждого из этих случаев, решая, как в предыдущем параграфе, дифференциальное уравнение изогнутой оси балки с соответствующими граничными условиями. Но можно использовать и более простой прием, если вспомнить, что, при потере устойчивости на длине стержня должна укладываться одна полуволна синусоиды. Рассмотрим некоторые характерные случаи закрепления стержня по концам и получим общую формулу для различных видов закрепления. 1. Стержень длиной l заделан одним концом и сжат продольной силой. Из сравнения вида изогнутой оси балки для рассматриваемого и основного случаев можем сделать вывод, что ось стержня, заделанного одним концом, находится в тех же условиях, как и верхняя половина шарнирно опертого стержня длиной 2l. Таким образом, критическая сила для стержня длиной l с одним защемленным концом может быть найдена так же как и для шарнирно опертой балки длиной 2l, то есть 2. Стержень длиной l, у которого оба конца жестко заделаны. Средняя часть стержня, с двумя жестко закрепленными, концами находится в тех же условиях, что и шарнирно опертая балка длиной l/2. Таким образом, критическая сила для стержня длиной l с двумя защемленными концами может быть определена так же как и для шарнирно опертой балки длиной l/2, то есть 3. Стержень длиной l, у которого один конец жестко заделан, а другой шарнирно оперт. Критическая сила для стержня длиной l с защемленным и шарнирно опертым концами может быть определена так же как и для шарнирно опертой балки длиной 0,7l, то есть Все полученные решения можно объединить в одну общую формулу где μl = lпр – приведенная длина стержня; l – фактическая длина стержня; μ– коэффициент приведенной длины, показывающий во сколько раз необходимо изменить длину стержня, чтобы критическая сила для этого стержня стала равна критической силе для шарнирно опертой балки. (Другая интерпретация коэффициента приведенной длины: μпоказывает, на какой части длины стержня для данного вида закрепления укладывается одна полуволна синусоиды при потере устойчивости.)
Задача Эйлера	Рассмотрим шарнирно опертый по концам стержень, сжатый продольной силой F. Положим, что по какой-то причине стержень получил малое искривление оси, вследствие чего в нем появился изгибающий момент M: M=-F, где y – прогиб стержня в произвольном сечении с координатой x. Для определения критической силы можно воспользоваться приближенным дифференциальным уравнением упругой линии: где E – модуль Юнга; J – осевой момент инерции сечения стержня относительно оси z в данном случае; EJ – жесткость стержня при изгибе. Знаки левой и правой части согласованны в данной системе координат. Проведя преобразования, можно увидеть, что минимальное значение критическая сила примет при n=1 (на длине стержня укладывается одна полуволна синусоиды) и J=Jmin (стержень искривляется относительно оси с наименьшим моментом инерции) Это выражение обычно называют формулой Эйлера, а определяемую с ее помощью критическую силу – эйлеровой силой.
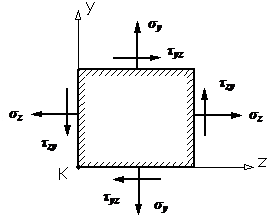
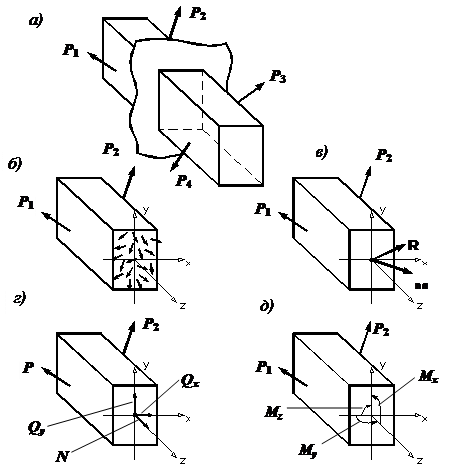
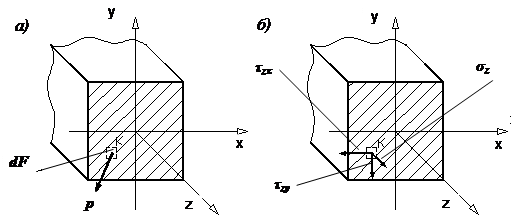
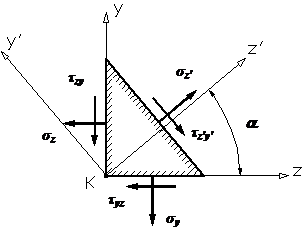
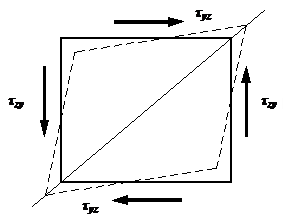
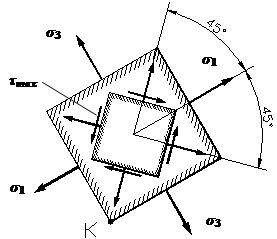
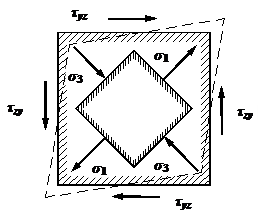
Закон парности касательных напряжений	Элементарный параллелепипед должен находиться в равновесии. В частности, он не должен вращаться вокруг оси x, проходящей через точку К (см. рис. 1), поэтому суммарный момент всех сил, возникающих по его граням, относительно этой оси должен быть равен нулю: В формуле (1) в скобки заключены соответствующие силы, а их плечи указаны за скобками. Рис.1. После элементарных упрощений выражения (1) найдем: Соотношение (2) и называется законом парности касательных напряжений: на любых двух взаимно перпендикулярных площадках касательные напряжения, направленные по перпендикуляру к линии пересечения этих площадок, равны по величине. При этом касательные напряжения либо сходятся к линии пересечения площадок, либо расходятся от нее.
Зона упрочнения	участок кривой деформирования образца, на котором материал вновь приобретает свойство оказывать сопротивление нагрузке, однако с ростом удлинения образца нагрузка возрастает значительно медленнее, чем на упругом участке.

И

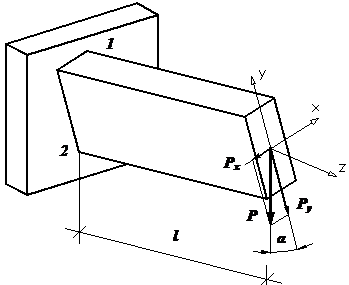
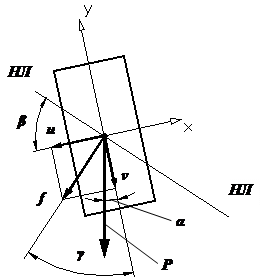
Изгиб косой	Косой изгиб - вид изгиба, при котором плоскость действия изгибающего момента не содержит ни одной из главных центральных осей инерции поперечного сечения балки. Впервые задача о косом изгибе балки была решена в 1843 г. Сен-Венаном. Рассмотрим как вычисляются наибольшие нормальные напряжения при косом изгибе. Покажем это на конкретном примере. Рассмотрим консольную балку прямоугольного поперечного сечения длиной l, нагруженную вертикальной силой P (рис. 1). Пусть балка расположена по отношению к нагрузке таким образом, что ее главная центральная ось y (ось симметрии) составляет некоторый малый угол α с направлением действия нагрузки. Пусть такой перекос обусловлен, например, технологическим браком при сборке конструкции. Рис.1. Косой изгиб Разложим силу P на две составляющие: Воспользуемся принципом независимости действия сил и рассмотрим действие каждой из этих составляющих в отдельности. Нагрузки Py и Px вызывают в поперечном сечении, расположенном на некотором расстоянии z от правого конца балки, изгибающие моменты, абсолютные значения которых определяются по формулам: Оба изгибающих момента будут наибольшими в заделке: Суммарные нормальные напряжения при косом изгибе в произвольном поперечном сечении балки для некоторой точки с координатами x и y вычисляются по следующей формуле где – главные моменты инерции; h – высота, а b – ширина поперечного сечения балки. Значения изгибающих моментов и координат исследуемой точки подставляются в формулу (1) по их абсолютному значению, а знак каждого из слагаемых определяется в целом, согласно физическому смыслу. Наибольшие нормальные напряжения возникнут в поперечном сечении, расположенном в заделке, в точках 1 и 2, которые наиболее удалены от соответствующих нейтральных осей и имеют следующие абсолютные значения координат: y=h/2, x=b/2. 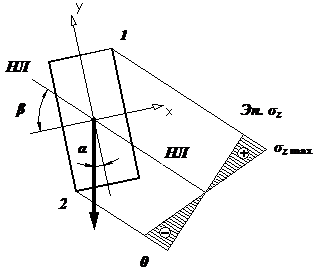При этом, очевидно, что в точке 1 напряжения будут растягивающими: а в точке 2 – точно такими же по величине, но сжимающими: В формулах (2) и (3) – моменты сопротивления балки при изгибе относительно главных центральных осей инерции. Определим положение нулевой (нейтральной) линии. Напомним, что нулевой линией (НЛ) (рис.2) называется геометрическое место точек поперечного сечения стержня, в которых нормальные напряжения равны нулю. Из этого определения легко и определяется положение НЛ. Приравнивая правую часть выражения (1) к нулю, получим: Отсюда Обозначим через β угол наклона НЛ к оси x. Тогда tgβ=y/x, и уравнение НЛ (4) принимает следующий вид: Из уравнения (5) видно, что в общем случае (когда Ix≠Iy) НЛ при косом изгибе не проходит перпендикулярно к силовой линии (рис. 2), поскольку . Лишь в частном случае, когда значения главных центральных моментов инерции равны между собой (Ix=Iy), угол между НЛ и силовой линией будет прямым (), и это означает, что изгиб будет прямым. Рис.2. Нулевая линия и эпюра напряжений при косом изгибе Заметим, что для балок с поперечным сечением типа квадрат, круг и т. п., у которых все центральные оси являются главными, косой изгиб невозможен. Построение эпюры нормальных напряжений при косом изгибе. Зная положение НЛ, легко построить эпюру σz. Для этого, например, справа от сечения (см. рис. 2) проведем перпендикуляр к НЛ. По нормали к нему и будем откладывать значения напряжений. Как уже отмечалось выше, они будут изменяться по линейному закону, при этом наибольшие растягивающие напряжения возникают в точке 1, а наибольшие сжимающие – в точке 2. Чем опасен косой изгиб? Выполним некоторые вычисления для рассмотренного нами случая. Пусть, например, α=10° (см. рис. 2), то есть перекос является относительно малым. При отсутствии перекоса, то есть при прямом изгибе, наибольшие нормальные напряжения в балке, например в точке 1, были бы равны: При косом изгибе в этой же точке они определяются по формуле Определим, во сколько раз наибольшие напряжения при наличии технологического брака больше, чем при его отсутствии. Составим отношение найденных выражений для напряжений: Например, при отношении h/b=4 получим то есть напряжения в балке возрастают почти на 70%. Таким образом, даже небольшой технологический перекос может привести к существенному увеличению нормальных напряжений в балке. В какой точке поперечного сечения балки возникает наибольшее касательное напряжение? В рассматриваемом нами примере нагрузки Py и Px вызывают во всех поперечных сечениях одинаковые перерезывающие силы, абсолютные значения которых соответственно равны: Наибольшие касательные напряжения от Qy возникают в точках, лежащих на оси x, а от Qx – в точках, лежащих на оси y. Эти напряжения определяются по формулам где F=bh – площадь поперечного сечения балки. Наибольшее касательное напряжение при косом изгибе возникает в центре тяжести поперечного сечения. Его можно найти как следующую геометрическую сумму: Определение прогибов при косом изгибе. Сначала найдем прогиб консоли от каждой из составляющих силы P в отдельности. Обозначим прогиб балки по направлению осей x и y соответственно через u и v (рис. 3). Тогда: Суммарный прогиб консоли равен: Найдем направление результирующего перемещения f. Для этого определим значение угла наклона γ этого перемещения к вертикальной оси y: Сопоставляя формулы (5) и (6), видим, что абсолютные значения углов β и γ равны между собой. Следовательно, направление суммарного прогиба балки при косом изгибе перпендикулярно нулевой линии (см.рис. 3). Рис.3. Прогиб балки при косом изгибе Отсюда можно сделать важный вывод о том, что направление суммарного прогиба балки f при косом изгибе (когда Ix≠Iy) не совпадает с направлением действующей силы P, то есть γ≠α.
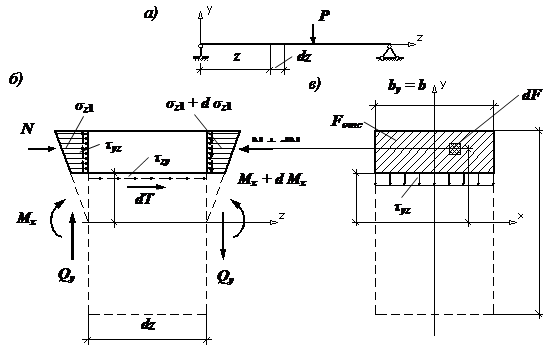
Изгиб	Изгибом называется такой вид деформации, при котором первоначально прямолинейная ось стержня искривляется. Стержень с прямолинейной осью, работающий на изгиб, называют балкой. Балки являются одним из важнейших элементов всех строительных конструкций, а также многих конструкций, применяемых в машиностроении, кораблестроении и в других отраслях техники. Первым вопрос о прочности балок поставил в 1638 г. Галилей в своей книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки». В 1826 г., то есть спустя почти два столетия, французский ученый Клод Луи Мари Анри Навье (Navier, 1785 – 1836 гг.) практически завершил создание теории изгиба балок. Этой теорией мы, по существу, пользуемся и по настоящее время. Гипотеза плоских сечений при изгибе балки Мысленно нанесем на боковой поверхности недеформированной балки сетку, состоящую из продольных и поперечных (перпендикулярных к оси балки) прямых линий. В результате изгиба балки мы увидим, что продольные линии примут криволинейное очертание, а поперечные линии практически останутся прямыми и перпендикулярными к изогнутой оси балки. Таким образом, поперечные сечения, плоские и перпендикулярные к оси балки до деформации, остаются плоскими и перпендикулярными к изогнутой оси после ее деформации. Это обстоятельство свидетельствует о том, что при изгибе (как при растяжении и кручении) выполняется гипотеза плоских сечений. Какие перемещения возникают при изгибе балки? В результате изгиба произвольная точка, лежащая на оси балки, перемещается в направлении вертикальной оси y и продольной оси z. Вертикальное перемещение обычно обозначают буквой v и называют его прогибом балки. Продольное перемещение точки обозначают буквой u. Касательная, проведенная к точке, расположенной на изогнутой оси балки, будет повернута по отношению к прямолинейной оси на некоторый угол. Этот угол, как показывают многочисленные опытные данные, оказывается равным углу поворота 𝜃 поперечного сечения балки, проходящего через рассматриваемую точку. Таким образом, три величины v, u и θ являются компонентами перемещения произвольного поперечного сечения балки при изгибе. В дальнейшем мы покажем, что u<<v, поэтому при расчете балки на изгиб продольным перемещением u пренебрегают. Какие внутренние усилия возникают в поперечном сечении балки при прямом изгибе? Рассмотрим, например, балку (рис. 1), нагруженную вертикальной сосредоточенной силой P. Для определения внутренних силовых факторов, возникающих в некотором поперечном сечении, расположенном на расстоянии z от места приложения нагрузки, воспользуемся методом сечений. Продемонстрируем два варианта использования этого метода, с которыми можно встретиться в учебной литературе. Рис.1. Внутренние силовые факторы, возникающие при прямом изгибе Первый вариант. Разрежем балку в намеченном нами поперечном сечении на расстоянии z от левого конца (рис. 1, а). Отбросим мысленно правую часть балки вместе с жесткой заделкой (или просто, для удобства, закроем их листком бумаги). Далее мы должны заменить действие отброшенной части на оставленную нами левую часть балки внутренними усилиями (силам упругости). Мы видим, что внешняя нагрузка пытается сместить видимую нами часть балки вверх (иными словами, осуществить сдвиг) с силой, равной P, а также изогнуть ее выпуклостью вниз, создавая момент, равный Pz. Вследствие этого, в поперечном сечении балки возникают внутренние силы, которые оказывают сопротивление внешней нагрузке, то есть противодействуют и сдвигу, и изгибу. Эти силы, очевидно, возникают во всех точках поперечного сечения балки, и распределены они по сечению по неизвестному пока нам закону. К сожалению, сразу же определить эту бесконечную систему сил невозможно. Поэтому мы сведем все эти силы к центру тяжести рассматриваемого поперечного сечения и заменим их действие статически эквивалентными внутренними усилиями: перерезывающей силой Qy и изгибающим моментом Mx. Как мы уже неоднократно отмечали выше, разрушение стержня в рассматриваемом сечении не произойдет только в том случае, если эти внутренние усилия Qy и Mx сумеют уравновесить внешнюю нагрузку. Поэтому мы легко находим, что Qy =P, а Mx =Pz. Заметим, что именно благодаря этим двум внутренним усилиям Qy и Mx при разгрузке рассматриваемая нами часть балки опустится вниз и выпрямится. Второй вариант. По-прежнему разрежем балку в интересующем нас месте на две части. Но отбросим теперь не правую, а левую часть балки, нагруженную силой P. Заменим действие отброшенной нами части на оставленную правую часть стержня внутренними усилиями. Эти усилия мы найдем непосредственно как действие отброшенной левой части на правую часть. Для этого осуществим параллельный перенос силы P в центр тяжести рассматриваемого поперечного сечения балки (рис. 1, б). Согласно известной лемме из курса теоретической механики, сила, приложенная в какой-либо точке тела, эквивалентна такой же силе, приложенной в любой другой точке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки ее приложения. Следовательно, в поперечном сечении стержня мы должны приложить силу P и момент Pz. Тогда перерезывающая сила Qy =P, а изгибающий момент Mx =Pz. То есть мы получаем тот же самый результат, но не производя процедуры уравновешивания. По каким правилам вычисляются изгибающий момент и перерезывающая сила, возникающие в поперечном сечении балки при изгибе? Если мы используем первый вариант, то эти правила следующие: 1) перерезывающая сила численно равна алгебраической сумме всех внешних сил (активных и реактивных), действующих на рассматриваемую нами часть балки; 2) изгибающий момент численно равен алгебраической сумме моментов этих же сил относительно главной центральной оси, проходящей через центр тяжести рассматриваемого поперечного сечения. Отметим, что изгиб, при котором в поперечном сечении балки возникают и изгибающий момент, и перерезывающая сила, называется поперечным. Если же в поперечном сечении балки возникает только изгибающий момент, то изгиб называется чистым. Что происходит с продольными волокнами балки при изгибе? Над этим вопросом задумывались многие ученые. Так, например, Галилей считал, что при изгибе балки все ее волокна одинаково растягиваются. Знаменитый немецкий математик Готфрид Вильгельм Лейбниц (Leibnitz, 1646 – 1716 гг.) полагал, что крайние волокна, расположенные на вогнутой стороне балки, не изменяют своей длины, а удлинения всех остальных волокон возрастают пропорционально удалению от этих волокон. Однако многочисленные опыты, например, опыты Артура Жюля Морена (Morin, 1795 – 1880 гг.), проведенные в 40-х гг. XIX в., показали, что балка при изгибе деформируется таким образом, что часть ее волокон испытывает растяжение, а часть – сжатие. Границей между областями растяжения и сжатия является слой волокон, которые лишь искривляются, не испытывая при этом ни растяжения, ни сжатия. Эти волокна образуют так называемый нейтральный слой. Линия пересечения нейтрального слоя с плоскостью поперечного сечения балки называется нейтральной осью или нулевой линией. При изгибе балки ее поперечные сечения поворачиваются именно относительно нейтральной оси. Как проверяется прочность балки при изгибе и как подбираются размеры ее поперечного сечения? Проверка прочности балки осуществляется, как правило, только по наибольшим нормальным напряжениям. Эти напряжения, как мы уже знаем, возникают в крайних волокнах того поперечного сечения балки, в котором «действует» наибольший по абсолютному значению изгибающий момент . Его значение мы определяем по эпюре изгибающих моментов. При поперечном изгибе в балке наряду с нормальными напряжениями возникают и касательные напряжения, но они в подавляющем числе случаев невелики и при расчете на прочность учитываются, в основном, только для балок двутаврового профиля, о чем мы будем говорить особо. Условие прочности балки при изгибе по нормальным напряжениям имеет вид: где допускаемое напряжение [σ] принимается таким же, как и при растяжении (сжатии) стержня из такого же материала. Помимо проверки прочности, по формуле (1) может быть произведен и подбор размеров поперечного сечения балки. При заданном допускаемом напряжении [σ] и известном максимальном абсолютном значении изгибающего момента требуемый момент сопротивления балки при изгибе определяется из следующего неравенства: Необходимо иметь в виду следующее очень важное обстоятельство. При изменении положения поперечного сечения балки по отношению к действующей нагрузке ее прочность может существенно изменится, хотя площадь поперечного сечения F и останется прежней. Пусть, например, балка прямоугольного поперечного сечения с отношением сторон h/b=3 расположена по отношению к силовой плоскости таким образом, что ее высота h перпендикулярна к нейтральной оси x. В этом случае отношение моментов сопротивления балки при изгибе равно: То есть такая балка в три раза прочнее той же самой балки, но повернутой на 90°. Напомним, что в выражении для момента сопротивления балки прямоугольного поперечного сечения при изгибе в квадрате стоит тот ее размер, который перпендикулярен нейтральной оси. Следовательно, сечение балки необходимо располагать таким образом, чтобы силовая плоскость совпадала с той из главных центральных осей, относительно которой момент инерции минимален. Или, что то же самое, необходимо добиваться того, чтобы нейтральной осью являлась ось, относительно которой главный момент инерции поперечного сечения максимален. В этом случае говорят, что балка испытывает изгиб в плоскости наибольшей жесткости. Сказанное выше еще раз подчеркивает важность темы «Определение положения главных центральных осей инерции поперечного сечения стержня», к которой студенты относятся, как правило, поверхностно. Определив из условия прочности (1) требуемый момент сопротивления при изгибе , мы можем перейти к определению размеров и формы поперечного сечения балки. При этом нам необходимо стремиться к тому, чтобы вес балки оказался минимальным. При заданной длине балки ее вес пропорционален площади поперечного сечения F. Покажем, например, что квадратное поперечное сечение является более экономным, чем круглое. В случае квадратного поперечного сечения, как мы знаем, момент сопротивления при изгибе определяется по формуле Для круглого поперечного сечения он равен: Если предположить, что площади поперечных сечений квадрата и круга равны между собой, то сторона квадрата a может быть выражена через диаметр круга d: Тогда момент сопротивления балки квадратного поперечного сечения будет равен: Сравнивая полученное значение момента сопротивления с моментом сопротивления балки круглого поперечного сечения Wx=0,125Fd, приходим к выводу, что квадратное поперечное сечение при той же площади имеет больший момент сопротивления, чем круглое (почти на 18%). Следовательно, квадратное поперечное сечение является более экономичным по сравнению с круглым. Анализируя распределение нормальных напряжений по высоте поперечного сечения балки (), легко прийти к заключению, что та часть материала, которая расположена вблизи нейтральной оси, почти не «работает» (это, в частности, и указывает на нерациональность круглого поперечного сечения по сравнению с квадратом). Для получения наибольшей экономии материала его нужно поместить как можно дальше от нейтральной оси. Наиболее благоприятный случай при заданной площади поперечного сечения F и высоте h получится при расположении каждой половины площади на расстоянии h/2 от нейтральной оси. Тогда момент инерции и момент сопротивления будут соответственно равны: Это тот предел, к которому можно приблизиться, применяя двутавровое поперечное сечение с наибольшим количеством материала в полках. Однако, вследствие необходимости выделить часть материала для стенки балки, полученное предельное значение для момента сопротивления недостижимо. Так, для прокатных балок двутаврового профиля: Для таких балок проверка прочности производится следующим образом: - в точках наиболее удаленных от нейтральной оси прочность двутавровой балки проверяется по формуле (1); - в точках, где полка соединяется со стенкой, то есть в тех точках, где велики и нормальные, и касательные напряжения, – по главным напряжениям: или же применяется одна из формул гипотез прочности; - в точках, расположенных на нейтральной оси, – по наибольшим касательным напряжениям: Чему равна потенциальная энергия деформации при изгибе? Потенциальная энергия деформации балки при поперечном изгибе определяется по следующей формуле где первый интеграл представляет собой потенциальную энергию сдвига, а второй – энергию чистого изгиба. Значение безразмерного коэффициента k, входящего в первое слагаемое выражения (2), зависит от формы поперечного сечения балки и вычисляется по формуле Например, для прямоугольного поперечного сечения k=1,2. Для большинства типов балок первое слагаемое в формуле (2) значительно меньше второго слагаемого. Поэтому при определении потенциальной энергии деформации при изгибе влиянием сдвига (первым слагаемым) часто пренебрегают.
Изгиб плоский	изгиб, при котором все силы, изгибающие балку, лежат в одной из плоскостей симметрии балки (в одной из главных плоскостей).
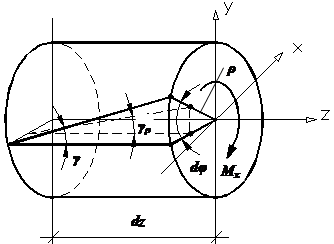
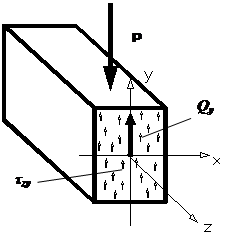
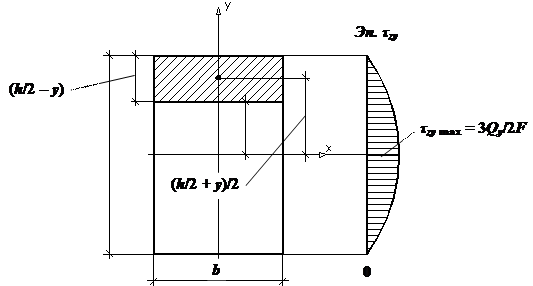
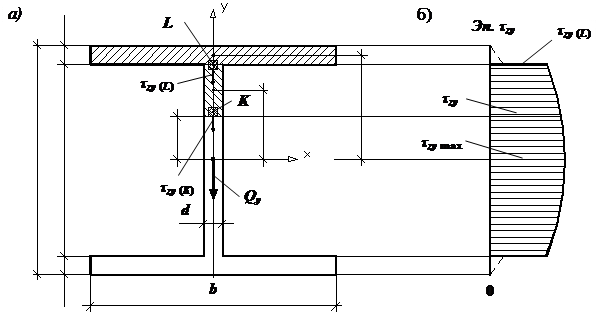
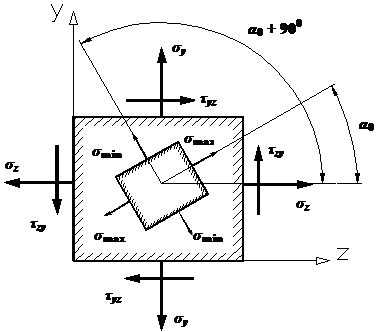
Изгиб поперечный	такой вид нагружения бруса, при котором из шести внутренних силовых факторов в сечении бруса отличными от нуля является изгибающий момент и поперечная сила. Нормальные напряжения: Закон Гука при изгибе: формула Навье: Максимальные напряжения: , где - момент сопротивления сечения при изгибе, . Касательные напряжения – формула Журавского: Для прямоугольного сечения: , для круглого сечения: , для любого сечения: . Главные напряжения при поперечном изгибе: Условие прочности по нормальным напряжениям условие прочности по касательным напряжениям Условия прочности по различным теориям прочности: I-я: ; II-я: (при коэфф.Пуассона =0,3); III-я: IV-я: теория Мора: Закон Гука при изгибе: Дифференциальное уравнение изогнутой оси балки Приближенное дифференциальное уравнение изогнутой оси балки: уравнение углов поворота уравнение прогибов Дифференциальные зависимости при изгибе:
Изгиб прямой	Вид изгиба, при котором силовая плоскость совпадает с одной из главных плоскостей инерции поперечного сечения (в противном случае имеет место косой изгиб). При плоском прямом изгибе плоскость изгиба и силовая плоскость совпадают. Силовой плоскостью называется плоскость, в которой действуют внешние нагрузки, а главной плоскостью – плоскость, которая проходит через продольную ось стержня z и одну из главных центральных осей инерции поперечного сечения (например, через ось x или ось y).
Изгиб сложный	изгиб, при котором нагрузки действуют в различных (произвольных) плоскостях.
Изгиб чистый	такой вид нагружения бруса, при котором из шести внутренних силовых факторов в сечении бруса отличным от нуля является только один изгибающий момент
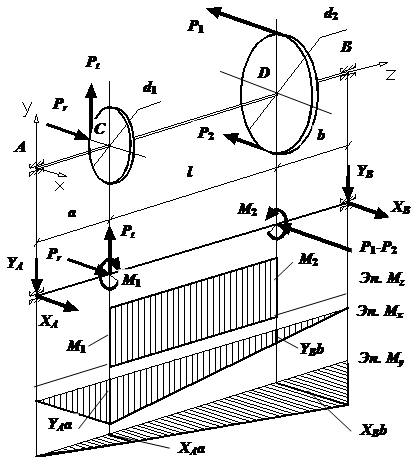
Изгиб с кручением	Сочетание деформаций изгиба и кручения очень часто встречается в машиностроении. Например, коленчатый вал воспринимает значительные скручивающие моменты и, кроме того, работает на изгиб. Оси моторных вагонов электропоезда, а также трамвайного вагона работают на изгиб с кручением. Разберем на конкретном примере. Рассмотрим вал диаметра d (рис. 1), на который насажены зубчатое колесо диаметром d1 и шкив ременной передачи диаметром d2. Пусть на зубчатое колесо действуют окружная сила Pt и радиальная сила Pr, а на шкив – силы натяжения ветвей ремня P1 и P2. Рис.1. Изгиб с кручением Приведем все эти силы к оси вала. При параллельном переносе силы Pt добавляется скручивающий момент M1=Ptd1/2, а при переносе сил P1 и P2 – скручивающий момент M2=P1d2/2-P2d2/2. При равномерном вращении вала (то есть при ω=const) должно выполняться условие M1=M2, из которого следует, что Ptd1=(P1-P2)d2. Подшипники, на которые опирается вал, рассматриваются нами как пространственные шарнирные опоры. При расчете на изгиб с кручением считается, что касательные напряжения от кручения намного больше, чем касательные напряжения от изгиба. Поэтому последними напряжениями пренебрегают и соответственно отпадает необходимость в построении эпюр поперечных сил Qx и Qy. Таким образом, нам необходимо построить эпюру крутящих моментов Mz и две эпюры изгибающих моментов Mx и My. Ординаты эпюр изгибающих моментов откладывают в соответствующей плоскости изгиба вала со стороны сжатых волокон. Для вала постоянного сечения опасным является то сечение, где одновременно возникают наибольшие крутящий момент Mz и результирующий изгибающий момент В рассматриваемом нами примере опасным является либо поперечное сечение, расположенное чуть правее точки С, либо сечение, расположенное чуть левее точки D (в зависимости от того, какой из изгибающих моментов будет больше: или ). В поперечном сечении опасными являются те две точки опасного поперечного сечения, в которых одновременно и нормальные напряжения от изгиба, и касательные напряжения от кручения имеют наибольшие значения. Эти точки расположены вблизи контура поперечного сечения вала. Поскольку валы, как правило, изготавливают из пластичного материала обе эти точки равноопасны. Рассмотрим как записывается условие прочности при изгибе с кручением. Расчет прочности при изгибе с кручением производится по третьей или по четвертой (энергетической) гипотезам прочности. В упомянутых опасных точках имеет место плоское напряженное состояние. Эквивалентное напряжение по третьей гипотезе прочности определяется по формуле Тогда условие прочности по этой гипотезе принимает вид: где – эквивалентный момент по гипотезе наибольших касательных напряжений, а Если же расчет вала вести по четвертой (энергетической) гипотезе прочности, то придем к следующему условию: в котором – эквивалентный момент по четвертой (энергетической) гипотезе прочности. Вернемся теперь вновь к вопросу об определении опасного поперечного сечения вала. После введения понятия эквивалентного момента, мы можем сказать, что опасным является то сечение, в котором эквивалентный момент будет наибольшим. Момент сопротивления: Диаметр вала:
Изгиб кривых брусьев большой кривизны	радиус нейтрального слоя Для прямоугольного сечения высотой h, с наружным радиусом R2 и внутренним R1: При h/R<1/2: . При наличии N: . Условие прочности: y= –h2 или y= h1.
Изгибающий момент	пара внутренних сил, перпендикулярная к плоскости поперечного сечения. Изгибающие моменты равны сумме моментов внешних сил относительно осей y и x соответственно: . Изгибающие моменты вызывают изгиб элемента.
Изотропный материал	материал, свойства которого одинаковы по всем направлениям.
Инварианты напряженного состояния	Сопоставление зависимостей напряженного и деформированного плоского состояний:
Инварианты деформированного состояния	тензор деформаций:
Интенсивность распределенной нагрузки	распределенная нагрузка, действующая на единицу длины или площади.
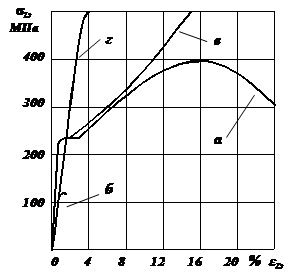
Испытание материала на сжатие	Строительные материалы, такие как бетон и цемент, испытывают в основном на сжатие. Дерево испытывают на сжатие как вдоль, так и поперек волокон. Сталь испытывают на сжатие реже, чем на растяжение. Образцы для испытания на сжатие имеют, как правило, форму кругового цилиндра с отношением высоты образца к диаметру не более 3. Для стали марки Ст. 3 диаграмма сжатия вплоть до предела текучести полностью повторяет диаграмму растяжения, то есть . Различие начинает сказываться после наступления текучести. При этом площадка текучести при сжатии менее четко выражена, чем при растяжении. При больших деформациях различие становится особенно ощутимым, и в первую очередь из-за того, что сжатие сопровождается увеличением площади поперечного сечения образца, вследствие чего испытание требует постоянно возрастающей нагрузки. Следовательно, при сжатии пластичного материала получить такую характеристику, как предел прочности, не представляется возможным. Исследуемый образец, не претерпевая разрушения, расплющивается, и дальнейшее испытание ограничивается возможностями пресса. В расчетной практике предел прочности пластичного материала на сжатие условно принимается таким же, как и на растяжение. Диаграмма сжатия хрупкого материала по виду напоминает диаграмму растяжения, но предел прочности на сжатие, как правило, в несколько раз больше, чем на растяжение (). Разрушение образца при сжатии происходит обычно путем сдвига одной части относительно другой, происходящим примерно под углом 45° к оси образца. Наглядное представление о сравнительных механических характеристиках низкоуглеродистой стали и серого чугуна при растяжении и сжатии дают диаграммы, показанные на рис. 1. Рис.1. Сравнительные свойства низколегированной стали и серого чугуна при испытании на растяжение и сжатие: а – диаграмма растяжения низкоуглеродистой стали; б – диаграмма растяжения серого чугуна; в – диаграмма сжатия низкоуглеродистой стали; г – диаграмма сжатия серого чугуна
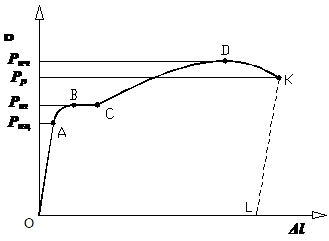
Испытание материала на растяжение	Механические характеристики материала определяются в результате испытания образца на специальных прессах. Форма образца может быть различной. Как правило, это стержень с участком постоянного поперечного сечения (круглого или прямоугольного) длиной l0. Концы образца имеют специальные утолщения для их закрепления в испытательной машине. Перед началом испытания замеряется площадь поперечного сечения средней части образца F0. Значения растягивающей силы P и удлинения средней части образца ∆l в каждый момент нагружения определяются специальными устройствами. При испытании нагрузка увеличивается медленно и плавно. Современные испытательные машины снабжены записывающим прибором, который при испытании образца автоматически вычерчивает график зависимости между нагрузкой P и абсолютным удлинением ∆l. Такой график называется диаграммой растяжения. Идея построения такого графика была предложена Яковом Бернулли, поэтому он иногда называется диаграммой Бернулли. 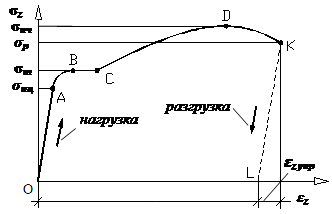Рассмотрим, например, диаграмму растяжения образца, изготовленного из стали марки Ст.3 (рис.1). Заметим, что эта диаграмма характеризует поведение именно образца, а не материала, из которого он сделан. Рис.1. Диаграмма растяжения образца из стали марки Ст. 3 в осях P – ∆l В начальной стадии испытания, до точки А с ординатой Pпц (индекс «пц» – сокращение от слова пропорциональность), зависимость между силой P и удлинением ∆l носит линейный характер, то есть удлинение образца растет пропорционально росту внешней нагрузки. Этот факт свидетельствует о линейной деформируемости образца. Затем диаграмма искривляется и при некотором значении растягивающей силы Pт (индекс «т» – сокращение от слова текучесть) наблюдается значительный рост удлинения образца без увеличения нагрузки. Это явление называется текучестью. Практически горизонтальный участок диаграммы BC называется площадкой текучести, а точка B – критической точкой диаграммы. При некотором значении растягивающей силы Pт, соответствующем критической точке B, на поверхности образца, если он, например, полирован, мы заметим появление сначала нескольких полосок, параллельных между собой и расположенных под углом примерно 45° к оси образца. Далее появляется вторая система линий, пересекающая первую и наклоненную к оси под тем же углом, что и первая. Такая система сопряженных линий называется линиями Людерса – Чернова. Эти линии впервые были описаны в 1859 г. немецким металлургом В. Людерсом и независимо от него в 1884 г. русским металлургом Д.К. Черновым (1839 – 1921 гг.). Упомянутые линии представляют собой следы сдвигов частиц материала. Направления этих линий соответствуют площадкам, на которых при растяжении возникают наибольшие касательные напряжения. За точкой C удлинение образца начинает расти быстрее нагрузки. Число линий Людерса – Чернова растет, они сливаются друг с другом и теряют ясность своих очертаний. Этот участок диаграммы называется зоной упрочнения. В наивысшей точке диаграммы (в точке D) при силе равной Pmax=Pпч (индекс «пч» – сокращение от слова прочность) на образце внезапно появляется местное сужение – шейка, которая представляет собой результат накопления деформаций сдвига. Сопротивление образца растяжению, после образования шейки, падает, и его разрыв происходит в точке K при нагрузке Pp<Pпч (индекс «р» – сокращение от слова разрыв). При разрыве образца, как правило, появляется поперечная трещина в центре тяжести поперечного сечения (посредине шейки), а остальная часть сечения скалывается под углом 45° к оси образца так, что на одной части разорванного образца образуется выступ, а на другой – кратер. Линия разгрузки образца KL представляет собой прямую линию, параллельная участку ОА. Следовательно, полное удлинение образца в момент разрыва (в точке K) состоит из двух частей: упругого, исчезающего после снятия нагрузки, и остаточного, равного длине отрезка ОL. Для того чтобы исключить влияние абсолютных размеров образца, диаграмму, изображенную на рис. 1, перестраивают: ординаты делят на начальную площадь поперечного сечения F0, а абсциссы – на начальную расчетную длину образца l0. В результате получается так называемая условная диаграмма растяжения. Она строится в координатах εz-σz (рис. 2) и отличается от диаграммы Бернулли только масштабом. Рис. 2. Диаграмма растяжения образца из стали марки Ст. 3 в осях εz-σz Условной эта диаграмма называется потому, что напряжения и деформации вычисляются по первоначальным размерам образца. Справедливость такого подхода определяется только практическими соображениями. На условной диаграмме (см. рис. 2) отмечены следующие основные механические характеристики материала: - предел пропорциональности – наибольшее напряжение, до которого выполняется закон Гука - предел текучести – напряжение, при котором материал «течет» - предел прочности – наибольшее напряжение, которое выдерживает материал без разрушения Например, для стали марки Ст. 3 упомянутые выше характеристики соответственно равны: σпц≈210 МПа, σт≈240 МПа, σпч≈400 МПа. Сталь марки Ст. 3. относится к так называемым пластичным материалам, которые имеют площадку текучести и разрушаются при больших остаточных деформациях. Необходимо, правда, отметить, что не для всех пластичных материалов площадка текучести имеет четко выраженный характер. Для таких материалов вводится понятие условного (или технического) предела текучести, представляющего собой напряжение, которое возникает в материале образца при относительном его удлинении, равном 0,2%. Иногда условный предел текучести обозначают σ0,2. Однако существуют и такие материалы, например чугун, которые характерны тем, что они вообще не имеют площадки текучести. Их разрушение происходит без образования шейки. Диаграмма сжатия для них обрывается сразу же после достижения предела прочности и при очень малых остаточных деформациях. Такие материалы называют хрупкими.
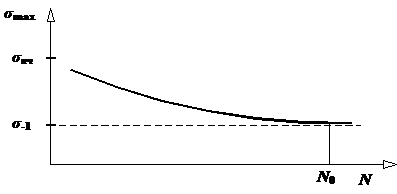
Испытание материалов на усталость	Наиболее распространенными являются испытания образцов на чистый изгиб при симметричном цикле, поскольку именно этот цикл напряжений является самым опасным для материала (вспомним пример с медной проволокой), а проведение этого эксперимента значительно проще, чем для других видов циклов. Для проведения такого эксперимента изготавливают партию из 6–10 совершенно одинаковых образцов, имеющих в пределах рабочей части строго круговую цилиндрическую форму. Диаметр образцов обычно составляет от 5 до 10 мм. Первый образец нагружают таким образом, чтобы возникающие в нем максимальные нормальные напряжения были заведомо ниже предела прочности материала (σmax≈0,7σпч), но выше предела выносливости. Для последующих образцов максимальное напряжение уменьшают. С помощью счетчика оборотов, имеющегося на испытательной машине, фиксируют число циклов нагружения, которое выдержит каждый образец до разрушения. 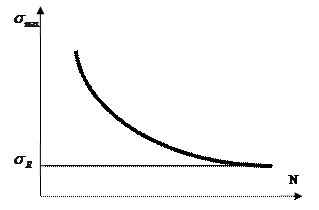По результатам испытаний строят график зависимости числа циклов N, которое выдерживает образец без разрушения, от максимального напряжения σmax, создаваемого в образце (рис. 1). Кривая σmax=f(N) называется кривой усталости или кривой Велера (по имени служащего немецких железных дорог Августа Велера (Wohler, 1819 – 1914 гг.), опубликовавшего в 1870 г. результаты своих экспериментов с образцами на усталость). Рис. 1. Кривая Велера Из рис. 1 видно, что по мере уменьшения напряжения σmax число циклов N начинает очень быстро расти, поэтому кривая усталости имеет значительную протяженность вдоль оси абсцисс. Для многих материалов эта кривая асимптотически приближается к некоторому значению максимального напряжения, начиная с которого образцы не проявляют никаких признаков разрушения. Поэтому при соответствующем числе циклов испытания можно прекратить. Практика проведения испытаний показывает, что образцы, выдержавшие без разрушения 10^7 циклов, могут при данном нагружении проработать неограниченное время. Поэтому продолжительность испытаний заранее оговаривается. Для того чтобы иметь наглядное представление о порядке указанного значения числа циклов, заметим, что ось железнодорожного вагона на пути от Москвы до Владивостока испытывает около 3×10^6 циклов. Предварительно задаваемая наибольшая продолжительность эксперимента на усталость называется базой испытаний N0. Еще раз напомним, что максимальное по абсолютному значению напряжение цикла, при котором до базы испытания не происходит усталостного разрушения, называется пределом выносливости. Кривые усталости для цветных материалов не имеют асимптоты, и их ординаты с ростом N падают до нуля. Для цветных материалов вводится понятие условного предела выносливости. За его значение принимается наибольшее напряжение, при котором образец выдерживает не менее 10^8 циклов.

К

Консоль	балка с одним защемленным и другим свободным концом или часть балки, продолжающаяся за опору.
Концентрация напряжений	повышение напряжений в местах изменения формы или нарушения сплошности материала
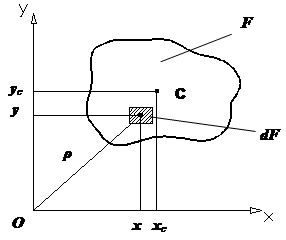
Координаты центра тяжести поперечного сечения стержня	Из формул следует, что статический момент площади фигуры относительно центральной оси (то есть оси, проходящей через центр тяжести фигуры) равен нулю. Сопоставляя и , мы легко получим формулы, позволяющие определить положение центра тяжести поперечного сечения стержня: Если площадь всей фигуры можно разбить на n простых частей, для которых известны и площадь Fi, и положение центра тяжести xi и yi, то вместо формул (1) мы получим (рис.1): Рис.1. Поперечное сечение стержня
Коэффициент асимметрии цикла	отношение минимального напряжения цикла к максимальному.
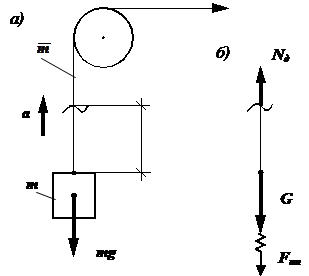
Коэффициент динамичности	или Динамический коэффициент, показывает во сколько раз воздействие динамической нагрузки на конструкцию будет больше, чем в случае приложения равной по величине статической нагрузки. Определим коэфиициент динамичности при поперечном ударе. Рассмотрим удар груза весом G, падающего с высоты h на некоторую упругую систему, например балку (рис. 1). Рис.1. Падение груза на балку Обозначим vд – динамический прогиб балки в месте падения груза. Работа, совершаемая падающим грузом, равна: Согласно принятому второму допущению, работа полностью переходит в потенциальную энергию деформации балки V. По теореме Клапейрона потенциальная энергия деформации равна половине произведения некоторой динамической силы Fд=vд/δ на соответствующее ей динамическое перемещение vд: Приравнивая выражения (1) и (2), а также учитывая, что статический прогиб балки в месте падения груза G, вызванный его статическим приложением, равен vст=δG, после несложных преобразований получим следующее квадратное уравнение относительно динамического прогиба балки: Отсюда Легко убедиться, что второй корень квадратного уравнения (3) имеет отрицательное значение vд, и поэтому он нас не интересует. Динамический прогиб балки в месте падения груза можно представить в виде: где kд – коэффициент динамичности. Тогда Принятое нами допущение о линейной зависимости между внешней силой и перемещением позволяет сделать вывод о том, что динамические напряжения в балке от действия ударной нагрузки во столько же раз больше напряжений, которые возникли бы в ней при статическом приложении такой же нагрузки, во сколько раз динамический прогиб больше статического, поэтому: В частном случае, когда высота падения h=0, то есть в случае внезапного приложения нагрузки, kд=2. Из формулы (4) следует, что для уменьшения коэффициента динамичности необходимо увеличить vст. Поэтому для смягчения удара применяют пружинные и резиновые прокладки, допускающие большие деформации.
Коэффициент запаса прочности	показывает во сколько раз необходимо снизить уровень напряжений в конструкции, считая от предела текучести или предела временного сопротивления, что бы при ее эксплуатации не допустить разрушения изделия. Призван компенсировать недостатки расчетных методик, рассеяния свойств материала, неучтенные факторы условий эксплуатации и т.п.
Коэффициент запаса прочности при сложном напряженном состоянии	число, на которое следует умножить все компоненты тензора напряжений (или s1, s2, s3), чтобы данное напряженное состояние стало предельным.
Коэффициент Пуассона	Пусть в результате деформации первоначальная длина стержня l станет равной l1. Изменение длины ∆l=l1-l называется абсолютным удлинением стержня. Оно измеряется в единицах длины, например, в сантиметрах (см). Отношение абсолютного удлинения стержня к его первоначальной длине называется относительным удлинением или продольной деформацией. Эта безразмерная величина обозначается εz (эпсилон) и вычисляется по формуле При растяжении продольная деформация считается положительной, а при сжатии – отрицательной. Поперечные размеры стержня в результате деформирования также изменяются, при этом при растяжении они уменьшаются, а при сжатии – увеличиваются. Если материал является изотропным, то его поперечные деформации в направлении осей x и y равны между собой: Опытным путем установлено, что при растяжении (сжатии) в пределах упругих деформаций отношение поперечной деформации к продольной является постоянной для данного материала величиной. Абсолютная величина этого отношения называется коэффициентом поперечной деформации или коэффициентом Пуассона – по имени французского ученого Симеона Дени Пуассона (Poisson, 1781–1840 гг.). Коэффициент Пуассона μ также как и модуль Юнга Е характеризует упругие свойства материала. Для изотропных материалов коэффициент Пуассона находится в пределах от 0 до 0,5 (пробка μ=0; сталь μ=0,3; каучук μ=0,5). Коэффициент Пуассона не может принимать значение большее, чем 0,5. Докажем это. Определим изменение объема стержня, имеющего, например, прямоугольное поперечное сечение с размерами b и h, при его растяжении. Длина стержня l увеличится и станет равной Поперечные размеры b и h уменьшатся: Площадь поперечного сечения после деформации будет равна: Учитывая, что деформация εz мала и пренебрегая величиной по сравнению с единицей, получим: Тогда объем стержня после деформации определится по формуле Трудно себе представить, что при растяжении объем стержня уменьшится. Тогда из условия найдем, что 1-2μ≥1. Или, окончательно, μ≤0,5.
Коэффициент снижения основного допускаемого напряжения (коэффициент продольного изгиба)	показывает во сколько раз отличаются напряжения в продольно сжатом стержне при потере им устойчивости от случая простого сжатия.
Кривая усталости (кривая Веллера)	Кривая усталости (рис.) строится на основании результатов усталостных испытаний при симметричном цикле. Кривая усталости показывает, что с увеличением числа цикла максимальное напряжение, при котором происходит разрушение материала, значительно уменьшается. При этом для многих материалов, например углеродистой стали, можно установить такое наибольшее напряжение цикла, при котором образец не разрушается после любого числа циклов (горизонтальный участок диаграммы), называемое пределом выносливости ().
Критическая сила	Нагрузка Fкр, превышение которой вызывает потерю устойчивости первоначальной формы (положения) тела. С момента наступления критического состояния до момента разрушения деформации системы нарастают крайне быстро, и практически нет времени принять меры по предотвращению грозящей катастрофы. Таким образом, при расчете на устойчивость критическая нагрузка подобна разрушающей при расчете на прочность. При этом условие устойчивости можно записать в следующем виде При определении критической силы, вызывающей потерю устойчивости сжатого стержня, предполагается, что стержень идеально прямой и сила F приложена строго центрально. Рассматриваемый метод решения основан на том, что при достижении силой F критического состояния (F=Fкр) стержень находится в безразличном состоянии и ему присущи две формы равновесия: прямолинейная и криволинейная (в таких случаях говорят, что происходит ветвление, или бифуркация, равновесных состояний). Для выявления криволинейной формы равновесия достаточно приложить к стержню малую поперечную возмущающую нагрузку Q, которая вызовет малый прогиб. Если F < Fкр, то при удалении Q стержень будет сохранять прямолинейную форму равновесия. Если F > Fкр, то равновесие стержня становится неустойчивым и сколь угодно малое возмущение достаточно для того, чтобы возникли большие прогибы. Задачу о критической нагрузке сжатого стержня с учетом возможности существования двух форм равновесия при одном и том же значении силы решил академик Петербургской Академии наук Л. Эйлер в 1744 году.
Критическое напряжение	напряжения, соответствующее критической силе при потере устойчивости сжатого стержня Вспомним, что – квадрат минимального радиуса инерции. Тогда формулу можно записать так:
Круговая частота	представляет собой число колебаний в 2π секунд.
Крутящий момент	пара внутренних сил, лежащая в плоскости поперечного сечения. Крутящий момент в поперечном сечении равен сумме моментов всех внешних сил по одну сторону от сечения, взятых относительно центральной оси стержня. Крутящий момент вызывает кручение элемента.
Кручение	Мысленно заделаем, например, левый конец стержня круглого поперечного сечения в стену и приложим к его правому свободному концу внешний момент, вращающий относительно оси стержня z. Этот внешний момент мы будем называть скручивающим моментом и обозначать его Mскр. Такая внешняя нагрузка вызовет в стержне деформацию кручения, которая характеризуется тем, что одно поперечное сечение поворачивается на некоторый угол относительно другого сечения. Если угол поворота мал, то можно предположить, что расстояние между этими сечениями останется прежним. В поперечных сечениях стержня, при такой деформации, возникнет только одно внутреннее усилие – крутящий момент, который мы будем обозначать Mz. Угол, на который повернется нагруженное крайнее правое поперечное сечение стержня относительно неподвижного левого сечения, называется углом закручивания стержня и обозначается буквой φ. Кручение - вид нагружения бруса, при котором из шести составляющих главного вектора и главного момента внутренних сил от нуля отличается только крутящий момент. Круглый стержень, испытывающий деформацию кручения, принято называть валом. Кручение элементов конструкции и деталей машин встречается очень часто. Одним из наиболее характерных случаев является кручение вала машины. На кручение работают оси локомотивов, стержень винтовой цилиндрической пружины и т. д. Скручивающий момент вычисляется по следующей формуле где – скручивающий момент, Н∙м.; N – мощность, Вт; ω – угловая частота вращения вала, рад/c. Если ω измеряется в оборотах в минуту, то формула (1) принимает вид: Допущения положенные в основу теории кручения круглых стержней. Считается, что при малых углах закручивания вала: - поперечные сечения, плоские и перпендикулярные к его оси до деформации, остаются плоскими (не коробятся) и перпендикулярными к оси вала и после деформации (это допущение принято называть гипотезой плоских сечений или гипотезой Бернулли); - радиусы поперечных сечений при деформации не искривляются и не изменяют своей длины; - длина вала в результате закручивания также не изменяется. Таким образом, поперечное сечение вала ведет себя при кручении, как жесткий диск, и тогда деформацию кручения можно рассматривать как результат сдвига одного поперечного сечения относительно другого. Следовательно, в точках поперечного сечения вала возникают только касательные напряжения. Теория кручения, основанная на перечисленных выше допущениях, хорошо подтверждается многочисленными опытными данными. Одним из первых исследователей, экспериментально изучавших кручение круглых стержней, был французский ученый Шарль Огюстен Кулон (Coulomb, 1736 – 1806 гг.). Кручение стержней прямоугольного поперечного сечения. Упомянутые допущения, сформулированные для круглого вала, не могут быть приняты для стержня прямоугольного поперечного сечения. При кручении такого стержня отдельные точки поперечного сечения перемещаются вдоль его оси. И поэтому все сечение, в целом, перестает быть плоским (оно коробится). Происходит так называемая депланация поперечного сечения стержня. Эта задача является значительно более сложной по сравнению со случаем кручения стержня круглого поперечного сечения и методами сопротивления материалов она не может быть решена. Зависимость между углом сдвига и относительным углом закручивания. Рассмотрим часть вала длиной dz. Предположим, что правое поперечное сечение вала провернулось на угол dφ относительно левого сечения. Для произвольного продольного волокна, отстоящего от оси вала на расстоянии ρ, возникнет абсолютный сдвиг, равный ρdφ (рис. 1). Рис.1. Кручение Тогда угол сдвига Входящая в формулу (2) величина называется относительным углом закручивания. Таким образом, между углом сдвига и относительным углом закручивания существует следующая зависимость: Закон Гука при кручении. Так же, как и при сдвиге: или, с учетом зависимости (3), то есть, касательные напряжения в произвольной точке поперечного сечения вала, отстоящей от центра тяжести сечения на расстоянии ρ, пропорциональны относительному углу закручивания. При этом в точках, равноудаленных от центра тяжести поперечного сечения, численные значения касательных напряжений одинаковы. Из формулы (4) следует, что касательные напряжения, возникающие в поперечном сечении вала при кручении, изменяются по линейному закону (пропорционально ρ – расстоянию от точки, в которой мы вычисляем напряжения, до центра тяжести). Они равны нулю в центре вала и достигают максимального значения τmax в точках контура поперечного сечения (рис. 2). Рис.2. Касательные напряжения при кручении Из рис. 2 видно, что средняя часть поперечного сечения вала практически не участвует в сопротивлении кручению. В связи с этим на практике находят широкое применение полые валы. Такие валы, при той же площади поперечного сечения F, могут воспринять больший скручивающий момент. Выражение крутящего момента через касательные напряжения, возникающие в поперечном сечении вала. При повороте поперечного сечения каждая его точка (кроме, разумеется, точки, лежащей на оси вала) перемещается по некоторой дуге окружности радиуса ρ. Поэтому направление касательного напряжения, возникающего в этой точке, должно быть перпендикулярно к радиусу ρ, проведенному в эту точку. Элементарная внутренняя сила, возникающая на площадке dF (см. рис.2), равна , а ее момент относительно оси z (или центра тяжести поперечного сечения вала): Суммируя эти элементарные моменты по всей площади, получим выражение для крутящего момента, возникающего в поперечном сечении вала: Зависимость между относительным углом закручивания и крутящим моментом. Подставив выражение (4) в формулу (5), найдем: С учетом того, что интеграл в выражении (6) представляет собой полярный момент инерции поперечного сечения Iρ, получим следующую форму записи закона Гука при кручении, но уже не для материала, а для стержня: Который читается следующим образом: крутящий момент, возникающий в поперечном сечении стержня, пропорционален относительному углу закручивания. Напомним, что для стержня круглого поперечного сечения Тогда относительный угол закручивания равен: Из формулы (7) следует, что произведение GIρ характеризует жесткость стержня при кручении. Напомним, что модуль сдвига G характеризует жесткость материала при сдвиге (кручении), а полярный момент инерции Iρ является мерой сопротивления вращению поперечного сечения относительно оси стержня. Вычисление касательных напряжений в произвольной точке поперечного сечения вала. Наибольшие касательные напряжения при кручении. Подставив выражение (7) в формулу (4), получим: Формула (8) позволяет вычислить касательное напряжение в любой точке поперечного сечения вала. Наибольшие касательные напряжения τmax возникают в точках контура поперечного сечения при ρ=d/2=r. Они равны: Введя обозначение , окончательно получим: Величина Wρ называется моментом сопротивления при кручении (или полярным моментом сопротивления) и является геометрической характеристикой поперечного сечения вала. Момент сопротивления при кручении определяет способность вала сопротивляться кручению. Он измеряется в единицах длины в кубе (как правило, в см^3). Заметим, что буквенное обозначение W, выбранное для обозначения момента сопротивления при кручении, очень похоже на перевернутую букву M, что способствует лучшему запоминанию формулы (9). Для стержня круглого поперечного сечения: Для полого вала, имеющего внутренний диаметр d и внешний – D, полярный момент сопротивления равен: где α=d/D. Условие прочности при кручении. Прочность вала считается обеспеченной, если наибольшие касательные напряжения, возникающие в его опасном поперечном сечении, не превышают допускаемых касательных напряжений при кручении: Формула (11) служит для проверочного расчета вала на прочность. Заметим, что незначительное превышение расчетного напряжения τmax над допускаемым напряжением [τ]k разрешается (не более 5%). При проектировочном расчете требуемый полярный момент сопротивления определяется по следующей формуле, вытекающей из условия прочности (11): Отсюда легко можно найти требуемый диаметр вала. Например, для вала сплошного поперечного сечения, используя (10), получим: Для вала постоянного диаметра опасным является сечение, в котором возникает наибольший крутящий момент Mzmax. Если же вал имеет переменное по длине поперечное сечение, то может оказаться, что наибольшие касательные напряжения возникают не там, где крутящий момент максимален. Следовательно, в этом случае вопрос об опасном сечении должен быть исследован дополнительно. Допускаемое напряжение [τ]k для пластичных материалов назначается в зависимости от их предела текучести τm при кручении (сдвиге): Для хрупких материалов – в зависимости от предела прочности τпч: Вычисление угла закручивания вала. Из (7) следует, что угол закручивания вала определяется по формуле Если диаметр d постоянен по длине вала l и крутящий момент Mz имеет во всех поперечных сечениях одинаковое значение, то Условие жесткости при кручении. За меру жесткости при кручении принимается относительный угол закручивания вала θ. Условие жесткости имеет вид: где [θ] – значение допускаемого относительного угла закручивания, рад/м, которое зависит от назначения вала и условий его работы. Если [θ] задано в град/м, то преобразовывать формулу (13) не следует. Проще просто перевести [θ] в рад/м, учитывая, что 1 рад ≈ 57,3 град. Неравенство (13) позволяет определить требуемый диаметр вала из условия жесткости. Так, для сплошного вала мы получим Напомним, что вал должен удовлетворять и условию прочности, и условию жесткости. Поэтому из двух значений диаметра, найденных нами по формулам (12) и (14), мы должны взять наибольшее значение. Потенциальная энергия деформации при кручении вала. При кручении, как и при других видах деформации стержня, работа внешней силы (скручивающего момента) расходуется на создание в деформируемом теле определенного запаса энергии (потенциальной энергии деформации), которая определяется по формуле:

Л

Линия балки упругая

Проекция нейтрального слоя на плоскость изгиба (плоскость симметрии).

М

Малоцикловая усталость	усталость материала, при которой усталостное повреждение или разрушение происходит при упруго-пластическом деформировании. Условно принимают, что при N<50000 циклов имеет место малоцикловая усталость.
Массивное тело	тело, все три измерения которого мало отличаются друг от друга.
Материал идеально упругий	материал, который полностью восстанавливает свою форму и размеры после снятия нагрузки независимо от величин нагрузок и температуры тела.
Материал изотропный	материал, свойства которого во всех направлениях одинаковы.
Материал однородный	материал, свойства которого во всех точках одинаковы.
Метод сечений	Метод сечений позволяет определить внутренние силы (точнее говоря, внутренние силовые факторы), которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки. Рассмотрим, например, идеально упругий призматический стержень прямоугольного поперечного сечения (рис. 1, а). Рис.1 Мысленно выделим внутри стержня какие-либо две частицы K и L, расположенные на бесконечно малом расстоянии друг от друга. Для большей наглядности предположим, что между этими частицами имеется некоторая пружинка, удерживающая их на определенном расстоянии друг от друга. Пусть натяжение пружинки равно нулю. Приложим теперь к стержню растягивающую силу P (рис. 1, б). Пусть в результате деформации стержня частица K перейдет в положение K1, а частица L – в положение L1. Соединяющая эти частицы пружинка при этом растянется. После снятия внешней нагрузки частицы вернутся в первоначальное положение K и L благодаря усилию, которое возникло в пружинке. Сила, которая возникла между частицами (в пружинке) в результате деформации идеально упругого стержня, называется силой упругости или внутренней силой. Она, как уже отмечалось, может быть найдена методом сечений. Метод сечений подразделяется на четыре этапа. Для лучшего запоминания формулировки метода и его четырех этапов иногда вводится аббревиатура РОЗУ, представляющая начальные буквы наименований соответствующих этапов: разрежем, отбросим, заменим, уравновесим. Мысленно разрежем стержень, находящийся в равновесии под действием некоторой системы Pi (рис. 2, а), на две части плоскостью, перпендикулярной к его оси z. Рис.2 Напомним, что реакции связей также относятся к внешним силам, поэтому среди сил, показанных на рис. 2, могут быть как активные, так и реактивные силы. Отбросим одну из частей стержня, например, переднюю и рассмотрим оставленную нами часть. Поскольку мы как бы разрезали бесчисленное множество пружинок, соединявших бесконечно близкие частицы тела, разделенного теперь на две части, в каждой точке поперечного сечения стержня необходимо приложить силы упругости, которые возникли между этими частицами вследствие деформации тела. Иными словами, действие отброшенной передней части стержня вместе с приложенными к ней внешними силами мы заменим внутренними силами (рис. 2, б). Эти внутренние силы оказывают противодействие внешней нагрузке, приложенной к оставленной части тела. Бесконечную систему внутренних сил по правилам теоретической механики с помощью известной теоремы Пуансо (1804 г.) можно привести к одной точке – к центру тяжести поперечного сечения. В результате мы получим главный вектор R и главный момент M (рис. 2, в). Разложим их на составляющие по осям x, y и z. Заметим, что оси x и y представляют собой главные оси, проходящие через центр тяжести поперечного сечения. В итоге мы получим шесть внутренних силовых факторов, возникающих в поперечном сечении стержня при его деформировании: три силы N, Qx, Qy (рис. 2, г) и три момента Mx, My, Mz (рис. 2, д). Сила N называется продольной силой, Qx, Qy – поперечными (или перерезывающими) силами, момент относительно оси z Mz – крутящим моментом, моменты относительно осей x, y Mx, My – изгибающими моментами. Необходимо отметить, что внутренние силовые факторы – векторные величины, составляющие главного вектора R и главного момента M по осям координат. Поэтому ошибочно говорить, например, что продольная сила N является проекцией главного вектора R на ось стержня, поскольку проекция вектора – это скалярная, а не векторная величина. Как мы уже отмечали выше, разрушение тела не произойдет только в том случае, если эти шесть внутренних усилий сумеют уравновесить внешнюю нагрузку, действующую на рассматриваемую нами часть стержня. Поэтому уравновесим оставленную нами часть стержня. Записываем уравнения равновесия: ΣX=0; ΣY=0; ΣZ=0; ΣMx=0; ΣMy=0; ΣMz=0. Из этих уравнений и определяются внутренние усилия, возникающие в рассматриваемом поперечном сечении стержня. При этом оказывается, что: - продольная сила N равна сумме проекций всех сил (активных и реактивных), действующих на любую из частей рассеченного стержня, на ось z; - поперечные силы Qx, Qy равны сумме проекций всех сил, действующих на любую из частей стержня, на оси x и y соответственно; - крутящий момент Mz равен сумме моментов всех сил, действующих на любую из частей стержня, относительно продольной оси z; - изгибающие моменты Mx, My равны сумме моментов всех сил, действующих на любую из частей стержня, относительно осей x и y соответственно.
Метод Мора	Рассмотрим балку, изображенную на рис. 1, а. Рис. 1. Определение перемещений балки методом Мора Эту балку будем называть заданной. Обозначим MxP и QyP, соответственно, изгибающий момент и перерезывающую силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки ∆КР в точке K. Введем в рассмотрение вспомогательную балку, представляющую собой ту же самую балку. Нагрузим ее только одной силой (рис. 1, б). Эту единичную силу мы приложим в точке K, то есть в той самой точке, где мы и собираемся определить прогиб. Внутренние усилия, возникающие во вспомогательной балке, обозначим и . Воспользуемся теперь теоремой о взаимности работ, согласно которой работа внешних сил, приложенных к вспомогательной балке на соответствующих перемещениях заданной балки, равна взятой с обратным знаком работе внутренних сил заданной балки на соответствующих перемещениях вспомогательной балки. Тогда При определении перемещений в балке, как правило, можно пренебрегать влиянием перерезывающей силы, то есть второе слагаемое в (1) можно отбросить. Тогда, учитывая, что , окончательно получим: Эту формулу в 1874 г. получил Мор. Определение перемещений по этой формуле часто называют определением перемещений методом Мора, а саму формулу – интегралом Мора. Необходимо иметь в виду, что входящие в интеграл Мора изгибающие моменты берутся в произвольном поперечном сечении и поэтому представляют собой аналитические функции от текущей координаты z. Заметим, что если мы хотим в некоторой точке K определить угол поворота поперечного сечения θкр, то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент (рис. 1, в). Приведем порядок вычисления перемещений балки методом Мора: 1) к вспомогательной балке в той точке, где требуется определить перемещение, прикладываем единичное усилие (при определении прогиба прикладываем единичную силу , а при определении угла поворота – единичный момент ); 2) для каждого участка балки составляем выражения для изгибающих моментов заданной MxP и вспомогательной балок; 3) вычисляем интеграл Мора для всей балки по соответствующим участкам; 4) если вычисленное перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичного усилия (отрицательный знак указывает на то, что действительное направление искомого перемещения противоположно направлению единичного усилия). Пусть, например, для шарнирно опертой балки постоянной изгибной жесткости EIx=const, длиной l, нагруженной равномерно распределенной нагрузкой интенсивностью q (рис.2, а), требуется определить прогиб посредине пролета f и угол поворота на левой опоре θA. Начнем с определения прогиба. В том месте, где нам нужно определить прогиб, к вспомогательной балке прикладываем единичную силу (рис.2, б). Записываем выражения для изгибающих моментов для каждого из двух участков (0≤z1≤l/2; 0≤z2≤l/2) заданной и вспомогательной балок: Вычисляем интеграл Мора. Учитывая симметрию балки, получим: Переходим к определению угла поворота поперечного сечения балки на левой опоре. Рис.2. Определение прогиба и угла поворота методом Мора Нагружаем вспомогательную балку единичным моментом , прикладывая его в том месте, где мы ищем угол поворота (рис. 2, в). Записываем выражения для изгибающих моментов в заданной и вспомогательной балках только для одного участка (0≤z≤l): Тогда интеграл Мора будет иметь вид: Полученный нами положительный знак в выражении для угла поворота поперечного сечения балки указывает на то, что поворот сечения происходит по направлению единичного момента .
Метод сил	Наиболее распространенный (но не единственный) метод раскрытия статической неопределимости Канонические уравнения метода сил: . . . . . . . . . . . . ; ; . коэффициенты находят по способу Верещагина:
Метод начальных параметров	интегрируем:
Механическое состояние материала	поведение материала под действием механической нагрузки. Применительно к центральному растяжению образца из мягкой стали различают, например, следующие механические состояния материала: упругости, общей текучести, упрочнения, местной текучести и разрушения.
Механические свойства	характеристики материала, описывающие его поведение при внешних силовых воздействиях.
Минимальное напряжение цикла	наименьшее по алгебраическому значению напряжение цикла.
Многоцикловая усталость	усталость материала, при которой усталостное повреждение или разрушение происходит в основном при упругом деформировании. Условно принимают, что при N>50000 циклов имеет место многоцикловая усталость.
Модуль продольной упругости, Модуль упругости первого рода, Модуль Юнга	Коэффициент пропорциональности E, стоящий в формуле σ=Eε, называется модулем продольной упругости или модулем Юнга – по имени английского ученого Томаса Юнга (Iounge, 1773–1829 гг.). Его значение для данного материала может быть установлено только опытным путем. В справочниках обычно приводится среднее значение модуля Юнга. Иногда модуль Юнга называют и «модулем упругости первого рода». Из формулы σ=Eε видно, что чем больше модуль Юнга, тем меньше (при том же значении напряжения) деформация материала. Следовательно, модуль продольной упругости характеризует жесткость материала при растяжении (сжатии). Из этой же формулы видно, что модуль Юнга измеряется в тех же единицах, что и нормальное напряжение σ. Так, например, для всех марок сталей E=2∙10^5 МПа, для алюминиевых сплавов E=0,7∙10^5 МПа, для пленки скорлупы яйца E=8 МПа, а для алмаза E=12∙10^5 МПа. К сожалению, само название – модуль продольной упругости – провоцирует иногда студента на неверное истолкование его физического смысла. Так, на вопрос о том, что он характеризует, зачастую можно услышать следующий неверный ответ: «Модуль Юнга характеризует упругость материала. Поэтому, чем он больше, тем больше упругость материала». Напомним, что упругость – это способность восстанавливать первоначальные размеры и форму после снятия внешней нагрузки. Следовательно, к упругости, в этом смысле слова, модуль Юнга не имеет никакого отношения. Закон Гука, в котором фигурирует модуль продольной упругости E, говорит нам о том, что напряжение пропорционально деформации только в пределах упругих деформаций. И именно в том смысле следует понимать слово «упругость» в упомянутом термине.
Модуль Сдвига, Модуль упругости второго рода	Величина, характеризующая упругие свойства материала при чистом сдвиге. В случае малых деформаций, когда справедлив закон Гука, т.е. имеет место линейная зависимость между касательными напряжениями и сдвиговыми деформациями, модуль упругости представляет собой коэффициент пропорциональности между этими соотношениями.
Момент инерции осевой, полярный, центробежный	Осевым моментом инерции площади фигуры называется интеграл произведений элементарных площадей на квадраты их расстояний до рассматриваемой оси. Так, моменты инерции произвольной фигуры (см. рис. 1) относительно осей x и y соответственно равны: Рис.1. Поперечное сечение стержня Полярным моментом инерции площади фигуры относительно данной точки (полюса) называется интеграл произведений элементарных площадей на квадраты их расстояний до полюса: Если через полюс проходят две взаимно перпендикулярные оси x и y, то . И тогда Из формул (1) и (2) видно, что значения осевых и полярного моментов инерции всегда положительны, поскольку координаты x, y и расстояние ρ входят в них в квадрате. Центробежным моментом инерции площади фигуры называется интеграл произведений элементарных площадей на их расстояния до осей x и y: Моменты инерции измеряются в единицах длины в четвертой степени (как правило, см^4). Понятие о моменте инерции впервые ввел в науку в 1673 г. французский ученый Христиан Гюйгенс (Huygens, 1629–1695 гг.).
Моменты инерции собственные, переносные, главные центральные	Осевые и центробежный моменты инерции относительно осей, проходящих через центр тяжести поперечного сечения стержня, иногда называются собственными моментами инерции. По какой формуле вычисляются моменты инерции фигуры относительно оси, параллельной центральной? Какие моменты инерции называются переносными? Пусть две взаимно перпендикулярные оси x и y проходят через центр тяжести C поперечного сечения стержня. Проведем другие оси координат x’ и y’, параллельные осям x и y. Обозначим a и b координаты центра тяжести С в новых осях x’ и y’ (рис.1, а). Рис. 1. Параллельный перенос и поворот координатных осей Тогда осевые и центробежный моменты инерции фигуры относительно новых осей x’ и y’ будут определяться по следующим формулам: Очень часто эти формулы необоснованно приписывают немецкому ученому Якобу Штейнеру (Steiner, 1796–1863 гг.). Однако на самом деле они были доказаны еще в 1749 г. Эйлером. Первые слагаемые в формулах (1) ранее нами были названы собственными моментами инерции. Вторые слагаемые в этих формулах называются переносными моментами инерции. Отметим, что координаты a и b подставляются в формулы (1) с учетом их знаков, что является крайне важным, в частности, для третьей из этих формул. Как изменяются собственные моменты инерции при повороте координатных осей? Пусть нам известны собственные моменты инерции Ix, Iy и Ixy относительно двух взаимно перпендикулярных осей x и y, проходящих через центр тяжести C поперечного сечения стержня. Проведем через точку C другие оси x’ и y’, повернутые относительно осей x и y на угол α (рис. 1, б). Будем считать этот угол положительным, если поворот осей происходит против хода часовой стрелки. Можно показать, что моменты инерции поперечного сечения относительно новых осей x’ и y’ будут определяться по формулам: Из формул (2) видно, что Следовательно, сумма собственных осевых моментов инерции поперечного сечения является величиной постоянной, то есть она не изменяется при повороте координатных осей. Из этих же формул (2) можно получить следующую важную зависимость: Как уже отмечалось выше, две взаимно перпендикулярные оси, проходящие через центр тяжести фигуры, относительно которых центробежный момент инерции равен нулю, называются главными центральными осями инерции. Тогда при из третьей формулы (2) после несложных преобразований можно определить направления этих осей: Из полученного выражения (5) мы найдем два значения угла α0, которые отличаются друг от друга на угол 90°. Они и определяют положение двух главных центральных осей инерции. Какие собственные осевые моменты инерции называются главными центральными моментами инерции? При повороте центральных осей и приближении их к главным центральным осям больший из собственных осевых моментов инерции становится еще больше, стремясь к своему максимальному значению Imax, а меньший – еще меньше, приближаясь к минимальному значению Imin. Моменты инерции фигуры относительно главных центральных осей Imax и Imin называются главными центральными моментами инерции. Они могут быть вычислены по следующим формулам, вытекающим из соотношений (2) и (4): Из (6) легко получить следующее условие, аналогичное (3): Как для сложной фигуры определить, какая из главных центральных осей является осью максимум, то есть той осью, относительно которой осевой момент инерции принимает наибольшее значение Imax? По определению осевой момент инерции равен интегралу произведений элементарных площадей на квадрат их расстояний до соответствующей оси. Поэтому чем больше элементарные площади удалены от оси и чем больше таких площадей, тем больше и осевой момент инерции. Чему равны главные центральные моменты инерции простейших фигур: прямоугольника и круга? Для прямоугольного поперечного сечения (рис. 2, а) оси x и y являются главными центральными осями, поскольку они проходят через центр тяжести фигуры и являются осями симметрии. Рис. 2. Прямоугольное и круглое поперечные сечения стержня Главные моменты инерции прямоугольника равны: Необходимо запомнить, что размер стороны, параллельной рассматриваемой оси, входит в выражение для главного момента инерции прямоугольника в первой степени, а размер стороны, перпендикулярной к оси, – в третьей степени. Для круглого поперечного сечения любые две взаимно перпендикулярные оси, проходящие через центр тяжести фигуры, являются главными центральными осями (рис. 2, б). Очевидно также, что для круга Imax=Imin. Если d – диаметр круга, то Учитывая, что Iρ=Ix+Iy, можно легко получить следующую формулу для полярного момента инерции стержня круглого поперечного сечения:
Момент сопротивления осевой	В том случае, когда поперечное сечение балки симметрично относительно нейтральной оси, нормальные напряжения в точках, наиболее удаленных от нее (при |y|=h/2), определяются по формуле Геометрическую характеристику поперечного сечения балки, равную и называют осевым моментом сопротивления при изгибе. Он измеряется в единицах длины в кубе (как правило, в см^3). Тогда наибольшие нормальные напряжения равны Заметим, что формула (1) по внешнему виду напоминает формулу для наибольших касательных напряжений при кручении стержня. И здесь буквенное обозначение W, выбранное для обозначения осевого момента сопротивления при изгибе, очень похоже на перевернутую букву M, что также способствует лучшему запоминанию очень важной формулы (1). Чему равны моменты сопротивления при изгибе для балок прямоугольного и круглого поперечных сечений? Рис. 1. Прямоугольное и круглое поперечные сечения стержня Для прямоугольного поперечного сечения (см. рис. 1) момент сопротивления при изгибе относительно нейтральной оси x равен: Из этой формулы видно, что при той же самой площади поперечного сечения балки ее момент сопротивления существенно возрастает с увеличением высоты балки h. Если балка имеет квадратное поперечное сечение со стороной a, то В случае круглого поперечного сечения балки момент сопротивления при изгибе равен Заметим, что для катанных профилей, таких, например, как швеллер, двутавр и уголок, значения моментов сопротивления балки при изгибе (а также другие геометрические характеристики) определяются по сортаментам, которые приводятся в приложениях практически к каждому учебнику по сопротивлению материалов.
Мора круги	графический способ определения напряжений на наклонных или главных площадках.

Н

Нагрузка	совокупность активных внешних сил, действующих на рассматриваемое тело.
Нагрузка погонная	При расчете балок часто приходится сталкиваться с погонной нагрузкой. Так называется нагрузка, приходящаяся на единицу длины балки. Ее интенсивность, как правило, обозначается буквой q. Как уже отмечалось в первой беседе, единицы погонной нагрузки – ньютон на метр, килоньютон на метр (Н/м, кН/м) или килограмм силы на метр, килограмм силы на сантиметр (кгс/см, кгс/м) и т. д. Определение значения погонной нагрузки, действующей на балку, рассмотрим на следующем примере. Пусть, например, помещение комнаты представляет собой в плане прямоугольник со сторонами 9 и 5 м. Пять балок пола уложены параллельно меньшей из сторон прямоугольника через 1,5 м и оперты концами на стены. Пусть давление на пол p=4 кН/м^2 кН/м^2. Подсчитаем интенсивность погонной нагрузки q, приходящуюся на одну балку. Будем предполагать, что давление p и соответственно нагрузка на площадь, расположенную между двумя смежными балками, распределяется поровну между этими балками. Следовательно, ширина полосы, с которой давление «собирается» на одну балку с двух сторон, будет равна b=1,5 м. Тогда погонная нагрузка q=pb=4×1,5=6 кН/м.
Наклеп материала	повышение прочности и уменьшение пластичности материала вследствие предварительной нагрузки выше предела текучести.
Напряжения	Очевидно, что в общем случае нагружения внутренние силы в стержне распределены и по его длине, и по его поперечному сечению неравномерно. Для суждения об интенсивности внутренних сил, возникающих, например, в некоторой точке поперечного сечения стержня, вводится понятие о напряжении в этой точке. Это понятие является ключевым понятием в сопротивлении материалов. Напряжением в точке тела K (обозначим его буквой p) называется интенсивность внутренней силы dR, возникающей на бесконечно малой площадке dF в окрестности данной точки (рис. 1, а). В количественном выражении напряжение, возникающее в точке тела на площадке dF, равно: p=dR/dF. Заметим, что приведенное выражение, конечно же, неправомерно рассматривать как процедуру дифференцирования, при которой роль аргумента играет площадь поперечного сечения. Рис. 1. Напряжение в точке тела поперечного сечения Понятие о напряжении в точке твердого тела в некотором смысле напоминает понятие о давлении, которое действует, например, внутри жидкости. В технике под термином «давление» понимают величину, численно равную силе, действующей на единицу поверхности. Однако, хотя эти два понятия и сопоставимы, необходимо отметить следующее. Согласно закону Блеза Паскаля (Paskal, 1623 – 1662 гг.), давление в точке жидкости одинаково во всех направлениях. Если же мы проведем через точку K твердого тела другое сечение, то в новый разрез попадет другая пружинка и иной в общем случае будет и внутренняя сила. Следовательно, иным будет и напряжение, хотя оно и возникает в той же самой точке K. Таким образом, при произвольном приложении внешней нагрузки напряжения, возникающие в некоторой точке тела на разных площадках, проходящих через данную точку, отличаются друг от друга. Понятие о напряжении в точке деформируемого твердого тела ввел в 1822 г. французский ученый Огюстен Луи Коши (Cauchy, 1789 – 1857 гг.). Основную роль в расчетах прочности конструкций играет не полное напряжение p, а его составляющие на оси координат x, y и z: нормальное напряжение (σz – сигма), направленное по перпендикуляру к площадке (параллельно оси z), и касательные напряжения (τzx, τzy), лежащие в плоскости сечения и направленные соответственно вдоль осей x и y (рис. 1, б). Первый индекс z у касательных напряжений τzx, τzy характеризует нормаль к площадке, на которой они возникают. Заметим, что иногда касательные напряжения называются тангенциальными напряжениями (от латинского слова tangens – касающийся) или скалывающими. Между полным p, нормальным σz и касательными напряжениями τzx и τzy существует следующая очевидная зависимость: Отметим, что касательные напряжения служат мерой тенденции одной части сечения смещаться относительно другой его части. Единица измерения нормальных и касательных напряжений в системе СИ – паскаль (Па). Один паскаль – это напряжение, при котором на площадке в один квадратный метр возникает внутренняя сила, равная одному ньютону (то есть равная приблизительно весу одного яблока). Как мы увидим в дальнейшем, эта единица напряжения очень мала. В сопротивлении материалов чаще используются другие единицы: 1 МПа = 10^6Па; 1 кН/см^2 ≈10^7Па = 10 МПа. В технической системе единиц напряжения, как правило, измеряются в килограммах силы на миллиметр (или сантиметр) в квадрате (кгс/мм^2 или кгс/см^2) . Следует запомнить, что 1 кгс/мм^2≈1 кН/см^2 = 10 МПа. Необходимо отметить следующее. Ведя речь о напряжениях или о внутренних силовых факторах, мы не рекомендуем говорить, что они действуют в поперечном (или в некотором другом) сечении стержня, как поступают авторы некоторых учебниках по сопротивлению материалов. Правильнее говорить, что они возникают в рассматриваемом сечении стержня, поскольку при деформировании стержня и напряжения, и внутренние силовые факторы противодействуют внешней нагрузке, то есть они не играют активной роли. В крайнем случае слово «действуют» следует употреблять, заключая его в кавычки. Наконец, еще раз подчеркнем, что нельзя говорить о напряжении в данной точке тела, не указывая положения площадки, на которой оно возникает.
Напряжения и площадки главные	По каким формулам вычисляются нормальные и касательные напряжения, возникающие на наклонных площадках, проходящих через рассматриваемую точку? При изучении плоского напряженного состояния (НС) мы будем рассматривать только такие наклонные площадки, которые перпендикулярны граням параллелепипеда, на которых отсутствуют нормальные и касательные напряжения (рис. 1). Рис. 1. Напряжения на наклонной площадке, проходящей через точку К Наклон площадки будем определять углом α, который образует внешняя нормаль z’ к этой площадке с осью z. Угол 𝛼 считается положительным, если он отсчитывается от оси z против хода часовой стрелки. Тогда нормальные и касательные напряжения, возникающие на наклонной площадке, проходящей через точку К, определяются соответственно по следующим формулам: Формулы (1) позволяют нам фактически определять напряжения, возникающие на любой площадке, проходящей через заданную точку. Таким образом, плоское НС в точке тела определено, если нам известны (заданы) напряжения, возникающие на двух взаимно перпендикулярных площадках, проходящих через эту точку тела. Из формул (1) видно, что нормальные и касательные напряжения являются непрерывными функциями угла α и, следовательно, могут иметь экстремальные значения: максимумы и минимумы. Найдем угол наклона площадки , при котором нормальное напряжение принимает экстремальное значение. Для этого возьмем производную и приравняем ее к нулю: Тогда Из формулы (3) мы найдем два угла и , которые и определяют положение двух взаимно перпендикулярных площадок, на которых возникают экстремальные в рассматриваемой точке К нормальные напряжения σmax и σmin (рис.2). Рис.2. Главные площадки и главные напряжения Необходимо отметить, что σmax всегда направлено в ту сторону, где сходятся касательные напряжения 𝜏zy=𝜏yz. Объяснение этого правила следует из рассмотрения рис. 3. Рис. 3. Деформация элемента под «действием» касательных напряжений Видно, что касательные напряжения «создают» дополнительное удлинение одной из диагоналей. Заметим, что формула (3) внешне напоминает формулу , по которой определяется положение главных центральных осей инерции. Чему равны касательные напряжения на площадках, на которых возникают экстремальные нормальные напряжения? Из формулы (2) можно сделать следующий, очень важный вывод: касательные напряжения на этих площадках равны нулю. Какие площадки и какие напряжения называются главными? Площадки, проходящие через исследуемую точку, на которых касательные напряжения отсутствуют, называются главными площадками, а возникающие на этих площадках нормальные напряжения – главными напряжениями. По каким формулам вычисляются экстремальные нормальные напряжения в исследуемой точке тела? Исключив из формул (1) угол 2α, мы получим следующее уравнение Значения экстремальных нормальных напряжений можно найти из полученного уравнения (4), если положить в нем =0, поскольку на главных площадках касательные напряжения отсутствуют. Тогда: Заметим, что формулы (5) внешне похожи на формулы, по которым вычисляются значения главных центральных моментов инерции поперечного сечения стержня. Отметим также важную закономерность, которая вытекает из выражений (5): Следовательно, при плоском НС сумма нормальных напряжений, возникающих на любых двух взаимно перпендикулярных площадках, проходящих через некоторую точку тела, остается постоянной. Как обозначаются главные напряжения? В общем случае нагружения (при объемном НС) среди бесчисленного множества площадок, проходящих через некоторую точку тела, всегда можно найти три взаимно перпендикулярные главные площадки. Следовательно, в окрестности любой точки деформированного твердого тела всегда можно выделить элементарный параллелепипед, ориентированный в пространстве таким образом, что по его граням будут возникать только нормальные (главные) напряжения. Главные напряжения обозначаются через σ1, σ2, σ3. Индексы расставляются лишь после того, как эти напряжения вычислены, при этом должно выполняться следующее неравенство: σ1≥σ2≥σ3. Таким образом, σ1 – наибольшее по алгебраической величине, а σ3 – наименьшее по алгебраической величине нормальное напряжение, возникающее в исследуемой точке тела. В частном случае нагружения может получиться так, что все три главных напряжения в исследуемой точке тела равны между собой. Тогда любая площадка, проведенная через эту точку, является главной. В заключение отметим, что именно по значениям главных напряжений дается оценка прочности материала в исследуемой точке деформированного твердого тела. При плоском НС на грани элементарного параллелепипеда с нормалью х полностью отсутствует не только касательное, но и нормальное напряжение. Тогда получается, что эта площадка тоже является главной? Да. И главное напряжение на этой площадке равно нулю. Иногда такую площадку называют нулевой главной площадкой. Пусть, например, для случая плоского НС мы по формулам (5) нашли, что экстремальные нормальные напряжения в исследуемой точке равны 𝛔max=200 МПа, а 𝛔min=50 МПа. Как в этом случае расставить индексы у главных напряжений? В этом случае σ1=200 МПа, σ2=50 МПа, σ3=0 МПа. Если же, например, получилось, что σmax=-100 МПа, а σmin=-250 МПа, то тогда σ1=0 МПа, σ2=-100 МПа, σ3=-250 МПа. По какой формуле вычисляются наибольшие касательные напряжения в исследуемой точке тела и на каких площадках они возникают? Найдем угол наклона площадки α1, при котором касательное напряжение , определяемое по формуле (6.3), принимает экстремальное значение. Для этого возьмем производную и приравняем ее к нулю: Отсюда Сопоставляя равенства (6) и (3), мы видим, что следовательно, или Таким образом, для данной точки существуют две взаимно перпендикулярные площадки, на которых возникают равные по закону парности экстремальные касательные напряжения τmax. Эти площадки расположены под углом 45° к главным площадкам (рис. 4), на которых «действуют» главные напряжения σ1 и σ3. Рис. 4. Площадки, на которых возникают наибольшие касательные напряжения Абсолютное значение экстремальных касательных напряжений определяется по формуле В общем случае нагружения на площадках, на которых возникают наибольшие касательные напряжения, возникают и нормальные напряжения. Последние равны половине суммы главных напряжений σ1 и σ3. Если же, например, на площадках, где возникают наибольшие касательные напряжения, нормальные напряжения отсутствуют, то эти площадки называются площадками чистого сдвига. Вернемся к чистому сдвигу. Чему в этом случае равны главные напряжения и в каких направлениях они возникают? Напомним, что при чистом сдвиге в поперечных сечениях стержня возникают только касательные напряжения τzy. По закону парности касательных напряжений τyz=τzy. Напряженное состояние в рассматриваемой точке является плоским. Пусть dy=dz (рис. 5). Рис.5. Чистый сдвиг По формуле (2) найдем, что Тогда По формуле (4) получим: Следовательно, главные напряжения при чистом сдвиге равны: Их направления показаны на рис. 5. Наибольшие касательные напряжения равны: Таким образом, чистый сдвиг можно рассматривать как простую комбинацию растяжения и сжатия под углом 45°.
Напряжения допускаемые	Испытания материала на растяжение и сжатие позволяют определить предельные напряжения σпред, то есть те напряжения, при которых материал образца непосредственно разрушается или же в нем возникают большие пластические деформации. Таким образом, в качестве предельного напряжения принимается: - для пластичного материала – предел текучести (то есть считается, что разрушение пластичного материала начинается при появлении в нем заметных пластических деформаций): - для хрупкого материала – предел прочности, значение которого при растяжении и сжатии различно: Для обеспечения прочности реального стержня необходимо так выбрать его размеры и материал, чтобы наибольшее нормальное напряжение, возникающее в некоторой точке, было меньше предельного напряжения: σzmax<σпред. Однако даже в том случае, когда наибольшее расчетное напряжение σzmax в стержне будет близко к предельному напряжению, гарантировать его прочность еще нельзя. Дело в том, что внешние нагрузки, воздействующие на реальный стержень, не могут быть нами определены достаточно точно. Да и расчетные напряжения в стержне в ряде случаев могут быть вычислены лишь приближенно. Наконец, возможны отклонения действительных механических характеристик материала, применяемого для стержня, от характеристик, заложенных в расчете. Из сказанного следует, что стержень должен быть спроектирован с некоторым расчетным коэффициентом запаса прочности: Ясно, что чем больше n, тем прочнее деталь. Однако совершенно очевидно, что очень большой коэффициент запаса прочности приводит к перерасходу материала и это делает стержень тяжелым и неэкономичным. В зависимости от назначения конструкции и целого ряда других обстоятельств устанавливается допускаемый (или нормативный) коэффициент запаса прочности, который обозначается [n]. Прочность стержня считается обеспеченной, если n≥[n]. Это условие и называют условием прочности. Используя выражение (1), перепишем условие прочности в виде: Отсюда можно получить и другую форму записи условия прочности: Отношение предельного напряжения к допускаемому коэффициенту запаса прочности (то есть отношение, стоящее в правой части последнего неравенства) называется допускаемым напряжением. Оно обозначается [σ] и определяется по формуле В случае, когда предельные и соответственно допускаемые напряжения при растяжении и сжатии различны, их обозначают и . Пользуясь понятием допускаемого напряжения, можно условие прочности сформулировать следующим образом: прочность стержня будет обеспечена, если возникающее в нем наибольшее напряжение не превышает допускаемого напряжения. Тогда окончательно условие прочности при растяжении (сжатии) записывается в следующем виде: В случае, когда расчетное напряжение получается значительно ниже допускаемого, площадь опасного поперечного сечения стержня должна быть уменьшена. Если расчетное напряжение незначительно, но все же превышает допускаемое напряжение, такое незначительное превышение в расчетах на прочность допускается, но не более, чем на 5%. К сожалению, приходится констатировать, что студенты не всегда правильно понимают условие прочности (2). Так, на естественный вопрос, что произойдет со стержнем (конструкцией), если расчетное напряжение превысит допускаемое напряжение [σ], например, на 10%, можно услышать ответ, что конструкция разрушится. Это неверно. Она может и не разрушиться, если, например, выполняется условие, что . Еще раз подчеркнем, что допускаемое напряжение представляет собой долю от предельного напряжения. Поэтому незначительное превышение расчетного напряжения над допускаемым напряжением означает лишь только снижение надежности конструкции. В этом случае расчетный коэффициент запаса прочности получается меньше допускаемого (n<[n]).
Напряжения касательные	составляющие полного вектора напряжений, лежащие в плоскости рассматриваемого сечения и обозначаются .
Напряжения касательные при поперечном изгибе	Вырежем из балки прямоугольного поперечного сечения (рис. 1, а) элемент длиной dz и дополнительным продольным сечением рассечем его на две части (рис.1, б). Рис.1. Касательные напряжения при изгибе Рассмотрим равновесие верхней части, в поперечных сечениях которой из-за отличия изгибающих моментов возникают разные сжимающие напряжения. Для того чтобы эта часть балки находилась в равновесии (то есть выполнялось условие равновесия ΣZ=0), в ее продольном сечении должна возникнуть касательная сила dT. Тогда Отсюда где интегрирование ведется только по отсеченной части площади поперечного сечения балки Fотс. Эта часть площади (рис. 1, в) нами заштрихована. В формуле (1) – статический момент отсеченной (заштрихованной) части площади поперечного сечения относительно нейтральной оси x. Будем предполагать, что касательные напряжения τyz, возникающие в продольном сечении балки, равномерно распределены по ее ширине by в месте сечения. Это допущение, известное под названием гипотезы Журавского, справедливо только в том случае, когда ширина поперечного сечения много меньше его высоты, то есть сечение является узким. Тогда и соответственно Учитывая формулу (1), найдем, что Но, согласно формуле Шведлера – Журавского, dMx/dz=Qy, а τyz=τzy. Тогда окончательно касательные напряжения 𝜏zy, возникающие в точках поперечного сечении балки, находящихся на расстоянии y от нейтральной оси x, определяются по следующей формуле Приближенная формула (2) впервые была получена в 1855 г. Дмитрием Ивановичем Журавским, и поэтому она носит его имя. Проанализируем формулу Журавского. Для конкретного сечения балки перерезывающая сила Qy и момент инерции поперечного сечения относительно нейтральной оси Ix являются постоянными величинами. Поэтому из формулы (2) следует, что по высоте поперечного сечения касательные напряжения изменяются по тому же закону, что и отношение статического момента отсеченной части поперечного сечения к ширине поперечного сечения by, в котором они вычисляются. Во всех точках поперечного сечения, расположенных на расстоянии y от нейтральной оси, то есть по всей ширине сечения by, касательные напряжения одинаковы. Во всех самых удаленных от нейтральной оси точках поперечного сечения касательные напряжения равны нулю, поскольку в этом случае Fотс=0. Наибольшие касательные напряжения возникают в точках поперечного сечения, расположенных на нейтральной оси. Напомним, что в этих точках нормальные напряжения равны нулю. Как выглядят эпюры касательных напряжений для балок прямоугольного и двутаврового поперечных сечений? Напомним, что при выводе формулы Журавского мы предполагали, что балка имеет прямоугольное поперечное сечение (рис. 2), поэтому где y – расстояние от точки, в которой определяется касательное напряжение, до нейтральной оси x. Подставляя выражения (3) в формулу (2), получим: Отсюда видно, что для балки прямоугольного профиля касательные напряжения изменяются по высоте поперечного сечения по закону квадратичной параболы (см. рис. 2). Рис. 2 Эпюра касательных напряжений для прямоугольного поперечного сечения балки При , то есть для точек, наиболее удаленных от нейтральной оси, τzy=0. Для точек, расположенных на нейтральной оси (при y=0), касательные напряжения достигают максимального значения: Характерной особенностью двутаврового сечения балки является то обстоятельство, что в том месте, где полка соединяется со стенкой, происходит резкое изменение ширины поперечного сечения by (рис. 3). Рис. 3. Эпюра касательных напряжений для двутаврового поперечного сечения балки Определим касательное напряжение в некоторой точке K. Для этого проведем через эту точку сечение. Ширина этого сечения равна толщине стенки, то есть by=d. Рассмотрим верхнюю отсеченную часть площади поперечного сечения, которая состоит из площади полки F1 и площади части стенки F2 (обе эти площади на рис. 3, а заштрихованы). Статический момент этой отсеченной части площади поперечного сечения относительно нейтральной оси x равен: Эпюра касательных напряжений, возникающих в точках стенки двутавра, имеет вид, показанный на рис. 3, б. Касательные напряжения τzy, возникающие в точках полки двутавра, по формуле Журавского вычислять нельзя, поскольку при ее выводе использовалось допущение о равномерности распределения касательных напряжений по ширине поперечного сечения, что справедливо только в том случае, если ширина сечения by невелика. Однако очевидно, что эти напряжения малы и не оказывают практического влияния на прочность балки. Их эпюра показана штриховой линией (см. рис. 3, б). Касательное напряжение в точке L, то есть в том месте, где полка соединяется со стенкой, вычисляется по формуле Как и для балки прямоугольного поперечного сечения, наибольшие касательные напряжения в балке двутаврового профиля возникают в точках, лежащих на нейтральной оси x. По какой формуле можно вычислить значения касательных напряжений для балки прямоугольного поперечного сечения, если оно не является узким? Точное решение задачи, полученное Сен-Венаном, показывает, что касательные напряжения при поперечном изгибе балки не одинаковы по ширине поперечного сечения. Наибольшие касательные напряжения возникают в точках, расположенных по краям нейтральной оси. Значения этих напряжений можно определить по следующей формуле где k – коэффициент, зависящий от отношения сторон b/h. Так, например, при b/h=0,5 коэффициент k=1,033, то есть для узкого поперечного сечения формула Журавского дает практически точное значение. Если же сечение широкое, например, b/h=4, то тогда коэффициент k=1,988. Следовательно, формула Журавского занижает максимальные касательные напряжения почти в два раза. Как выглядит эпюра касательных напряжений для балки круглого поперечного сечения? Прежде чем ответить на этот вопрос, попробуем сначала выяснить, какое вообще направление имеет касательное напряжение, возникающее в некоторой точке контура поперечного сечения стержня. Рассмотрим поперечное сечение стержня, имеющее совершенно произвольную форму (рис. 4, а). Предположим, что в некоторой точке К его контура возникает касательное напряжение τ, направленное под каким-то углом по отношению к контуру. Разложим это напряжение на две составляющие: τn – по нормали и τt – по касательной к контуру сечения. Если напряжение τn действительно существует, то по закону парности касательных напряжений на поверхности стержня должно существовать и равное ему по значению касательное напряжение . Но поверхность стержня при изгибе не нагружена внешними силами, параллельными оси балки z. Поэтому касательное напряжение на поверхности стержня =0 и, следовательно, τn=0. Таким образом, при изгибе балки касательное напряжение, возникающее в некоторой точке контура поперечного сечения, всегда направлено по касательной к контуру. Покажем, что в вершине угла прямоугольного поперечного сечения балки касательное напряжение при изгибе равно нулю (рис. 4, б). Рис.4. Касательное напряжение в точке контура поперечного сечения стержня Предположим, что в вершине угла, в точке M, возникает некоторое касательное напряжение τ. Разложим его на составляющие τzx и τzy. Но касательные напряжения на поверхности балки отсутствуют (τxz=τyz=0). Поэтому по закону парности касательных напряжений должны быть равны нулю и составляющие τzx и τzy. Следовательно, в точке M 𝜏=0. С учетом изложенного выше, задача вычисления касательных напряжений в произвольной точке балки круглого поперечного сечения заметно усложняется. Однако, если сделать предположение о том, что в точках, расположенных на некоторой линии ab (рис. 5), касательные напряжения τ направлены так, что все они пересекаются в точке О, и дополнительно предположить, что вертикальные проекции этих напряжений равномерно распределены вдоль линии ab, то формулу Журавского можно использовать для вычисления вертикальных проекций τzy. Вычисление всех остальных величин, входящих в формулу (2), производится так же, как и, например, для прямоугольного поперечного сечения. Рис.5. Эпюра касательных напряжений для балки круглого поперечного сечения В частности, наибольшие касательные напряжения, возникающие в точках, расположенных на нейтральной оси x, вычисляются по формуле Согласно гипотезе Бернулли считается, что при изгибе балки ее продольные волокна не оказывают давления друг на друга. Такое предположение для чистого изгиба вполне естественно. Но насколько это допущение справедливо при поперечном изгибе балки? Рассмотрим, например, жестко защемленную балку прямоугольного поперечного сечения, нагруженную сверху равномерно распределенной поперечной нагрузкой q. Тогда в точках, принадлежащих верхним волокнам балки, возникнут нормальные напряжения: В нижних же волокнах, ввиду отсутствия поверхностной нагрузки, σy=0. При существующих на практике значениях внешней нагрузки напряжение настолько мало по сравнению с наибольшим нормальным напряжением σz, возникающем в поперечном сечении балки, что им можно пренебречь. Покажем это. Для рассматриваемой балки наибольший изгибающий момент возникает в заделке. Он равен В этом случае Тогда . Для реальных балок отношение l/h>10, поэтому окончательно получим:
Напряжения нормальные	составляющие полного вектора напряжений, направленные по нормали к рассматриваемому сечению и обозначаются σ
Напряжения нормальные при растяжении-сжатии	Из гипотезы Бернулли следует, что все продольные волокна стержня деформируются одинаково. Поэтому можно считать, что при растяжении (сжатии) напряжения во всех точках поперечного сечения стержня одинаковы и направлены по нормали к поперечному сечению. Такие напряжения, напомним, называются нормальными напряжениями. Если в рассматриваемом поперечном сечении стержня возникает продольное усилие N, а F – площадь этого поперечного сечения, то, с учетом изложенного выше, нормальные напряжения при растяжении (сжатии) вычисляются по формуле Для нормального напряжения σ, как и для продольной силы N, принимается следующее правило знаков: при растяжении оно считается положительным, а при сжатии – отрицательным. Какие напряжения возникают в наклонных сечениях стержня, то есть в сечениях, которые не являются поперечными? Начнем ответ со следующих рассуждений. Да, мы уже умеем определять нормальные напряжения, которые возникают в опасном поперечном сечении стержня. Но можем ли мы утверждать, что эти нормальные напряжения являются наибольшими и именно их значения следует использовать для оценки прочности стержня? Нам уже известно, что касательные напряжения в поперечном сечении стержня при растяжении (сжатии) не возникают. Но возникают ли они в наклонных сечениях? Таким образом, нам необходимо научиться определять напряжения на любых площадках, проходящих через некоторую точку К тела, и находить именно те площадки, на которых нормальные и касательные напряжения достигают наибольших значений. А теперь ответим на поставленный вопрос. Разрежем стержень, растягиваемый силами P, плоскостью, проходящей через точку К и наклоненной под углом α к поперечному сечению (рис. 1, а). Отбросим правую часть стержня. Рис.1. Напряжения в наклонных сечениях Внешняя нормаль к этому наклонному сечению будет составлять с осью z такой же угол α. Действие отброшенной нами правой части стержня на левую часть заменим внутренними усилиями (рис. 1, б). Чтобы левая часть стержня находилась в равновесии, в каждой точке наклонного сечения стержня должно возникнуть продольное противодействующее усилие. Очевидно, что равнодействующая всех этих внутренних усилий N равна внешней силе P. Будем считать, что внутренние усилия равномерно распределены по всей площади наклонного сечения F1=F/cosα. Тогда полное напряжение в каждой точке наклонного сечения будет равно: где – нормальное напряжение, возникающее в этих же точках (в том числе и в точке К), но в поперечном сечении стержня (рис. 1, в). Разложим полное напряжение p, возникающее в некоторой точке К наклонного сечения, на две составляющие – нормальное и касательное напряжения (рис. 1, г). Они будут равны: Проследим, как будет меняться каждое из этих напряжений с изменением угла наклона сечения α от нуля до 90°. При увеличении угла α нормальное напряжение в точке К будет постепенно уменьшаться от своего максимального значения до нуля. Касательное напряжение при этом будет сначала возрастать от нулевого до максимального значения при α=45°, а затем убывать. При угле α=90° касательное напряжение снова станет равным нулю. Следовательно, наибольшее нормальное напряжение действительно возникает в точках поперечного сечения стержня. В продольном сечении оно равно нулю. Отсюда следует, что продольные волокна стержня не давят друг на друга. Наибольшие касательные напряжения возникают в сечениях, расположенных под углом 45° к оси стержня. В поперечном и в продольном сечениях стержня они равны нулю.
Напряжения нормальные при чистом изгибе	Допущения, принимаемые при выводе формулы для нормальных напряжений при чистом изгибе балки. 1) гипотеза плоских сечений при изгибе балки. Мысленно нанесем на боковой поверхности недеформированной балки сетку, состоящую из продольных и поперечных (перпендикулярных к оси балки) прямых линий. В результате изгиба балки мы увидим, что продольные линии примут криволинейное очертание, а поперечные линии практически останутся прямыми и перпендикулярными к изогнутой оси балки. Таким образом, поперечные сечения, плоские и перпендикулярные к оси балки до деформации, остаются плоскими и перпендикулярными к изогнутой оси после ее деформации. Это обстоятельство свидетельствует о том, что при изгибе (как при растяжении и кручении) выполняется гипотеза плоских сечений. 2) Помимо упомянутой гипотезы плоских сечений принимается ещё одно допущение: считается, что продольные волокна балки при ее изгибе не надавливают друг на друга (то есть напряжения σy=0). Эти два допущения вместе называют гипотезой Бернулли. Рассмотрим балку прямоугольного поперечного сечения, испытывающую чистый изгиб (Qy=0). Двумя бесконечно близкими поперечными сечениями выделим элемент балки длиной dz (рис. 1. а). В результате изгиба поперечные сечения балки повернутся, образовав между собой угол dθ. Пусть при этом верхние волокна испытывают сжатие, а нижние – растяжение. Радиус кривизны нейтрального волокна обозначим ρ. Для удобства далее будем условно считать, что волокна изменяют свою длину, оставаясь при этом прямыми (рис. 1. б). Тогда абсолютное и относительное удлинения волокна, отстоящего на расстоянии y от нейтрального волокна, будут соответственно равны: По закону Гука Рис.1. Нормальные напряжения при чистом изгибе Покажем теперь, что продольные волокна, не испытывающие при изгибе балки ни растяжения, ни сжатия, проходят через главную центральную ось x. Поскольку длина балки (а точнее, длина ее оси) при изгибе не изменяется, продольное усилие N, возникающее в поперечном сечении, должно равняться нулю. Элементарное продольное усилие . Тогда или, с учетом выражения (1), Множитель E/ρ≠0 можно вынести за знак интеграла, так как он не зависит от переменной интегрирования. В итоге получим Выражение (2) представляет собой статический момент площади поперечного сечения балки относительно нейтральной оси x. Он равен нулю только в том случае, когда эта ось проходит через центр тяжести поперечного сечения. Следовательно, нейтральная ось (или нулевая линия) при изгибе балки проходит через центр тяжести поперечного сечения. Очевидно, что изгибающий момент связан с нормальными напряжениями, возникающими в точках поперечного сечения стержня. Поэтому перейдем к его вычислению. Элементарный изгибающий момент, создаваемый элементарной силой , равен , тогда где – момент инерции поперечного сечения относительно нейтральной оси x, а отношение k=1/ρ называется кривизной оси балки. Произведение EIx в формуле (3) называется жесткостью поперечного сечения балки при изгибе. Чем больше эта величина, тем меньше кривизна оси балки при том же значении изгибающего момента. Формула (3) представляет собой закон Гука для стержня при изгибе: изгибающий момент, возникающий в поперечном сечении, пропорционален кривизне оси балки. Выражая из (3) радиус кривизны ρ и подставляя его значение в (1), получим окончательно следующую формулу для нормальных напряжений 𝜎z, возникающих в произвольной точке поперечного сечения балки, отстоящей на расстоянии y от нейтральной оси x: Отметим, что в формулу (4), которая, кстати, впервые была получена Навье, следует подставлять абсолютные значения изгибающего момента Mx и координаты y. Будет ли напряжение в данной точке растягивающим или же сжимающим легко установить по характеру изгиба балки или, что является тем же самым, по эпюре изгибающих моментов, ординаты которой откладываются нами со стороны сжатых волокон балки. Из формулы (4) видно, что нормальные напряжения σz изменяются по высоте поперечного сечения балки по линейному закону. Напомним, что по ширине сечения они считаются постоянными. На рис. 1, в показана эпюра нормальных напряжений. Наибольшие напряжения при изгибе балки возникают в точках, наиболее удаленных от нейтральной оси. Несложный анализ эпюры нормальных напряжений показывает, что при изгибе балки материал, расположенный вблизи нейтральной оси, практически не работает. Поэтому в целях снижения веса балки рекомендуется выбирать такие формы поперечного сечения, у которых большая часть материала удалена от нейтральной оси как, например, у двутаврового профиля.
Напряжения нормальные при поперечном изгибе	В отличие от чистого изгиба, при поперечном изгибе в сечении балки помимо изгибающего момента Mx возникает и перерезывающая сила Qy. Поэтому в поперечном сечении наряду с нормальными напряжениями σz возникают и касательные напряжения τzy. На основании закона парности касательных напряжений в продольных сечениях балки возникают касательные напряжения τyz=τzy. Возникновение касательных напряжений τyz в плоскостях, параллельных нейтральной плоскости, покажем на следующем простом примере. Мысленно представим себе балку прямоугольного поперечного сечения высотой h, шарнирно опертую по концам. Поместим поверх этой балки точно такую же балку. Приложим к этим двум балкам посредине пролета сосредоточенную силу P. Если пренебречь трением между этими балками, изгиб каждой из них будет происходить независимо от изгиба другой балки. При этом у обеих балок будут сжаты верхние и растянуты нижние волокна. В результате нижние продольные волокна верхней балки сместятся относительно верхних волокон нижней балки. Иную картину мы будем наблюдать в сплошной балке высотой 2h. Никакого смещения верхней части балки относительной нижней мы, естественно, не обнаружим. Отсутствие этого смещения и объясняется возникновением, в данном случае в нейтральном слое, касательных напряжений τyz. Поскольку при поперечном изгибе в поперечных сечениях стержня возникают касательные напряжения τzy, поперечные сечения балки искривляются (рис. 1) и, следовательно, гипотеза плоских сечений нарушается. Рис. 1. Нарушение гипотезы плоских сечений Однако теоретические и экспериментальные исследования показали, что если балка является достаточно длинной (l/h>10), то влияние искривления поперечного сечения на значения нормальных напряжений невелико. Поэтому влиянием сдвигов на закон распределения нормальных напряжений при изгибе пренебрегают и нормальные напряжения вычисляют по формуле
Напряжения переменные	Рассмотрим, ось вагона, имеющую круглое поперечное сечение диаметром d, нагруженную силами P и вращающуюся с постоянной угловой скоростью 𝜔=const (рис. 1, а). Подшипники, на которые опирается вал, будем рассматривать как шарнирные опоры. Рис.1. Напряжения, переменные во времени На участке AB между опорами вал испытывает чистый изгиб (эпюра изгибающих моментов Mx построена на сжатых волокнах). Проследим за изменением нормального напряжения в точке К, расположенной вблизи контура поперечного сечения (рис. 1, б). Напомним, что напряжения при изгибе в произвольной точке поперечного сечения равно: При повороте вала расстояние y от точки К до нейтральной оси x будет изменяться от 0, когда точка находится на оси x, до ymax=d/2, когда точка К занимает крайнее верхнее или крайнее нижнее положение. В некоторый момент времени t это расстояние может быть определено по формуле y(t)=(d/2)sinωt. Тогда Из последней формулы видно, что напряжение в точке К изменяется по синусоидальному закону (рис. 1, в). За один полный оборот оси рассматриваемая точка попадает из зоны растяжения в зону сжатия (или наоборот). Мысленно представим теперь, что к этой же оси вагона помимо двух сил P (рис. 1, а), вызывающих ее изгиб, по концам приложены и две растягивающие постоянные силы P1. Тогда напряжение в точке К будет равно алгебраической сумме напряжений, возникающих как от растяжения, так и от изгиба: В этом случае график изменения напряжений в рассматриваемой точке K во времени будет представлять собой синусоиду, но смещенную вверх относительно оси t на величину P1/F.
Напряжения и состояния предельные	Прежде всего, отметим, что речь будет идти об оценке прочности не всего тела, а о прочности материала в отдельно взятой его точке. Напомним, что в случае линейного НС оценка прочности в исследуемой точке тела довольно легко производится путем непосредственного сопоставления возникающего в ней расчетного напряжения либо с предельным 𝜎пред, либо с допускаемым напряжением [𝜎]. Коэффициент запаса прочности равен отношению предельного напряжения к расчетному: n=σпред/σ. Состояние материала, при котором хотя бы в одной точке тела отмечено возникновение текучести или признаков хрупкого разрушения, рассматривается как предельное, то есть соответствующее началу нарушения прочности всего тела. Соответствующее этому состоянию напряжение называется предельным. Для пластичных материалов за предельное напряжение принимается предел текучести σm, а для хрупких – предел прочности σпч. Расчет на прочность, основанный на таком представлении о предельном состоянии тела, называется расчетом по опасной точке или расчетом по допускаемым напряжениям. В современной практике, однако, применяют и другие методы расчета, например, по предельным нагрузкам или несущей способности, по расчетным предельным состояниям и т. д. Эти методы основаны на иных представлениях о предельных состояниях тела.
Напряжения температурные	Если при нагреве (охлаждении) стержня ничто не препятствует изменению его длины, то никаких напряжений в нем не возникает. При нагреве линейные размеры тела увеличиваются, а при охлаждении – уменьшаются. Абсолютное удлинение стержня, вызванное изменением его температуры на ∆t градусов Цельсия, определяется по формуле где α – коэффициент линейного расширения материала стержня, а l – его длина. Для стали, например, коэффициент линейного расширения примерно равен α=0,0000115. Если стальной стержень с первоначальной длиной l=1 м равномерно нагреть на 20℃, то его длина увеличится на 0,23 мм. Иная картина имеет место для статически неопределимого стержня. Предположим, что мы нагреваем стержень, жестко защемленный по концам (см., например, рис. 1, а (P=0)). Рис. 1. Статически неопределимый стержень при растяжении (сжатии) Стержень хотел бы удлиниться на величину но этому препятствуют заделки. В них возникают реактивные силы RA=RB, которые в итоге приводят к сжатию стержня. Таким образом, при нагреве (охлаждении) статически неопределимого стержня в нем всегда возникают напряжения, которые принято называть температурными напряжениями. Определим температурные напряжения σt в рассмотренном нами случае. Отбросим мысленно нижнюю заделку и действие отброшенной связи на стержень заменим реактивной силой RB (см. рис. 1, б (P=0)). Удлинение стержня ∆l, равное нулю, может быть представлено в виде Отсюда Тогда температурные напряжения в стержне равны
Напряжения эквивалентные	напряжение, которое следует создать в растянутом образце, чтобы его напряженное состояние стало равноопасным заданному напряженному состоянию. Из приведенных рассуждений следует, что эквивалентное напряжение – это лишь некоторая воображаемая условная расчетная величина, а не какое-то реально возникающее напряжение. Значение эквивалентного напряжения зависит не только от заданного типа НС (то есть от значений, соответствующих ему главных напряжений), но и от принятого для расчета прочности критерия эквивалентности НС. Поэтому, в частности, нельзя говорить, что эквивалентное напряжение возникает в некоторой точке. Следует говорить об определении (или вычислении) эквивалентного напряжения для исследуемой точки.
Напряженное состояние в точке тела	Напряженным состоянием (НС) в точке тела называют совокупность нормальных и касательных напряжений, возникающих на всевозможных площадках, проходящих через данную точку. Для оценки прочности материала в первую очередь интересуют наибольшие значения нормальных и касательных напряжений, возникающих в данной точке тела. Для их определения нам необходимо знать нормальные и касательные напряжения на любых трех взаимно перпендикулярных площадках, проходящих через данную точку тела. Кроме того, необходимо знать и направления «действия» этих наибольших нормальных и касательных напряжений или, иными словами, на каких площадках, проходящих через данную точку тела, они возникают. Исследование напряженного состояния в точке тела начинается с того, что в окрестности исследуемой точки, например точки К (рис. 1), из нагруженного тела, находящегося в равновесии, мысленно вырезается элементарный параллелепипед со сторонами dx, dy и dz. Ввиду малости этого параллелепипеда можно считать, что напряженное состояние во всех его внутренних точках одинаково (то есть однородно) и совпадает с напряженным состоянием в непосредственно исследуемой точке К. Поэтому мы будем предполагать, что как по граням, так и по любым другим сечениям элементарного параллелепипеда нормальные и касательные напряжения распределяются равномерно. Эти предположения позволяют исследовать закон изменения напряжений по наклонным сечениям элементарного параллелепипеда, считая, что эти сечения проходят через исследуемую нами точку К. Рис.1. Элементарный параллелепипед Какие различают виды НС в точке тела? В дальнейшем мы увидим, что в окрестности любой точки деформированного твердого тела всегда можно выделить элементарный параллелепипед, ориентированный в пространстве таким образом, что по его граням будут возникать только нормальные напряжения. В зависимости от того, испытывает ли такой параллелепипед «растяжение» («сжатие») в одном, в двух или в трех направлениях, различают следующие виды НС (рис. 2). Рис. 2. Виды напряженного состояния в точке тела: а – линейное (одноосное); б – плоское (двухосное); в – объемное (трехосное) С линейным НС мы уже сталкивались при изучении центрального растяжения (сжатия) стержня. В задачах сопротивления материалов наиболее часто встречается плоское НС. Его характерным признаком является полное отсутствие нормальных и касательных напряжений на двух параллельных гранях элементарного параллелепипеда. Именно этому случаю НС мы и уделим в дальнейшем основное внимание. В частности, мы будем полагать, что напряжения не возникают на гранях элементарного параллелепипеда с нормалью x. Тогда вместо объемного параллелепипеда, с целью упрощения, мы будем на рисунках показывать плоский элемент, то есть проекцию параллелепипеда на плоскость yz. При этом штриховкой мы будем указывать внутреннюю область этого элемента. Объемное НС в курсе сопротивления материалов практически не изучается. Какие правила знаков для нормальных и касательных напряжений принимаются в сопротивлении материалов при изучении плоского НС? Установим следующие правила знаков. Для нормальных напряжений оно формулируется очень просто: нормальное напряжение, соответствующее растяжению, считается положительным, а сжатию – отрицательным. Несколько сложнее выглядит правило для касательных напряжений. Касательное напряжение будем считать положительным, если одновременно выполняются (или одновременно не выполняются) следующие два условия: - во-первых, направление напряжения совпадает с положительным направлением соответствующей координатной оси; - во-вторых, внешняя нормаль к площадке, на которой оно возникает, направлена в ту же сторону, что и другая соответствующая координатная ось. Например, все напряжения на рис. 3, возникающие по граням элементарного параллелепипеда, показаны положительными. Поскольку, как уже отмечалось, во всех точках элементарного параллелепипеда НС считается однородным, одноименные напряжения, возникающие на параллельных гранях элемента, численно равны друг другу. Рис. 3. Положительные направления нормальных и касательных напряжений Отметим, что при анализе НС в некоторой точке тела нормальные σz, σy и касательные τzy, τyz напряжения, возникающие по граням элементарного параллелепипеда, считаются заданными.
Напряженное состояние равноопасное	такое напряженное состояние, для которого коэффициенты запаса прочности по всем компонентам тензора напряжений равны.
Напряженное состояние линейное	если одно главное напряжение отлично от нуля, а два других равны нулю ); полное напряжение: нормальное напряжение: касательное напряжение: на перпендикулярных площадках:
Напряженное состояние плоское (двухосное)	если два главных напряжения отличны от нуля, а одно равно нулю );
Напряженное состояние объемное	если все три главных напряжения отличны от нуля ); ; ; максимальные касательные напряжения ; напряжения по октаэдрической площадке интенсивность напряжений первый инвариант: ; обобщенный закон Гука: ; относительная объемная деформация ; среднее напряжение ; модуль объемной деформации: ; Потенциальная энергия ; удельная потенциальная энергия энергия изменения объема: ; энергия изменения формы: тензор напряжений: тензор для главных напряжений:
Нейтральная ось	линия, во всех точках которой нормальные напряжения равны нулю. При этом в точках сечения, наиболее удаленных от нейтральной оси нормальные напряжения принимают свои экстремальные значения – минимум и максимум.

О

Оболочка	тело, одно измерение которого мало по сравнению с двумя другими.
Обобщенные силы и перемещения	Внешняя нагрузка, действующая на балку, обычно представляет собой группу сил. Упругую работу группы сил по теореме Клапейрона можно записать в виде: где множитель P зависит только от сил этой группы и называется обобщенной силой, а ∆ зависит от перемещений и называется обобщенным перемещением. Таким образом, под обобщенной силой будем понимать любую нагрузку (сосредоточенные силы, моменты, распределенную нагрузку), а под обобщенным перемещением – тот вид перемещения, на котором обобщенная сила производит работу. Пусть, например, группа сил состоит из двух равных постоянных сил P, образующих пару. Момент этой пары (рис. 1) равен M=Pa. Рис. 1. Обобщенная сила и обобщенное перемещение Допустим, что в результате деформации системы элемент AB повернулся на угол θ. Пути, пройденные точками приложения сил P по направлениям их действия, соответственно равны AA’=OA∙θ и BB’=OB∙θ. Суммарная работа обеих сил: Следовательно, если обобщенной силой является момент M, то обобщенным перемещением – угол поворота θ.
Однородный материал	материал, в каждой точке которого механические свойства одинаковы и не зависят от величины выделенного объема.
Опасное сечение	поперечное сечение стержня, где возникают наибольшие напряжения, растягивающие и сжимающие.
Опорные закрепления	В сопротивлении материалов применяются три вида опорных закреплений (рис. 1): Рис.1. Типы опорных закреплений балок 1) шарнирно неподвижная опора; 2) шарнирно подвижная опора; 3) жесткая заделка. Шарнирно неподвижной опорой (рис. 1, а, опора А) называется такое закрепление конца балки, при котором балка может поворачиваться, но не может перемещаться ни в горизонтальном (влево или вправо), ни в вертикальном (вверх или вниз) направлениях, то есть не может перемещаться ни в каком направлении. Следовательно, в такой опоре может возникнуть реакция, которую удобно представить в виде двух составляющих: вертикальной RA и горизонтальной HA. Такая опора на расчетной схеме условно изображается посредством двух стерженьков. Нижние их концы шарнирно прикреплены к «земле», а верхние концы соединены между собой и с балкой шарниром. Шарнирно подвижная опора (рис. 1, б, опора B) представляет собой устройство, при котором конец балки может свободно перемещаться в горизонтальном направлении, может поворачиваться при изгибе, но не может перемещаться в вертикальном направлении. Соответственно этому со стороны подвижной опоры может возникнуть только одна, вертикальная реакция RB. Эта опора изображается посредством одного стерженька, шарнирно соединенного и с землей, и с балкой. Жесткой заделкой называется закрепление (рис. 1, в, опора С), при котором конец балки не может ни поворачиваться, ни перемещаться. В заделке могут возникнуть реактивный момент MC (момент жесткой заделки) и реакции RC и HC. Балка при таком закреплении показывается заделанной в часть стены, которая штрихуется.
Опорные реакции	Способы определения опорных реакций изучаются в курсе теоретической механики. Поэтому мы остановимся только на некоторых практических вопросах, касающихся методики их вычисления, в частности для шарнирно опертой балки с консолью (рис. 1). Рис.1. Определение опорных реакций Для такой балки нам необходимо найти три упомянутые ранее реакции: RA, HA и RB. Направления этих реакций мы выбираем произвольно. Направим, например, обе вертикальные реакции вверх, а горизонтальную реакцию – влево. Для вычисления их значений можно составить три уравнения статики: 1) Сумма проекций всех сил (активных и реактивных) на ось z равна нулю: ΣZ=0. Поскольку в сопротивлении материалов принято считать, что на балку действуют только вертикальные нагрузки (перпендикулярные к ее оси), то из этого уравнения мы легко находим, что горизонтальная реакция неподвижной шарнирной опоры HA=0. 2) Сумма моментов всех сил относительно опоры А равна нулю: ΣMA=0. Договоримся о правиле знаков для момента силы. Будем считать момент силы положительным, если он вращает балку относительно некоторой точки против хода часовой стрелки. Кстати, происхождение термина «момент силы» неизвестно. По-видимому, этот термин произошел от латинского слова movimentum, что означает способность силы двигать (вращать) объект, используя какой-либо рычаг (плечо силы). Вернемся к рассматриваемому примеру. Предварительно нам необходимо найти равнодействующую распределенной погонной нагрузки. Очевидно, что она равна площади эпюры этой нагрузки q∙c и приложена в центре тяжести этой эпюры, то есть посредине участка длиной c. Тогда 3) Сумма моментов всех сил относительно опоры B равна нулю: ΣMB=0 Или Знак «минус» в полученном результате говорит о том, что предварительное направление опорной реакции RA нами было выбрано неверно. Заменим направление реакции RA на противоположное (см. рис. 1) и про знак «минус» навсегда забудем. Теперь сделаем проверку. Сумма проекций всех сил на ось y должна быть равна нулю: ΣY=0. Силы, направление которых совпадает с положительным направлением оси y, проектируются (или проецируются) на эту ось со знаком «плюс»: то есть опорные реакции найдены нами верно. Теперь перейдем к жестко защемленной балке. В этом случае для определения опорных реакций составляются следующие уравнения статики: ΣZ=0; ΣY=0; ΣMc=0. Из первого уравнения определяется реакция HC (обычно она равна нулю), из второго – RC, а из третьего – момент в заделке MC. Проверка, как правило, не производится.
Осевое усилие	Осевое усилие равно сумме проекций всех сил на ось z, действующих с одной стороны сечения: . Осевое усилие вызывает растяжение или сжатие элемента.
Оси главные	В зависимости от положения координатных осей центробежный момент инерции может быть положительным, отрицательным, а также равным нулю. Рассмотрим, например, квадрат (рис. 1, а). Рис. 1. Изменение центробежного момента инерции фигуры при повороте координатных осей Центробежный момент инерции квадрата Ixy относительно осей x,y положителен, так как координаты x,y у всех элементов площади положительные. При повороте осей вокруг начала координат на угол 90° (рис. 1, б) знак центробежного момента инерции становится отрицательным, так как в этом случае координаты x всех элементарных площадей положительны, а координаты y – отрицательны. Очевидно, что можно найти такое положение двух взаимно перпендикулярных осей x,y, при котором Ixy=0. Такие оси называются главными осями. Для квадрата такие оси изображены на рис. 1, в. Если фигура имеет ось симметрии, то эта ось является одной из главных осей (другая ось перпендикулярна ей). Главные оси, проходящие через центр тяжести поперечного сечения стержня, называются главными центральными осями. Понятие о главных осях впервые введено в 1755 г. Яношем Сегнером (Segner, 1704 – 1777 гг.) и, независимо от него, в 1758 г. Леонардом Эйлером (Euler, 1707 – 1783 гг.). Заметим, что иногда главные оси называют главными осями инерции. Встречаются ли помимо круглого поперечного сечения такие поперечные сечения, у которых любые центральные оси являются главными? Для всех поперечных сечений, у которых Imax=Imin, любые две взаимно перпендикулярны оси, проходящие через центр тяжести, всегда будут главными. Это правило вытекает из полученного нами ранее условия Imax+Imin=Ix+Iy=const, согласно которому ни один из осевых моментов инерции Ix или Iy не может быть меньше или больше, чем Imax=Imin. Следовательно, осевые моменты инерции Ix и Iy тоже равны между собой и при повороте осей вообще не изменяются. Тогда любые две взаимно перпендикулярные оси, проходящие через центр тяжести поперечного сечения, являются главными центральными осями. Например, момент инерции квадрата относительно любой оси, проходящей через цент тяжести, равен a^4/12. И все-таки, для чего нам необходимо знать положение главных центральных осей, а также значения главных центральных моментов инерции поперечного сечения стержня? Их определение, напрямую связано именно с обеспечением прочности, жесткости и устойчивости стержня (то есть, с теми основными вопросами, которые и изучаются в сопротивлении материалов), но при более сложных, чем центральное растяжение (сжатие) и сдвиг, видах деформации. Рассмотрим следующий пример. Предположим, что нам необходимо заделать одним концом в стену обычную ученическую линейку, поперечное сечение которой представляет собой прямоугольник, у которого один размер (высота) намного больше другого размера (толщины). Предполагается, что на другом конце к этой линейке будет приложена вертикальная сила P. Как нам следует расположить линейку в пространстве по отношению к этой нагрузке, чтобы напряжения в ней и прогиб свободного конца были минимальными? Ответ на этот вопрос очевиден – «ребром». То есть таким образом, чтобы силовая плоскость (плоскость, в которой расположена внешняя нагрузка) была перпендикулярна к оси максимум поперечного сечения линейки. Правда, при этом нам необходимо помнить о том, что с ростом силы P линейка попытается «выскользнуть» из-под нагрузки. И в этом легко убедиться, выполнив соответствующий эксперимент. При некотором значении нагрузки Pкр, называемой критической, линейка внезапно изогнется вбок с одновременным закручиванием. Это явление, которое называется потерей устойчивости плоской формы изгиба, вряд ли произойдет с линейкой, расположенной «плашмя». Очевидно, что расположенная таким образом линейка скорее сломается, чем потеряет устойчивость. А как нам расположить под вертикальной сосредоточенной силой стержень, поперечное сечение которого представляет собой, например, швеллер с приваренным к его полке неравнобоким уголком? Ответ на этот вопрос следующий: и в этом случае, с точки зрения прочности и жесткости, стержень нужно расположить так, чтобы силовая плоскость была перпендикулярна к оси максимум данного поперечного сечения. В заключение отметим, довольно часто говорят просто главные оси инерции и главные моменты инерции, подразумевая, что эти понятия имеют отношения к центру тяжести поперечного сечения стержня.
Ось бруса	геометрическое место точек центров тяжестей поперечных сечений бруса, то есть сечений, нормальных к оси бруса.
Относительное сужение после разрыва	, представляющее собой отношение уменьшения площади поперечного сечения образца в месте разрыва к начальной площади поперечного сечения образца: Для стали марки Ст3 характеристики пластичности следующие: δ=25…27% (при испытании коротких образцов); ψ=60…70%.
Относительное удлинение после разрыва	(%) – это отношение приращения расчетной длины образца после разрыва к ее первоначальному значению, вычисляемое по формуле: . Заметим, что относительное удлинение после разрыва зависит от отношения расчетной длины образца к его диаметру. С увеличением этого отношения значение уменьшается, так как зона шейки (зона местной пластической деформации) у длинных образцов занимает относительно меньше места, чем в коротких образцах. Кроме того, относительное удлинение зависит и от места расположения шейки (разрыва) на расчетной длине образца. При возникновении шейки в средней части образца местные деформации в области шейки могут свободно развиваться и относительное удлинение будет больше, чем в случае, когда шейка возникает ближе к головке образца, тогда местные деформации будут стеснены.
Отнулевой или пульсирующий цикл напряжений	изменение переменного во времени напряжения от нуля до максимального положительного значения (или от нуля до минимального отрицательного значения) в течении одного периода.

П

Перемещения способом фиктивной нагрузки определение
Перемещение балок при изгибе	Для того чтобы судить о работе балок, недостаточно иметь информацию только о напряжениях, которые возникают в ней при деформировании. Весьма прочные балки могут оказаться непригодными к эксплуатации из-за недостаточной их жесткости. Если балка сильно прогибается под нагрузкой, то в ней могут возникнуть изгибные колебания с большими амплитудами, приводящие к дополнительным напряжениям. Для проверки жесткости балки необходимо уметь определять перемещения отдельных точек ее оси. В результате изгиба ось балки становится криволинейной. Изогнутую ось балки принято называть упругой линией балки. Кривизна упругой линии балки может быть определена из формулы: Напомним, что вертикальное перемещение произвольной точки, лежащей на оси балки, при изгибе (прогиб балки) обозначается буквой v, продольное перемещение – буквой u, а угол поворота поперечного сечения балки – буквой θ. Проверка жесткости балки сводится к требованию, согласно которому ее наибольший прогиб vmax, называемый стрелой прогиба, не должен превышать определенной доли от пролета балки l: Здесь число m устанавливается нормами проектирования и колеблется обычно в пределах от 300 до 1000. Для ответственных сооружений, например, для мостов, m=1000. Отсюда видно, что прогибы балки при изгибе малы по сравнению с ее пролетом. Это позволяет нам в дальнейшем изложении ввести следующие упрощения: - во-первых, при малых прогибах v угол наклона касательной к изогнутой оси балки и, следовательно, угол поворота поперечного сечения балки можно определять с помощью выражения - во-вторых, горизонтальным перемещением u можно пренебречь, так как оно по сравнению с прогибом v и углом поворота поперечного сечения θ является величиной более высокого порядка малости. В результате мы можем считать, что угол поворота поперечного сечения равен первой производной от прогиба балки и что каждая точка оси балки перемещается только по вертикали. Следовательно, для определения полной картины деформации нам необходимо получить уравнение упругой линии балки v=v(z). Если эта функция известна, то, определив прогибы балки в ряде точек, можно построить кривую прогибов и найти наибольший прогиб, который и позволит нам судить о жесткости балки. В заключение отметим, что в ряде задач, главным образом статически неопределимых, возникает необходимость и в определении угла поворота поперечного сечения балки. Как записывается дифференциальное уравнение изгиба балки? Для определения уравнения изогнутой оси балки можно воспользоваться законом Гука (1): Из курса высшей математики нам известно следующее выражение для кривизны некоторой кривой: В пределах упругих деформаций квадрат угла поворота поперечного сечения балки ничтожно мал по сравнению с единицей. Поэтому , то есть вторая производная от прогиба представляет собой кривизну изогнутой оси балки в рассматриваемом месте. Тогда Это дифференциальное уравнение описывает изгиб балки в рамках гипотезы Бернулли. Продифференцировав его дважды по z, получим: Для балки постоянной жесткости (EIx=const) будем иметь Дифференциальное уравнение четвертого порядка (2) называется дифференциальным уравнением изгиба балки. Интегрируя уравнение (2) первый раз, получим выражение, дающее закон изменения перерезывающей силы по длине балки. Второе интегрирование определяет характер изменения изгибающего момента, третье интегрирование – углов поворота поперечных сечений, наконец, четвертое – прогибов балки по ее длине. При этом четыре постоянные интегрирования определяются из условий опирания балки. Как на практике осуществляется вычисление прогибов и углов поворота поперечных сечений балки? Они могут быть определены, например, с помощью универсального уравнения упругой линии балки. Мы приведем это уравнение без вывода. Прогиб балки в сечении с координатой z и угол поворота этого же сечения (рис. 1) определяются по следующим формулам: Здесь a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой. Заметим, что в формулы (3) входят только те внешние усилия (активные и реактивные), которые расположены левее сечения, в котором определяются перемещения балки. Если какая-нибудь нагрузка (нагрузки) имеют направление, противоположное тому, что указано на рис. 1, то у соответствующего слагаемого (слагаемых) в формулах (3) следует поменять знак на противоположный. В случае многократного повторения однотипных нагрузок необходимо использовать суммирование соответствующих слагаемых. Рис. 1. Прогиб и угол поворота поперечного сечения балки Прогиб v(0) и угол поворота θ(0) балки в начале координат (начальные параметры) определяются из условий закрепления балки. Продемонстрируем использование формул (3) на примере балки (см. рис. 2). Рис.2 Определим, например, прогиб балки на консоли при z=6 м, то есть v(6). Запишем универсальное уравнение упругой линии балки: Очевидно, что прогиб балки в начале координат (на левой шарнирной опоре) равен нулю. То есть v(0)=0. Для определения угла поворота в начале координат θ(0) необходимо составить дополнительное условие: прогиб на правой опоре равен нулю. Таким образом, будем иметь: Отсюда Тогда окончательно прогиб консоли равен: Знак «минус» говорит нам о том, что прогиб балки на консоли происходит вниз. Отметим также, что число, стоящее в числителе, измеряется в нашем примере в килоньютонах на метр в кубе (кН∙м^3). Примерный вид упругой линии балки показан на рис. 3. Рис. 3. Согласование упругой линии балки с эпюрой изгибающих моментов Упругая линия балки должна быть согласована с эпюрой изгибающих моментов. Напомним, что положительный изгибающий момент «изгибает» балку выпуклостью вниз (сжатые волокна сверху), а отрицательный – выпуклостью вверх (сжатые волокна снизу). Точка перегиба, то есть та точка, в которой кривизна балки равна нулю, находится под тем сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука. Как производится расчет простейших статически неопределимых балок? Он может быть произведен, например, с использованием универсального уравнения упругой линии балки. Рассмотрим, например, один раз статически неопределимую балку (рис. 4). Рис.4. Статически неопределимая балка Для определения трех реактивных усилий RA, RB, MA мы имеем пока только два уравнения статики: Третье дополнительное уравнение, необходимое для раскрытия статической неопределимости, можно получить, записав условия равенства нулю прогиба на шарнирной опоре: v(l)=0. При z=0, то есть в заделке, прогиб v(0)=0 и угол поворота сечения θ(0)=0. Поэтому условие отсутствия прогиба в точке B может быть представлено в виде: или Теперь мы имеем систему из трех уравнений с тремя неизвестными: Решая ее, находим: Таким образом, статическая неопределимость балки нами раскрыта.
Период колебаний	промежуток времени между двумя последующими максимальными отклонениями упругой системы от положения равновесия.
Периодическая нагрузка	переменная нагрузка с установившимся во времени характером изменения, значения которой повторяются через определенный промежуток (период) времени.
Пластина	элемент конструкции, у которого одно измерение (толщина) мало по сравнению с двумя другими. Пластина, криволинейная до нагружения, называется оболочкой.
Пластичность	способность материала накапливать до разрушения пластические (остаточные) деформации (свойство материала под действием внешних сил необратимо деформироваться без разрушения). Заметим, что пластичность – это положительное свойство материала. Она играет большую роль в обеспечении надежности конструкций. Пластические свойства материала оцениваются следующими двумя характеристиками, которые определяются при испытании на растяжение: - относительное остаточное удлинение образца при разрыве (в процентах), вычисляемое по формуле где l1 – конечная длина расчетной части образца; - относительное поперечное сужение образца при разрыве (в процентах), определяемое по формуле где F1 – площадь поперечного сечения образца в месте разрыва (иными словами, площадь поперечного сечения шейки).
Плоскость изгиба	плоскость расположения изогнутой оси балки.
Плоскость силовая	плоскость действия нагрузочных сил.
Площадки главные	площадки, совпадающие с гранями элементарного параллелепипеда, вырезанного в окрестностях исследуемой точки, на которых действуют главные напряжения.
Повторно-переменные нагрузки	силы непрерывно и периодически изменяющиеся во времени.
Ползучесть	явление изменения во времени напряжений и деформаций в нагруженной детали. Различают два случая ползучести - последействие и релаксацию.
Полная диаграмма критических напряжений	графическая зависимость критических напряжений от гибкости стержня.
Поперечная сила	Поперечные силы равны сумме проекций всех внешних сил (с одной стороны сечения) на оси х и y соответственно: Поперечные силы вызывают сдвиг в сечении элемента.
Последействие	или собственно ползучесть, явление роста деформаций при постоянных напряжениях
Потенциальная энергия деформации стержня	Согласно закону сохранения энергии, работа внешних сил не исчезает, а переходит в потенциальную энергию V, накапливаемую в упругом теле при его деформировании. Следовательно, потенциальная энергия деформации численно равна работе внешних сил при нагружении тела (или работе внутренних сил, совершаемой ими в процессе разгружения) V=A. Обращаем внимание на присутствие в этом предложении слова «численно». Его необходимо добавлять потому, что потенциальная энергия и работа являются разными понятиями и что они не могут быть равны друг другу. Таким образом, потенциальная энергия стержня, испытывающего, например, растяжение, кручение и прямой поперечный изгиб, равна: Как видно из этой формулы, потенциальная энергия деформации всегда положительна, поскольку она является квадратичной функцией обобщенных сил (или обобщенных перемещений, так как последние линейно связаны с обобщенными силами). Отсюда следует, что потенциальная энергия, накопленная в результате действия группы сил, не равна сумме потенциальных энергий, накопленных от действия каждой нагрузки в отдельности. Следовательно, принцип независимости действия сил при вычислении потенциальной энергии деформации не применим.
Поперечное сечение	сечение стержня, перпендикулярное (нормальное) к его центральной оси.
Предел выносливости	наибольшее (предельное) напряжение цикла , при котором не происходит усталостного разрушения образца после произвольно большого числа циклов. Так как испытания нельзя проводить бесконечно большое время, то число циклов ограничивают некоторым пределом, который называют базовым числом циклов. В этом случае, если образец выдерживает базовое число циклов (для черных металлов – N = 10^7), то считается, что напряжение в нем не выше предела выносливости. Кривые усталости для цветных металлов не имеют горизонтальных участков, поэтому для них за базовое число циклов увеличивается до N=10^8 и устанавливается предел ограниченной выносливости. Предел выносливости обозначается σR (или τR), где индекс R соответствует коэффициенту асимметрии цикла. Так, например, для симметричного цикла он обозначается σ-1, для отнулевого – σ0, для постоянного – σ+1. Установлено, что предел выносливости при симметричном цикле является наименьшим по сравнению с другими видами циклов, то есть σ-1<σR. Так, например,
Предел длительной прочности	напряжение, подсчитанное по первоначальной площади сечения образца, при котором происходит разрушение образца при данной температуре через заранее заданный промежуток времени. Этот промежуток времени называется базой испытания.
Предел неограниченной выносливости	Наибольшее по абсолютному значению напряжение цикла, при котором не происходит усталостного разрушения за бесконечно большое число циклов.
Предел ограниченной выносливости	Для расчета деталей, не предназначенных к длительной эксплуатации, возникает необходимость в определении наибольшего значения напряжения, которое может выдержать материал при заданном числе циклов N, значение которого меньше, чем базовое N0. В этом случае по кривой усталости и заданному числу циклов N определяется соответствующее напряжение σRN, называемое пределом ограниченной выносливости. В качестве базовой долговечности обычно принимают N0=10^6, 10^7 или 5∙10^7 циклов.
Предел пропорциональности	σпц называется наибольшее напряжение, до которого существует прямо пропорциональная зависимость между нагрузкой, и деформацией. Для Ст3 предел пропорциональности приблизительно равен σпц=195…200 МПа.
Предел прочности	отношение максимальной силы, которую способен выдержать образец из данного материала, к начальной площади поперечного сечения образца. В учебниках по сопротивлению материалов встречаются два понятия: «предел прочности» и «временное сопротивление разрыву». Первое из них относится к случаю, когда образец разрушается без образования шейки, что характерно для хрупких материалов. Второе относится к пластичным материалам. Временное сопротивление разрыву обозначают σв.
Предел текучести	σm называется наименьшее напряжение, при котором образец деформируется без заметного увеличения растягивающей нагрузки. Предел текучести является одной из основных механических характеристик прочности металлов. Для стали Ст3 σm=220…250 Мпа.
Предел упругости	σуп называется максимальное напряжение, при котором в материале не обнаруживается признаков пластической (остаточной) деформации. Предел упругости существует независимо от закона прямой пропорциональности. Он характеризует начало перехода от упругой деформации к пластической. У большинства металлов значения предела пропорциональности и предела упругости незначительно отличаются друг от друга. Поэтому обычно считают, что они практически совпадают. Для стали СтЗ σуп =205…210 МПа.
Предельное состояние	состояние, при котором конструкция или сооружение перестают удовлетворять заданным эксплуатационным требованиям или требованиям при возведении.
Принцип возможных перемещений	Этот принцип в 1788 г. был сформулирован для абсолютно твердых тел французским ученым Жозефом Луи Лагранжем (Lagrange, 1736–1813 гг.) и впервые применен к деформируемым телам Пуассоном в 1833 г. Принцип возможных перемещений формулируется следующим образом: если система находится в равновесии под действием приложенной к ней нагрузки, то сумма работ внешних и внутренних сил на всяком бесконечно малом возможном перемещении точек системы, допускаемых связями, равна нулю: Ав+Uв=0, где Ав – возможная работа внешних, а Uв – возможная работа внутренних сил. Заметим, что в процессе совершения системой возможного перемещения значения и направления внешних и внутренних сил считаются неизменными, то есть такими же, как и в исходном состоянии. Поэтому возможная работа внешних и внутренних сил определяется простым произведением соответствующих сил и перемещений, то есть в отличие от выражения для упругой работы в выражении для возможной работы коэффициента 1/2 нет. Учитывая принятое в сопротивлении материалов допущение о малости деформаций, а также линейную зависимость деформаций от нагрузок, в качестве возможных перемещений можно принимать и конечные упругие перемещения, вызванные любым видом внешней нагрузки и происходящие без нарушения связей.
Принцип Даламбера	Если движущееся тело (систему тел) в какой-то момент времени представить себе находящимся в покое, но помимо сил, производящих движение, приложить к нему силы инерции, то в таком покоящемся теле будут существовать такие же внутренние усилия, напряжения и деформации, какие имеют место во время его движения.
Принцип начальных размеров	Упругие тела являются относительно жесткими, благодаря чему перемещения точек тела весьма малы по сравнению с размерами самого тела.
Принцип независимости действия сил (принцип наложения, принцип суперпозиции, принцип сложения действия сил)	принцип, согласно которому суммарный результат, полученный одновременным действием нескольких сил, является суммой отдельных результатов, полученных действием этих сил в отдельности.
Принцип Сен-Венана	Суть принципа, который предложил в 1853 г. французский ученый Адемар Жан-Клод Барре де Сен-Венан (de Saint-Venant, 1797 – 1886 гг.), заключается в следующем. Вблизи от места приложения внешних сил распределение напряжений и деформаций стержня зависит от способа их приложения. Вдали от места нагружения распределение напряжений и деформаций практически не зависит от способа приложения нагрузки, а зависит только от ее статического эквивалента. Принцип Сен-Венана дает возможность вести расчет без учета местных (локальных) деформаций, возникающих вблизи точек приложения внешних сил и отличающихся от деформаций основного объема материала, что в большинстве случаев упрощает решение задачи. Справедливость принципа Сен-Венана не имеет теоретического доказательства, но она подтверждается опытными данными.
Прогиб балки	поступательные перемещения сечений, равные перемещениям их центров тяжести.
Пролет	вся балка или ее часть, расположенная между двумя соседними опорами.
Прочность	Прочностью называется способность конструкции сопротивляться разрушению. При этом под нарушением прочности понимается не только разрушение конструкции в буквальном смысле этого слова, но и возникновение в ней больших пластических деформаций. Говоря о достаточной прочности конструкции, полагают, что прочность будет обеспечена не только при заданном значении внешней нагрузки, но и при некотором возможном ее увеличении, то есть конструкция должна иметь определенный запас прочности. Количественно прочность характеризуют напряжения (МПa).

Р

Работа при растяжении
Работа	Работа внешних сил, действующих на упругую систему: работа при статическом действии обобщенной силы на упругую систему: Работа внутренних сил (сил упругости) в случае плоского изгиба:
Работа внутренних сил	Если нагруженное тело находится в равновесии, то внутренние силы (силы упругости) равны по значению внешним силам и противоположны им по направлению, поскольку они препятствуют развитию деформации. Поэтому работа внутренних сил U, с учетом их направления по отношению к деформации, всегда является отрицательной. При этом, очевидно, что работа внешних сил равна взятой с обратным знаком работе внутренних сил, то есть A=-U. Пусть элемент стержня длиной dz испытывает растяжение. Действие отброшенных частей стержня на рассматриваемый элемент заменим продольными «растягивающими» силами N, направленными от сечения. По отношению к элементу они являются как бы внешними. Тогда «вызываемое» ими удлинение элемента равно: Действие рассматриваемого элемента на отброшенные нами части стержня представляет собой для рассматриваемого элемента как бы внутренние усилия. Элементарная работа именно этих, постепенно увеличивающихся, внутренних продольных сил, противодействующих развитию удлинения, согласно теореме Клапейрона, равна: Теперь вычислим элементарную работу внутренних перерезывающих сил Qy при чистом сдвиге. Напомним, что в этом случае считается, что касательные напряжения равномерно распределены по всему сечению и определяются по формуле Абсолютный сдвиг dy правого сечения элемента длиной dz по отношению к левому сечению, с учетом закона Гука, равен: Тогда При поперечном изгибе касательные напряжения распределены по сечению неравномерно. В этом случае выражение для элементарной работы внутренних перерезывающих сил может быть представлено в виде: где k – коэффициент, зависящий от формы поперечного сечения стержня. Например, для прямоугольного поперечного сечения k=1,2. Определим теперь элементарную работу внутренних усилий при кручении. Поворот правого сечения элемента длиной dz по отношению к левому сечению, происходящий под действием внешних по отношению к нему крутящих моментов Mz, согласно закону Гука, равен: Тогда элементарная работа внутренних крутящих моментов на этом же угле поворота определяется по формуле Пусть теперь элемент стержня длиной dz испытывает чистый изгиб. И пусть его правое поперечное сечение повернется на угол dθ по отношению к левому сечению. Значение этого угла поворота мы определили ранее. Оно равно: Тогда внутренние изгибающие моменты совершат на этом угле поворота следующую элементарную работу: При одновременном растяжении, кручении и прямом поперечном изгибе стержня (с учетом того, что работа каждого из внутренних усилий на перемещениях, вызываемых остальными усилиями, равна нулю) получим следующее выражение для элементарной работы внутренних сил: Интегрируя последнее выражение по всей длине стержня, окончательно будем иметь:
Равновесие безразличное	новое положение системы после отклонения от исходного остается положением равновесия и после удаления внешнего воздействия.
Равновесие неустойчивое	система не возвращается в исходное положение, а отклоняется от него еще больше.
Равновесие устойчивое	при малом отклонении от положения равновесия система возвращается в первоначальное положение, как только будет устранена причина, вызывающая это отклонение
Равноустойчивый стержень	Мы уже отмечали, что если стержень одинаково закреплен в обеих главных плоскостях инерции, то при вычислении критической нагрузки в расчет необходимо вводить наименьший из главных моментов инерции. Поэтому рациональным будет такое поперечное сечение стержня, для которого главные моменты инерции равны между собой: Imax=Imin. Такой стержень и называется равноустойчивым. Так, например, если поперечное сечение стержня состоит из двух рядом расположенных двутавров, то Ix>>Iy. Раздвигая двутавры, мы будем увеличивать момент инерции поперечного сечения Iy. Для того чтобы такой стержень стал равноустойчивым, расстояние между центрами тяжести двутавров, так называемая раздвижка, обозначаемая далее буквой a, должно быть определено из условия, что Ix=Iy. Если для одного двутавра моменты инерции обозначить и (причем ), а площадь поперечного сечения – F1, то для определения раздвижки можно записать следующее равенство: Отсюда раздвижка двутавров равна
Радиус инерции	Момент инерции фигуры относительно какой-либо координатной оси может быть представлен в виде произведения площади фигуры на квадрат некоторой величины, называемой радиусом инерции: Новые геометрические характеристики в этих выражениях определяются по формулам и называются радиусами инерции поперечного сечения относительно осей x и y соответственно. Главным центральным осям соответствуют главные радиусы инерции: Например, для прямоугольника главные радиусы инерции равны: А для круглого поперечного сечения:
Размах напряжений цикла	алгебраическая разность максимального и минимального напряжения цикла.
Распределенная нагрузка	нагрузка, прилагаемая непрерывно к данной поверхности или линии. Единица измерения Н/м.
Растяжение (сжатие)	Растяжением (сжатием) называется такой вид деформации стержня, при котором происходит изменение его первоначальной длины. Растяжение (сжатие) стержня вызывается внешними силами, действующими вдоль его оси z, проходящей через центр тяжести поперечного сечения. При этом в любом поперечном сечении стержня возникает только одно внутреннее усилие – продольная сила N, которая является равнодействующей всех внутренних сил, возникающих в каждой точке этого поперечного сечения и направленных параллельно оси стержня. Условие прочности при растяжении (сжатии) записывается в следующем виде: В случае, когда расчетное напряжение получается значительно ниже допускаемого, площадь опасного поперечного сечения стержня должна быть уменьшена. По какой формуле осуществляется подбор требуемой площади поперечного сечения стержня при растяжении (сжатии)? Из неравенства (1) следует, что А как записывается условие жесткости? Оно имеет вид: ≤[∆l], где – допускаемое удлинение стержня.
Расчетная модель (схема)	Расчет любой реальной конструкции начинается с выбора расчетной схемы. Она представляет собой упрощенную, идеализированную схему, которая отражает наиболее существенные особенности объекта, определяющие его поведение под действием внешней нагрузки. Выбор расчетной схемы начинается со схематизации свойств материала и характера деформирования твердого тела. Вторым шагом является схематизация геометрической формы реального объекта. Формы элементов конструкций можно свести к следующим категориям: стержень, оболочка, пластина и массивное тело. Стержень – это твердое тело, у которого один размер (длина) значительно (раз в десять) превышает два других его размера. Представим себе некоторую плоскую фигуру, перемещающуюся в пространстве так, что центр тяжести этой фигуры все время остается на некоторой линии (прямой или кривой), а сама фигура остается перпендикулярной к этой линии. Описанная такой фигурой форма дает нам очертание стержня (прямолинейного или криволинейного). Линия, вдоль которой перемещается фигура, называется осью стержня, а сама фигура – его поперечным сечением. Оболочка – это твердое тело, ограниченное двумя криволинейными поверхностями, у которого один размер (толщина) много меньше двух других размеров. Пластина (или плита) – это тело, ограниченное двумя параллельными плоскостями. Массивное тело – это такое твердое тело, у которого все три размера имеют один порядок. В курсе сопротивления материалов, в основном, изучается напряженно-деформированное состояние призматических стержней с прямолинейной осью. Оболочки, пластины и массивные тела, как правило, не могут быть рассчитаны методами сопротивления материалов.
Реальный объект	исследуемый элемент конструкции, взятый с учетом всех своих особенностей: геометрических, физических, механических и других.
Резонанс	Явление повышения амплитуды при совпадении частот собственных колебаний и возмущающей силы, а само совпадение частот называется условием резонанса.
Релаксация	уменьшение напряжений в материале при постоянной деформации.

С

Сдвиг чистый	Сдвигом называется такой вид деформации, при котором одна часть стержня смещается относительно другой (как скользят, например, карты в колоде) или такой вид нагружения бруса, при котором в его поперечных сечениях из шести составляющих главного вектора и главного момента внутренних сил, от нуля отличается только поперечная (перерезывающая) сила. Деформация сдвига будет происходить, например, в том случае, если к стержню приложить две равные по значению и противоположно направленные силы P, перпендикулярные к его оси z (рис. 1, а). Расстояние между этими силами ∆z должно быть очень малым, чтобы моментом P∙∆z, создаваемым этими силами, можно было пренебречь. Рис.1. Деформация сдвига Применив метод сечений (разрезав стержень между силами P), можно легко установить, что в поперечном сечении стержня возникает только одно внутреннее усилие – поперечная (перерезывающая) сила Qy=P. Далее мы увидим, что сдвиг возникает и при кручении стержня. При сдвиге в точках поперечного сечения стержня возникают только касательные напряжения . Будем считать, что касательные напряжения распределены по всей площади поперечного сечения равномерно (рис. 2). Рис. 2. Касательные напряжения при чистом сдвиге Тогда, если в поперечном сечении стержня площадью F возникает перерезывающая сила Qy=P, то касательные напряжения в любой точке этого сечения будут равны Касательные напряжения τzy измеряются в тех же единицах, что и нормальные напряжения σz: мегапаскалях, килоньютонах на квадратный сантиметр (МПа, кН/см^2), а также в килограммах силы на квадратный сантиметр или миллиметр (кгс/см^2, кгс/мм^2). В результате деформации сдвига одно поперечное сечение стержня смещается относительно другого на некоторую величину ∆y, называемую абсолютным сдвигом. Малый угол γ, на который изменится первоначально прямой угол (рис. 1, б), называется углом сдвига или относительным сдвигом. Угол сдвига выражается в радианах. Закон Гука при сдвиге: Касательное напряжение, отвечающее безопасной работе материала при сдвиге, называется допускаемым напряжением и обозначается [τ]. Величина допускаемых напряжений зависит от свойств материала, характера нагрузки и может быть определена по 3-ей теории прочности: , а так как при чистом сдвиге , то Условие прочности при сдвиге: По формуле (1) осуществляется проверочный расчет соединений, работающих на срез. Для определения требуемой площади поперечного сечения (проектировочный расчет) необходимо воспользоваться следующим неравенством, вытекающим из формулы (1): Какая зависимость существует между модулем сдвига и модулем Юнга? Для изотропных материалов эта зависимость имеет вид: Значение коэффициент Пуассона μ лежит в пределах 0≤μ≤0,5. Следовательно, E/3≤G≤E/2. Например, для стали любой марки: Аналогичное значение модуля сдвига для стали может быть получено в результате проведения эксперимента на сдвиг (или на кручение). Как выглядит диаграмма 𝛄 – 𝛕zy при сдвиге? Вид диаграммы γ – τzy аналогичен диаграмме εz – σz при растяжении, которую мы рассматривали выше. Так, для пластичного материала на ней, в частности, имеются точки, характеризующие предел пропорциональности при сдвиге τпц, предел текучести τm, а также предел прочности τпч. Последний соответствует срезу образца. Для многих материалов между пределом текучести при сдвиге τm и пределом текучести при растяжении σm существует следующая зависимость: Чему равна потенциальная энергия деформации при сдвиге? Если участок стержня длиной ∆z испытывает чистый сдвиг, то накапливаемая в нем потенциальная энергия деформации определяется по формуле
Сила инерции	Рассмотрим следующий пример. К грузу массой m привяжем веревку. Другой конец веревки будем удерживать в руке. Начнем вращать массу в горизонтальной плоскости с постоянной угловой скоростью. Будем пренебрегать весом груза. Тогда на массу будет действовать только одна сила – сила натяжения веревки, направленная от груза к руке (так называемая центростремительная сила). Эта сила выводит массу из присущего ей, по свойству инерции, состояния покоя или равномерного и прямолинейного движения и сообщает массе центростремительное ускорение. Согласно третьему закону Ньютона, масса противодействует этой силе. Это противодействие со стороны движущейся с ускорением массы приложено к веревке. Оно ее растягивает с силой, которую и называют силой инерции. Эту силу инерции, реально действующую со стороны движущейся массы на упругую связь (в нашем примере – на веревку), необходимо отличать от фиктивной силы, которую в теоретической механике, согласно принципу французского ученого Жан де Рона Д’Аламбера (d’Alembert, 1717 – 1783 гг.), условно прикладывают к самой движущейся массе и также называют силой инерции. Таким образом, в сопротивлении материалов, говоря о силе инерции, мы будем иметь в виду реальную силу, которая представляет собой действие (или, точнее, противодействие), оказываемое движущейся с ускорением массы на упругую связь. Сила инерции, как и внешняя нагрузка, деформирует связь, вызывает в ней внутренние усилия и может привести к разрушению связи. Проиллюстрируем сказанное и на следующем примере. Пусть груз массой m, находящийся на консоли невесомой балки, совершает свободные колебания (рис. 1, а). Рис.1. Сила инерции Отбросим массу (рис.1,б) и действие движущейся массы на невесомую балку (иногда называемую безмассовым упругим скелетом) заменим силой инерции , где v(t) – прогиб балки в точке расположения массы, а точками обозначена вторая производная от прогиба по времени t. Напомним, что обозначение производной по времени точкой было предложено английским ученым Исааком Ньютоном (Newton, 1642–1727 гг.) Заметим, что ошибочно прикладывать реальную силу инерции к самой движущейся массе (рис.1,в), как это делается в некоторых учебниках по сопротивлению материалов. Понятие «сила инерции» в 1803 г. ввел французский ученый Лазар Никола Маргерит Карно (Carnot, 1753 – 1823 гг.).
Симметричный цикл напряжений	изменение переменного напряжения от минимального до максимального значения в течение одного периода, причем максимальное и минимальное напряжения равны друг другу по модулю и противоположны по знаку.
Сложное сопротивление	вид нагружения, представляющий собой комбинацию (сочетание) нескольких простых видов сопротивления.
Слой нейтральный	граница между сжатыми и растянутыми волокнами на изогнутой балке, то есть волокна, длина которых при изгибе не изменяется.
Смятие	пластическая деформация местного характера, возникающая на поверхности контакта при действии сжимающих сил.
Собственный вес стержня	Знакомясь с теорией растяжения и сжатия стержня, мы пренебрегали влиянием его собственного веса. Дело в том, что при тех значительных внешних нагрузках, с которыми приходится сталкиваться при расчете реального стержня относительно небольшой длины, увеличение напряжения в нем за счет собственного веса в процентном выражении весьма невелико и поэтому собственный вес такого стержня действительно можно не учитывать. Другую картину мы будем наблюдать при расчете очень длинных стержней, например, канатов, применяемых для подъема руды, или штанг насосов, используемых для откачивания воды в рудниках. Здесь собственный вес стержня уже будет играть большую роль. Рассмотрим жестко закрепленный верхним концом стержень длиной l и площадью поперечного сечения F. Пусть вес единицы объема материала стержня (удельный вес) равен γ. Тогда вес всего стержня G=γFl. Наибольшие нормальные напряжения, которые возникнут в поперечном сечении стержня вблизи заделки, будут равны Из условия прочности σmax≤[σ] можно определить предельную длину стержня: Рассмотрим, например, пеньковый канат, удельный вес которого γ=0,01 мН/м^3. При допускаемом напряжении [σ]=5 МПа предельная длина получается равной: Как известно, глубина многих рудников бывает гораздо больше полученного значения. Иногда определяют не предельную, а так называемую разрывную длину стержня: где σпч – предел прочности. Например, для каната, изготовленного из стали марки Ст.3 с пределом прочности σпч=400 МПа и удельным весом γ=0,078 МН/м^3, получим:
Собственные колебания	колебательные движения, которые совершает система, освобожденная от внешнего активного силового воздействия и предоставленная сама себе.
Сопротивление материалов	учебная дисциплина, занимающаяся расчетом элементов конструкций на прочность, жесткость, устойчивость и долговечность, а также изучением механических свойств материалов. «Сопротивление материалов» учит не только рассчитывать простейшие элементы самолета, корабля, здания, моста и т. п., но и определять их размеры с учетом безопасности и экономичности. Основателем науки о сопротивлении материалов по праву считается итальянский ученый Галилео Галилей (Galilei, 1564 – 1642 гг.), который первым, в своей книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки» (1638 г.), поставил вопрос о прочности твердых тел и первым попытался дать на него ответ. Теоретические положения сопротивления материалов опираются на законы и теоремы общей механики, которые одинаково верны как для тел абсолютно твердых, так и для деформируемых твердых тел, то есть для реальных твердых тел, которые под действием внешней нагрузки незначительно, но все же изменяют свои первоначальные размеры и форму. К основным понятиям, известным из механики абсолютно твердого тела, в сопротивлении материалов прибавляются новые понятия. Из этих новых понятий двумя важнейшими являются деформация и напряжение.
Сосредоточенная нагрузка	силы и моменты, площадь действия которых мала по сравнению с размерами объекта (приложены в точке).
Состояние предельное	в опасной точке детали - переход материала в окрестности данной точки из упругого состояния в пластическое или разрушение детали, выражающееся в образовании трещин.
Сплошность	свойство материала, определяемое его способностью сплошь (без пустот) заполнять пространство, ограниченное поверхностью тела. Вследствие этого свойства материал считается непрерывным, что позволяет использовать для определения напряжений и деформаций математический аппарат дифференциального и интегрального исчисления.
Сплошной материал	материал, не имеющий разрывов, пустот, пор, трещин, включений и т.д.
Среднее напряжение цикла	постоянная (положительная или отрицательная) составляющая цикла напряжений, равная алгебраической полусумме максимального и минимального напряжения цикла.
Срез	разрушение, происходящее от сдвига в плоскости максимальных касательных напряжений.
Статическая вязкость	способность материала поглощать энергию, идущую на деформирование образца.
Статический момент площади поперечного сечения	Рассмотрим произвольную плоскую фигуру (поперечное сечение стержня) площадью F. Проведем через произвольную точку О оси координат x и y. Выделим элемент площади dF с координатами x и y (рис. 1). Рис.1. Поперечное сечение стержня По аналогии с понятием момента силы относительно оси введем понятие статического момента (или просто момента) площади фигуры относительно оси. Величину, равную произведению площади dF на расстояние y до оси x (иными словами, произведение элементарной площади на плечо), назовем статическим моментом элемента площади относительно оси x: По аналогии статический момент элемента площади dF относительно оси y будет равен: Просуммировав такие произведения по всей площади F, мы получим статические моменты площади всей фигуры относительно осей x и y соответственно: Статический момент площади фигуры относительно оси измеряется в единицах длины в кубе (как правило, в см^3). Он может быть положительным, отрицательным и, как мы увидим в дальнейшем, равным нулю. Пусть xc, yc – координаты центра тяжести фигуры. Продолжая аналогию с моментом силы, можно записать следующие выражения: Таким образом, статическим моментом площади фигуры относительно оси называется произведение площади фигуры на расстояние от ее центра тяжести до этой оси.
Статическая нагрузка	нагрузка, значение, направление и место приложения которой изменяется столь незначительно, что при расчете элементов конструкций их принимают независящими от времени и поэтому пренебрегают влиянием сил инерций, обусловленной такой нагрузкой.
Статическая неопределимость	Свойство расчетной схемы конструкции, при котором число неизвестных реакций связей превышает число уравнений равновесия.
Статически неопределимые системы при растяжении-сжатии	Системы, для которых не удается определить все опорные реакции из уравнений статики, называются статически неопределимыми. Рассмотрим, например, нагруженный стержень, заделанный обоими концами (рис. 1, а). В заделках возникают реакции, направленные вдоль оси стержня: RA и RB. Для их определения мы имеем только одно уравнение статики: Назовем эту расчетную схему заданной системой (ЗС). Рис. 1. Статически неопределимый стержень при растяжении (сжатии) Для раскрытия статической неопределимости необходимо записать дополнительное уравнение. Это уравнение связано с деформацией ЗС и называется уравнением перемещений. Поступим следующим образом. Отбросим, например, нижнюю заделку и действие отброшенной связи на стержень заменим некоторой реактивной силой RB, которую мы в дальнейшем будем рассматривать как активную силу (рис. 1, б). Полученный таким образом стержень назовем основной системой (ОС). Это название происходит от слова «основа» для дальнейшего расчета. Полученный нами стержень уже является статически определимым. Он заделан одним концом и нагружен двумя активными силами P и RB. Правда, значение силы RB мы пока не знаем. Очевидно, что удлинение ЗС равно нулю, то есть ∆l=0. Поэтому неизвестную нам силу RB мы можем найти из условия, что и удлинение ОС тоже равно нулю: ∆l=∆lOC=0. Это уравнение и является тем самым дополнительным уравнением (уравнением перемещений), которое свидетельствует о том, что заданная и основная системы деформируются одинаково. Используя принцип суперпозиции, запишем удлинение ОС в виде: Отсюда легко находим, что Таким образом, статическая неопределимость нами раскрыта. Вернемся к ЗС. Из уравнения (1) находим опорную реакцию RA: Теперь мы можем перейти к построению эпюры продольных сил, определению напряжений и деформаций в стержне, оценке его прочности и жесткости.
Статически определимые системы	Задачи, в которых все реакции связей определяются из условий равновесия.
Степень статической неопределимости	разность между числом искомых неизвестных усилий и числом независимых уравнений равновесия, которые для данной расчетной системы можно составить.
Стержень (брус)	элемент конструкции, один из размеров которого (длина) много больше двух других.

Т

Текучесть	свойство материала, проявляющееся в быстром росте пластических деформаций без заметного увеличения нагрузки.
Термическая усталость	Разрушение, вызванное знакопеременной пластической деформацией, являющейся следствием циклических изменений температуры
Теорема о взаимности перемещений (теорема Максвелла)	Пусть и (рис.1). Тогда, с учетом принятого нами обозначения перемещения от единичной силы, будем иметь: . Рис. 1. Теорема о взаимности перемещений Это выражение носит название теоремы о взаимности перемещений. Она была доказана в 1864 г. Максвеллом и формулируется следующим образом: Перемещение точки приложения первой единичной силы, вызванное действием второй единичной силы, равно перемещению точки приложения второй единичной силы, вызванному действием первой единичной силы (рис. 1). Если Р1=1 и Р2=1, то , т.е. , в общем случае . Обобщенное перемещение (формула или интеграл Мора): . Для плоской системы: Вычисление интегралов Мора способом Верещагина. Перемножение эпюр, имеющих вид трапеций: При действии равномерно распределенной нагрузки на шарнирно опертую балку эпюра строится в виде выпуклой квадратичной параболы, площадь , т.е. Для "глухой" заделки при равномерно распределенной нагрузке имеем вогнутую квадратичную параболу, для которой
Теорема о взаимности работ (теорема Бетли)	Эта теорема, доказанная в 1872 г. итальянским ученым Энрико Бетти (Betti, 1823 – 1892 гг.), формулируется следующим образом: возможная работа сил первого состояния на соответствующих перемещениях, вызванных силами второго состояния, равна возможной работе сил второго состояния на соответствующих перемещениях, вызванных силами первого состояния. Приведем доказательство этой теоремы. Наметим на балке две точки 1 и 2 (рис. 1, а). Рис. 1. Теорема Бетти Приложим статически в точке 1 силу P1. Она вызовет в этой точке прогиб ∆11, а в точке 2 – ∆21. Для обозначения перемещений мы используем два индекса. Первый индекс означает место перемещения (где), а второй – причину, вызывающую это перемещение (от какого усилия). Так, например, ∆21 означает прогиб балки в точке 2 от нагрузки P1. После того, как закончен рост силы P1, приложим в точке 2 к деформированному состоянию балки статическую силу P2 (рис. 1, б). Балка получит дополнительные прогибы: ∆12 в точке 1 и ∆22 в точке 2. Составим выражение для работы, которую совершают эти силы на соответствующих им перемещениях: Здесь первое и третье слагаемые представляют собой упругие работы сил P1 и P2. Согласно теореме Клапейрона, они имеют коэффициент 1/2. У второго слагаемого этого коэффициента нет, поскольку сила P1 своего значения не изменяет и совершает возможную работу на перемещении ∆12, вызванном другой силой P2. Изменим теперь порядок нагружения балки. Сначала прикладываем к балке силу P2, а затем P1 (рис. 1, в, г). Тогда Очевидно, что A1=A2. Из этого равенства и следует теорема Бетти: Заметим, что теорема Бетти справедлива как для случая внешних, так и для случая внутренних сил. – работа силы Р1 первого состояния на перемещении по ее направлению, вызванном силой Р2 второго состояния. Аналогично: – работа силы Р2 второго состояния на перемещении по ее направлению, вызванном силой Р1 первого состояния.
Теорема Кастильяно	Пусть на упругое тело в точке K действует одна внешняя сила P. Если нагрузка получит приращение dP, то потенциальная энергия деформации увеличится на величину dV=dP∆KP и станет равной Отсюда следует, что то есть производная от потенциальной энергии деформации по внешней силе дает перемещение, соответствующее этой силе. Эта теорема в 1875 г. была доказана итальянским ученым Карло Альберто Кастильяно (Castigliano, 1847 – 1884 гг.). Если к телу приложено несколько нагрузок, теорема Кастильяно формулируется следующим образом: перемещение точки приложения обобщенной силы по направлению ее действия равно частной производной от потенциальной энергии деформации по этой силе, то есть Для определения перемещения (линейного или углового) в точке, где по условию задачи внешнее усилие (сила или момент) отсутствует, необходимо приложить в этом месте фиктивную обобщенную силу. Далее следует написать выражение для потенциальной энергии деформации от всех сил, включая и фиктивную, и взять от этого выражения производную по фиктивной силе. В полученном выражении для обобщенного перемещения фиктивную нагрузку необходимо принять равной нулю. Продемонстрируем применение теоремы Кастильяно на следующем примере. Определим угол поворота поперечного сечения в точке K жестко защемленной балки, нагруженной распределенной нагрузкой q (рис. 1, а). Приложим к заданной балке на ее свободном конце в точке K фиктивный момент Mф (рис. 1, б). Рис. 1. Определение перемещений по теореме Кастильяно Изгибающий момент в произвольном сечении балки равен: Потенциальная энергия деформации при изгибе балки (при пренебрежении влиянием перерезывающей силы) вычисляется по формуле Угол поворота равен: Принимая в полученном выражении Mф=0, окончательно найдем: Теорему Кастильяно можно использовать и для раскрытия статической неопределимости. Рассмотрим, например, один раз статически неопределимую балку (рис. 2, а). Для определения опорных реакций RA и RB, а также момента в жесткой заделке MA мы имеем только два уравнения статики: ΣY=0 и ΣMA=0. Мысленно удалим лишнюю связь – правую опору и вместо нее введем в рассмотрение неизвестную опорную реакцию RB, которую мы будем рассматривать как активную силу (рис. 2, б). Однако перемещение полученной таким образом статически определимой балки в точке приложения силы RB должно быть равно нулю, поэтому ∆BP=0. Рис. 2. Раскрытие статической неопределимости по теореме Кастильяно Составим выражение для изгибающего момента в произвольном сечении статически определимой балки: Потенциальная энергия деформации балки будет равна: Так как перемещение в месте приложения неизвестной силы RB равно нулю, то Тогда Решая последнее уравнение, находим реакцию правой опоры: Теперь, составляя уравнения статики для исходной балки (см. рис. 2, а), мы можем легко определить две остальные опорные реакции:
Теорема Клайперона	Согласно этой теореме, упругая работа внешней силы при статическом приложении равна половине произведения ее окончательного значения на соответствующее этой силе перемещение. Эту теорему в 1852 г. впервые сформулировал французский ученый Бенуа Поль Эмиль Клапейрон (Clapeyron, 1799 – 1864 гг.). Докажем эту теорему. Определим работу, которую совершает сила P1, действующая, например, на балку, изображенную на рис. 1, а. Будем считать, что нагрузка прикладывается к балке статически, то есть она медленно возрастает от нуля до заданной величины P1. Пусть в некоторый момент сила, достигшая значения P<P1, вызвала в месте своего приложения прогиб балки, равный ∆. Увеличим это значение силы на бесконечно малую величину dP. Такое изменение нагрузки приведет к дополнительному прогибу d∆. Очевидно, что элементарная дополнительная работа определяется по формуле Тогда полная работа, совершенная внешней силой, будет равна: Для линейно деформируемой системы (график зависимости между прогибом ∆ и силой P для такой системы показан на рис. 1, б) прогиб балки пропорционален внешней нагрузке, то есть ∆=δP, (2) где δ – перемещение от силы, равной единице . Коэффициент δ часто называют и податливостью системы. Дифференцируя уравнение (2), найдем Подставляя (3) в (1) и учитывая, что, согласно (2), , окончательно получим что и требовалось доказать. А если на упругое твердое тело действует несколько внешних сил? Представим себе балку, шарнирно опертую по краям (см., например, рис. 1) и нагруженную силами P1, P2, …, Pn. Пусть ∆1, ∆2, …, ∆n перемещения точек приложения этих сил по направлениям их действия. Тогда, согласно теореме Клапейрона: Важно отметить, что, записывая выражение для упругой работы внешних сил, мы принимаем во внимание только активные силы и совсем не учитываем силы реактивные – реакции опор. Поскольку перемещения на опорах отсутствуют, работа реакций всегда равна нулю.
Теорема Лагранжа	Частная производная от потенциальной энергии деформации по любому обобщенному перемещению равна обобщенной силе, действующей по направлению этого перемещения, то есть
Теорема о трех моментах
Теории прочности	по существу, это гипотезы, стремящиеся выявить механическое состояние материала при сложном напряженном состоянии и определить, таким образом, критерии прочности материалов: условие пластичности - для упругопластических материалов, и условие прочности - для хрупких материалов. 1-ая теория прочности (теория наибольших нормальных напряжений): . 2-ая теория прочности (теория наибольших относительных деформаций): , условие прочности . 3-я теория прочности (теория наибольших касательных напряжений): , условие прочности: . При . 4-я теория прочности (энергетическая теория): Для плоского напряженного состояния: При . Теория прочности Мора: , когда допускаемые напряжения на растяжение и сжатие не одинаковы (чугун).

У

Угловая деформация	это угол сдвига.
Ударная вязкость	способность материала сопротивляться удару, выявляемая на стандартных образцах путем удара, падающим грузом.
Ударная нагрузка	под ударной понимается всякая быстроизменяющаяся нагрузка. Под ударом понимается взаимодействие движущихся тел, которое происходит в результате их соприкосновения. Удар сопровождается резким изменением скоростей частиц этих тел за весьма малый промежуток времени, при этом сила удара достигает, как правило, очень большого значения. В качестве примера можно привести действие кузнечного молота на кусок металла, удар падающего груза при забивке свай, воздействие колеса вагона на рельс при перекатывании через стык и т. п. За исключительно короткий промежуток времени, в течение которого совершается удар, очень трудно произвести какие-либо измерения, связанные с определением силы удара. Поэтому обычно производится условный расчет на удар, по которому определяются внутренние силы и перемещения, возникающие в стержне после удара. При этом сначала определяется наибольшее динамическое перемещение точки стержня, по которой наносится удар, а затем и напряженное состояние самого стержня. Методика расчета на удар в сопротивлении материалов основывается на следующих основных допущениях: 1) деформация стержня, вызванная ударной нагрузкой, описывается законом Гука, а сам стержень является линейно деформируемой системой, при этом модуль Юнга имеет такое же значение, как и при статическом нагружении стержня; 2) работа, совершаемая падающим грузом, полностью переходит в потенциальную энергию деформации стержня; 3) масса стержня, воспринимающего удар, пренебрежимо мала по сравнению с массой падающего груза; 4) удар считается неупругим, то есть после соприкосновения падающего груза со стержнем он не отскакивает и продолжает движение вместе со стержнем при его деформации.
Удлинение стержня абсолютное	Данное выражение иногда также называют законом Гука, но уже не для материала, а для всего стержня. Произведение EF, стоящее в знаменателе формулы, характеризует жесткость стержня при растяжении (сжатии).
Упругая линия	изогнутая ось балки в пределах упругих деформаций материала.
Упругий материал	материал, обладающий способностью восстанавливать первоначальную форму и размеры тела после снятия внешней нагрузки. Линейно-упругий материал – материал, подчиняющийся закону Гука.
Упругость	способность материала восстанавливать первоначальные размеры и форму детали после снятия внешних нагрузок.
Уравнение кривой усталости	математическая зависимость, связывающая между собой долговечность (количество циклов нагружения) конструкции и уровень действующих напряжений.
Условие прочности балки	требование, чтобы максимальные расчетные нормальные напряжения не превышали допускаемых напряжений для материала балки.
Условие прочности при растяжении-сжатии
Условие жесткости при растяжении-сжатии	, где - изменение размеров детали; - допускаемая величина этого изменения. Учитывая, что при растяжении (сжатии) абсолютное удлинение в общем виде определяется как алгебраическая сумма величин по участкам , условие жесткости при растяжении (сжатии) запишем следующим образом:
Условия совместности деформаций	уравнения, связывающие между собой деформации или перемещения отдельных частей тела и добавляемые к уравнениям равновесия тела, для решения статически неопределимых задач.
Условный предел текучести	напряжение, при котором остаточное удлинение достигает 0,2% от рабочей длины образца:
Усталость материалов	Усталостью называют явление разрушения материала в результате постепенного накопления в нем повреждений (микротрещин), приводящих к возникновению усталостной трещины при многократном повторном нагружении. Как легче всего разломать медную проволоку? Несколькими повторными перегибами в одном каком-то ее сечении. В этом случае говорят, что проволока ломается, потому что ее материал «устал». При этом «усталость» материала не связана с изменением его физико-механических свойств. Излом детали от усталости имеет характерный вид. В поперечном сечении почти всегда можно наблюдать две зоны. Одна из них – гладкая, притертая, образованная вследствие постепенного развития трещины, а другая – крупнозернистая, образовавшаяся при окончательном изломе сечения детали, ослабленного развивающейся трещиной. Усталостному разрушению подвержены многие детали машин и элементы конструкций. Это оси вагонов, шатуны моторов, гребные винты и т. п. Термин «усталость» впервые ввел в рассмотрение в 1828 г. французский ученый Жан Виктор Понселе (Poncelet, 1788 – 1867 гг.). Кроме свойств материала детали, на усталостную прочность оказывают влияние следующие факторы: 1) наличие концентраторов напряжений; 2) масштабный фактор, то есть влияние абсолютных размеров детали (чем больше размеры детали, тем ниже усталостная прочность); 3) качество обработки поверхности (с уменьшением шероховатости поверхности детали растет усталостная прочность); 4) эксплуатационные факторы (температура, коррозия, частота нагружения, радиационное облучение и т.д.); 5) наличие поверхностного слоя, упрочненного различными технологическими методами. Влияние концентрации напряжений. Вблизи выточек, у краев отверстий, в местах изменения формы стержня, у надрезов и т. п. наблюдается резкое увеличение напряжений по сравнению с номинальными напряжениями, вычисленными по обычным формулам сопротивления материалов. Такое явление называется концентрацией напряжений, а причина, вызывающая значительный рост напряжений, – концентратором напряжений. Зона распространения повышенных напряжений носит местный характер, поэтому эти напряжения часто называют местными. При напряжениях, переменных во времени, наличие концентратора напряжений на образце приводит к снижению предела выносливости. Это объясняется тем, что многократное изменение напряжений в зоне очага концентрации напряжений приводит к образованию и дальнейшему развитию трещины с последующим усталостным разрушением образца. Для того чтобы оценить влияние концентрации напряжений на снижение сопротивления усталости образца с учетом чувствительности материала к концентрации напряжений, вводят понятие эффективного коэффициента концентрации, который представляет собой отношение предела выносливости стандартного образца без концентратора напряжений к пределу выносливости образца с концентратором напряжений заданного типа: Влияние абсолютных размеров поперечного сечения. С увеличением размеров поперечных сечений образцов происходит уменьшение предела выносливости. Это влияние учитывается коэффициентом влияния абсолютных размеров поперечного сечения (ранее этот коэффициент назывался масштабным фактором). Упомянутый коэффициент равен отношению предела выносливости гладких образцов диаметром d к пределу выносливости гладкого стандартного образца диаметром, равным 7,5 мм: Шероховатость поверхности. Обработка поверхности детали оказывает существенное влияние на предел выносливости. Это связано с тем, что более грубая обработка поверхности детали создает дополнительные места для концентраторов напряжений и, следовательно, приводит к возникновению дополнительных условий для появления микротрещин. Отношение предела выносливости образца с данной шероховатостью поверхности к пределу выносливости образца со стандартной обработкой поверхности, соответствующей ГОСТ 2789–73, называется коэффициентом влияния шероховатости поверхности: Значение этого коэффициента определяется по таблицам или графикам, которые приводятся в справочниках по сопротивлению материалов или в другой научной литературе. Совместное влияние перечисленных трех факторов учитывается общим коэффициентом снижения предела выносливости при симметричном цикле: Поэтому предел выносливости детали при симметричном цикле будет равен:
Усталостное разрушение	разрушение материала под действием повторно-переменных напряжений. Физические причины усталостного разрушения материалов достаточно сложны и еще не до конца изучены. Одной из основных причин усталостного разрушения принято считать образование и развитие трещин. Механизм усталостного разрушения во многом связан с неоднородностью реальной структуры материалов (различие размеров, очертаний, ориентации соседних зерен металла; наличие различных включений – шлаков, примесей; дефекты кристаллической решетки, дефекты поверхности материала – царапины, коррозия и т. д.). В связи с указанной неоднородностью при переменных напряжениях на границах отдельных включений и вблизи микроскопических пустот и различных дефектов возникает концентрация напряжений, которая приводит к микропластическим деформациям сдвига некоторых зерен металла (при этом на поверхности зерен могут появляться полосы скольжения) и накоплению сдвигов (которое на некоторых материалах проявляется в виде микроскопических бугорков и впадинок – экструзий и интрузий); затем происходит развитие сдвигов в микротрещины, их рост и слияние; на последнем этапе появляется одна или несколько макротрещин, которая достаточно интенсивно развивается (растет). Края трещины под действием переменной нагрузки притираются друг об друга, и поэтому зона роста трещины отличается гладкой (полированной) поверхностью. По мере роста трещины поперечное сечение детали все больше ослабляется, и, наконец, происходит внезапное хрупкое разрушение детали, при этом зона хрупкого долома имеет грубозернистую кристаллическую структуру (как при хрупком разрушении).
Усталость расчет	В расчетах на усталость прочность детали принято оценивать по значению расчетного коэффициента запаса n, который сравнивается со значением допускаемого коэффициента запаса прочности [n], установленного соответствующими нормами. Условие прочности при таком проверочном расчете записывается в виде: n≥[n]. При симметричном цикле расчетный коэффициент запаса прочности определяется как отношение предельного напряжения к расчетному. При расчете на усталость понятие предельного напряжения относится не к материалу, а к конкретной детали. Еще раз напомним, что предел выносливости детали при симметричном цикле существенно отличается от соответствующего предела выносливости стандартного образца, который обычно рассматривается как механическая характеристика материала. Таким образом, расчетный коэффициент запаса при симметричном цикле определяется по формуле Формула для коэффициента запаса при кручении аналогична. При асимметричном (несимметричном) цикле расчетный коэффициент запаса прочности равен: где коэффициент Важно отметить, что влияние факторов, снижающих предел выносливости, сказывается только на предельных амплитудных напряжениях цикла σa и не отражается на предельных средних напряжениях σm. Коэффициент запаса n для асимметричного цикла может быть определен и непосредственно по диаграмме предельных амплитуд. Сначала определяется коэффициент запаса не для реальной детали, а для гладкого стандартного образца nσ(об). Для этого отметим точку M (см. рис. 1) с координатами σa и σm, характеризующими амплитудное и среднее напряжения заданного рабочего цикла. Соединим эту точку прямой линией с началом координат. Продолжим полученный отрезок ОМ до пересечения с кривой AСB (или ACB’). Полученная таким образом точка N соответствует предельному циклу. Тогда коэффициент запаса n для стандартного образца будет равен: Рис.1. Диаграмма предельных амплитуд Для оценки прочности детали еще необходимо учесть, что ее предел выносливости зависит от размеров детали, состояния ее поверхности и наличия концентраторов напряжений. В случае возникновения в опасной точке детали плоского напряженного состояния, например при совместном изгибе и кручении, общий расчетный коэффициент запаса прочности n определяется из формулы где nσ – расчетный коэффициент запаса прочности по нормальным напряжениям σ, а nτ – по касательным напряжениям τ.
Устойчивое, неустойчивое и безразличное равновесие	Рассмотрим длинный стержень (рис. 1), нагруженный осевой сжимающей силой P. Пока нагрузка на стержень невелика P=P1, его прямолинейное положение равновесия является устойчивым, поскольку, получив малое боковое отклонение от вертикали, он под действием упругих сил быстро возвратится в первоначальное прямолинейное положение равновесия (см. рис. 1, а), после исчезновения причин, вызвавших это отклонение. Рис.1. Виды равновесия По мере увеличения нагрузки стержень это делает все медленнее и медленнее. И наконец, при некоторой нагрузке P2>P1 (см. рис. 1, б) он замрет в близком, изогнутом положении равновесия даже после исчезновения причин, вызвавших это отклонение. В этом случае говорят, что первоначальное прямолинейное положение равновесия является безразличным, поскольку наряду с прямолинейной формой равновесия стержня возможна и близкая к ней, изогнутая форма равновесия. При дальнейшем, даже весьма малом, увеличении нагрузки P3>P2 прямолинейное положение равновесия становится неустойчивым. Слегка отклоненный от вертикали стержень будет изгибаться и после исчезновения причин, вызвавших это отклонение, пока не займет положение равновесия, которому соответствуют уже значительные прогибы (см. рис. 1, в). Какая нагрузка называется критической? Нагрузка, превышение которой вызывает потерю устойчивости прямолинейной формы равновесия стержня, называется критической. Она обозначается Pкр. Из изложенного выше примера следует, что Pкр =P2. Можно утверждать, что потеря устойчивости равносильна разрушению стержня. При P>Pкр прямолинейная форма равновесия становится неустойчивой, стержень изогнется и это, в свою очередь, приведет к практически неограниченному росту напряжений. Что называется формой потери устойчивости стержня? При потере устойчивости прямолинейная ось стержня искривляется. Конфигурация изогнутой оси стержня называется формой потери устойчивости. Форма потери устойчивости зависит от условий закрепления стержня и места приложения сжимающей нагрузки по его длине.
Устойчивость сжатого стержня	Под устойчивостью понимают способность конструкции сохранять прямолинейную форму равновесия, отвечающее действующей на нее нагрузке. Иными словами, положение равновесия конструкции устойчиво в том случае, если, получив произвольное малое отклонение от этого положения равновесия, конструкция снова к нему возвращается после исчезновения причин, вызвавших это отклонение. Проблема устойчивости возникает, например, при расчете длинного стержня на сжатие. Прежде всего, заметим, что, говоря об устойчивости сжатого стержня, мы будем подразумевать устойчивость его прямолинейной формы равновесия. Отметим и следующее. Все, что говорилось ранее о центральном сжатии стержней применительно лишь к коротким стержням. Такие стержни, выполненные из хрупкого материала, разрушаются под углом 45°, вследствие сдвига, а из пластичного материала вовсе не разрушаются, и их можно сжать практически в лепешку. Иначе ведут себя при сжатии длинные стержни. Опыт, который можно провести, например, с ученической линейкой, показывает, что при некотором значении сжимающей силы прямолинейная линейка внезапно изгибается, теряя при этом способность нести внешнюю нагрузку. Может случиться так, что при некоторой нагрузке, называемой критической, такой стержень, отвечающий и условию прочности, и условию жесткости, внезапно изогнется (потеряет устойчивость прямолинейной формы равновесия). Это может привести к неминуемой катастрофе всей конструкции, в состав которой входит данный стержень. Очень часто такой внезапный переход от прямолинейной формы равновесия к криволинейной называется выпучиванием стержня. Обычно потеря устойчивости системы сопровождается большими перемещениями, возникновением пластических деформаций или разрушением. Возможны также случаи, когда система, потеряв устойчивость, переходит в режим незатухающих колебаний. Особая опасность потери устойчивости заключается в том, что она происходит внезапно и при низких значениях напряжений, когда прочность материала еще далеко не исчерпана.
Устойчивость расчет	В 1744 г. Эйлер впервые получил формулу для определения теоретической нагрузки, при которой происходит потеря устойчивости стержня. Эту нагрузку, как правило, называют эйлеровой. Она равна: где Е – модуль Юнга; Imin – минимальный главный центральный момент инерции поперечного сечения (очевидно, что при потере устойчивости изгиб стержня произойдет именно в плоскости наименьшей жесткости, то есть поперечные сечения стержня будут поворачиваться вокруг той из главных осей, относительно которой момент инерции минимален); μ – коэффициент приведения длины стержня, зависящий от формы потери устойчивости; l – длина стержня. Произведение μl=l0 называется приведенной, или свободной, длиной стержня. Для шарнирно опертого стержня, сжатого по концам, Эйлером была получена следующая формула В этом случае μ=1. Форма потери устойчивости такого стержня представляет собой одну полуволну синусоиды (рис. 1, а). И этот случай принято считать основным случаем потери устойчивости. Некоторые другие способы закрепления концов стержня (нагрузка по-прежнему приложена по его торцам) легко могут быть приведены к основному случаю путем сопоставления формы изогнутой оси с формой потери устойчивости шарнирно опертого стержня. Рис. 1. Влияние закрепления концов стержня на значение критической нагрузки Рассмотрим еще два наиболее часто встречающихся случая закрепления концов стержня. 1) Стержень с жестко защемленным одним и совершенно свободным другим концом. При потере устойчивости он изогнется, как показано на рис. 1, б. Форма потери устойчивости этого стержня представляет собой четверть синусоиды. Следовательно, в этом случае приведенная длина равна 2l (полуволна синусоиды имеет длину 2l), а эйлерова сила в четыре раза меньше, чем для основного случая: 2) Оба конца стержня жестко защемлены. В этом случае форма потери устойчивости такова, что одна полуволна синусоиды занимает половину длины стержня (рис. 1, в). Поэтому приведенная длина стержня равна l/2 (μ=l/2), а эйлерова нагрузка то есть в четыре раза больше, чем для основного случая. Отметим, что критической Pкр принято называть истинную, а эйлеровой Pэ – теоретическую нагрузку, при которой происходит потеря устойчивости стержня. Формула Эйлера получена при предположении, что в момент потери устойчивости напряжения сжатия в стержне не превышают предела пропорциональности, то есть Об этом, в частности, говорит присутствие в формуле (1) модуля Юнга Е, который свидетельствует о том, что вплоть до момента потери устойчивости выполнялся закон Гука. Поэтому, если потеря устойчивости происходит при напряжении меньшем, чем σпц, то Pэ=Pкр. Для стержней, теряющих устойчивость при напряжении, превышающем предел пропорциональности σпц, использование формулы Эйлера не только принципиально неправильно, но и крайне опасно по своим последствиям, поскольку критическая нагрузка (истинная нагрузка, при которой происходит потеря устойчивости) меньше эйлеровой: Pэ>Pкр. Установим пределы применимости формулы Эйлера. Пределы ее применимости можно легко установить, предварительно введя понятие гибкости стержня, предложенное Феликсом Станиславовичем Ясинским (1856 – 1899 гг.). Определим эйлеровы напряжения, исходя из формулы Эйлера (1): Здесь – геометрическая характеристика поперечного сечения, называемая минимальным радиусом инерции, которая измеряется в сантиметрах; – безразмерная геометрическая характеристика, называемая гибкостью сжатого стержня. С учетом формулы (2), находим, что Величину, стоящую в правой части этого неравенства, обозначим и назовем предельной гибкостью. Тогда В отличие от гибкости стержня, представляющей собой его геометрическую характеристику, предельная гибкость зависит только от физико-механических свойств материала и не зависит от его размеров. Предельная гибкость – постоянная для данного материала величина. Например, для стали марки Ст. 3 . Используя понятие предельной гибкости, пределы применимости формулы Эйлера можно представить в виде: Таким образом, формула Эйлера дает истинное значение нагрузки, при которой происходит потеря устойчивости стержня, только в том случае, когда гибкость рассчитываемого стержня больше или равна предельной гибкости для материала, из которого он изготовлен. По какой формуле определяется критическая нагрузка для стержней малой и средней гибкости (при )? В случае, когда формула Эйлера неприменима, критическая нагрузка определяется по эмпирической формуле, предложенной Ясинским, на основе опытов, проведенных рядом исследователей. Она имеет вид: где а и b – коэффициенты, зависящие от свойств материала и измеряющиеся в единицах напряжения. Например, для стали марки Ст. 3 a=31 кН/см^2, b=0,114 кН/см^2; для дерева a=2,93 кН/см^2, b=0,0194 кН/см^2. Для очень коротких стержней (при некоторой гибкости, обозначаемой λ0) критическое напряжение, то есть напряжение, при котором происходит потеря устойчивости стержня, может оказаться равным предельному напряжению (при сжатии: пределу текучести для пластичных материалов или пределу прочности для хрупких). Тогда, при : - для пластичных материалов - для хрупких Можно ли увеличить критическую нагрузку стержня, заменив, например, одну марку стали на другую, имеющую больший предел текучести? Для стержней с одинаковыми геометрическими размерами и с одинаковыми условиями закрепления концов замена одной марки стали на другую может изменить, а может и не изменить критическую нагрузку. Критическая нагрузка не изменится, если она определяется по формуле Эйлера (при ), поскольку входящий в эту формулу модуль Юнга практически не зависит ни от химического состава стали, ни от ее термической обработки (для всех марок стали E=2∙10^5 МПа). Однако для стержней средней гибкости (при ), а также для коротких стержней (при ) такая замена марки стали приведет к увеличению критической нагрузки. В первом случае это объясняется тем, что эмпирические коэффициенты а и b в формуле Ясинского существенно зависят от марки стали, а во втором стержень, по существу, рассчитывается не на устойчивость, а на прочность. Как осуществляется расчет центрально сжатого стержня на устойчивость и что такое коэффициент уменьшения основного допускаемого напряжения (коэффициент продольного изгиба)? При назначении размеров длинного сжатого стержня, в первую очередь, приходится заботиться о том, чтобы он в процессе эксплуатации не потерял устойчивость прямолинейной формы равновесия. Поэтому напряжения в сжатом стержне не должны превышать критических напряжений: Исследования показали, что незначительные местные ослабления стержня (например, заклепочные отверстия) не оказывают существенного влияния на значение критической нагрузки, поэтому в формуле (3) берется вся площадь поперечного сечения (площадь брутто). Условие прочности при сжатии, как известно, имеет вид: Расчет сжатого стержня на устойчивость можно по форме привести к расчету на простое сжатие. Однако при этом необходимо учесть, что длинный стержень (стержень большой гибкости) может потерять устойчивость, то есть исчерпает несущую способность, при меньшем напряжении, чем допускаемое напряжение [σ]. Поэтому условие устойчивости сжатого стержня можно представить в виде: где φ – коэффициент, называемый коэффициентом уменьшения основного допускаемого напряжения или коэффициентом продольного изгиба. Очевидно, что этот коэффициент зависит от материала стержня и от его гибкости λ и изменяется в пределах от 0 (при λ→∞) до 1 (при λ =0). Этот метод расчета очень удобен в том смысле, что он не связан с пределами применимости формулы Эйлера и может быть использован практически при всех значениях гибкости. Заметим, что проектировочный расчет по формуле (4), связанный с подбором размеров поперечного сечения стержня приходится осуществлять методом последовательных приближений. Это обусловлено тем, что площадь поперечного сечения стержня в неявном виде входит и в правую часть выражения (5), поскольку коэффициент продольного изгиба φ зависит от гибкости стержня λ, а последняя, в свою очередь, от радиуса инерции
Учет сил инерции	Пусть груз массой m поднимают на тросе с ускорением a (рис. 1, а). И пусть погонная масса троса (масса троса, приходящаяся на единицу его длины) равна . Рис. 1. Ускоренное поднятие (опускание) груза Определим продольное динамическое усилие Nд, возникающее в некотором сечении троса, находящемся на расстоянии z от груза. Отбросим движущиеся массы груза и участка троса длиной z и заменим их действие на безмассовый упругий скелет троса силой их веса и суммарной силой инерции направленной в сторону, противоположную ускорению a (рис. 1, б). Из уравнения равновесия находим: Если бы груз был неподвижен, то Тогда, окончательно получим: Эффект действия динамической нагрузки на практике, как правило, оценивается коэффициентом динамичности, представляющим собой отношение динамического усилия (перемещения) к статическому усилию (перемещению): В рассматриваемом нами случае он оказывается равным: Таким образом, при поднятии груза с ускорением a внутреннее динамическое продольное усилие в тросе Nд может в несколько раз превысить статическое усилие Nст. Так, например, в скоростных лифтах, в которых большая скорость подъема может быть достигнута только благодаря большим ускорениям, динамическое усилие и соответственно динамическое напряжение в тросе бывает очень большим. Если груз опускается с ускорением a, то в формуле (1) перед вторым слагаемым нужно поставить знак «минус». Заметим, что при свободном падении груза, когда a=-g, динамическое усилие в тросе будет равно нулю.
Учет собственного веса стержня

Х

Хрупкость

свойство материала разрушаться без предшествующей значительной пластической деформации.

Ц

Цикл напряжений	совокупность всех значений переменных напряжений за время одного периода изменения нагрузки. Обычно цикл напряжений характеризуется двумя основными параметрами цикла: - максимальное напряжение цикла; - минимальное напряжение цикла; - среднее напряжение цикла - амплитудное напряжение цикла R – коэффициент асимметрии цикла напряжений
Цикл асимметричный	Цикл нагружения, при котором максимальные и минимальные напряжения цикла (например, и ) не равны между собой. При этом асимметричный цикл может быть знакопеременным или знакопостоянным;
Цикл знакопеременный	максимальное и минимальное напряжения не равны по абсолютной величине и противоположны по знаку
Цикл знакопостоянный	максимальное и минимальное напряжения не равны по абсолютной величине и имеют одинаковый знак
Цикл отнулевой (пульсационный)	максимальное или минимальное напряжения равны нулю (σmax=0 или σmin=0, R=0 или R=∞).
Цикл симметричный	Цикл нагружения, при котором максимальное значение напряжений ( или ) и минимальное значение напряжений ( или ) численно равны между собой, но противоположны по знаку.

Ч

Частота колебаний	представляет собой число колебаний в единицу времени. Величина, обратная периоду колебаний.
Чистый изгиб	тип простой деформации, при которой в поперечных сечениях стержня при действии внешних сил возникают только изгибающие моменты.

Э

Эффективный коэффициент концентрации	Влияние концентрации напряжений на предел выносливости зависит от чувствительности материала к концентрации напряжений
Элемент конструкции	некоторая часть конструкции (сооружения, механизма), предназначенная для расчета.
Энергия упругой деформации	В науке под энергией понимается способность совершать работу. При растяжении (сжатии) внешние силы совершают работу на перемещениях, которые получают точки их приложения в результате деформирования стержня. Вследствие этой работы, внутри тела накапливается потенциальная энергия деформации V. Последняя измеряется в системе СИ в джоулях (1 ДЖ = 1 Н∙м). Один джоуль – это примерно потенциальная энергия яблока, находящегося на кухонном столе, по отношению к полу. Энергию можно запасти, например, в пружине. Однако, как заметил Гук, поведение пружины является прототипом поведения деформируемого твердого тела при воздействии на него внешней нагрузки. Таким образом, любое деформирмируемое упругое тело является как бы аккумулятором энергии. Потенциальная энергия деформации при растяжении (сжатии) определяется по формуле
Эпюры крутящих моментов	Крутящий момент, возникающий в поперечном сечении стержня, определяется методом сечений. Он равен алгебраической сумме скручивающих моментов, приложенных к любой из частей стержня (иными словами, действующих по одну сторону от рассматриваемого сечения стержня). Эпюра крутящих моментов представляет собой график, показывающий изменение крутящего момента по длине вала Mz(z). При построении эпюры крутящих моментов обычно используется следующее правило знаков: Если при взгляде на поперечное сечение стержня мы видим, что внешний скручивающий момент вращает рассматриваемую часть стержня против хода часовой стрелки, то он вызывает в этом сечении положительный крутящий момент, который, в свою очередь, противодействуя этому скручивающему моменту, будет направлен по ходу часовой стрелки.
Эпюры продольных сил	В тех случаях, когда продольные силы, возникающие в различных поперечных сечениях стержня, неодинаковы, закон их изменения по длине стержня представляется в виде графика N(z), называемого эпюрой продольных сил N. Эта эпюра наглядно демонстрирует нам, какие участки стержня испытываю растяжение, а какие – сжатие. При этом продольную силу N, противодействующую растяжению стержня, принято считать положительной, а сжатию – отрицательной. Эпюра N необходима для оценки прочности стержня. По этой эпюре определяется опасное сечение стержня. Как правило, это то его поперечное сечение, в котором продольная сила принимает наибольшее по абсолютной величине значение. Построение эпюры N производится с помощью метода сечений. Для определения продольной силы N, возникающей в некотором поперечном сечении стержня, необходимо найти алгебраическую сумму всех внешних сил (активных и реактивных), действующих на любую из рассматриваемых частей стержня. Продемонстрируем его применение на следующем примере (рис.1). Мы покажем, как определяется продольная сила N только в одном, намеченном нами поперечном сечении (рис.1, а). В других поперечных сечениях стержня она может быть определена по аналогии. Прежде всего, нам необходимо найти опорную реакцию R (рис.1, б), возникающую в заделке. Направим ее, например, вверх. Рис. 1. Определение продольного усилия N в стержне при растяжении (сжатии) Составим уравнение равновесия ΣZ=0 для всего стержня: ΣZ=-R+P3-P2+P1=0. Отсюда находим, что R=P3-P2+P1=60-40+30=+50 кН. Знак «плюс» в полученном результате говорит о том, что предварительное направление опорной реакции R вверх было выбрано нами верно. Разрежем теперь стержень по намеченному сечению и мысленно отбросим его нижнюю часть. Действие отброшенной части стержня нам необходимо заменить продольной силой N. Это мы можем осуществить следующими двумя способами. Первый способ – будем всегда направлять продольную силу N от сечения, то есть будем предполагать, что она противодействует растяжению стержня. В этом случае положительный результат, полученный после уравновешивания оставленной части стержня, укажет нам на то, что внутренняя сила действительно соответствует растяжению, а отрицательный – что она противодействует сжатию. По существу, первый способ является формальным. Второй способ – будем направлять продольную силу, согласно здравому смыслу. То есть будем ориентироваться на значения внешних сил, действующих на рассматриваемую часть стержня, и помнить о том, что сила N должна их уравновесить. Тогда знак «плюс» в решении покажет, «угадали» или «не угадали» мы истинное направление продольной силы. Проиллюстрируем первый способ. Направим, не задумываясь, внутреннюю силу N от сечения (рис. 1, в). Для удобства вычисления значения продольной силы N закроем отброшенную нами нижнюю часть стержня, например листком бумаги. Разрушение стержня в рассматриваемом нами поперечном сечении не произойдет в том случае, если внутреннее усилие N уравновесит внешние силы R и P3, то есть те силы, которые мы видим. Записываем уравнение равновесия: ΣZ=+N+P3-R=0; N=R-P3=+50-60=-10 кН. Знак «минус» в полученном результате говорит нам о том, что в рассматриваемом сечении возникает продольное усилие N, противодействующее сжатию стержня. Аналогичный результат мы получим и при отбрасывании верхней части стержня. Убедимся в этом, воспользовавшись теперь (для иллюстрации) вторым способом. Закром верхнюю часть стержня листком бумаги. Мы увидим, что внешняя сила P1=30 кН растягивает, а сила P2=40 кН сжимает нижнюю часть стержня. Продольное усилие N, возникающее в рассматриваемом нами поперечном сечении стержня, должно уравновесить эти две силы. Поскольку P2>P1, сила N должна быть направлена к сечению стержня, то есть противодействовать сжатию. Тогда N=P2-P1=40-30=10 кН. С учетом принятого выше правила знаков, на эпюре продольных сил найденное значение N должно быть отложено со знаком «минус». Таким образом, мы получили тот же самый результат.
Эпюры перерезывающих сил Qy и изгибающих моментов Mx	Данные эпюры строятся для наглядного представления о характере изменения этих внутренних силовых факторов по длине балки, а также с целью определения тех опасных сечений, в которых возникают, соответственно, наибольшие касательные и нормальные напряжения. Напомним, что: 1) перерезывающая сила численно равна алгебраической сумме всех внешних сил (активных и реактивных), действующих на рассматриваемую нами часть балки; 2) изгибающий момент численно равен алгебраической сумме моментов этих же сил относительно главной центральной оси, проходящей через центр тяжести рассматриваемого поперечного сечения (иногда говорят просто – относительно самого сечения). Правила знаков используемые для вычисления перерезывающей силы Qy и изгибающего момента Mx? Эти правила, к сожалению, непростые для запоминания, формулируются следующим образом. Для перерезывающей силы: внешняя сила, действующая на рассматриваемую часть балки и стремящаяся «повернуть» эту часть относительно сечения по ходу часовой стрелки, вызывает в сечении положительную перерезывающую силу. Такая внешняя сила входит в алгебраическую сумму для определения Qy со знаком «плюс» (рис. 1, а). Рис.1. Правила знаков для перерезывающей силы и изгибающего момента Заметим, что и положительная перерезывающая сила Qy, в свою очередь, тоже «стремится вращать» любую из частей балки по ходу часовой стрелки. Теперь приведем правило знаков для изгибающего момента: внешняя нагрузка, изгибающая рассматриваемую часть балки выпуклостью вниз, вызывает в сечении положительный изгибающий момент. Поэтому момент, создаваемый такой нагрузкой, входит в алгебраическую сумму для определения Mx со знаком «плюс» (рис. 1, б). Обращаем внимание уважаемого Читателя на то, что в этом правиле говорится об изгибающем моменте, то есть моменте, который изгибает балку, а не вращает ее. Из рис. 1, б видно, что положительный изгибающий момент Mx как бы «стремится изогнуть» любую из частей балки также выпуклостью вниз. Для удобства определения знака изгибающего момента рекомендуется поперечное сечение балки мысленно представлять в виде условной жесткой заделки. Дифференциальные зависимости между интенсивностью равномерно распределенной нагрузки q, перерезывающей силой Qy и изгибающим моментом Mx? Эти зависимости, имеющие вид: впервые были установлены в 1852 г. немецким ученым Иоганом Вильгельмом Шведлером (Schwedler, 1823–1894 гг.). Позднее они были получены и русским ученым Дмитрием Ивановичем Журавским (1821–1891 гг.). Формулы (1) используются для контроля правильности построения эпюр Qy и Mx. Очень часто их называют также формулами Шведлера – Журавского. Необходимо подчеркнуть, что в приведенных формулах распределенная нагрузка q считается положительной, если она направлена вниз. Правила построения и проверки эпюр Qy и Mx. Приведем основные правила, которые вытекают непосредственно из метода сечений, а также являются следствием формул (1) Шведлера – Журавского. Отметим, что некоторые из этих правил справедливы только при обходе эпюр Qy и Mx слева направо: 1) Если на некотором участке балки отсутствует распределенная нагрузка (q=0), то эпюра Qy на этом участке представляет собой прямую, параллельную оси балки (рис. 2). Действительно, поскольку q=0, то и dQy/dz=0. Следовательно, Qy=const. Эпюра моментов на этом же участке (где q=0) – также прямая линия. Причем, если Qy >0, то прямая линия идет вверх, а если Qy <0, прямая линия идет вниз. Если Qy =0, то изгибающий момент постоянен, поскольку dMx/dz=0. 2) Под сосредоточенной силой P на эпюре Qy (рис. 2, а) имеется скачок на величину этой силы и по ее направлению, а на эпюре Mx – излом, угол которого всегда направлен навстречу нагрузке. 3) Если на некотором участке балки имеется равномерно распределенная нагрузка, то эпюра Qy на этом участке представляет собой наклонную прямую (рис. 2, б), идущую вниз, если нагрузка q направлена вниз, и идущую вверх, если нагрузка q направлена вверх. Эпюра Mx на этом участке, согласно третьей формуле (1), изменяется по квадратичной параболе, причем выпуклость параболы всегда направлена навстречу нагрузке. Если эпюра перерезывающей силы проходит через нулевое значение, то в этом сечении балки на эпюре Mx имеется экстремум (последнее вытекает из зависимости dMz/dz=Qy=0). Отметим, что в точках, соответствующих началу и концу участка, в пределах которого действует распределенная нагрузка, параболическая и прямолинейная части эпюры Mx переходят одна в другую плавно (без излома). 4) Сосредоточенный внешний момент M (рис. 2, в) никак не отражается на эпюре Qy. На эпюре Mx в месте приложения этого момента имеется скачок на его величину. Заметим, что построение эпюр перерезывающих сил и изгибающих моментов ввел в практику расчета стержней на изгиб в 1859 г. французский ученый Жак Антуан Шарль Бресс (Bresse, 1822 – 1883 гг.). Рис. 2. Правила согласования эпюр перерезывающих сил и изгибающих моментов В заключение отметим, что, как это ни странно, студенты зачастую неверно «штрихуют» эпюры. Смысл «штриховки» заключается в том, что каждая ее линия (ордината эпюры) в принятом масштабе дает значение внутреннего усилия, возникающего в соответствующем поперечном сечении стержня. Поэтому так любимая студентами «штриховка» эпюр под углом 45° лишена всякого смысла.

Я

Ядро сечения

Ядром сечения называется малая область вокруг центра тяжести поперечного сечения стержня. Она характеризуется тем, что всякая сжимающая сила, приложенная внутри этой области, вызывает во всех точках поперечного сечения (и соответственно во всем стержне) только напряжения сжатия. Понятие о ядре сечения впервые ввел Бресс в 1854 г. Рассмотрим следующий пример. Пусть стержень имеет прямоугольное поперечное сечение с размерами b и h и одна из координат точки приложения нагрузки (точка A) равна нулю, например xP=0, yP=0 (рис. 1). Рис.1. Ядро сечения Тогда напряжения в крайних точках K и L поперечного сечения стержня будут определяться по формулам Из этих формул видно, что при е=0 во всех точках поперечного сечения, в том числе и в крайних точках K и L, будут возникать одинаковые сжимающие напряжения. При e < b/6 напряжения по-прежнему будут сжимающими, но будут изменяться по ширине сечения. При e = b/6 в точках K и L они будут равны: Если e > b/6, то нейтральная линия разделит поперечное сечение на две части. В одной из них напряжения будут сжимающими, а в другой – растягивающими. Для всех этих случаев (см. рис. 1) показаны эпюры напряжений. Таким образом, если мы не хотим, чтобы в поперечном сечении внецентренно сжатого стержня возникали растягивающие напряжения (а многие строительные материалы, как известно, очень плохо работают на растяжение), то эксцентриситет нагрузки не должен выходить за некоторую область вокруг центра тяжести этого сечения. Эту область и называют ядром сечения. Определим форму ядра сечения для прямоугольного и для круглого поперечных сечений стержня. Рис.2. Форма ядра для прямоугольного и круглого ядра сечения Для прямоугольника ядро сечения имеет форму ромба (рис. 2, а), а для круглого сплошного стержня – круга (рис. 2, б). Заметим, что для любого поперечного сечения форма ядра всегда представляет собой выпуклую фигуру.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00