Главная
Лекция 7 (продолжение). Примеры решения на сложное сопротивление
Расчет
валов на изгиб с кручением
С сочетанием изгиба и кручения брусьев круглого поперечного сечения наиболее часто приходится встречаться при расчете валов, реже других деталей и брусьев некруглого сечения.
Если внешние
силы, действующие на вал не лежат в одной плоскости, например в валах
редукторов, то каждую из них раскладывают на ее составляющие по двум
направлениям: вертикальному и горизонтальному. Затем строят эпюры изгибающих
моментов в вертикальной и горизонтальных плоскостях. Величину суммарного
изгибающего момента находят по формуле:
Для построения эпюры полных изгибающих моментов по вышеприведенной формуле находят моменты на границах силовых участков и, по ним собственно, строят эпюру. Плоскости действия этих моментов в разных сечениях вала различны, но ординаты эпюры условно для всех сечений совмещают с плоскостью чертежа.
Эпюра крутящих моментов строится так же, как и при чистом кручении.
Опасное сечение вала устанавливается с помощью эпюр полных изгибающих моментов М и крутящих моментов Мк по одной из теорий прочности. Если в сечении вала постоянного диаметра с наибольшим изгибающим моментом М действует наибольший крутящий момент Мк , то это сечение является опасным.
Если же такого явного совпадения нет, то опасным может оказаться сечение, в котором ни М ни Мк не являются наибольшими. Еще больше осложняется задача при валах переменного диаметра; у таких валов наиболее опасным может оказаться такое сечение, в котором действуют значительно меньшие изгибающие и крутящие моменты, чем в других сечениях.
В случаях, когда опасное сечение не может быть установлено непосредственно по эпюрам М и Мк , необходимо проверить прочность вала в нескольких предположительно опасных сечениях.
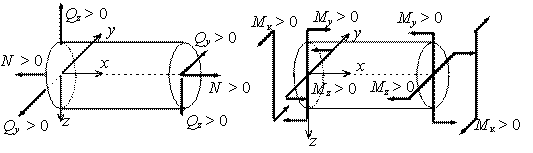
После установления опасного сечения вала находят в нем опасные точки. В сечении возникают одновременно нормальные напряжения от изгибающего момента и касательные напряжения от крутящего момента и поперечной силы. В валах круглого сечения, длина которых во много раз больше диаметра, величины наибольших касательных напряжений от поперечной силы относительно невелики и при расчете прочности валов на совместное действие изгиба и кручения не учитываются.
Наибольшие
напряжения в сечении вала, как нормальные так и
касательные, возникают в точках, расположенных по периметру сечения и они
равны: 
, 
Где 
соответственно осевой и полярный моменты сопротивления
поперечного сечения бруса.
Расчет валов на прочность при изгибе с кручением, как уже отмечалось выше, производится с применением теорий прочности. При этом расчет валов из пластичных материалов выполняется на основе третьей или четвертой теорий прочности, а из хрупких – по теории Мора.
По третьей
теории прочности 
По четвертой теории прочности
, 
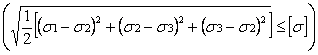Эти условия прочности можно выразить и через моменты
По теории прочности Мора
где 
Мприв – приведенный
момент по теории прочности Мора
Таким образом, расчет вала круглого поперечного сечения на совместное действие изгиба и кручения по форме совпадает с расчетом на прямой изгиб, но в расчетной формуле роль изгибающего момента играет приведенный момент, величина которого зависит от изгибающих и крутящего моментов, а также от принятой теории прочности.
Поясним теперь вышеизложенное примером.
Пример 1.
На вал круглого сплошного сечения посажены три шкива, через шкивы переброшены ремни, ветви которых параллельны друг другу и наклонены к горизонту на первом шкиве под углом 30о, на втором - под углом 45о, и на третьем – под углом 60о. От первого шкива ремень идет к электродвигателю: в этом ремне, как в ремне ведущего шкива, усилие в сбегающей ветви вдвое больше, чем в набегающей, от второго и третьего шкивов ремни идут к станкам; в этих ремнях усилие в набегающей ветви в двое больше чем в сбегающей.
Станки
потребляют мощность 100кВт, первый 60 и второй 40 кВт, вал делает 1000 об/мин.
Диаметры шкивов соответственно – 
80 МПа. Собственными весами вала и шкивов пренебречь.
Решение.
Вал подвергается изгибу, а части его, расположенные между шкивами, и
скручиванию. Крутящий момент определяют по формуле:
Моменты, передаваемые каждым из шкивов на вал равны:
По полученным значениям ординат, строится эпюра крутящих моментов Мк (рис.1, б)
Обозначим
натяжение набегающей ветви ремня, надетого на первый шкив, через 
, тогда натяжение сбегающей ветви по условию равно 
. Для вращающего шкив момента, равного крутящему моменту Мк ,
имеем
где 
- диаметр первого шкива;
Отсюда
Для второго и третьего шкивов аналогично
Таким образом, в сечениях, где посажены шкивы, вал нагружен наклонными силами
;
;
.
Рис.1
Для вычисления наибольшего изгибающего момента определяются сначала изгибающие моменты в вертикальной и горизонтальной плоскостях. Для этого раскладывают силы: R1, R2, R3 на вертикальную и горизонтальную составляющие. Вертикальная нагрузка от первого шкива будет равна:
От второго шкива
От третьего шкива
Горизонтальная нагрузка от первого шкива равна
От второго шкива
От третьего шкива
При этом
нагрузка 
направлена влево, а 
вправо т.е. в противоположные стороны.
Далее, для
нагрузок
и
, действующих в вертикальной плоскости, определяют
вертикальные составляющие реакций опор:
Делаем проверку
Вертикальные составляющие реакций опор определены верно.
После этого производят построение эпюры изгибающих
моментов 
(рис 1, г)
Аналогично
этому от нагрузок, 
и
действующих в горизонтальной плоскости, определяем
горизонтальные составляющие реакций опор:
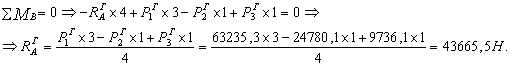
Делаем проверку
Горизонтальные
составляющие реакций опор определены верно. Строим эпюру изгибающих моментов 
(рис. 1, е)
Строим эпюру
результирующих изгибающих моментов (рис.1, ж),
осуществив геометрическое сложение эпюр 
и 
:
Максимальный результирующий изгибающий момент под шкивом 1 и крутящий момент имеют максимальные значение в этом сечении. Поэтому это сечение является самым опасным.
Расчетный момент по третьей теории прочности равен
Необходимый диаметр вала находим по формуле:
Ближайшее стандартное значение d=190 мм.
Пример 2.
Шкив с диаметром D1=
1 м и углом наклона ветвей к горизонту 
=40°
делает n=600 об/мин и
передает мощность N1 = 60
кВт. Два других шкива имеют одинаковый диаметр D2=
D3= 0,8 м и одинаковые
углы наклона ветвей ремня к горизонту 
=60°, и каждый из них передает мощность 
(рис. 1, а).
Требуется подобрать диаметр вала при 
= 700 кГс/см2
= 70 МПа.
Рис. 1
Рис. 2
Решение.
1. Выясним, какие виды деформации испытывает вал.
Для этого усилия, которые приложены к шкиву
(например, шкиву с диаметром D1)
приведем к оси вала (рис. 2). Перенос усилий
2t1 и t1 к оси вала требует
приложения таких же усилий в противоположном направлении. Тогда усилия,
перечеркнутые одной чертой, образуют пару с моментом 
, а усилия, перечеркнутые двумя чертами, образуют пару с
моментом 
. Суммарно эти моменты дают скручивающий момент
.
Кроме того, на вал передается усилие, действующее
перпендикулярно оси вала и по величине равное F1 = 2t1 +
t1 =3t1. Скручивающий момент M1K вызывает деформацию кручения, а усилие F 1 – деформацию изгиба.
Таким образом, имеем совместное действие
изгиба с кручением, и следовательно, для подбора
диаметра необходимо использовать гипотезы прочности. Так как вал изготовлен из
пластичного материала, воспользуемся третьей гипотезой прочности, согласно
которой
.
Анализируя эту формулу
видим, что нам необходимо определить скручивающие моменты, передаваемые на вал каждым шкивом, и выяснить характер распределения крутящих
моментов по длине вала, т.е. построить эпюру крутящих моментов (эп. Tz). Кроме того, для выяснения характера распределения
изгибающих моментов по длине вала, т.е. для построения эпюры изгибающих
моментов (эп. 
) нам необходимо определить усилия, которые действуют на вал
перпендикулярно оси вала. Имея эп. Tz и эп. , мы сможем выяснить, в каком сечении совместное действие
изгиба и кручения наиболее опасно, т.е. для какого сечения выражение 
будет наибольшим. Для
этого опасного сечения мы и подберем диаметр.
2. Определим
скручивающие моменты, передаваемые шкивами на вал:
3. По полученным данным строим эпюру крутящих моментов.
Так как знак крутящего момента выбирается произвольно, то примем крутящий момент,
возникающий от действия скручивающего момента 
положительным. Тогда эп. 
будет иметь вид,
указанный на рис. 1, б.
4. Определим окружные усилия t1, t2
и t3, воспользовавшись
выводом, полученным в пункте 1 настоящей задачи:
, отсюда
Аналогично 
5. Определим давления на вал:
а) горизонтальная плоскость
= 3×194,8 = 584,4 кГс =
5,84 кН; (см. пункт 1 настоящей задачи);
б) вертикальная плоскость
= 3×121,8 = 365,4 кГс =
3,65 кН.
Рис. 3
6. Так как усилия 
и 
действуют в разных
плоскостях, то спроектируем их на горизонтальную и вертикальную оси (рис.
3, а, б).
= –584,4×0,766 = –447,6 кГ =
–4,48 кН,
= –584,4×0,643 = –375,8 кГ =
–3,76 кН,
= 365,4×0,5=182,7 кГ = 1,83 кН,
= –365,4×0,87 = –316,4 кГ =
–3,16 кН.
7. Построим эпюры изгибающих
моментов от горизонтальных сил (эп. МГОР) и от вертикальных сил (эп. МВЕРТ).
Рассмотрим горизонтальную плоскость. Для этого представим вал как балку на двух
опорах (опоры ставим в местах установки подшипников) и
нагрузим ее силами, действующими в горизонтальной плоскости. Так как силы Х1 и
Х2, Х3 имеют разные знаки, то и приложить на балку их надо
так, чтобы они действовали в разные стороны. Например, Х1 направить вниз, а Х2 и Х3 – вверх (см. рис.1, в) или наоборот, для решения задачи
это несущественно.
Определим реакции опор ХА и ХВ
(рис. 1, в):
; – Х2×0,4 – Х1×0,3 + ХВ×0,9 + Х3×1,1 = 0;
; 
;
Проверка:
; 182,7 + 75 – 447,6 + 7 + 182,7 = 0;
447,6 – 447,6 = 0.
Определим изгибающие моменты в сечениях С, А, D,
В, Е, т.е. на границах силовых участков
МС = 0; МА
= 182,7×0,4 = 73,1 кГм = 0,731 кНм;
MD = 182,7×0,7 + 75,1×0,3 = 150,4 кГм = 1,5 кНм;
МЕ = 0; МВ
= 182,7×0,2 = 36,5 кГм = 0,365 кНм.
По полученным
результатам строим эпюру МГОР
(рис. 1, г). Аналогично рассмотрим вертикальную плоскость. Покажем вал как
балку на двух опорах и нагрузим ее силами У1, У2
и У3 (рис. 1, д).
Определим
реакции опор УА и УВ:
; У2×0,4 – У1×0,3
+ УВ×0,9
– У3×1,1
= 0,
; У2×1,3 – УА×0,9
+ У1×0,6
– У3×0,2
= 0,
Проверка:
; –316,4 + 637,2 – 375,8 + 371,4 – 316,4 = 0,
1008,6 –
1008,6 = 0.
Определим
изгибающие моменты в сечениях
С, А, D, В, Е.
МС = 0; МА
= – 316,4×0,4 = – 126,6 кГм = – 1,266 кНм;
MD = – 316,4×0,7 + 637,2×0,3 = – 30,3 кГм = – 0,303 кНм;
МЕ = 0; МВ
= – 316,4×0,2 = – 63,3 кГм = –0,633 кНм.
По полученным результатам строим эпюру MВЕРТ (рис.1,
е).
8. На основании эпюр MГОР и MВЕРТ строим эпюру суммарного момента М. Суммарный момент в любом сечении вала
можно определить как геометрическую сумму моментов в вертикальной и
горизонтальной плоскостях (рис. 4).
, тогда МС = 0;
= 146,1 кГм = 1,46 кНм,
= 153,4 кГм = 1,53 кНм,
= 73,1 кГм = 0,73 кНм,
.
Рис.4
Суммарная эпюра
будет прямолинейной на тех участках вала, где MГОР и MВЕРТ одновременно убывают или одновременно возрастают
(по абсолютной величине). На тех участках где MГОР возрастает, а MВЕРТ убывает
(или наоборот), эпюра суммарных моментов будет очерчиваться кривой линией без
экстремумов. Эпюра суммарных моментов показана на рис. 1, ж.
9. Определим опасное сечение. Таковым, очевидно,
будет сечение в месте посадки шкива с диаметром D1,
т.к. здесь мы имеем максимальный суммарный момент 
= 153,4 кГм и 
= 48,7 кГм (по кручению все сечения вала равноопасны,
т.к. во всех сечениях крутящий момент одинаков).
10. Определим диаметр вала:
Округляем
диаметр до стандартной величины в большую сторону d = 70 мм.
Пример 3.
Подобрать круглое поперечное сечение вала, если диаметры шкивов d1 = d2 = 200 мм, d3 = 300
мм; углы наклона ремней к горизонту 
30°, 
= 45° (см.
рис.); мощность на ведущем шкиве 3 N3 = 5кВт; мощность на ведомых шкивах 1 и 2 N1 = N2 = N3 /
2; расстояния а
= 0,25 м, b = 0,4м; допускаемые напряжения = 80 МПа. Расчет проводить по третьей теории
прочности.
а)
б)
Решение.
1. Определяем крутящие моменты на валу и строим их эпюру
2. Определяем окружные усилия
, 
;
3. Определяем горизонтальные и вертикальные проекции сил, действующих на вал.
Для определения проекций сил пользуемся направлениями осей, принятыми на рис.б.
4. Строим эпюру изгибающих моментов в горизонтальной плоскости
Определяем опорные реакции (рис. а)
; 
; 
Проверка
; 
-
верно
Строим эпюру (рис. а).
5. Строим эпюру изгибающих моментов в вертикальной плоскости
Определяем опорные реакции (рис. а)
; 
; 
Проверка
; 
-
верно
Строим эпюру (рис. а).
6. Строим эпюру суммарного изгибающего момента
Для построения суммарной эпюры изгибающего момента значения ординат в характерных точках берем с эпюр моментов в горизонтальной и вертикальной плоскостях (рис. а).
В точке А:
В точке В:
В точке С:
Строим эпюру (рис. а).
7. Определяем приведенный момент в опасном сечении вала
Опасным сечением вала будет являться сечение в точке В, так как в ней крутящий и суммарный изгибающий моменты имеют наибольшие значения.
1) Подбираем безопасный диаметр вала
Принимаем d = 35 мм.
Пример 4.
Стальной вал
постоянного сечения (рис.1, а)
вращается с частотой n об/мин и передает мощность N кВт. Подобрать диаметр
вала, если заданы предел текучести материала 
и запас прочности 
.
Числовые
данные к задаче: а = 0,3 м; b = 0,3 м; c = 0,2 м; D1 = 0,3 м; D2 = 0,6 м; N = 20 кВт; n1
= 120 об/мин; материал Ст50; =300 МПа; запас прочности по отношению к пределу текучести 
.
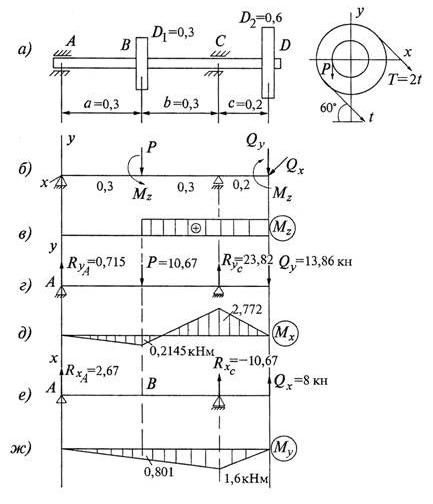
Рис. 1
Решение.
1. Определение нагрузок, передающихся на вал
1.1. Определение крутящего момента по формуле
1.2. Определение окружных усилий по формулам и разложение их на вертикальную и горизонтальную составляющие
Выполняем вычисления и показываем все найденные силы на расчетной схеме вала (рис.1, б)
2. Построение
эпюр моментов 
2.1. Построение эпюры крутящих
моментов 
Эпюра
крутящих моментов располагается между шкивами, т.к. скручивается только этот
участок вала. Величина крутящего момента определена в п.1.1.: 
=1,60 кНм (рис.1, в)
2.2. Построение эпюры изгибающих моментов относительно осей Х – Мх изгиб вертикальной плоскости
Схема нагрузок показана на рис. 1, г.
Находим опорные реакции
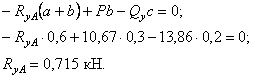
Проверка:
Точность 
Вычисляем моменты в характерных точках:
По вычисленным значениям моментов строится эпюра (рис.1, д).
2.3.
Построение эпюры изгибающих моментов 
(изгиб в
горизонтальной плоскости)
Схема нагрузок, действующих в этой плоскости, показана на рис.1, е).
Находим опорные реакции:
Проверка:
Вычисляем моменты в характерных точках:
По найденным
значениям строится эпюра изгибающих моментов в горизонтальной плоскости (рис. 1, ж).
3. Подбор
сечения (определение диаметра вала)
Материал Ст50,
=380 МПа, запас 
=3.
Находим допускаемое напряжение:
Опасным в данном случае является сечение С, так как в этом сечении все моменты наибольшие, что видно по эпюрам. Выписываем величины моментов в сечении С:
Вычисляем приведенный расчетный момент:
По
формуле для кругового сечения вычисляем диаметр вала:
Пример 5.
Дано: редукторный
ступенчатый вал (рис. 1). материал – сталь, = 160 МПа; Т
= 0,14 кНм; D1
=
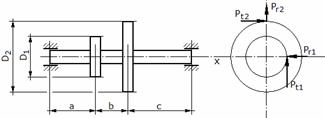
Рис.1
Требуется:
1) определить окружные и радиальные
усилия, приняв соотношение между ними 
2) построить эпюры изгибающих моментов в двух плоскостях;
3) построить эпюру суммарного изгибающего момента;
4) построить эпюру крутящего момента;
5) используя IV теорию прочности определить диаметр вала на отдельных участках, округлив их до стандартных размеров;
6) начертить эскиз вала;
Решение.
1. Определение окружных и радиальных усилий
Окружные усилия создают относительно оси вращения моменты, равные по величине моменту, передаваемого валом, поэтому:
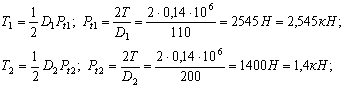
по соотношению между окружными и радиальными усилиями, находим последние:
2. Построение эпюр изгибающих моментов в двух плоскостях
а) в горизонтальной плоскости
В горизонтальной плоскости действуют радиальное усилие шкива 1 и окружное усилие шкива 2 (рис. 2, б). Находим горизонтальные реакции опор:
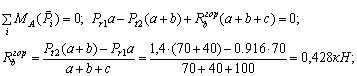
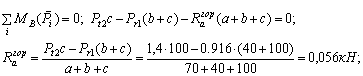
Вал имеет 3 участка, границами участков являются опоры и шкивы. Горизонтальный изгибающий момент линейно меняется по участкам вала (т.к. нет распределенной нагрузки).
На 1ом участке изгибающий момент равен:
в сечении A изгибающий момент равен 0 (т.к. нет внешних моментов), в сечении C:
На 3ем участке изгибающий момент равен:
в сечении B момент равен 0 (т.к. нет внешних моментов), в сечении D:
По вычисленным значениям моментов строим эпюру горизонтального изгибающего момента (рис.2, в).
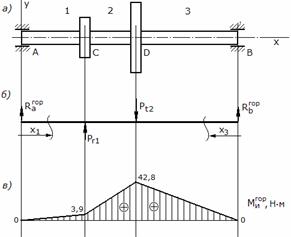
Рис.2
б) в вертикальной плоскости
В вертикальной плоскости действуют окружное усилие шкива 1 и радиальное усилие шкива 2 (рис. 3, б). Находим вертикальные реакции опор:
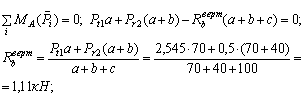
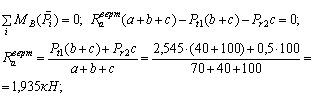
Вертикальный изгибающий момент линейно меняется по участкам вала (т.к. нет распределенной нагрузки).
На 1ом участке изгибающий момент равен:
в сечении A изгибающий момент равен 0 (т.к. нет внешних моментов), в сечении C:
На 3ем участке изгибающий момент равен:
в сечении B момент равен 0 (т.к. нет внешних моментов), в сечении D:
По вычисленным значениям моментов строим эпюру вертикального изгибающего момента (рис. 3, в).
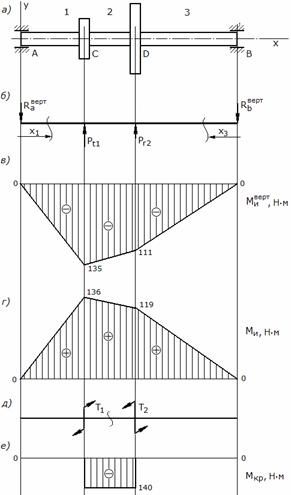
Рис.3
3. Построение эпюры суммарного изгибающего момента
Суммарный изгибающий момент определяется как:
Определяем суммарный изгибающий момент в сечениях по границам участков:
в сечениях A и B суммарный изгибающий момент равен 0;
в сечении C:
в сечении D:
По вычисленным значениям моментов строим эпюру суммарного изгибающего момента (рис. 3, г).
4. Построение эпюры крутящего момента
Окружное усилие шкива 1 создает относительно продольной оси вала момент, который стремится вращать вал по часовой стрелке (если смотреть с положительного направления оси x); окружное усилие шкива 2 создает момент, который стремится вращать вал против часовой стрелки (рис. 3, д).
Крутящий момент возникает только в сечениях участка вала между шкивами, на участках между шкивом и опорой крутящий момент равен 0.
Проводим произвольное сечение на участке 2 между шкивами и рассматриваем равновесие одной из частей (например, правой). Крутящий момент возникающий в сечении равен сумме внешних моментов, действующих по одну сторону от сечения; в данном случае крутящий момент равен по величине моменту T2 = 140 Нм и направлен в противоположную ему сторону; и если смотреть на торец отсеченной части вала, то крутящий момент стремится вращать отсеченную часть против часовой стрелки, поэтому он имеет отрицательный знак.
Строим эпюру крутящих моментов (рис. 3, е).
5. Определение диаметров вала по участкам, исходя из условия прочности по IV теории
По IV теории условие прочности выглядит:
где Wz – момент сопротивления сечения вала; в данном случае вал круглого сечения:
где d – диаметр сечения вала.
Определяем диаметры вала по участкам, исходя из условия прочности:
– 1ый участок:
Наибольший суммарный изгибающий момент на 1ом участке действует в сечении C, крутящий момент на 1ом участке не возникает, поэтому эквивалентный момент равен:
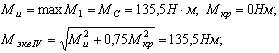
исходя из условия прочности определяем необходимый момент сопротивления и диаметр сечения вала на 1ом участке:
– 2ой участок:
Наибольший суммарный изгибающий момент на 2ом участке действует в сечении C, крутящий момент на 2ом участке равен моменту, передаваемого валом, с отрицательным знаком, поэтому эквивалентный момент равен:
исходя из условия прочности определяем необходимый момент сопротивления и диаметр сечения вала на 2ом участке:
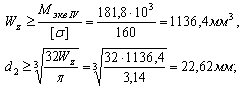
- 3ий участок:
Наибольший суммарный изгибающий момент на 3ем участке действует в сечении D, крутящий момент на 3ем участке не возникает, поэтому эквивалентный момент равен:
исходя из условия прочности определяем необходимый момент сопротивления и диаметр сечения вала на 3ем участке:
Выбираем диаметры вала по участкам, исходя из ряда Ra 40 нормальных линейных размеров (ГОСТ 6636–69):
– для
1ого участка принимаем диаметр 
– для
2ого участка принимаем 
– для
3его участка принимаем 
6. Эскиз вала
Эскиз вала с указанием необходимых размеров представлен на рис. 4.
Рис.4
Пример 6.
Рассчитать радиус круглого цилиндрического вала с прямой осью, несущего два шкива, весом каждый по 1 кН и с одинаковыми диаметрами D = 0,5 м. Длина вала l = 0,5 м (рис. 1). Натяжение в ведущих ремнях Р1 = 0,8 кН, в ведомых Р2 = 0,2 кН. Ремни левого шкива расположены вертикально, правого – горизонтально, Radm = 65 МПа. Собственным весом вала пренебречь. Использовать критерии прочности наибольших касательных напряжений и удельной потенциальной энергии формоизменения.
Решение.
Определяем величину внешних усилий (моментов пар сил и сосредоточенных сил), передаваемых на вал со стороны шкивов. Величина внешних скручивающих моментов МI и MII определится разностью натяжений в ремнях:
MI = 800·0,25 – 200·0,25 = 150 Нм;
MII = 200·0,25 – 800·0,25 = –150 Нм.
Кроме кручения вал испытывает изгиб в вертикальной плоскости от веса шкивов G1 = G2 = 1 кН и от суммарной силы натяжения в ремнях левого шкива РI = 0,8 + 0,2 = 1 кН, а также изгиб в горизонтальной плоскости от суммарной силы натяжения в ремнях правого шкива РII = 0,8 + 0,2 = 1 кН. Схема загружения вала в вертикальной и горизонтальной плоскостях, а также эпюры крутящего момента Т и изгибающих моментов Мв и Мг показаны на рис. 2. Самым напряженным является сечение, где расположен левый шкив и в котором
Т = 150Нм, Мв = 180Нм; Мг = 20Нм.
Для расчета
диаметра вала воспользуемся формулам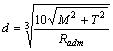и 
и 
, имея в виду, что в них
.
В результате получим по критерию наибольших касательных напряжений:
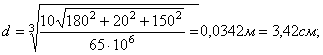
по критерию удельной потенциальной энергии формоизменения:
Вал, рассчитанный по критерию удельной потенциальной энергии формоизменения, более экономичен.
Пример 7.
Дано: а =400 мм, N1=50 кВт, n=900 об/мин, 
=600.
Для вала
изображенного на рис.1 требуется:
1) составить
расчетную схему вала;
2) определить
мощность на всех ведомых элементах вала;
3) определить
величину усилий и вращающего момента на ведущем и
ведомых элементах. Собственным весом вала и укрепленных на нем деталей пренебречь;
4) разложить
нагрузки на вертикальные и горизонтальные составляющие и построить эпюры:
изгибающих моментов в вертикальной плоскости Мверт., изгибающих моментов в
горизонтальной плоскости Мгор., суммарных изгибающих
моментов 
, крутящих моментов Мкр;
5) установить
опасное сечение;
6) По третьей
теории прочности вычислить диаметр вала при =90 МПа и округлить
до ближайшего значения по ГОСТ6636-69.
Указания.
Соотношение усилий принять следующие:
- в
плоскоременной передаче Т=2t;
- на зубчатых
колесах Ррад=0,42Рокр..
-
скручивающий момент 
Решение.
1. Определяем
мощность на ведомом колесе (рис.1)
2. Определяем
величину вращающего момента и усилий на ведущем и
ведомых элементах.
Крутящие
моменты определяем по заданным N и n
тогда
Определяем
усилия, действующие на шкив (рис. 3)
отсюда 
Определяем
давление на вал, т.к.
то 
Определяем
окружное и радиальное усилия, действующие на зубчатое колесо
Б (рис.4)
отсюда 
Определяем
окружное и радиальное усилия, действующие на зубчатое колесо
В (рис.5)
отсюда 
3. Найдем
проекции окружных и радиальных сил на горизонтальное и вертикальное направления
(x, y) (рис. 3, 4, 5):
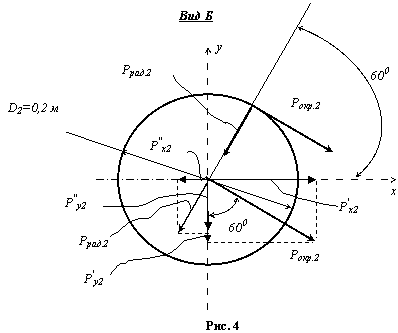
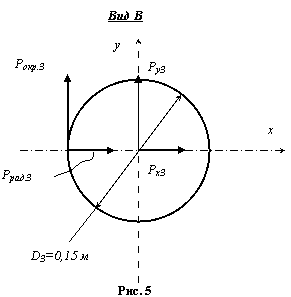
Эскиз вала и
расчетная схема приведены на рис. 6, а, б.
4. Построим
эпюру изгибающих моментов от сил, действующих в вертикальной плоскости (рис. 6,
в).
Определяем
опорные реакции:
Проверка:
Определяем
изгибающие моменты Мверт.:
Эпюра Мверт. показана на рис. 6, г.
5. Построим
эпюру изгибающих моментов от сил, действующих в горизонтальной плоскости Мгор.
(рис. 6, д).
Определяем
опорные реакции:
Проверка:
Определим
изгибающие моменты Мгор:
Эпюра Мгор приведена на рис. 6, е.
6. Построим
эпюру суммарных изгибающих моментов Ми:
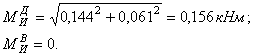
Эпюра МИ приведена на рис. 6, ж.
7. Построим
эпюру крутящих моментов, для чего нагрузим вал только скручивающими моментами
(рис. 6, з):
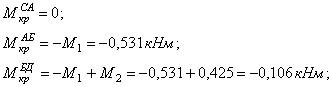
Эпюра Мкр
приведена на рис. 6, и.
8. Анализируя
эпюры Мкр
и Ми, видим, что опасным
будет сечение Б, где действует изгибающий момент Ми= 0,673 кНм и крутящий момент Мкр = -0,531 кНм.
По третьей
теории прочности найдём расчётный момент:
9. Определим
диаметр вала.
Условие
прочности:
где
тогда
Принимаем d =
Пример 8.
Для стального
вала, схема которого приведена на рис.1. Частота вращения вала n =200 об/мин; диаметры
шкивов D1=0,7
м; D2=0,5
м; диаметр зубчатого колеса D3=0,3 м;
передаваемая шкивами мощность N1 = 15 кВт;
N2 = 6 кВт, сила весов шкивов Q1 =
800 Н; Q2 = 500 Н.
Соотношение
между силами натяжения ветвей ременной передачи показано на схеме; соотношение
между силами, действующими в зубчатой передаче FR =0,3Ft3 , = 80 МПа.
Требуется
определить диаметр вала по III
теории прочности.
Решение.
1. Определим какой вид деформаций испытывает вал от
действия сил t1, t2,
, FR , Q1, Q2.
Для этого
приводим каждую силу к центру вала (рис. 1,а,б,в)
Учитывая, что
натяжение ремней ведущей ветви (2t1 и 2t2) больше натяжений для ведомых ветвей (t1 и t2 ), получаем для крутящих моментов: сечение С:
(против часовой
стрелки); (1)
сечение Е: 
(по часовой стрелке);
сечение D: 
(по часовой стрелке).
Условие
статического равновесия вала при кручении:
; T1 – T2 – T3 = 0.
(2)
Крутящий
момент определим по формуле: 
, Нм, (3)
где N - мощность в кВт,
n - число оборотов
вала в минуту.
Учитывая (2 и
3), можно записать условия (1) через мощности:
N1 – N2 – N3 = 0.
Тогда, N3 = N1 – N2 = 15 – 6 = 9 кВт,
Находим
крутящие моменты по формуле (3):
Крутящие
моменты действуют в точках С, D и Е.
По найденным
значениям приводим расчетную схему и эпюру крутящих моментов, Эп Т (рис.1,б,в).
Теперь
определим усилия , t1 и t2
по формулам, полученным из (2):
Н;
Н;
Н.
Найдем
давление на вал от сил натяжения ремней (2t1, t1, 2t2, t2), приведенных к центру вала (рис. 1, а,г,б,д).
и
Сила,
действующая на вал со стороны шестерни:
Н.
Силы R1, R2, FR
вызывают изгиб вала.
Из рис. 2,б видно,
что составляющие на оси Х и Y от сил R2 ,, FR соответственно равны:
Н;
Н;
Н;
Н;
Н;
Н.
Выберем силы,
вызывающие изгиб вала в вертикальной плоскости:
- со стороны
ведущего шкива (в точке С)
Н (направлена вниз);
- со стороны
ведомого шкива (в точке Е)
Н (направлена вниз);
- со стороны
шестерни (в точке D)
Н (направлена вверх).
Перенесем эти
силы на расчетную схему и построим эпюру изгибающих моментов в вертикальной
плоскости Эп МY0Z
(рис.1, г,д).
Рис.1
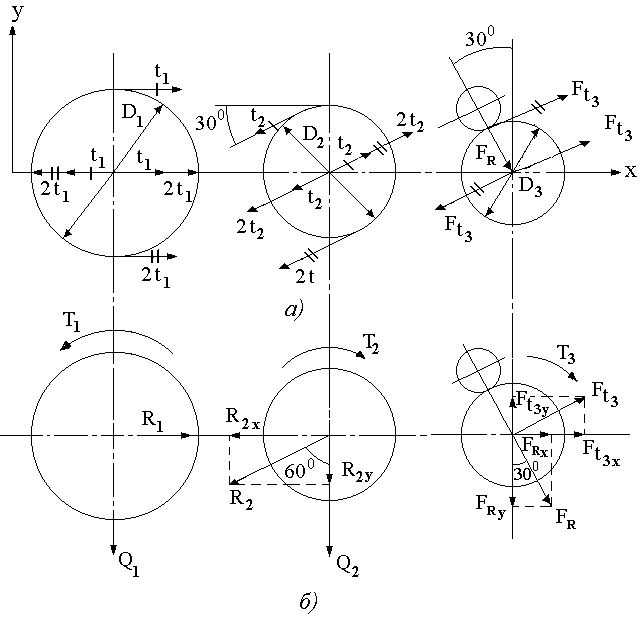
Рис.
2
Определим
реакции опор YA
и YВ:
Проверка: 
- 632 – 800 +
2983 + 701 – 2252 = 0.
Для
построения эпюры определяем значения изгибающих моментов в точках А, С, В, D,
Е:
МА = 0;
МС = - 632×0,2 = - 1264 Нм;
МВ = - 632×0,8 – 800×0,6
= - 986 Нм;
МД = - 632×1 – 800×0,8
+ 2982×0,2
= - 676 Нм;
МЕ = 0.
Построим
эпюру Эп. МY0Z.
Выберем силы,
вызывающие изгиб вала в горизонтальной плоскости:
со стороны
ведущего шкива (в точке С):
F1 = R1 = 6255 H (направлена вправо);
со стороны
ведомого шкива (в точке Е):
F2 = R2х = 3034 H (направлена влево);
со стороны
шестерни (в точке D):
F3 = 
= 2530 + 438 = 2968 H (направлена вправо).
Расставим эти
силы на схеме (рис. 1,е).
Определим реакции опор ХА и ХВ :
Проверка:
-XA + F1 – XB + F3
– F2 = 0;
- 5845 + 6255
– 344 + 2968 – 3034 = 0.
Для
построения эпюры находим значения изгибающих моментов в точках А, С, D,
В, Е:
МА = 0;
МС = - 5845×0,2 = - 1169 Нм;
МВ = - 5845×0,8 + 6255×0,6
= - 923 Нм;
МД = - 3034 ×0,3 = - 910 Нм;
МЕ = 0.
Построим
эпюру изгибающих моментов в горизонтальной плоскости МXOZ (рис. 1,ж)
Переходим к
построению суммарной эпюры изгибающих моментов Эп.МСУМ.
(рис.1,з). Определяем значение
изгибающего момента для каждой точки по формуле :
(4)
Найдем
опасное сечение вала. Опасным сечением будет являться та точка, где крутящий и
изгибающий моменты одновременно достигают наибольшей величины, т.е. эквивалентный момент имеет максимальное значение.
Эквивалентный момент рассчитываем по формуле:
(5)
Из анализа
эпюр 
и Т видно, что это
точка В.
Диаметр вала
определяем по формуле:
(6)
Принимаем d = 50 мм. Размер принят из стандартного ряда чисел для
диаметров валов.
Пример 9.
Дано: N=70 кВт,
n1 =400 об/мин, а=1,3м, в=1,8м, с=1,7м, D1=1,4м, D2=1,3м, =800, =700
Требуется
определить диаметр вала по III
теории прочности.
Решение.
1. Определяем
вращающие моменты на шкивах 1 и 2
Так как
дополнительных условий нет, считаем, что вращающие моменты на ведомых шкивах
одинаковы и равны
2. Изображаем
расчетную схему для определения крутящих моментов и строим эпюру крутящих моментов.
3. Определяем
окружные усилия из условий
Откуда
4. Определяем
вертикальные и горизонтальные составляющие внешней нагрузки, действующей со
стороны шкивов на вал. Знаки составляющих берем с учетом принятой схемы и
системы координатных осей
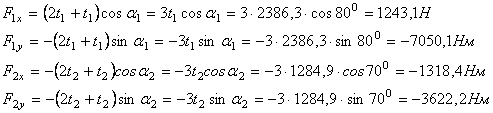
5. Изображаем
расчетную схему для определения изгибающих моментов в вертикальной плоскости
6. Определяем
опорные реакции от вертикальных составляющих нагрузки. Следует иметь в виду,
что знаки сил учтены в расчетной схеме.
Проверяем
правильность нахождения опорных реакций, используя третье уравнение статики
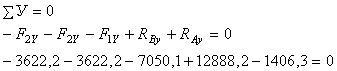
Реакции опор
найдены правильно.
7. Определяем
изгибающие моменты в вертикальной плоскости и строим эпюру МВ.
Так как
согласно расчетной схеме внешние нагрузки носят сосредоточенный характер, то
достаточно определить значения моментов в опорах и в местах расположения
шкивов, соединив эти значения прямыми линиями.
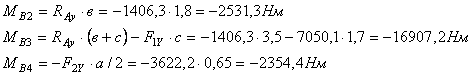
8. Изображаем
расчетную схему для определения изгибающих моментов в горизонтальной плоскости.
9. Определяем
опорные реакции от горизонтальных составляющих нагрузки. Следует иметь в виду,
что знаки сил учтены в расчетной схеме.
Проверяем
правильность нахождения опорных реакций, используя третье уравнение статики
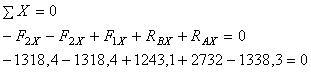
Реакции опор
найдены правильно.
10.
Определяем изгибающие моменты в горизонтальной плоскости и строим эпюру МГ
11.
Определяем суммарные изгибающие моменты и строим эпюру 
.
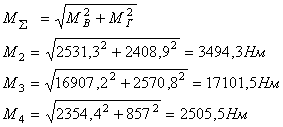
Рассмотрение
эпюр Т и достоверно указывает,
что наиболее опасным сечением является сечение 3.
12.
Определяем расчетный момент в сечении 3 по III теории прочности
13.
Определяем необходимый диаметр вала, учитывая, что 
=100 МПа, 
Принимаем d=120 мм
Пример 10.
На стальной
ломаный стержень круглого поперечного сечения, расположенный в горизонтальной
плоскости и имеющий прямые углы в точках B и
C (рис. а),
действует вертикальная нагрузка.
Допускаемое
нормальное напряжение 
кН/см2; 
м; 
м; 
м; 
кН/м; 
кН.
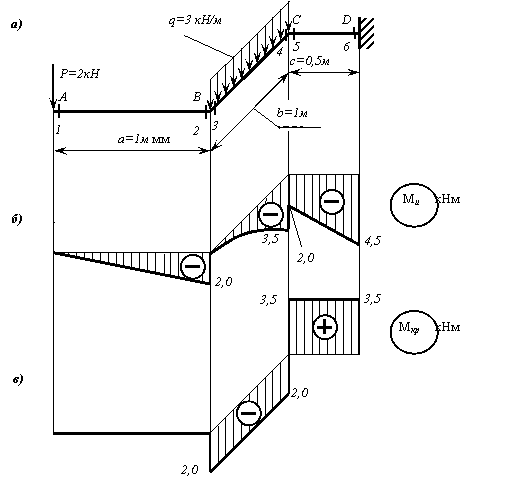
Требуется:
1) построить
отдельно в аксонометрии эпюры изгибающих и крутящих моментов,
2) установить
опасное сечение, найти для него эквивалентный момент по третьей гипотезе
прочности
3) подобрать диаметр стержня.
Решение.
1. Строим
эпюры изгибающих и крутящих моментов.
Разбиваем
длину стержня на три участка: AB, BC и CD. Делаем сечения по
границам каждого из этих участков и вычисляем значения изгибающего 
и крутящего 
:
, 
;
кНм
(сжаты волокна снизу), 
;
, 
кНм;
кНм
(сжаты волокна снизу),
кНм;
кНм
(сжаты волокна снизу),
кНм;
кНм
(сжаты волокна снизу),
кНм.
По найденным
значениям строим эпюры изгибающих 
и крутящих 
моментов. При
построении эпюры изгибающих моментов придерживаемся
следующих правил: плоскость эпюры на каждом из участков ломаного стержня
совпадает с плоскостью изгиба соответствующего участка; ординаты эпюры
откладываются со стороны сжатых волокон.
Эпюра
изгибающих моментов показана на рис. б. Под незагруженными
участками AB и CD она линейна, а под
распределенной нагрузкой изменяется по квадратичной параболе.
Для крутящего
момента сохраняем обычное правило знаков. Эпюра крутящих моментов может быть ориентирована
в пространстве как угодно, но ее ординаты всегда откладываются по нормали к оси
стержня (рис. в).
2.
Устанавливаем опасное сечение.
Несложный
анализ построенных эпюр показывает, что опасным является сечение 6, в котором возникают и наибольший
изгибающий, и наибольший крутящий моменты:
кНм, 
кНм.
3. Вычисляем
эквивалентный момент по третьей
гипотезе прочности:
кНм
кНсм.
4. Подбираем
диаметр стержня.
Из условия
прочности требуемый осевой момент сопротивления
см3.
Отсюда
см.
Принимаем,
округляя, 
мм.
Пример 11.
На рис.1,а изображена в аксонометрии ось ломаного
стержня круглого поперечного сечения, расположенная в горизонтальной плоскости
и имеющая прямые углы в точках А и В. На стержень
действует вертикальная нагрузка. Дано: l=2 м, Р=30 кН, q=15 кН/м.
Требуется:
1) построить
отдельно (в аксонометрии) эпюры изгибающих и крутящих моментов;
2) установить опасное сечение и найти для него расчетный момент по четвертой теории прочности.
Решение.
1. Разобьем
стержень на участки (рис.1, а).
Изгибающий момент в любом сечении стержня определяем как алгебраическую сумму
моментов (относительно соответствующей оси) внешних сил действующих по одну
сторону от сечения.
Чтобы
предварительно не определять реакций в заделке, рекомендуется брать сумму
моментов сил, действующих со стороны свободного конца стержня.
I-й
участок (ЕА):
II-й
участок (АВ)
Для
определения изгибающих моментов в сечениях II-го участка полезно мысленно перенести распределенную нагрузку действующую на I-ом участке в точку А. При переносе
надо добавить момент, лежащий в плоскости чертежа, т.е. в плоскости уох, и равный 
кНм (рис. 1,б). Так как плоскость действия этого момента перпендикулярна оси
второго участка, то он вызывает кручение стержня, а изгиб производит сила 
кН (рис. 1,б), поэтому:
III-й
участок (ДВ)
IV-й
участок (ВС)
Перенесем
силу Р
параллельно самой себе из точки Д в точку В. При переносе надо добавить момент 
кНм, который будет вызывать кручение стержня (рис.1, б), поэтому:
Эпюра
изгибающих моментов представлена на рис.2, а.
Построим
эпюру крутящих моментов. Стержень на участке ЕА не испытывает кручения, так как
q лежит в той же плоскости, что и продольная ось участка ЕА.
Крутящий
момент в сечениях участка АВ:
Участок ДВ не
испытывает кручения, так как Р лежит в той же плоскости, что и продольная ось участка ДВ.
Крутящий
момент в сечениях участка ВС:
Эпюра Мкр показана на рис. 2, б.
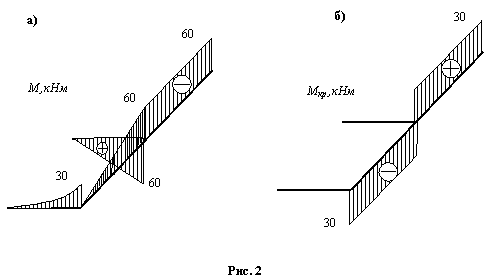
2.
Определение опасного сечения
Анализируя
эпюры М и Мкр (рис.2,а, б), видим, что необходимо проверить
расчетные моменты в сечении В для второго и четвертого
участков, а также в сечении С.
Тогда:
Отсюда видно,
что опасным сечением будет либо сечение В, либо сечение
С, так как расчетный момент в этих сечениях одинаковый.
Пример 12.
Идеализированная
расчетная схема коленчатого вала представлена на рис.1. Левый и правый концы
вала имеют шарнирное закрепление в вертикальной и горизонтальной плоскостях,
перпендикулярных оси стержня. Правый конец, кроме того, жестко закреплен от
продольного перемещения и поворота сечения вокруг оси стержня. Требуется,
подобрать радиус круглого сечения шатунной шейки (горизонтальная
участок вала длиной 
) и размеры прямоугольного сечения кривошипа (вертикальные
участки вала длиной 
) так, чтобы удовлетворялись условия статической и
усталостной прочности вала. Примем следующие исходные данные: 
кН, 
кН, 
кН, 
, 
см, 
см, 
см, 
. Для кривошипа отношение сторон прямоугольного сечения 
. Материал вала – сталь С275 с допускаемым напряжением
190 МПа. Пределы выносливости для симметричного цикла примем: при изгибе 
МПа, при кручении 
МПа.
Рис.1
Теоретические
сведения.
Коленчатый вал является плоской рамой, испытывающей действие пространственных циклических нагрузок, в которой возможно усталостное разрушение, поэтому кроме расчета на статические нагрузки требуется учет влияния на напряжения динамического действия нагрузок. Известно, что под действием длительных, циклически меняющихся нагрузок материалы конструкций обнаруживают значительное понижение прочности. Это явление носит название усталости материала. Способность материала сопротивляться усталостному разрушению называют выносливостью. Важной характеристикой материала является предел выносливости, определяемый экспериментально. Следует отметить, что расчет на циклические нагрузки (усталостную прочность) носит эмпирический характер, требует наличия большого количества экспериментальных данных, обычно приводимых в справочниках в виде таблиц и графиков. Используемый в рассматриваемой задаче расчет на усталостную прочность является достаточно приближенным, так как многие необходимые для расчета величины эмпирических коэффициентов принимаются условно. Более точный расчет коленчатых валов рассматривается в специальных курсах.
Один из
способов расчета на усталостную прочность сводится к определению действительного
коэффициента запаса усталостной прочности 
и сравнению его с
нормируемым коэффициентом запаса n. В
данном расчете примем 
. Условием усталостной прочности является условие
. (1)
Для "балочного" напряженного состояния, которое имеет место в опасных точках коленчатого вала коэффициент запаса усталостной прочности находится по формуле Гафа и Полларда
(2)
где 
– запас прочности по
нормальным напряжениям в предположении, что касательные напряжения равны нулю; 
– запас прочности по
касательным напряжениям, когда 
. Коэффициенты и определяются следующим
образом:
,
(3)
.
(4)
В формулах
(3), (4) 
и 
– пределы выносливости
при изгибе и кручении для симметричного цикла; 
, 
– амплитудные значения
цикла напряжений при изгибе и кручении, 
, 
– средние напряжения
цикла при изгибе и кручении. Остальные величины, входящие в формулы (3), (4),
являются эмпирическими коэффициентами, учитывающими
- 
, 
– влияние среднего
напряжения на величину сопротивления усталости;
- 
, 
– масштабный фактор и
степень шероховатости поверхности;
- 
, 
– влияние концентрации
напряжений на сопротивление усталости.
Эти
коэффициенты в инженерных расчетах определяют по специальным справочникам.
Решение.
Определение внутренних усилий. Прежде всего надо найти внутренние усилия в сечениях вала, т. е. построить эпюры усилий. Для этого сначала определим опорные реакции. В заданных закреплениях на концах вала возникает шесть опорных реакций, показанных на рис. 2.
Рис.2
Составим шесть уравнений статики
Из них получим 
, 
, 
, 
, 
, 
кНм.
При вычислении
внутренних усилий используем местные системы координатных осей для каждого
участка стержня. Направление оси 
, совпадающей с осью стержня, следует сохранять на всех
участках рамы. На рис. 5.33 оно соответствует обходу вдоль оси стержня
слева направо. Оси 
и 
– главные центральные
оси инерции поперечного сечения. Ось будем всегда
направлять перпендикулярно плоскости чертежа, ось 
лежит в плоскости
рисунка и меняет свое направление при переходе с одного участка рамы на другой
(см. рис. 2). При определении усилий используем правила знаков для
внутренних усилий, поясняемые рис. 3.
Рис.3
Тогда, используя метод сечений, найдем внутренние усилия в расчетных сечениях 1–10:
; 
; 
;
; 
;
; 
; 
;
; 
;
; 
;
;
;
; 
,
; 
; 
;
; 
;
; 
;
; 
;
; 
; 
.
Эпюры
внутренних усилий, построенные по принятым в условии задачи исходным данным,
показаны на рис. 4. Эпюры изгибающих моментов откладываем со стороны растянутых
волокон. Обратим внимание на соблюдение дифференциальных зависимостей между 
и 
, а так же между 
и 
.
Рис.4
Предварительный подбор сечений шатунной
шейки и кривошипа. После построения эпюр можно подобрать размеры поперечных
сечений. Предварительный подбор сечений производим из условия статической
прочности без учета напряжений от продольной и поперечных сил, а для
прямоугольного сечения, кроме того, не учитываем напряжения от крутящего
момента. При предварительном подборе сечения допускаемое напряжение примем
пониженным – 
МПа, имея в виду снижение прочности металла за счет усталости
при циклически меняющихся напряжениях и необходимости удовлетворения еще
условию усталостной прочности. Сначала определим радиус круглого сечения шатунной шейки. Выберем опасное сечение,
сравнив величины суммарных изгибающих моментов в потенциально опасных сечениях
3, 4–5 и 6 (см. рис. 2). Суммарный изгибающий момент находится по формуле
.
В сечении 3 
кНсм, 
, тогда 
кНсм; в
сечении 4(5) 
кНсм, 
кНсм и 
кНсм; наконец, в сечении 6 
кНсм, 
кНсм и 
кНсм.
Видно, что
опасным будет сечение 4(5), в котором действует суммарный момент 
кНсм. Условие
статической прочности в опасной точке этого сечения, полученное из третьей
теории прочности, имеет вид:
,
где 
– приведенный момент,
а 
– момент сопротивления
изгибу. Из условия статической прочности найдем необходимый радиус сечения
шатунной шейки. В рассматриваемом примере
кНсм.
Из условия 
кН/см2 получим 
см. Так как в использованном условии прочности не
учтена продольная сила, немного увеличим сечение. Достаточно округлить
полученный размер в большую сторону. Примем 
см.
Теперь
предварительно подберем размеры прямоугольного сечения кривошипа из условия прочности в угловых точках сечения, где
действуют только максимальные нормальные напряжения от изгиба, а касательные
напряжения равны нулю. Условие прочности в этих точках имеет вид 
.
Прежде чем
находить размеры сечения, подумаем, как рационально расположить сечение.
Поскольку в рассматриваемом примере 
, то для обеспечения рациональной работы кривошипа сечение
надо развернуть так, чтобы наибольшая сторона 
была расположена вдоль
оси . Тогда 
, 
и 
. Условие прочности в этом случае
запишется так:
.
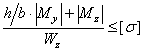Чтобы выбрать
опасное сечение, надо сравнить значение числителя в условии прочности в
потенциально опасных сечениях правого (расчетным считаем правый кривошип, т.к.
в нем крутящий момент не равен нулю) кривошипа (сечения 7, 8 на рис. 2). При самым опасным сечением
будет сечение 7, в котором 
кНсм. Из условия прочности, считая
допускаемое напряжение равным 95 МПа, найдем размер сечения кривошипа.
кН/см2.
Отсюда 
2,72 см. Округляя размер в большую сторону примем 
см, 
см.
Построение эпюр
напряжений. Построим эпюры напряжений в опасных сечениях с тем, чтобы найти
положение дополнительных опасных точек и завершить в дальнейшем окончательную
проверку статической прочности. Чтобы найти точное положение опасных точек в круглом сечении шатунной шейки, определим направление суммарного изгибающего
момента. Изобразим пары и в виде векторов с
учетом их знаков (в опасном сечении и в соответствии с
эпюрами отрицательны), определяя их направление по правилу правого винта (см.
рис.5). Нейтральная линия для круглого сечения перпендикулярна плоскости изгиба
и совпадает с линией действия вектора полного изгибающего момента 
. На рис. 5.35 построены эпюры нормальных напряжений,
вызванных действием изгибающего момента , продольной силы N, и эпюра касательных
напряжений от крутящего момента 
.На эпюрах напряжений учтены знаки усилий.
Максимальные напряжения от продольной силы, изгиба и кручения найдены по
формулам соответственно 
,
и 
.
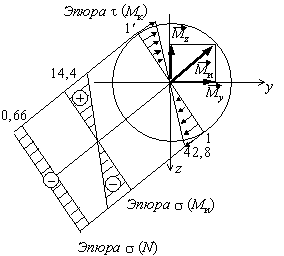
Рис.5
Построим эпюры
распределения напряжений в прямоугольном
сечении кривошипа (рис. 6). При
определении максимальных нормальных напряжений,
вызванных продольной силой и изгибающими моментами, использованы формулы , 
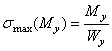и 
. Максимальные касательные напряжения крутящего момента и от
поперечных сил найдены по формулам 
, 
, 
, 
. Знаки нормальных напряжений соответствуют знакам усилий 
, и . Стрелками показаны направления касательных напряжений,
вызванных усилиями , и с учетом их знаков.
Рис.6
Проверка усталостной прочности шатунной шейки. Нормальные напряжения от изгиба изменяются по симметричному циклу, а нормальные напряжения от продольной силы постоянны, поэтому характеристики цикла, по которому меняются полные нормальные напряжение,
, 
.
Касательные напряжения от кручения изменяются по пульсирующему (отнулевому) циклу с такими характеристиками
.
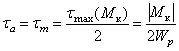Найдем эти характеристики, считая радиус шатунной шейки равным 3,1 см. Тогда
см3, 
см3, 
см2
и
кН/см2, 
кН/см2;
кН/см2.
Сосчитаем
коэффициенты запаса по формулам 
, ,
.
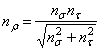Примем следующие значения эмпирических коэффициентов:
, 
, 
.
Тогда
,
,
,
то есть условие усталостной прочности шатунной шейки выполняется.
Проверка статической прочности шатунной шейки и кривошипа. Проверка статической прочности производится на кратковременное двукратное увеличение нагрузки с учетом напряжений от всех внутренних усилий. Допускаемое напряжение при этом принимается равным 190 МПа.
По построенным ранее эпюрам напряжений выбираем опасные точки. Для круглого сечения шатунной шейки опасными могут быть точки 1, 1¢ (рис. 5). Для пластичного материала опасной является только точка 1, в которой нормальные напряжения от изгиба и продольной силы имеют один знак (в рассматриваемом примере знак "минус"). В этой точке, кроме того, действуют максимальные касательные напряжения, вызванные кручением. Таким образом, точка 1 находится в "балочном" напряженном состоянии. Проверку прочности в этой точке необходимо осуществлять по теориям прочности, соответствующим материалу. При подборе сечения в условии прочности точки 1 не учитывалась продольная сила. Теперь учтем ее влияние. В соответствии с условием окончательной проверки прочности увеличим найденные ранее напряжения в 2 раза. Сложим нормальные напряжения от изгиба и продольной силы в точке 1
МПа.
Касательные
напряжения в точке 1 
МПа. Подставим их в условие прочности по третьей теории 
МПа < 190 МПа.
Таким образом,
условие прочности в точке 1 шатунной шейки выполняется.
то есть найденный радиус поперечного сечения см, удовлетворяющий условию и статической, и усталостной
прочности является окончательным.
Для прямоугольного сечения кривошипа опасными могут быть три группы
точек, показанных на рис. 6. В рассматриваемом примере будем проверять
прочность в точках 1 (здесь нормальные напряжения от , и имеют один знак), 2 и 3 (в них складываются имеющие одинаковые
направления касательные напряжения от крутящего момента и поперечных сил).
Увеличим показанные на рис. 6 напряжения в 2 раза и проверим прочность в каждой
из опасных точек.
- В угловой
точке 1 действуют максимальные по модулю нормальные напряжения, равные сумме
напряжений от , и . Точка находится в линейном
напряженном состоянии и условие прочности в этой точке
МПа < 190 МПа
выполняется.
- В точке 2 по середине длинной стороны прямоугольника действуют и нормальные
МПа,
и касательные напряжения
МПа.
Точка
находится в "балочном" напряженном состоянии и проверку прочности
производим по третьей теории прочности
МПа < 190 МПа.
- Точка 3 по середине короткой стороны прямоугольника тоже находится в "балочном" напряженном состоянии. В ней действуют нормальные и касательные напряжения:
МПа,
МПа.
Условие прочности в этой точке по третьей теории прочности
МПа < 190 МПа.
Поскольку
условия прочности во всех опасных точках выполняются, окончательные размеры
поперечного сечения кривошипа см, см.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
