Главная
Лекция 7 (продолжение). Примеры решения на сложное сопротивление
Расчет балок при косом изгибе
Пример 1.
Для стальной балки требуется:
1. Определить положение нейтральной линии;
2. Построить эпюру нормальных напряжений в долях силы Р вдоль оси, перпендикулярной нейтральной линии;
3. Определить грузоподъемность балки, если R = 240 МПа.

Решение.
1. Определим геометрические характеристики сечения.
По таблице стандартных профилей находим
![]()
![]()
![]()
![]()

где х и у – собственные оси швеллера.
ХСY – главная центральная система координат.
Ось х параллельна оси Х, а ось у параллельна оси Y.
Определим главные центральные моменты инерции относительно осей Х и Y.
![]() .
.
![]() .
.
2. Рассмотрим плоскость OYZ (вертикальную плоскость) и построим эпюру Мх.
Рассмотрим плоскость OХZ (горизонтальную плоскость) и построим эпюру Му.
3. Опасным является сечение в заделке, так как относительно этого сечения изгибающие моменты являются наибольшими.
![]() (растянуто верхнее
волокно).
(растянуто верхнее
волокно).
![]() (растянуто правое
волокно).
(растянуто правое
волокно).


Силовая
плоскость (плоскость действия результирующего момента ![]() ) проходит через I и III квадранты. Тогда нейтральная линия
должна проходить через II и IV квадранты.
) проходит через I и III квадранты. Тогда нейтральная линия
должна проходить через II и IV квадранты.
Определим угол наклона нейтральной линии к оси Х
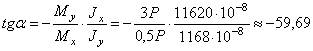
![]()
![]() ,
,
![]()
Знак «минус»
показывает, что угол ![]() откладываем от оси Х против хода часовой стрелки.
откладываем от оси Х против хода часовой стрелки.
4. Определим координаты угловых точек сечения А, L, B, K в главной центральной системе координат ХY
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Подсчитаем напряжения в точках А, L, B, K.
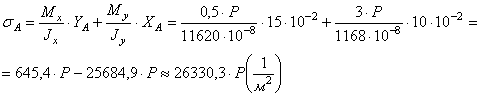


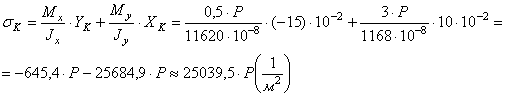
Продлим нейтральную линию и на перпендикуляре построим эпюру напряжений.
5. Определим грузоподъемность балки
![]()
Условия
прочности ![]()
![]()
![]() Мн
Мн
![]() Мн.
Мн.
Пример 2.
Балка
загружена нагрузкой, показанной на рис.1. Сила ![]() кН действует в вертикальной плоскости,
кН действует в вертикальной плоскости, ![]() кН – в горизонтальной, пара сил
кН – в горизонтальной, пара сил ![]() кНм – в плоскости, расположенной
под углом
кНм – в плоскости, расположенной
под углом ![]() к оси
к оси ![]() .
.

Рис.1
Требуется:
1) из условия прочности подобрать номер двутавра;
2) найти
полное перемещение точки ![]() оси балки (см. рис. 1);
оси балки (см. рис. 1);
3)
нарисовать сечение балки в масштабе и показать на нем нейтральную линию и
полное перемещение точки ![]() .
Определить угол между нейтральной линией и полным перемещением.
.
Определить угол между нейтральной линией и полным перемещением.
Решение.
Разложим нагрузку на вертикальную (рис. 2, а) и горизонтальную (рис. 2, в) составляющие и построим эпюры ![]() и
и ![]() (рис. 2, б, г). Чтобы правильно поставить знаки изгибающих моментов,
необходимо на рисунках показывать направление осей
(рис. 2, б, г). Чтобы правильно поставить знаки изгибающих моментов,
необходимо на рисунках показывать направление осей ![]() и
и ![]() , так как в соответствии с правилом знаков для изгибающего
момента в задачах сложного сопротивления знак момента зависит от направления
осей. Эпюры моментов строим со стороны растянутых волокон в той плоскости, в
которой действует нагрузка. По эпюрам выбираем опасные сечения. В
рассматриваемом примере их два: сечение
, так как в соответствии с правилом знаков для изгибающего
момента в задачах сложного сопротивления знак момента зависит от направления
осей. Эпюры моментов строим со стороны растянутых волокон в той плоскости, в
которой действует нагрузка. По эпюрам выбираем опасные сечения. В
рассматриваемом примере их два: сечение ![]() , в котором действуют
, в котором действуют ![]() кНм и
кНм и ![]() кНм, и сечение
кНм, и сечение ![]() с изгибающими
моментами –
с изгибающими
моментами – ![]() кНм и
кНм и ![]() кНм.
кНм.
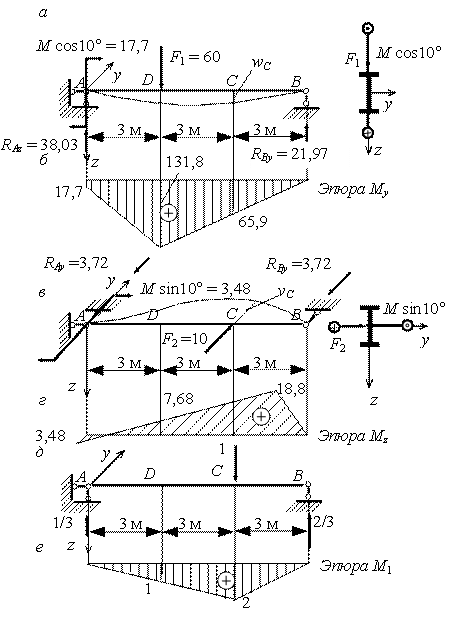
Рис.2
Условие
прочности в опасных точках двутавра имеет вид  . Поскольку отношение моментов сопротивления
. Поскольку отношение моментов сопротивления ![]() зависит от номера
двутавра, а он неизвестен, примем это отношение условно равным 10. Тогда
условие прочности
зависит от номера
двутавра, а он неизвестен, примем это отношение условно равным 10. Тогда
условие прочности  в опасных
точках сечения
в опасных
точках сечения ![]() примет вид:
примет вид:
![]() ,
,
где
допускаемое напряжение для стали принято ![]() = 160 МПа, величины
изгибающих моментов переведены из кНм в кНсм. Из написанного условия прочности
найдем необходимый момент сопротивления
= 160 МПа, величины
изгибающих моментов переведены из кНм в кНсм. Из написанного условия прочности
найдем необходимый момент сопротивления
![]() см3.
см3.
По сортаменту
прокатной стали подбираем номер двутавра. Для двутавра № 50 с такими
характеристиками: ![]() см3 и
см3 и ![]() см3 условие
прочности в опасных точках сечения
см3 условие
прочности в опасных точках сечения ![]()
![]() кН/см2
кН/см2
не
выполняется, поэтому увеличиваем двутавр. Проверим прочность для двутавра № 55,
у которого ![]() см3 и
см3 и ![]() см3:
см3:
![]() кН/см2.
кН/см2.
Убедимся в
том, что условие прочности выполняется и в опасных точках опасного сечения ![]() :
:
![]() кН/см2.
кН/см2.
Обратите
внимание на величину напряжений от изгибающего момента ![]() , действующего в горизонтальной плоскости, которую показывает
второй член в сумме. Видно, что, несмотря на то, что
, действующего в горизонтальной плоскости, которую показывает
второй член в сумме. Видно, что, несмотря на то, что ![]() в рассмотренном
примере существенно меньше
в рассмотренном
примере существенно меньше ![]() , напряжения от
, напряжения от ![]() больше чем напряжения от
больше чем напряжения от ![]() (или они примерно одинаковы). Это говорит об опасности изгиба
в горизонтальной плоскости, особенно для двутавров, у которых
(или они примерно одинаковы). Это говорит об опасности изгиба
в горизонтальной плоскости, особенно для двутавров, у которых ![]() .
.
Найдем
перемещение точки ![]() . Будем искать по формуле
. Будем искать по формуле  сначала
вертикальную составляющую перемещения, вызванную вертикальной составляющей
нагрузки. Формулу Максвелла – Мора
сначала
вертикальную составляющую перемещения, вызванную вертикальной составляющей
нагрузки. Формулу Максвелла – Мора  интегрируем по
правилу Верещагина, перемножая эпюры
интегрируем по
правилу Верещагина, перемножая эпюры ![]() и
и ![]() (рис. 2, б, е). Если хотя бы одна эпюра на участке имеет форму трапеции,
используем для перемножения правило трапеций.
(рис. 2, б, е). Если хотя бы одна эпюра на участке имеет форму трапеции,
используем для перемножения правило трапеций.
![]() кНм3.
кНм3.
Аналогично
определим по ![]() горизонтальную
составляющую перемещения (эпюру М1 от горизонтальной единичной силы, направленной
вдоль оси y, можно не строить, т.к. она такая
же, как от вертикальной единичной нагрузки), перемножая эпюры
горизонтальную
составляющую перемещения (эпюру М1 от горизонтальной единичной силы, направленной
вдоль оси y, можно не строить, т.к. она такая
же, как от вертикальной единичной нагрузки), перемножая эпюры ![]() и
и ![]() (рис. 2, г, е).
(рис. 2, г, е).
![]() кНм3.
кНм3.
Положительные
знаки перемещений свидетельствуют о том, что перемещения происходят по
направлениям единичных сил, т.е. вертикальное перемещение – вниз (по направлению
оси ![]() ), горизонтальное – по направлению оси
), горизонтальное – по направлению оси ![]() . Сосчитаем найденные составляющие перемещения в
"см", разделив их на соответствующие жесткости.
. Сосчитаем найденные составляющие перемещения в
"см", разделив их на соответствующие жесткости.
![]() кНсм2,
кНсм2,
![]() кНсм2,
кНсм2,
![]() см,
см,
![]() см.
см.
Из сравнения
величин ![]() и
и ![]() видно, что
горизонтальная составляющая перемещения, даже при небольшой горизонтальной
нагрузке много больше (особенно для двутавра) вертикальной составляющей.
видно, что
горизонтальная составляющая перемещения, даже при небольшой горизонтальной
нагрузке много больше (особенно для двутавра) вертикальной составляющей.
Выполним
последнюю часть задачи. Нарисуем сечение балки в масштабе, покажем на нем
нейтральную линию и полное перемещение. Уравнение нейтральной линии  в опасном сечении С имеет вид (при составлении уравнения нейтральной линии не забывайте
учитывать знаки изгибающих моментов в рассматриваемом сечении. В данной задаче
оба момента положительны):
в опасном сечении С имеет вид (при составлении уравнения нейтральной линии не забывайте
учитывать знаки изгибающих моментов в рассматриваемом сечении. В данной задаче
оба момента положительны):
![]() или
или ![]() .
.
Нейтральная
линия, построенная по этому уравнению, и эпюра нормальных напряжений в сечении ![]() показаны на рис. 3. Знаки
напряжений соответствуют положительным знакам изгибающих моментов. Угловые
точки 1, 1¢
– это опасные точки сечения, в которых мы ранее находили напряжения.
показаны на рис. 3. Знаки
напряжений соответствуют положительным знакам изгибающих моментов. Угловые
точки 1, 1¢
– это опасные точки сечения, в которых мы ранее находили напряжения.
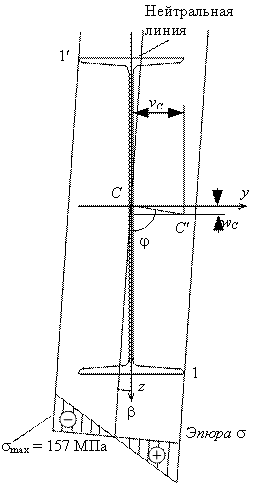
Рис.3
Найдем угол ![]() (см. рис. 3)
между нейтральной линией и осью
(см. рис. 3)
между нейтральной линией и осью ![]() :
:
![]()
Отложим в
масштабе найденные ранее вертикальную ![]() и горизонтальную
и горизонтальную ![]() составляющие
перемещения с учетом их направления. Полное перемещение точки
составляющие
перемещения с учетом их направления. Полное перемещение точки ![]() – отрезок
– отрезок ![]() на рис. 3 равен
геометрической сумме
на рис. 3 равен
геометрической сумме ![]() и
и ![]() . Угол
. Угол ![]() между полным перемещением
и осью
между полным перемещением
и осью ![]()
![]() .
.
Таким образом,
угол между полным перемещением ![]() и нейтральной линией
и нейтральной линией ![]() , что близко к
, что близко к ![]() .
.
Пример 3.
Для стержня (рис.1) определить внутренние силовые факторы в произвольном поперечном сечении и их построить эпюры.
Дано: F1 = 100 Н, F2 = 300 Н, q = 75 Н/м, a = 0,3 м, b = 0,2 м, l = 2 м.


а)
б)
Рис.1
Решение.
Рассекаем брус на произвольном расстоянии z от его свободного конца. Отбрасываем правую часть. Располагаем оси координат в центре тяжести сечения. Действие правой части бруса на его левую часть заменяем внутренними силами: N, Qx, Qy, Mx, My, Ткр (рис. 1, б).
Уравновешиваем, то есть, записываем уравнения равновесия и определяем значения внутренних силовых факторов.
![]() ;
;
QX = - 100Н.
![]() ;
;
при z = 0 Qy = 0;
при z = l Qy = -150 Н.
![]() ;
;
N = - 300Н.
![]() ;
;
при z = 0 Mx = - 45 Нм;
при z = l Mx = -195 Нм.
![]() ;
;
при z = 0 My = 30 Нм; при z = l My = - 170 Нм.
![]() ; Ткр = 15 Нм.
; Ткр = 15 Нм.
Строим эпюры внутренних силовых факторов (рис.2). Опасное сечение в данном брусе будет находиться в заделке, так как в этом сечении значения всех внутренних силовых факторов имеют наибольшие величины.

Рис.2
Пример 4.
Консольная балка прямоугольного поперечного сечения с соотношением
сторон ![]() нагружена в вертикальной и в
горизонтальной плоскостях сосредоточенными силами
нагружена в вертикальной и в
горизонтальной плоскостях сосредоточенными силами ![]() кН,
кН, ![]() кН, сосредоточенным
моментом
кН, сосредоточенным
моментом ![]() кНм
и равномерно распределённой нагрузкой
интенсивностью
кНм
и равномерно распределённой нагрузкой
интенсивностью ![]() кН/м (рис.1).
кН/м (рис.1).
Определить
рациональную ориентацию поперечного сечения (ребром или плашмя), а также его
размеры b и h из условия прочности
при допускаемом нормальном напряжении ![]() кН/см2. Построить эпюру нормальных напряжений по
контуру опасного поперечного сечения.
кН/см2. Построить эпюру нормальных напряжений по
контуру опасного поперечного сечения.
![]()

Рис. 1
Решение.
Для прямоугольного поперечного сечения условие
прочности при одновременном изгибе в двух плоскостях можно записать в виде:
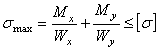 ,
,
где ![]() – максимальное
значение нормального напряжения, возникающего в поперечном сечении балки;
– максимальное
значение нормального напряжения, возникающего в поперечном сечении балки; ![]() и
и ![]() – изгибающие моменты;
– изгибающие моменты; ![]() и
и ![]() – осевые моменты сопротивления
поперечного сечения относительно главных центральных осей x и y соответственно.
– осевые моменты сопротивления
поперечного сечения относительно главных центральных осей x и y соответственно.
1. Строим
эпюры изгибающих моментов ![]() и
и ![]() по значениям, вычисленным
для характерных сечений (рис. 2).
по значениям, вычисленным
для характерных сечений (рис. 2).
Воспользуемся
принципом суперпозиции и сначала рассмотрим изгиб балки в вертикальной плоскости.
Сечение 1:
![]() кНм.
кНм.
Сечения 2 и 3:
![]() кНм.
кНм.

Рис. 2
Сечения 4 и 5:
![]() кНм.
кНм.
Сечение 6:
![]()
На участке
балки, нагруженном равномерно
распределённой нагрузкой интенсивностью q,
необходимо сделать дополнительное сечение 7.
Перерезывающая сила ![]() , возникающая в этом сечении, равна
, возникающая в этом сечении, равна
![]()
и при ![]() м
она обращается в нуль.
м
она обращается в нуль.
Следовательно,
в этом поперечном сечении балки изгибающий момент ![]() принимает экстремальное значение:
принимает экстремальное значение:
![]() кНм.
кНм.
Теперь
рассмотрим изгиб балки в горизонтальной
плоскости.
Сечение 1:
![]() кНм.
кНм.
Сечения 2 –7:
![]() кНм.
кНм.
2. Определяем
необходимые размеры поперечного сечения балки
при его расположении ребром.
Осевые моменты
сопротивления равны:
![]() ;
; ![]() .
.
Условие
прочности принимает вид:
![]()
Отсюда, после
несложных преобразований,
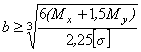 .
.
Отметим, что
при косом изгибе расположение опасного с точки зрения прочности сечения не
всегда очевидно. Поэтому нам необходимо исследовать несколько сечений, «похожих» на опасные сечения.
Сечение 1:
 см.
см.
Сечение 7:
 см.
см.
Из двух
полученных выше значений размера b нам следует
выбрать большее значение. Таким образом, для случая
расположения балки ребром принимаем
следующие размеры поперечного сечения:
![]() см;
см; ![]() см.
см.
3. Теперь
определим необходимые размеры поперечного сечения балки при ее расположении плашмя.
Осевые моменты
сопротивления в этом случае равны:
![]() ;
; ![]() .
.
Условие
прочности принимает вид:
![]() .
.
Отсюда
![]() .
.
Из условия
прочности сечения 1 получим:
 см,
см,
а из условия
прочности сечения 7 –
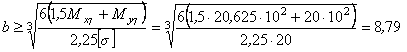 см.
см.
Из двух
найденных выше значений принимаем для размера b большее значение: ![]() см. Тогда
см. Тогда
![]() см.
см.
Анализируя
полученные результаты, видим, что расположение поперечного сечения балки плашмя является более рациональным, поскольку
в этом случае размер ![]() см оказывается меньше, чем при
расположении балки ребром (
см оказывается меньше, чем при
расположении балки ребром (![]() см).
см).
4. Строим
эпюру нормальных напряжений по контуру опасного
сечения 1. Осевые моменты сопротивления:
![]() см
см![]() ;
; ![]() см
см![]() .
.
Максимальные
значения нормальных напряжений при изгибе в вертикальной и горизонтальной плоскостях
соответственно равны:
![]() кН/см
кН/см![]() ;
;
 кН/см
кН/см![]() .
.
Эпюры ![]() и
и ![]() от изгиба в
вертикальной и горизонтальной плоскостях соответственно представлены на рис. 3.
от изгиба в
вертикальной и горизонтальной плоскостях соответственно представлены на рис. 3.
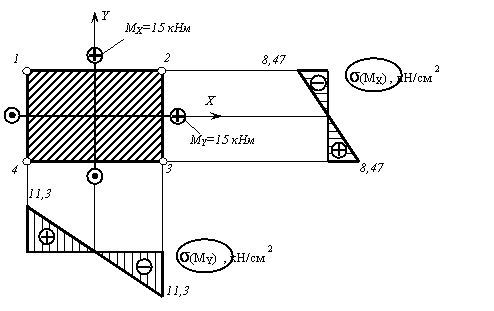
Рис. 3
Определяем
значения напряжений в угловых точках поперечного сечения с учётом их знака:
![]() кН/см
кН/см![]() ;
; ![]() кН/см
кН/см![]() ;
;
![]() кН/см
кН/см![]() ;
; ![]() кН/см
кН/см![]() .
.
Эпюра нормальных напряжений ![]() по контуру поперечного
сечения, расположенного плашмя,
представлена на рис. 4.
по контуру поперечного
сечения, расположенного плашмя,
представлена на рис. 4.

Рис. 4
Пример 5.
Для балки с
постоянным прямоугольным поперечным сечением (рисунок 1) требуется:
1) Построить
эпюры изгибающих моментов Mx
и My.
2) Проверить
балку на прочность по нормальным
напряжениям в самых опасных точках
заделки.
Дано
допускаемое значение нормального напряжения: ![]() = 835 МПа.
= 835 МПа.
Значения
сосредоточенных сил: Р1=3 кН; Р2=10
кН; Р3=6 кН. Размеры
сечения: b=6 см=
Линейные
размеры приведены на схеме.

Решение.
Применяем
метод сечений. Начиная со свободного торца, разбиваем балку на участки, проводя
их границы через сечения, в которых приложены внешние силы.
1. Построим эпюру для изгибающего момента Mx. Для этого рассмотрим только все вертикальные силы на балке, то есть те, которые стремятся совершить деформацию изгиба относительно оси x. (В вертикальной плоскости, в плоскости чертежа.)

Рис.1
I участок. ![]()
Проводим
произвольное сечение. Отбрасываем правую часть балки вместе с заделкой.
Рассматриваем моменты всех сил, приложенных к оставленной левой части балки.
Заменяем действие отброшенной (правой) части внутренним изгибающим моментом Mx, считая его
положительным (последовательность рассуждений отображена на рисунок 1).
Составляем
уравнение равновесия для моментов относительно точки K – центра
тяжести сечения:
![]() .
. ![]() .
.
II участок. ![]()
![]() .
. ![]() ;
; ![]() ;
; ![]()
На границах
участка: ![]() (кНм);
(кНм); ![]() (кНм).
(кНм).
III участок. ![]()
![]() .
. ![]() ;
; ![]()
На границах
участка: ![]() (кНм);
(кНм);
![]() (кНм).
(кНм).
Строим эпюру Mx в плоскости
чертежа.
2. Построим эпюру для изгибающего момента My. Для этого рассмотрим только все горизонтальные
силы на балке, то есть те, которые стремятся совершить деформацию изгиба
относительно оси y. (В горизонтальной плоскости, то
есть в плоскости, перпендикулярной чертежу.) Изгибающий момент My, так же, как и момент Mx, справа от сечения считаем положительным
(см. рис. 1). (Последовательность рассуждений аналогична той, что
использовалась для построения эпюры Mx,
и на схеме не отображена.)
I участок. ![]()
![]() .
. ![]() .
. ![]()
На границах
участка: ![]() (кНм);
(кНм); ![]() (кНм).
(кНм).
II участок. ![]()
![]() .
. ![]() ;
; ![]()
На границах
участка: ![]() (кНм);
(кНм); ![]() (кНм).
(кНм).
III участок. ![]()
![]() .
. ![]() ;
;
![]()
![]()
На границах
участка: ![]() (кНм);
(кНм); ![]() (кНм).
(кНм).
Строим эпюру My в горизонтальной плоскости.
3. Определим
нормальные напряжения в четырех опасных точках сечения в заделке по формуле:
 ;
;
Рассчитаем
моменты инерции прямоугольника:
![]() (м4);
(м4);
![]() (м4).
(м4).
Значения
изгибающих моментов в заделке определяем по эпюрам (рис. 1):
![]() (Нм);
(Нм);
![]() (Нм).
(Нм).
Определим напряжение в точке А.
Её координаты:
x= – b/2= –
![]() (Па).
(Па).
Определим напряжение в точке B.
Её координаты: x= – b/2= –
![]() (Па).
(Па).
Определим напряжение в точке C.
Её координаты: x=b/2=0,03 м; y=h/2=0,05 м.
![]() (Па).
(Па).
Определим напряжение в точке D.
Её координаты: x=b/2=0,03 м; y= – h/2= – 0,05.
![]() (Па).
(Па).
Значения
напряжения максимальны в точках А и С.
Проверим,
соблюдается ли в этих точках условие прочности:
![]() МПа <
МПа < ![]() =835 МПа.
=835 МПа.
Следовательно,
расчет подтверждает выполнение условия прочности.
4. Строим
эпюру нормальных напряжений в сечении, находящемся в заделке (рис.2).

Рис.2
Пример
6.
Для заданной консольной балки (рис.1)
1. построить эпюры изгибающих моментов и поперечных сил.
2. Подобрать
поперечное сечение при ![]() и
и ![]() .
.
3. Для опасного сечения определить: момент сопротивления, положение нейтральной линии, максимальные напряжения и построить эпюры распределения нормальных напряжений по сечению в аксонометрии.

Рис.1
Дано: а =0,4 м, ![]() =300, М=20
кНм, Р=16
кН, q=30 кН/м.
=300, М=20
кНм, Р=16
кН, q=30 кН/м.
Решение:
Все нагрузки,
действующие на консольную балку, расположены в различных плоскостях, проходящих
через ось балки, поэтому мы имеем дело со сложным изгибом. Для решения
поставленной задачи нагрузки, действующие в произвольных силовых плоскостях
нужно разложить на составляющие, расположенные в главных плоскостях ![]() и
и ![]() .
.
Плоскость ![]()
Проекция силы ![]() на плоскость
на плоскость ![]() проецируется с учетом
угла
проецируется с учетом
угла ![]()
![]()
Момент ![]() действует в плоскости
действует в плоскости ![]() , поэтому проецируется в натуральную величину.
, поэтому проецируется в натуральную величину.
Нагрузка ![]() лежит в плоскости,
перпендикулярной
лежит в плоскости,
перпендикулярной ![]() , поэтому ее проекция на плоскость
, поэтому ее проекция на плоскость ![]() будет равна нулю.
Покажем плоскость
будет равна нулю.
Покажем плоскость ![]() со спроецированной
нагрузкой (рис. 2).
со спроецированной
нагрузкой (рис. 2).
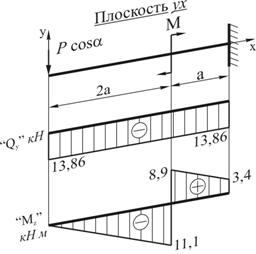
Рис.2
Поперечная сила по всей длине балки будет одинакова и равна
![]()
Изгибающий момент в сечении, где приложен момент М
Слева от сечения
![]()
Справа от сечения
![]()
Изгибающий момент в защемлении
![]()
Строим эпюры ![]() и
и ![]() (рис. 2).
(рис. 2).
Плоскость ![]()
Покажем
плоскость ![]() и спроецируем на нее
всю нагрузку.
и спроецируем на нее
всю нагрузку.
Проекция силы Р
![]()
Поперечная сила от свободного конца до начала приложения нагрузки q
![]()
Поперечная сила от начала действия нагрузки q до защемления
![]() ,
,
где ![]() - координата
- координата ![]() , отсчитываемая от начала распределенной нагрузки.
, отсчитываемая от начала распределенной нагрузки.
В сечении начала действия распределенной нагрузки
![]()
В защемлении балки
![]()
Поперечная сила меняет знак, значит, на эпюре изгибающих моментов будет экстремум в сечении с координатой
![]()
Изгибающий момент на свободном конце балки равен нулю.
В сечении начала действия распределенной нагрузки
![]()
Экстремальное значение изгибающего момента
![]()
В сечении защемления
![]()
Строим эпюры (рис. 3).
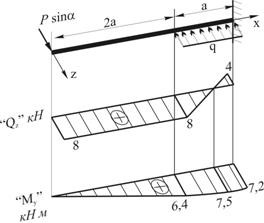
Рис.3
По двум эпюрам
![]() и
и ![]() определяем опасное
сечение.
определяем опасное
сечение.
Вероятнее
всего опасным сечением будет точка приложения сосредоточенного момента М. Для данного сечения ![]() ;
; ![]() . Расположим сечение таким образом, что бы большая сторона
сечения была перпендикулярна оси, относительно которой изгибающий момент будет
максимальным (рис. 4).
. Расположим сечение таким образом, что бы большая сторона
сечения была перпендикулярна оси, относительно которой изгибающий момент будет
максимальным (рис. 4).

Рис.4
Момент
сопротивления прямоугольного сечения с учетом ![]() :
:
относительно
оси ![]()
![]()
относительно
оси ![]()
![]()
Условие прочности при сложном изгибе
![]()
![]()
![]()
Принимаем ![]()
Моменты сопротивления сечения
![]()
![]()
Для определения угла наклона нейтральной линии необходимо определить отношение осевых моментов инерции.

Тангенс угла наклона нейтральной линии
![]()
![]() (рис. 5).
(рис. 5).
Для проверки
правильности построения нейтральной линии рассмотрим знаки напряжений от изгиба
относительно осей ![]() и
и ![]() .
.
Момент ![]() сжимает нижние волокна
и растягивает верхние. Ставим около точек В
и С знак плюс, а около точек А и Д
знак минус.
сжимает нижние волокна
и растягивает верхние. Ставим около точек В
и С знак плюс, а около точек А и Д
знак минус.
Момент ![]() сжимает правые волокна
и растягивает левые. Ставим около точек В
и А знак плюс, а около точек С и Д
знак минус.
сжимает правые волокна
и растягивает левые. Ставим около точек В
и А знак плюс, а около точек С и Д
знак минус.
Очевидно, что максимальные напряжения будут в точках, где совпадают знаки (точка В – максимальное положительное нормальное напряжение; Точка D – максимальное отрицательное напряжение).
Тогда
нейтральная линия должна пройти через четверти сечения, содержащие в себе точки С и А, как мы и изобразили на рис. 5,
отложив угол ![]() от оси
от оси ![]() .
.
Рассмотри напряженное состояние поперечного сечения. На нейтральной линии (н. л.) нормальные напряжения будут равны нулю.
В точках наиболее удаленных от нейтральной линии (точки В и D) нормальные напряжения имеют максимальные значения
![]()
![]()
В точках А и С напряжения по модулю равны
![]()
Для изображения эпюры распределения нормальных напряжений по сечению начнем со стороны BC.
Напряжения
будем откладывать параллельно оси ![]() , перпендикулярной поперечному сечению.
, перпендикулярной поперечному сечению.
В точке В откладываем
параллельно оси ![]() в сторону
положительных значений в масштабе значение
в сторону
положительных значений в масштабе значение![]()

Рис.5
По стороне ВС напряжения будут изменяться
пропорционально от максимального значения в точке В до нулевого значения на нейтральной линии. Поэтому соединяем
точку В с точкой пересечения
нейтральной линией стороны ВС. Из
точки С
проведем прямую, параллельную оси ![]() до пересечения с
продолжением прямой проведенной из точки В
к точке пересечения нейтральной линии стороны ВС. Получили отрезок, дающий нам значение и знак напряжения в точке
С
до пересечения с
продолжением прямой проведенной из точки В
к точке пересечения нейтральной линии стороны ВС. Получили отрезок, дающий нам значение и знак напряжения в точке
С
![]()
Те же действия проделываем со стороной АD. Получаем напряжение в точке А
![]()
Соединяя значения точек А и В – получаем распределение нормальных напряжений по стороне АВ. Соединяем значения напряжений точек С и D – получаем распределение нормальных напряжений по стороне СD.
Образованная плоскость, соединяющая значения напряжений для точек А, В, С и D является эпюрой распределения нормальных напряжений по сечению. Для определения напряжения в любой точке сечения проводится перпендикуляр к сечению до пересечения с плоскостью эпюры. Величина перпендикуляра даст знак и значение напряжения для данной точки.
Пример 7.
Стальная балка АВ, расчетная схема и поперечное сечение которой показаны на рис. 1, а, (c = 0,03 м) нагружена силами Р1 и Р2.
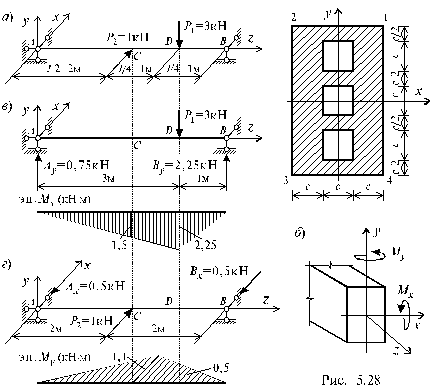
Рис.1
Требуется:
1. Построить эпюры изгибающих моментов в главных плоскостях инерции;
2. Установить по эпюрам изгибающих моментов опасное сечение балки. Найти для опасного сечения положение нулевой линии;
3. Вычислить наибольшие растягивающие и сжимающие нормальные напряжения;
4. Определить значение полного прогиба в середине пролета балки и указать его направление.
Решение.
1. Построить эпюры изгибающих моментов в главных плоскостях инерции. Ввиду симметричности сечения балки относительно осей x и y (рис. 5.28, а), можно сделать вывод, что эти оси - главные. Для построения эпюр изгибающих моментов, используя принцип независимости действия сил, представим косой изгиб как изгиб в двух главных плоскостях инерции бруса (рис. 1, б, г). Определив опорные реакции, составим аналитические выражения изгибающих моментов и вычислим их значения в характерных сечениях. Построим эпюры изгибающих моментов Mx и My (рис. 1, в, г), откладывая ординаты со стороны растянутых волокон. В соответствии с принятым правилом знаков, Mx < 0, My > 0.
2. Установить по эпюрам изгибающих моментов опасное сечение балки. Найти для опасного сечения положение нулевой линии. Сравнивая ординаты эпюр Mx и My , делаем вывод, что опасными могут быть сечения D или С, т.к. в них предположительно возникают наибольшие по величине изгибающие моменты. Для того, чтобы установить, какое из них является наиболее опасным, нужно вычислить возникающие в сечениях C и D наибольшие нормальные напряжения и сравнить их. Теоретически доказано, что если контур поперечного сечения так вписывается в прямоугольник, что четыре крайние точки сечения совпадают с углами прямоугольника, то максимальное нормальное напряжение будет в одном из углов прямоугольника и определится по формуле:
![]() ,
,
где все величины берутся по абсолютной величине. У нас именно такой случай. Осевые моменты инерции сечения вычислим по следующим зависимостям:
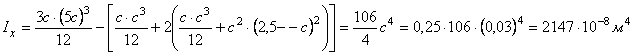
![]() .
.
Моменты сопротивления сечения Wx и Wy определятся следующим образом:
![]() м3;
м3;
![]() м3.
м3.
Таким образом, наибольшие напряжения в сечениях С и D равны:
сечение С
![]()
сечение D
![]() .
.

Рис. 2
Сравнивая эти значения, заключаем
-
опасным является сечение D.
Подставив значения Ix ,
Iy , Mx , My в
формулу  получим:
получим:
![]() , откуда
, откуда ![]() .
.
Нулевая линия
пройдет в тех четвертях поперечного сечения, в которых изгибающие моменты
будут вызывать нормальные напряжения разных знаков. В нашем случае это будут
первая и третья четверти. Поэтому, отложив угол ![]() от оси x против хода часовой стрелки, проведем
нулевую линию (рис. 2).
от оси x против хода часовой стрелки, проведем
нулевую линию (рис. 2).
3. Вычислить
наибольшие растягивающие и сжимающие нормальные напряжения. Вершины
стрелок нормальных напряжений, определяемых по формуле
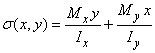 будут лежать на плоскости,
пересекающей плоскость поперечного сечения по нулевой линии. При взгляде на
плоскость напряжений вдоль нулевой линии мы увидим ее в виде прямой, ординаты
которой показаны в виде эпюры
будут лежать на плоскости,
пересекающей плоскость поперечного сечения по нулевой линии. При взгляде на
плоскость напряжений вдоль нулевой линии мы увидим ее в виде прямой, ординаты
которой показаны в виде эпюры ![]() на рис. 2. Наибольшие нормальные напряжения будут иметь
место в точках 2 и 4 и различаться только знаком. Действительно, подставляя в
формулу
на рис. 2. Наибольшие нормальные напряжения будут иметь
место в точках 2 и 4 и различаться только знаком. Действительно, подставляя в
формулу 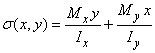 координаты точек 2 и
4, получаем:
координаты точек 2 и
4, получаем:
точка 2
![]() ;
;
точка 4
![]() .
.
Отложив в
удобном масштабе полученные величины напряжений, построим эпюру напряжений ![]() (рис. 2).
(рис. 2).
4. Определить значение полного прогиба в середине пролета балки и указать его направление. Полный прогиб (перемещение центра тяжести сечения С) вычисляем по формуле:
![]() ,
,
где ![]()
![]() - проекции
полного прогиба на главные оси. Эти величины можно определить методом
начальных параметров. Начало координат поместим на левом конце балки в точке А.
- проекции
полного прогиба на главные оси. Эти величины можно определить методом
начальных параметров. Начало координат поместим на левом конце балки в точке А.
Прогиб в плоскости x0z. Начальные параметры:
![]()
![]()
![]() кН.
кН.
Составим выражение прогибов fx (z) с помощью универсального уравнения упругой линии балки:
![]() . (1)
. (1)
Величину j0 определим из условия, что при fx (l) = 0. Подставляя в выражение (1) z = l = 4 м, получим:
![]() ;
;
![]() .
.
Окончательно выражение прогибов fx (z) будет иметь вид:
![]() . (2)
. (2)
Для определения прогиба в середине пролета подставим z = 0,5l = 2 м в выражение (2):
![]() кНм3.
кНм3.
Учитывая, что Е = 2×108 кН/м2 и Iy = 891×10-8 м4, получаем:
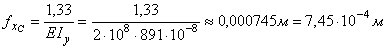 .
.
Прогиб в плоскости y0z. Начальные параметры:
![]()
![]()
![]() кН.
кН.
Выражение для прогибов fy (z) получаем с помощью метода начальных параметров:
![]() . (3)
. (3)
Подставляя z = l = 4 м в выражение (3) и учитывая, что в т. В прогиб равен нулю, получаем уравнение для определения ![]() :
:
![]() ,
,
откуда
![]() .
.
Окончательно выражение для прогибов fy (z) будет иметь вид:
![]() . (4)
. (4)
Для определения прогиба в середине пролета подставим z = 0,5 l = 2 м в выражение (4):
![]() ;
;
![]() .
.
Определим величину модуля вектора полного прогиба
![]()
![]() м.
м.
Направление
вектора полного прогиба показано на рис. 3. При этом,
угол ![]() определим по формуле:
определим по формуле:
 ;
; ![]() .
.

Рис.3
Пример 8.
Для консольной
двутавровой балки, загруженной горизонтальной силой F1
= 0,56 кН и вертикальной силой F2 = 5,84 кН
(рис. 1), построить эпюру нормальных напряжений в защемлении и найти максимальное нормальное напряжение ![]() .
.
![]()
![]()
![]()
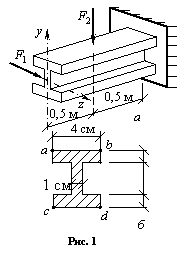
Решение.
Нормальные
напряжения определяем по формуле ![]() Подсчитаем
вначале величины изгибающих моментов в защемлении (по модулю):
Подсчитаем
вначале величины изгибающих моментов в защемлении (по модулю):
My =![]() = 560 Hм;
= 560 Hм;
Mz =![]() = 2920 Hм.
= 2920 Hм.
При этом момент Mz растягивает верхние волокна и сжимает нижние, а момент My растягивает левые волокна и сжимает правые.
Моменты инерции сечения, состоящего из прямоугольников, относительно осей z и y равны:
Iz = 116,67 см4 =![]()
Iy = 29,5 см4 =![]() .
.
Для построения эпюры нормальных напряжений вычисляем напряжения в угловых точках a, b, c, d (рис. 1, б). В точке а оба момента Mz и My вызывают растяжение, поэтому напряжение имеет величину:
![]()
В точке b момент Mz вызывает растяжение, а My – сжатие, поэтому
![]()
В точке с момент Mz вызывает сжатие, а My – растяжение, поэтому
![]()
В точке d оба момента Mz и My вызывают сжатие, поэтому

![]()
Определив
напряжения в угловых точках и зная, что нормальные напряжения изменяются по
закону плоскости, строим эпюру ![]() (рис. 2). Из эпюры
видно, что наибольшее нормальное напряжение
(рис. 2). Из эпюры
видно, что наибольшее нормальное напряжение ![]() = 138 МПа.
= 138 МПа.
Пример 9.
Для стальной
балки, лежащей на двух опорах и нагруженной силой F = 60 кН, лежащей в плоскости zy и
составляющей угол ![]() = 30o с
вертикальной осью y (рис. 1),
подобрать прямоугольное сечение при условии, что h = 2b, Ry = 160 МПа,
= 30o с
вертикальной осью y (рис. 1),
подобрать прямоугольное сечение при условии, что h = 2b, Ry = 160 МПа, ![]() = 1.
= 1.
![]()

Решение.
Разложив силу на две составляющие по главным осям сечения балки, определим опорные реакции, действующие в главных плоскостях, и построим эпюры изгибающих моментов Mz и My, рис. 2, а.
Наибольшие моменты действуют в среднем сечении, где
![]()
![]()
В этом сечении наибольшие нормальные напряжения возникают в точках а (растяжение) и b (сжатие), рис. 2, б. Для них условие прочности запишется так:
![]()
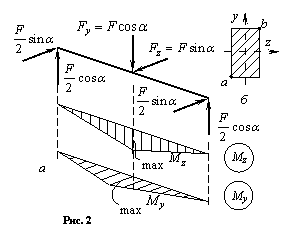
Вычисляем моменты сопротивления Wz и Wy при заданном соотношении высоты h и ширины b:
![]()
![]()
Подставляем в
условие прочности значения Mz , My
, Wz и Wy. В итоге
получим![]()
![]()
![]() ,
,
откуда ![]()
![]()
Онлайн-калькулятор "Косой изгиб, подбор сечения"
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов