Главная
Лекция
14 (продолжение). Метод конечных элементов
Содержание
Понятие о методе конечных элементов
Переход к общей системе координат
Объединение конечных элементов
Определение перемещений, усилий и
напряжений
Понятие о методе конечных элементов
Современная вычислительная техника позволяет проводить расчеты сооружений с более подробным описанием их внутренней структуры и с более точным учетом действующих нагрузок. Для этого разработаны специальные методы расчета, среди которых наибольшее распространение получил метод конечных элементов (МКЭ).
Метод конечных элементов – это метод расчета сооружений, основанный на рассмотрении сооружения как совокупности типовых элементов, называемых конечными элементами (КЭ).
В дискретном методе мы рассмотрели три типовых стержневых элементов, которые используются и в МКЭ как конечные элементы. Например, элемент 3-его типа в МКЭ называется ферменным (рис. 1,а), а 1-го типа – плоским стержневым конечным элементом (рис. 1,б). При расчете пространственных рам используется КЭ бруса (рис. 1,в). В расчетах плоских тел (плит или пластин) используются треугольный (рис. 1,г) или четырехугольный (рис. 1,д) конечные элементы. При расчете пространственных сооружений могут использоваться призменный КЭ (рис. 1,е) или тетраэдальный КЭ (рис. 1,ж) и др. Для расчета различных сооружений разработано множество других КЭ.
Рис. 1
МКЭ – дискретный метод. В этом методе сооружение делится на определенное число КЭ, соединенных между собой в узлах конечно-элементной модели. А нагрузка, действующая на сооружение, переносится в узлы. Это позволяет определять НДС сооружения через узловые усилия и перемещения конечно-элементной модели.
Как мы знаем, можно выбирать разные расчетные схемы сооружения. Но и в пределах одной расчетной схемы можно выбирать разные расчетные модели по МКЭ, потому что сооружение можно разбить не только на разное количество однотипных КЭ, но и представить его как комбинацию различных типов КЭ. С другой стороны, при расчете сооружения могут быть реализованы различные варианты МКЭ в формах метода сил, метода перемещений и смешанного метода. В настоящее время широкое распространение получил МКЭ в форме метода перемещений.
Вариационные основы МКЭ
При решении многих задач статики, динамики и устойчивости сооружений определяется их полная потенциальная энергия U:
U = W – V. (1)
Здесь W – работа внешних сил, V – работа внутренних сил. Обычно все они представляются в виде функций,
зависящих от перемещений, деформаций, напряжений элементов расчетной модели
сооружения.
Исследование этого выражения позволяет выявить важные
законы механики, называемые принципами. Например, в теоретической механике
известен принцип Лагранжа-Дирихле: для
того чтобы механическая система находилась в равновесии, ее полная
потенциальная энергия должна быть постоянной. Из этого принципа следует,
что приращение полной потенциальной энергии системы, находящейся в равновесии,
должно равняться нулю:
Вычисление приращения функции обычно заменяется
вычислением его приближенного значения − дифференциала. В этом случае
получается вариационное уравнение Лагранжа
где символ 
означает вариацию, вычисление
которого схоже с вычислением дифференциала функции. Это уравнение позволяет
свести задачу определения НДС сооружения к отысканию экстремума полной
потенциальной энергии.
С учетом (1) вариационное уравнение Лагранжа принимает
вид
Оно формулируется как принцип Лагранжа: вариация работы внутренних сил равна
вариации работы внешних сил.
Принцип Лагранжа используется для сведения континуальной
задачи расчета сооружений к дискретной задаче путем аппроксимации
(приближенного определения) непрерывных полей перемещений, деформаций,
напряжений внутри конечного элемента по его узловым перемещениям.
В строительной механике используются и другие
вариационные принципы, аналогичные принципу Лагранжа, такие как принципы Кастильяно, Рейсснера, Ху-Вашицу и др. Однако мы воспользуемся только вариационным
принципом Лагранжа как основой варианта МКЭ в форме метода перемещений.
Аппроксимация КЭ
Имея КЭ разного типа, при выборе конечно-элементной
модели сооружения можно вводить узлы с разным числом степеней свободы. Например,
в плоской системе могут рассматриваться узлы как с тремя степенями свободы
(рис. 2,а), так и с двумя (рис. 2,б) или даже с одной степенью свободы. В
первом случае учитываются два линейных (поступательных) и одно угловое
перемещение узла, во втором – два линейных перемещения, а в третьем −
лишь одно поступательное перемещение. В пространственной системе узлы могут
иметь шесть (рис.2, в) или три степени свободы (рис.2, г).
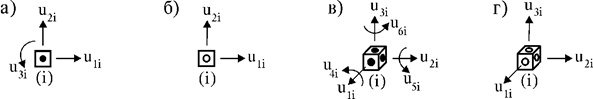
Рис.2
Для упорядочения степеней свободы и соответствующих
перемещений узлов КЭ все они нумеруются в определенном порядке и собираются в
общий вектор перемещений u.
Чтобы воспользоваться принципом Лагранжа, вводятся так
называемые координатные функции, аппроксимирующие непрерывное поле
перемещений внутри КЭ через перемещения ее узлов:
Здесь 
– вектор перемещений внутренних точек КЭ,
C – матрица координатных функций,
– вектор коэффициентов. Элементы
матрицы C выбираются в виде
полиномов, непрерывных внутри КЭ. Если в полиноме учитывается минимальное число
членов, то такой КЭ называется симплекс-элементом.
При учете большего числа членов полинома КЭ называется комплекс-элементом.
В качестве простейшего примера рассмотрим ферменный КЭ с
узлами i и j (рис. 3, а) в местной системе координат 
. Его узлы имеют по одной поступательной степени свободы по оси и соответствующие им узловые
перемещения 
и 
. Допустим, что в узлах КЭ приложены силы 
и 
(рис. 3, б).
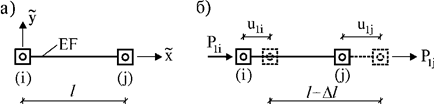
Рис. 3
Перемещения внутренних точек элемента будем аппроксимировать
полиномом первой степени
Запишем его в матричной форме:
где 
называется матрицей координатных функций, а 
является вектором неизвестных коэффициентов.
Подставив 
и 
в наш полином, получим два равенства:
С другой стороны, 
и 
(рис. 3, б). Учитывая их,
предыдущие равенства перепишем так:
Тогда их можно записать в матричной форме
и представить как матричное уравнение
связывающее вектор узловых перемещений 
и вектор координат 
через представленную выше матрицу Ф.
Определим вектор :
Тогда
или
Входящая сюда матрица 
называется матрицей форм. Она
позволяет аппроксимировать поле перемещений внутренних точек КЭ через
перемещения узлов.
По аналогии с перемещениями поле внутренних усилий 
в КЭ можно аппроксимировать через вектор узловых сил P по формуле
Например, для рассмотренного КЭ имеем
Матрица жесткости КЭ
Известные в механике
геометрические и физические соотношения для континуальных систем можно записать
в виде, аналогичном рассмотренным ранее
уравнениям дискретного подхода. Например,
для дискретной системы:
для континуальной системы:
Здесь 
и 
– вектора деформаций и напряжений, а
и 
– матрицы
равновесия и податливости континуальной системы. В отличие от дискретного подхода,
уравнения континуального подхода удовлетворяются во всех точках системы.
При рассмотрении конечного элемента как континуальной
системы принцип Лагранжа 
можно записать в виде
где левая и правая части представляют возможные работы
внутренних и внешних сил, а интегрирование ведется по объему КЭ V.
После этого осуществляется переход к дискретной модели КЭ
с использованием матрицы форм H. Тогда после ряда преобразований получается матричное уравнение,
связывающее вектор узловых перемещений u с вектором узловых усилий P КЭ:
Ku=P,
в которой симметричная
квадратная матрица
называется матрицей жесткости конечного
элемента. Физический смысл элемента kij этой матрицы – это
реакция (реактивная сила), возникающая в i-ом
направлении от заданного
единичного перемещения в j-ом
направлении.
К примеру, для рассмотренного ферменного КЭ, находящегося
в одноосном напряженном состоянии, геометрическое уравнение будет 
. Сравнив его с матричным
уравнением 
, видим, что матрица равновесия является дифференциальным оператором с
одним членом, т.е. 
. Из уравнения связи между деформацией и напряжением 
видно, что матрица податливости
будет 
.
Для определения матрицы жесткости КЭ вычислим:
Интегрирование по объему V сводится к интегрированию по длине l КЭ, т.к. 
(F − площадь сечения КЭ). Тогда
При рассмотрении прямоугольного
КЭ толщиной t и размерами 2a и 2b
с четырьмя узлами i, j, k, m и восемью узловыми перемещениями (рис. 4), матрица
жесткости будет иметь размеры 8
8.
Рис. 4
Для краткости записи матрицу жесткости этого КЭ можно
представить в блочной форме с 16 блоками одинаковой размерности 22:
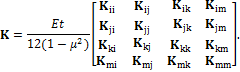
Здесь 
– коэффициент Пуассона. Элементы каждого блока
матрицы K определяются по разным формулам. Например,
Перенос нагрузки в узлы
В расчетной модели сооружения по МКЭ нагрузка должна быть
приложена только в узлах. Поэтому действующую на систему внеузловую
нагрузку необходимо переносить в узлы.
Порядок переноса нагрузки в узлы расчетной модели в
простых случаях остается таким же как и ранее.
Например, в стержневых системах используется таблица метода перемещений.
Если к прямоугольному КЭ
действует изменяющаяся по линейному закону распределенная нагрузка
(рис. 5, а), то узловые силы (рис. 5, б) определяются по
формулам
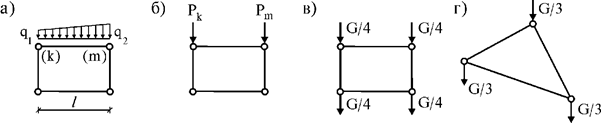
Рис. 5
При переносе объемной нагрузки, например собственного веса четырехугольного КЭ, в каждый узел нужно прикладывать четвертую часть его веса G (рис. 5, в). При переносе собственного веса треугольного КЭ в каждый узел прикладывается его третья часть (рис. 5, г).
В общем случае вектор узловой нагрузки определяется по формуле
Переход к общей системе координат
Каждый КЭ в МКЭ вначале
рассматривается в местной системе координат. Затем осуществляется переход к
глобальной (общей) системе координат. Рассмотрим порядок такого перехода.
Пусть
некоторый узел i в местной системе
координат 
имеет перемещения 
,
которые следует преобразовать в перемещения узла 
в общей системе координат x-y (рис. 15.2 а).
Поворот координатных осей осуществляется с помощью матрицы преобразования координат. Для плоской системы она имеет вид
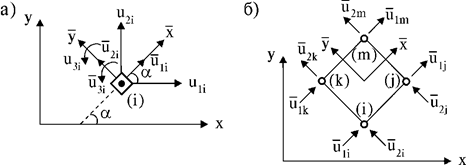
Рис. 6
Если координатные системы ортогональны и поворот осуществляется на угол α, то
Для шарнирного узла с двумя степенями свободы
Эти матрицы позволяют использовать матрицы и вектора
геометрических и жесткостных характеристик КЭ,
полученных в местной системе координат, для получения соответствующих
характеристик КЭ в общей системе координат. Например, преобразование вектора
координат прямоугольного КЭ с четырьмя шарнирными узлами i-j-k-m (рис. 6, б), рассматриваемого в местной системе координат 
, в общую систему координат x-y осуществляет матрица
.
Блоки 
этой матрицы имеют вид (2). Имея матрицу
жесткости КЭ 
в местной системе координат, можно определять
ее матрицу жесткости в общей системе координат по формуле
Объединение конечных элементов
Пусть в расчетной модели сооружения имеется m КЭ
и n узлов, а вектора ее перемещений и
узловых нагрузок определены так:
После построения матриц жесткостей всех конечных элементов
и определения
векторов узловых нагрузок 
в общей системе
координат следует сформировать матрицу жесткости и вектор нагрузки всего
сооружения. Это можно проделать так.
Вначале матрицы жесткости всех КЭов
собираются в единую диагональную матрицу 
, а вектора узловых нагрузок − в единый вектор 
:
Они еще не учитывают связи между соседними конечными
элементами в узлах их примыкания.
Для объединения КЭов в
единую систему используется энергетический принцип: энергия конечно-элементной модели системы
равняется сумме энергий всех ее КЭ. В этом случае матрица жесткости
объединенной системы будет определяться по формуле
где Г –
объединяющая матрица. Элементы этой матрицы состоят только из нулей и единиц, а
отдельные ее блоки соответствуют узлам КЭ и строятся по принципу: если КЭ
содержит данный узел, то записывается единичная матрица, если нет – нулевая
матрица. А соответствующие узловые нагрузки будут объединяться по формуле
Однако получение матрицы жесткости K и вектора
нагрузки P таким способом
требует больших вычислительных затрат. Задача упрощается, если составить так
называемую матрицу индексов, определяющую соответствие номеров узловых
перемещений КЭов узловым перемещениям всей модели.
Тогда матрицу жесткости K можно
получать рассылкой в ее блоки отдельных блоков матриц жесткостей КЭов по информации, заключенной в матрице индексов. При
этом рассылка идет с суммированием рассылаемого блока матрицы жесткости КЭ с
имеющимся блоком в матрице K. Такой метод называется методом сложения жесткостей.
Вектор узловой нагрузки P
формируется аналогично.
В результате этих действий формируется разрешающее
уравнение МКЭ, по виду совпадающее с уравнением МКЭ для
отдельного КЭ:
Ku=P .
Но уже здесь K
и P − матрица жесткости и
вектор нагрузки всей системы. Матрицу K
часто называют глобальной матрицей жесткости.
Учет граничных условий
Разрешающее уравнение МКЭ нельзя сразу решить
относительно перемещений u. Причина
в том, что при его составлении не учтены граничные условия закрепления
сооружения в опорах. Поэтому матрица жесткости K является вырожденной (т.е. ее определитель равняется нулю). Чтобы
выйти из положения, вектор перемещений приходится делить на две части – на
перемещения по закрепленным (з) и незакрепленным (н) направлениям:
Так как опоры сооружения обычно бывают достаточно
жесткими, их перемещения можно принять равными нулю (
), а нагрузку, приходящуюся на опоры, не учитывать. В
таком случае разрешающее уравнение преобразуется в уравнение меньшего размера.
Однако такая процедура существенно меняет структуру матрицы жесткости K и усложняет дальнейшее решение.
Поэтому используется другой прием: все элементы строк
и столбцов матрицы жесткости, соответствующие закреплениям, приравниваются
нулю, и лишь вместо их диагональных элементов ставятся единицы. В таком случае
разрешающее уравнение упрощается без нарушения ее структуры и принимает вид:
Здесь
E −
единичная матрица, 
и 
− блоки
матрицы жесткости и вектора нагрузки, соответствующие незакрепленным
направлениям.
Определение перемещений, усилий и напряжений
После решения разрешающего уравнения и определения
вектора узловых перемещений u из
этого вектора можно выбирать перемещения отдельных КЭов
и определять перемещения в интересующих точках любого i-го КЭ по формуле
Усилия в узлах и напряжения внутри КЭов
вычисляются по формулам
В конкретных случаях последнюю формулу можно
упростить. Например, напряжения ферменного элемента определяются так:
Порядок расчета МКЭ
В настоящее время разработаны вычислительные
комплексы, позволяющие рассчитывать на компьютере сложные и разнообразные
сооружения на различные воздействия. К таким относятся расчетные комплексы
NASTRAN, ANSIS, ЛИРА, СУМРАК и др.
Эти расчетные комплексы рассчитаны на использование
мощных компьютеров, разнообразной вспомогательной аппаратуры, сложных
компьютерных программ. Они состоят из трех основных частей:
1. Препроцессор
– предназначен для подготовки и ввода исходных данных в компьютер. Используется
для формирования расчетной модели сооружения (автоматического разбиения на КЭ
по задаваемой сетке), определения координат узлов, геометрических и физических
характеристик КЭов, проверки правильности и полноты
исходных данных. Дает возможность обзора расчетной модели в разных ракурсах на
мониторе.
2. Процессор
– блок математического расчета МКЭ. Входящие в него компьютерные программы
предназначены для: составления и решения разрешающего уравнения; вычисления
перемещений и деформаций, внутренних усилий и напряжений; проверки на прочность
и жесткость; решения задач динамики и устойчивости.
3. Постпроцессор – предназначен для обработки результатов расчета,
представления их в виде эпюр, в удобной для анализа табличной, графической и
анимационной формах.
Алгоритм расчета сооружений МКЭ состоит из следующих основных этапов:
1. Выбор расчетной модели.
2. Перенос нагрузки в узлы.
3. Определение матриц жесткостей КЭов.
4. Перевод матриц жесткостей КЭов
в общую систему координат.
5. Сборка глобальной матрицы жесткости K.
6. Учет граничных условий.
7. Решение разрешающего уравнения Ku=P.
8. Вычисление внутренних усилий.
9. Обработка результатов расчета.
Примеры расчета по методу конечных элементов
Заданную конструкцию (раму, ферму и т.д.) разобьем на
отдельные элементы (желательно простые – прямой стержень; участок стержня и т.
д.). Элементы определяются самим расчетчиком. Попробуем проделать это на
отдельных конструкциях.
Пример 1 (рис.7).
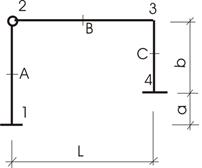
Рис.7
Можно:
1) Выделить три элемента: 1 – 2; 2 – 3; 3 – 4 (рис. 8).
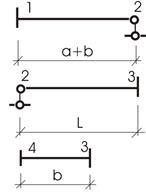
Рис.8
2) 6 элементов: 1 – А; А – 2; 2 – В; В – 3; 3 – С; С – 4 и т. д.
Если мы учтем одно из правил изменения внутренних усилий, а именно: на незагруженном участке внутренние усилия меняются по линейному закону, то это позволит нам при распределении внешней нагрузки в узлы конструкции использовать конечные элементы в виде стержней, соединяющихся в узлах.
Распределение внешней нагрузки разберем ниже.
Пример 2 (рис. 9).
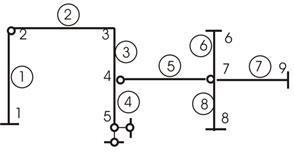
Рис.9
Пронумеруем узлы. Пронумеруем элементы (они обозначены цифрой в кружочках). Выделим их отдельно (рис. 10).
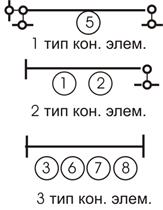
Рис.10
При узловой нагрузке в этих элементах будут возникать внутренние усилия:
- в первом элементе возникает только продольное усилие (рис. 11,а).
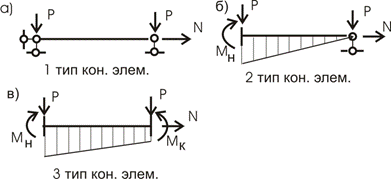
Рис.11
- во втором (рис. 11,б) и третьем (рис. 11,в) элементах, помимо продольного усилия, в заделках возникает изгибающий момент и он вызывает перерезывающую силу – Q.
Примем правило:
- меньший номер при нумерации узлов будем считать началом – «н», а больший номер – концом – «к» стержня;
- изгибающий момент будем направлять так, чтобы он растягивал нижние волокна.
Из рассуждений видим, что в каждом элементе возникают неизвестные силы:
- продольное усилие;
- изгибающий момент.
Перерезывающую силу можем представить (выразить) через изгибающий момент. Такой подход снижает количество неизвестных.
Определив характер неизвестных, сформируем порядок их определения.
Обратимся к примеру.
Пример 3 (рис. 12).
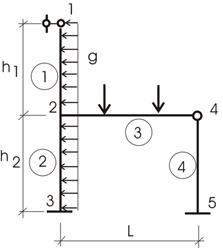
Рис.12
1. Пронумеруем узлы в произвольном порядке.
2. Жесткое соединение стержней обозначим заделкой (можно и другим способом), подобно методу перемещений (делается это для наглядности).
3. Нумеруем элементы (в произвольном порядке). Номер элемента обведем в кружочек.
4. Нагрузку, действующую на элемент, распределяем на его узлы.
Элемент 1 (рис. 13). Строим эпюру изгибающих моментов и определяем опорные реакции. Можем воспользоваться схемами метода перемещений. Исходя из решения, получаем узловую нагрузку на элемент.
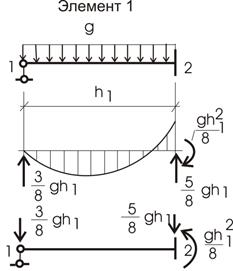
Рис.13
Элемент 2. Нагрузка на элемент показана на рисунке 14.
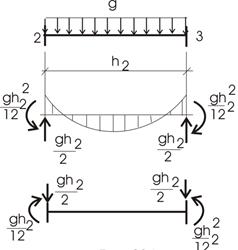
Рис.14
Элемент 3 (рис. 15).
Если табличных решений нет, данную балку можем решить одним из рассмотренных выше способов.
Воспользуемся уравнением 3-х моментов неразрезной балки:
Опорные реакции обозначены на рисунке 15.
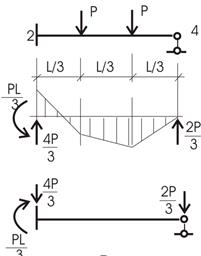
Рис.15
Отсутствие нагрузки на элементе 4 дает нулевую нагрузку на его узлы. Полученная узловая нагрузка для каждого элемента дает общую схему нагружения конструкции в целом (рис. 236).
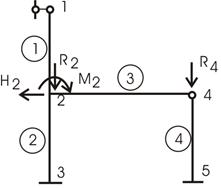
Рис.16
Для наглядности дальнейших расчетов вычертим эпюры неизвестных изгибающих моментов и продольных усилий согласно принятым нами правилам (рис. 17,а,б).
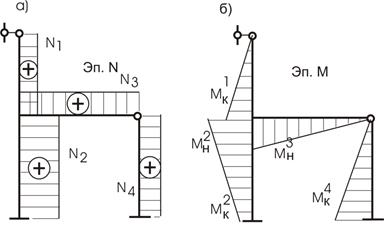
Рис.17
По этим эпюрам мы легко просчитаем количество неизвестных и составим матрицу-столбец неизвестных усилий (представим матрицу усилий в виде матрицы-строки):
где Ni – продольное усилие в i – ом элементе; 
и 
- изгибающие моменты в начале (н) и конце (к) i-го элемента.
Связь между усилиями и внешней нагрузкой
осуществляется посредством уравнений равновесия. Для этого воспользуемся
вырезанием узлов (в любой последовательности). При составлении уравнений
равновесия примем правила:
- ось х направим вправо;
- ось y направим вверх;
- изгибающий момент положительный, если он направлен относительно узла против часовой стрелки (рис. 18).
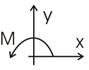
Рис.18
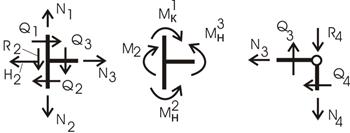
Рис.19
Вырезаем узел 2 (рис. 19). Моменты и линейные усилия (N и Q) представим для наглядности на отдельных рисунках.
Перерезывающие силы выразим через изгибающие моменты
Перепишем уравнения равновесия, перенеся грузовые слагаемые в правую часть
Вырезаем узел 4 (рис. 19 справа).
Тогда после подстановки Q4 и Q3 уравнения (а), (б) примут вид:
Полученные уравнения равновесия позволяют сформировать матрицу равновесия А из коэффициентов при неизвестных и матрицу Р – вектора нагрузки, а именно:
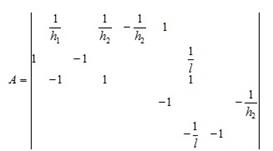
Количество строк матрицы соответствует количеству уравнений равновесия, а количество столбцов – количеству неизвестных. И если количество столбцов больше количества строк (прямоугольная матрица), то это говорит о статически неопределимой задаче. Вектор нагрузки (в виде матрицы-строки) запишется:
Тогда уравнения равновесия запишутся в матричной
форме:
Для решения статически неопределимой задачи, как мы
знаем, потребуются уравнения совместности деформации.
Раскроем их физическую суть.
Нужно помнить, что каждому виду воздействия (усилию) соответствует свой вид деформации, и для упругих систем запишем:
где В – коэффициент пропорциональности, назовем его коэффициентом податливости. Поскольку перерезывающая сила отсутствует в списке неизвестных, мы о ней говорить больше не будем.
Выявим физическую суть коэффициента податливости для
продольного усилия.
Рассмотрим 1 тип конечного элемента (рис. 20):
Загрузим данный элемент силой N=1 и вычислим перемещение точки приложения N=1 по ее направлению по формуле Мора
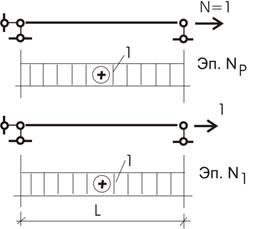
Рис.20
Тогда общее уравнение (перемещение) от силы N запишется:
или коэффициент податливости
Для элемента второго типа, кроме загружения силой N=1 (результат нам уже известен) нужно загрузить жесткий узел моментом M=1 и определить от этой нагрузки угол поворота заделки по данному направлению (рис. 21).
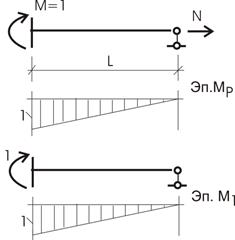
Рис.21
Тогда
или
Учитывая, что данный элемент подвергается воздействию
двух усилий, общий коэффициент податливости (он уже будет представлять
диагональную матрицу второго порядка) примет вид:
В матрице податливости элемента ноль в первой строке указывает на то, что продольное усилие (N) не вызывает поворота в заделке, а ноль во второй строке указывает, что изгибающий момент не вызывает продольного удлинения стержня.
Третий тип элемента (рис. 22).
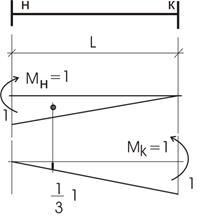
Рис.22
Элемент подвергается трем воздействиям: N – продольной силой, Мн и Мк – изгибающими моментами в начале (н) и конце (к) элемента. Матрица податливости В для данного элемента будет третьего порядка, а именно:
где 
- продольное перемещение от N=1 и равно 
;
нули в первой строке указывают на то, что продольная сила не вызывает поворота ни
в начале, ни в конце элемента; 
- угол поворота начала (н) элемента от 
,
и он будет равен, как и у элемента 2-го типа 
;
- угол поворота конца (к) элемента от
воздействия ,
и 
- угол поворота начала (н) элемента от воздействия
.
Нужно отметить, 
- угол поворота конца
(к) элемента от .
Тогда матрица
податливости для 3-го типа элемента запишется:
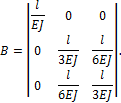
Матрица податливости конструкции в целом будет
представлять собой совокупность матриц податливости отдельных элементов,
расположенных по диагонали:
где n – количество конечных элементов; i – порядковый номер элемента.
Остальные
элементы матрицы податливости конструкции равны нулю, что означает: воздействие
усилий i-го
конечного элемента не вызывает перемещений в других конечных элементах.
Матрица податливости для рассматриваемой рамы представится:
.
Общая зависимость перемещений и усилий для конструкции в целом представится в виде:
где 
- матрица-столбец перемещений узлов
конструкции (не учитывая опорные узлы);
- матрица-столбец усилий, которую мы разобрали
выше.
Выясним
структуру матрицы перемещений -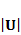 
.
Поскольку конечные элементы, сходящиеся в один узел,
имеют одинаковые перемещения, ограничимся только перемещениями узлов.
Шарнирный узел имеет возможность перемещаться только линейно: по горизонтали и вертикали, а жесткий узел еще имеет и угол поворота.
Примем правило (рис. 23):
- горизонтальное перемещение будем считать первым (1) направлением;
- вертикальное перемещение – вторым направлением;
- угол поворота – третьим направлением.
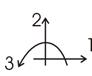
Рис.23
Стрелочки
указывают на положительное направление перемещений. Тогда вектор перемещений 
примет вид:
где у 
- первый индекс указывает на номер узла, а
второй индекс – на номер перемещения.
Для рассматриваемой рамы вектор перемещения запишется
(в виде матрицы-строки)
Подведем итог нашим рассуждениям:
Получили 2 группы уравнений:
- уравнения равновесия (геометрические уравнения)
- уравнения совместности деформации (физические уравнения)
Из второй группы уравнений находим усилия
где 
- обратная матрица податливости, которая
названа матрицей жесткости конструкции, т. е.
тогда выражение для усилий перепишется:
Подставим выражения для усилий в первую группу уравнений, получим:
откуда находим перемещения узлов
а затем и усилия – S.
Пример 4 (рис. 24).
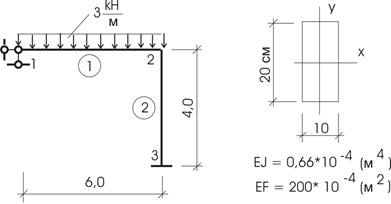
Рис.24
1. Расчетная модель получена введением жесткой связи в узел 2, пронумеровав узлы слева направо и вниз. Получаем 2 участка.
2. Перенесем внешнюю нагрузку в узлы рамы (по схеме рис. 25).
Рис.25
3. Строим схему загружения рамы.
4. Представляем эпюры внутренних расчетных усилий.
По ним составляем вектор внутренних усилий (представим его в виде строки)
5. Составляем уравнения равновесия, вырезая узел 2 из представленной рамы (рис.26).
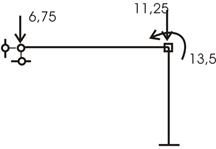
Рис.26
или
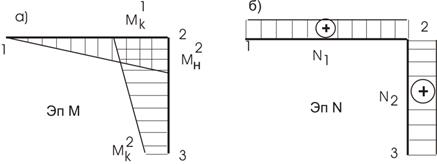
Рис.27
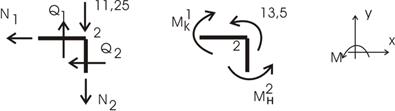
Рис.28
Матрица равновесия представится в виде
Вектор нагрузки (запишем строкой)
6. Составляем вектор перемещений
и матрицу
податливости
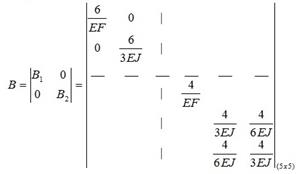
Умножим равенство на EF, подставим значения, получим
Используя программу расчета, все параметры, Р, А, В вносим в компьютер и получаем:
а) величину усилий
Построим эпюры полученных усилий: для Nрасч (рис. 29,а) и если эпюру N мы получаем в окончательном виде, то для эпюры Мок нужно к полученной эпюре Мрасч. (рис. 29,б) добавить эпюры на конечных элементах из МР (рис. 29,в). Эпюра Мок представлена на рисунке 29,г.
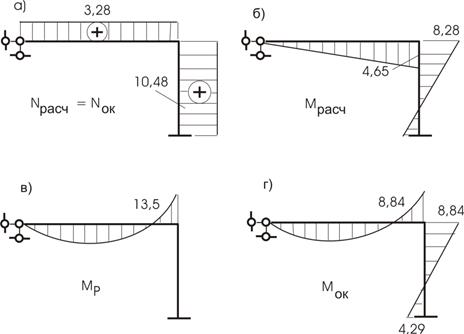
Рис.29
Остается построить эпюру Qок. по эпюре Мок, как это мы делали в методе перемещений (рис. 30).
Рис.30
б) величину перемещений:
u21=20,20/EF;
u22=42,11/EF;
u23=2730/EF.
По этим данным при необходимости строится деформированная схема конструкции (рамы).
Вопросы для самопроверки
- Перечислите основные современные численные методы расчета конструкций.
- В чем суть (основная идея) метода конечных элементов?
- Что такое дискретизация расчетной области конструкции при расчете МКЭ?
- В чем суть дискретной модели рассчитываемой конструкции по МКЭ?
- Перечислите основные шаги общего алгоритма статического расчета по МКЭ?
- Конечные элементы, их типы. Степени свободы конечного элемента. Конечно-элементная расчетная схема. Приведение нагрузки на систему к узловой.
- Матрица жесткости конечного элемента. Ее структура. Связь между перемещениями узлов элемента и усилиями, действующими на них.
- Дайте определение числовой матрице.
- Какая матрица называется квадратной, прямоугольной, единичной, матрицей-вектором?
- Как складываются, вычитаются и перемножаются матрицы?
- Что такое обратная матрица и для чего она используется?
- Каков смысл коэффициентов матрицы влияния изгибающих моментов?
- По каким формулам вычисляются элементы матрицы жесткости конечного элемента?
- По каким формулам вычисляются элементы матрицы геометрической жесткости конечного элемента?
- По каким формулам вычисляются элементы матрицы масс конечного элемента?
- Сформулируйте метод разложения по собственным формам?
- Собственные формы какой матрицы участвуют в расчетах?
- Как определяются функции матриц?
- Преобразование матрицы жесткости конечного элемента при повороте координатных осей.
- Матрица жесткости системы конечных элементов. Ее структура. Связь между перемещениями узлов конечно-элементной схемы и усилиями, действующими на них.
- Векторы перемещений и усилий, действующих на элемент. Векторы перемещений и усилий, действующих и на систему элементов, их структура и связь между собой.
- Соединение конечных элементов. Условие равновесия узлов в конечно-элементной схеме. Формирование системы разрешающих уравнений метода конечных элементов.
- Формирование глобальной матрицы жесткости конечно-элементной схемы из матриц жесткости конечных элементов.
- Определение внутренних усилий в стержневых конечных элементах после нахождения узловых перемещений в конечно-элементной схеме. Учет направленности осей местной системы координат конечного элемента по отношении к глобальной системе осей координат конечно-элементной схемы.
- Учет связей и заданных узловых перемещений в системе разрешающих уравнений метода конечных элементов.
- На какие элементы делится плита при её расчёте методом конечных элементов?
- Зависимость между какими величинами представляет в методе конечных элементов матрица жесткости отдельного элемента?
- Общая процедура расчета стержневых систем методом конечных элементов в форме метода перемещений. Реализация алгоритма МКЭ в современных программных комплексах.
- Препроцессор, процессор, постпроцессор, библиотеки конечных элементов.
- Сформулируйте в матричной форме решение задачи определения перемещений для произвольного силового воздействия?
- Сформулируйте в матричной форме решение задачи определения внутренних сил для произвольного силового воздействия?
- Сформулируйте в матричной форме решение задачи определения перемещений для гармонического воздействия?
- Сформулируйте в матричной форме решение задачи определения внутренних сил для гармонического воздействия?
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
