Главная

Лекция 14 (продолжение). Расчет статически неопределимых неразрезных балок

Содержание

Основные понятия

Частный случай метода сил - уравнение трех моментов

Построение эпюры моментов по моментно-фокусным отношениям

Вопросы для самопроверки

Основные понятия

Рассмотренный в предыдущей главе данной лекции метод сил применим к расчету многих стержневых систем, имеющих большое практическое применение и прежде всего к расчету многопролетных балок, арок и ферм. Основная система метода сил, связанная с выбором статически определимой основной системы и устранением противоречий между основной и заданной системами, полностью сохраняется и в расчете всех рассмотренных в этой главе расчетных схем. Однако в каждом расчете есть некоторая особенность, которую нужно знать.

Неразрезной называется непрерывная статически неопределимая балка, перекрывающая несколько пролетов (не менее 2) и проходящая над всеми промежуточными опорами, с которыми она соединена шарнирно. Крайние опоры могут быть или шарнирными, или защемленными (рис.1). В первом случае (рис.1, а) при действии вертикальной нагрузки горизонтальная реакция в неподвижной опоре равна нулю, и потому число лишних вертикальных реакций (и степень статической неопределимости) будет равно числу промежуточных опор. Во втором случае (рис.1, б) степень статической неопределимости равна числу шарнирных опор.

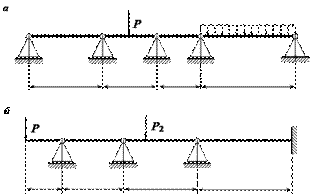
Рис.1. Типы неразрезных балок с край ними шарнирными опорами (а)

и жестким защемлением (б)

Неразрезные балки конструируют таким образом, чтобы были исключены вероятности отрыва балки от опор.

Следует отметить одно из важных свойств неразрезных балок – при нагружении одного пролета балка изогнется на протяжении всех пролетов (рис. 2).

Рис.2

Неразрезные балки нашли широкое применение в металлических, железобетонных и деревянных конструкциях в качестве основного элемента или части конструкции, например, в мостовых конструкциях, элементы стропильных систем, подкрановые балки.

Рассмотрим неразрезную балку (рис.3). Балка нагружена сосредоточенной силой P и имеет четыре опоры: крайняя левая опора жесткая, три остальные опоры шарнирно подвижные. Степень статической неопределимости балки равна n=3 и может быть определена по формуле n=С-3.

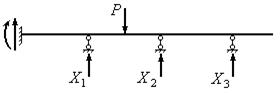
Рис.3

Решая эту задачу в традиционном плане, было бы естественным взять в качестве “лишних” связей неизвестные реакции и . Однако, традиционное решение задачи путем отбрасывания внешних связей оказывается при расчете неразрезных балок весьма громоздким. В связи с этим обычно такие задачи решают путем врезания шарниров в тело балки таким образом, чтобы при этом балка была статически определимой и оставалась геометрически неизменяемой. Вариант основной системы в такой постановке приведен на рис.4.

Рис.4. Вариант основной системы

Шарниры можно врезать в любом месте балки при условии ее геометрической неизменяемости. Но проще врезать шарниры на промежуточных опорах. В результате мы получаем статически определимую (разрезную) балку, состоящую из нескольких независимых друг от друга балок. В качестве “лишних” неизвестных при этом принимаются внутренние опорные моменты. Вид эквивалентной системы представлен на рис.5.

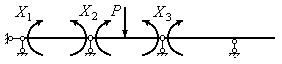
Рис.5. Эквивалентная система

Смысл канонических уравнений метода сил при таком выборе основной системы принципиально меняется. Если в прежней постановке идея метода сил состояла в определении перемещений в месте отброшенных связей и приравниванию этих перемещений нулю, то при расчете неразрезных балок такой подход не годится. Исходя из энергетической природы метода Мора, момент может совершать работу только на угле поворота сечения. Но углы поворота сечений, в которых приложены опорные моменты, кроме крайнего левого, в процессе деформации не равны нулю. А вот взаимные углы поворота двух прилегающих к опоре сечений на опоре, где поставлен шарнир, равны нулю (рис.6).

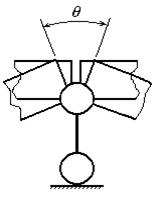
Рис.6

В этом и состоит физический смысл системы канонических уравнений метода сил при расчете неразрезных балок.

Частный случай метода сил - уравнение трех моментов

Рассмотрим общий случай расчета неразрезной балки.

Примем некоторые правила:

- пролет балки (расстояние между соседними опорами, рис. 7) будем именовать по номеру правой опоры;

Рис.7

- нумерацию опор производим слева направо, начиная с нуля.

Степень статической неопределимости будем подсчитывать по упрощенному выражению

Основная система для неразрезной балки получается однозначно путем введения шарниров на опорах (рис. 8), что определяет в качестве неизвестных обобщенные изгибающие моменты на опорах. Направление их возьмем из предположения, что они растягивают нижние волокна. При такой основной системе единичные изгибающие моменты и не будут вызывать перемещений на опоре i (угол поворота на опоре i, рис. 8,а).

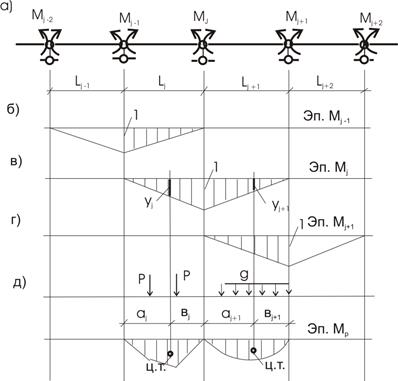
Рис.8

Это позволяет упростить систему канонических уравнений:

Рассмотрим подробно одно общее уравнение системы, состоящее из 3-х моментов; скажем,для опоры i-ой

Вычислим значения коэффициентов перемножением эпюр (рис. 8,б,в,г):

Грузовое слагаемое:

Из подобия треугольников ординаты y_i и y_i+1 определяются:

Подставим значения ординат в выражение :

Нетрудно убедиться, что выражения и есть опорные реакции при загружении пролетов фиктивной нагрузкой по характеру и значениям, равным изгибающим моментам от внешней нагрузки в соответствующих пролетах, а именно (рис. 8,д).

Определим реакцию i - го пролета (рис. 9,а):

Аналогично находим (рис. 9,б):

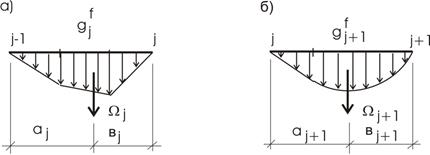
Рис.9

Подставим все полученные значения в уравнение

Произведем преобразования:

- умножим уравнение на ;

- введем обозначение

- проведенная длина i – го пролета, где J₀ – произвольный момент инерции.

Преобразования дают уравнение в виде:

Это и есть уравнение трех моментов для неразрезной балки постоянного сечения. В уравнение входят три момента на трёх соседних опорах, поэтому оно носит название «уравнение трёх моментов». В этом уравнении неизвестными являются изгибающие моменты на опорах. Если у неразрезной балки все опоры шарнирные, то таких уравнений можно составить столько, сколько у балки промежуточных опор.

Имея систему канонических уравнений метода сил в форме (1), нет необходимости строить единичные эпюры.

Из анализа уравнения 3–х моментов следует:

– неразрезные балки из разных материалов испытывают одни и те же усилия при прочих равных условиях работы;

– опорные моменты зависят не от абсолютных значений моментов инерции, а от их соотношений в пролетах, тем самым наглядно подтверждается свойство статически неопределимых систем о перераспределении внутренних усилий пропорционально жесткостям стержней.

Порядок расчета неразрезной балки на постоянную нагрузку.

1. Определяют степень статической неопределимости

2. Записывают столько уравнений трех моментов сколько неизвестных опорных моментов есть в решаемой задаче. Для этого в общее уравнение (1) поочередно подставляют номер опоры, для которой составляется уравнение.

3. Строят грузовую эпюру М_Р и вычисляют .

Каждый нагруженный пролет рассматривается как балка на двух шарнирных опорах.

Для вычисления грузовых членов нужно уметь вычислять площади эпюр. Для симметричных эпюр это не составляет труда. Полезно знать, где лежит центр тяжести несимметричной треугольной эпюры моментов.

Если крайние пролеты неразрезной балки имеют нагруженные консоли, то изгибающие моменты на этих опорах определяются сразу по определению изгибающего момента.

4. Решают систему уравнений (1) , находят неизвестные моменты в опорных сечениях.

5. Строят эпюру изгибающих моментов М в неразрезной балке.

Для этого откладывают на опорах в масштабе полученные опорные моменты и соединяют концы этих отрезков прямыми линиями. В пролетах, где нет внешней нагрузки, построенная эпюра моментов будет окончательной. Там, где задана нагрузка, на прямые линии "навешивают" балочные эпюры М_Р.

6. Используя формулу Журавского, по эпюре М строят эпюру поперечных сил Q.

Чтобы убедиться в правильности построения эпюр М и Q необходимо провести проверку равновесия неразрезной балки по уравнениям:

Замечание: При наличии на концах балки нагруженных консолей, изгибающие моменты на крайних опорах войдут в уравнение трех моментов, как известные величины, а при отсутствии консолей эти моменты будут равны 0.

Если конец неразрезной балки защемлен, то для применения уравнения (1) необходимо, отбросив заделку, ввести с ее стороны дополнительный пролет (рис.9.1). Такая система будет деформироваться также, как балка с жесткой заделкой.

Рис. 9.1

Пример 1.

Рассмотрим пример на рис. 10.

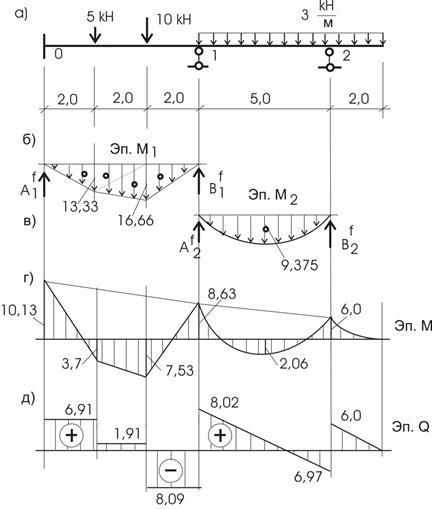
Рис.10

Решение.

В нашем примере неизвестные моменты М₀ и М₁.

Момент на опоре 2 вычисляется

Записываем уравнения для М₀ и М₁:

здесь при EJ – const , тогда

Определим фиктивные реакции.

Пролет 1 (рис. 10,б).

Пролет 2.

Учитывая симметричность загружения, можем обойтись без уравнения статики (рис. 10,в).

Полученные значения подставим в уравнения и произведем преобразования:

или

Зная моменты на опорах, строим эпюру опорных моментов. Окончательная эпюра М_ок строится как результат сложения М_оп с М_пр (рис. 10,г). Момент на консоли строится обычным путем. Уже известным приемом по М_ок строится Q (рис. 10,д).

Построение эпюры моментов по моментно-фокусным отношениям

Говоря о расчете неразрезных балок, остановимся на частном загружении, а именно загружении балки только в одном пролете. В этом случае эпюра изгибающих моментов строится по моментно-фокусным отношениям.

Было подмечено, что при загружении одного пролета (рис. 11) значения изгибающих моментов от загруженного пролета от опоры к опоре:

- затухают, становятся все меньщими;

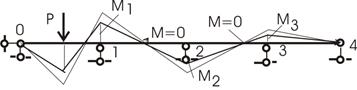
Рис.11

- имеют переменные знаки, а значит имеется точка в пролете, в котором M = 0;

- с ростом нагрузки увеличиваются опорные моменты пропорционально, при этом точка, в которой M = 0, не меняет своего положения.

Последнее обстоятельство позволило записать:

где k_i – коэффициент, который назван фокусным отношением. Различаются правые и левые фокусные отношения в зависимости от того, в какую сторону от загруженного пролета распространяются опорные моменты (в нашем примере правые фокусные отношения).

Для вычисления значения фокусных отношений рассмотрим i – ый пролет балки с нагрузкой, располагающейся где-то в пролете слева (рис. 12).

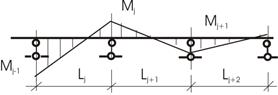
Рис.12

Запишем для M_i уравнение трех моментов:

Разделим уравнение на M_i

Как видно из рисунка,

Из этих выражений мы можем записать:

Значок «пр» у фокусного отношения означает, что вычисления ведем для правых фокусных отношений. Подставим полученные значения и в уравнение и получим:

Откуда и определим :

Приведя подобные, получим:

Аналогично произведя преобразования, получим выражение для левых фокусных отношений (рис. 13):

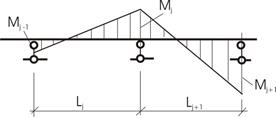
Рис.13

Как видно из полученных выражений, вычисления фокусных отношений приведут нас к началу (левые фокусные отношения) или к концу балки (правые фокусные отношения).

Начальное или конечное опирания могут быть: шарнирным опиранием или заделкой.

Шарнирное опирание (рис.14)

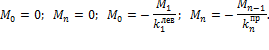
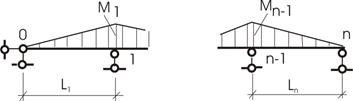
Рис.14

Заделка (рис.15,а).

Заделку можем представить с нулевым пролетом (рис. 15,б), тогда

где , тогда

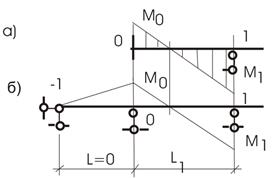
Рис.15

Выводы:

1. Ближайшее фокусное отношение у шарнирной опоры равно бесконечности.

2. Ближайшее фокусное отношение у опоры – заделки равно 2.

Пример 2.

Рассмотрим пример (рис. 16)

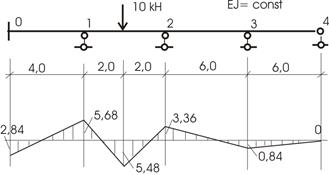
Рис.16

Решение.

Значения моментов на первой и второй опорах найдем, записав для них уравнения трех моментов:

Нужно определить фокусные отношения:

а) левые

б) правые

Подставим эти выражения в систему уравнений

Приведя подобные и решив систему уравнений, плучим :

Тогда

Эпюра моментов показана на рисунке 16.

Пример 3.

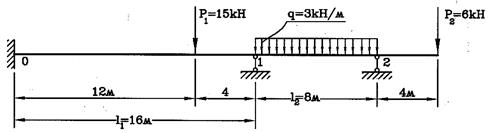
Определить реакции опор неразрезной балки, представленной на рис.17.

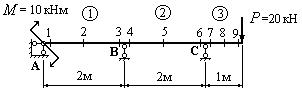
Рис.17

Решение.

1. Разобьем балку на участки и проставим на каждом участке “характерные” сечения (рис.17).

2. Определяем степень статической неопределимости: n=4-3=1.

3. Выбираем основную систему (рис.18).

Рис.18. Основная система

4. Изображаем эквивалентную систему (рис.19).

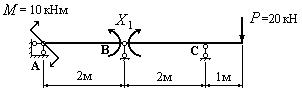
Рис.19. Эквивалентная система

Каноническое уравнение метода сил имеет вид:

Физический смысл этого уравнения – равенство нулю взаимного угла поворота двух, прилегающих к опоре В сечений, вызванного внешними силами и опорными моментами принятыми в качестве “лишней” неизвестной.

5. Изображаем грузовое состояние системы (рис.20,а) и строим эпюру грузовых изгибающих моментов (рис.20,б).

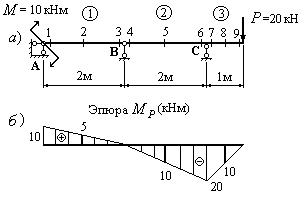
Рис.20

6. Изображаем единичное состояние системы (рис.21,а) и строим эпюру единичных изгибающих моментов (рис.21,б).

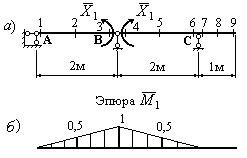
Рис.21

7. Используя формулу Симпсона, определяем грузовое перемещение и единичное перемещение , перемножая соответствующие эпюры изгибающих моментов:

8. Подставляя (б) и (в) в (а), находим :

9. Определяем суммарные изгибающие моменты в “характерных” сечениях путем сложения эпюр и строим суммарную эпюру изгибающих моментов (рис.22).

кНм;

кНм;

кНм;

кНм;

кНм;

кНм;

Рис.22. Суммарная эпюра изгибающих моментов

10. Вырезаем участки (рис.23), составляем уравнения равновесия, определяем значения поперечной силы и строим суммарную эпюру поперечных сил (рис.24).

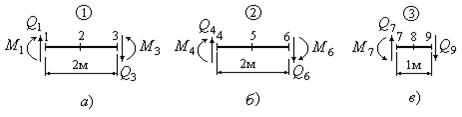
Рис.23

Составляем уравнение равновесия для участка №1:

Откуда:

Поперечная сила на участке будет постоянной, так как на участке отсутствует распределенная нагрузка. Поэтому при определении поперечной силы на участке достаточно составить только одно уравнения равновесия.

Составляем уравнение равновесия для участка №2:

Откуда:

Составляем уравнение равновесия для участка №3:

Откуда:

Строим суммарную эпюру поперечных сил (рис.24).

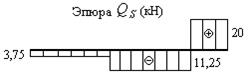
Рис.24. Эпюра суммарных поперечных сил

11. Пользуясь эпюрой поперечных сил (рис.24), определяем опорные реакции и проставляем их на рис.25.

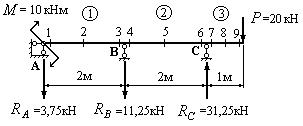
Рис.25. Опорные реакции неразрезной балки

Пример 4.

Требуется построить эпюры изгибающих моментов М и поперечных сил Q для балки, показанной на рис.26.

Рис.26

Решение.

Так как левый конец балки защемлен, то для применения уравнений трех моментов вводим дополнительный фиктивный пролет l₀=0 (рис.27).

Рис.27

В качестве основной выбирают систему разрезных балок, полученную из заданной системы врезкой шарниров над каждой опорой. За неизвестные принимают опорные изгибающие моменты М₀ и М₁ (рис.28).

Изгибающий момент на опоре 3 по определению равен М₃ = -64=-24 кНм, а М_-1=0

Рис.28

Неизвестные опорные моменты М₀ и М₁ находят из уравнений трех моментов (1), записанных для n = 0 и n = 1

Для n = 0

Для n =1

Для вычисления правых частей этих уравнений строим эпюры изгибающих моментов в каждом пролете от свой нагрузки как для балки на двух шарнирных опорах, в том числе и для балки с опорами 1 и 2. Эпюра на консоли строится отдельно (рис.29)

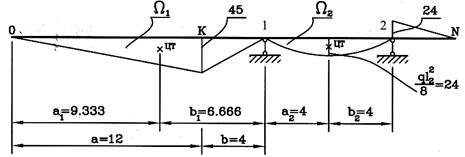
Рис.29

Подсчитываем площади, определяем положение центов тяжести эпюр на каждом участке и подставляем в (а).

Подставляя

После сокращений получаем систему уравнений

2M₀ + M₁ = - 56,25 (б)

M₀ + 3M₁ = - 90,75

Решая систему (б), находим опорные моменты

M₁=-25,05; M₀= - 15,6 (в)

Строят эпюру изгибающих моментов М (рис.2.9)

1. На опорах в удобном масштабе откладывают отрезки, равные по величине найденым и известным (М₁) значениям моментов.

2. Концы отрезков соединяют пунктирной линией.

3. На пунктирную линию в каждом пролете “навешивают” балочные эпюры М, построенные в основной системе на рис.29

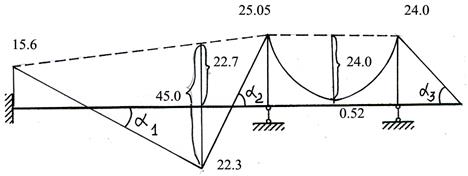
Рис.30

4. Убрав вспомогательные линии, необходимые для построения окончательной эпюры, получают график, показанный на рис.31.

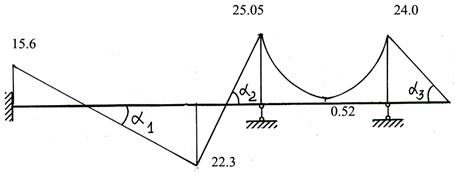
Рис.31

Строят эпюру поперечных сил Q (рис.32)

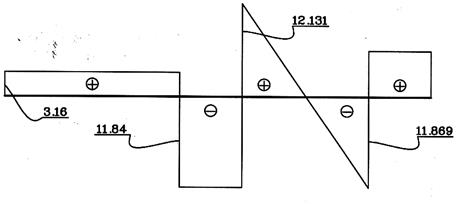
Рис.32

Вопросы для самопроверки

- Какую балку мы называем неразрезной?

- Как определить степень статической неопределимости неразрезной балки?

- Как выбирается основная система при расчете балки методом сил?

- Что принимают за основные неизвестные при расчете неразрезной балки?

- Каков физический смысл уравнения трех моментов?

- Каков порядок построения эпюры изгибающих моментов?

- Как проверить правильность эпюр М и Q?

- Как выбирается основная система при расчете неразрезных балок с помощью уравнения трех моментов.

- Общие сведения о неразрезных балках. Уравнение трёх моментов.

- Определение изгибающих моментов, поперечных сил и опорных реакций в неразрезных балках.

- Моментные фокусы и моментно-фокусные отношения.

- Применение моментно-фокусных отношений для построения эпюр.

- Огибающие эпюры усилий для неразрезных балок.

- Многопролетные неразрезные балки. Основная система Клапейрона. Формула трех моментов. Метод прогонки для решения системы разрешающих уравнений метода сил в этом случае.

- Случай загружения одного пролета в многопролетной неразрезной балке. Характерный вид эпюр для этого случая. Фокусные точки и фокусные отношения.

- Постройте эпюры моментов и поперечных сил для балки с двумя защемленными концами при следующих нагрузках: равномерно распределенная нагрузка на всем пролете; сосредоточенная сила посредине пролета.

- Почему на протяжении двух соседних пролетов неразрезной балки эпюра моментов не может быть однозначной?

- Расчет неразрезной балки на действие подвижной нагрузки. Построение огибающих эпюр в неразрезной балке. Линии влияния изгибающего момента в неразрезных балках.

- Неразрезная балка на упруго оседающих опорах. Коэффициенты жесткости и податливости опор. Определение коэффициентов системы разрешающих уравнений метода сил для балки на упруго оседающих опорах.

- Расчет неразрезной балки на упруго оседающих опорах методом сил. Особенности системы разрешающих уравнений метода сил в этом случае. Влияние жесткости опор балки на вид эпюр изгибающего момента.

- Что называют статически определимыми и статически неопределимыми системами?

- Что называется степенью статической неопределимости системы?

- Как определяется степень статической неопределимости?

- Чем принципиально отличаются статически неопределимая балка от статически определимой?

- Какие методы могут быть использованы для расчета статически неопределимых балок?

- Как решают простейшие статически неопределимые балки?

- Как записывается уравнение трех моментов?

- Какие балки называют статически неопределимыми?

- В каком случае балка является статически неопределимой?

- Какие условия равновесия обычно записывают для определения опорных реакций?

- Какое дополнительное уравнение к трем основным уравнениям статики добавляет врезка в сечении балки шарнира?

- Какой порядок расчета используется при решении статически неопределимых балок?

- В какой последовательности выполняют расчет статически неопределимой балки?

- Для чего и как проводятся деформационная проверка при решении статически неопределимых балок?

- Что представляет собой основная система?

- В чём заключается выбор основной системы?

- Что понимается под выражением «каноническое уравнение» метода сил?

- Что выражает каждое из канонических уравнений?

- Как составляют канонические уравнения метода сил?

- Каков физический смысл произведений ?

- Какие перемещения называют главными и побочными. Какими свойствами они обладают?

- В каком порядке производится расчёт статически неопределимых систем?

- Перемножением каких эпюр определяют коэффициенты и свободные члены системы канонических уравнений?

- Как определяются значения неизвестных Х_i?

- Какими приёмами можно построить окончательную (суммарную) эпюру изгибающих моментов?

- Как производится статическая проверка правильности раскрытия статической неопределимости системы?

- Как проводят деформационную проверку правильности построения окончательной эпюры М статически неопределимой системы?

- Как производится определение перемещений в статически неопределимых системах?

- Какие системы называют геометрически неизменяемыми?

- Объясните смысловую сторону метода сил?

- Каким методом ведется проверка балки на жесткость?

- Запишите условие прочности балки по нормальным напряжениям?

- Объясните, как, используя условия прочности по нормальным напряжениям, подбираются балки из ГОСТа?

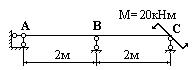
- Определить изгибающий момент на промежуточной опоре В для балки, изображенной на рисунке.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00