Главная
Лекция 14 (продолжение). Задачи для самостоятельного
решения.
Содержание
Расчет статически неопределимых балок
Расчет статически неопределимых рам
Расчет статически неопределимых балок
Задача 1.
Балка
длиной l и весом Q, с моментом инерции I лежит на трех
одинаковых упругих опорах (по концам и посредине длины балки). Жесткость стойки
равна С. Чему равна реакция средней стойки?
Ответ: R=(Q/8)(I92EI+5Cl3)/(72EI+Cl3).
Задача 2.
Деревянная
балка квадратного сечения 30х30 см, длиной 3 м подвешена на трех стальных тягах
длиной 2 м и площадью поперечного сечения по 8 см2
каждая. Две тяги поддерживают балку по концам, третья – посредине. На балку
действует посредине ее длины сила F=130
кН. Определить величины напряжений в тягах и
наибольшее нормальное напряжение в балке.
Ответ:
![]() (в
балке).
(в
балке).
Задача 3.
Двутавровая
балка № 55 установлена на трех двутавровых стойках № 20. Стойки делят длину
балки на два пролета по 1,5 м. Высота стоек 3 м. После установки балки средняя
стойка нагрета на 40 0С. Определить напряжения в стойках и
наибольшее нормальное напряжение в балке от нагревания стойки.
Ответ:
![]()
Задача 4.
Двутавровая
балка № 18 длиной 6 м лежит на трех деревянных стойках круглого сечения
диаметром 25 см и высотой 4 м. две стойки поддерживают балку по концам, третья
– в середине пролета. Балка нагружена по всей длине равномерно распределенной
нагрузкой интенсивности q=20
кН/м. Определить напряжения в стойках и наибольшее нормальное напряжение в
балке.
Ответ:
![]()
Задача 5.
Стальная
балка с моментом инерции I
и длиной l оперта по концам на жесткие шарнирные
опоры, а в двух промежуточных сечениях – на стальные колонны высотой Н. Все три
пролета равны между собой. Балка загружена равномерно распределенной нагрузкой
по всей длине. Найти необходимую площадь поперечного сечения опор из условия,
чтобы усилия в стойках и реакции крайних опор были одинаковы.
Ответ:
А=486НI/(7l3).
Задача 6.
Четырехпролетная неразрезная балка с
равными пролетами из деревянного бруса длиной 8 м с соотношением высоты
поперечного сечения к ширине равным 1,5. Балка загружена по всей длине
равномерно распределенной нагрузкой интенсивности q=7 кН/м. определить размеры бруса при [σ]=8 МПа.
Ответ:
b=10
см.
Задача 7.
Стальная
двутавровая балка № 22 длиной 4 м опирается по концам на шарнирные жесткие опоры,
а посредине длины – на деревянную стойку высотой 8 м и площадью поперечного
сечения 400 см2. В одном метре от опор
приложены две силы F=30
кН каждая. Найти напряжения в стойке и наибольшее напряжение в балке.
Ответ:
![]()
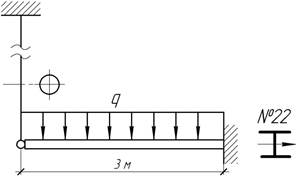
Задача 8.
Двутавровая
стальная балка № 22 длиной 3 м защемлена одним концом, а свободный конец
поддерживается стальной тягой диаметром 25 мм и длиной 8 м. Определить
напряжение в тяге и наибольшее нормальное напряжение в балке, если q=30кН/м. Как изменится
напряжение, если тяга окажется на 2,5 мм длиннее проектной длины?
Ответ:
1) ![]() 2)
2)![]() .
.
Задача 9.
Какое
предельное значение может иметь сила F,
чтобы правый конец балки не отрывался от
гладкой опоры?
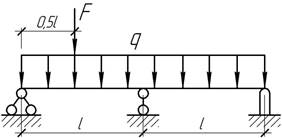
Ответ:
F=4ql.
Задача 10.
Как
должны относиться пролеты балки l и а, чтобы реакция правой опоры оказалось равной нулю?
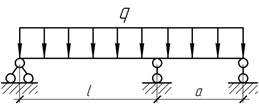
Ответ:
а=0,433l.
Задача 11.
Найти
осадку Δ пружины, жесткость которой равна С.
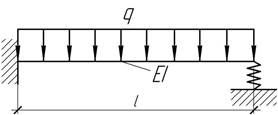
Ответ:
Δ=3ql/(8kc), k=1+3EI/cl3.
Задача 12.
На
какую высоту нужно поднять опору В балки АВ жесткостью
EI,
чтобы напряжение в сечении а были равны нулю?
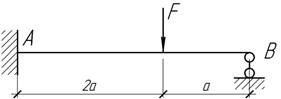
Ответ:
Δ=4Fa3/(3EI).
Задача 13.
При
каком значении z
изгибающий момент под силой F
будет максимальным?
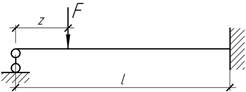
Ответ:
z=0,365l.
Задача 14.
На
какую величину необходимо опустить средние опоры балки, чтобы изгибающие моменты
в сечениях над этими опорами обратились в нуль?
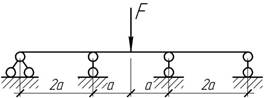
Ответ:
Δ=Fa3/(2EI).
Задача 15.
При
какой величине зазора Δ все три реакции равны между собой?
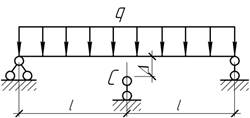
Ответ:
Δ=(7/72)ql4/(EI).
Задача 16.
При
какой величине Δ изгибающий момент в сечение С
равен нулю?
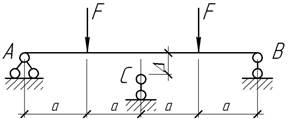
Ответ:
Δ=Fa3/(2EI).
Задача 17.
Для
трехопорной балки задана эпюра изгибающего момента.
Определить величину неизвестного момента М.
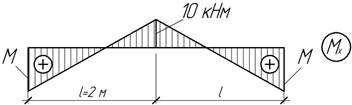
Ответ:
М=20 кНм.
Задача 18.
Как
распределяется нагрузка между балками, которые отличаются только высотой поперечного
сечения?
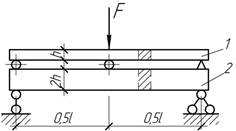
Ответ:
F1=F/9, F2=8F/9.
Задача 19.
На
какие углы α следует при защемлении повернуть концы балки постоянной
жесткости EI,
чтобы после приложения нагрузки q
моменты в сечениях А, В и С были одинаковы?
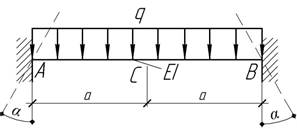
Ответ:
α=qa3/(12EI).
Задача 20.
Ползун
СД жестко связан с двумя стержнями АС и ВД разной изгибной жесткости. Найти реакции
в опорных закреплениях А и В при действии на ползун
силы F.
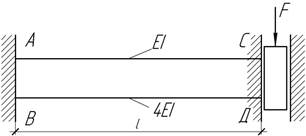
Ответ:
![]()
Задача 21.
При
каком расстоянии z
перемещения в пролете АВ равны нулю?
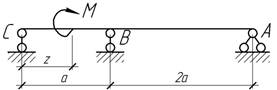
Ответ:
z=0,577а.
Задача 22.
На
стальную балку прямоугольного сечения 4х10 см параллельно ее оси наклеен тензодатчик. Определить величину силы F, если ![]() м.
м.
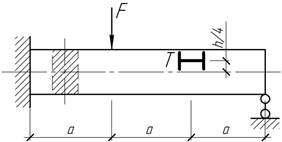
Ответ:
F=30
кН.
Задача 23.
На
сколько нужно сместить опору В, чтобы сделать равными
по абсолютной величине изгибающие моменты в пролете и в защемлении?
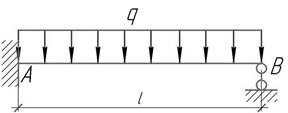
Ответ:
Приподнять на Δ=0,013ql4/EI.
Задача 24.
Балка
поддерживается в точке С упругой опорой с
коэффициентом податливости α. Полная нагрузка на балку равна Q и распределена
равномерно по ее длине. Чему равно давление на опору С.
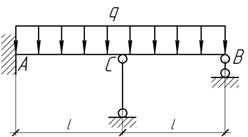
Ответ:
![]() где К=I+6EIα/l3.
где К=I+6EIα/l3.
Задача 25.
Балки
расположены перекрестно, причем при отсутствии нагрузки низ верхних балок касается
верха нижних балок без нажима. Чему равны опорные реакции и наибольшие нормальные
напряжения в каждой из балок при действии силы А=12 кН
и а=1 м.
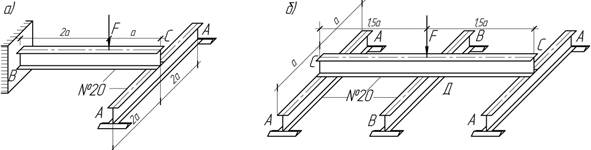
Ответ:
а) ![]() б)
б) ![]()
Задача 26.
Какое предельное значение может иметь сила F, чтобы правый конец балки не отвалился от гладкой опоры?
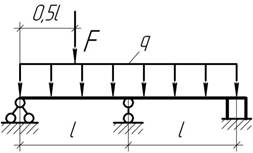
Ответ:
F=4ql
Задача 27.
Как должны относиться пролеты балки l и а, чтобы реакция правой опоры оказалась равной нулю?
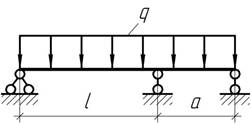
Ответ:
а=0,433l
Задача 28.
На какую высоту нужно поднять опору В балки АВ жесткостью EI, чтобы напряжение в сечении А были равны нулю?
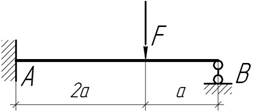
Ответ:
![]()
Задача 29.
На сколько
нужно сместить опору В, чтобы сделать равными по
абсолютной величине изгибающие моменты в пролете и в защемлении?
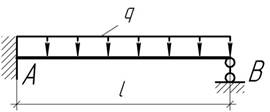
Ответ: Приподнять на ![]()
Задача 30.
На какие углы α следует при
защемлении повернуть концы балки постоянной жесткости EI, чтобы после приложения нагрузки q моменты
в сечениях А, В и С были одинаковы?
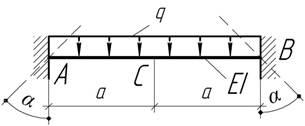
Ответ: α=qa3/(12EI)
Задача 31.
При каком значении z изгибающий момент под силой F будет максимальным?
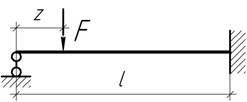
Ответ:
z=0,365l
Задача 32.
При каком значении х коэффициент запаса трехопорной балки АВ наибольший? Балка находится в условиях прямого изгиба, поперечное сечение постоянно, материал одинаково сопротивляется растяжению и сжатию.
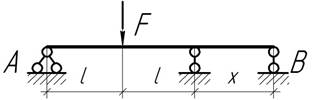
Ответ:
х=0,25l
Задача 33.
На какую величину необходимо опустить средние опоры балки, чтобы изгибающие моменты в сечениях над этими опорами обратились в нуль?
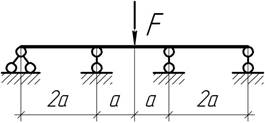
Ответ:
![]()
Задача 34.
При каком
расстоянии z
перемещение в пролете АВ равны нулю?
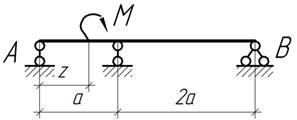
Ответ:
z=0,577а
Задача 35.
Для трехопорной балки заданы эпюра изгибающего момента. Определить величину неизвестного момента М?
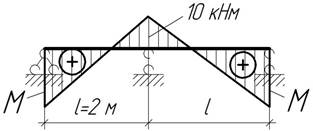
Ответ: М=20 кНм
Задача 36.
Определить опорные реакции однопролетной балки, показанной на рисунке.
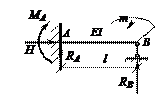
Ответ: H = 0, RB = –3m/(2l), RA = 3m/(2l); MA
= –m/2.
Задача 37.
Определить опорные реакции и построить эпюры изгибающих моментов М и поперечных сил Q для балки с консолью (см. рис.). Жесткость балки на изгиб постоянна и равна EI.
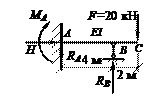
Ответ: H = 0; RB = 35 кН, RA = –15 кН; МА = 20 кНм, МС = 0; МВ = –40 кНм; QАВ = –15 кН, QВС = 20 кН.
Задача 38.
Определить опорные реакции, построить эпюры изгибающих моментов и поперечных сил для двухпролетной балки, изображенной на рисунке. Принять, что F1 = F.
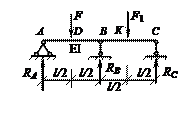
Ответ: RA = 0,3125F; RB = 1,375F; RC = RA; MK = MD; MA = MC = 0;
MD = 0,15625Fl; MB =
–0,1875Fl; QAD = RA; QDB
= –0,6875F;
QBK = –QDB; QKC = –RC.
Задача 39.
Определить опорные реакции двухпролетной балки, показанной на рисунке. Принять F1 = 2F.

Ответ: RA = 0,21875F; RB = 2,0625F;
RC = 0,71875F.
Задача 40.
1) Определить опорные реакции, построить эпюры изгибающих моментов и поперечных сил для двухпролетной балки, нагруженной на опоре С сосредоточенным моментом m (рис. 1).
2) Определить опорные реакции для один раз статически неопределимой балки, показанной на рис. 2.
3) Определить опорные реакции, построить эпюры изгибающих моментов и поперечных сил для двухпролетной балки с консолью (рис. 3).
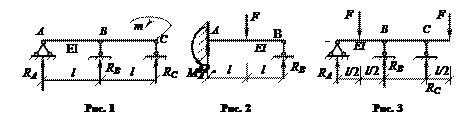
Ответ к рис.1: RA = –m/(4l); RB = 3m/(2l); RC = 5m/(4l).
Ответ к рис.2: RA = 11F/16; RB = 5F/16; MA = 3Fl/8.
Ответ к рис.3: RA = 0,53125F; RB = –0,0625F; RC = 1,53125F.
Задача 41.
На рисунке изображена консольная балка, нагруженная двумя сосредоточенными силами. Во сколько раз уменьшится максимальный изгибающий момент (на опоре В), если поставить дополнительно в точке А шарнирно подвижную опору?
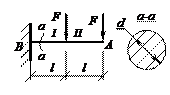
Ответ: уменьшится в 8 раз.
Расчет статически неопределимых рам
Задача 1.
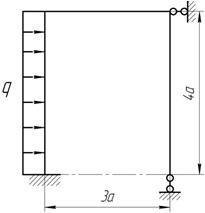
Построить эпюру М методом сил, если жесткости элементов рамы постоянны и равны EI, а=2 м, q=30 кН/м.
Задача 2.
Дано: P=qa; q=1кН/м; М=qa2; a=1 м; EI=const. Построить эпюру М и сделать статическую проверку RB-?, ЭМΣ-?

Задача 3.
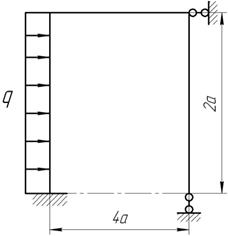
Построить эпюру М методом сил, если жесткости элементов рамы постоянны и равны. а=3 м, q=20 кН/м.
Задача 4.
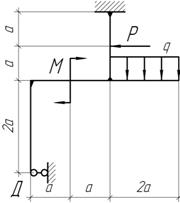
Дано: P=qa; q=1кН/м; М=qa2; a=1 м. Построить эпюру М и сделать статическую проверку RР-?, ЭМΣ-?
Задача 5.
Дано: P=qa; q=1кН/м; М=qa2; a=1 м; EI=const. Построить эпюру М и сделать статическую проверку RB-?, ЭМΣ-?
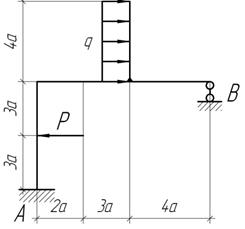
Задача 6.
Дано: P=qa; q=1кН/м; М=qa2; a=1 м; EI=const. Построить эпюру М и сделать статическую проверку RС-?, ЭМΣ-?
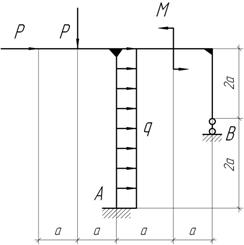
Задача 7.
Построить эпюру M, воспользовавшись методом сил.
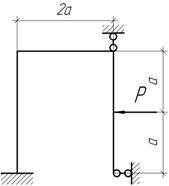
Задача 8.
Дано: q=60кН/м; Мa=4 м. Построить эпюру внутренних изгибающих моментов Мсум. Подобрать сечение двутавра
из условия прочности ![]()
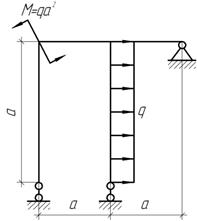
Задача 9.
Дано: P=qa; q=1кН/м; М=qa2. Построить эпюру М и сделать статическую проверку RА-?, ЭМΣ-?
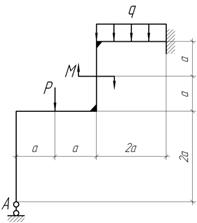
Задача 10.
Дано: P=qa; q=10 кН/м; М=qa2; a=1 м; ![]() . Построить эпюру М и сделать
статическую проверку. Подобрать номер двутаврового сечения.
. Построить эпюру М и сделать
статическую проверку. Подобрать номер двутаврового сечения.

Задача 11.
Дано: P=qa; q=1кН/м; М=qa2; a=1 м. Построить эпюру М и сделать статическую проверку RB-?, ЭМΣ-?
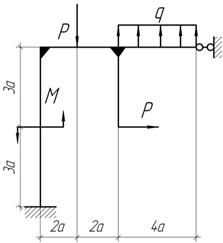
Задача 12.
Дано: q=3,0 кН/м; a=4 м. Построить эпюру внутренних изгибающих моментов и
подобрать сечение двутавра. ![]()
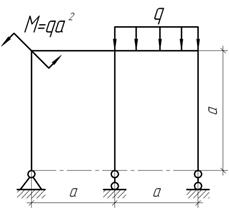
Задача 13.
Дано: P=qa; q=1кН/м; М=qa2; a=1 м. Построить эпюру М и сделать статическую проверку RР-?, ЭМΣ-?

Задача 14.
Построить эпюру М методом сил, если рамы постоянны и равны EI, а=2 м, q=30 кН/м.
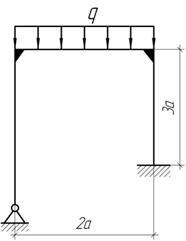
Задача 15.
Раскрыть статическую неопределимость рамы.
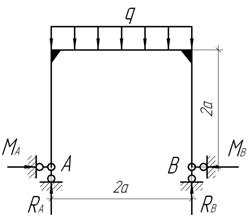
Ответ: ![]()
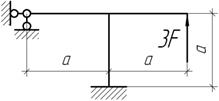
Задача 16.
Дано: q=10 кН/м; F=20 кН; М=30 кНм; а=2м. Построить Эп N, Q, M - ?
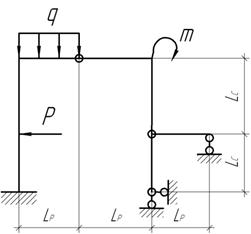
Задача 17.
Дано: Р=2 кН; m=4 кНм; q=2 кН/м; Lc=2 м; Lp=2 м; ![]() EI=const. Построить методом сил
эпюры внутренних усилий M,
Q,
N.
EI=const. Построить методом сил
эпюры внутренних усилий M,
Q,
N.
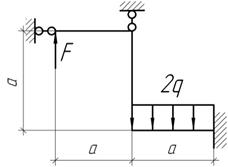
Задача 18.
Дано: q=10 кН/м; F=20 кН; М=30 кНм; а=2м. Построить Эп N, Q, M - ?
Задача 19.
Дано: q=10 кН/м; F=20 кН; М=30 кНм; а=2м. Построить Эп N, Q, M - ?
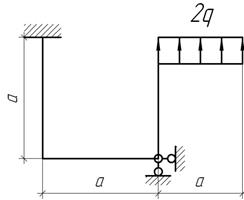
Задача 20.
Дано: q=10 кН/м; F=20 кН; М=30 кНм; а=2м. Построить Эп N, Q, M - ?
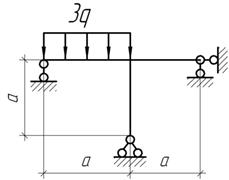
Задача 21.
Дано: q=10 кН/м; F=20 кН; М=30 кНм; а=2м. Построить Эп N, Q, M - ?
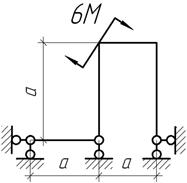
Задача 22.
Дано: q=10 кН/м; F=20 кН; М=30 кНм; а=2м. Построить Эп N, Q, M - ?
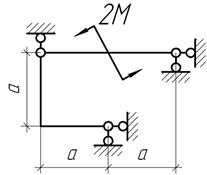
Задача 23.
Ригель ВС рамы АВС выполнен короче проектной длины на величину Δ. Чему равен наибольший изгибающий момент, возникающий при сборке?
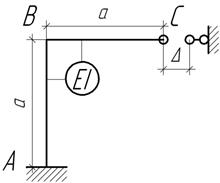
Задача 24.
Какой из приведенных вариантов не является основной системой?

email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов

