Главная
Лекция 14 (продолжение). Примеры решения на построение эпюр в статически неопределимых системах по методу сил.
Расчет статически неопределимых
балок
Пример 1.
Построить эпюру изгибающих моментов и поперечных сил для однопролетной балки, показанной на рис. а.
Решение.
Для
определения опорных реакций H, RA, RB, MA составим уравнения
равновесия: 
откуда H = 0,
далее
тогда 
тогда 
Для
определения трех опорных реакций МА,
RВ, RА имеем систему
двух уравнений. Таким образом, задача является статически неопределимой. Для ее
решения необходимо привлечь одно дополнительное уравнение 
Отбросим одну
лишнюю опорную реакцию RВ = Х1. В результате получим консольную балку, показанную на
рис. б. Для этой полученной
консольной балки строим эпюру изгибающих моментов МF от внешней нагрузки.
Для
определения вертикального смещения 
точки В построим эпюру
изгибающих моментов 
от единичной силы,
приложенной в направлении отброшенной опорной реакции RB
(рис. в). Затем, используя правило
Верещагина, находим перемещение:
Для
определения перемещения 
необходимо умножить по
правилу Верещагина эпюру саму на себя:
Подставим
полученные результаты в формулу :
откуда 
Из полученных ранее выражений определяем остальные опорные реакции:
Положительные значения опорных реакций показывают, что выбранные нами предварительно их направления правильны (рис. а). Отрицательные значения показывают, что выбранные предварительно направления опорных реакций необходимо заменить на противоположные.
Проводим сечение I – I и отбрасываем мысленно левую часть, тогда
; 
тогда 
.
Экстремальное значение изгибающего момента в пролете будет в сечении, где поперечная сила равна нулю, т.е. на расстоянии х = 3l/8 от правой опоры:
.
Затем строим эпюру поперечных сил:
QA = RA = 5ql/8; QB
= –RB = –3ql/8.
Задача 2.
Построить эпюру изгибающих моментов и поперечных сил для двухпролетной балки, показанной на рис. а.
Решение.
Для определения опорных реакций RA, RB, RC составим уравнения равновесия:
откуда RC = 0,25F – 0,5RB;
откуда RA = 0,75F –
0,5RB.
Для
определения трех опорных реакций RA, RB, RC имеем
систему двух уравнений. Привлекаем дополнительное условие Отбросим одну
лишнюю опорную реакцию RB =
Х1. В результате получим
однопролетную балку, показанную на рис. б.
Для полученной однопролетной балки строим эпюру изгибающих моментов МF от внешней силы F. Предварительно находим 
откуда Rc = 0,25F. Далее записываем откуда определяем Ra = 0,75F.
Для построения
эпюры МF
достаточно определить изгибающие моменты в трех точках (рис. б): Ma = Mc = 0; Md = 
= 0,375Fl.
Для
определения прогиба в точке В построим эпюру
изгибающих моментов от единичной силы,
приложенной в направлении отброшенной опорной реакции RB (рис. 4.7.4, в). Используя правило Верещагина,
вычисляем интеграл Мора 
Разбиваем эпюры МF и на три участка так, чтобы в пределах одного участка не было
переломов эпюр. Перемножаем последовательно участки:
Для
определения перемещения необходимо умножить по
правилу Верещагина эпюру саму на себя:
Подставляя полученные результаты в формулу находим
Из полученных ранее выражений вычисляем остальные опорные реакции:
RC = 0,25F –
0,5RB = 0,25F – 
–0,09375F;
RA = 0,75F –
0,5RB = 0,75F –0,40625F.
Положительные значения опорных реакций показывают, что предварительно выбранные их направления правильны (рис. а), а отрицательные значения показывают, что выбранные без расчета направления опорных реакций необходимо заменить на противоположные, как, например, у опорной реакции RC.
Зная опорные реакции, легко построить эпюру изгибающих моментов М (рис. г):
MA = MC = 0; MD = RA 0,5l = 0,203125Fl; MB = RCl = –0,09375Fl,
а также эпюру поперечных сил Q:
QAB = RA; QDB = RA – F = 0,59375F; QBC = –RC
= 0,09375F.
Пример 3.
Раскрыть статическую неопределимость балки методом сил и определить точки С приложения силы Р (рис. а).
Решение.
Балка один раз статически неопределима, ибо в задаче возникает три неизвестные опорные реакции RA , RB , mA , а уравнений равновесия можно составить только два. В качестве лишней связи выбираем опору В. На рис. б, в изображены основная и эквивалентная системы. Каноническое уравнение метода сил имеет вид
.
(1)
Для
определения коэффициентов 
, 
для основной системы
строим эпюры отдельно от действия внешней нагрузки (рис. г) и от единичной силы
(рис. д).
На основании формулы Мора и способа Верещагина находим
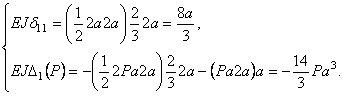
Подстановка полученных выражений в каноническое уравнение (1) приводит к выражению:
откуда находим:
.
(2)
Теперь, используя (2), из уравнений равновесия для эквивалентной системы
находим опорные реакции:
На рис. е,ж изображены окончательные эпюры перерезывающих сил и изгибающих моментов.
Для определения прогиба в точке С прикладываем в этой точке основной системы единичную силу Р = 1 (рис. з). Перемножая эпюру от этой силы на результирующую (рис. ж), находим:
Деформационная
проверка правильности построенных эпюр состоит в определении перемещения точки В, которое заведомо равно нулю.
Используя формулу Мора и способ Верещагина, перемножаем эпюру моментов на эпюру
от единичной силы 
В результате
находим:
Следовательно, эпюра моментов в данной задаче построена правильно.
Пример 4.
Решим предыдущий пример (рис. а) несколько проще. Выберем основную систему так, как показано на рис. б, т.е. разрежем балку в защемлении и вставим шарнир.
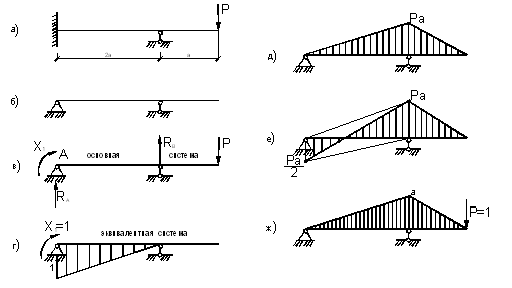
Этим самым мы освободим одну простую лишнюю связь. Эквивалентная система приведена на рис. в, а эпюры от единичного момента и внешней нагрузки – на рис. г, д. Коэффициенты канонического уравнения:
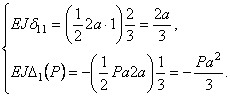
Подставляя
полученные значения коэффициентов в каноническое уравнение, найдём 
, т.е. то же значение опорного момента 
, что и в предыдущей задаче.
Далее для
эквивалентной системы строим эпюры Q, M. Эпюра
моментов может быть получена весьма просто сложением эпюр моментов,
изображённых на рис. г, д, при условии, что ординаты
единичной эпюры увеличены 
раза. После определения опорных реакций RA , RB из уравнений равновесия
, 
обычным способом строится эпюра Q. Перемножая эпюры на рис. е, ж, находим:
Деформационная проверка даёт
что подтверждает правильность решения.
Пример 5.
Рассмотрим дважды статически неопределимую балку (рис. а). Раскроем её статическую неопределённость методом сил.
Решение.
Возможны, как и в примерах 3 и 4, два варианта выбора эквивалентной системы (рис. б, в). Более рациональной является эквивалентная система на рис. в, где в опорах врезаны внутренние шарниры.
Канонические уравнения метода сил имеют вид:
(1)
Для
определения коэффициентов 
строим для основной системы эпюры от внешней нагрузки (рис. г) и единичных моментов (рис. д).
В результате их перемножения по способу Верещагина, находим:
Подставляя полученные значения коэффициентов в канонические уравнения (1), находим:
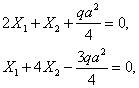
откуда следует:
Эпюра моментов от Х1 и Х2 построена на рис. е. Складывая её с эпюрой моментов от внешних сил (рис. г), находим суммарную эпюру моментов (рис. ж).
Найдём далее из уравнений равновесия частей эквивалентной системы опорные реакции. Из рис. в следует:
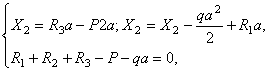
откуда находим:
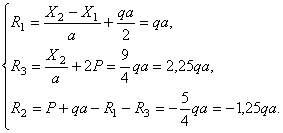
Эпюра перерезывающих сил строится по известным правилам (см. рис. з). Далее производится деформационная проверка. Угол поворота сечения в опоре 1 (защемление) и взаимный угол поворота сечений над опорой 2 равны нулю.
Сделаем проверку второго из этих условий:
Деформационная проверка подтверждает правильность полученного решения.
Пример 6.
Построить эпюру изгибающих моментов для статически неопределимой балки (рис. 1, а).
Рис.1
Решение.
Степень статической неопределимости балки:
.
Основная и эквивалентная система приведены на рис.1,б,в. Так выбор основной системы является наиболее рациональным, но не единственным. Можно было, например, заменить жесткую заделку на шарнирно-неподвижную опору; тогда основная система представляла бы собой статически определимую шарнирную балку, а лишняя неизвестная – сосредоточенный момент X, приложенный к левой опоре.
Эпюра
изгибающих моментов от внешней нагрузки 
(рис.1, д) имеет размерность кНм, а
единичная эпюра моментов 
(рис.1, ж) в метрах.
Каноническое
уравнение метода сил:
Вычисляем
коэффициенты 
и 
, перемножая соответствующие эпюры по правилу Верещагина:
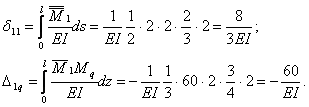
Реакция лишней
связи:
Таким образом,
исходная статически неопределимая система, загруженная распределенной нагрузкой
, приведена к статически определимой системе (жестко
защемленная балка), загруженной распределенной нагрузкой и сосредоточенной
силой 
(рис.1, з).
На рис.2,а,б
представлены эпюры поперечных сил 
и изгибающих моментов
для заданной системы.
Отметим, что
эпюры и (рис.2) построены непосредственно методом сечений,
причем по условиям задачи построение эпюры не является
обязательным. Тем не менее, эта эпюра позволила определить сечение, в котором
будет экстремум на эпюре .
Рис.2
Использование
формулы метода сил 
в виде:
не дает ответа
на вопрос о месте нахождения экстремума и делает правильное построение эпюры более сложной задачей, требующей определенных навыков.
Пример 7.
Для балки
(рис. 1) задано: l1 = 2 l2 , P = q l1,
.
Требуется:
1. Определить степень статической неопределимости системы и составить уравнение совместности деформаций;
2. Определить коэффициенты и решить каноническое уравнение метода сил;
3. Построить эпюры моментов М и поперечных сил Q.
Рис.1
Решение.
1. Определить степень статической неопределимости системы и составить уравнение совместности деформаций. Подсчитаем степень статической неопределимости системы s=m-n= 4-3 = 1, следовательно система один раз статически неопределима. Основную систему получим путем отбрасывания опоры в точке А и замены ее действия неизвестным усилием X1 (рис.2). Каноническое уравнение метода сил в данном случае запишется в следующем виде:
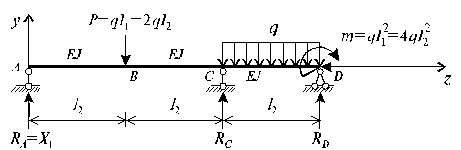
Рис.2
2. Определить
коэффициенты и решить каноническое уравнение метода сил. От силы X1 строим эпюру M1 (рис. 3). Для
определения величины воспользуемся выражением 
. Фактически эпюру M1
нужно умножить саму на себя и проинтегрировать это произведение:
Рис.3
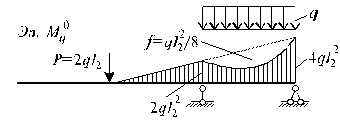
Рис.4
Для определения свободного коэффициента в каноническом уравнении строим в основной системе эпюру моментов MP от внешней нагрузки (рис. 4) и получаем:
При вычислении
было учтено, что эпюры
М1
и МP имеют разный знак,
т.к. вызывают растяжение разных волокон - об этом говорит
отрицательный знак при . Кроме этого, криволинейный участок в эпюре МP был представлен как
разность трапеции и параболического сегмента.
Напишем уравнение совместности деформаций в виде
и, подставляя найденные величины перемещений, получим:
, откуда 
.
3. Построить эпюры изгибающих моментов и поперечных сил. Окончательную эпюру изгибающих моментов получим по формуле:
.
Последняя
формула означает, что окончательное значение момента в любом сечении
определяется путем сложения значения момента в эпюре МP с величиной момента в эпюре М1, увеличенной на коэффициент
(рис. 5, а). Эпюру QОК для заданной системы можно построить следующим
образом. Заменив в заданной системе опорные реакции RA на X1,
получим статически определимую эквивалентную систему, тождественную
заданной. Далее, определяя остальные опорные реакции RC и RD
и по методу сечений составляя аналитические выражения изменения поперечных сил
на каждом участке, по ним определив ординаты в характерных сечениях, строится эпюра QОК
(рис. 5, б).
Рис.5
Пример 8.
Балка, показанная на рис. 1, с шарниром в точке Е загружена сосредоточенной парой М. Требуется определить внутренние усилия и построить изогнутую ось балки.
Рис.1
Решение.
Как было показано выше, заданная балка является один раз статически неопределимой. Выберем основную систему, отбросив одну лишнюю связь, например, подвижную опору в точке D (рис. 2).
Рис.2
Опорную
реакцию в точке D будем считать
лишней неизвестной и обозначим буквой Х. Уравнением
для определения лишней неизвестной является уравнение совместности деформаций.
Для выбранной основной системы это условие, приравнивающее нулю прогиб балки в
точке D: 
. Прогиб в точке D
можно найти как сумму прогиба, вызванного заданной нагрузкой (парой сил М) и прогиба от лишней неизвестной Х, т. е. условие совместности деформаций
можно записать так:
.
Будем искать
прогиб методом Максвелла – Мора с использованием правила Верещагина. Сначала
найдем 
. Для этого построим в основной системе эпюры изгибающего
момента от заданной нагрузки (пары М
в данной задаче) – ММ и изгибающего момента от единичной обобщенной
силы, соответствующей искомому перемещению, – М1. Чтобы построить эпюру ММ, найдем опорные реакции.
Горизонтальная реакция НА
в балках при отсутствии горизонтальной составляющей нагрузки всегда равна нулю
– это следует из уравнения равновесия "сумма проекций всех сил на
горизонтальную ось равна нулю". Для определения трех других опорных
реакций RA, RB
и RC
составим три уравнения равновесия:
; 
; 
;
; 
; 
;
; 
; 
.
При составлении уравнений статики было принято, что все реакции действуют вверх, полученные знаки учтены в направлении реакций на рис. 3, а.
Рис.3
Первое уравнение равновесия связано с наличием шарнира в точке Е балки и показывает, что изгибающий момент в шарнире равен нулю, то есть сумма моментов всех сил слева (или справа) от шарнира равна нулю. Эпюра изгибающих моментов ММ от заданной нагрузки показана на рис. 3, б. Чтобы построить эпюру изгибающих моментов от единичной обобщенной силы, приложим эту силу к балке. Поскольку определяем прогиб в точке D, то согласно методу Максвелла – Мора прикладываем в точке D сосредоточенную силу, равную единице (рис. 3, в). Находим опорные реакции и строим эпюру М1 аналогично выполненному ранее построению эпюры ММ (рис. 3, г). Вычисляем прогиб в точке по формуле Максвелла – Мора, перемножая эпюры ММ и М1:
.
Теперь ищем
прогиб в точке D от лишней
неизвестной Х – 
.
Строим эпюру МХ (рис. 3, е) и перемножаем ее с эпюрой М1,
пользуясь правилом Верещагина:
.
Складываем и , находим
полное перемещение и в соответствии с условием совместности деформаций
приравниваем его нулю:
.
Отсюда 
.
Итак, мы нашли лишнюю неизвестную Х из условия совместности деформаций. Прикладываем ее к заданной системе, не меняя направления, так как значение Х получилось положительным. Строим окончательные эпюры внутренних усилий и от заданных нагрузок (пары сил М), и от лишней неизвестной Х. Эти эпюры показаны на рис. 4, б, в.
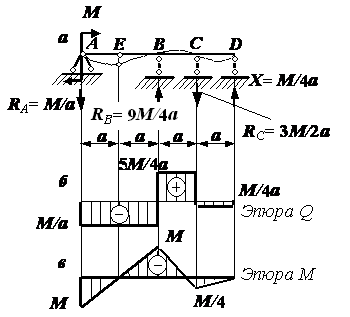
Рис.4
Заканчиваем решение
проверкой результатов. Часто можно обнаружить ошибку, если построить изогнутую
ось балки. Изогнутая ось должна удовлетворять как эпюре моментов, которая
показывает, в какую сторону направлена выпуклость оси балки после изгиба, так и
условиям закрепления балки. На рис. 4, а
показана деформированная ось балки, удовлетворяющая указанным условиям.
Заметим, что из-за наличия шарнира возможен перелом изогнутой оси в точке Е, так как сечения, примыкающие к
шарниру поворачиваются на разные углы. Если не удается построить изогнутую ось
так, чтобы она удовлетворяла всем условиям, то следует искать ошибку. Эта
проверка носит качественный характер и не
всегда дает возможность найти ошибку в вычислениях. Проверкой, подтверждающей
правильность вычисления лишней неизвестной, является условие 
, то есть результатом перемножения окончательной эпюры М с эпюрой изгибающих моментов от
единичной обобщенной силы М1 (по
правилу Верещагина) должен быть ноль. Делая эту проверку, мы еще раз проверяем равенство
нулю прогиба в точке D в нашей
задаче, поскольку смыслом этого перемножения является согласно методу Максвелла
– Мора определение перемещения по направлению обобщенной силы (прогиба в точке D в решаемой задаче). Проверим решение
нашей задачи:
.
Пример 9.
Балка (см. рис.) имеет одну шарнирно-неподвижную и две шарнирно-подвижные опоры.
Дано: m – внешний момент, длина l, изгибная жесткость EJ.
Требуется:
1) Построить
эпюру изгибающих моментов .
2) Выполнить деформационную проверку.
Решение.
Для расчетной основной системы имеем каноническое уравнение метода сил:
.
Коэффициенты уравнения вычисляем при помощи правила Верещагина:
Из уравнения получаем неизвестную реакцию:
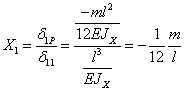
Эпюру 
строим по формуле по
точкам:
Построение всех эпюр показано на рисунке.
Выполним
деформационную проверку, для чего эпюру “перемножим” на
единичную эпюру 
для проверочной основной системы.
Считаем что задача решена правильно, хотя для полной проверки надо было выполнить повторное решение данной задачи для проверочной основной системы.
Пример 10.
Дано: Балка из двутавра №22; 
=232cм3; 
=2550см4
Требуется:
1) Раскрыть статическую неопределимость для заданной балки
2) Построить
эпюру поперечных сил и изгибающих моментов
Решение.
1) Определим степень статической неопределимости для данной системы n=5-3=2.
Выбираем основную систему (О.С.) и запишем канонические уравнения метода сил для этой расчетной ОС (рис. б)
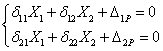
1.1) Строим
эпюру 
по участкам
Эта грузовая эпюра показана на рис. д.
1.2) Находим коэффициенты канонических уравнений метода сил при помощи правила Верещагина:
1.3) Подставляем полученные коэффициенты в каноническое уравнение метода сил.
получаем неизвестные реакции
2) Строим
эпюры и по точкам
Все построенные эпюры представлены на рис. в, ж.
Пример 11.
Требуется
раскрыть статическую неопределимость балки, нагруженной равномерно
распределенной нагрузкой интенсивностью q и
сосредоточенным моментом 
(см. рис.), и
построить эпюры поперечных сил 
и изгибающих моментов 
.
Решение.
1. Определяем степень статической
неопределимости балки.
Заданная балка является один раз статически
неопределимой, поскольку для нахождения четырех реактивных усилий
и 
мы имеем только три
уравнения статики:
.
2. Составляем уравнения
равновесия.
Из первого уравнения статики 
мы легко находим, что
горизонтальная реакция жесткой заделки 
.
Второе уравнение дает:
или
.
Сумма моментов всех внешних и
реактивных усилий относительно точки A приводит
к следующему уравнению:
.
Отсюда
.
3. Для раскрытия статической неопределимости
нам необходимо записать одно
дополнительное условие, касающееся деформации
балки.
Таким условием может являться, например,
условие отсутствия прогиба балки при 
, то есть на опоре B: 
.
Воспользуемся универсальным уравнением упругой линии балки.
Прогиб балки в произвольном сечении с
координатой z, согласно этому уравнению, определяются по следующей формуле
,
где 
и 
– прогиб
и угол поворота поперечного сечения балки в начале координат соответственно; a и b –
абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P; c и d – координаты начала и конца участка,
нагруженного распределенной нагрузкой q.
В случае многократного повторения однотипных
нагрузок в уравнении упругой линии балки необходимо использовать суммирование
соответствующих слагаемых.
Заметим, что в приведенную выше формулу для
прогиба 
входят только те
внешние усилия (активные и реактивные), которые расположены левее
сечения с координатой z,
в котором определяется прогиб балки.
Поскольку в
нашем примере в заделке 
, условие отсутствия прогиба в точке B примет вид
или
.
Таким образом, мы имеем систему
из трех уравнений с тремя неизвестными:
;
;
.
Решая ее, находим, что
.
4. Строим эпюры поперечных сил и изгибающих моментов .
Сечение 1. Отбросим мысленно правую часть балки. Мы видим реакцию опоры 
и погонную нагрузку q, распределенную на бесконечно малой длине.
Равнодействующая погонной нагрузки равна нулю. Поэтому
.
Знак «плюс» нами взят потому, что сила вращает видимую нами
часть балки относительно первого сечения по ходу часовой стрелки.
Изгибающий момент в сечении балки, равен
алгебраической сумме моментов всех усилий, которые расположены левее
рассматриваемого сечения. Мы видим реакцию опоры , у которой плечо равно нулю, и момент в заделке 
. Поэтому
.
Сечение 2. Закроем левую часть балки. Получим:
; 
.
По найденным значениям строим эпюры поперечных
сил 
(рис. б) и изгибающих моментов (рис. в).
В сечении 3 на эпюре – экстремум, поскольку эпюра поперечной силы для этого сечения проходит через
нулевое значение, то есть 
. Определим расстояние 
от этого сечения до левой опоры.
Поперечная сила равна:
.
Отсюда
.
Тогда экстремальное
значение изгибающего момента в сечении 3
равно:
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
