Главная
Лекция 2 (продолжение). Примеры решения на осевое растяжение – сжатие
Расчет статически определимых
стержней на растяжение-сжатие
Пример 1.
Круглая
колонна диаметра d сжимается
силой F. Определить увеличение диаметра ![]() , зная модуль упругости Е
и коэффициент Пуассона
, зная модуль упругости Е
и коэффициент Пуассона ![]() материала колонны.
материала колонны.

Р е ш
е н и е.
Продольная деформация по закону Гука равна
![]() .
.
Используя закон Пуассона, находим поперечную деформацию
![]() .
.
С другой
стороны, ![]() .
.
Следовательно, ![]() .
.
Пример 2.
Построить эпюры продольной силы, напряжения и перемещения для ступенчатого бруса.

Р е ш
е н и е.
1. Определение опорной реакции. Составляем уравнение равновесия в проекции на ось z:
![]() ,
, ![]() ,
,
откуда RE = 2qa.
2. Построение
эпюр Nz,
![]() , W.
, W.
Э п ю р а Nz. Она строится по формуле
![]() .
.
Имеем
![]() ,
,
![]()
![]() ,
,
![]() .
.
Э п ю р а ![]() .
Напряжение равно
.
Напряжение равно ![]() . Как
следует из этой формулы, скачки на эпюре
. Как
следует из этой формулы, скачки на эпюре ![]() будут обусловлены не только скачками Nz, но также резкими изменениями
площади поперечных сечений. Определяем значения
будут обусловлены не только скачками Nz, но также резкими изменениями
площади поперечных сечений. Определяем значения ![]() в характерных точках:
в характерных точках:
![]()
![]()
![]()
![]()
![]() и строим эпюру
и строим эпюру ![]() .
.
Э п ю р а W. Она строится по формуле
![]() .
.
Построение ведем от защемления к свободному концу. Находим перемещения в характерных сечениях:
Wo = WE = 0,
![]()
![]()
![]()
![]()
и строим эпюру W.
Пример 3.
Для стержня,
изображенного на рисунке, построить эпюру нормальной силы и определить
удлинение стержня, если F1 = 100 кН, F2 = 50 кН, q =
40 кН/м, а =
Решение.
1. Разбиваем брус на участки АВ, ВС, CD
2. Определяем значение нормальной силы на каждом участке
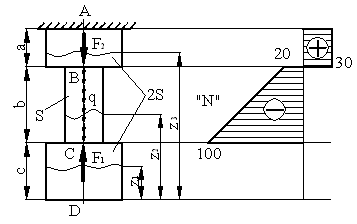
CD ![]()
![]()
CB ![]()
![]()
при z2=1,5 м, N2=-100 кН,
при z2=3,5 м, N2=-20 кН,
BА ![]()
![]() кН
кН
1) Строим эпюру нормальной силы
2) Определяем удлинение стержня
![]()
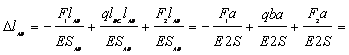
![]()

![]()
Пример 4.
Построить
эпюру ![]() для колонны
переменного сечения (рис. а). Длины
участков
для колонны
переменного сечения (рис. а). Длины
участков ![]() 2 м. Нагрузки: сосредоточенные
2 м. Нагрузки: сосредоточенные ![]() =40 кН,
=40 кН, ![]() =60 кН,
=60 кН, ![]() =50 кН; распределенная
=50 кН; распределенная ![]() =20 кН/м.
=20 кН/м.

Решение:
Пользуемся методом сечений. Рассматриваем (поочередно) равновесие отсеченной (верхней) части колонны (рис. в).
Из уравнения ![]() для отсеченной части
стержня в произвольном сечении участка
для отсеченной части
стержня в произвольном сечении участка ![]() продольная сила
продольная сила
![]() (
(![]() ),
),
при ![]() =0
=0 ![]() кН;
кН;
при ![]() =2 м
=2 м ![]() кН,
кН,
в сечениях
участков ![]() имеем соответственно:
имеем соответственно:
![]() кН,
кН,
![]() кН,
кН,
![]() кН,
кН,
Итак, в четырех
сечениях продольные силы отрицательны, что указывает на деформацию сжатия
(укорочения) всех участков колонны. По результатам вычислений строим эпюру
продольных сил ![]() (рис. б), соблюдая масштаб. Из анализа эпюры
следует, что на участках, свободных от нагрузок, продольная сила постоянна, на
нагруженных – переменна, в точках приложения сосредоточенных сил – изменяется
скачкообразно.
(рис. б), соблюдая масштаб. Из анализа эпюры
следует, что на участках, свободных от нагрузок, продольная сила постоянна, на
нагруженных – переменна, в точках приложения сосредоточенных сил – изменяется
скачкообразно.
Пример 5.
Построить
эпюру ![]() для стержня
переменного сечения (рис. а).
для стержня
переменного сечения (рис. а).

Решение.
1. Определяем вид деформации стержня. Все силы лежат на оси стержня, значит, имеем осевое растяжение-сжатие, будем строить эпюру продольных сил N.
2. Проводим ось, параллельную оси стержня.
3. Разбиваем стержень на два участка. В качестве участка загружения будем понимать часть стержня между двумя ближайшими точками приложения сил. Отметим, что изменение площади поперечного сечения не влияет на определение границ участков.
4.
Делаем сечения в начале и конце первого участка загружения и определяем N. В сечении 1 (рис. б)
![]() N1
= F1 = 6кН; в
сечении 2 (рис. в)
N1
= F1 = 6кН; в
сечении 2 (рис. в) ![]() N2
= F1 = 6кН. Знак определяем по правилу: N1, N2
> 0,
так как сила F1 растягивает продольные
волокна. Откладываем значения N1, N2, например, выше оси (строгого правила для
продольной силы не существует) и соединяем прямой линией. Внутри ставим в
кружочке знак «+» (рис. е). Переходим
ко второму участку. В сечении 3 (рис. г)
N2
= F1 = 6кН. Знак определяем по правилу: N1, N2
> 0,
так как сила F1 растягивает продольные
волокна. Откладываем значения N1, N2, например, выше оси (строгого правила для
продольной силы не существует) и соединяем прямой линией. Внутри ставим в
кружочке знак «+» (рис. е). Переходим
ко второму участку. В сечении 3 (рис. г)
![]() N3 = F1
– F2 = 6 – 10 = - 4кН; в сечении 4 (рис. д)
N3 = F1
– F2 = 6 – 10 = - 4кН; в сечении 4 (рис. д) ![]() N4
= F1 – F2 = 6 – 10 =
- 4 кН. Поскольку N3, N4
< 0. откладываем полученные
значения ниже оси и внутри эпюры ставим в кружочке знак «-». Числовые значения N1 – N4 обязательно
проставляем на эпюре (рис. е).
N4
= F1 – F2 = 6 – 10 =
- 4 кН. Поскольку N3, N4
< 0. откладываем полученные
значения ниже оси и внутри эпюры ставим в кружочке знак «-». Числовые значения N1 – N4 обязательно
проставляем на эпюре (рис. е).
5. Эпюру штрихуем и обозначаем.
6.
Эпюру проверяем. Так как к стержню не приложены распределенные нагрузки, на
эпюре не образуются наклонные прямые. В сечении (1) приложена
сила F1 = 6 кН ![]() на эпюре в этом
сечении скачок равный 6; на границе первого и второго участков приложена сила F2
=10 кН
на эпюре в этом
сечении скачок равный 6; на границе первого и второго участков приложена сила F2
=10 кН ![]() на эпюре имеем скачок
на величину 6 + 4 =10; скачок, равный 4 в сечении (4) соответствует реакции в
заделке, которую мы заранее не определяли. Эпюра построена верно.
на эпюре имеем скачок
на величину 6 + 4 =10; скачок, равный 4 в сечении (4) соответствует реакции в
заделке, которую мы заранее не определяли. Эпюра построена верно.
Пример 6.
Построить
эпюру ![]() для прямого стержня.
для прямого стержня.

Решение.
1. Вид деформации – осевое растяжение-сжатие, строим эпюру N.
2. Проводим вертикальную ось, параллельную оси стержня.
3. Имеем один участок загружения.
4.
Делаем сечение в начале и конце участка. В целях упрощения решения задачи
оставшиеся после отбрасывания жесткой заделки части стержня, изображать не
станем. Будем эту процедуру проделывать мысленно. Для наглядности можно просто
закрывать отброшенную часть стержня листом бумаги. Имеем N1
= 0; ![]() кН.
кН.
5. Откладываем N1, N2 от оси, например, вправо и соединяем прямой линией (см. рис.).
6. Ставим знак, штрихуем и обозначаем эпюру.
7. Проверка эпюры: так как на стержень действует равномерно-распределенная нагрузка, на графике должна быть наклонная прямая. Сосредоточенных сил нет, поэтому нет и скачков (скачок в заделке соответствует реакции в заделке).
Пример 7.
Построить
эпюру ![]() для стержня
переменного сечения.
для стержня
переменного сечения.
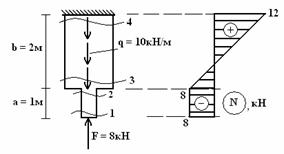
Решение.
1. Вид деформации – осевое растяжение-сжатие.
2. Проводим вертикальную ось.
3. Делим на участки загружения – в данном примере будет два участка.
4.
Делаем сечения на первом участке: N1 = -F= -8 кН; N2 = -F = -8 кН. Откладываем значения,
например, влево от оси, соединяем прямой линией. Делаем сечение на втором
участке ![]() кН;
кН; ![]() кН. Значение N3 < 0, откладываем влево от оси; N4
>
0 – вправо и соединяем прямой.
кН. Значение N3 < 0, откладываем влево от оси; N4
>
0 – вправо и соединяем прямой.
5. Ставим знаки, штрихуем и обозначаем эпюру (см. рис.).
6.
Проверка эпюры: на первом участке нет распределенной нагрузки – на эпюре
прямая, параллельная оси; на втором участке распределена нагрузка – на эпюре
наклонная прямая. В сечении (1) приложена сосредоточенная сила F = 8 кН ![]() на эпюре скачок,
равный 8.
на эпюре скачок,
равный 8.
Пример 8.
Построить эпюру Nz для стержня, приведенного на рисунке.

Р е ш
е н и е.
Стержень
нагружен только сосредоточенными осевыми силами, поэтому продольная сила в
пределах каждого участка постоянна. На границе участков Nz
претерпевает разрывы. Примем направление обхода от свободного конца (сеч. Е) к защемлению (сеч. А). На участке DE продольная сила положительна, так как сила ![]() вызывает растяжение,
т.е. NED = +F. В сечении D продольная сила
меняется скачком от NDE = NED = F до NDС = NDЕ –3F = –2F (находим из условия
равновесия бесконечно малого элемента dz, выделенного на
границе двух смежных участков CD и DE).
вызывает растяжение,
т.е. NED = +F. В сечении D продольная сила
меняется скачком от NDE = NED = F до NDС = NDЕ –3F = –2F (находим из условия
равновесия бесконечно малого элемента dz, выделенного на
границе двух смежных участков CD и DE).

Заметим, что скачок равен по величине приложенной силе 3F и направлен в сторону отрицательных значений Nz, так как сила 3F вызывает сжатие. На участке CD имеем NСD = NDС = –2F. В сечении C продольная сила изменяется скачком от NСD = –2F до NСВ = NСD + 5F = 3F. Величина скачка равна приложенной силе 5F. В пределах участка CВ продольная сила опять постоянна NСВ = NВС =3F. Наконец, в сечении В на эпюре Nz опять скачок: продольная сила меняется от NВС = 3F до NВА = NВС –2F = F. Направление скачка вниз (в сторону отрицательных значений), так как сила 2F вызывает сжатие стержня. Эпюра Nz приведена на рисунке.
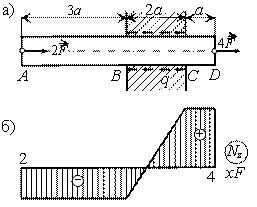
Пример 9.
Стержень, нагруженный, как показано на рисунке, удерживается в опоре силами трения, равномерно распределенными по ее толщине. Построить эпюру продольной силы.
Р е ш
е н и е.
Из условия равновесия стержня в проекции на ось z находим интенсивность сил трения:
![]() ,
, ![]() , откуда q = 3F/a.
, откуда q = 3F/a.
Эпюру Nz строим по формуле ![]() . Согласно этой зависимости на участках АВ и CD продольная сила постоянна, так
как погонной нагрузки нет (q = 0). На участке ВС продольная
сила изменяется по
линейному закону (q = const). В сечениях А и D, где приложены сосредоточенные
силы, на эпюре Nz имеют место скачки,
равные по величине приложенным силам. Примем направление обхода слева направо.
В сечении А сила 2F вызывает сжатие, поэтому
NAB = -2F. На участке ВС
продольная сила изменяется от NB = NA = -2F до
. Согласно этой зависимости на участках АВ и CD продольная сила постоянна, так
как погонной нагрузки нет (q = 0). На участке ВС продольная
сила изменяется по
линейному закону (q = const). В сечениях А и D, где приложены сосредоточенные
силы, на эпюре Nz имеют место скачки,
равные по величине приложенным силам. Примем направление обхода слева направо.
В сечении А сила 2F вызывает сжатие, поэтому
NAB = -2F. На участке ВС
продольная сила изменяется от NB = NA = -2F до ![]() . На участке CD продольная сила
постоянна и равна NСD = 4F.
. На участке CD продольная сила
постоянна и равна NСD = 4F.
Пример 10.
Стержень, изображенный на рисунке (а), нагружен уравновешенной системой в виде сосредоточенных и распределенных сил. Эпюра продольной силы показана на рисунке (б). Определить значения и направления приложенной к стержню нагрузки.

Р е ш
е н и е.
В сечениях 1,
2, 3, 4 на эпюре имеются скачки, что связано с приложенными здесь
сосредоточенными силами. Скачку вверх соответствует сила, вызывающая растяжение
в рассматриваемом сечении; при скачке вниз сила вызывает сжатие. Величина
скачка равна приложенной силе. Будем перемещаться по стержню слева направо. В
сечении 1 приложена растягивающая сила F1
= 20 кН, направленная влево. Далее на участке 12 на стержень действует
распределенная нагрузка постоянной интенсивности, равной согласно
дифференциальной зависимости ![]() тангенсу угла наклона
прямой, т.е. q12 =(60-20)/2
= 20 кН/м. Погонная нагрузка вызывает растяжение и направлена влево.
Приложенная в сечении 2 сила F2
= 100 кН вызывает сжатие и направлена вправо. На участке 23 распределенной
нагрузки нет, так как продольная сила постоянна. В сечении 3 приложена
растягивающая сила F3 = 80
кН (направлена влево). На участке 34 действует
распределенная нагрузка интенсивности
q34 = (-40 -
40)/1 = -80
кН/м, вызывающая сжатие и направленная вправо. Наконец, в сечении 4 приложена
сила F4 = 40 кН,
направленная влево.
тангенсу угла наклона
прямой, т.е. q12 =(60-20)/2
= 20 кН/м. Погонная нагрузка вызывает растяжение и направлена влево.
Приложенная в сечении 2 сила F2
= 100 кН вызывает сжатие и направлена вправо. На участке 23 распределенной
нагрузки нет, так как продольная сила постоянна. В сечении 3 приложена
растягивающая сила F3 = 80
кН (направлена влево). На участке 34 действует
распределенная нагрузка интенсивности
q34 = (-40 -
40)/1 = -80
кН/м, вызывающая сжатие и направленная вправо. Наконец, в сечении 4 приложена
сила F4 = 40 кН,
направленная влево.
Пример 11.
Стержень
переменного сечения с заданным отношением площадей A1/A2=2 подвержен действию нагрузок, показанных на
рис. а. Цель расчета – подобрать
площади поперечного сечения стержня так, чтобы на каждом участке соблюдалось
условие прочности. (При этом должно выполняться заданное отношение площадей.)
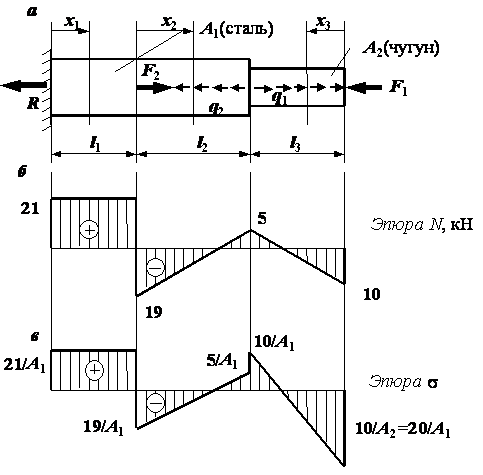
Решение.
Определяем продольную силу и строим эпюру распределения N вдоль оси стержня. Для этого сначала из уравнения равновесия всего стержня находим опорную реакцию:
![]() .
.![]()
Затем, используя метод сечений, определяем продольную силу в произвольном сечении на каждом участке стержня:
на первом
участке ![]()
![]() ;
;
на втором
участке ![]()
![]() ;
;
на третьем
участке ![]()
![]() .
.
Ищем значения N на границах участков. На первом участке продольная сила постоянна и не зависит от x. В начале второго участка
![]() ,
,
в конце второго участка
![]() .
.
Аналогично для третьего участка
![]() ,
, ![]() .
.
По
полученным точкам строим эпюру N. На
рис. б эпюра N построена для следующих исходных
данных: ![]() м,
м, ![]() м; F1 = 10 кН, F2 = 40 кН, q1 = 15 кН/м, q2 = 20 кН/м.
м; F1 = 10 кН, F2 = 40 кН, q1 = 15 кН/м, q2 = 20 кН/м.
Зная продольную силу, находим напряжения в стержне и строим эпюру распределения напряжений по длине стержня (рис. в). Заметим, что на эпюре продольных сил скачки (т.е. резкие изменения усилий при переходе в соседнее сечение) имеют место под сосредоточенными силами на величину этих сил, на эпюре напряжений скачки появляются так же и в местах изменения поперечного сечения.
Для
подбора сечения стержня по эпюре напряжений выбираем опасные сечения с
максимальными напряжениями. Причем для хрупких материалов важным является не
только абсолютное значение напряжения, но и его знак. Более опасным является
растягивающее напряжение, так как разрушающее напряжение при растяжении у
хрупкого материала много меньше прочности при сжатии. Например, на эпюре ![]() , показанной на рис. в, опасным
является не только сечение в начале третьего участка
, показанной на рис. в, опасным
является не только сечение в начале третьего участка ![]() , где действуют максимальные сжимающие напряжения, но и
сечение в конце третьего участка
, где действуют максимальные сжимающие напряжения, но и
сечение в конце третьего участка ![]() с максимальными
растягивающими напряжениями. Таким образом, для стержня, показанного на
рисунке, должны выполняться условия прочности в трех опасных сечениях:
с максимальными
растягивающими напряжениями. Таким образом, для стержня, показанного на
рисунке, должны выполняться условия прочности в трех опасных сечениях:
для
чугунной части
![]() , откуда
, откуда ![]() ,
,
![]() и
и ![]() ;
;
для стальной части
![]() , тогда
, тогда ![]() .
.
Из трех
значений A1, найденных из условий
прочности в опасных сечениях выбираем то, которое удовлетворяет всем условиям. Значение А2 находим по заданному
соотношению: ![]() .
.
Для проверки вычислений находим действительные коэффициенты запаса прочности на каждом участке и сравниваем их с нормируемым коэффициентом запаса. На самом опасном участке (в опасном сечении) действительный коэффициент запаса прочности должен равняться нормируемому, а на остальных участках должен быть больше нормируемого.
Пример 12.
Построить эпюры нормальных сил и нормальных напряжений для бруса, изображенного на рисунке. Собственный вес бруса в расчете не учитывать.

Решение.
Для определения внутренних усилий разбиваем прямолинейный брус на участки. Границами участков являются точки продольной оси, соответствующие изменению площади поперечного сечения и точкам приложения сосредоточенных сил. Из рассмотрения рис. а определяем, что брус необходимо разбить на четыре участка.
Проводим сечение I – I. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой N1 (рис. б). Запишем уравнение равновесия, проектируя силы на ось бруса:
![]() откуда N1 = F.
откуда N1 = F.
Очевидно, что
на всем первом участке (![]() ) нормальная сила N1 постоянна
по величине. Откладываем в масштабе значение нормальной силы N1 = F в пределах участка I – I (рис. е).
) нормальная сила N1 постоянна
по величине. Откладываем в масштабе значение нормальной силы N1 = F в пределах участка I – I (рис. е).
Проводим сечение II – II и, отбрасывая верхнюю часть бруса, заменяем ее действие нормальной силой N2 (рис. в). Проектируем все силы на ось бруса:
![]() откуда N2 = –F.
откуда N2 = –F.
Аналогично находим нормальные силы в сечении III – III (рис. г):
![]() откуда N3 = –F
откуда N3 = –F
и в сечении IV – IV (рис. д):
![]() откуда N4 = 0.
откуда N4 = 0.
Откладывая в масштабе значения нормальных сил N2, N3, N4 в пределах соответствующих участков, получаем эпюру нормальных сил (рис. е). Полученную таким путем эпюру принято штриховать прямыми линиями, перпендикулярными к оси бруса. Каждая такая линия в принятом масштабе дает величину нормальной силы в соответствующем поперечном сечении бруса. Знак «плюс» показывает, что в пределах данного участка – растяжение, а знак «минус» – сжатие.
Для построения
эпюры нормальных напряжений ![]() воспользуемся формулой
для каждого участка:
воспользуемся формулой
для каждого участка:
![]()
Эпюра нормальных напряжений (рис. ж) показывает, что наибольшего значения нормальные напряжения достигают в пределах третьего участка (участок III).
Пример 13.
Определить
величину продольной силы в сечении I – I бруса, находящегося в равновесии, если ![]() = 20 кН = 2
= 20 кН = 2![]() кг,
кг, ![]() = 10 кН = 1
= 10 кН = 1![]() кг,
кг, ![]() = 10 кН = 1
= 10 кН = 1![]() кг,
кг, ![]() = 60º (см. рис.).
= 60º (см. рис.).
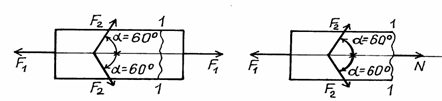
а) б)
Решение.
Пользуясь методом сечений:
а) рассекаем брус по заданному сечению;
б) отбрасываем любую, например, правую часть (рис, б);
в) заменяем ее действие на оставшуюся часть неизвестной продольной силой N, направив ее от сечения, т.е. предполагая, что продольная сила – растягивающая;
г) составляем условие равновесия и вычисляем N:
![]() ;
; ![]() ;
;
![]() = 1
= 1![]() кг = 10 кН,
кг = 10 кН,
т.е. ![]() .
.
Таким образом, продольная сила в поперечном сечении бруса численно равна алгебраической сумме проекций на его ось всех внешних сил, приложенных по одну сторону от сечения.
Пример 14.
Построить эпюру
продольных сил и вычислить диаметр стального короткого бруса, если ![]() = 40 кН = 4
= 40 кН = 4![]() кг,
кг, ![]() = 30 кН = 3
= 30 кН = 3![]() кг,
кг, ![]() = 80 кН = 8
= 80 кН = 8![]() кг; допускаемое напряжение на растяжение и сжатие принять
кг; допускаемое напряжение на растяжение и сжатие принять ![]() = 160 МПа = 1600 кг/см2
(см. рис.).
= 160 МПа = 1600 кг/см2
(см. рис.).
Решение.
1. Используя
формулу ![]() , для каждого из 3-х участков получим (рис. а):
, для каждого из 3-х участков получим (рис. а):
сечение 1 – 1 ![]() = – 4000 кг = –40 кН,
= – 4000 кг = –40 кН,
сечение 2 – 2 ![]() = – 4000 + 3000 = –1000 кг = –10 кН,
= – 4000 + 3000 = –1000 кг = –10 кН,
сечение 3 – 3 ![]() = – 4000 + 3000 + 8000=7000кг = 70 кН.
= – 4000 + 3000 + 8000=7000кг = 70 кН.
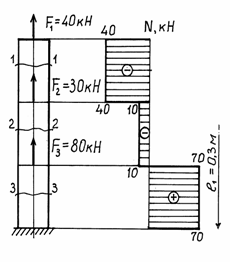
2. Проводим
рядом с брусом ось, параллельную его продольной оси, и, выбрав масштаб, откладываем
по длине каждого участка найденные значения продольных сил ![]() ,
, ![]() и
и ![]() , т.е. строим эпюру N
(рис. б).
, т.е. строим эпюру N
(рис. б).
3. Определяем опасное сечение – сечение, в котором нормальные напряжения максимальны (для пластичных материалов берем по абсолютной величине), т.е.
![]() ,
,
где А – площадь поперечного сечения бруса.
В нашем случае
для всех трех участков площадь поперечного сечения А постоянна и по абсолютной
величине N3>N2>N1. Опасное
сечение – любое сечение участка 3, где ![]() = 7000 кг = 70 кН. Тогда из условия прочности на растяжение и
сжатие для расчета площади поперечного сечения применим формулу
= 7000 кг = 70 кН. Тогда из условия прочности на растяжение и
сжатие для расчета площади поперечного сечения применим формулу
![]() ;
; ![]() .
.
Отсюда
![]()
Пример 15.
Для стального
ступенчатого бруса (![]() ), нагруженного осевыми внешними силами F1
= 150 кН = 15
), нагруженного осевыми внешними силами F1
= 150 кН = 15![]() кг, F2 = 100 кН = 10
кг, F2 = 100 кН = 10![]() кг, при длине
участков
кг, при длине
участков ![]() = 30 cм, b = 20 см,
= 30 cм, b = 20 см,
![]() = 15 см и площади поперечного сечения A = 10 см2 требуется:
= 15 см и площади поперечного сечения A = 10 см2 требуется:
1. Определить
внутренние продольные силы ![]() и построить их эпюру.
и построить их эпюру.
2. Вычислить для каждого участка напряжения ![]() и построить их эпюру.
и построить их эпюру.
3. Выполнить полную абсолютную деформацию бруса и определить перемещение сечения I – I (см. рис.).

а) б) в)
Решение.
1. Определяем внутренние продольные силы. Имеем два силовых участка длиной (а + b) и c. Для первого участка, имеем
![]() =
= ![]() = 15·103 кг
= 150 кН (растяжение);
= 15·103 кг
= 150 кН (растяжение);
для второго участка:
![]() =
= ![]() –
– ![]() = 15
= 15![]() – 20
– 20![]() = –5
= –5![]() кг = –50 кН (сжатие).
кг = –50 кН (сжатие).
Выбираем
масштаб и строим эпюру ![]() (рис. б).
(рис. б).
2. Вычисляем нормальные напряжения.
На участках а и b площадь поперечного сечения одинакова и равна 2А=20 см2. Тогда
![]()
на участке с:
![]()
Выбираем
масштаб и строим эпюру ![]() (рис. в).
(рис. в).
2. Полная деформация бруса:
![]()
= 0,00973 – 0,00375
= 0,00562 см = 0,0562![]() м.
м.
3. Поскольку верхнее сечение защемлено, то перемещение заданного сечения I – I численно будет равно абсолютной деформации участков бруса b и c, т.е.
![]()
Пример 16.
Стальной стержень
(![]() МПа) находится под действием внешних силы Р1 и
Р2 (рис. а).
МПа) находится под действием внешних силы Р1 и
Р2 (рис. а).
Требуется:
1. построить
эпюры продольных сил N, нормальных
напряжений σ и перемещений
сечений ![]() ;
;
2. определить
насколько изменится длина всего стержня если дано: Р1=2 кН; Р2=3,2 кН , ![]() =160 МПа.
=160 МПа.

Решение.
Построение эпюры продольных сил

![]()
Эпюра продольных сил N приведена на рис. б.
Условие
прочности ![]() отсюда
отсюда ![]()
Участок АВ
![]() .
.
Участок ВС
![]() .
.
Участок ДС
![]() .
.
Окончательно
принимаем ![]() .
.
Построение
эпюры нормальных напряжений ![]()

По данным
значениям строим эпюру ![]() рис. в.
рис. в.
Построение
эпюры ![]() .
.
Деформация
участка ![]()

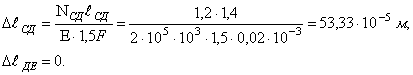
Деформации
характерных сечений ![]()
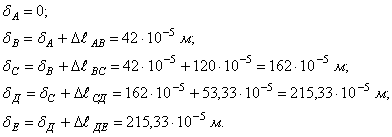
Эпюра ![]() показана на рис. г.
Длина всего стержня увеличится на
показана на рис. г.
Длина всего стержня увеличится на ![]()
Пример 17.
Стальной
стержень (модуль Юнга ![]() кН/см2) с размерами
кН/см2) с размерами ![]() см;
см; ![]() см,
см, ![]() см и площадью
поперечного сечения нижнего участка
см и площадью
поперечного сечения нижнего участка ![]() см2, а
верхнего –
см2, а
верхнего – ![]() см2
нагружен внешними осевыми силами
см2
нагружен внешними осевыми силами ![]() кН и
кН и ![]() кН (см. рис.).
Построить эпюры продольных сил
кН (см. рис.).
Построить эпюры продольных сил ![]() и нормальных
напряжений
и нормальных
напряжений ![]() . Оценить прочность стержня, если предельное напряжение
(предел текучести)
. Оценить прочность стержня, если предельное напряжение
(предел текучести) ![]() кН/см2, а допускаемый коэффициент запаса
кН/см2, а допускаемый коэффициент запаса ![]() . Найти удлинение стержня
. Найти удлинение стержня ![]() .
.
![]()
![]()
![]()

Решение.
1. Определяем значение опорной реакции ![]() , возникающей в заделке.
, возникающей в заделке.
Учитывая, что
![]() , направим опорную реакцию
, направим опорную реакцию ![]() вниз. Тогда из
уравнения равновесия
вниз. Тогда из
уравнения равновесия ![]() находим:
находим:
![]() кН.
кН.
2.
Строим эпюру продольных сил ![]() .
.
Разбиваем длину стержня на три участка (рис. а). Границами участков являются те сечения, в которых приложены внешние силы и (или) изменяется размер поперечного сечения стержня.
Воспользуемся методом сечений (РОЗУ). Делаем по одному сечению в произвольном месте каждого из трех участков стержня.
Начнем с
сечения 1 – 1. Отбросим (или закроем
листком бумаги) верхнюю часть стержня (рис. б).
Само сечение 1 – 1 мысленно считаем неподвижным. Мы видим, что внешняя сила ![]() растягивает рассматриваемую нижнюю часть стержня. Отброшенная нами
верхняя часть стержня противодействует этому растяжению. Это противодействие мы заменим внутренней продольной силой
растягивает рассматриваемую нижнюю часть стержня. Отброшенная нами
верхняя часть стержня противодействует этому растяжению. Это противодействие мы заменим внутренней продольной силой ![]() , направленной от сечения и соответствующей растяжению.
Разрушения стержня не произойдет только в том случае, если возникающая в
сечении 1 – 1 внутренняя продольная
сила
, направленной от сечения и соответствующей растяжению.
Разрушения стержня не произойдет только в том случае, если возникающая в
сечении 1 – 1 внутренняя продольная
сила ![]() уравновесит внешнюю силу
уравновесит внешнюю силу ![]() . Поэтому очевидно, что
. Поэтому очевидно, что
![]() кН.
кН.
Переходим к
сечению 2 – 2 (рис. в). Внешняя сила ![]() растягивает
рассматриваемую нами нижнюю часть стержня, а сила
растягивает
рассматриваемую нами нижнюю часть стержня, а сила ![]() ее сжимает (напомним,
что 2 – 2 мы мысленно считаем неподвижным). Причем, согласно условию
задачи,
ее сжимает (напомним,
что 2 – 2 мы мысленно считаем неподвижным). Причем, согласно условию
задачи, ![]() . Чтобы уравновесить эти две силы, в сечении 2 – 2 должна возникнуть внутренняя сила
. Чтобы уравновесить эти две силы, в сечении 2 – 2 должна возникнуть внутренняя сила ![]() , противодействующая сжатию,
то есть направленная к сечению. Она равна:
, противодействующая сжатию,
то есть направленная к сечению. Она равна:
![]() кН.
кН.
Делаем
сечение 3 – 3 (рис. г). Отбросим теперь часть стержня, расположенную
ниже этого сечения. Внутренняя продольная сила ![]() должна уравновесить
внешнюю (реактивную) сжимающую силу R. Поэтому она направлена к сечению и равна:
должна уравновесить
внешнюю (реактивную) сжимающую силу R. Поэтому она направлена к сечению и равна:
![]() кН.
кН.
Легко
убедиться в том, что полученный результат не изменится, если мы отбросим не
нижнюю, а верхнюю часть стержня. В этом случае продольная сила ![]() также противодействует
сжатию. Она равна:
также противодействует
сжатию. Она равна:
![]() кН.
кН.
При
построении эпюры продольных сил ![]() будем пользоваться
следующим правилом знаков: внутренняя
продольная сила, возникающая в поперечном сечении стержня, считается положительной, если она
противодействует растяжению стержня,
и отрицательной, если она
противодействует его сжатию.
будем пользоваться
следующим правилом знаков: внутренняя
продольная сила, возникающая в поперечном сечении стержня, считается положительной, если она
противодействует растяжению стержня,
и отрицательной, если она
противодействует его сжатию.
Это правило знаков вводится для того, чтобы можно было наглядно видеть, какая часть стержня испытывает деформацию растяжения, а какая часть – деформацию сжатия. Это обстоятельство может оказаться крайне важным, в частности для стержней из хрупкого материала, которые имеют разные допускаемые напряжения на растяжение и на сжатие.
Таким
образом, мы установили, что в любом
сечении нижнего участка стержня внутренняя продольная сила противодействует растяжению и равна ![]() кН. В любом сечении
среднего и верхнего участков стержня имеет место деформация сжатия, поэтому
кН. В любом сечении
среднего и верхнего участков стержня имеет место деформация сжатия, поэтому ![]() кН.
кН.
Для
построения эпюры продольных сил ![]() проводим тонкой линией ось, параллельную оси
стержня z (рис. д). Вычисленные значения продольных сил
в выбранном масштабе и с учетом их знака откладываем от этой вертикальной оси.
В пределах каждого из участков стержня продольная сила остается постоянной,
поэтому мы как бы «заштриховываем» горизонтальными
линиями соответствующий участок.
проводим тонкой линией ось, параллельную оси
стержня z (рис. д). Вычисленные значения продольных сил
в выбранном масштабе и с учетом их знака откладываем от этой вертикальной оси.
В пределах каждого из участков стержня продольная сила остается постоянной,
поэтому мы как бы «заштриховываем» горизонтальными
линиями соответствующий участок.
Отметим, что каждая линия «штриховки» (то есть ордината эпюры) в принятом масштабе дает значение продольной силы в соответствующем поперечном сечении стержня.
Полученную эпюру обводим жирной линией.
Анализируя
полученную эпюру, мы видим, что в местах приложения внешних сил на эпюре ![]() имеет место
скачкообразное изменение продольной силы на величину, равную значению
соответствующей внешней силы. Причем изменение поперечного размера стержня, как
это видно из рис. д,
никак не сказывается на характере эпюры
имеет место
скачкообразное изменение продольной силы на величину, равную значению
соответствующей внешней силы. Причем изменение поперечного размера стержня, как
это видно из рис. д,
никак не сказывается на характере эпюры ![]() .
.
3. Строим эпюру нормальных напряжений ![]() .
.
Нормальное напряжение, возникающее в k–м поперечном сечении стержня при растяжении (сжатии), вычисляется по следующей формуле
![]() ,
,
где ![]() и
и ![]() – продольная сила и
площадь k–го поперечного сечения стержня
соответственно.
– продольная сила и
площадь k–го поперечного сечения стержня
соответственно.
В первом поперечном сечении стержня нормальное
напряжение равно
![]() кН/см2,
кН/см2,
во втором –
![]() кН/см2,
кН/см2,
в третьем –
![]() кН/см2.
кН/см2.
Строим по
вычисленным значениям эпюру ![]() (рис. е). В пределах каждого из участков
стержня напряжения постоянны, то есть эпюра напряжений параллельна оси. Заметим,
что в отличие от эпюры N, на эпюре
(рис. е). В пределах каждого из участков
стержня напряжения постоянны, то есть эпюра напряжений параллельна оси. Заметим,
что в отличие от эпюры N, на эпюре ![]() «скачок» имеет место
не только в местах приложения внешних сил, но и там, где происходит изменение
размеров поперечного сечения стержня.
«скачок» имеет место
не только в местах приложения внешних сил, но и там, где происходит изменение
размеров поперечного сечения стержня.
4. Оцениваем прочность стержня.
Сопоставляем наибольшее (по модулю) нормальное
напряжение ![]() , которое в нашем примере возникает во втором сечении
стержня, с допускаемым напряжением
, которое в нашем примере возникает во втором сечении
стержня, с допускаемым напряжением ![]() . Напомним, что
допускаемое напряжение представляет собой долю от предельного напряжения
. Напомним, что
допускаемое напряжение представляет собой долю от предельного напряжения ![]() , то есть от напряжения, при котором начинается разрушение
материала. Разрушение стали, как пластичного
материала, начинается при появлении значительных остаточных деформаций.
Поэтому для стали предельное
напряжение равно пределу текучести:
, то есть от напряжения, при котором начинается разрушение
материала. Разрушение стали, как пластичного
материала, начинается при появлении значительных остаточных деформаций.
Поэтому для стали предельное
напряжение равно пределу текучести: ![]() . Тогда
. Тогда
![]() кН/см2.
кН/см2.
Условие прочности имеет вид ![]() . В
нашем случае
. В
нашем случае
![]() кН/см2 >
кН/см2 > ![]() кН/см2,
кН/см2,
следовательно, прочность стержня на втором участке не обеспечена.
Таким
образом, площадь поперечного сечения стержня на втором участке, равную ![]() см2, нам необходимо увеличить.
см2, нам необходимо увеличить.
Несложный анализ показывает, что на других участках стержня условие прочности выполняется.
Из условия прочности определяем требуемую площадь поперечного сечения стержня на втором участке:
![]() см2.
см2.
Принимаем на
втором участке ![]() см2.
см2.
5. Вычисляем
удлинение всего стержня ![]() .
.
При переменных по длине стержня значениях продольной силы и площади поперечного сечения удлинение вычисляется по формуле
![]() ,
,
где E – модуль Юнга, а ![]() – длина соответствующего участка стержня.
– длина соответствующего участка стержня.
Тогда
![]() см.
см.
Таким образом, длина стержня уменьшается на 1,7 мм.
Пример 18.
Для стального
ступенчатого бруса (см. рис.1) (![]() МПа), нагруженного силами, кратными F= 30 кН, с длиной участков
l= 0,4 м при
допускаемом нормальном напряжении
МПа), нагруженного силами, кратными F= 30 кН, с длиной участков
l= 0,4 м при
допускаемом нормальном напряжении ![]() = 160 МПа требуется:
= 160 МПа требуется:
1. Определить величину продольных сил на каждом участке бруса и построить их эпюру.
2. Подобрать площади поперечных сечений для каждого участка бруса.
3. Вычислить полную деформацию бруса и построить эпюру перемещений.
4. Определить перемещение заданного сечения А-А.
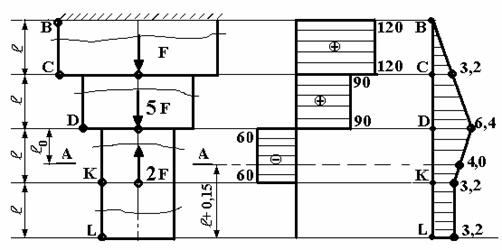
N, кН
![]() , м
, м
а)
б) в)
Рис.1
Решение.
1. Определение величины продольных сил. Разбиваем брус на четыре участка и определяем продольные силы N.
Участок KL:
рассекаем брус поперечным сечением и отбрасываем ту его часть, на которой
расположена заделка. Заменяем ее действие неизвестной, продольной силой N1, предположительно направив ее на растяжение, т.е. от сечения (рисунок 2).
Составляем уравнение статического равновесия, выбрав положительное направление
оси Z, и определяем величину продольной силы N1:
![]() ; N1 = 0;
; N1 = 0;

Рис. 2
Рис. 3
Участок DK: аналогично участку KL делаем сечение в любом месте по длине участка DK; отбрасываем верхнюю часть с заделкой, заменяем верхнюю отброшенную часть бруса неизвестной продольной силой N2 , также направив ее на растяжение (рисунок 3) и составляем условие статического равновесия:
![]() ; 2F + N2 = 0;
; 2F + N2 = 0;
N2 = - 2F = -2×30 = - 60 кН.
Отрицательное значение продольной силы N2 говорит о том, что действительное направление этой силы противоположное, т.е. не на растяжение, а на сжатие. Исправляем свою ошибку, направив силу N2 в обратную сторону, и отбросив минус в ее значении.

Рис. 4
Рис.5
Участок СD: продольную силу N3 определяем аналогично определению продольных сил на участках KL и DK (рисунок 4).
![]() ; 2F – 5F+ N3 = 0;
; 2F – 5F+ N3 = 0;
N3 = 5F –2F = 3F = 3 ×30 = 90 кН.
В данном случае получили знак продольной силы N3 положительный. Это говорит о том, что выбранное направление силы N3 сделано верно .
Участок ВC: для расчетной схемы (рис. 5) аналогично выше изложенному получаем:
![]() ; 2F – 5F - F+ N4
= 0;
; 2F – 5F - F+ N4
= 0;
N4 = 5F + F – 2F = 4F = 4×30 = 120 кН.
Знак у продольной силы N4 положительный – направление ее выбрано верно.
Далее строим эпюру продольных сил. Условимся откладывать
положительные значения продольных сил справа от оси, а отрицательные
(сжимающие) – слева от оси (рисунок 4,б):
1. Участок KL: продольная сила N1 = 0;
2. Участок DK: продольная сила N2 = 60 кН вызывает сжатие. Следовательно, откладывается в отрицательную сторону.
3. Участок СD: величина продольной силы N3 = 90 кН, она направлена на растяжение и, соответственно, откладывается в положительную сторону от оси эпюры.
4. Участок ВС: здесь продольная сила N4 = 120 кН растягивает стержень и откладывается в положительную сторону.
Правило проверки эпюры продольных сил: в точке приложения к брусу внешней сосредоточенной нагрузки на эпюре появляется скачок, равный величине внешней нагрузки и направленный в сторону действия этой нагрузки.
2. Подбор площадей поперечных сечений для каждого участка бруса. Величины площадей поперечных участков находятся из условия прочности при растяжении и сжатии.
![]() ; отсюда
; отсюда ![]() .
.
Участки KL и DK: Площади поперечных сечений участков KL и DK, согласно расчетной схемы, одинаковы и будут равны
![]()
Участок СD:
![]()
Участок ВС:
![]()
3. Вычисление полной деформации бруса и построение эпюры перемещений.
Полная деформация бруса равна алгебраической сумме деформаций его участков:
![]() .
.
Для определения полной деформации бруса необходимо определить деформации всех отдельных участков.
Абсолютное линейное удлинение (укорочение) участка бруса длиной l согласно закону Гука равно:
![]()
Определяем деформации отдельных участков.
Участок KL:
![]() т.к. N1 = 0;
т.к. N1 = 0;
Участок DK: ![]()
Участок CD: ![]()
Участок ВC: ![]()
Полная линейная деформация бруса будет равна:
![]() (0 – 0,32 + 0,32 + 0,32 + 0,32)×10-3 =
0,32×10-3м.
(0 – 0,32 + 0,32 + 0,32 + 0,32)×10-3 =
0,32×10-3м.
Построение эпюры перемещений начинаем от защемления
(сечения В), т.к. по условию задачи
это сечение не может перемещаться, т.е. ![]() .
.
Перемещение
сечения С
численно будет равно деформации участка ВС: ![]() м.
м.
Для остальных участков аналогично получим:
![]() ;
;
![]() ;
;
![]() .
.
Построение эпюры перемещений (рис.1, в) выполняется аналогично построению эпюры продольных сил; проводим ось эпюры перемещений параллельно оси стержня и откладываем в выбранном масштабе значения величин перемещений сечений бруса с учетом их знаков и соединяем их прямыми линиями.
4. Определение перемещения заданного сечения. Перемещение заданного сечения А-А будет складываться из перемещения точки D и деформации отрезка длиной l0 (рис. 1,а):
![]() ;
;
![]()
![]()
![]()
![]() .
.
На расчетной
схеме рисунок 1 проводим на уровне сечения А-А линию
до пересечения ее с эпюрой перемещений ![]() . Эта линия должна отсечь на этой эпюре отрезок, равный
вычисленному значению
. Эта линия должна отсечь на этой эпюре отрезок, равный
вычисленному значению ![]() м (см. рис.1,б).
м (см. рис.1,б).
Пример 19.
Для изображенного на рис. а стержня простроить эпюру нормальных сил и перемещений поперечных сечений.
|
а) в) г) |
|
Решение.
1. Определение опорной реактивной силы
Уравнение равновесия сил, направленных по оси Z, имеет вид
![]() ,
,
откуда
![]() .
.
2. Определение внутренних
нормальных сил N методом сечений и построение эпюры N(z)
Стержень имеет
три участка, границами которых служат сечения, где приложены внешние силы ![]() . Для обнаружения нормальных сил на этих участках используем
метод сечений. Мысленно рассекаем стержень на каждом из участков на расстояниях
. Для обнаружения нормальных сил на этих участках используем
метод сечений. Мысленно рассекаем стержень на каждом из участков на расстояниях
![]() и рассматриваем
равновесие одной из частей рассеченного стержня, заменяя действие отброшенных
частей внутренними нормальными силами
и рассматриваем
равновесие одной из частей рассеченного стержня, заменяя действие отброшенных
частей внутренними нормальными силами ![]() (рисунок 1, б). В результате получаем уравнения
равновесия
(рисунок 1, б). В результате получаем уравнения
равновесия
![]() .
.
С учетом ![]() находим
находим
![]() .
.
Нормальные силы на каждом из участков известны, что позволяет легко построить график-эпюру нормальных сил (рис. в).
Из эпюры находим опасное сечение или участок, где нормальные силы максимальны. Таким оказывается второй участок, на котором
![]() .
.
3. Расчет на прочность
Для опасных сечений второго участка составляем условие прочности
![]() .
.
Различают три типа расчета на прочность.
Проверочный расчет на прочность
Известны все
величины в условии прочности. Пусть, например ![]() .
.
Тогда
![]() ,
,
что меньше
допускаемого значения ![]() . Следовательно, стержень удовлетворяет условию прочности.
. Следовательно, стержень удовлетворяет условию прочности.
Проектировочный расчет на прочность
Требуется
найти диаметр ![]() круглого поперечного
сечения стержня, для которого площадь сечения определяется формулой
круглого поперечного
сечения стержня, для которого площадь сечения определяется формулой ![]() .
.
Тогда
![]() ,
,
тогда
![]() .
.
Сохраняя значения ![]() , получаем
, получаем
![]() .
.
Округляя, принимаем ![]() .
.
Расчетное напряжение
![]()
![]() , что меньше допускаемого на 5,8 %.
, что меньше допускаемого на 5,8 %.
Определение допускаемой нагрузки
Имеем
![]() .
.
Пусть ![]() , тогда
, тогда
![]() .
.
4. Построение эпюры перемещений
Поскольку в задаче мы имеем три участка с различными значениями нормальных сил, то формулу удобно записать в виде
 ,
,
где ![]() – номер участка;
– номер участка; ![]() – постоянная в начале i-го участка;
– постоянная в начале i-го участка; ![]() – текущая координата сечения i-го
участка;
– текущая координата сечения i-го
участка; ![]() – жесткость i-го участка,
– жесткость i-го участка, ![]() – координаты начального сечения i-го
участка.
– координаты начального сечения i-го
участка.
На первом участке ![]() имеем
имеем
 .
.
Следовательно, эпюра − прямая линия.
При ![]() имеем
имеем ![]() , т. е.
, т. е. ![]() при жестком
защемлении.
при жестком
защемлении.
При ![]() получаем
получаем
![]() .
.
На втором участке![]() имеем
имеем
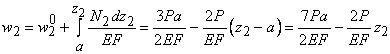 .
.
Эпюра на втором участке − прямая линия.
При ![]() получаем
получаем
![]() .
.
На третьем участке ![]() имеем
имеем
 .
.
При ![]() получаем
получаем
![]() .
.
Используя
полученные данные, строим график-эпюру перемещений ![]() поперечных сечений
(рисунок 1, г).
поперечных сечений
(рисунок 1, г).
5. Расчеты на жесткость
Согласно (5), полное удлинение стержня не должно превышать условия жесткости стержня:
![]() .
.
Отсюда можно найти другое допускаемое значение силы:
![]() .
.
Сравнивая два значения, видим что Рдоп наименьшее.
Пример 20.
Построить
эпюры ![]() для стержня,
изображенного на рисунке, при нагружении силой P и
равномерно распределенной нагрузкой q. Составить условие
прочности.
для стержня,
изображенного на рисунке, при нагружении силой P и
равномерно распределенной нагрузкой q. Составить условие
прочности.
|
а) в) г) |
|
Решение.
1. Определение опорной реакции
Уравнение равновесия сил (рис. а)
![]() ,
,
откуда ![]() .
.
2. Определение внутренних усилий ![]() методом сечений
методом сечений
Стержень
содержит два участка с разным характером нагружения. На первом участке делаем
сечение на расстоянии ![]() и из условия равновесия
левой отсеченной части находим (рисунок 1, б)
и из условия равновесия
левой отсеченной части находим (рисунок 1, б)
![]() .
.
Следовательно,
на первом участке график-эпюра ![]() прямая линия.
прямая линия.
Строим эпюру
по двум точкам. При ![]() имеем
имеем ![]() , а при
, а при ![]() получаем
получаем ![]() .
.
На втором
участке отсекаем на расстоянии ![]() правую часть стержня.
Действие левой части на правую заменяем усилием
правую часть стержня.
Действие левой части на правую заменяем усилием ![]() (рис. б).
Из уравнения равновесия отсеченной части правой части находим
(рис. б).
Из уравнения равновесия отсеченной части правой части находим
![]() .
.
Следовательно,
на втором участке ![]() имеем постоянное
значение.
имеем постоянное
значение.
Эпюра ![]() приведена на рис. в. На расстоянии
приведена на рис. в. На расстоянии ![]() усилие
усилие ![]() . Найдем это расстояние:
. Найдем это расстояние:
![]() ;
; ![]() .
.
Максимальное
значение ![]() возникает в
защемлении. Это сечение является опасным по прочности.
возникает в
защемлении. Это сечение является опасным по прочности.
Контроль правильности построенной эпюры осуществляется с помощью правил дифференциальной зависимости Д. Журавского
![]() :
:
1) на незагруженном участке ![]() и
и ![]() ;
;
2) на равномерно загруженном участке ![]() и
и ![]() , т.е. эпюра − прямая линия, возрастающая с ростом
, т.е. эпюра − прямая линия, возрастающая с ростом ![]() , если угловой коэффициент
, если угловой коэффициент
![]() , и убывающая, если
, и убывающая, если ![]() .
.
Оба правила в нашей задаче соблюдены.
3. Расчет на прочность
Условие прочности стержня
![]() .
.
Пусть поперечное сечение стержня − прямоугольное с соотношением
сторон ![]() . Тогда
. Тогда ![]() .
.
Допускаемое напряжение ![]() (дерево),
(дерево), ![]() ,
, ![]() . Требуется определить размеры поперечного сечения h и b. Тогда:
. Требуется определить размеры поперечного сечения h и b. Тогда:
![]() ,
,
откуда ![]() .
.
Округляем
значение ![]() до значения
до значения ![]() , тогда
, тогда ![]()
![]() . Проверяем стержень на прочность с подобранными размерами
поперечного сечения:
. Проверяем стержень на прочность с подобранными размерами
поперечного сечения:
![]() ,
,
что больше
допустимого значения ![]() .
.
Перенапряжение
составит ![]() , т.е.
, т.е. ![]() . Отклонение от
. Отклонение от ![]() допускается в пределах
допускается в пределах
![]() .
.
4. Построение эпюры перемещений ![]()
На первом участке:
![]() ,
,
или
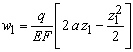 .
.
Эпюра –
парабола. В сечении ![]() , где
, где ![]() , перемещение достигает максимального значения:
, перемещение достигает максимального значения:
![]() .
.
Выпуклость параболы определяется знаком второй производной ![]() , т.к.
, т.к. ![]() . Следовательно, кривая перемещений обращена выпуклостью к
верху.
. Следовательно, кривая перемещений обращена выпуклостью к
верху.
При ![]() имеем
имеем
![]() .
.
На втором участке ![]() получаем
получаем
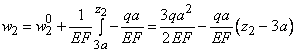 .
.
Эпюра − прямая линия. При ![]() имеем
имеем ![]() , а при
, а при ![]()
![]() .
.
Строим прямую линию на втором участке (рис. г). Задача решена.
Определение напряжений и перемещений
в брусе при растяжении-сжатии с учетом собственного веса
Определить
диаметр d, а также удлинение участка CD для круглого стержня, нагруженного
силой F, принимая во внимание
собственный вес. Удельный вес ![]() , допускаемое напряжение [
, допускаемое напряжение [![]() ]
и модуль упругости Е материала
стержня заданы.
]
и модуль упругости Е материала
стержня заданы.
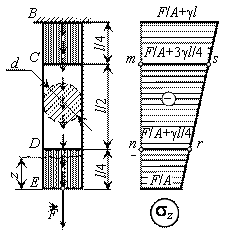
Решение
Для призматического стержня при действии собственного веса и сосредоточенной силы F на свободном конце имеем:
-
продольная сила в
произвольном сечении
![]() ,
,
- нормальное напряжение в этом же сечении
![]() .
.
Из условия прочности находим искомый диаметр
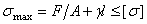 и
и
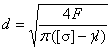 ,
,
oткуда ![]() .
.
Удлинение участка CD находим по общей формуле
![]() .
.
Здесь ![]() – это площадь трапеции
mnrs, которая равна
– это площадь трапеции
mnrs, которая равна
![]() .
.
Следовательно, ![]() .
.
Пример 22.
Стержень переменного
сечения с соотношением площадей поперечных сечений A1/A2 =2
находится под действием сосредоточенных сил и собственного веса (рис. а). Материал стержня на всех участках
одинаков. Требуется построить эпюры распределения продольной силы и напряжений
вдоль оси стержня и определить перемещение сечения а–а.

Решение.
Строим эпюры изменения продольной силы и напряжений вдоль оси стержня. Собственный вес стержня принято учитывать, заменяя его распределенной по всей длине нагрузкой. Интенсивность распределенной нагрузки равна собственному весу, действующему на единицу длины стержня, т. е.
на первом и втором участках
![]() ,
,
на третьем участке
![]() ,
,
где ![]() – объемный вес материала стержня.
– объемный вес материала стержня.
Эпюры продольной силы и напряжений строим, используя метод сечений. Заметим, что угол наклона эпюры продольной силы зависит от величины q и, следовательно, при построении эпюры N в масштабе угол ее наклона на первом и втором участке должен быть больше, чем на третьем участке, так как A1 по условию больше, чем A2 (рис. б). Угол же наклона эпюры напряжений зависит от объемного веса g, и поэтому угол наклона эпюры напряжений на всех участках одинаков (рис. в).
Находим
перемещение (опускание) сечения а–а.
Это перемещение можно искать разными способами. По первому способу для
определения перемещения используем формулу ![]() . Здесь F –
сосредоточенная сила, вызывающая перемещение участка длиной l; G
– собственный вес рассматриваемого
участка. Эту формулу можно использовать на участках постоянного сечения между
сосредоточенными силами. Отсчет надо вести от неподвижного сечения, т.е.
заделки. Например, в рассматриваемой задаче перемещение сечения
а–а складывается из удлинения участка
длиной l1, которое мы
обозначим
. Здесь F –
сосредоточенная сила, вызывающая перемещение участка длиной l; G
– собственный вес рассматриваемого
участка. Эту формулу можно использовать на участках постоянного сечения между
сосредоточенными силами. Отсчет надо вести от неподвижного сечения, т.е.
заделки. Например, в рассматриваемой задаче перемещение сечения
а–а складывается из удлинения участка
длиной l1, которое мы
обозначим ![]() , и удлинения участка длиной
, и удлинения участка длиной ![]() . При определении удлинения
. При определении удлинения ![]() в формуле
сила F равна сумме F1, F2 и собственного веса всех расположенных ниже участков.
Вес участка стержня длиной l1:
в формуле
сила F равна сумме F1, F2 и собственного веса всех расположенных ниже участков.
Вес участка стержня длиной l1:
![]() . Таким образом, по формуле
. Таким образом, по формуле
![]() .
.
Удлинение ![]() происходит под
действием сосредоточенной силы, состоящей из силы F2, веса участков стержня, расположенных ниже сечения а–а, и собственного веса участка
происходит под
действием сосредоточенной силы, состоящей из силы F2, веса участков стержня, расположенных ниже сечения а–а, и собственного веса участка ![]() . То есть
. То есть
![]() .
.
Окончательно
опускание сечения а–а равно ![]() .
.
Если построена
эпюра распределения напряжений, то для определения перемещения заданного
сечения удобно использовать второй
способ, применяя формулу ![]() . В этой формуле
. В этой формуле ![]() , а
, а ![]() – это площадь эпюры
напряжений. Таким образом, если найти площадь
двух трапеций на участке между неподвижным сечением (заделкой) и
сечением а–а (заштрихованные площади
– это площадь эпюры
напряжений. Таким образом, если найти площадь
двух трапеций на участке между неподвижным сечением (заделкой) и
сечением а–а (заштрихованные площади ![]() и
и ![]() эпюры
эпюры ![]() на рис. в)
и разделить полученную величину на модуль упругости, мы получим искомое
перемещение сечения а–а:
на рис. в)
и разделить полученную величину на модуль упругости, мы получим искомое
перемещение сечения а–а:
![]() .
.
При вычислении перемещения обращайте внимание на единицы измерения величин, входящих в формулы. Рекомендуем окончательный результат получить в сантиметрах.
Пример 23.
Построить
эпюры нормальных сил и нормальных напряжений для бруса, изображенного на рис. а. Принять a = 0,4 м; площадь поперечного сечения бруса на участках III и IV А = 20 см2; сосредоточенная сила F = 0,5 кН, собственный вес ![]() = 0,0078 кг/см3 = 76,44 кН/м3.
= 0,0078 кг/см3 = 76,44 кН/м3.
Решение.
Для
определения внутренних усилий разбиваем брус с прямолинейной осью на четыре участка.
Проводим сечение I – I (рис. а) и отбрасываем верхнюю часть бруса,
заменяя действие отброшенной части нормальной силой N1 (рис.
б). Так как сечение I –I может быть проведено в любом месте
участка I, то длина оставшейся части участка
будет переменной величиной, и поэтому обозначим ее через x (рис. б), причем ![]() . Запишем уравнение равновесия, проектируя силы, действующие
на оставшуюся часть бруса, на направление оси бруса:
. Запишем уравнение равновесия, проектируя силы, действующие
на оставшуюся часть бруса, на направление оси бруса:

а б в г д е ж
![]() откуда
откуда ![]()
Через ![]() обозначен собственный
вес оставшейся части бруса первого участка, в пределах которого площадь
поперечного сечения равна 2А, а длина
оставшейся части обозначена через x. Подставим численные
значения в полученную формулу:
обозначен собственный
вес оставшейся части бруса первого участка, в пределах которого площадь
поперечного сечения равна 2А, а длина
оставшейся части обозначена через x. Подставим численные
значения в полученную формулу:
![]() .
.
Записанное
выражение показывает, что эпюра нормальных сил в пределах первого участка
представляет собой наклонную прямую линию. Для построения этой прямой определим
значение нормальной силы N1 в начале
первого участка (x = 0): N1(x = 0) = 500 Н и в конце первого
участка (x = a= 0,5 м): N1 (х =
0,5 м) =![]()
Полученные значения откладываем в масштабе в соответствующих точках эпюры нормальных сил (рис. е). Найденные точки соединяем прямой линией, затем штрихуем первый участок эпюры прямыми линиями, перпендикулярными к оси бруса.
Проводим
сечение II – II и повторяем порядок
расчета, описанный выше для сечения I – I.
Переменная величина х участка II – II будет изменяться в пределах ![]() . Составим уравнение равновесия (рис. в)
. Составим уравнение равновесия (рис. в)
![]() откуда
откуда ![]()
где ![]() – собственный вес
части бруса, расположенного ниже сечения II
– II.
– собственный вес
части бруса, расположенного ниже сечения II
– II.
Окончательно имеем
![]()
Определяем значение нормальной силы N2 в начале второго участка (х= 0,5 м):
![]()
и в конце этого же участка (х = хmax = 1 м):
![]()
Полученные значения N2 откладываем в масштабе в начале и в конце второго участка (рис. е).
Проводим сечение III – III и для оставшейся части бруса составляем уравнение равновесия (рис. г)
![]()
откуда ![]() где
где ![]() – собственный вес
оставшейся части бруса третьего участка;
– собственный вес
оставшейся части бруса третьего участка; ![]() – собственный вес первого и второго участков.
– собственный вес первого и второго участков.
Тогда для
участка ![]()
![]()
где нормальная сила N3 в начале третьего участка будет N3(х=0) = –194,2 Н; а в конце третьего участка получаем N3 (х = a = 0,5 м) = –117,8 Н. Найденные значения N3 переносим на эпюру нормальных сил.
И наконец, рассматривая равновесие оставшейся части бруса, после проведения сечения IV – IV получаем (рис. д)
![]()
откуда ![]() где
где ![]() Н – собственный вес участков I
– I и II – II,
Н – собственный вес участков I
– I и II – II, ![]() – собственный вес третьего и оставшейся части четвертого
участков.
– собственный вес третьего и оставшейся части четвертого
участков.
В этом случае имеем
![]()
т.е. в начале четвертого участка N4 (х = 0,5 м) = 382,2 Н, а в конце этого же участка N4 (х = 1 м) = 458,64 Н. Вычисленные значения N4 откладываем в масштабе на эпюре нормальных сил (рис. е).
Эпюра нормальных сил показывает, что первый и четвертый участок подвержены растяжению, а второй и третий – сжатию.
Для вычисления
значений нормальных напряжений ![]() и построения эпюры
нормальных напряжений используем формулу:
и построения эпюры
нормальных напряжений используем формулу:
![]()
![]()
![]()
![]()
Эпюра нормальных напряжений показывает, что самое большое нормальное напряжение возникает в сечении, проходящем через точку Л четвертого участка (рис. ж), т.е. на опоре.
Пример 24.
Дано: брус
постоянной жёсткости (см. рис.) длиной 2l, площадью поперечного
сечения A, нагружен сосредоточенной силой F, распределённой нагрузкой интенсивностью q и собственным весом![]() .
.
Требуется: построить эпюру N.

Эп N
Решение.
1. Определение опорной реакции
Составим сумму проекций всех сил на продольную ось бруса Z:
![]()
2. Установление силовых участков
Изучив
действие внешних нагрузок F, ![]() , q на брус, нетрудно установить, что
имеется два силовых участка:
, q на брус, нетрудно установить, что
имеется два силовых участка:
- первый
участок, ![]() , на котором N зависит от F и
, на котором N зависит от F и ![]() ;
;
- второй
участок, ![]() , на внутреннюю силу N оказывают влияние F,
, на внутреннюю силу N оказывают влияние F, ![]() ,q.
,q.
3. Составление
аналитических выражений для нормальной силы![]()
С
учётом метода сечений брус рассекаем на две части, отбрасываем верхние
отсечённые части, заменяя их действие силами![]() . Целесообразно силы N1 и
N2 направить по внешней нормали к сечению, то есть
предполагать, что они вызывают растяжение бруса.
. Целесообразно силы N1 и
N2 направить по внешней нормали к сечению, то есть
предполагать, что они вызывают растяжение бруса.
![]()
4. Вычисление значений N в характерных сечениях бруса
Определим значения N на границах силовых участков:
- при ![]() ;
;
- при ![]() .
.
- при ![]() ;
;
- при ![]() .
.
- при ![]() ;
;
![]() .
.
По полученным
результатам расчёта строим эпюру N с учётом масштаба (см. рис.).
Примечание. В расчётно-проектировочной работе необходимо результаты расчётов доводить до числовых величин. Для проверки правильности построения эпюры N нужно воспользоваться следующими дифференциальными зависимостями:
![]() .
.
Перемещения поперечных сечений
брусьев в статически определимых задачах при растяжении-сжатии
Пример 25.
Определить
перемещение нижнего конца стержня, изображенного на рис. а. Задачу решить без учета собственного веса материала бруса.
Принять ![]() a = 0,5 м; А = 10 см2;
сосредоточенная сила F = 10 кН.
a = 0,5 м; А = 10 см2;
сосредоточенная сила F = 10 кН.
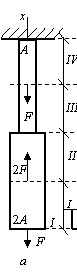

Решение.
Для рассматриваемого случая эпюра нормальных сил представлена на рис. е. Для стержня со ступенчатым изменением площади и нормальных сил перемещения поперечных сечений вычисляются по формуле (1.7). Рассматривая рис. а и рис. е, запишем формулу для определения перемещения нижнего конца стержня в виде:
![]()
![]()
Знак «минус» в
ответе показывает, что общая длина стержня уменьшится, т.е. нижний конец
стержня переместится вверх вдоль его оси на величину ![]() мм.
мм.
Пример 26.
Определить перемещение
нижнего конца стержня, изображенного на рис. а. Принять![]() объемный вес материала стержня
объемный вес материала стержня ![]() = 76440 Н/м3.
= 76440 Н/м3.

Решение.
Для рассматриваемого случая эпюра нормальных сил представлена на рис. б.
Эпюра нормальных сил построена с учетом сосредоточенных внешних сил и с учетом собственного веса материала бруса. Выделим на эпюре нормальных сил (рис. б) ее постоянные нормальные составляющие и треугольные участки эпюры, учитывающие собственный вес соответствующего участка. Разделение составляющих эпюры нормальных сил на рис. б произведено пунктирными линиями.
Теперь
перемещение поперечного сечения от постоянной составляющей эпюры нормальных сил
будет определяться по формуле ![]() а перемещение от действия собственного веса –
по формуле
а перемещение от действия собственного веса –
по формуле ![]()
Для рассматриваемого случая формула для определения перемещения нижнего конца стержня будет иметь вид
![]()
![]()
![]()
Знак «+» показывает, что общая длина стержня
увеличится, т.е. нижний конец стержня переместится вниз вдоль его оси на
величину ![]() м
(рис. а).
м
(рис. а).
Определим перемещение сечения а –
а (рис. а). Для этого мысленно
разрежем эпюру нормальных сил в соответствующем сечении а – а и отбросим нижнюю
часть эпюры. На основании оставшейся части эпюры нормальных сил (рис. в) определяем перемещение сечения а –
а, используя формулы ![]() и
и ![]()
![]()
![]()
![]()
![]()
Полученный ответ показывает, что поперечное сечение а – а переместится вниз вдоль оси стержня.
Пример 27.
Для стального бруса квадратного сечения сжатого силой Р с учетом собственного веса при исходных данных приведенных ниже, требуется (см. рис. а):
1. Определить количество расчетных участков;
2. Составить
аналитические выражения для нормальных сил Nz ,
нормальных напряжений ![]() и вычислить их
значения для каждого из участков с учетом их собственных весов;
и вычислить их
значения для каждого из участков с учетом их собственных весов;
3. Построить
эпюры Nz
и ![]() ;
;
4. Вычислить перемещение верхнего конца колонны от действия силы Р и собственного веса.
Дано: Р = 20 кН;
l1 = l2 = l3 = 0,4 м; модуль упругости стали Е = ![]() кН/м2; F1 =
кН/м2; F1 = ![]() м2;
F2 =
м2;
F2 = ![]() м2;
F3 =
м2;
F3 = ![]() м2;
м2;
![]() = 78
кН/м3 .
= 78
кН/м3 .
Решение.
1. Определение
количества участков. Так как нормальная сила Nz зависит от величин внешних сил, в
данном случае включающих в себя и собственный вес колонны, а последний, в свою
очередь, от размеров поперечного сечения Fi и объемного веса ![]() g, то границами
участков следует назначать те сечения, в которых приложены внешние
сосредоточенные силы и где происходит скачкообразное изменение площади поперечного
сечения или объемного веса материалов конструкций.
g, то границами
участков следует назначать те сечения, в которых приложены внешние
сосредоточенные силы и где происходит скачкообразное изменение площади поперечного
сечения или объемного веса материалов конструкций.
Исходя из
вышесказанного, учитывая ![]() =const,
брус будет иметь три участка:
=const,
брус будет иметь три участка:
1 участок - от 0 до сечения В (где приложена сила Р);
2 участок - от сечения В до сечения С;
3 участок - от сечения С до сечения D.
Следует
заметить, что при определении нормальных напряжений используются те же
участки.

2. Составить аналитические выражения для нормальных сил Nz, нормальных напряжений sz и вычислить их значения для каждого из участков, с учетом их собственных весов. Для этого воспользуемся методом сечений.
1 участок
(0 - В) ![]() .
.
Проведя
сечение 1 - 1 на расстоянии z1
от начала координат (точка 0), рассмотрим равновесие верхней части.
При этом, к рассматриваемой части прикладываются в
центре ее тяжести собственный вес и нормальная сила ![]() , заменяющую действие отброшенной нижней части бруса на
верхнюю рассматриваемую (рис. б).
Составив уравнение равновесия рассматриваемой верхней части колонны по оси z ,
получим:
, заменяющую действие отброшенной нижней части бруса на
верхнюю рассматриваемую (рис. б).
Составив уравнение равновесия рассматриваемой верхней части колонны по оси z ,
получим:
![]() .
.
В свою очередь, собственный вес верхней части колонны определяется следующим образом:
![]() кН.
кН.
Тогда выражение для нормальной силы будет иметь вид:
![]() кН,
кН,
а для
нормальных напряжений ![]() :
:
![]() кН/м2.
кН/м2.
Так как, ![]() и
и ![]() линейно зависят от z1 ,
то для построения их графиков (эпюр) достаточно определить значения этих
величин на границах участка, т.е.
линейно зависят от z1 ,
то для построения их графиков (эпюр) достаточно определить значения этих
величин на границах участка, т.е.
при z1 = 0 ![]()
при z1 = 0,4 м ![]() кН;
кН;
![]() кН/м2.
кН/м2.
Знаки минус при ![]() и
и ![]() указывают на то, что принятое направление для этих величин
не совпадает с действительным, т. к. в принятой схеме продольная сила не
растягивает, а сжимает первый участок.
указывают на то, что принятое направление для этих величин
не совпадает с действительным, т. к. в принятой схеме продольная сила не
растягивает, а сжимает первый участок.
2 участок (В - С) ![]() .
.
Аналогично
предыдущему проводим сечение 2-2 на расстоянии z2
(рис. в). Для верхней части
составляем уравнение равновесия ![]() .
.
В это
уравнение войдут: собственный вес первого участка ![]() ; собственный вес отсеченной части второго участка
; собственный вес отсеченной части второго участка ![]() ; сосредоточенная сила Р = 20 кН, а также сила
; сосредоточенная сила Р = 20 кН, а также сила ![]() .
.
Тогда уравнение равновесия примет вид:
![]() ,
,
отсюда
![]() =
= ![]() =
= ![]() кН.
кН.
Учитывая постоянство площади поперечного сечения на втором участке, выражение для нормального напряжения может быть записано таким образом:
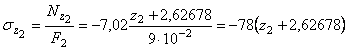 кН/м2.
кН/м2.
Вычислим
значения ординат ![]() и
и ![]() в граничных сечениях второго участка:
в граничных сечениях второго участка:
при z2 = 0,4 м ![]() кН,
кН,
![]() кН/м2;
кН/м2;
при z2 = 0,8 м ![]() кН,
кН,
![]() кН/м2.
кН/м2.
3 участок (С - D)
![]() .
.
Составив
уравнение равновесия ![]() (рис. г) для верхней части бруса, получим:
(рис. г) для верхней части бруса, получим:
![]() ,
,
откуда
![]()
![]() кН.
кН.
Выражение для напряжения:
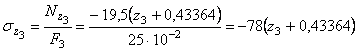 кН/м2.
кН/м2.
Вычислим
значения ординат ![]() и
и ![]() в граничных сечениях
третьего участка:
в граничных сечениях
третьего участка:
при z3 = 0,8 м ![]() (0,8) = -19,5 (0,8 + 0,43364) = -24,056
кН,
(0,8) = -19,5 (0,8 + 0,43364) = -24,056
кН,
![]() (0,8) = -78 (0,8 + 0,43364) = -96,224
кН/м2;
(0,8) = -78 (0,8 + 0,43364) = -96,224
кН/м2;
при z3 = 1,2 м ![]() (1,2) = -19,5 (1,2 + 0,43364) = -31,856
кН,
(1,2) = -19,5 (1,2 + 0,43364) = -31,856
кН,
![]() кН/м2.
кН/м2.
3. Построение
эпюр Nz и![]() . По причине
линейной зависимости нормальной силы и напряжений от координаты z для построения их эпюр достаточно значений Nz и
. По причине
линейной зависимости нормальной силы и напряжений от координаты z для построения их эпюр достаточно значений Nz и ![]() в
граничных сечениях каждого из участков (см. рис. д, е). Необходимым условием правильности построения этих графиков
является выполнение следующих требований:
в
граничных сечениях каждого из участков (см. рис. д, е). Необходимым условием правильности построения этих графиков
является выполнение следующих требований:
- скачок в эпюре Nz должен находиться в точке приложения сосредоточенного усилия и быть равным по величине значению этой силы;
- скачки
в эпюре ![]() должны
совпадать с точками приложения внешней силы Р и изменения площади поперечного
сечения колонны.
должны
совпадать с точками приложения внешней силы Р и изменения площади поперечного
сечения колонны.
После анализа полученных эпюр (рис. д, е) легко можно убедиться, что построения выполнены правильно.
4. Вычисление перемещения верхнего конца колонны от действия всех сил. Полное перемещение согласно закону Гука может быть вычислено по формуле
 .
.
В данном случае это выражение принимает следующий вид:
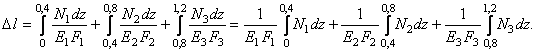
Так как
величины определенных интегралов равны площадям, очерченным соответствующими подынтегральными
функциями, то для вычисления перемещений ![]() достаточно
вычислить площади эпюры Nz на каждом из этих участков и
разделить их на Ei Fi . Следовательно,
достаточно
вычислить площади эпюры Nz на каждом из этих участков и
разделить их на Ei Fi . Следовательно,
 .
.
Пример 28.
![]()
![]()
![]()
![]()
![]() Найти
закон изменения площадей поперечного сечения бруса равного сопротивления,
испытывающего растяжение под действием силы
и собственного веса.
Найти
закон изменения площадей поперечного сечения бруса равного сопротивления,
испытывающего растяжение под действием силы
и собственного веса.

Решение.
В каждом
сечении бруса равного сопротивления нормальные напряжения должны быть равны
постоянной величине (![]() ). Запишем условие равновесия элемента длиной dx:
). Запишем условие равновесия элемента длиной dx:
![]() или
или ![]()
Имеем dG – собственный вес элемента бруса длиной dx:
![]() тогда
тогда ![]() или
или ![]()
Интегрируя последнее выражение, находим
![]()
где С – произвольная постоянная интегрирования, которая находится из граничных условий. Окончательно запишем
![]()
Постоянную
интегрирования находим из условия, что при х
= 0 имеем А(х) = А0, т.е. получаем ![]() .
.
Таким образом, закон изменения площади поперечного сечения А(х) получает вид
![]() ,
,
т.е. в брусе равного сопротивления площади поперечных сечений изменяются по логарифмическому закону.
Онлайн-калькулятор "Расчет прочности при растяжении-сжатии"
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов


