Главная

Лекция 2. Осевое растяжение – сжатие

Содержание

Продольные силы в поперечных сечениях

Напряжение в поперечных сечениях стержня

Деформации и перемещения. Закон Гука

Потенциальная энергия деформации

Напряженное и деформированное состояние при растяжении и сжатии

Расчеты на прочность и жесткость при растяжении и сжатии

Расчеты статически определимых стержней

Учет собственного веса при растяжении и сжатии

Подбор сечений с учетом собственного веса (при растяжении и сжатии)

Деформации при действии собственного веса

Композитный брус

Расчет статически определимых стержневых систем

Понятие о статически неопределимых системах

Основные положения. Связи необходимые и дополнительные.

Степень статической неопределимости. Методика ее определения

Раскрытие статической неопределимости

Примеры типовых расчетов статически неопределимых систем

Расчет конструкций по допускаемым нагрузкам

Расчет статически определимых систем по способу допускаемых нагрузок

Расчет статически неопределимых систем по способу допускаемых нагрузок

Расчет гибких нитей

Вопросы для самопроверки

Продольные силы в поперечных сечениях

Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только продольные силы N, а прочие силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.

Это самый простой и часто встречающийся вид деформации. Обычно он наблюдается когда внешняя нагрузка действует вдоль продольной оси стержня. Продольной осью стержня называется линия, проходящая через центры тяжести поперечных сечений.

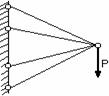
Обычным является растяжение стержня силами, приложенными к его концам. Передача усилий к стержню может быть осуществлена различными способами, как это показано на рис. 2.1.

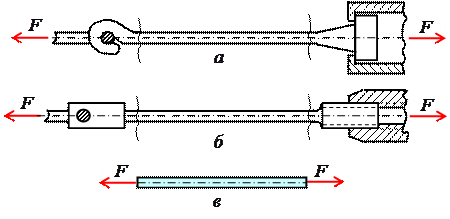
Рис. 2.1

Во всех случаях, однако, система внешних сил образует равнодействующую F, направленную вдоль оси стержня. Поэтому независимо от условий крепления растянутого стержня, расчетная схема в рассматриваемых случаях (рис. 2.1, а, б) оказывается единой (рис. 2.1, в) согласно принципу Сен – Венана.

Если воспользоваться методом сечений (рис. 2.2), то становится очевидным, что во всех поперечных сечениях стержня возникают нормальные силы N_z, равные силе F (рис. 2.2, б).

Сжатие отличается от растяжения, формально говоря, только знаком силы N_z. При растяжении нормальная сила N_z направлена от сечения (рис. 2.2, б), а при сжатии – к сечению.

Рис. 2.2

Растягивающие продольные силы принято считать положительными (рис. 2.3, а), а сжимающие – отрицательными (рис. 2.3, б).

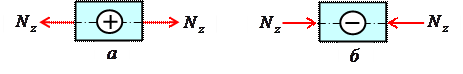
Рис. 2.3

Вместе с тем между растяжением и сжатием могут обнаружиться и качественные различия, как, например, при изучении процессов разрушения материала или при исследовании поведения длинных и тонких стерж-ней, для которых сжатие сопровождается, как правило, изгибом.

При расчете стержней, испытывающий деформацию растяжения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от N_z), возникающих в стержне, и нахождение линейных перемещений в зависимости от внешней нагрузки.

Продольные силы (N_z), возникающие в поперечных сечениях стержня, определяются по внешней нагрузке с помощью метода сечений.

График, показывающий изменение продольных сил по длине оси стержня, называется эпюрой продольных сил (эп. N_z). Он дает наглядное представление о законе изменения продольной силы.

Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.

Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти N_max при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.

Перед построением эпюр необходимо освободить брус, в котором будем строить эпюры от опорных связей (выделить объект равновесия) и приложить к нему все действующие внешние силы (активные и реактивные). Затем необходимо установить границы участков, в пределах которых закон изменения внутренних сил постоянный. Границами таких участков являются сечения, где приложены сосредоточенные силы или начинается и кончается распределенная нагрузка, а также сечения, где имеется перелом стержня.

Применяя метод сечений и учитывая правила знаков изложенные выше, получаем уравнения изменения внутренних сил в пределах длины каждого участка бруса. Затем, используя, полученные зависимости строим графики (эпюры) этих усилий. Ординаты эпюр в определенном масштабе откладываем от базисной линии, которую проводим параллельно оси бруса.

Рассмотрим стержень постоянного поперечного сечения, жестко защемленный правым концевым сечением и нагруженный заданной внешней сосредоточенной нагрузкой F и распределенной q (рис. 2.4, а).

Прежде всего определим опорную реакцию R₁, задавшись ее направлением вдоль оси z.

ΣF_z=0, -R₁ - 22 + 24∙0,6 = 0, R₁= -7,6 кН.

Знак минус говорит о том, что действительное направление опорной реакции R₁ противоположно показанному на рис. 2.4, а. Исправляем его и в дальнейших расчетах знак минус у опорной реакции R₁ не учитываем (рис. 2.4, в, г).

Под участком будем понимать часть стержня, на которой N_z представляется некоторым аналитическим выражением. На другом участке N_z будет определяться другой функцией.

Границами участка являются начало и конец стержня, сечения, где приложены сосредоточенные нагрузки, начинается и заканчивается распределенная нагрузка.

В нашем случае стержень разбивается на два участка. В пределах первого участка мысленно рассечем стержень на две части нормальным сечением (рис. 2.4, б, в).

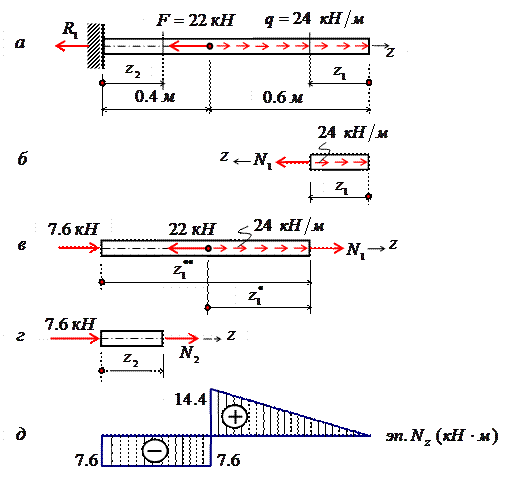
Рис. 2.4

Направления продольных сил (рис. 2.4, б – г) приняты в предположении, что они являются растягивающими (т. е. положительными). Если в результате расчета значение N_i получится со знаком «минус», то это будет означать, что в действительности стержень в этом сечении сжат.

Поскольку обе части стержня являются равноправными, то N₁ на первом участке в сечении, определяемом координатой z₁, можно определить рассматривая равновесие его правой (рис. 2.4, б) либо левой (рис. 2.4, в) частей.

В нашем случае для определения N₁ предпочтительнее рассмотреть равновесие правой части – к ней приложено меньше сил (рис. 2.4, б). Начало координат совмещаем с правым концевым сечением первого участка. Ось z направляем налево. Пределы изменения положения сечения вдоль продольной оси 0≤z₁≤0,6 м. Спроектируем все силы, действующие на правую часть, на продольную ось.

ΣF_z=0, N₁ - 24∙z₁ = 0, N₁ =24∙z₁, N₁(0)= 0, N₁(0,6)= 14,4 кН.

Поскольку функция N₁ =24∙z₁ получилась линейная, то для построении графика ее изменения вдоль продольной оси (эп. N_z) достаточно вычислить значения продольной силы на границах первого участка, отложить их перпендикулярно продольной оси вверх (стержень растянут) и провести через них прямую линию (рис. 2.4, д).

Таким образом, в пределах первого участка стержень растянут и нормальная сила изменяется по линейному закону.

Этот же результат можно получить, рассматривая равновесие левой части стержня.

Здесь при выборе системы координат рассмотрим два варианта. При первом варианте начало координат совмещаем с левым концевым сечением второго участка. Ось z направляем направо. Пределы изменения положения сечения вдоль продольной оси 0,4 м≤≤1,0 м. Спроектируем все силы, действующие на левую часть, на продольную ось.

ΣF_z=0, N₁ +7,6 – 22 + 24∙( - 0,4)= 0, N₁ =24- 24∙, N₁(0,4)= 14,4 кН, N₁(1,0)= 0.

Во втором варианте введем скользящую систему координатных осей. Начало координат совмещаем с левым концевым сечением первого участка. Ось z направляем направо. Пределы изменения положения сечения вдоль продольной оси 0≤≤0,6 м. Имеем

ΣF_z=0, N₁ +7,6 – 22 + 24∙ = 0, N₁ =14,4- 24∙, N₁(0)= 14,4 кН, N₁(0,6)= 0.

Заметим, что при выборе скользящей системы координат, функция N₁=f(z, q) меняется от нуля, что делает последующие расчеты менее трудоемкими.

Сравнивая все три варианта определения N₁, приходим к выводу, что когда мы оставляем ту часть стержня, к которой приложено меньше внешних нагрузок, то расчеты оказываются более простыми.

При некотором навыке можно сразу составить выражение для N₁, не изображая отдельные части бруса, на которые он расчленяется поперечными сечениями (рис. 2.4, б, в). Например,

при 0≤z₁≤0,6 м, N₁ =24∙z₁;

при 0,4 м≤≤1,0 м, N₁ =7,6 + 22 - 24∙(-0,4);

при 0≤≤0,6 м, N₁ = -7,6 + 22 - 24∙.

Таким образом, на основании метода сечений продольная сила в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, на его продольную ось.

Причем проекция внешней силы берется со знаком плюс, если сила растягивает часть стержня от точки ее приложения до рассматриваемого сечения и, наоборот, со знаком минус – если сжимает.

Осталось определить значение продольной силы N₂ в произвольном сечении, определяемом координатой z₂, на втором участке (рис. 2.4, г). Так как продольная сила N₂ численно равна алгебраической сумме внешних сил, приложенных к стержню слева от сечения (рассматриваем равновесие левой части стержня), то N₂= -7,6 кН (реакция R₁=7,6 кН сжимает часть стержня длиной z₂). Здесь принимаем скользящую систему координат, с началом в левом концевом сечении второго участка. Ось z направляем направо.

Эпюра N_z на втором участке представлена на рис 2.4, д в виде прямоугольника со знаком минус, поскольку N₂= -7,6 кН =const. Таким образом, в пределах второго участка стержень претерпевает сжатие постоянной нормальной силой.

Каждая ордината эп. N_z (рис. 2.4, д) в принятом масштабе равна величине продольной силы, действующего в том поперечном сечении стержня, которому соответствует эта ордината.

Видно, что на участке между точками приложения сосредоточенных сил R₁ и F продольная сила имеет постоянное значение, а на участке, где приложена распределенная внешняя нагрузка, меняется по линейному закону (рис. 2.4, д).

Характерно, что скачки на эп. N_z обусловлены наличием в соответствующих сечениях сосредоточенных сил R₁ и F.

Рассмотрим несколько примеров определения внутренних сил.

Пример 1.

Пусть имеется стержень постоянного поперечного сечения, нагруженный силами 2Р и 3Р вдоль продольной оси стержня, показанный на рис.2.4.1. Определить величину внутренних сил.

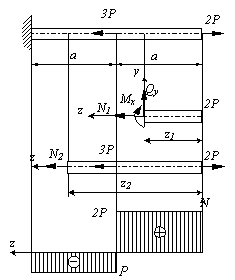
Рис.2.4.1

Решение.

Стержень может быть разделен на два участка, граничными точками которых являются точки приложения сосредоточенных сил и точка закрепления. Если начало координат расположить на правом конце стержня, а ось z направить справа налево, то, используя метод сечений, рассекая последовательно участки, отбрасывая левую часть, заменяя ее действие внутренними усилиями N, Q_y, M_x и уравновешивая оставшуюся часть, получим:

I участок:

Как видно, при растяжении в поперечных сечениях стержня возникает только один внутренний силовой фактор - нормальная сила N.

II участок:

Таким образом, нормальная сила равна алгебраической сумме проекций сил, приложенных к отсеченной части на продольную ось

Полученные результаты для большей наглядности удобно представить в виде графика, (эпюры N), показывающего изменение продольной силы вдоль оси стержня (рис.2.4.1). Построим на первом участке линию параллельную оси z на высоте 2Р, на втором участке – линию со значением -Р. Области ограниченные графиком и осью z принято штриховать и обозначать знак этой области. Видно, что наибольшая продольная сила возникает на первом участке стержня и, как следствие, при прочих равных условиях, он скорее может разрушиться, чем второй участок.

Пример 2.

Построить эпюру продольных сил для жестко защемленной балки (рис.2.4.2).

Решение:

1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке.

2. Определяем продольную силу в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.

3. По найденным значениям строим эпюру .

Положительные значения откладываются (в выбранном масштабе) над осью эпюры, отрицательные – под осью.

Рис.2.4.2

Пример 3.

Два стержня, соединенные в т. А, находятся под действием силы Р (рис.2.5, а). Определить усилия, действующие в стержнях.

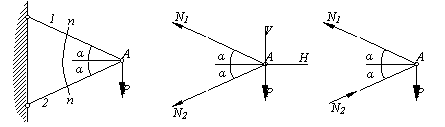
а) б) в)

Рис.2.5

Решение.

Воспользуемся методом сечений. Рассечем стержни в произвольном месте сечения n-n. Отбросим левую отсеченную часть. Заменим отброшенную часть, приложив усилия N₁ и N₂ в сечениях к правой части. Направление усилий целесообразно выбрать так чтобы они растягивали отсеченные части (рис.2.5, б).

Уравновесим отсеченную часть, запишем уравнения

Решая, из первого уравнения получим

из второго уравнения окончательно имеем

Так как величина силы N₂ < 0, то её направление следует изменить на противоположное (рис.2.5, в). Согласно рисунку нормальная сила N₁ растягивает отсеченную часть стержня 1 - она положительна, сила N₂ сжимает отсеченную часть стержня 2 - она отрицательна.

Пример 4.

Абсолютно жесткий брус подвешен на двух стержнях и находится под действием силы Р (рис.2.6, а). Определить усилия в стержнях.

Решение.

Используя метод сечений, получим отсеченную часть, показанную на рис.2.6, б.

Запишем уравнения равновесия и :

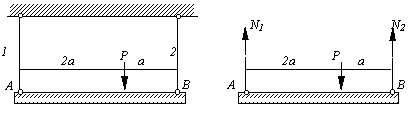
Рис.2.6

Решая систему уравнений, получим

Напряжение в поперечных сечениях стержня

Нормальная сила N приложена в центре тяжести сечения, является равнодействующей внутренних сил в сечении и, в соответствии с этим, определяется следующим образом:

Но из этой формулы нельзя найти закон распределения нормальных напряжений в поперечных сечениях стержня. Для этого обратимся к анализу характера его деформирования.

Если на боковую поверхность этого стержня нанести прямоугольную сетку (рис. 2.2, б), то после нагружения поперечные линии а-а, b-b и т.д. переместятся параллельно самим себе, откуда следует, что все поверхностные продольные волокна удлинятся одинаково. Если предположить также, что и внутренние волокна работают таким же образом, то можно сделать вывод о том, что поперечные сечения в центрально растянутом стержне смещаются параллельно начальным положениям, что соответствует гипотезе плоских сечений (гипотезе Бернулли).

Значит, все продольные волокна стержня находятся в одинаковых условиях, а следовательно, нормальные напряжения во всех точках поперечного сечения должны быть также одинаковы и равны

где A - площадь поперечного сечения стержня.

В сечениях, близких к месту приложения внешних сил, гипотеза Бернулли нарушается: сечения искривляются, и напряжения в них распределяются неравномерно. По мере удаления от сечений, в которых приложены силы, напряжения выравниваются, и в сечениях, удаленных от места приложения сил на расстояние, равное наибольшему из размеров поперечного сечения, напряжения можно считать распределенными по сечению равномерно. Это положение, называемое принципом Сен-Венана, позволяет при определении напряжений в сечениях, достаточно удаленных от мест приложения внешних сил, не учитывать способ их приложения, заменять систему внешних сил статически эквивалентной системой. Например, экспериментально установлено, что во всех трех случаях нагружения стержня (рис. 2.7, а) значения напряжений в сечениях, удаленных от крайних сечений на расстояние не менее высоты сечения h, одинаковы: (рис. 2.7, б), а в сечениях, близких к местам приложения внешних сил, распределения напряжений по сечению существенно различны (рис. 2.7, в).

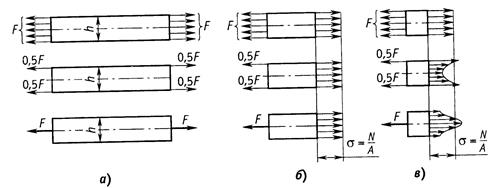
Рис.2.7

Высказанное предположение о равномерном распределении нормальных напряжений в поперечном сечении справедливо для участков, достаточно удаленных от мест: резкого изменения площади поперечного сечения (рис. 2.2, в); скачкообразного изменения внешних нагрузок; скачкообразного изменения физико-механических характеристик конструкций.

Нормальные напряжения при сжатии определяют также, как и при растяжении, но считают отрицательными.

Следует помнить, что длинные (тонкие) стержни, нагруженные сжимающими силами, могут потерять устойчивость. Расчет стержней на устойчивость рассмотрен в разделе «Устойчивость».

В инженерных сооружениях встречаются растянутые или сжатые элементы, имеющие отверстия. В сечениях с отверстием определяют осредненные нормальные напряжения по формуле

где - площадь поперечного сечения нетто; A - площадь поперечного сечения брутто; - площадь его ослабления.

Деформации и перемещения. Закон Гука

Рассмотрим однородный стержень с одним концом, жестко заделанным, и другим - свободным, к которому приложена центральная продольная сила Р (рис. 2.8). До нагружения стержня его длина равнялась l - после нагружения она стала равной (рис. 2.8). Величину называют абсолютной продольной деформацией (абсолютным удлинением) стержня. В большинстве случаев оно мало по сравнению с его первоначальной длиной l (∆l<<l).

Рис. 2.8

Если в нагруженном стержне напряженное состояние является однородным, т.е. все участки стержня находятся в одинаковых условиях, деформация остается одной и той же по длине стержня и равной

Величина ε называется относительной продольной деформацией.

Если же по длине стержня возникает неоднородное напряженное состояние, то для определения его абсолютного удлинения необходимо рассмотреть бесконечно малый элемент длиной dz (рис. 2.8). При растяжении он увеличит свою длину на величину и его деформация составит:

В пределах малых деформаций при простом растяжении или сжатии закон Гука записывается в следующем виде (нормальные напряжения в поперечном сечении прямо пропорциональны относительной линейной деформации ):

Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости материала первого рода (модуль продольной упругости). Его величина постоянна для каждого материала. Он характеризует жесткость материала, т.е. способность сопротивляться деформированию под действием внешней нагрузки.

Из совместного рассмотрения уравнений (2.5) и (2.6) получим:

откуда с учетом того, что

окончательно получим:

Если стержень изготовлен из однородного изотропного материала с Е = const, имеет постоянное поперечное сечение A = const и нагружен по концам силой Р, то из (2.7) получим

Зависимость (2.8) также выражает закон Гука. Знаменатель EA называется жесткостью при растяжении - сжатии или продольной жесткостью.

При решении многих практических задач возникает необходимость, наряду с удлинениями, обусловленными действием механических нагрузок, учитывать также удлинения, вызванные температурным воздействием. В этом случае пользуются принципом независимости действия сил, и полные деформации рассматривают как сумму силовой и температурной деформаций:

где - коэффициент температурного расширения материала; t -перепад температуры тела. Для однородного стержня, нагруженного по концам продольными силами Р и равномерно нагретого по длине, получим:

Потенциальная энергия деформации

Внешние силы, приложенные к упругому телу и вызывающие изменение геометрии тела, совершают работу W на соответствующих перемещениях. Одновременно с этим в упругом теле накапливается потенциальная энергия его деформирования U. При действии динамических внешних нагрузок часть работы внешних сил превращается в кинетическую энергию движения частиц тела К. Приняв энергетическое состояние системы до момента действия данных сил равным нулю, и в условиях отсутствия рассеивания энергии, уравнение баланса энергии можно записать в следующем виде:

W = U + K. (2.11)

При действии статических нагрузок К = 0, следовательно,

W = U. (2.12)

Это означает, что при статическом нагружении работа внешних сил полностью преобразуется в потенциальную энергию деформации. При разгрузке тела производится работа за счет потенциальной энергии деформации, накопленной телом. Таким образом, упругое тело является аккумулятором энергии. Это свойство упругого тела широко используется в технике, например, в заводных пружинах часовых механизмов, в амортизирующих рессорах и др. В случае простого растяжения (сжатия) для вывода необходимых расчетных зависимостей потенциальной энергии деформации рассмотрим решение следующей задачи.

На рис. 2.9, а изображен растягиваемый силой Р стержень, удлинение которого соответствует отрезку , ниже показан график изменения величины удлинения стержня в зависимости от силы Р (рис. 2.9, б). В соответствии с законом Гука этот график носит линейный характер.

Пусть некоторому значению силы Р соответствует удлинение стержня . Дадим некоторое приращение силе - соответствующее приращение удлинения составит . Тогда элементарная работа на этом приращении удлинения составит:

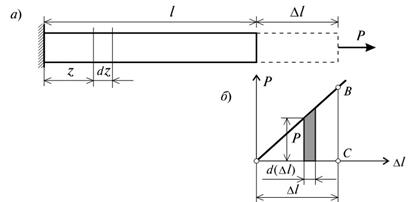
Рис.2.9

вторым слагаемым, в силу его малости, можно пренебречь, и тогда

Полная работа равна сумме элементарных работ, тогда, при линейной зависимости “нагрузка - перемещение”, работа внешней силы Р на перемещении будет равна площади треугольника ОСВ (рис. 2.9), т.е.

В свою очередь, когда напряжения и деформации распределены по объему тела V равномерно (как в рассматриваемом случае) потенциальную энергию деформирования стержня можно записать в виде:

Поскольку, в данном случае имеем, что , то

т.е. подтверждена справедливость (2.12).

С учетом (2.8) для однородного стержня с постоянным поперечным сечением и при Р = const из (2.17) получим:

Единицей измерения потенциальной энергии деформации является 1Hм = 1Дж.

Напряженное и деформированное состояние при растяжении и сжатии

Рассмотрим более подробно особенности напряженного состояния, возникающего в однородном растянутом стержне. Определим напряжения, возникающие на некоторой наклонной площадке, составляющей угол  с плоскостью нормального сечения (рис. 2.10, а).

Из условия , записанного для отсеченной части стержня (рис. 2.10, б), получим:

где A - площадь поперечного сечения стержня, - площадь наклонного сечения. Из (2.19) легко установить:

Раскладывая напряжение р по нормали и касательной к наклонной площадке (рис. 2.10, в), с учетом (2.20) получим:

Рис. 2.10

Полученные выражения показывают, что для одной и той же точки тела величины напряжений, возникающих в сечениях, проходящих через эту точку, зависят от ориентации этой площадки, т.е. от угла . При из (2.21) следует, что . При , т.е. на продольных площадках, . Это означает, что продольные слои растянутого стержня не взаимодействуют друг с другом. Касательные напряжения принимают наибольшие значения при , и их величина составляет . Важно отметить, что . Следовательно, в любой точке тела на двух взаимно перпендикулярных площадках касательные напряжения равны между собой по абсолютной величине. Это условие является общей закономерностью любого напряженного состояния и носит название закона парности касательных напряжений.

Теперь перейдем к анализу деформаций в растянутом стержне. Наблюдения показывают, что его удлинение в продольном направлении сопровождается пропорциональным уменьшением поперечных размеров стержня (рис. 2.11).

Если обозначить:

то, как показывают эксперименты, для данного материала и является безразмерным коэффициентом Пуассона. Величина является важной характеристикой материала и определяется экспериментально. Для реальных материалов принимает значения 0,1...0,45.

Рис. 2.11

При растяжении стержня возникают не только линейные, но и угловые деформации.

Рассмотрим прямой угол АВС (рис. 2.12, а), образованный отрезками АВ и АС, в недеформированном состоянии.

Рис. 2.12

При растяжении стержня точки А, В и С займут положение А¢, B¢, C¢ соответственно. Величина

называется угловой деформацией или угловым сдвигом в точке А.

Совместим точки А и А¢ и рассмотрим взаимное расположение отрезков АВ и А¢B¢ (рис. 2.12, б). На этом рисунке отметим вспомогательные точки K и L и прямую n, перпендикулярную отрезку А¢B¢. Из рис. 2.12, б имеем:

откуда с учетом получим:

Для определения спроектируем ломаную на ось n

откуда, учитывая малость угла , т.е. , получим:

В результате совместного рассмотрения (2.22) и (2.23) получим:

Откуда .

Следовательно,

Сопоставляя выражение с выражением из (2.21) окончательно получим закон Гука для сдвига:

где величина называется модулем сдвига или модулем упругости материала второго рода.

Расчеты на прочность и жесткость при растяжении-сжатии

Основной задачей расчета конструкции является обеспечение ее безопасной эксплуатации. Важнейшим условием, обеспечивающим безопасную эксплуатацию конструкции, является условие прочности. Существуют различные методы обеспечения прочности конструкций. Мы чаще всего будем пользоваться одним из этих методов – расчетом по допускаемым напряжениям. Согласно этому методу для конструкций, работающих на растяжение-сжатие, условие прочности, составленное для опасного сечения, можно записать в таком виде:

где – максимальное напряжение в конструкции; – характеристика материала, называемая допускаемым напряжением.

Допускаемое напряжение находится по формуле

где – предельное напряжение, при достижении которого в стержне наступает предельное состояние материала: появляются пластические деформации, если материал стержня – пластичный, или происходит разрушение, если стержень выполнен из хрупкого материала; n – нормируемый коэффициент запаса прочности.

Кроме формулы (2.26), возможен второй вариант условия прочности

называется действительным коэффициентом запаса прочности, показывающим во сколько раз надо увеличить максимальное напряжение в стержне, чтобы материал стержня оказался в опасном (предельном) состоянии.

Условие прочности в зависимости от цели поставленной задачи позволяет выполнять расчеты на прочность двух видов: проектный и проверочный. Для спроектированного стержня можно также определять допускаемую нагрузку.

Проектный расчет выполняют с целью определения размеров поперечных сечений элемента конструкции при известных рабочих нагрузках и материале (допускаемых напряжений). Площадь поперечного сечения определяют из выражения

Форма сечения стержня не влияет на его прочность при растяжении (сжатии). Форму сечения стержня необходимо знать только для определения размеров сечения при известном значении площади.

Зная площадь сечения и его форму, находят размеры сечения.

Проверочный расчет выполняют для спроектированной конструкции с целью проверки ее прочности. При проверочном расчете должны быть известны площадь опасного сечения, нагрузка и материал (допускаемое напряжение). Проверочный расчет выполняют по формуле (2.26).

Определение допускаемой нагрузки для спроектированного элемента конструкции, размеры поперечного сечения которого и материал (допускаемые напряжения) известны. Условие прочности в этом случае записывают в виде

Зная значение , определяют допускаемую нагрузку .

Так как допускаемые напряжения не имеют точного значения, а выбираются приближенно, то при проверочном расчете максимальные рабочие напряжения могут превышать допускаемые на 5%. По этой же причине можно округлять полученные в расчетах значения площади опасного поперечного сечения или допускаемой нагрузки так, чтобы максимальные напряжения отличались от допускаемых не более чем на 5%. По этой же причине можно округлять полученные в расчетах значения площади опасного поперечного сечения или допускаемой нагрузки та, чтобы максимальные напряжения отличались от допускаемых не более чем на 5%.

При проектировании элементов конструкций стремятся сделать их во всех сечениях равнопрочными.

Рассмотренные три вида расчетов на прочность можно выполнять не только при растяжении или сжатии, а при любом виде деформации (сдвиге, кручении, изгибе).

При проектировании строительных конструкций расчет на прочность стальных элементов, подверженных центральному растяжению или сжатию, следует выполнять по формуле

где – коэффициент условий работы, принимаемый по СНИП (см. табл.2.1) или другим нормам.

Таблица 2.1

Элементы конструкции
Колонны общественных зданий и опор водонапорных башен Элементы стержневых конструкций покрытий и перекрытий: а) сжатых при расчетах на устойчивость б) растянутых в сварных конструкциях Сплошные составные балки, колонны, несущие статическую нагрузку и выполненные с помощью болтовых соединений, при расчетах на прочность Сечения прокатных и сварных элементов, несущих статическую нагрузку, при расчетах на прочность Сжатые элементы из одиночных уголков, прикрепляемые одной полкой	0,95 0,95 0,95 1,1 1,1 0,75
Примечание: В случаях, не оговоренных в настоящих нормах, в формулах следует принимать .

Для хрупких строительных материалов условия прочности принимают вид:

при растяжении:

при сжатии:

где и – допускаемые напряжения при растяжении и сжатии; n_t и n_c – нормативные коэффициенты запаса прочности по отношению к пределу прочности (n_t, n_c>1).

Для центрально сжатых бетонных элементов формула (2.33) записывается в виде:

где – коэффициент, принимаемый для бетона тяжелого, мелкозернистого и легкого равным 1,00; для ячеистого автоклавного – 0,85; для ячеистого неавтоклавного – 0,75.

В некоторых случаях работоспособность элемента конструкции определяется не только его прочностью, но и жесткостью, т.е. способностью элемента воспринимать нагрузки без недопустимых упругих деформаций. При расчетах на жесткость определяют максимальные перемещения сечений и сопоставляют их с допускаемыми перемещениями.

Условие жесткости, ограничивающее изменение длины элемента, имеет следующий общий вид:

где - изменение размеров детали;

[] - допускаемая величина этого изменения.

Учитывая, что при растяжении (сжатии) абсолютное удлинение в общем виде определяется как алгебраическая сумма величин по участкам

условие жесткости при растяжении (сжатии) запишем следующим образом:

Так как перемещение, согласно закону Гука, зависит от нагрузки и размеров поперечного сечения, условие жесткости позволяет решать те же три вида задач, что и условие прочности.

Расчеты статически определимых стержней

Статически определимый стержень – это стержень, который можно рассчитать, используя только уравнения равновесия (уравнения статики).

В любой науке, которая называется «точной» и в которой используются аналитические методы описания состояний и явлений, не обойтись без моделей. В нашем случае при решении различных задач мы каждый раз будем выбирать для рассматриваемого объекта расчетную схему.

Расчетная схема – это упрощенная схема конструкции или ее элементов, освобожденная от несущественных в данной задаче особенностей. При этом расчетная схема должна отражать все наиболее существенное для характера работы данной конструкции и не содержать второстепенных факторов, мало влияющих на результаты ее расчета. Построение и обоснование расчетной схемы – ответственный этап проектирования и расчета конструкции.

Перейдем к рассмотрению конкретных примеров.

Пример 5.

Чугунная труба-стойка высотой H=l=3м с наружным диаметром D=25 см и внутренним диаметром d=20 см нагружена сжимающей силой F=50 т, модуль упругости чугуна . Найти напряжение в поперечном сечении колонны, абсолютное и относительное укорочения .

Решение.

Как уже говорилось выше, решение задачи начинается с выбора расчетной схемы. В данном случае стойка изображается как вертикальный стержень длиной H=l=3м, жестко закрепленный в нижней части (условное изображение фундамента или земли). К верхней части стержня приложена сосредоточенная сжимающая сила (направление к стержню). При этом линия действия силы должна совпадать с осью стержня. Кроме того, рядом необходимо изобразить поперечное сечение стойки с указанием основных размеров. В данном примере – это кольцо. Расчетная схема для решения задачи изображена на рис. 2.13, а.

Далее строим эпюру продольной силы и определяем максимальное внутреннее усилие, возникающее в колонне. Поскольку внешняя нагрузка постоянна по высоте, то возникает только одна сжимающая продольная сила

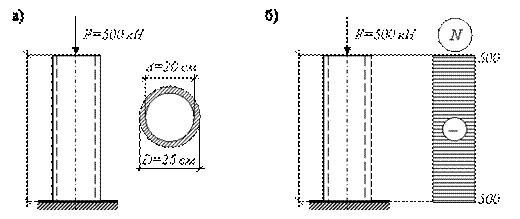
Рис. 2.13

Максимальное нормальное напряжение определяется по формуле:

где A [м²] – площадь трубы:

тогда:

Абсолютное и относительное укорочения стойки определяем по формулам:

Знак "минус" обозначает уменьшение размера (укорочение).

Пример 6.

Стальной стержень круглого сечения растягивается усилием F=10 т. Относительное удлинение не должно превышать l/2000, а напряжение – 1200 кг/см². Найти наименьший диаметр, удовлетворяющий этим условиям, если модуль упругости стали

Решение.

Как и ранее, решение задачи начинается с изображения расчетной схемы и построения эпюра продольных сил (рис. 2.14).

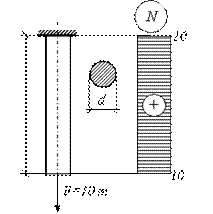
Рис.2.14

По условию задачи напряжение не должно превышать 1200 кг/см², в связи с чем данная величина может быть принята за расчетное сопротивление материала стойки на растяжение, то есть . По аналогии заданное относительное удлинение можно принять за предельно допустимое для данной стойки, то есть . В результате необходимо подобрать диаметр стойки, удовлетворяющий условию прочности и условию жесткости.

Продольное растягивающее усилие равно по величине внешней нагрузке, действующей на стержень N=10 т=0,1 MH_.

Требуемая площадь поперечного сечения колонны из условия прочности будет определяться выражением:

Зная требуемую площадь, выразим необходимый из условия прочности диаметр:

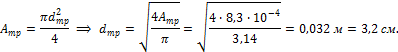
Условие жесткости при центральном растяжении-сжатии:

Выражаем из предельного неравенства требуемую из условия жесткости площадь поперечного сечения:

Диаметр стойки из условия жесткости определим по формуле:

Окончательно принимаем из двух диаметров больший, d=3,6 см.

Пример 7.

Определить грузоподъемность и удлинение балки, если R=160 МПа ; A=12 см²;

Расчетная схема бруса и эпюра продольных сил изображены на рис. 2.15.

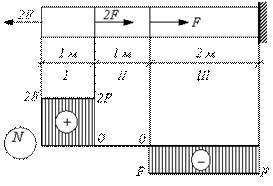
Рис.2.15

Решение.

Грузоподъемность бруса – это максимальная нагрузка, которую он может выдержать, не разрушаясь. Таким образом, необходимо определить требуемую нагрузку из условия прочности:

Согласно эпюре , тогда условие прочности примет вид:

Отсюда грузоподъемность бруса будет равна:

Для определения удлинения стержня разбиваем его на участки. Каждый участок, должен иметь постоянную жесткость EA и величину продольной силы. Таким образом, для данного бруса получаем три участка (на рис. 2.15 они обозначены римскими цифрами), тогда абсолютная деформация в общем виде будет определяться выражением:

в котором каждое слагаемое определяется отдельно:

где - значения продольных сил соответственно на первом, втором и третьем участках; - длины соответственно первого, второго и третьего участков; - значения модулей упругости материалов бруса для каждого участка; - площади поперечных сечений стержня на первом, втором и третьем участках.

Поскольку жесткости всех трех участков одинаковые (балка изготовлена из одного материала и имеет постоянное по всей длине поперечное сечение), можно обозначить и вынести этот множитель за скобки. В результате получим выражение в виде:

где

Пример 8.

Проверить прочность чугунного бруса (рис.2.16, а). Принять МПа; МПа, допускаемый коэффициент запаса прочности [n]= 4.

Решение.

Строим эпюры продольных сил N и нормальных напряжений (рис.2.16, б и в).

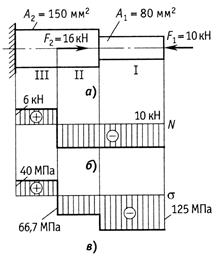
Рис.2.16

Напряжения на участках бруса

Так как материал бруса имеет различную прочность при растяжении и сжатии, проверку прочности следует выполнять для сжатого и растянутого участков, несмотря на то, что на участке I напряжение значительно больше по абсолютному значению.

Коэффициенты запаса прочности

- прочность обеспечена;

- прочность обеспечена.

Из решения задачи можно сделать следующие выводы:

1) прочность стержня не обеспечена, так как на одном его участке коэффициент запаса прочности меньше требуемого;

2) на участках I и II коэффициент запаса прочности завышен, следовательно, эти участки бруса можно сделать меньшего диаметра. При проектировании элементов конструкций следует стремиться к тому, чтобы во всех сечениях коэффициент запаса прочности был равен или близок к требуемому.

Проверку прочности бруса можно было выполнить, используя условие прочности в виде , определив предварительно допускаемые напряжения по формулам

Учет собственного веса при растяжении и сжатии

Подбор сечений с учетом собственного веса (при растяжении и сжатии)

При установлении внешних сил, растягивающих или сжимающих элементы конструкций, мы до сих пор игнорировали собственный вес этих элементов. Возникает вопрос, не вносится ли этим упрощением расчета слишком большая погрешность? В связи с этим подсчитаем величины напряжений и деформаций при учете влияния собственного веса растянутых или сжатых стержней.

Пусть вертикальный стержень (рис.2.17, а) закреплен своим верхним концом; к нижнему его концу подвешен груз Р. Длина стержня l, площадь поперечного сечения F, удельный вес материала и модуль упругости Е. Подсчитаем напряжения по сечению АВ, расположенному на расстоянии x от свободного конца стержня.

а)                   б)

Рис.2.17

Рассечем стержень сечением АВ и выделим нижнюю часть длиной x с приложенными к ней внешними силами (рис.2.17, б) — грузом Р и ее собственным весом . Эти две силы уравновешиваются напряжениями, действующими на площадь АВ от отброшенной части. Эти напряжения будут нормальными, равномерно распределенными по сечению и направленными наружу от рассматриваемой части стержня, т. е. растягивающими. Величина их будет равна:

Таким образом, при учете собственного веса нормальные напряжения оказываются неодинаковыми во всех сечениях. Наиболее напряженным, опасным, будет верхнее сечение, для которого x достигает наибольшего значения l; напряжение в нем равно:

Условие прочности должно быть выполнено именно для этого сечения:

Отсюда необходимая площадь стержня равна:

От формулы, определяющей площадь растянутого стержня без учета влияния собственного веса, эта формула отличается лишь тем, что из допускаемого напряжения вычитается величина .

Чтобы оценить значение этой поправки, подсчитаем ее для двух случаев. Возьмем стержень из мягкой стали длиной 10 м; для него , а величина. Таким образом, для стержня из мягкой стали поправка составит 78,5/140 т. е. около 0,6%. Теперь возьмем кирпичный столб высотой тоже 10 м; для него , а величина . Таким образом, для кирпичного столба поправка составит 18/1,2, т.е. уже 15%.

Вполне понятно, что влиянием собственного веса при растяжении и сжатии стержней можно пренебрегать, если мы не имеем дела с длинными стержнями или со стержнями из материала, обладающего сравнительно небольшой прочностью (камень, кирпич) при достаточном весе. При расчете длинных канатов подъемников, различного рода длинных штанг и высоких каменных сооружений (башни маяков, опоры мостовых ферм) приходится вводить в расчет и собственный вес конструкции.

В таких случаях возникает вопрос о целесообразной форме стержня. Если мы подберем сечение стержня так, что дадим одну и ту же площадь поперечного сечения по всей длине, то материал стержня будет плохо использован; нормальное напряжение в нем дойдет до допускаемого лишь в одном верхнем сечении; во всех прочих сечениях мы будем иметь запас в напряжениях, т. е. излишний материал. Поэтому желательно так запроектировать размеры стержня, чтобы во всех его поперечных сечениях (перпендикулярных к оси) нормальные напряжения были постоянны,

Такой стержень называется стержнем равного сопротивления растяжению или сжатию. Если при этом напряжения равны допускаемым, то такой стержень будет иметь наименьший вес.

Возьмем длинный стержень, подверженный сжатию силой Р и собственным весом (рис.2.18). Чем ближе к основанию стержня мы будем брать сечение, тем больше будет сила, вызывающая напряжения в этом сечении, тем большими придется брать размеры площади сечения. Стержень получит форму, расширяющуюся книзу. Площадь сечения F будет изменяться по высоте в зависимости от x, т. е. F=f(x).

Установим этот закон изменения площади в зависимости от расстояния сечения x от верха стержня.

Рис.2.18

Площадь верхнего сечения стержня F₀ определится из условия прочности:

где — допускаемое напряжение на сжатие; напряжения во всех прочих сечениях стержня также должны равняться величине

Чтобы выяснить закон изменения площадей по высоте стержня, возьмем два смежных бесконечно близких сечения на расстоянии x от верха стержня; расстояние между сечениями dx; площадь верхнего назовем F(x), площадь же смежного F(x)+dF(x).

Приращение площади dF(x) при переходе от одного сечения к другому должно воспринять вес элемента стержня между сечениями. Так как на площади dF(x) он должен вызвать напряжение, равное допускаемому , то dF(x) определится из условия:

Отсюда:

После интегрирования получаем:

При x=0 площадь F(x)=F₀; подставляя эти значения, имеем:

и

Отсюда

Если менять сечения точно по этому закону, то боковые грани стержня получат криволинейное очертание (рис.2.18), что усложняет и удорожает работу. Поэтому обычно такому сооружению придают лишь приближенную форму стержня равного сопротивления, например в виде усеченной пирамиды с плоскими гранями. Приведенный расчет является приближенным. Мы предполагали, что по всему сечению стержня равного сопротивления передаются только нормальные напряжения; на самом деле у краев сечения напряжения будут направлены по касательной к боковой поверхности.

В случае длинных канатов или растянутых штанг форму стержня равного сопротивления осуществляют тоже приближенно, разделяя стержень по длине на ряд участков; на протяжении каждого участка сечение остается постоянным (рис.2.19) — получается так называемый эквивалентный ступенчатый стержень.

Рис.2.19

Определение площадей при выбранных длинах производится следующим образом. Площадь поперечного сечения первого нижнего участка будет по формуле равна:

Чтобы получить площадь поперечного сечения второго участка, надо нагрузить его внешней силой Р и весом первого участка :

Для третьего участка к внешней силе добавляются веса первого и второго участков. Подобным же образом поступают и для других участков.

Деформации при действии собственного веса

При определении влияния собственного веса на деформацию при растяжении и сжатии стержней придется учесть, что относительное удлинение различных участков стержня будет переменным, как и напряжение . Для вычисления полного удлинения стержня постоянного сечения определим сначала удлинение бесконечно малого участка стержня длиной dx, находящегося на расстоянии x от конца стержня (рис.2.20).

Рис.2.20

Абсолютное удлинение этого участка равно

Полное удлинение стержня равно:

Величина представляет собой полный вес стержня. Таким образом, для вычисления удлинения от действия груза и собственного веса можно воспользоваться прежней формулой:

подразумевая под S внешнюю силу и половину собственного веса стержня.

Что же касается деформаций стержней равного сопротивления, то, так как нормальные напряжения во всех сечениях одинаковы и равны допускаемым , относительное удлинение по всей длине стержня одинаково и равно

Абсолютное же удлинение при длине стержня l равно:

Деформацию ступенчатых стержней следует определять по частям, выполняя подсчеты по отдельным призматическим участкам. При определении деформации каждого участка учитывается не только его собственный вес, но и вес тех участков, которые влияют на его деформацию, добавляясь к внешней силе. Полная деформация получится суммированием деформаций отдельных участков.

Пример 9.

Определить объем кладки мостовой опоры высотой 42 м, нагруженной сжимающей силой F=400 т, для двух вариантов:

1 вариант - опора постоянного сечения;

2 вариант - опора ступенчатая из трех частей одинаковой высоты.

Объемный вес материала кладки , расчетное сопротивление материала кладки на сжатие

Решение.

Объем кирпичной кладки вычисляется по формуле:

где A[м²] - площадь поперечного сечения столба; H[м] - высота столба.

Таким образом, для решения задачи необходимо знать площади поперечных сечений мостовой опоры.

1.Вариант. Расчетная схема и эпюра внутренних усилий для данного варианта изображена на рис. 2.21.

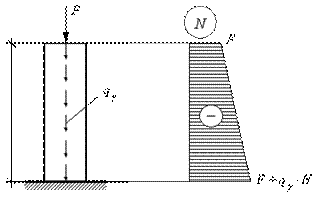
Рис.2.21

Максимальная сжимающая продольная сила возникает у основания опоры и определяется выражением (для удобства будем подставлять значения внутренних усилий по абсолютной величине):

Записываем условие прочности:

Подставляя в это выражение значение получим:

Отсюда требуемая площадь из условия прочности кладки на сжатие равна:

Объем кладки для первого варианта будет равен:

2 вариант. Расчетная схема и эпюра внутренних усилий для данного варианта изображена на рис. 2.22.

Мостовая опора состоит из трех ступеней, высота каждой . Площади поперечных сечений ступеней соответственно , в связи с чем в пределах каждой ступени от действия собственного веса будут возникать различные по величине продольные силы и напряжения.

Таким образом, для решения задачи необходимо рассмотреть условие прочности для каждой ступени отдельно.

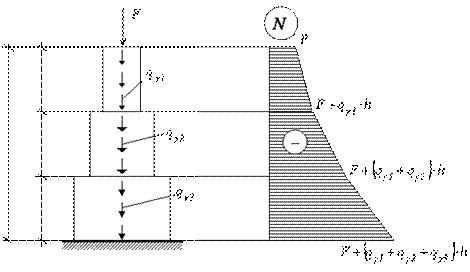
Рис.2.22

1-я ступень. Максимальная сжимающая продольная сила для первой ступени (рис. 2.22):

По аналогии с вариантом 1, записываем для первой ступени условие прочности и подставляем в него исходные данные:

Отсюда требуемая площадь первой ступени равна:

2-я ступень. Максимальная сжимающая продольная сила для второй ступени (рис. 2.22):

Записываем для второй ступени условие прочности и подставляем в него исходные данные:

Отсюда требуемая площадь второй ступени равна:

3-я ступень. Максимальная сжимающая продольная сила для третьей ступени (рис. 2.22):

Записываем для третьей ступени условие прочности, из которого по аналогии с предыдущими записями определяем требуемую площадь поперечного сечения:

Объем кладки мостовой опоры для второго варианта определяется выражением:

Таким образом, мостовая опора, состоящая из ступеней различной площади, выгоднее по расходу материала, чем опора постоянного по всей высоте сечения.

Пример 10.

Определить полное удлинение стержня, с учетом собственного веса, а также перемещение сечения m-n. Площадь поперечного сечения – А, модуль упругости – Е, объемный вес материала - . Расчетная схема стержня изображена на рис. 2.23.

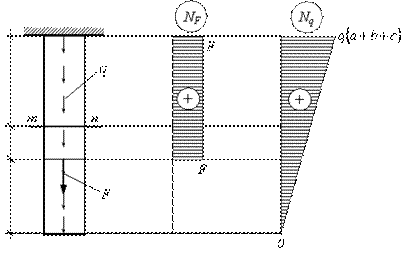
Рис.2.23

Решение.

Для решения задачи используем принцип независимости действия сил, а именно: отдельно построим эпюры продольных сил от действия сосредоточенной силы F и от действия собственного веса, то есть от равномерно распределенной продольной нагрузки . Расчетная схема и эпюры продольных сил и изображены на рис. 2.23.

Полное удлинение стержня будет складываться из удлинения, полученного стержнем от действия сосредоточенной силы F и от действия собственного веса:

Или в другом виде:

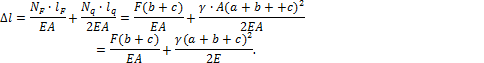
Для того, чтобы определить перемещение сечения m-n отбрасываем часть стержня ниже сечения m-n, а ее действие заменяем сосредоточенной силой , равной продольной силе в сечении m-n:

В результате получаем новую расчетную схему, которая приведена на рис. 2.24.

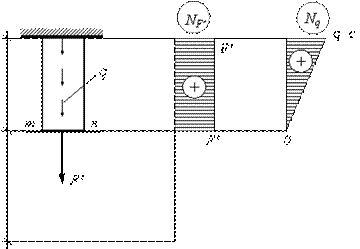
Рис.2.24

А теперь решаем новую задачу о нахождении полного удлинения уже для данного стержня (рис. 2.23):

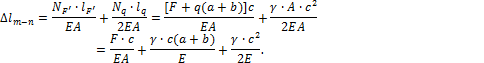
Композитный брус

Брус, состоящий из различных материалов, называется композитным. Будем полагать, что соединение материалов по всей длине бруса обеспечивает их совместную работу. При этом сечения остаются плоскими, а линейная деформация отдельного волокна равномерная. Чтобы сохранить эти предположения для торцевых сечений, нагрузку можно осуществить, например, через жесткую обойму. Рассмотрим брус, состоящий из различных материалов на рис.2.24.1, а. При постоянстве деформации ε_х напряжения распределяются по сечению неравномерно на рис.2.24.1, б, что объясняется различием модулей продольной упругости составляющих материалов.

Рис.2.24.1

Очевидно,

Откуда

Тогда

т.е. напряжения распределяются прямо пропорционально модулям упругости.

При определении перемещений и удлинений можно использовать формулы для однородного бруса с заменой ЕА на .

Расчет статически определимых стержневых систем

Статически определимая стержневая система – это система, в которой все неизвестные реакции опор и внутренние усилия можно определить из уравнений равновесия (статики).

Для «решения» любой стержневой системы необходимо выделить в ней объект равновесия. В связи с этим, все системы можно разделить на два типа:

1 тип – системы, состоящие из абсолютно жестких (недеформируемых) стержней и одиночных невесомых (деформируемых) стержней. Для стержневых систем этого типа объектами равновесия являются недеформируемые стержни.

2 тип – системы, состоящие из нескольких деформируемых стержней, соединенных в одной точке. Точки соединения двух и более стержней называются узлами, которые и являются объектами равновесия для систем 2-го типа.

Все соединения в элементах систем шарнирные, однако существуют определенные правила, по которым вводятся реакции и усилия в стержнях:

- в шарнире, соединяющем абсолютно жесткий элемент системы с «землей» или с другой конструкцией, всегда возникают две реакции – горизонтальная H и вертикальная R;

- в шарнире, соединяющем деформируемый стержень с абсолютно жестким стержнем или с другой конструкцией, всегда возникает одна реакция, направленная вдоль этого стержня и равная по величине усилию, возникающему в нем.

В абсолютно жестких стержнях никогда не возникает внутренних усилий, они не деформируются!

- в шарнире, соединяющем несколько деформируемых стержней (узловой шарнире), возникают усилия, направленные вдоль этих стержней и сходящиеся в этом узле.

Порядок решения большинства задач о проверке прочности статически определимых стержневых систем при расчете по допускаемым напряжениям сводится к следующим этапам:

1) находим внутренние усилия (продольную силу при растяжении-сжатии) и выявляем опасные сечения;

2) определяем напряжения;

3) после выявления максимальных напряжений используем условие прочности (формулы (2.26), (2.28), (2.32)) при растяжении-сжатии).

Пример 11.

Абсолютно жесткий брус CD поддерживается стальным стержнем AB, имеющим площадь поперечного сечения 100 мм² (рис.2.25, а). Определить из условия прочности стержня AB допускаемую нагрузку [P] и проверить, обеспечена ли жесткость системы, если допускается перемещение сечения D бруса под действием силы P не более 2 мм. Допускаемое напряжение принять равным МПа, модуль упругости Па.

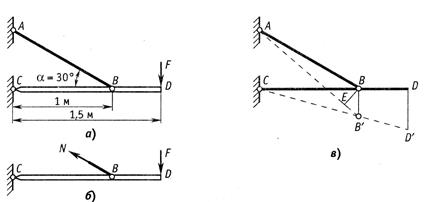
Рис.2.25

Решение.

Используя метод сечений, определим соотношение между продольной силой N в стержне AB и нагрузкой P. Из условия равновесия сил (рис.2.25, б) находим

Допускаемая продольная сила [N] для стержня AB из условия его прочности

Допускаемая нагрузка на систему

[P]=[N]/3=15/3=5 кН.

При нагружении системы стержень AB удлиняется на , а абсолютно жесткий брус поворачивается, оставаясь прямолинейным. Система после деформации стержня AB показана штриховой линией на рисунке 2.25, в. Из треугольника ABC определяем длину l стержня AB: l=1/cos30⁰=1,153 м.

На основании принципа начальных размеров принимаем, что значение угла не изменяется, а точки B и D перемещаются по вертикали.

Из прямоугольного треугольника BB^’E находим

; так как , то

Перемещение точки D определяем из подобия треугольников и

Жесткость системы не обеспечена.

Следует заметить, что нельзя повысить жесткость системы, применив для стержня AB более прочную сталь, так как характеристикой свойств материала, влияющей на жесткость, является модуль упругости, значение которого для всех марок сталей примерно одинаково. Повысить жесткость системы можно, либо увеличив площадь поперечного сечения стержня AB, либо уменьшив его длину.

Пример 12.

Определить допускаемую нагрузку [P] для системы из двух стержней, изготовленных из дюралюминиевых труб одинакового поперечного сечения (рис.2.26, а). Допускаемое напряжение принять МПа.

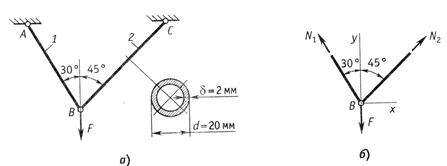
Рис.2.26

Решение.

Используя метод сечений, вырезаем узел B и из уравнений равновесия сил

находим неизвестные продольные силы, возникающие в стержнях, через нагрузку P (рис.2.26, б)

Допускаемую нагрузку [P] определяем из условия прочности наиболее нагруженного стержня 1:

Следует отметить, что стержень 2 недогружен. Напряжение в нем

что примерно на 30% ниже допускаемого. Для стержня 2 можно использовать трубу меньшего поперечного стержня.

Пример 13.

Рассмотрим стержневую систему, состоящую из абсолютно жесткого (недеформируемого) стержня AC, шарнирно закрепленного в точке A и невесомого (деформируемого) стержня BD, шарнирно закрепленного по концам, загруженную в точке C сосредоточенной силой F (рис. 2.27).

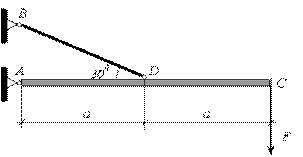
Рис.2.27

Решение.

Объектом равновесия в данном случае будет являться стержень AC, для которого и будем составлять уравнения равновесия.

Под действием внешней нагрузки, на основании введенных выше правил, в точке A будут возникать две реакции и , а в стержне BD возникает усилие , направленное по стержню (рис. 2.28).

Определим несущую способность (грузоподъемность) заданной системы, то есть допустимую нагрузку F, если площадь сечения стержня , расчетное сопротивление материала стержня R=200 МПа.

Для этого можно составить следующие уравнения равновесия:

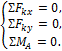
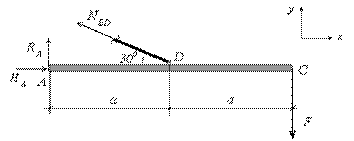
Рис.2.28

Поскольку в конечном итоге решение задачи будет сводиться к определению усилия в стержне BD, то оставляем в рассмотрении уравнение равновесия, содержащее только , то есть уравнение моментов относительно точки A. Распишем данное уравнение:

отсюда неизвестное усилие

Записываем условие прочности для стержня BD и выражаем нагрузку F:

Пример 14.

Определить необходимые размеры поперечных сечений металлических тяг в стержневой системе из условия прочности, если тяга № 1 – из стали, расчетное сопротивление , поперечное сечение - швеллер; тяга № 2 – из алюминия, расчетное сопротивление , круглого поперечного сечения. Стержневая система изображена на рис. 2.29.

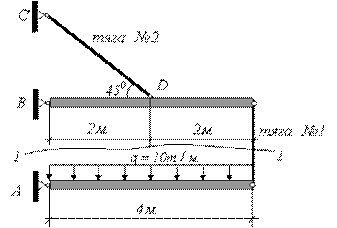
Рис.2.29

Решение.

Под действием внешней нагрузки в точках опор системы A, B и C возникают реакции . Кроме того, в тягах возникают усилия соответственно и .

Для решения данной задачи необходимо по очереди рассмотреть равновесие двух абсолютно жестких стержней. Сначала рассекаем систему сечением 1-1 по тяге № 1 и рассматриваем равновесие нижнего бруса (рис. 2.30, б), а затем - равновесие верхнего бруса (рис. 2.30, а). Из условий равновесия для нижней части будем находить усилие в первой тяге , а из условия равновесия для верхней - (при этом усилие считается уже известным).

Для определения усилия необходимо записать уравнение моментов относительно точки A (рис. 2.30, б):

отсюда - усилие растяжения.

Теперь, считая усилие известным, необходимо рассмотреть равновесие средней части, для чего записать уравнение моментов относительно точки B (рис. 2.30, а):

отсюда - усилие растяжения.

а)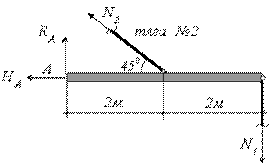

б)

Рис.2.30

Далее, для каждой тяги записываем условие прочности и выражаем площади поперечных сечений - площадь тяги № 1, - площадь тяги № 2.

Тяга № 1:

По сортаменту принимаем швеллер [ №10],

Фактическая площадь сечения должна быть не меньше требуемой!

Тяга № 2:

Алюминиевая тяга имеет круглое сечение, тогда требуемый диаметр:

Фактическая площадь круглого сечения:

Пример 15.

Определить усилия, возникающие в стержнях системы (рис. 2.31) под действием внешней нагрузки.

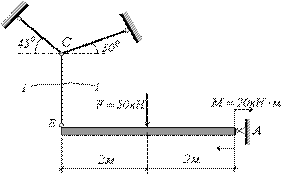
Рис.2.31

Решение.

Под действием внешней нагрузки в точке опоры системы А возникают реакции , а также усилия в стержнях

В качестве объектов равновесия в этой задаче выступают абсолютно жесткий брус AB и узел C. Поэтому, для определения неизвестных усилий сначала рассекаем систему сечением 1-1 по стержню BC и рассматриваем равновесие нижней части (рис. 2.32, б), а затем рассматриваем равновесие узла C (рис. 2.32, а).

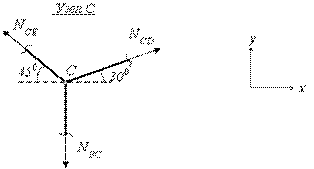
Рис.2.32

Для определения усилия необходимо записать уравнение моментов относительно точки A (рис. 2.32, б):

отсюда - усилие растяжения.

Теперь, считая усилие известным, необходимо рассмотреть равновесие узла С, для чего записать уравнения сумм проекций всех сил на вертикальную и горизонтальную оси (рис. 2.32, а):

В результате получаем систему двух уравнений с двумя неизвестными:

Решая систему определяем усилия в стержнях CD и CE:

Пример 16.

Два стальных (Е = 210⁵ МПа) стержня, шарнирно соединенные в точке А, находятся под действием силы Р (рис. 2.33). Первый стержень имеет длину с и площадь поперечного сечения F, второй длину а и площадь - 2F.

1) Найти величины нормальных напряжений, действующих в стержнях.

2) Найти абсолютную и относительную деформации стержней.

Дано: Р = 130 кН, с = 1,5 м, а = 2 м, F = 12 см.

Рис.2.33 Рис.2.34

Решение.

Стержни прикреплены к стене и соединены между собой шарнирами (точках В, С и А). Шарниры предполагаются идеальными, т. е. такими, трение в которых отсутствует. Нагрузка Р приложена в узле А. Поэтому стержни будут испытывать только продольные (растягивающие или сжимающие) усилия, т.е. в поперечных сечениях стержней возникает только один внутренний силовой фактор - продольная сила N.

1. Для определения усилий рассмотрим равновесие узла А (рис. 2.34), к которому приложены нагрузка Р и два неизвестных усилия N₁, и N₂, действующие со стороны стержней АВ и АС и направленные вдоль их осей.

При определении неизвестных усилий в стержнях обычно принято считать их растянутыми и соответственно этому направлять векторы сил от узла. Знак плюс в решении для усилия будет подтверждать правильность сделанного предположения о направлении усилия, а знак минус укажет на то, что в действительности усилие направлено противоположно и соответствующий стержень сжат.

Полагая оба стержня растянутыми, направим усилия N₁, и N₂ так, как показано на рис.2.34. Для плоской системы сил, пересекающихся в одной точке, как известно из курса теоретической механики, можно составить только два независимых уравнения равновесия - в виде сумм проекции всех сил на две оси, не параллельные друг другу.

В качестве таких осей выберем оси Х и Y (рис. 2.34). Тогда уравнения равновесия представятся в виде:

Из этой системы (1) можно было бы определить неизвестные усилия N₁, и N₂, если бы были известны значения и . Определим эти величины. Для этого рассмотрим данную стержневую систему (рис. 2.34). Из точки А опустим перпендикуляр АD на прямую ВС, получим два прямоугольных треугольника и .

Рис.2.35

Из треугольника ABD определим AD:

м.

Из треугольника ADG получим:

Теперь определим неизвестные усилия N₁, и N₂ из системы двух линейных уравнений (1). Перепишем уравнения в следующем виде:

Решим эту систему используя метод Крамера

2. Определим нормальные напряжения, действующие в стержнях.

Напряжения в стержнях определяются по формуле

Для первого стержня

для второго стержня

3. Найдем абсолютную и относительную деформации стержней.

Абсолютная деформация стержня длиной l равна:

Абсолютная деформация первого стержня

Абсолютная деформация второго стержня

Относительную деформацию определим из закона Гука

Относительная деформация первого стержня

Относительная деформация второго стержня

Понятие о статически неопределимых системах

Основные положения. Связи необходимые и дополнительные.

Для решения задач сопротивления материалов необходимо знать все внешние силы, действующие на конструкцию, включая реакции наложенных на нее связей. Из теоретической механики известно, что для равновесия твердого тела, нагруженного плоской системой сил, достаточно наложить на тело три связи, а нагруженного пространственной системой сил – шесть связей. Соответственно для таких систем можно составить три и шесть независимых уравнений равновесия. Если при рассмотрении заданной системы, находящейся в равновесном состоянии от действия заданных внешних нагрузок, все реакции в связях закрепления можно определить с помощью уравнений равновесия, без использования дополнительных условий, то такая система называется статически определимой.

В реальной практике встречаются такие конструкции, при расчете которых одних лишь уравнений равновесия оказывается недостаточно, в связи с чем требуется формулирование дополнительных уравнений, связанных с условиями деформирования конструкции.

Системы, в которых количество наложенных связей больше, нежели число независимых уравнений равновесия, называются статически неопределимыми.

В машиностроении и строительных конструкциях такие системы находят широкое применение. В одних случаях статическая неопределимость является сущностью самой конструкции.

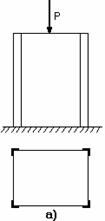
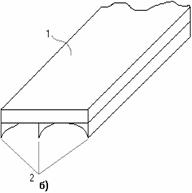
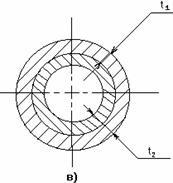
Рис. 2.36

Примерами таких конструкций могут быть: армированные уголками стойки (рис.2.36, а); панель крыла самолета, состоящая из обшивки 1 с продольными ребрами 2 (рис. 2.36, б); составной цилиндр, полученный путем напряженной посадки двух труб из различных материалов (рис. 2.36, в). В других случаях, с целью повышения жесткости и надежности системы, вводятся дополнительные связи сверх тех минимально необходимых, которые обеспечивают ее кинематическую неизменяемость. Наложение на систему дополнительных связей превращает ее в статически неопределимую. Напомним, что кинематическая неизменяемость плоской системы обеспечивается тремя, а пространственной – шестью связями.

Конструкции, состоящие из стержней, соединенных шарнирами, называются шарнирно-стержневыми. В этих конструкциях есть стержни, которые обеспечивают геометрическую неизменяемость конструкции и при удалении которых система превращается в механизм. Такие стержни будем называть необходимыми. Если же при удалении некоторых стержней геометрическая неизменяемость конструкции не нарушается, то такие стержни назовем лишними. Лишними такие связи называются только потому, что они не являются необходимыми для обеспечения равновесия конструкции и ее геометрической неизменяемости, хотя постановка их диктуется условиями эксплуатации. По условиям прочности и жесткости конструкции лишние связи могут оказаться необходимыми.

В статически определимой системе есть только необходимые стержни, в статически неопределимой – число лишних стержней равно степени статической неопределимости.

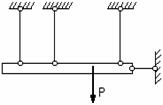
а) б) в)

Рис. 2.37

На рис.2.37 приведены схемы 3-х плоских систем с «лишними» связями: а – стержневой подвески; б – стержня, закрепленного обоими концами; в – стержневого кронштейна. В схеме, показанной на рис. 2.37, в, вся система состоит из упругих звеньев. Подсчет числа наложенных связей производится в этом случае следующим образом. Каждый стержень связан с опорной поверхностью двумя связями. Всего таких связей 8. Шарнир, соединяющий концы стержней, снимает связи, ограничивающие относительный или взаимный их поворот. При соединении двух стержней одним шарниром снимается одна связь, трех стержней – две связи, четырех – три и т.д. В данном случае снимаются три связи. Следовательно, всех связей, наложенных на эту систему оказывается пять, две из которых могут считаться «лишними».

Статически неопределимые конструкции характеризуются рядом особенностей, по сравнению со статически определимыми системами. Заключаются они в том, что в элементах статически неопределимых систем напряжения возникают не только от действия внешних сил, но и в результате изменения температуры, неточности изготовления деталей, неточностей их сборки, смещения мест опорных креплений и ряда других причин. Объясняется это тем, что деформация одного из элементов в статически неопределимой системе приводит к деформации и других ее элементов.

Например, если один из стержней системы (рис. 2.37, в) изготовлен по длине неточно, то соединение концов стержней одним шарниром возможно только путем деформации всех стержней.

Сила, возникающая при деформации одного из стержней, вызывает усилия в других стержнях, находящихся с ним в шарнирном соединении. Смонтированная система приходит в равновесие, следовательно, совокупность сил системы обеспечивает ее равновесие. Эти силы вызывают соответствующие, называемые начальными, напряжения в стержнях.

В статически неопределимых конструкциях при изменении температуры ее элементов по сравнению с температурой, при которой осуществлялась сборка, возникают дополнительные усилия и напряжения, которые принято называть температурными.

Распределение усилий между элементами системы зависит от их жесткости. Если увеличить жесткость какого- либо элемента, то он примет на себя большее усилие. Изменяя соотношение жесткостей элементов конструкций, можно менять распределение усилий между ними.

Эти особенности статически неопределимых конструкций должны учитываться при проектировании или применении таких систем.

Статически неопределимые системы обладают повышенной «живучестью». Разрушение одного или нескольких элементов (в зависимости от числа дополнительных связей) не вызывает потерю несущей способности конструкции в целом. Так разрушение даже двух стержней в системе, показанной на рис. 2.37, в не приводит к потере способности воспринимать силу P оставшимися двумя стержнями, конечно, при условии их достаточной прочности.

Степень статической неопределимости. Методика ее определения.

Статически неопределимые системы характеризуются степенью статической неопределимости, которая равна числу «лишних» связей и может быть вычислена как разность между числом неизвестных сил и числом независимых уравнений равновесия. По числу единиц этой разности системы бывают 1,2,3….n раз статически неопределимыми.

Для расчетов составляется силовая схема заданной системы, на которой указываются все известные и неизвестные силовые факторы.

При составлении силовой схемы в случае определения внутренних силовых факторов применяется метод сечений, согласно которому каждое звено системы разделяется на две части в произвольном сечении, затем отбрасываются части, примыкающие к опорным элементам, а их действие на оставшиеся части заменяется продольными силами. После этого на схеме показываются все заданные внешние силы и реакции опор.

Затем по этой схеме устанавливается возможное число независимых уравнений равновесия. Степень статической неопределимости подсчитывается, как разность между числом неизвестных сил и числом независимых уравнений равновесия.

На рис.2.38, а изображен кронштейн, состоящий из двух стержней, шарнирно скрепленных между собой. В связи с тем, что на конструкцию действует лишь вертикальное усилие Р, а система является плоской (т.е. все элементы конструкции и вектор внешних сил лежат в одной плоскости), получается, что усилия в стержнях легко определяются из условий равновесия узла A, т.е.

Раскрывая эти уравнения, получаем замкнутую систему линейных уравнений относительно неизвестных усилий N₁ и N₂ в которой количество уравнений равно количеству неизвестных:

Если конструкцию кронштейна усложнить, добавив еще один стержень (рис.2.38, б), то усилия в стержнях N₁, N₂ и N₃ прежним способом определить уже не удастся, т.к. при тех же двух уравнениях равновесия (2.37) имеются уже три неизвестных усилия в стержнях. В таких случаях говорят, что система один раз статически неопределима.

Рис.2.38

На рис.2.39 приведены примеры статически неопределимых систем. В стержне с жестко заделанными концами (рис.4.2, а) возникают две реакции, а уравнение равновесия можно составить только одно, следовательно, конструкция один раз статически неопределима. Не нарушая равновесия стержня, можно отбросить одну из опор.

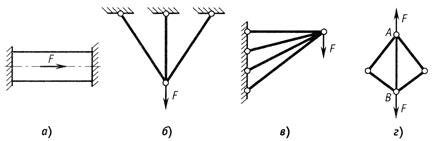
Рис.2.39

Для системы из трех стержней (рис.2.39, б) можно составить два уравнения равновесия, а неизвестных сил в системе три, следовательно, система один раз статически неопределима. Один из стержней не нужен для равновесия системы, и его можно отбросить. Рассуждая аналогично, можно установить, что система из четырех стержней (рис.2.39, в) дважды статически неопределима.

Для определения внутренних сил в системе из пяти стержней (рис.2.39, г) необходимо вырезать и рассмотреть раздельно равновесие узлов A и B. К каждому узлу примыкают три стержня (всего пять стержней и, следовательно, пять неизвестных сил), а уравнений равновесия для каждого узла можно составить два, т.е. всего четыре уравнения. Система один раз статически неопределима.

Напомним, что для пространственной системы сил можно составить шесть независимых уравнений равновесия: три уравнения, выражающие сумму проекций всех сил на три взаимно перпендикулярные оси (), и три - сумму моментов всех сил относительно этих же осей (). Для общего случая сил, лежащих в одной плоскости - три независимых уравнения (например: ). В частных случаях плоской системы можно составить два независимых уравнения равновесия: для системы параллельных сил (например: ) и для системы сил, линии действия которых пересекаются в одной точке (). Для сил, линии действия которых лежат на одной прямой, можно записать только одно независимое уравнение (например: ).

На рис. 2.40 показаны примеры составления силовых схем и определения степени статической неопределимости по формуле

S=n-m,

где n - общее число неизвестных сил, включая реакции опор; m - число возможных для данной системы независимых уравнений статики.

Раскрытие статической неопределимости

Операции по определению неизвестных силовых факторов в статически неопределимых системах принято называть раскрытием статической неопределимости. Производятся они следующим образом. В начале исходя из силовой схемы составляются уравнения равновесия.

При решении любых задач число уравнений должно быть равно числу неизвестных. Для определения сил в стержнях статически неопределимых систем следует составлять уравнения, дополняющие уравнения равновесия до числа неизвестных сил. Дополнительные уравнения, называемые уравнениями совместности перемещений или деформаций, составляют, определяя перемещения отдельных стержней системы и устанавливая между ними связь.

Принцип совместности деформирования выражает условие, заключающееся в том, что конструкция должна деформироваться без разъединения и непредусмотренного взаимного перемещения отдельных ее звеньев.

Для облегчения записей уравнений перемещений строят схему деформаций всех упругих элементов или схему деформированной системы. Для любой статистически неопределимой системы всегда можно составить столько дополнительных уравнений, сколько раз система статически неопределима.

В силу различной взаимозависимости элементов, различия накладываемых связей и условий деформирования, уравнения совместности деформаций систем записываются по разному. Но все они выражают соотношения деформаций (перемещений) отдельных упругих элементов системы. Например, на схеме,

на рис. 2.40, в

а на рис. 2.40, г.

т. к. весь стержень не может не удлиниться, ни укоротиться. На схеме (рис. 2.40, а) можно установить геометрическое соотношение деформаций стержней 1, 2 и 3.

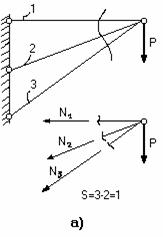
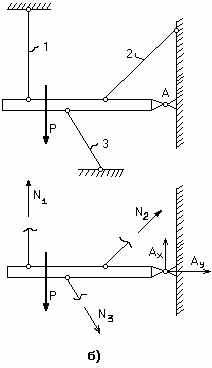
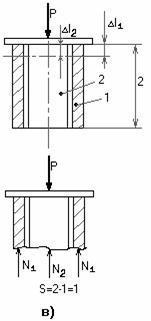
Рис.2.40

После получения указанных геометрических соотношений величины абсолютных изменений, длины стержней заменяют по закону Гука их выражениями через усилия :

Полученные таким образом уравнения, содержащие в качестве неизвестных продольные силы, и являются дополнительными уравнениями. Они включают также показатели жесткости отдельных звеньев конструкции, вводя тем самым зависимость распределения сил внутри системы от жесткости ее элементов. Вместе с уравнениями статистики общее число уравнений равно числу неизвестных сил. Решая их, определяют неизвестные внутренние (продольные) силы.

В заключение может быть выполнена энергетическая проверка решения задачи. Она заключается в составлении и удовлетворении равенства работы внешних сил А и суммы потенциальной энергии деформации элементов системы U.

Сложные статически неопределимые системы, в том числе статически неопределимые фермы (элементы ферм работают на растяжение, сжатие) и статически неопределимые рамы, рассматриваются в курсе строительной механики стержневых систем. В курсе сопротивления материалов рассматриваются обычно простейшие статически неопределимые системы, к которым относятся:

а) прямые стержни постоянного, кусочно-постоянного и переменного сечений, закрепленные с двух сторон, от нагрузки действующей вдоль оси стержня;

б) системы шарнирно соединяемых стержней с возможным включением жестких недеформируемых элементов.

При решении статически неопределимых систем, в стержнях которых действуют продольные силы, можно отметить основные этапы:

1) анализ работы конструкции с указанием действующих силовых факторов и выяснением деформации ее элементов, определение степени статической неопределимости;

2) статическая сторона задачи – составляют уравнения равновесия для системы или отсеченных ее частей;

3) геометрическая сторона задачи – выясняют, как деформируются стержни системы, изображают систему в деформированном виде, устанавливают связи между перемещениями отдельных элементов системы, составляют уравнения совместности перемещений;

4) физическая сторона задачи – выражает деформации элементов, согласно закону Гука, через действующие в них неизвестные усилия;

5) синтез – определяют неизвестные силы, решая совместно систему уравнений равновесия и перемещений.

Статически неопределимые конструкции характеризуются рядом особенностей, по сравнению со статически определимыми системами. Так, при эксплуатации конструкции возможно изменение ее температуры, вызванное условиями работы или сменой времен года. С изменением температуры изменяются линейные размеры элементов конструкции: увеличиваются при нагреве, уменьшаются при охлаждении на величину

где - температурный коэффициент линейного расширения (см. раздел «Справочные данные»); - длина элемента; - изменение температуры, (⁰С).

В статически определимых системах длина стержня может свободно изменяться при их нагреве или охлаждении (рис.2.41, а, б).

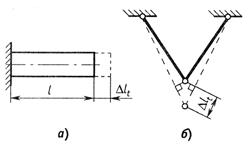
Рис.2.41

В статически неопределимых системах при изменении температуры возникают дополнительные силы. Если нагреть стержень, жестко закрепленный по концам (рис.2.42, а), то его длина не может изменяться: этому препятствуют жесткие заделки. В опорах (заделках) возникают реакции, сжимающие стержень.

Так как неизвестных сил две, а уравнение равновесия можно составить только одно: , то система один раз статически неопределима.

Решая геометрическую часть задачи, составляем уравнение перемещений. Отбросим одну из опор и заменим ее действие неизвестной силой . Теперь стержень при нагреве может удлиниться на величину (рис.2.42, б).

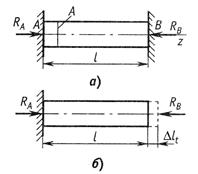
Рис.2.42

Так как длина стержня остается неизменной, перемещение сечения B должно быть равно нулю, следовательно, сила должна сжать стержень на величину, равную его удлинению при нагреве:

Решая физическую часть задачи, с учетом равенства получаем

Тогда продольная сила в сечениях стержня

напряжение в стержне

Отметим, что напряжение в стержне не зависит от площади сечения.

Элементы конструкций изготовляют с определенной точностью. При сборке статически неопределимых систем, имеющих неточно изготовленные стержни, стержни приходится деформировать (удлинять или укорачивать), при этом в них возникают напряжения, называемыми начальными или монтажными.

Рассмотрим систему, один из стержней которой изготовлен короче, чем требуется, на величину (рис.2.43, а). Определим внутренние силы и напряжения, возникающие в стержнях системы при ее сборке. Стержни имеют одинаковые размеры и изготовлены из одного материала.

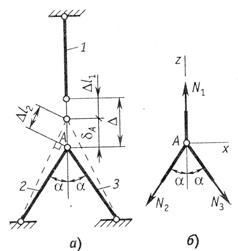
Рис.2.43

При сборке системы все три стержня необходимо удлинить, приложив к ним растягивающие силы. В собранном виде система показана штриховыми линиями (см. рис.2.43, а). Вырежем узел A (рис.2.43, б), составим уравнения равновесия сил

откуда

Система один раз статически неопределима. Рассмотрим геометрическую часть задач и составим уравнение перемещений. Из схемы, представленной на рис.2.43, а, следует, что

Уравнение перемещений принимает вид

Используя закон Гука, выразим удлинение через неизвестные силы в стержнях

Решив уравнение перемещений совместно с уравнениями равновесия, получим

Начальные напряжения часто специально создают в статически неопределимых системах, таких, например, как соединения с натягом и резьбовые соединения. Создавая в элементах статически неопределимой системы начальные напряжения, знак которых противоположен знаку напряжения от внешних сил, можно повысить прочность конструкции или увеличить допускаемую для нее нагрузку.

Распределение усилий между элементами системы зависит от их жесткости. Если увеличить жесткость какого- либо элемента, то он примет на себя большее усилие. Изменяя соотношение жесткостей элементов конструкций, можно менять распределение усилий между ними.

Эти особенности статически неопределимых конструкций должны учитываться при проектировании или применении таких систем.

Статически неопределимые системы обладают повышенной «живучестью». Разрушение одного или нескольких элементов (в зависимости от числа дополнительных связей) не вызывает потерю несущей способности конструкции в целом. Так разрушение даже двух стержней в системе, показанной на рис.2.39, в не приводит к потере способности воспринимать силу P оставшимися двумя стержнями, конечно, при условии их достаточной прочности.

В заключение отметим следующие основные свойства статически неопределимых систем.

1. Статически неопределимая система ввиду наличия добавочных лишних связей, по сравнению с соответствующей статически определимой системой оказывается более жесткой, а при идентичном характере нагружения значения усилий получаются меньшими. Следовательно, и более экономичными.

2. Разрушение лишних связей в нагруженном состоянии, не ведет к разрушению всей системы в целом, так как удаление этих связей приводит к новой геометрически неизменяемой системе, в то время как потеря связи в статически определимой системе приводит к изменяемой системе.

3. Для расчета статически неопределимых систем необходимо предварительно задаваться геометрическими характеристиками поперечных сечений элементов, т.е. фактически их формой и размерами, так как их изменение приводит к изменению усилий в связях и новому распределению усилий во всех элементах системы.

4. При расчете статически неопределимых систем необходимо заранее выбрать материал конструкции, так как необходимо знать его модули упругости.

5. В статически неопределимых системах температурное воздействие, осадка опор, неточности изготовления и монтажа вызывают появление дополнительных усилий.

Решение статически неопределимых систем можно вести, используя три метода:

- расчет по упругой стадии деформации (допускаемым напряжениям);

- расчет по разрушающим нагрузкам;

- расчет по предельному пластическому состоянию.

В машиностроении отдается предпочтение первому методу, а в строительстве – второму и третьему.

Если в качестве физических уравнений используется закон Гука, то такой способ расчета носит название расчета по упругой стадии деформаций. После определения внутренних усилий – продольных сил в стержнях статически неопределимой системы – встает задача обеспечения ее прочности. При расчете по упругой стадии деформаций считается, что предельное состояние конструкции наступает тогда, когда один, наиболее напряженный, стержень переходит в предельное состояние (разрушится или потечет). Поэтому после определения усилий по этому способу находим напряжения в стержнях и выбираем стержень, в котором действует максимальное напряжение. Из условия прочности этого наиболее напряженного стержня либо вычисляем допускаемую нагрузку, либо подбираем сечения стержней. Следует отметить, что в большинстве статически неопределимых конструкций в результате расчета по этому способу только в одном стержне напряжения будут равны допускаемым, остальные же стержни будут недогружены. Достичь равенства напряжений во всех элементах конструкции и, следовательно, добиться выполнения требования, чтобы напряжения во всех стержнях равнялись допускаемым, в общем случае невозможно.

Второй способ расчета статически неопределимых стержневых систем носит название расчета по предельному пластическому состоянию. Благодаря наличию лишних стержней в статически неопределимой системе, наступление состояния текучести в одном (наиболее напряженном) стержне еще не приводит к нарушению геометрической неизменяемости всей конструкции. Остальные стержни, оставаясь упругими, препятствуют пластическим деформациям этого стержня. Конструкция продолжает выполнять свое назначение, перейдя из упругой стадии работы в упругопластическую. При увеличении нагрузки в пластическую стадию работы вовлекаются все новые стержни. И только тогда, когда в системе потекут все лишние стержни и хотя бы один необходимый, конструкция превращается в механизм и не может выполнять свои функции. Это состояние и считается предельным при расчете по предельному пластическому состоянию. Таким образом, расчет по предельному пластическому состоянию сводится к следующему:

1) определяем, сколько стержней должно потечь, чтобы конструкция превратилась в механизм. Дальнейший расчет возможен по двум вариантам:

- если в предельном состоянии текут все стержни системы, то, составляя уравнения равновесия конструкции в предельном состоянии, находим из него значение предельной нагрузки ;

- если в предельном состоянии течет только часть стержней, то, не определяя порядка перехода стержней в пластическое состояние, рассматриваем все кинематически возможные варианты предельного состояния конструкции. Находим из уравнений равновесия предельную нагрузку для каждого варианта. Выбираем из всех вариантов минимальное значение предельной нагрузки ;

2) из условия прочности конструкции по предельному состоянию либо вычисляем допускаемую нагрузку, либо подбираем сечения стержней.

Отметим, что расчет по предельному пластическому состоянию является более экономичным, чем расчет по упругой стадии деформаций. Поэтому при сравнении результатов расчета по двум способам должно получиться, что допускаемая нагрузка, найденная расчетом по предельному пластическому состоянию, всегда не меньше нагрузки, полученной расчетом по упругой стадии деформации. Соответственно площади сечений стержней, найденные расчетом по предельному состоянию, должны быть не больше площадей сечений, полученных расчетом по упругой стадии деформаций.

Примеры типовых расчетов статически неопределимых систем

Рассмотрим основные этапы расчета статически неопределимых систем на примере простейших конструкций.

Пример 17.

Определить продольные силы в сечениях ступенчатого стержня, жестко закрепленного по концам (рис.2.44, а).

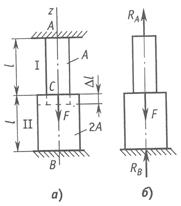
Рис.2.44

Решение.

Под действием силы P в заделках возникают опорные реакции и . Единственное уравнение равновесия имеет вид

следовательно, система один раз статически неопределима. Для раскрытия статической неопределимости отбросим одну из опор, например верхнюю (рис.2.44, б), и составим для стержня уравнение совместности перемещений. Так как длина стержня не изменяется (он жестко закреплен по концам), удлинение верхней части стержня должно быть равно укорочению нижней, т.е. перемещение сечения C.

Уравнение совместности перемещений можно записать в ином виде, определив перемещение верхнего сечения A под действием сил и P. Так как это сечение закреплено, его перемещение равно нулю

Очевидно, оба уравнения совместности перемещений равнозначны.

На основании закона Гука, уравнение совместности перемещений запишем в виде

Решив совместно уравнение равновесия и уравнение перемещений, получим

Используя метод сечений, находим

Отметим, что в более жесткой нижней части стержня возникает бóльшая по абсолютному значению продольная сила.

Пример 18.

К стержню, закрепленному обоими концами, приложена осевая сила Р (рис.2.45). Определить опорные реакции R₁ и R₂, если известны l₁, l₂ и Р.

Решение.

1. Статическая сторона задачи.

Первое и третье условия удовлетворялись тождественно. Таким образом, рассмотрение статической стороны задачи приводит к одному уравнению с двумя неизвестными

R₁+R₂=P (а)

Следовательно, данная задача один раз (S=2-1=1) статически неопределима и для ее решения нужно составить еще одно уравнение, содержащее те же неизвестные R₁ и R₂.

Рис.2.45

2. Геометрическая сторона задачи.

Установим связь между деформациями участков длиной l₁ и l₂.

В случае неразрывности участок длинной l₂ укоротится на столько, насколько растянется участок длиной l₁:

Это и есть условие совместности, выраженное в деформациях.

3. Физическая сторона задачи.

Для совместного решения (а) и (b) нужно, пользуясь законом Гука, выразить деформации (b) через усилия:

а т. к. N₁=R₁ и N₂=R₂

то

отсюда

4. Определение неизвестных.

Решая (с) совместно с (а) получим:

Определив реакции опор, используя метод сечений, можно вычислить внутренние продольные силы. Эпюра продольных сил представлена на рис. 2.36, б.

5. Энергетическая проверка.

Работа А внешней силы Р на перемещении равна сумме потенциальной энергии деформации U верхней и нижней частей стержня: А=U

тогда

Учитывая, что

получим

или

т. е. равенство удовлетворяется.

Пример 19.

Определить продольные силы в стержнях, на которых подвешена абсолютно жесткая балка AC, нагруженная силой P (рис.2.46, а). Стержни изготовлены из одного материала и имеют одинаковые площади поперечного сечения. Длины стержней равны

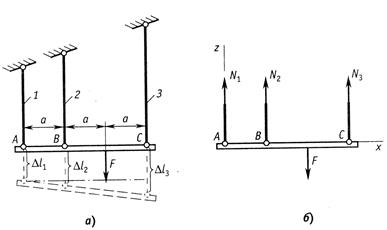
Рис.2.46

Решение.

Используя метод сечений, рассечем стержни и рассмотрим равновесие отсеченной части (рис.2.46, б). Составляем уравнение равновесия сил

Так как неизвестных сил три, а уравнений равновесия два, система один раз статически неопределима. Для решения задачи нужно составить одно уравнение совместности перемещений.

Рассмотрим геометрическую часть задачи. Так как балка AC по условию задачи абсолютно жесткая, то в результате удлинения стержней она переместится вниз и повернется на некоторый угол, оставаясь прямолинейной. Положение системы после деформации стержней показано штриховыми линиями на рисунке 2.46, а.

Составим уравнение, связывающее перемещение сечений A, B и C стержней

откуда

Используя закон Гука, выразим перемещения через силы, действующие на стержни

или

Решив полученное уравнение перемещений совместно с уравнениями равновесия, найдем

Пример 20.

Определить продольные силы, возникающие в стержнях системы (рис.2.47, а). Материал, площади поперечных сечений и длины всех стержней одинаковы.

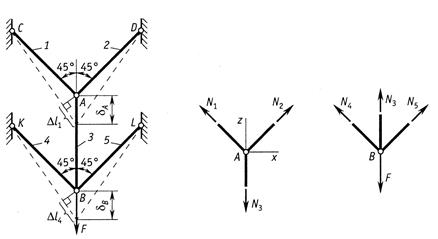
а) б)

Рис.2.47

Решение.

Применив метод сечений, вырезаем узлы A и B, заменив действие отброшенных частей системы силами (рис.2.47, б), составляем уравнения равновесия сил для каждого узла

для узла A , откуда

для узла B , откуда

Имеем четыре уравнения равновесия и пять неизвестных сил, следовательно, система один раз статически неопределима.

Рассмотрим геометрическую сторону задачи. При нагружении системы силой P все ее стержни растягиваются и деформированная система занимает положение, показанное штриховыми линиями на рисунке 2.47, а.

Если бы стержень 3 был абсолютно жестким, то при деформации системы перемещения узлов A и B были бы одинаковыми. Так как стержень 3 растягивается, перемещение узла B больше перемещения узла A на удлинение этого стержня

Из схемы, представленной на рисунке 2.47, а, находим соотношение между перемещениями узлов и деформациями стержней

Запишем уравнение перемещений через деформации стержней

Используя закон Гука, выразим деформации стержней через действующие в них продольные силы

или

Решив полученное уравнение совместно с уравнениями равновесия, находим

Пример 21.

Определить усилия в стержнях системы, возникающие в результате действия силы Р. Деформациями массивной балки АС пренебречь, рис.2.48.

Дано: E₁=E₂=E₃=E; F₁=2F₂=2F₃=2F; l₁=l; l₂=1,2l; l₃=1,6l

Рис.2.48

Решение.

1. Статическая сторона задачи.

отсюда

2. Геометрическая сторона задачи.

Под действием силы Р балка АС опустится и наклонится, заняв положение А₁С₁ (рис.2.48, б).

Исходя из силовой схемы, определяем степень статической неопределимости: S=3-2=1. Следовательно, для определения трех неизвестных сил N₁, N₂ и N₃ требуется одно дополнительное уравнение. Оно составляется из условия совместности деформации стержней по схеме деформированной системы:

или

3. Физическая сторона задачи.

По закону Гука имеем:

Подставляя это в (b), получаем:

4. Определение неизвестных.

Решая совместно уравнения (с) и (а), находим:

5. Энергетическая проверка.

Работа А внешней силы Р на перемещении равна сумме потенциальной энергии деформации стержней системы U: А=U

где

Подставляя все в (d), получим

33.811,2=33.811,2;

т. е. равенство (d) удовлетворяется.

Пример 22.

Определить усилия в стержнях, возникающие при сборке узла А из-за неточности изготовления элементов системы (устранение технологического зазора ) рис. 2.49, а.

Дано: E₁=E₂=E; F₁=2F₂=2F; l₁=l₂=l;

Рис. 2.49

Решение.

1. Статическая сторона задачи.

тогда и

2. Геометрическая сторона задачи.

После принудительной сборки конструкции шарнир А займет положение А₁ (рис. 2.49, б). Стержни 1 и 2 окажутся растянутыми. В соответствии с этим схема деформированной системы имеет вид, показанный на рис. 2.49, б.

Степень статической неопределимости S=3-2=1. Исходя из схемы деформированного состояния, составляем условие совместимости деформаций:

Строго говоря, удлинение получится, если из точки В описать дугу радиуса , однако, в силу малости деформаций, можно получить, опуская перпендикуляр из точки А на новое направление стержня .

В собранном состоянии угол между стержнями будет меньше, чем . Однако, в силу малости деформаций, изменение угла отразится на 5 или 6 знаке косинуса, что несущественно.

3.Физическая сторона задачи.

Согласно закону Гука

Подставляя это в (в) получим:

4. Определение неизвестных.

Решая систему уравнений (с) и (а), с учетом, что N₁=R₁, а N₂=R₂ имеем:

где N₁ и N₂ так называемые монтажные усилия.

Пример 23.

Определить усилия в стержнях системы, возникающие в результате поворота двухсторонней винтовой стяжки <<С>> на угол . Жесткость стяжки равна жесткости третьего стержня (рис. 2.50).

Дано: E₁=E₂=E₃=E, F₁=2F₃=2F₂=2F; шаг винтовой нарезки гайки- h; l₁=l.

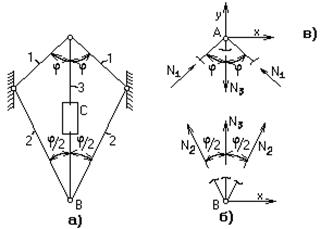
Рис.2.50

Решение.

1.Статическая сторона задачи.

Составляем уравнения равновесия узла А (рис. 2.50, в). Учитывая симметрию относительно оси Y, имеем:

Отсюда

Составляем уравнения равновесия узла B (рис. 2.50, с).

отсюда

Тогда степень статической неопределенности подсчитывается так: S=3-2=1

2. Геометрическая сторона задачи.

При повороте гайки на угол стержень 3, состоящий из двух частей, ввинтится в гайку на величину

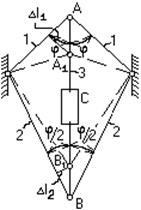
Рис. 2.51

За счет ввинчивания стержня 3 точки А и В сблизятся на величину , а за счет растяжения этого стержня и стяжки они разойдутся на величину (рис. 2.51). Тогда, на основании схемы деформированной системы, условие совместности деформаций будет иметь вид:

3. Физическая сторона задачи.

Согласно закону Гука.

Здесь l₁=l₂ по условию, а l₂ и l₃ можно определить из равенства проекций стержней на горизонтальную и вертикальную оси (рис. 2.50, а):

Подставляя (d) в (с), получим:

4. Определение неизвестных.

Решая систему, составленную из уравнений (а), (в) и (е), получим:

Пример 24.

Определить усилия в стержнях системы, возникающие в результате повышения температуры всех стержней на (рис. 2.52, а)

Дано: F₁=F₂=F; E₁=0,5E; E₂=E; l₁=l

Рис.2.52

Решение.

1. Статическая сторона задачи.

С учетом симметрии относительно оси Y имеем:

отсюда

2. Геометрическая сторона задачи.

В результате термического расширения точка А переместится в А₁ (рис. 2.52, б). Исходя из схемы деформированной конструкции можно составить условие совместности деформаций:

3. Физическая сторона задачи.

Крайние стержни 1 длиннее среднего стержня 2; кроме того, у крайних стержней коэффициент линейного расширения больше, чем у среднего. По этой причине точка А у первых стержней опустилась бы ниже, чем точка А у второго стержня, если бы они деформировались отдельно. Но так как они в точке А связаны шарниром, то возникает силовое взаимодействие боковых и среднего стержней. Боковые стержни, удлиняясь за счет термического воздействия, будут одновременно укорачиваться в результате действия возникающего усилия, средний же стержень будет удлиняться как за счет термического расширения, так и за счет механического действия на него крайних стержней.

Следовательно

где

подставляя (с) в (б), получим:

4. Определение неизвестных.

Решая систему уравнений (а) и (d) с учетом, что R₁=N₁ и R₂=N₂, получим:

Пример 25.

Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис. 2.53). Исходные данные: а = 2,1 м, b = 2,4 м, с = 1,5 м, F = 12см², Е = 210⁵ МПа.

Требуется найти:

1. усилия и напряжения в стержнях, выразив их через силу Q;

2. допускаемую нагрузку [Q], приравняв большее из напряжений в двух стержнях допускаемому напряжению = 160 МПа;

3. предельную грузоподъемность системы Q_пр. и допускаемую нагрузку [Q_пр], если предел текучести = 240 МПа и запас прочности n = 1,5;

4. сравнить величины допускаемых нагрузок [Q] и [Q_пр].

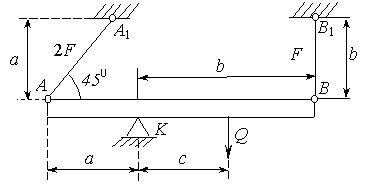
Рис.2.53

Решение.

Усилия N₁, и N₂ в стержнях АА₁, и ВВ₁, шарнирно прикрепленных по концам, направлены вдоль осей этих стержней. Реакция опоры К имеет горизонтальную составляющую Н_К, и вертикальную составляющую R_К, т.к. эта опора препятствует горизонтальному и вертикальному перемещению точки К бруса.

Таким образом, всего имеется четыре неизвестные реакции (рис.2.54), а уравнений равновесия для плоской системы сил можно составить всего три. Следовательно, данная система один раз статически неопределима. Статически неопределимые системы рассчитывают путем совместного решения уравнений, полученных в результате рассмотрения статической, геометрической и физической сторон задачи.

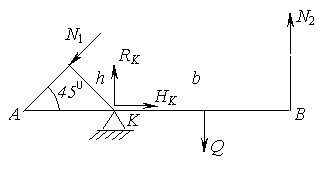
Рис. 2.54

1. Найдем усилия и напряжения в стержнях, выразив их через силу Q.

Статическая сторона задачи. По условию задачи необходимо определить усилия N₁, и N₂ стальных стержней АА₁, и ВВ₁, a в определений реакций Н_К, и R_К нет необходимости. Поэтому достаточно из трех возможных уравнений равновесия использовать одно, в которое не входили бы реакция Н_К, и R_К . Таким является уравнение в виде суммы моментов всех сил относительно шарнира К:

где м.

Подставляя в уравнение значения h, b, с, получим

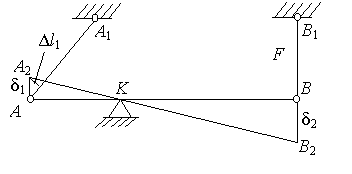
Рис.2.55

Геометрическая сторона задачи. Под действием внешней силы Q абсолютно жесткий брус повернется вокруг точки К. Шарниры А и В после деформации переходят в положение А₂ и В₂ соответственно, т.е. перемещаются по вертикали на величины и (рис.2.55).

Из подобия треугольников AA₂К и ВВ₂К находим

Выразим укорочение стержня АА₁ и удлинение стержня ВB₁, через перемещения и .

откуда

или с учетом равенства (b)

Физическая сторона задачи. Используя закон Гука, записанный для абсолютных деформаций, выразим удлинения стержней через усилия

Подставим выражения (c) в условие (d)

после сокращения получим

Решаем совместно уравнения статики (a) и уравнение (e):

Определяем напряжения в стержнях 1 и 2:

2. Найдем допускаемую нагрузку [Q], приравняв большее из напряжений в двух стержнях допускаемому напряжению = 160 МПа.

откуда

3. Найдем предельную грузоподъемность системы Q_пр. и допускаемую нагрузку [Q_пр], если предел текучести = 240 МПа и запас прочности n = 1,5.

При увеличении нагрузки Q cверх значения [Q] напряжения в обоих стержнях сначала увеличивается прямо пропорционально нагрузке. При увеличении нагрузки до некоторой величины Q>[Q] напряжение во второй стержне достигают предела текучести , а усилие N₂ - предельного значения N_2пр = c₁F. При этом напряжение в первом стержне остается меньше . В процессе дальнейшего увеличения нагрузки напряжения во втором стержне остаются постоянными, равными пределу текучести, а в первом - возрастают, пока также не становятся равными , усилие N₁ при этом равно . Это состояние системы называется предельным, соответствующим исчерпанию ее грузоподъемности. Дальнейшее, даже незначительное увеличение нагрузки связано с весьма большими деформациями системы. Величину Q, вызываюшую предельное состояние, обозначают Q_пр и называют предельной нагрузкой.

Для определения Q_пр, подставим в уравнение (a) значения сил, соответствующих предельному состоянию, когда Q = Q_пр, N₁ = N_1пр, N₂ = N_2пр:

откуда

4. Сравним величины допускаемых нагрузок [Q] и [Q_пр]

Следовательно, при расчете на прочность данной системы по предельной нагрузке грузоподъемность ее увеличивается на 38%.

Расчет конструкций по допускаемым нагрузкам.

Расчет статически определимых систем по способу допускаемых нагрузок.

В предыдущем изложении методов расчета мы исходили из основного условия прочности . Это неравенство требует выбора размеров конструкции с таким расчетом, чтобы наибольшее напряжение в самом опасном месте не превосходило допускаемого.

Но можно стать на другую точку зрения. Можно задать условие, чтобы действительная нагрузка на всю конструкцию не превосходила некоторой допускаемой величины. Условие это можно выразить таким неравенством:

За допускаемую нагрузку надо выбрать некоторую 1/k часть той нагрузки, при которой конструкция перестанет функционировать правильно, перестанет выполнять свое назначение. Такая нагрузка обычно называется предельной, иногда—разрушающей в широком смысле слова (под разрушением конструкции подразумевают прекращение ее нормальной работы).

В качестве примера возьмем систему из двух стальных стержней АВ и АС (рис.2.56), нагруженных силой P.

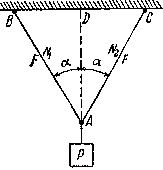
Рис.2.56

 Рассчитывая эту систему обычным путем, найдем усилия N₁ = N₂ no формуле:

(из равновесия узла А). Отсюда площадь каждого из стержней равна:

По способу допускаемых нагрузок имеем:

Введя в качестве коэффициента запаса для конструкции в целом ту же величину k, которая была принята в качестве коэффициента запаса для напряжений, мы получим, что величина

Предельной, опасной величиной P_пр будет та, при которой напряжения в стержнях дойдут до предела текучести:

Таким образом, допускаемая величина Р равна:

Условие прочности принимает вид

а учитывая, что

получаем:

Отсюда:

Таким образом, расчет по допускаемым нагрузкам привел в данном случае к тем же результатам, что и расчет по допускаемым напряжениям. Это всегда имеет место для статически определимых конструкций при равномерном распределении напряжений, когда материал по всему сечению используется полностью.

Расчет статически неопределимых систем по способу допускаемых нагрузок

Совсем другие результаты мы получим, если будем применять способ допускаемых нагрузок к статически неопределимым системам, стержни которых изготовлены из материала, обладающего способностью к большим пластическим деформациям, например из малоуглеродистой стали.

В качестве примера рассмотрим систему из трех стержней, нагруженных силой Q (рис. 2.57). Пусть все стержни сделаны из малоуглеродистой стали с пределом текучести . Длины крайних стержней, как и выше, обозначим ; длину среднего . Допускаемое напряжение .

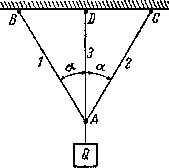
Рис.2.57

Как и раньше, при расчете этой статически неопределимой системы зададимся отношением площадей стержней; примем, что все три стержня будут иметь одинаковую площадь F. Получим:

1.

2.

3.

Используя закон Гука, получим:

Следовательно:

Так как , средний стержень напряжен больше, чем крайние; поэтому подбор площади сечения F надо произвести по формуле:

Ту же величину площади надо дать и боковым стержням; в них получается некоторый дополнительный запас.

Применим способ допускаемых нагрузок; условием прочности будет:

Что в данном случае следует понимать под предельной нагрузкой конструкции? Так как конструкция выполнена из материала, имеющего площадку текучести, то, по аналогии с простым растяжением стержня из такого материала, за предельную нагрузку следует взять груз, соответствующий достижению состояния текучести для всей конструкции в целом. Назовем эту нагрузку . Пока сила Q не достигла этого значения, для дальнейшей деформации (опускания точки A) требуется возрастание нагрузки. Когда же Q сделается равным , дальнейший рост деформаций будет происходить уже без увеличения нагрузки, — конструкция выйдет из строя.

Для определения величины рассмотрим постепенный ход деформации нашей стержневой системы. Так как средний стержень напряжен сильнее крайних, то в нем раньше, чем в других, напряжение дойдет до предела текучести. Нагрузку, соответствующую этому моменту, обозначим Q_Т; она будет равна:

где — усилие в среднем стержне, соответствующее его пределу текучести.

Напряжения в крайних стержнях, имеющих ту же площадь, в этот момент еще не дойдут до предела текучести, и эти стержни будут упруго сопротивляться дальнейшей деформации. Для того чтобы эта деформация происходила, необходимо дальнейшее увеличение нагрузки до тех пор, пока в крайних стержнях напряжения тоже не дойдут до предела текучести. Лишь тогда будет достигнута предельная грузоподъемность конструкции .

Так как при нагрузке Q_Т напряжения в среднем стержне дойдут уже до предела текучести , то при дальнейшем возрастании груза они, а стало быть и усилие N₃, останутся без увеличения. Наша статически неопределимая система превратится в статически определимую, состоящую из двух стержней АВ и АС и нагруженную в точке А силой Q, направленной вниз, и известным усилием , равным (рис.2.58).

Рис.2.58

Такая схема работы нашей конструкции будет иметь место, пока

Для иллюстрации хода деформации рассматриваемой конструкции изобразим графически зависимость между силой Q и перемещением f точки А (рис. 2.59) . Пока опускание точки А равно удлинению среднего стержня и определяется формулой

Рис.2.59

Как только Q будет заключаться в промежутке перемещение точки А должно быть вычислено, как опускание этого узла в системе двух стержней АС и АВ, нагруженных в точке А силой . Так как:

и, в свою очередь:

Отсюда

Для f₁₂ (на втором участке) получаем уравнение прямой, но уже не проходящей через начало координат. После достижения нагрузкой Q значения напряжения в крайних стержнях достигнут предела текучести, и система будет деформироваться без увеличения нагрузки. График перемещения идет теперь параллельно оси абсцисс.

Для определения предельной грузоподъемности всей системы мы должны для системы двух стержней, нагруженных силой , найти то значение Q, при котором напряжения и в крайних стержнях дойдут до предела текучести. Такая задача решена в предыдущем параграфе; подставляя в выражение (а) вместо Р величину , получаем:

Отсюда

Допускаемая нагрузка будет равна

а учитывая, что

получаем

Окончательно:

и

Эта величина меньше, чем полученная обычным методом расчета, т. е.

При Q=40 кН, (сталь) получаем: по обычному способу

по способу допускаемых нагрузок:

Таким образом, метод расчета по допускаемым нагрузкам позволяет спроектировать статически неопределимую систему из материала, обладающего площадкой текучести, экономичнее, чем при расчете по допускаемым, напряжениям. Это понятно: при способе расчета по допускаемым напряжениям мы считали за предельную нагрузку нашей конструкции величину Q_Т, при которой до предела текучести доходил лишь материал среднего стержня, крайние же были недонапряжены. При методе расчета по допускаемым нагрузкам предельная грузоподъемность определяется величиной . При нагрузке полностью используется материал всех трех стержней.

Таким образом, новый метод расчета позволяет реализовать скрытые при старом способе запасы прочности в статически неопределимых системах, добиться повышения их расчетной грузоподъемности и действительной равнопрочности всех частей конструкции. Не представит никаких затруднений распространить этот метод на случай, когда соотношение площадей среднего и крайних стержней не будет равно единице.

Изложенные выше теоретические соображения проверялись неоднократно на опыте, причем всегда наблюдалась достаточно близкая сходимость величин предельной нагрузки — вычисленной и определенной при эксперименте. Это дает уверенность в правильности теоретических предпосылок метода допускаемых нагрузок.

Расчет гибких нитей

В технике встречается еще один вид растянутых элементов, при определении прочности которых важное значение имеет собственный вес. Это — так называемые гибкие нити. Таким термином обозначаются гибкие элементы в линиях электропередач, в канатных дорогах, в висячих мостах и других сооружениях.

Пусть (рис.2.60) имеется гибкая нить постоянного сечения, нагруженная собственным весом и подвешенная в двух точках, находящихся на разных уровнях. Под действием собственного веса нить провисает по некоторой кривой АОВ.

Горизонтальная проекция расстояния между опорами (точками ее закрепления), обозначаемая l, носит название пролета.

Нить имеет постоянное сечение, следовательно, вес ее распределен равномерно по ее длине. Обычно провисание нити невелико по сравнению с ее пролетом, и длина кривой АОВ мало отличается (не более чем на 10%) от длины хорды АВ. В этом случае с достаточной степенью точности можно считать, что вес нити равномерно распределен не по ее длине, а по длине ее проекции на горизонтальную ось, т. е. вдоль пролета l.

Рис.2.60

Эту категорию гибких нитей мы и рассмотрим. Примем, что интенсивность нагрузки, равномерно распределенной по пролету нити, равна q. Эта нагрузка, имеющая размерность сила/длина, может быть не только собственным весом нити, приходящимся на единицу длины пролета, но и весом льда или любой другой нагрузкой, также равномерно распределенной. Сделанное допущение о законе распределения нагрузки значительно облегчает расчет, но делает его вместе с тем приближенным; если при точном решении (нагрузка распределена вдоль кривой) кривой провисания будет цепная линия, то в приближенном решении кривая провисания оказывается квадратной параболой.

Начало координат выберем в самой низшей точке провисания нити О, положение которой, нам пока неизвестное, очевидно, зависит от величины нагрузки q, от соотношения между длиной нити по кривой и длиной пролета, а также от относительного положения опорных точек. В точке О касательная к кривой провисания нити, очевидно, горизонтальна. По этой касательной направим вправо ось x.

Вырежем двумя сечениями — в начале координат и на расстоянии x от начала координат (сечение m — n) — часть длины нити. Так как нить предположена гибкой, т. е. способной сопротивляться лишь растяжению, то действие отброшенной части на оставшуюся возможно только в виде силы, направленной по касательной к кривой провисания нити в месте разреза; иное направление этой силы невозможно.

   На рис.2.61 представлена вырезанная часть нити с действующими на нее силами. Равномерно распределенная нагрузка интенсивностью q направлена вертикально вниз. Воздействие левой отброшенной части (горизонтальная сила Н) направлено, ввиду того, что нить работает на растяжение, влево. Действие правой отброшенной части, сила Т, направлено вправо по касательной к кривой провисания нити в этой точке.

Cоставим уравнение равновесия вырезанного участка нити. Возьмем сумму моментов всех сил относительно точки приложения силы Т и приравняем ее нулю. При этом учтем, опираясь на приведенное в начале допущение, что равнодействующая распределенной нагрузки интенсивностью q будет qx, и что она приложена посредине отрезка x. Тогда

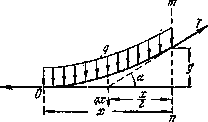
Рис.2.61

откуда

Отсюда следует, что кривая провисания нити является параболой. Когда обе точки подвеса нити находятся на одном уровне, то . Величина f в данном случае будет так называемой стрелой провисания. Ее легко определить. Так как в этом случае, ввиду симметрии, низшая точка нити находится посредине пролета, то a=b=1/2; подставляя в уравнение (2.39) значения x=b=1/2 и y=f получаем:

Из этой формулы находим величину силы Н:

Величина Н называется горизонтальным натяжением нити.

Таким образом, если известны нагрузка q и натяжение H, то по формуле (2.40) найдем стрелу провисания f. При заданных q и f натяжение Н определяется формулой (2.41). Связь этих величин с длиной s нити по кривой провисания устанавливается при помощи известной из математики приближенной формулы)

Составим еще одно условие равновесия вырезанной части нити, а именно, приравняем нулю сумму проекций всех сил на ось x:

Из этого уравнения найдем силу Т — натяжение в произвольной точке

Откуда следует, что сила Т увеличивается от низшей точки нити к опорам и будет наибольшей в точках подвеса — там, где касательная к кривой провисания нити составляет наибольший угол с горизонталью. При малом провисании нити этот угол не достигает больших значений, поэтому с достаточной для практики степенью точности можно считать, что усилие в нити постоянно и равно ее натяжению Н. На эту величину обычно и ведется расчет прочности нити. Если все же требуется вести расчет на наибольшую силу у точек подвеса, то для симметричной нити ее величину определим следующим путем. Вертикальные составляющие реакций опор равны между собой и равны половине суммарной нагрузки на нить, т. е. ql/2. Горизонтальные составляющие равны силе Н, определяемой по формуле (2.41). Полные реакции опор получатся как геометрические суммы этих составляющих:

Условие прочности для гибкой нити, если через F обозначена площадь сечения, имеет вид:

Заменив натяжение Н его значением по формуле (2.41), получим:

   Из этой формулы при заданных l, q, F и можно определить необходимую стрелу провисания f. Решение при этом упростится, если в q включен лишь собственный вес; тогда , где — вес единицы объема материала нити, и

т. е. величина F не войдет в расчет.

Если точки подвеса нити находятся на разных уровнях, то, подставляя в уравнение (2.39) значения x=-a и x=b, находим и :

Отсюда из второго выражения определяем натяжение

а деля первое на второе, находим:

Имея в виду, что b+a=l, получаем:

Или

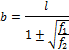
Подставив это значение b в формулу определенного натяжения Н, окончательно определяем:

Два знака в знаменателе указывают на то, что могут быть две основные формы провисания нити. Первая форма при меньшем значении Н (знак плюс перед вторым корнем) дает нам вершину параболы между опорами нити. При большем натяжении Н (знак минус перед вторым корнем) вершина параболы расположится левее опоры А. Получаем вторую форму кривой. Возможна и третья (промежуточная между двумя основными) форма провисания, соответствующая условию ; тогда начало координат O₃ совмещается с точкой А. Та или иная форма будет получена в зависимости от соотношений между длиной нити по кривой провисания АОВ (рис.2.60) и длиной хорды АВ.

Если при подвеске нити на разных уровнях неизвестны стрелы провисания и , но известно натяжение Н, то легко получить значения расстояний а и b и стрел провисания и . Разность h уровней подвески равна:

Подставим в это выражение значения и , и преобразуем его, имея в виду, что a+b=l:

откуда

а так как a+b=l то

 Следует иметь в виду, что при a>0 будет иметь место первая форма провисания нити, при a<0 — вторая форма провисания и при a=0 — третья форма. Подставляя значения a и b в выражения для стрел провисания и , получаем величины и :

Теперь выясним, что произойдет с симметричной нитью, перекрывающей пролет l, если после подвешивания ее при температуре и интенсивности нагрузки температура нити повысится до а нагрузка увеличится до интенсивности (например, из-за ее обледенения). При этом предположим, что в первом состоянии задано или натяжение H₁, или стрела провисания (Зная одну из этих двух величин, всегда можно определить другую.)

При подсчете деформации нити, являющейся по сравнению с длиной нити малой величиной, сделаем два допущения: длина нити равна ее пролету, а натяжение постоянно и равно Н. При пологих нитях эти допущения дают небольшую погрешность.

В таком случае удлинение нити, вызванное увеличением температуры, будет равно

где — коэффициент линейного температурного расширения материала нити.

При повышении температуры нить удлиняется. В связи с этим увеличится ее стрела провисания и, как следствие, уменьшится ее натяжение. С другой стороны, из-за увеличения нагрузки, как видно из формулы (2.41), натяжение увеличится. Допустим, что окончательно натяжение увеличивается. Тогда удлинение нити, вызванное увеличением натяжения, будет, согласно закону Гука, равно:

Если окажется меньше, чем то величина будет отрицательной. При понижении температуры будет отрицательной величина .

   Таким образом, длина нити во втором ее состоянии будет равна длине при первом ее состоянии с добавлением тех деформаций, которые произойдут от повышения температуры и натяжения:

Изменение длины нити вызовет изменение и ее стрелы провисания. Вместо , она станет .

Теперь заменим в последнем уравнении и их известными выражениями, а деформации и — также их полученными ранее значениями. Тогда уравнение для S₂ примет следующий вид:

В этом уравнении заменим и их значениями по формуле (2.40):

Тогда, после некоторых преобразований, уравнение для расчета натяжения может быть написано в виде:

Определив из этого уравнения натяжение H₂, можно найти по формуле (2.40) и стрелу .

В случае, если при переходе от первого ко второму состоянию нагрузка не изменяется, а изменяется лишь температура, то в последнем уравнении интенсивность заменяется на . В случае, если при переходе от первого ко второму состоянию не изменяется температура, а изменяется лишь нагрузка, то в этом уравнении средний член в квадратной скобке равен нулю. Полученное уравнение пригодно, конечно, и при понижении температуры и уменьшении нагрузки.

В тех случаях, когда стрела провисания не является малой по сравнению с пролетом, выведенные выше формулы, строго говоря, неприменимы, так как действительная кривая провисания нити, цепная линия, будет уже значительно отличаться от параболы, полученной нами благодаря предположению о равномерном распределении нагрузки по пролету нити, а не по ее длине, как то имеет место в действительности.

Точные подсчеты показывают, что значение погрешности в величине натяжения Н, вызванной этим предположением, таково: при отношении f/l<1/20 погрешность не превосходит 0,3%, при f/l=1/10 ошибка составляет уже 1,3%, а при f/l=1/5 погрешность несколько, превосходит 5%.

Вопросы для самопроверки

- Что называется стержнем?

- Какой вид нагружения стержня называются осевым растяжением (сжатием)?

- Какие силы являются внешними, какие внутренними?

- Какие внутренние силовые факторы возникают в сечении бруса при растяжении и сжатии?

- Дайте определение эпюры внутреннего силового фактора.

- Что называют нормальной силой?

- В чем сущность метода сечений? Из каких операций состоит метод?

- Как определяется значение нормальной силы в поперечном сечении?

- Какое правило знаков используют для нормальных сил?

- Какие нагрузки называют распределенными? Указать размерности различных внешних сил (в системе СИ).

- Как вычисляется значение нормальной силы N в произвольном поперечном сечении бруса?

- Что представляет собой эпюра нормальных сил и как она строится?

- Какой вид имеет эпюра нормальной силы на прямолинейном участке, свободном от распределенной нагрузки?

- Какой вид имеет эпюра нормальной силы на участке, подверженном равномерно распределенной продольной нагрузке?

- Какова особенность эпюры N в месте действия осевой сосредоточенной силы?

- Что является количественной мерой интенсивности внутренних сил в точке?

- Какое напряжение называют нормальным? Какое касательным?

- Как распределены нормальные напряжения σ_х в поперечных сечениях центрального растянутого бруса и чему они равны?

- В каких сечениях растянутого (сжатого) стержня возникают наибольшие нормальные напряжения?

- В каких сечениях растянутого (сжатого) стержня возникают наибольшие касательные напряжения?

- Какие напряжения возникают в наклонных сечениях стержня при растяжении или сжатии?

- Каково соотношение между наибольшими нормальными и наибольшими касательными напряжениями в точке растянутого (сжатого) стержня?

- Что называется жесткостью поперечного сечения при растяжении?

- Как формулируется закон Гука? Запишите формулы абсолютной и относительной продольной деформации бруса?

- Что представляют собой эпюра продольных перемещений?

- Как учитывается собственный вес бруса в аналитическом выражении для продольной силы?

- Как объяснить наличие множителя 1/2 в формуле удлинения вертикального бруса постоянного сечения от собственного веса?

- В чем смысл и какова формула поверочного расчета?

- Как назначаются допускаемые напряжения для пластичных и хрупких материалов?

- Как выполняется проектировочный расчет?

- Какие три характерных вида задач встречаются при расчете на прочность конструкции?

- Почему считается возможным отклонение до 5% фактического напряжения от допустимого?

- Почему необходимо выполнять условие жесткости? Приведите примеры.

- При проведении расчета на прочность по предельным состояниям с чем сравнивают фактические напряжения?

- Как распределяются по сечению силы упругости при растяжении и сжатии? (Использовать гипотезу плоских сечений).

- Как вычисляется значение продольной силы в произвольном поперечном сечении стержня?

- Какого характера напряжения возникают в поперечном сечении при растяжении и сжатии: нормальные или касательные?

- Как распределены нормальные напряжения в поперечных сечениях центрально-растянутого или центрально-сжатого стержня и по какой формуле они определяются?

- Получите формулу нормальных напряжений при растяжении-сжатии? Какие предпосылки используются при выводе этой формулы?

- Как записывается условие прочности бруса при растяжении (сжатии)? Какие виды задач решаются с помощью условия прочности?

- В каких единицах измеряется напряжение?

- Как изменится величина напряжения, если площадь поперечного сечения возрастет в 4 раза?

- Как назначаются знаки продольной силы и нормального напряжения?

- Как связаны гипотеза плоских сечений (гипотеза Бернулли) и закон распределения нормальных напряжений в поперечном сечении растянутого (сжатого) стержня?

- Раскройте понятие эпюр продольных сил, нормальных напряжений и перемещений. Для чего они строятся? Каких правил придерживаются при построении эпюр?

- Что показывает эпюра продольной силы?

- Что представляют собой эпюры внутренних силовых факторов? С какой целью их строят?

- Опишите технику построения эпюры продольных сил в брусе, загруженном несколькими сосредоточенными силами по оси бруса?

- Как вычислить значение продольной силы в произвольном поперечном сечении бруса?

- Как вычислить напряжения в поперечном сечение бруса при растяжении и сжатии? Как они распределены по поперечному сечению?

- Как определяют абсолютное удлинение ступенчатого бруса, нагруженного несколькими силами?

- Как определяется удлинение призматического бруса от собственного веса?

- Какое влияние оказывает собственный вес стержня при проектирования сооружения?

- Что понимается под брусом равного сопротивления?

- Запишите формулы для определения удлинения бруса. Что характеризует произведение АЕ и как оно называется?

- Какие деформации бруса называются абсолютными и какие относительными?

- Что называется удлинением стержня (абсолютной продольной деформацией)? Что такое относительная продольная деформация? Каковы размерности абсолютной и относительной продольных деформаций?

- Опишите технику определения продольных и поперечных деформаций бруса при растяжении-сжатии?

- Стальной стержень длиной 1,5 м вытянулся под нагрузкой на 3 мм. Чему равно относительное удлинение? Чему равно относительное сужение? (= 0,25)

- Как определяются продольные перемещения точек бруса при ступенчато переломанном сечении и продольных силах, постоянных в пределах отдельных участков?

- Что характеризует модуль упругости материала? Какова единица измерения модуля упругости?

- Что называется модулем упругости Е? Как влияет величина Е на деформации стержня?

- Что называется жесткостью поперечного сечения стержня при растяжении (сжатии)?

- Относительные деформации и перемещения.

- Что понимается под жесткостью при растяжении или сжатия стержня?

- Принципы расчета на жесткость.

- Типы задач при расчетах на жесткость.

- Примеры влияния жёсткости на работоспособность конструкции.

- Сформулируйте закон Гука. Напишите формулы для абсолютной и относительной продольных деформаций стержня.

- Что происходит с поперечными размерами стержня при его растяжении (сжатии)?

- Что характеризует коэффициент поперечной деформации?

- Что такое коэффициент Пуассона? В каких пределах он изменяется?

- Как определяется коэффициент Пуассона?

- Какие три характерных типа задач встречаются при расчете прочности конструкции?

- Какая разница между статически определимой и статически неопределимой стержневой системой?

- Какие системы называют статически неопределимыми? Как установить степень статической неопределимости системы?

- В какой последовательности рассчитывают статически неопределимые системы?

- Что представляют собой дополнительные уравнения условия совместности перемещений?

- Сколько уравнений статики нужно составить для системы сил, лежащих на одной прямой?

- Сколько уравнений статики нужно составить для системы сил, расположенных как угодно в плоскости, но сходящихся в одной точке?

- Сколько уравнений статики нужно составить для системы сил, расположенных как угодно в плоскости и не сходящихся в одной точке?

- Какое влияние оказывает на стержневую статически неопределимую системы изменение температуры?

- Какие напряжения называются температурными?

- Как учитываются в статически неопределимых стержневых системах монтажные напряжения?

- Как отражается увеличение жесткости отдельных элементов статически неопределимых систем на усилиях в этих и других элементах?

- Как ведется расчет статически неопределимых систем по методу разрушающих нагрузок?

- Объясните метод расчета статически неопределимых стержневых систем по предельному состоянию?

- Во сколько раз (примерно) поперечная деформация меньше продольной при осевом растяжении (сжатии) стальных стержней?

- При проведении испытаний были получены различные значения коэффициента Пуассона для стали: 0,15; 0,28; 0,4. Укажите, какие значения ошибочны?

- Вычислите продольную силу, возникающую в поперечном сечении растянутого стержня, если нормальные напряжения в этом сечении равны 140 МПа, а его площадь составляет 100 мм²?

- Определение нормальных и касательных напряжений на наклонных площадках при растяжении – сжатии. Вывод формулы.

- Какая нить называется абсолютно гибкой нитью?

- Как определяется стрела провисания нити и когда она считается малой?

- Как изменяется сила натяжения в нити от низшей точки нити к опорам? В каком месте может произойти обрыв нити?

- Какая влияет температура на натяжение нити?

- Как влияют упругие деформации на длину и натяжение нити?

- В поперечном сечении растянутого бруса возникают напряжения, которые называются …

- Жесткостью поперечного сечения при растяжении называют …

- Безопасная прочность бруса при растяжении определяется по формуле…

- Допустимые напряжения для пластичных материалов определяют по формуле …

- Допустимые напряжения при растяжении хрупких материалов определяют по формуле …

- Опасным поперечным сечением бруса является сечение, в котором действуют наибольшие …

- Центральным растяжением называют такой вид деформации, при котором в поперечном сечении возникает только одно внутреннее усилие - …

- С увеличением жесткости поперечного сечения бруса абсолютное удлинение …

- Площадь поперечного сечения бруса из условия безопасной прочности при растяжении определяется по формуле …

- Значение продольной силы в поперечном сечении бруса вычисляют из условия …

- Напряжения в системе СИ имеют размерность …

- Удлинение растянутого стержня определяется по формуле …

- При поверочном расчете сравнивают …

- При проектировочном расчете определяют …

- Условие жесткости при растяжении определяется выражением …

- Отличие расчета на прочность по предельным состояниям от расчета по допустимым напряжениям состоит в …

- Проекция главного вектора внутренних сил в поперечном сечении нагруженного бруса на продольную ось бруса называется:

1) критической силой;

2) касательным напряжением;

3) поперечной силой;

4) продольной силой;

5) нормальным напряжением.

- Деформации (линейные ε и угловые γ) считаются практически малыми, если они не превосходят…

1) 0,12 (или 12%);

2) 0,05 (или 5%);

3) 0,2 (или 20%);

4) 0,1 (или 10%).

- Если предел пропорциональности материала и соответствующая ему деформация равны σ_П=100 МПа, ε_П=0,0014, тогда величина модуля упругости равна...

1) 83110 Мпа;

2) 55782 Мпа;

3) 71429 Мпа;

4) 65822 Мпа.

- Каков физический смысл модуля Юнга?

1. коэффициент пропорциональности между поперечной и продольной деформацией;

2. коэффициент пропорциональности между нормальным напряжением и линейной деформацией;

3. коэффициент пропорциональности между касательным напряжением и угловой деформацией.

- Чему равняется максимальная по абсолютной величине продольная сила, возникающая в представленном на рисунке стержне?

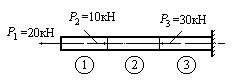
- Чему равно нормальное напряжение (в МПа) на третьем участке изображенного на рисунке стержня, если площадь поперечного сечения стержня равна см²?

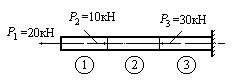
- Определить величину внешней силы (в кН), приложенной к стержню, изображенному на рисунке.

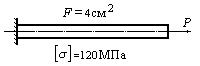
- Найти площадь поперечного сечения (в см²) для приведенного на рисунке стержня из условия прочности.

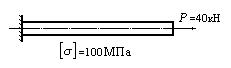
- Определить площадь поперечного сечения (в см²) для приведенного на рисунке стержня из условия жесткости.

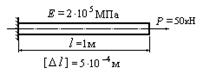
- Вертикально расположенный ступенчатый брус нагружен на свободном конце растягивающей силой P. Найти распределение продольной силы, нормального напряжения и осевого перемещения по длине бруса. Заданы площадь F, длина l, удельный вес γ, модуль Юнга E.

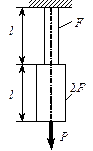
- Вертикально расположенный ступенчатый брус нагружен на свободном конце сжимающей силой P. Найти распределение продольной силы, нормального напряжения и осевого перемещения по длине бруса. Известны площадь F, длина l, удельный вес γ, модуль Юнга E.

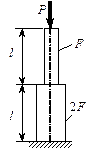
- На середине лестницы AB, установленной под углом α, находится человек весом P. Считая лестницу балкой с поперечным сечением площадью F , моментом инерции I, длиной AB=l и модулем Юнга E, определить внутренние усилия и перемещения. Силами трения пренебречь.

- Консольный кран несёт нагрузку P. Определить внутренние усилия и перемещения балки AB, считая тягу BC нерастяжимой. Принять для балки AB площадь и момент инерции поперечного сечения равными F, I; модуль Юнга – E. Геометрические размеры указаны на рисунке.

- Определить усилие (в кН) в стержне ВС фермы, изображенной на рисунке:

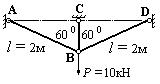
Онлайн-калькулятор "Расчет прочности при растяжении-сжатии"

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00