Главная
Лекция 18. Ползучесть
материалов
Содержание
Испытание материалов на ползучесть
Последействие и релаксация материалов
Основы теории ползучести
При изучении предыдущих частей данного учебного пособия предполагалось, что напряженное и деформированное состояние тела остается неизменным во времени, если неизменны внешние воздействия. Однако, в действительности полная деформация любой точки заданного тела при действии внешних сил, формируется в течении определенного промежутка времени. Далее известно, что все материалы обладают свойством старения, т.е. физико-механические характеристики во времени меняются, поэтому учет временных процессов, протекающих в элементах конструкций в период действия внешних сил имеет важное значение в плане совершенствования методов их расчета.
Ползучестью называется процесс нарастания остаточной деформации во времени при постоянных нагрузке или напряжении и температуре.
В современной технической литературе термин «ползучесть» часто заменяют термином «вязкоупругость».
Явление ползучести в принципе присуще всем материалам, но не все они обладают им в одинаковой мере. В металлах ползучесть обнаруживается лишь при высоких температурах, а в цветных металлах (свинец, медь и др.) может проявляться и при обычных температурах. Наиболее ощутим процесс ползучести в бетоне, грунтах, полимерах. Опыт показывает, что деформации ползучести могут быть весьма существенными и заметно влиять на работу конструкции. Известны случаи разрушения котельных труб под постоянным давлением вследствие ползучести материала. Установлено, что в результате ползучести бетона напряжения в арматуре железобетонных конструкций могут увеличиться в 2...2,5 раза, а перемещения в 3...4 раза. Накопление деформаций ползучести в лопатках и дисках турбин может привести к опасному уменьшению зазора между концами лопаток и кожухом двигателя, к заклиниванию и поломке лопаток. В других случаях чрезмерное удлинение детали в условиях ползучести может привести к уменьшению поперечного сечения и разрушению детали при напряжениях, гораздо меньших, чем те, которые она может выдержать при обычном статическом нагружении без длительной выдержки под нагрузкой. Поэтому учет фактора ползучести имеет существенное значение для правильного работы конструкций при действии внешних сил.
Хотя явление ползучести было известно давно, экспериментально его исследовал одним из первых В.Вебер в 1835 г. в опытах по воздействию крутящего момента на кварцевые волокна. В них обнаружилось удивительное для неживой материи свойство хранить «память» о воздействиях, которые она испытывала в прошлом.
Предположим, что в начальный момент времени деформации имеют значения ε(0), равное упругой деформации или суммарной упругой и пластической деформацией (рис.18.1). Обычно считается, что время нагружения (или разгрузки) образца пренебрежимо мало по сравнению с временем проведения эксперимента, в связи с чем можно положить, что напряжение и деформация ε(0) появляются мгновенно.
С увеличением времени t наблюдается возрастание деформаций. Если процесс сопровождается
уменьшением скорости деформирования ![]() (точкой обозначена производная по времени t) и при
(точкой обозначена производная по времени t) и при ![]() ,
, ![]() , то эта стадия ползучести называется установившейся (1) (рис.18.1) Если
деформация ползучести имеет тенденцию к беспредельному увеличению и в итоге
сопровождается разрушением материалов конструкции, то эта стадия ползучести
называется неустановившейся (2)
(рис.18.1).
, то эта стадия ползучести называется установившейся (1) (рис.18.1) Если
деформация ползучести имеет тенденцию к беспредельному увеличению и в итоге
сопровождается разрушением материалов конструкции, то эта стадия ползучести
называется неустановившейся (2)
(рис.18.1).
Полная деформация в произвольный момент времени определяется как сумма начальной деформации ε(0) и деформации ползучести εП, т.е.
![]()
Заметим, что характер протекания ползучести во времени очень чувствителен в зависимости от интенсивности напряжений и температуры. Увеличение интенсивности напряжений или градиента температуры, как правило, приводит к возрастанию деформаций ползучести.
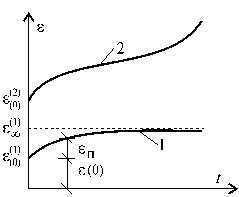
Рис.
18.1
Если увеличение деформаций ползучести пропорционально увеличению напряжений, то имеем дело с линейной ползучестью, в противном случае - с нелинейной ползучестью. Установлено, что ползучесть металлов при высоких температурах нелинейная, а бетона, пластмасс при малых напряжениях – линейная. В частности, линейная ползучесть бетона при сжатии имеет место при напряжениях, меньших приблизительно половины призменной прочности.
На ползучесть различных материалов кроме перечисленных оказывают значительное влияние и другие факторы. Например, на ползучести бетона сказываются влажность, свойства заполнителя, вид цемента, водоцементное отношение, масштабный фактор и т.д.
В некоторых случаях наблюдается изменение механических свойств материала по истечении длительного времени при неизменных внешних условиях и в ненагруженном состоянии. В бетоне, например, это явление обусловлено длительными химическими процессами, происходящими в цементном камне, в пластмассах, каучуках и в материалах органического происхождения – медленно протекающими окислительными процессами. Отмеченные явления приводят к так называемому старению материалов. В результате старения они через определенный промежуток времени не могут быть использованы в качестве конструкционных. Установлено, что деформация ползучести при старении зависит не только от продолжительности действия нагрузки, но и от возраста самого материала, который нагружается не сразу после его изготовления.
Известны четыре вида ползучести:
- неупругая
обратимая ползучесть, которая считается неопасной для
конструкций, т.к. она протекает при напряжениях сдвига ниже критических (![]() );
);
- логарифмическая ползучесть протекает в области относительно низких температур;
- высокотемпературная
ползучесть – которая протекает при (0,4...0,6)![]() , где
, где ![]() , - температура плавления материала;
, - температура плавления материала;
- диффузионная
ползучесть реализуется при очень высоких температурах порядка
(0,8...0,9)![]() .
.
Испытание материалов на ползучесть
Сопоставление материалов по их сопротивлению
ползучести часто проводится с помощью условной характеристики, называемой
пределом ползучести. Существуют два определения для предела ползучести. Первое
относится к случаю относительно непродолжительной работы материала при высоких
уровнях напряжения и температуры, когда существенную роль играют процессы,
происходящие на стадии неустановившейся ползучести. Например, работа лопаток
авиационных газовых турбин. В соответствии с первым определением пределом ползучести называется
напряжение, при котором остаточная деформация в условиях длительного
статического напряжения достигает определенной величины за заданный промежуток
времени, равный времени эксплуатации детали (например, 0,1% за 300 часов) при
температуре T. Второе определение
относится к случаю длительной работы конструкции в стационарных условиях при
относительно невысоких напряжении и температуре, когда стадией неустановившейся
ползучести практически можно пренебречь, а учитывать только деформацию ползучести,
накапливаемую на стадии установившейся ползучести с постоянной скоростью.
Например, работа лопаток паровой турбины тепловой станции. В соответствии со
вторым определением пределом ползучести
называется напряжение, при котором скорость ползучести на установившейся стадии
![]() равна
заданной величине (например, 10-8 ч-1) при температуре T. Отметим, что предел ползучести является не только
характеристикой материала, но учитывает также фактор времени.
равна
заданной величине (например, 10-8 ч-1) при температуре T. Отметим, что предел ползучести является не только
характеристикой материала, но учитывает также фактор времени.
Предел ползучести рекомендуется определять при допусках на удлинение от 0,1 до 1% при длительности испытания от 50 до 10000 ч. Если предел ползучести определяется по скорости ползучести, то общая продолжительность испытания должна составлять не менее 2000-3000 ч, при условии продолжительности прямолинейного участка кривой ползучести не менее 500 ч. Скорость ползучести определяется по формуле
![]()
где ∆l - абсолютное приращение длины образца за время ∆t; l0 - расчетная длина.
Порядок определения условного предела
ползучести следующий: испытывают серию образцов (не менее четырех) при данной
температуре и трех-четырех уровнях напряжения. Количество образцов в серии
должно обеспечивать задаваемую точность определения предела ползучести.
Результатом испытания являются первичные кривые ползучести в координатах
«деформация ![]() -
время t»
(рис.18.2, а). В случае нахождения
предела ползучести по заданной деформации, при обработке первичных кривых
ползучести определяются величины относительных деформаций, соответствующих
заданной длительности, например 10000 ч. Затем по найденным величинам
деформации строится график зависимости напряжения σ от деформации
-
время t»
(рис.18.2, а). В случае нахождения
предела ползучести по заданной деформации, при обработке первичных кривых
ползучести определяются величины относительных деформаций, соответствующих
заданной длительности, например 10000 ч. Затем по найденным величинам
деформации строится график зависимости напряжения σ от деформации ![]() (рис.18.2, б),
из которого по заданному допуску (например, 1% деформации) находится значение
искомого напряжения.
(рис.18.2, б),
из которого по заданному допуску (например, 1% деформации) находится значение
искомого напряжения.
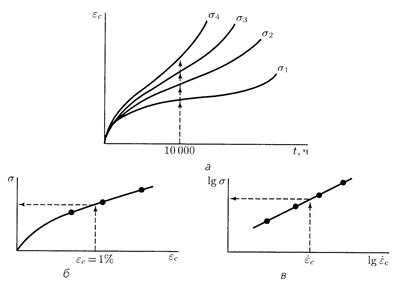
Рис.18.2
В случае определения предела ползучести по
заданной скорости ползучести, на основании обработки первичных кривых
ползучести находят средние скорости ползучести на прямолинейных участках каждой
кривой. Затем строят график зависимости логарифма напряжения σ от логарифма скорости ползучести ![]() (рис.18.2, в).
Эта зависимость в логарифмической системе координат изображается прямой, что
позволяет легко определить напряжение, соответствующее заданной скорости
ползучести
(рис.18.2, в).
Эта зависимость в логарифмической системе координат изображается прямой, что
позволяет легко определить напряжение, соответствующее заданной скорости
ползучести ![]() . Эти способы позволяют находить искомое
напряжение с погрешностью, не превышающей 5 МПа.
. Эти способы позволяют находить искомое
напряжение с погрешностью, не превышающей 5 МПа.
При определении предела ползучести по
деформации в обозначении этой величины указывается допуск на деформацию, время
и температура испытания. Например, ![]() -
предел ползучести при допуске на деформацию 0,2% за 100 ч испытания при
температуре 700 0С. При определении предела ползучести по скорости
он обозначается, например,
-
предел ползучести при допуске на деформацию 0,2% за 100 ч испытания при
температуре 700 0С. При определении предела ползучести по скорости
он обозначается, например, ![]() , что означает, что испытания велись при 1100
0С и при скорости испытания
, что означает, что испытания велись при 1100
0С и при скорости испытания ![]() %/ч.
%/ч.
Суть расчета конструкции на ползучесть заключается в том, что деформация деталей не будет превышать допустимого уровня, при котором нарушится конструктивная функция, т.е. взаимодействие узлов, за весь срок эксплуатации конструкции. При этом должно выполняться условие
![]() ,
,
разрешив которое, получаем уровень рабочих напряжений. Обратим внимание на тот факт, что при расчете на ползучесть речь не идет о недопущении разрушения конструкции. Решается лишь задача недопущения чрезмерной ее деформации. Например, деформация ползучести лопаток авиационной газовой турбины, работающих при температурах до 1200 0С, не нарушит условий работы турбины за весь срок ее эксплуатации.
Для практики наиболее важна высокотемпературная ползучесть. При высокотемпературных испытаниях образец нагревается специальной печью, которая содержится в конструкции испытательной машины.
Как отмечалось выше, процесс ползучести завершается разрушением материала. Сопротивление материала такому разрушению называется длительной прочностью. Время до разрушения (долговечность) tp зависит от величины напряжения и температуры.
Испытания на длительную прочность проводятся аналогично испытаниям образцов на ползучесть и на тех же испытательных машинах. Отличие заключается в том, что в испытаниях на длительную прочность не интересуются изменением деформации образца в процессе его нагружения постоянной нагрузкой, а фиксируют лишь время до его разрушения и деформацию при разрушении. Экспериментальная зависимость tp от напряжения σ при заданной температуре отражается в виде кривой длительной прочности в логарифмических координатах lgσ - lgtp, которую обычно представляют в виде ломаной линии, состоящей из двух прямых (рис.18.3).
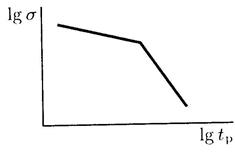
Рис.18.3
Точка перелома соответствует переходу от вязкого разрушения к хрупкому. Хрупкое разрушение связано с накоплением повреждений в материале, в частности в поликристаллических материалах с развитием многочисленных трещин по границам между зернами. При вязком разрушении трещины развиваются внутри зерен.
В образцах, изготовленных из одного и того же материала при различных нагрузках, могут наблюдаться и хрупкое, и вязкое разрушения. Как правило, при уменьшении напряжения и соответственно увеличении длительности пребывания образца под нагрузкой деформации к моменту разрушения уменьшаются, а характер разрушения становится хрупким. Иногда в указанных координатах кривая длительной прочности имеет вид прямой, что соответствует одному из указанных видов разрушения.
Зависимость времени до разрушения
одновременно от уровня напряжений и температуры дает кинетическая теория
разрушения, развитая Журковым на основе
экспериментов, проведенных на широком классе материалов (металлах, галлоидных соединениях, полимерах, стеклах) в большом
диапазоне изменения долговечности, температуры и напряжений. Была установлена следующая зависимость
![]()
где σ
- напряжение при растяжении; T- абсолютная температура; ![]() - постоянные, определяемые экспериментально и
зависящие от физико-химической природы твердого тела и его структуры; k -
постоянная Больцмана.
- постоянные, определяемые экспериментально и
зависящие от физико-химической природы твердого тела и его структуры; k -
постоянная Больцмана.
Прочность материала при ползучести
оценивается пределом длительной прочности,
т.е. таким минимальным напряжением, которое при заданной длительности работы
при определенной температуре приводит материал к разрушению. Предел длительной
прочности с увеличением времени действия нагрузки (от долей минут до десятков
лет) значительно снижается. Обозначается предел длительной прочности через σ с
двумя индексами, например, ![]() , где верхний индекс – это температура
испытания, а нижний – заданная продолжительность испытания до разрушения в часах.
, где верхний индекс – это температура
испытания, а нижний – заданная продолжительность испытания до разрушения в часах.
Если говорить о длительной прочности такого материала как бетон, то считается, что он определяется характером структурных дефектов, вызванных длительно действующей нагрузкой. Если дефекты не возникают, то это означает, что действующее напряжение не превосходит предела длительной прочности. При напряжениях, меньших предела длительной прочности, дефекты также могут возникать, но при условии, что их развитие прекращается во времени. Для достаточно большого времени нагружения, равного времени эксплуатации сооружения (~50...70 лет), предел длительной прочности бетона принимается равным ~0,8σв, где σв - призменная прочность бетона (временная).
Среди материалов, работающих в условиях комнатных температур, вопросы длительной прочности особенно важны для древесины и композитных материалов, выполненных на основе полимеров (стеклопластики, полимербетон и т.п.).
Для древесины можно привести следующие данные: предел временной прочности сосны при сжатии и растяжении вдоль волокон соответственно равен ~76 и ~115 МПа, а предел длительной прочности при тех же нагружениях ~44 и ~56 МПа; слоистый пластик ДСП-В (материал, изготовленный из тонких листов лущеного березового шпона, пропитанного синтетическими смолами) при кратковременном нагружении имеет предел прочности при сжатии и растяжении вдоль слоев шпона и вдоль волокон рубашки одинаковый и равный ~148 МПа, а предел длительной прочности ~75 МПа.
В испытаниях на длительную прочность также определяют характеристики пластичности: относительные удлинения и сужение образца при разрушении, дающие информацию о деформационной способности материала. Это особенно важно для большинства материалов, применяемых в энергомашиностроении, когда пластичность снижается от 10-15% при малой долговечности до 1-2% при сроках службы 1∙105-2∙105 ч.
Процесс ползучести следует рассматривать как
процесс накопления повреждений, приводящий к полному разрушению материала,
когда происходит исчерпание деформационной способности материала. За меру
повреждения можно принять отношение ![]() , где
, где ![]() -
накопленная деформация ползучести при заданном режиме нагружения и
продолжительности эксплуатации,
-
накопленная деформация ползучести при заданном режиме нагружения и
продолжительности эксплуатации, ![]() - деформация разрушения при заданном режиме
нагружения. Тогда кривые ползучести фактически отражают условия накопления
повреждений материала во времени. Такой подход
используется для оценки состояния материала элементов энергооборудования,
на которых происходят эксплуатационные измерения ползучести (например, в трубах
паропроводов современных энергоблоков), оценивая по величине накопленной
деформации степень поврежденности и определяя долю исчерпания заданного
ресурса.
- деформация разрушения при заданном режиме
нагружения. Тогда кривые ползучести фактически отражают условия накопления
повреждений материала во времени. Такой подход
используется для оценки состояния материала элементов энергооборудования,
на которых происходят эксплуатационные измерения ползучести (например, в трубах
паропроводов современных энергоблоков), оценивая по величине накопленной
деформации степень поврежденности и определяя долю исчерпания заданного
ресурса.
Последействие и релаксация материалов
Если в некоторый момент времени ![]() производить разгрузку, то накопленная
деформация ползучести начинает уменьшаться, асимптотически
стремясь к некоторому пределу
производить разгрузку, то накопленная
деформация ползучести начинает уменьшаться, асимптотически
стремясь к некоторому пределу ![]() рис.18.4. Такое явление носит название обратной ползучести. Частным
случаем обратной ползучести является рост необратимых и обратимых деформаций
при постоянном напряжении. Это явление носит название последействие.
рис.18.4. Такое явление носит название обратной ползучести. Частным
случаем обратной ползучести является рост необратимых и обратимых деформаций
при постоянном напряжении. Это явление носит название последействие.
Для условий эксплуатации изделий в течение длительного времени под постоянными нагрузками необходимо учитывать явление упругого последействия, которое заключается в том, что упругие деформации продолжают некоторое время возрастать после завершения нагружения. После разгрузки эта часть деформации исчезает не мгновенно, а постепенно, в течение некоторого времени. Деформации упругого последействия обычно невелики и проявляются, если деталь или образец нагружены до предела пропорциональности и длительное время находятся под этой нагрузкой. Чем однороднее материал, тем они меньше. Особенно ощутимы эти деформации в материалах органического происхождения, где с ними нельзя не считаться.
Явление необратимого последействия проявляется, если деталь или образец нагружены до предела упругости, но ниже предела текучести.

Рис.
18.4
Рис. 18.5
Обратимся к другому случаю, характеризующему свойства материалов и тесно связанному с ползучестью. Если имеется образец и обеспечить постоянство деформаций во времени в образце, как показывают эксперименты, то во времени происходит снижение напряжений (рис.18.5). Явления медленного уменьшения напряжений в образце при неизменной начальной деформации называется релаксацией. Она сопровождается переходом части упругих деформаций в пластические, поэтому соединения, выполненные с натягом, при длительной работе ослабевают. В металлических образцах при высоких температурах напряжение часто убывает до нуля. При испытаниях на релаксацию оценивают уменьшение макронапряжений во всем образце. Типичным примером детали, работающей в условиях релаксации напряжений, является болт фланцевого соединения. Плотность этого соединения определяется усилием натяга болта, который создается вследствие его упругой деформации. С течением времени натяг болта (уровень деформации) будет ослабевать, т.к. часть упругой деформации будет переходить в пластическую.
Испытания образцов на релаксацию напряжений проводят на тех же испытательных машинах и в тех же условиях, что и испытания образцов на ползучесть. Исключение заключается в том, что после приложения начальной полной нагрузки обеспечивается неизменность начальной деформации во времени. Это достигается путем периодического снижения нагрузки на образце по мере нарастания в нем деформации ползучести.
Уравнение релаксации напряжений имеет вид:
![]()
где ![]() -
упругая часть деформации, соответствующая напряжению
-
упругая часть деформации, соответствующая напряжению ![]() ;
; ![]() -
деформация ползучести, нарастающая во времени при снижающихся напряжениях.
Таким образом, релаксация напряжений является частным случаем ползучести при
изменяющемся напряжении.
-
деформация ползучести, нарастающая во времени при снижающихся напряжениях.
Таким образом, релаксация напряжений является частным случаем ползучести при
изменяющемся напряжении.
Увеличение деформаций ползучести ![]() приводит к снижению упругой деформации, причем
скорость снижения напряжений во времени зависит от скорости деформации
ползучести
приводит к снижению упругой деформации, причем
скорость снижения напряжений во времени зависит от скорости деформации
ползучести
![]()
Результаты испытаний на релаксацию напряжений представляются в виде кривой релаксации напряжений в координатах σ - t (рис.18.5).
В технической литературе часто встречается термин «замедленное разрушение». Этим термином характеризуется длительное разрушение, наблюдаемое в условиях, близких к условиям заданной деформации, когда происходит релаксация напряжений, сопровождаемая затухающей ползучестью. Накопление повреждений и исчерпание пластичности в этих условиях может привести со временем к разрушению даже при снижающихся напряжениях.
Возникновение релаксации напряжений, упругого и необратимого последействия является отражением того факта, что при нагружении и разгрузке с конечной скоростью материал находится в термодинамически неравновесном состоянии, так как поступающая извне энергия не может мгновенно распределиться по всему объему в соответствии с принципом минимума суммарной энергии системы. Возникают местные очаги с повышенной энергией, перераспределение которой по объему образца требует определенного времени. При этом часть избыточной энергии остается зафиксированной в материале в необратимой форме в виде дислокаций и других несовершенств кристаллической решетки, а также переходит в поверхностную энергию образующихся микротрещин.
Теории ползучести
Отметим, что в реальных условиях ползучесть, как правило, протекает при изменяющихся напряжениях и температурах, и для описания соответствующих процессов используются технические теории ползучести на базе характеристик, полученных при постоянных напряжениях и температуре.
Обычно для оценки сопротивления материала ползучести получают серию кривых ползучести по результатам испытания образцов при различных постоянных уровнях напряжения. Обрабатывая эту серию кривых ползучести, можно определить константы и параметры аналитических зависимостей соответствующих теорий ползучести и определить пределы ползучести. Сущность теорий ползучести состоит в выборе основных переменных, определяющих процесс ползучести, и установлении функциональных зависимостей между ними. Известны четыре основные теории ползучести, построенные на различных гипотезах.
Теория
течения. Основана на предположении существования постоянной
зависимости между скоростью пластической деформации, напряжением и временем ![]() . Полученное дифференциальное уравнение
теории течения справедливо при не слишком малых скоростях ползучести и медленно
изменяющихся напряжениях, достаточно больших в начале процесса. Оно нашло
применение в расчетах металлических узлов и соединений при высоких
температурах.
. Полученное дифференциальное уравнение
теории течения справедливо при не слишком малых скоростях ползучести и медленно
изменяющихся напряжениях, достаточно больших в начале процесса. Оно нашло
применение в расчетах металлических узлов и соединений при высоких
температурах.
Теория
упрочнения. Под упрочнением подразумеваются такие изменения в материале,
которые происходят по мере накопления деформаций ползучести и приводят к
снижению скорости ползучести при заданных напряжении и температуре. В
данной теории предполагается существование постоянной зависимости между
пластической деформацией, скоростью пластической деформации и напряжением ![]() .. Теория упрочнения удовлетворительно
описывает ползучесть при не очень сложных законах изменения внешних нагрузок.
.. Теория упрочнения удовлетворительно
описывает ползучесть при не очень сложных законах изменения внешних нагрузок.
Теории
наследственности и старения.
В этих теориях принята гипотеза о существовании постоянной зависимости между
пластической деформацией, напряжением и временем ![]() . Они описываются схожими интегральными
уравнениями. В теории старения механические характеристики принимаются зависящими от возраста материала.
. Они описываются схожими интегральными
уравнениями. В теории старения механические характеристики принимаются зависящими от возраста материала.
При линейной ползучести, если материал конструкции не обладает свойством старения, зависимость между напряжениями и деформацией можно представить в следующем виде:
![]()
где ![]() ;
; ![]() - определяет деформацию ползучести при единичном
напряжении σ = 1;
- определяет деформацию ползучести при единичном
напряжении σ = 1; ![]() .
.
Для функции ![]() справедливо равенство с(0) = 0.
справедливо равенство с(0) = 0.
Для получения зависимости между напряжением и деформацией при линейной ползучести в теории наследственности взят принцип наложения, согласно которому суммарная деформация ползучести при переменном напряжении может быть найдена как сумма деформаций ползучести, вызванных соответствующими приращениями напряжений. При этом каждая величина деформации ползучести зависит только от величины этого приращения напряжения и продолжительности его действия, но не зависит от величины и длительности действия других приращений.
Согласно принятому принципу наложения, получено выражение:
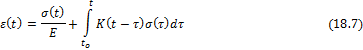
где t – время определения деформации; t0 – момент
времени приложения нагрузки; τ - момент времени
приращения нагрузки; функция ![]() указывает на приращение деформации от напряжения
указывает на приращение деформации от напряжения ![]() за
время
за
время ![]() .
.
Функция ![]() имеет
размерность 1/(сут∙МПа) и выражается различными уравнениями. Для ряда
материалов принимают, в частности:
имеет
размерность 1/(сут∙МПа) и выражается различными уравнениями. Для ряда
материалов принимают, в частности:
![]()
где γ, k - постоянные коэффициенты, характеризующие свойства материалов.
Первое слагаемое в выражении (18.7) соответствует упругой деформации, а интегральный член – деформации ползучести, накапливаемой в образце при действии нагрузки от момента времени t0 до t.
Если учесть свойства старения материалов, то величина деформаций ползучести конструкций зависят от возраста материала. В этом случае физические уравнения можно представить в следующем виде:
![]()
где ![]()
![]() или
или ![]()
Здесь β, n, A, B, γ - постоянные характеристики материалов конструкций.
В общем случае, когда переменными являются как напряжение, так и деформация соотношения между ними с учетом свойства наследственности и строения в рамках линейной теории записывается в виде:

Здесь вводим обозначения:
![]()
Теория ползучести, в основу которой положено выражение (18.10), носит название теории наследственного старения.
Соотношения наследственной теории ползучести были предложены Л.Больцманом в 1874 г. и развиты В. Вольтерра в 1909 г., а уравнения теории наследственного старения – Г.Н.Масловым и Н.Х.Арутюняном в 40-х годах XX столетия.
Линейное соотношение между напряжениями и деформациями (18.10) отличается от закона Гука для упругого материала только тем, что вместо величины 1/E здесь имеется интегральный оператор. Отсюда следует следующее простое правило построения решения задачи теории линейной ползучести, которое носит название принцип Вольтерра.
Решение задачи по теории линейной ползучести может быть получено из решения аналогичной задачи в упругой постановке, далее следует заменить упругие постоянные интегральные операторы и произвести необходимые операции над ними.
В частности, если в известных упругих решениях предполагать, что они записаны в изображениях Лапласа, т.е. заменить упругие постоянные изображениями соответствующих операторов теории ползучести и применить операции переходов от изображений к оригиналам искомых функций, получим решение соответствующее задаче с учетом ползучести материалов конструкции.
Отметим, что в настоящее время при решении многих инженерных задач, как в области механики твердого деформируемого тела, так и других отраслях, широко применяется метод интегрального преобразования Лапласа. Этот метод особенно эффективен при решении линейных дифференциальных, интегро-дифференциальных и интегральных уравнений, а также систем, состоящих из вышеуказанных типов уравнений. Суть его является следующей. Если имеется некая искомая функция y(t) от действительной переменной t, обозначая через y(s) образ искомой функции комплексной переменной s, т.е. изображение заданной функции по Лапласу, тогда формулы по определению оригинала и его изображения имеют следующие представления:
![]()
где i - мнимая единица, а c - некоторая постоянная, на действительной оси.
В качестве примера реализации изложенного подхода при решении инженерных задач рассмотрим расчет прогиба свободного конца консольной балки (рис.18.6), в момент времени t = 0 загруженной равномерно распределенной нагрузкой, постоянной во времени. Материал балки характеризуется линейной ползучестью, для которого
![]()

Рис.
18.6
По методу начальных параметров в упругой постановке задачи решение записывается в виде:

Заменим ![]() на
на
![]()
Тогда выражения перемещения (18.12) в изображениях Лапласа принимает вид:
![]()
Здесь K(s) определяется из (18.8):
![]()
С учетом (18.14), (18.13) принимает вид:
![]()
Выполняя операции обратного преобразования Лапласа, получим:
![]()
Отсюда следует, что при действии постоянной
нагрузки прогиб балки с течением времени возрастает по экспоненциальному закону
и при ![]() принимает следующее предельное значение:
принимает следующее предельное значение:
![]()
где yA - упругое перемещение, т.е. перемещение балки в точке А при t = 0.
В статически неопределимых упругих системах распределение усилий либо не зависит от упругих постоянных, либо зависит.
В первом случае, как и в статически определимых системах, напряженное состояние при ползучести совпадает с напряженным состоянием упругой системы, если функции E(t), K(t,τ) одинаковы для всех элементов конструкции. Меняется только деформированное состояние.
Во втором случае, который может встретиться, например, при расчете конструкций из разномодульных материалов, изменение во времени претерпевает не только деформированное, но и напряженное состояние.
Пример 1.
Для металлической двухпролетной
балки (рис.18.7, а), при
следующих исходных данных: q = 2 кН/м;
Р = 10 кН; ![]() = 20∙10-4 м4; Е0 = 2∙108 кН/м2;
а = 3 м; g = 2∙10-2 1/cут; k = 1,3;
= 20∙10-4 м4; Е0 = 2∙108 кН/м2;
а = 3 м; g = 2∙10-2 1/cут; k = 1,3;
![]() требуется определить перемещение за счет
изгиба конструкции в сечениях А и С, предполагая
материал конструкции упругим, далее - линейно
ползучим.
требуется определить перемещение за счет
изгиба конструкции в сечениях А и С, предполагая
материал конструкции упругим, далее - линейно
ползучим.
Решение:
1. Определить перемещение в точках
А и С за счет изгибаемых упругих деформаций конструкции.
Учитывая, что заданная система один раз статически неопределима, решение задачи рассмотрим по методу сил.

Рис.
18.7
Основная система изображена на рис.18.7, б. Эпюра моментов в основной системе от заданной системы внешних сил и единичной вертикальной силы X = 1, приложенной в месте и по направлению, отображенной связи показана на рис.18.7, в, г.
Перемножая эпюры моментов изображенных на рис.18.7, в, г по формуле Мора, последовательно определим вертикальное перемещение т.В от действия силы X = 1 и от действия системы внешних сил:
![]()

Опорная реакция в точке В принимает значение:

Далее вычисляются опорные реакции в заделке:
![]()
![]()
откуда
![]()
Проверяем правильность вычисления величины опорных реакций:
![]()
По методу начальных параметров последовательно определим величины упругих перемещений в точке А и С:
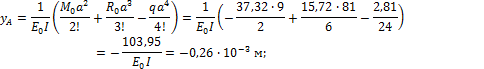
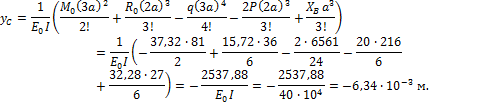
2. Определить перемещение в точках
А и С с учетом ползучести материала
конструкции.
Запишем выражения упругого перемещения:
![]()
По аналогу этих формул, запишем выражения перемещений с учетом ползучести материала балки в изображениях Лапласа:
![]()
![]()
Применяя изображения Лапласа запишем выражение функции K(t-τ) в изображениях в виде (18.14):
Подставляя (18.14) в (18.16) получим:
![]()
Переходя к оригиналам окончательно получим:
![]()
![]()
В условиях установившейся ползучести, при ![]() из
последних выражений вычисляются результирующие перемещения:
из
последних выражений вычисляются результирующие перемещения:
![]()
![]()
Как показывают численные расчеты за счет неограниченной ползучести перемещение заданной системы возросло в 2,3 раза:
![]()
![]()
Вопросы для самопроверки
1. Дайте определение о свойстве материалов, называемого ползучестью.
2. Дайте определение предела ползучести.
3. Дайте определение предела длительной прочности.
4. Дайте определение установившейся и неустановившейся ползучести.
5. Поясните, что такое упругое последействие.
6. Поясните, что такое релаксация.
7. Поясните понятие наследственной теории ползучести.
8. Поясните в чем заключается принцип Вольтерра.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов