Главная
Прямой
поперечный изгиб
- Балка АВ нагружена распределенной моментной нагрузкой
интенсивностью m и силой F=2m. Построить эпюры Q и M. Показать вид оси деформированной балки.
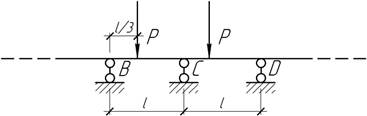
- Неразрезная балка постоянной жесткости EI имеет неограниченное число одинаковых пролетов, загруженных
силой Р на расстоянии l/3 от левой опоры. Построить эпюры поперечных сил и изгибающих
моментов.
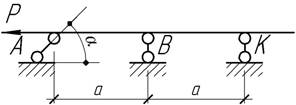
- Для балки построить эпюры поперечных сил и изгибающих
моментов, получить уравнение упругой линии и изобразить ее. α=600.
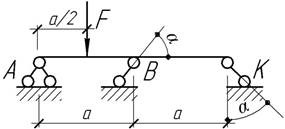
- Для балки определить опорные реакции, построить эпюры
поперечных сил и изгибающих моментов, получить уравнение упругой линии и
изобразить ее.
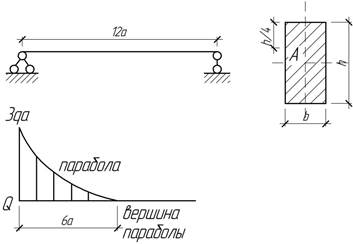
- Построить эпюры поперечных сил и изгибающих моментов.
- Построить эпюру изгибающих моментов. Определить перемещение
сечения А. Жесткость балки постоянна.
- Определить реакции опор. Стержень изогнут по дуге окружности.
- Для балки с двумя участками определить приложенные к ней
нагрузки, если известна эпюра поперечных сил и величина эквивалентного
напряжения (по гипотезе максимальных касательных напряжений) в точке А опасного сечения балки: 
- Балка составлена из двух брусков различных материалов с
отношениями модулей нормальной упругости Е1/Е2=2
и работает как одно целое. Найти максимальное растягивающие
и максимально сжимающие напряжения при изгибе балки положительным моментом М.
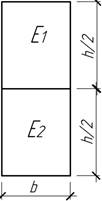
- Сечение балки состоит из двух одинаковых брусьев (В=10 см,
Н=30 см), между которыми вставлен стальной лист (b=1,2
см, h=23 см), жестко скреплены с ними. При каком значении изгибающего
момента наибольшие напряжения брусьев составят 10 МПа, каковы будут при этом
наибольшие напряжения в стальном листе? Ест=20Ед.
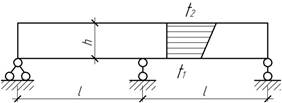
- Получить выражение для опорной реакции на средней опоре. Дано:
α, Е, l,
h.
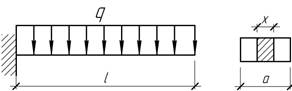
- Как должна изменяться ширина х балки прямоугольного
поперечного сечения, чтобы максимальные нормальные напряжения во всех ее
поперечных сечениях были постоянны. q, l, a – ширина сечения в
защемлении.
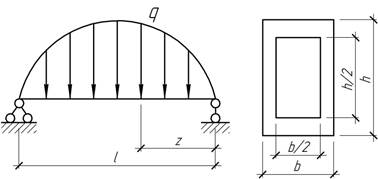
- По данному рисунку определить реакции
опор, построить эпюры внутренних усилий М, Q и найти Мmax.
- При каком значении z изгибающий момент под силой F будет максимальным?
- Балка
АВ защемляется обоими концами и должна нести равномерную нагрузку q. На какие углы α следует при защемлении
повернуть концы балки, чтобы после приложения нагрузки моменты в сечениях А, В и С были одинаковы?
-
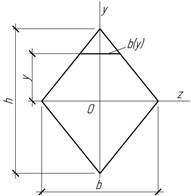
Для сечения изгибаемой балки в виде ромба определить закон распределения 
по высоте сечения и найти
- По заданным эпюрам Q и М установить
нагрузку, действующую на балку. Указать возможное расположение опор. m – максимальная интенсивность распределенного момента.
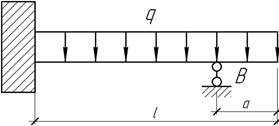
- Где по длине балки надо расположить опору В,
чтобы наибольший изгибающий момент имел наименьшее значение.
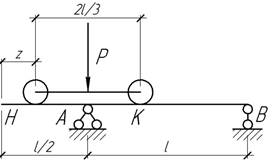
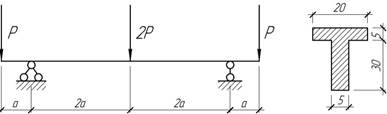
- По двутавровой балке АВ движется монтажная тележка весом Р. При каком положении тележки грузоподъемность балки будет:
1) наименьшей, 2) наибольшей?
- При какой силе Р максимальные
нормальные напряжения в балке АВ достигает 200 МПа. Материал – сталь. Размеры
считать заданными.
- Вычислить изменение отрезка (а, в). в, h, m, E – заданы.
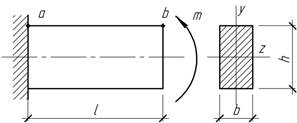
- Вычислить изменение отрезка (АВ). в, h,
Р, Е – заданы.
- Построить эпюры внутренних усилий.
- Стержень толщиной h
прижат к круговому лекалу радиуса R. Считая деформации упругими и перемещения малыми, найти
наибольшее нормальное напряжение и размер а зоны контакта. Принять F=4EI/Rl, h=R/700, 
- По уравнению упругой линии EIv=20z-15z2+2,5z3 для балки длиной l
установить: а) способы закрепления; б)
приложенные к балке нагрузки; в) длину балки.
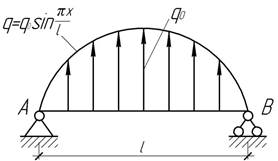
- Балка на двух опорах постоянного сечения загружена
распределенной нагрузкой, изменяющейся по синусоидальному закону 
. Определить наибольшие
нормальные и касательные напряжения.
- Бесконечная неразрезная балка постоянной жесткости лежит на
шарнирных опорах, расположенных с шагом l. На балку в каждом пролете действуют сосредоточенные пары сил с
моментами М каждая. Определить опорные реакции, построить эпюры поперечных сил
и изгибающих моментов.
- Построить эпюры поперечных сил и изгибающих моментов для
балки, нагруженной силой F
в середине левого пролета. F=1 кН, а=2 м,
α=600. В какую сторону сдвинется балка?
- Балка, опирающаяся правой катковой
опорой на наклонную стенку, нагревается на t0. Считая перемещения малыми и пренебрегая влиянием продольной
силы, определить реакцию катковой опоры.
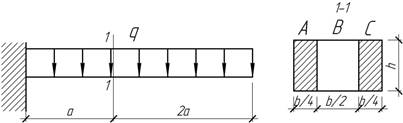
- Деревянная балка прямоугольного сечения, склеенная из трех
брусков А, В, С (ЕА=ЕС=Е, ЕВ=2Е),
нагружена равномерно распределенной нагрузкой. Определить наибольшие
касательные напряжения в сечении 1-1.
- Определить наибольшие нормальные напряжения в поперечном
сечении балки над опорой, если материал имеет разные модули упругости на
растяжение и сжатие (Ер=0,5Ес=104 МПа), Р=20 кН, а=1 м,
размеры сечения в см.
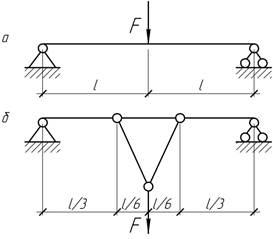
- На сколько повысится несущая
способность балки, если нагрузку F приложить так, как
показано на схеме б)?
- Найти координату х, при которой прочность балки будет
максимальной.
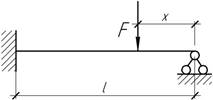
- На рисунке а) и б) изображены схемы двух балок одинаковой
длины и поперечного сечения. Правый конец балки по схеме а) может свободно
перемещаться в вертикальном положении, но не может поворачиваться. Сравнить
грузоподъемность балок.
- Найти угол α, при котором нормальные напряжения в опасном
сечении балки достигают максимальных значений.
- Для консольной балки, загруженной на конце силой F, определить наибольшее нормальное напряжение в поперечном
сечении, считая, что модули упругости I-го рода материала
балки при сжатии и растяжении различны, причем Ес=4Ер.
Поперечное сечение балки прямоугольное (ах2а).
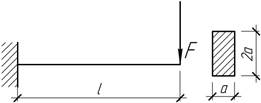
- Определить реакции опор и построить эпюры изгибающих моментов
и поперечных сил для балки, показанной на рисунке.
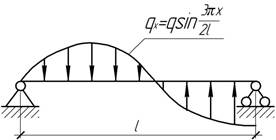
- Для бруса поперечной жесткости определить допускаемую нагрузку
q при заданных l, h, в и [σ].
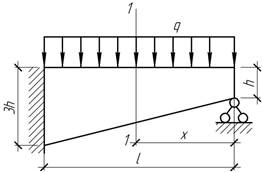
- На каком расстоянии (
) от опоры А надо приложить силу F, чтобы реакция RА была максимальной? EI=const.
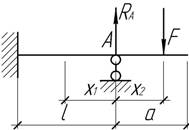
- Балка длиной l,
сечением аха находится под действием
нагрузки, равномерно распределенной по на верху и по низу, как показано на
рисунке.
Как изменится наибольшее напряжение, если балку распилить пополам продольным
сечением m-n? На сколько при
этом разойдутся торцевые сечения балки? Модуль упругости материала – Е.
- Балка нагружена распределенными
моментами [m]=[Нм/м] на половине пролета. Построить эпюры Q и М, установить опасное сечение.
Проверить правильность построения эпюр, объяснить кажущиеся противоречия в
эпюрах с точки зрения дифференциальных зависимостей.
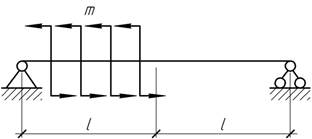
- Построить эпюры Qх и Мх,
установить опасное сечение. Проверить правильность построения эпюр и объяснить
кажущееся противоречия в эпюрах Qх
и Мх с точки зрения дифференциальных
зависимостей.
- По эпюре изгибающих моментов построить эпюру поперечных сил.
Изобразить балку с действующими на нее нагрузками.
- По заданной эпюре М для балки АВ установить действующие
нагрузки и построить эпюру Q.
- Замечено, что при разгрузке консольной или пролетной частей
нагрузки, балка может разрушаться. Когда это может случиться? Установить
оптимальные соотношения длин 
чтобы балка была наиболее
прочной.
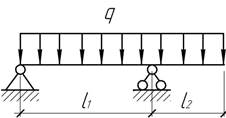
- Однопролетная балка на 2-х шарнирных опорах нагружена n сосредоточенными силами Р/n, расположенными на равном расстоянии одна друг от другой.
Определить Мmax
и проанализировать 
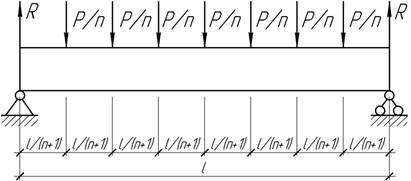
- Определить значение α (
), при котором максимальное нормальное напряжение
в опасном сечении балки прямоугольного сечения достигнет допускаемого значения,
если 
ширина сечения 
высота сечения 
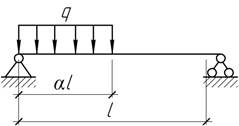
- Две балки одинаковой длины и выполненные из одного материала
изгибаются в вертикальной плоскости одной и той же нагрузкой. Сравнить балки по
весу, при условии их одинаковой прочности.
- При каком значении α максимальные нормальные напряжения
будут равны касательным?
- Для трехопорной балки построены
эпюры изгибающих моментов. Определить неизвестную ординату М.
- На консольную балку прямоугольного
поперечного сечения действует сила F=25
кН. Ширина балки постоянна и равна в=4 см, а высота
меняется по линейному закону от 6 см до 12 см. В каком сечении х возникают
максимальные напряжения?
- На балку действуют распределенные изгибающие моменты
интенсивностью m. Построить эпюры поперечных сил и изгибающих моментов.
- Для балки, показанной на рисунке, построить эпюры поперечных
сил и изгибающих моментов.
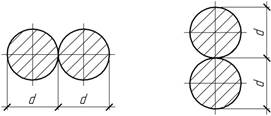
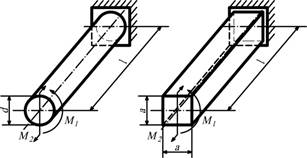
- Из конструктивных требований диаметр заделки принят равным 3d, а свободного – d. Определить диаметр d из условия прочности,
если l=2
м, [σ]=100 МПа, F=100 кН.
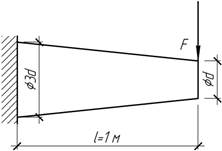
- Между двумя балками АВ и CD,
жесткостями на изгиб EI1=2EI и
EI2=EI установлен
каток «К». Найти силу взаимодействия между балками в точке К.
- Прямая упругая полоса (
) квадратного сечения аха
фиксируется без зазоров на цилиндрической поверхности радиуса R=30а
силами, направленными перпендикулярно к оси бруса. Найти нормальные напряжения
в центре тяжести сечения полосы.
-
Исходя из условия равнопрочности, определить соотношение
размеров поперечных сечений и массы двух брусьев одинаковой длины, если M1 = M2 = M. Материал
брусьев – сталь. Для квадратного сечения α = 0,208. Использовать 3ю теорию
прочности.
-
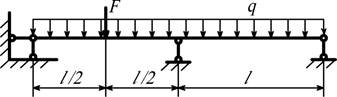
При каком значении силы F отсутствует реакция правой опоры. Дано: q, l
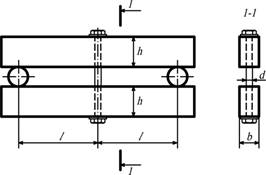
- Две одинаковые деревянные балки (h = 20 см, b = 12 см, l = 2,4 м) постепенно
стягиваются с помощью болта диаметром d = 1,5 см. Что произойдет раньше: излом балок или
разрыв болта, если предел прочности материала балки при изгибе σu=50 МПа, материала болта при растяжении σu=400 МПа, а коэффициент запаса n = 1,5?
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
