Главная

Стержни и стержневые системы, работающие на растяжение-сжатие

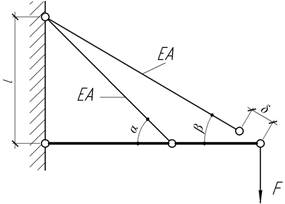
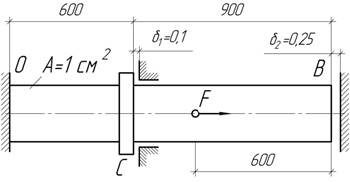
- Какая должна быть величина монтажного зазора δ, чтобы изображенная конструкция имела наименьший вес? Принять: α=45⁰, β=30⁰.

- Определить усилия в вертикальных связях.

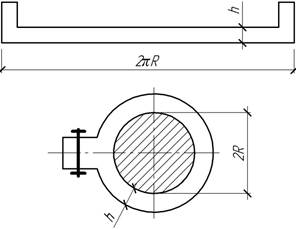
- Найти коэффициент запаса по пределу текучести стальной ленты толщиной h=1 мм и длиной 2πR, стянутой вокруг цилиндра. R=70 см, полагая

- Брус диаметром d имеет переменный вдоль радиуса модуль упругости. Найти [F] при заданном значении допускаемого напряжения [σ]. Считать справедливой гипотезу плоских сечений.

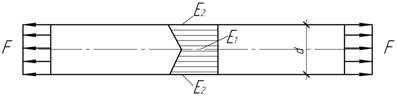
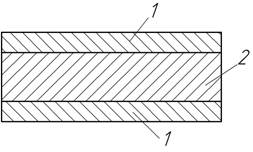
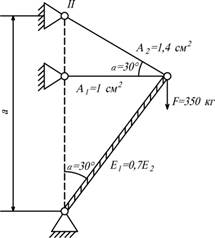
- Полоса из двух металлов 1 и 2 равномерно нагрета. Определить напряжения в обоих металлах, считая справедливой гипотезу плоских сечений. Коэффициент линейного расширения и площади поперечных сечений А₁ и А₂, модули упругости Е₁ и Е₂ материалов считать заданными. Решите эту задачу для случая, когда полоса изготовлена из пакета n металлов.

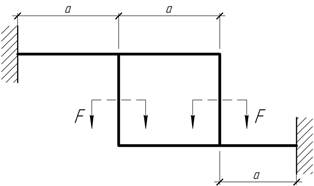
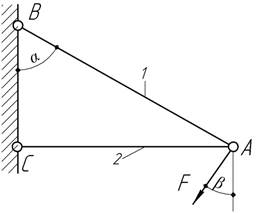
- Сила F вращается в плоскости АВС вокруг точки А. Подобрать площади поперечных сечений стержней и определить угол α из условия минимального веса стержней при самом невыгодном загружении конструкции. F и [σ] заданы.

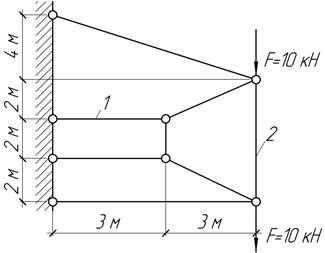
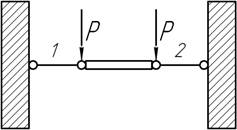
- Определить усилия в стержнях 1 и 2 системы, показанной на рисунке.

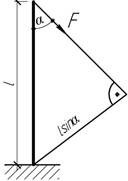
- Консольный стержень длиной l круглого поперечного сечения нагружен на свободном конце силой F, действующей под углом α. Определить наибольше нормальное напряжение в стержне и угол α, при котором это напряжение достигнет наибольшего значения.

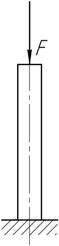
- Колонна нагружена осевой силой F, приложенной на ее свободном конце. спроектировать колонну минимального веса с учетом собственного веса, исходя из условия прочности.

- Невесомый стержень сжимается силами, приложенными вдоль его оси и равномерно распределенными по длине стержня (рисунок 5). Считая справедливым допущение о равномерном распределении нормальных напряжений в поперечном сечении стержня, определить касательное напряжение в произвольной точке сечения.

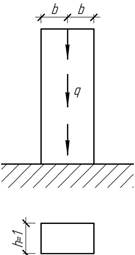
- Стержень нагружен осевыми силами с линейным изменением их интенсивности. Найти перемещение среднего сечения. Дано: q, l, E,A.

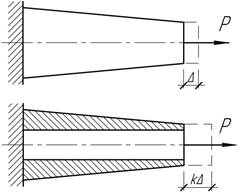
- Стержни с поперечной по длине площадью поперечного сечения при действии силы р на конце получают абсолютное удлинение Δ. Затем в стержне просверливается сквозное отверстие площадью А₀. После чего удлинение стержня (от той же силы) возрастает в к раз. Найти А₀.

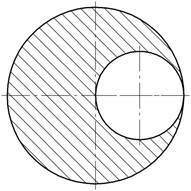
- На чертеже изображено поперечное сечение стержня, имеющего продольную внутреннюю полость. У какой точке сечения следует приложить к стержню силу, параллельную его оси, под действием которого во всех сечениях стержня возникают одинаковые напряжения?

- Где должен быть узел С, чтобы напряжения в стержнях были одинаковыми? Система симметричная.

- Абсолютно жесткий брус весом Q поддерживается двумя стержнями. Материал и поперечные сечения стержней одинаковы. Каким должен быть зазор δ, чтобы напряжения в стержнях после сборки были равны?

- Абсолютно жесткий брус весом Q поддерживается двумя стержнями. Материал и поперечные сечения стержней одинаковы. Каким должен быть зазор δ, чтобы напряжения в стержнях после сборки были равны?

- Стальной стержень прямоугольного сечения (axв) сжимается жесткими стальными плитами. Один конец плит и стержня защемлены. Определить перемещение левого конца стержня при нагреве только среднего стержня на Δt=100 ⁰С. Коэффициент трения между плитами стержня f=0,15. Коэффициент линейного расширения

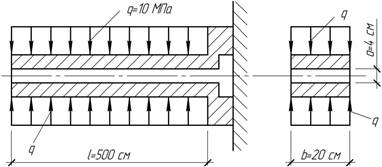
- Двухстержневая ферма воспринимает медленно вращающуюся в плоскости ферму постоянную по величине силу F. Определить величину угла φ, при котором объем материала стержней фермы будет минимальным.

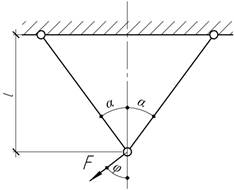
- Каким следует выбрать отношения а/в, чтобы вес ступенчатого бруса был минимальным, если

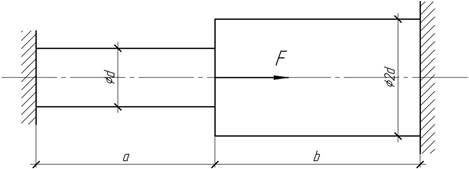
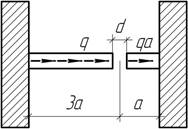
- При каком соотношении сил F₁ и F₂ сечение А-А не будет перемещаться?

- Стальная проволока наматывается на барабан с диаметром D=4 м. Найти работу, затрачиваемую на намотку, если длина проволоки l=1000 м, диаметр d=1 см. Намотка производится без натяжения.

- По абсолютно жесткой балке ВС, подвешенной на двух стержнях, перемещается сила F. На сколько нужно ускорить стержень 1 против проектной длины, чтобы балка была горизонтальной при заданном положении силы z=2а?

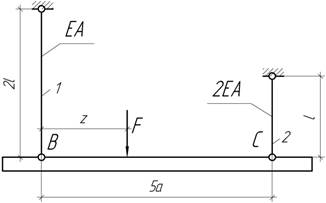
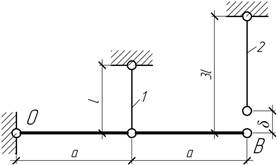
- Стержни, прикрепляющие узел В, имеют постоянный заданный объем V. Найти величину угла α, при которой допускаемая сила F, приложенная к узлу, будет наибольшей. Определить ее величину при заданном допускаемом напряжении для материала стержней [σ].

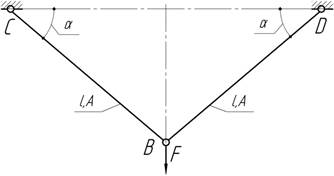
- Определить соотношение между углами α и β, при котором в стержнях не возникают температурные напряжения, если материал стержней и температура их нагрева одинаковы. Расстояние узла В от опорной поверхности СD постоянно (h=const).

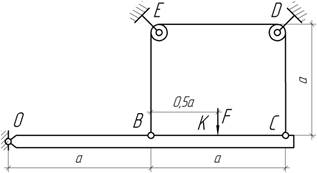
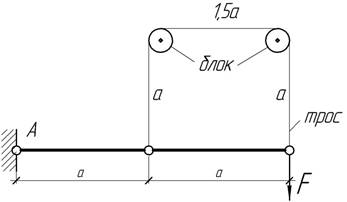
- Абсолютно жесткий стержень шарнирно закреплен в точке О и поддерживается тросом ВСДЕ, проходящим через блоки Д и Е. Определить величину δ перемещения точки приложения силы F. Найти сечение роса, которое остается неподвижным. Величины F, а и сечение троса А известны. Трением в блоках пренебречь.

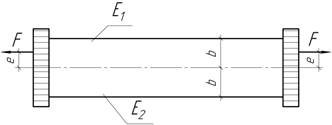
- Стержень квадратного поперечного сечения состоит из двух стержней, изготовленных из разных материалов, причем Е₁>Е₂. Оба стержня имеют одинаковые размеры поперечного сечения. Полагая, что концевые пластины абсолютно жесткие, получить выражение для такого эксцентриситета е приложения силы F, при котором оба стержня будут находиться в состоянии равномерного растяжения.

- Однородный стержень длиной l и площадью поперечного сечения А, жестко защемленный по концам, нагружен силами F. Установить, при каком положении сил, обеспечивается равнопрочность стержня.

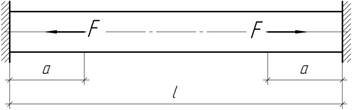
- На какую величину Δ надо укоротить правую тягу с помощью стяжной гайки К, чтобы призматический стержень весом G, подвешенный на трех одинаковых тягах, оставался горизонтальным? Известны: G, Е,А.

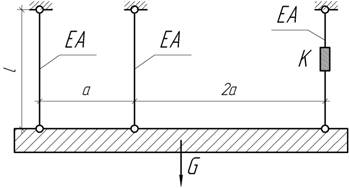
- Стержни 1 и 2 отличаются только длиной. На каком расстоянии х следует поставить опору В, чтобы обеспечить равнопрочность стержней? Деформациями детали ВСД пренебречь.

- Биметаллический стержень, состоящий из медного сердечника, к которому снизу и сверху присоединены две стальные полосы, равномерно нагревается на Т градусов. Полагая, что ширина стержня b, длина l и толщина каждого слоя t, определить напряжения в стальных и медной полосах, учитывая что Е_с=2Е_м и

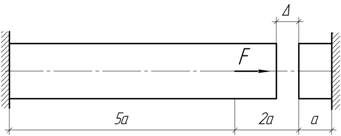
- Найти, при какой силе F напряжения во всех сечениях стержня жесткостью ЕА будут одинаковы.

- Каким следует выбрать отношение a/b, чтобы вес ступенчатого бруса был минимальным, если допускаемые напряжения его материала на растяжение и сжатие соответственно равны

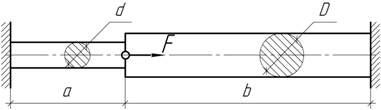
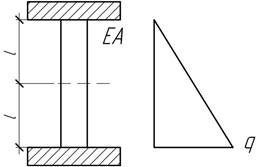
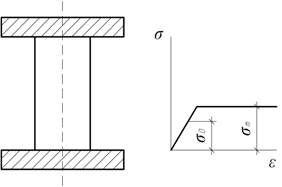
- Вычислить вертикальное перемещение узла В под действием силы F=200 кН, если диаграмма растяжения для материала стержней имеет вид кусочно-линейной функции, показанной на графике. Принять

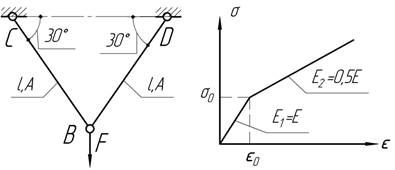
- Два шарнирно соединенных стержня до приложения силы F горизонтальны. Получить зависимость между силой F и опусканием δ узла В.

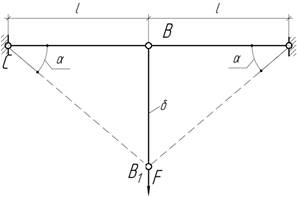
- Полубесконечная система состоит из жестких горизонтальных брусьев, подвешенных на стержнях одинаковой длины и жесткости ЕА. Определить перемещение точки С.

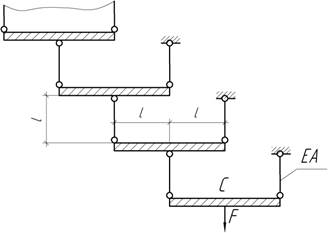
- Определить величину силы F=F₁, при которой буртик С стального стержня коснется кольцевой опоры. При каком значении F=F₂ правый торец стержня коснется опоры В? построить эпюру продольных сил и перемещений для следующих значений силы F: F₁, F₂, 2F₂.

- Очень длинная лента лежит на шероховатой поверхности и от силы F ее конец перемещается на величину λ. Найти закон изменения нормальных напряжений по ее длине, если объемный вес материала γ, модуль упругости Е, а коэффициент трения f.

- Абсолютно жесткий брус шарнирно закреплен в точке А и поддерживается тросом, как показано на рисунке. Определить вертикальное перемещение правого конца бруса. Жесткость троса ЕА и размер а заданы. Трением в блоках пренебречь.

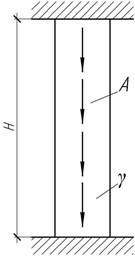
- Короткий стержень длиной Н, установленный вертикально, заделан с обоих концов. Определить реакцию опор и установить сечение, где продольная сила равна нулю, если модуль упругости на растяжение в два раза меньше, чем модуль упругости на сжатие.

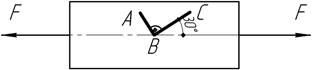
- Определить, как изменится угол АВС при осевом растяжении бруса силами F. Модуль упругости материала Е, коэффициент поперечной деформации μ, площадь сечения А.

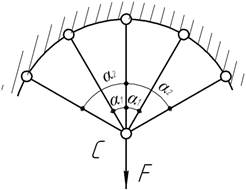
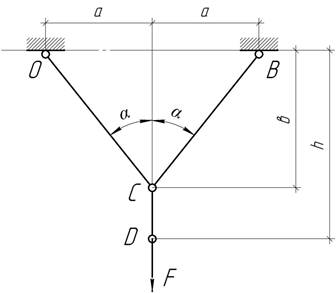
- К системе из трех стержней ОС, СВ, СD подвешен груз F. На какой высоте следует поместить шарнир С, чтобы вес всех стержней был минимальным? Размеры h и a изменению не подлежат.

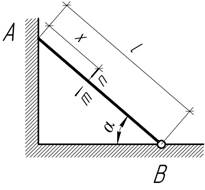
- Цилиндрический стержень АВ в точке В скреплен с основанием шарниром, а в точке А опирается на гладкую (без трения) стену веса g. Определить положение сечения «m-n», где сжимающие напряжения максимальны. Площадь поперечного сечения стержня А.

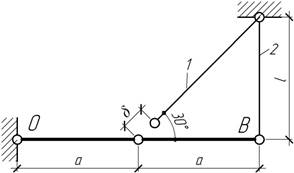
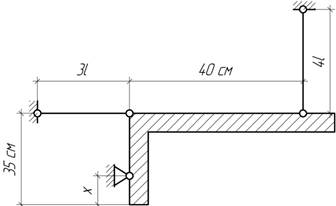
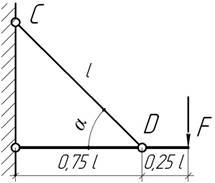
- Как установить тягу CD, чтобы напряжения в ней были минимальны?

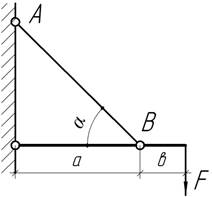
- Определить угол α, при котором расход материала на изготовление стержня АВ будет минимальным.

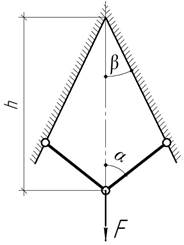
- Определить сечение стержня (их площади равны) по допускаемому напряжению и определить угол α из условия минимума объема стержней при заданных F, h, β.

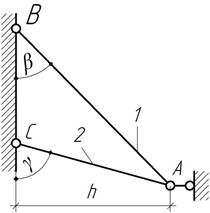
- При каком соотношении между углами γ и β () в изображенной на рисунке конструкции не возникает напряжений при ее нагревании. Материал стержней и температура нагрева их одинаковы.

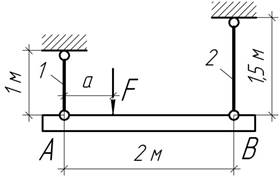
- Жесткий брус АВ подвешен на двух круглых тягах: тяга 1 диаметром 25 мм – медная, а тяга 2 диаметром 20 мм – стальная. На каком расстоянии а необходимо приложить силу F=30кН, чтобы в процессе деформации груз оставался горизонтальным? Какие в этом случае возникают напряжения?

Ответ: а

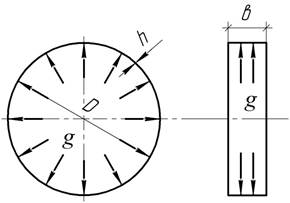
- Тонкостенное стальное кольцо, нагруженное внутренним давлением g, охлаждено так, что восстановились размеры недеформированного кольца. Определить изменение температуры и напряжение в кольце до охлаждения и после. Дано:

Ответ: t=20 ⁰С. Напряжения в кольце до охлаждения и после одинаковые и равны

- Определить усилия, возникающие в одинаковых стальных стержнях АВ и АС постоянного поперечного сечения А=100 мм² при действии силы F=30 кН. Длины стержней l=1м, угол наклона стержня в ненагруженном состоянии

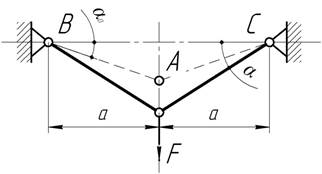
Ответ: N=110 кН.

- Под каким углом α следует приложить силу F к системе из двух стержней, чтобы узел перемещался горизонтально.

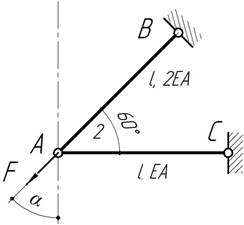
Ответ:

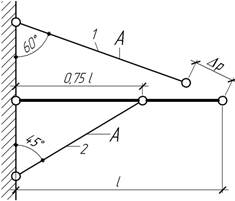
- При определении сварочных усилий в системе было принято, что стержень 1 короче проектной длины на Δ_р. При этом наибольшее усилие в системе оказалось 10 кН. Фактическая величина Δ_ф оказалась отличной от расчетной Δ_р. Насколько фактическое максимальное усилие будет отличаться от расчетного, если Δ_р=0,2 мм, Δ_ф=0,4 мм?

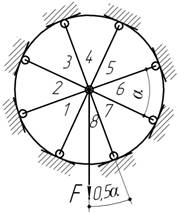
- Определить усилия в стержнях 1-8, сходящихся в общем узле, нагруженном силой F. Все стержни изготовлены из одного и того же материала и имеют одинаковые размеры (модуль упругости – Е, длина – L, площадь поперечного сечения - А).

- Найти вертикальное перемещение точки С. Все стержни изготовлены из одного и того же материала (модуль упругости - Е) и имеют одинаковую площадь поперечного сечения А. Угол при вершине В – прямой.

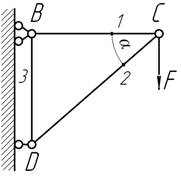
- При каком угле α перемещение узла С всегда будет направлено вдоль силы F? Жесткость стержня 1 – ЕА, стержня 2 - угол между стержнями – прямой.

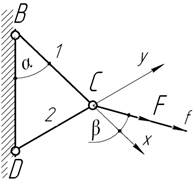
- На горизонтальные абсолютно жесткие стержни, шарнирно прикрепленные к неподвижному основанию в точках В и С, в плоскости чертежа действуют пары сил с моментами М. Жесткие стержни соединены одинаковыми упругими стержнями 1-4, усилия в которых надо определить.

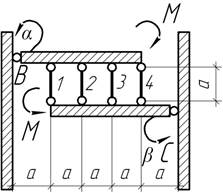
- Определить угол α, при котором перемещение узла D совпадает с направлением силы F. Е₁А₁=Е₂А₂=ЕА.

- При каком угле α перемещение узла С всегда будет направлено вдоль силы F? Жесткость стержня 1 – ЕА, стержня 2 - угол между стержнями – прямой. Получите ответ с помощью тензора податливости.

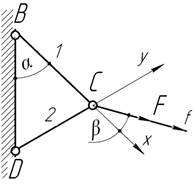
- Абсолютно жесткий брус подвешен на трех стержнях из одного и того же материала. Площадь поперечного сечения стержня 1 вдвое больше. Температура стержня 1 повышается, а стержней 2 понижается на t⁰. Определить усилие в стержнях, обусловленные изменением температур.

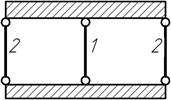
- К нижнему узлу В полубесконечной стержневой системы приложена сосредоточенная сила. Определить перемещение узла. Все стержни выполнены из одного и того же материала и имеют одинаковые размеры, α=60⁰.

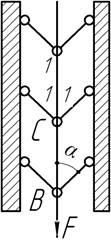
- Найти вертикальное перемещение точки С. Все стержни изготовлены из одного и того же материала (модуль упругости - Е) и имеют одинаковую площадь поперечного сечения А. Угол при вершине В – прямой. Решить данный пример с помощью энергетического метода.

- В каком порядке и на каких расстояниях разместить стержни 1, 2 и 3, чтобы вес удерживаемого ими жесткого бруса был наибольшим? Стержни изготовлены из различных материалов: Е₁=2Е₂=3Е₃; Задано расстояние L между левым стержнем «а» и равнодействующей Р сил веса бруса. Размеры стержней (l и А) одинаковы.

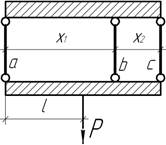
- Система из двух одинаковых стержней (допускаемое напряжение [σ]) нагружена силой Р. Размер l задан. Определить размер а, при котором вес стержней минимален.

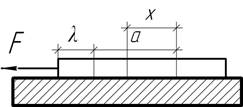
- Тяжелая тонкая полубесконечная лента лежит на шероховатой поверхности. Силой F конец ленты переместился на величину λ. Найти закон изменения нормальных напряжений по длине ленты и коэффициент трения f, считая известными погонный вес ленты q и модуль упругости Е.

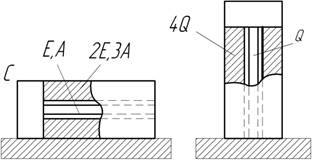
- Торцы двух элементов колонны соединяют жесткой плитой С, затем колонну устанавливают вертикально; вес элементов колонны Q и 4Q. Найти силы давления каждого элемента на опору.

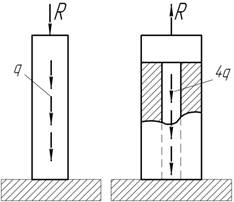
- Материал трех вертикальных стержней, удерживающих жесткий брус весом Р, следует диаграмме Прандтля. При каком значении Р будет исчерпана несущая способность системы? Площадь поперечного сечения левого стержня вдвое меньше, чем у каждого из двух других.

- Резиновые стержни, начальная длина которых равна соединены под углом к вертикали и затем нагружены силой Р. При каком значении этой силы в стержнях возникнут допустимые усилия [N]=100 Н? характеристика растяжения стержня представлена на рисунке.

- Упругие стержни 1 и 2 длиной L и жесткостью ЕА шарнирно соединены с жестким брусом и с вертикальными стенками. Определить величину потенциальной энергии, накопленной в стержнях при действии сил Р.

- Стержень имеет жесткость на расстояние ЕА; ВС – абсолютно жесткий. Найти зависимость Р-φ, полагая φ<<1.

- Стержень имеет жесткость на расстоянии ЕА=const. Сформулируйте условие замкнутости зазора.

- Два абсолютно жестких бруса АВ и СD соединены одинаковыми стержнями 1, 2, 3. Определить усилия в стержнях.

- Брус сжат напряжениями и помещен между двумя абсолютно жесткими плитами. На какую температуру t необходимо его нагреть, чтобы после остывания до первоначальной температуры его можно было свободно вынуть? Считая, что упругопластический материал бруса деформируется при сжатии в соответствии с идеализированной диаграммой σ-ε. Дано: α, Е.

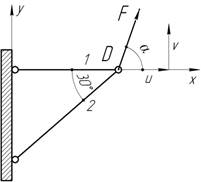
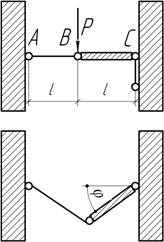
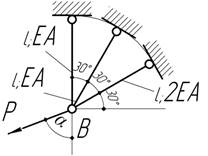
- Под каким углом α надо приложить силу к системе, чтобы узел В переместился по вертикали?

- Три стержня одинаковой длины соединены с абсолютно жесткой балкой и равномерно нагреты на t⁰. Определить усилия в стержнях.

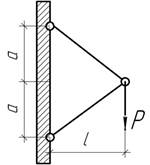
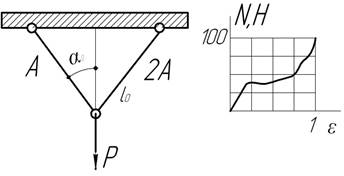
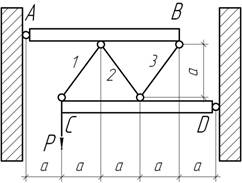
- Плоская двухстержневая ферма нагружена силой Р, совершающей вращательное движение в плоскости фермы. Определить угол α, при котором ферма будет иметь наименьший вес. [σ] известно.

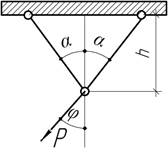
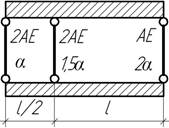
- Определить соотношение поперечных размеров стержней, обеспечивающее минимальную суммарную массу стальной стержневой конструкции, запроектированной по условию жесткости в вертикальном направлении.

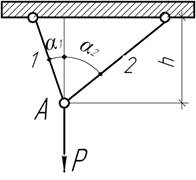
- При каком расстоянии h (а=const) конструкция будет иметь наименьший вес из условия ее прочности?

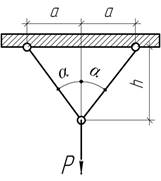
- При каком значении угла α направление перемещения узла С совпадает с направлением силы Р.

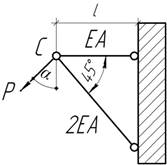
- Раскрыть статическую неопределимость системы

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00