Главная
Лекция 8 (продолжение). Задачи
для самостоятельного решения
Содержание
Расчет тонкостенных сосудов по безмоментной теории
Расчет тонкостенных сосудов по безмоментной теории
Задача 1.
Давление
воздуха в цилиндре амортизационной стойки шасси самолета в положении на стоянке
равно р=20 МПа. Диаметр цилиндра d=100 мм, толщина стенки
t=4
мм. определить главные
напряжения в цилиндре на стоянке и после взлета, когда давление в амортизаторе
уменьшится вдвое.
Ответ:
(на стоянке); 
(после взлета).
Задача 2.
Вода
поступает в водяную турбину по трубопроводу, наружный диаметр которого у машинного
здания равен 2 м, а толщина стенки t=25
мм. Машинное здание расположена на 200 м ниже уровня озера, из которого
забирается вода. Найти наибольшее напряжение в стенке трубопровода.
Ответ:
Задача 3.
Проверить
прочность стенки цилиндрического котла диаметром 2,5 м, находящегося под
рабочим давлением р=1 МПа, если толщина стенки t=12 мм, [σ]=100
МПа. Применить IV
гипотезу прочности.
Ответ:
Задача 4.
Котел
имеет диаметр цилиндрической части d=2
м и находится под рабочим давлением р=1,6 МПа.
Подобрать толщину стенки котла при допускаемом напряжении [σ]=100 МПа, используя
III
гипотезу прочности. Какая была бы необходимая толщина при использовании IV гипотезы прочности?
Ответ:
Задача 5.
Стальная
сферическая оболочка диаметром d=1
м и толщиной t=10
мм нагружена внутренним давлением р=4 МПа. Определить
главные напряжения и изменение диаметра.
Ответ:
мм.
Задача 6.
Цилиндрический
сосуд диаметром d=0,8
м имеет стенку толщиной t=4
мм. Определить величину допускаемого давления в сосуде, исходя из IV гипотезы прочности,
если [σ]=130 МПа.
Ответ:
[р]=1,5 МПа.
Задача 7.
Определить
коэффициент Пуассона материала цилиндрической оболочки, если при нагружении ее внутренним давлением деформации в направлении
датчиков составили 
Ответ:
ν=0,25.
Задача 8.
Дюралюминиевая
труба толщиной 
мм
и внутренним диаметром 
мм усилена плотно надетой на нее стальной
рубашкой толщиной 
мм.
Найти предельное внутреннее давление для двухслойной трубы по пределу текучести
и контактное напряжение между слоями в этот момент, полагая Ест=200 ГПа, 
Ед=70 ГПа,
Ответ:
Задача 9.
Водовод
диаметром d=480
мм в период пуска имел толщину стенки t=8
мм. В процессе эксплуатации вследствие коррозии толщина местами уменьшилась
вдвое. Какой максимальный столб воды может выдержит
трубопровод при двукратным запасе прочности, если предел текучести материала
трубы равен 
Задача 10.
Газопровод
диаметром d=1000
мм и толщиной стенки t=8
мм пересекает водохранилище при максимальной глубине укладки от уровня воды,
достигающей 60 м. в процессе эксплуатации газ перекачивается под давлением р=2,2 МПа, а при строительстве подводного перехода давление
в трубе отсутствует. Чему равны наибольшие напряжения в трубопроводе и когда
они возникают?
Задача 11.
Тонкостенный
цилиндрический сосуд имеет полусферические днища. Каково должно быть соотношение
между толщинами цилиндрической 
и сферической 
частей, чтобы в зоне перехода не возникло
напряжений изгиба?
Задача 12.
При
изготовлении железнодорожных цистерн их испытывают под давлением р=0,6 МПа. Определить эквивалентные напряжения в
цилиндрической части и в днище цистерны, принимая давление при испытаниях за расчетное. Расчет вести по III гипотезы прочности.
Задача 13.
Между
двумя концентрически расположенными бронзовыми
трубами протекает жидкость под давлением р=6 МПа.
Толщина наружной трубы равна 
При какой толщине внутренней трубы обеспечивается равнопрочность
обеих труб? Чему равны при этом наибольшие напряжения?
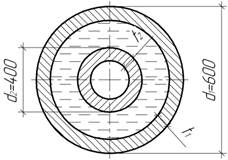
Задача 14.
Определите
коэффициент Пуассона материала оболочки, если нагружении
ее внутренним давлением деформации в направлении датчиков составили
Задача 15.
Тонкостенный
сферический сосуд диаметром d=1
м и толщиной t=1
см находится под действием внутреннего давления 
и внешнего 
Каков запас прочности стенок сосуда Пт, если 
Будет
ли правильным следующее решение:
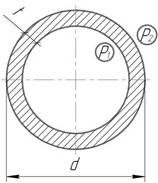
Задача 16.
Тонкостенная
труба с заглушенными концами находится под действием внутреннего давления р и изгибающего момента М. пользуясь III гипотезой прочности,
исследуйте зависимость расчетного напряжения 
от величины М при заданном р.
Задача 17.
На
какой глубине находятся точки с наибольшими меридиональными и окружными
напряжениями для приведенного справа конического сосуда? Определите величины
этих напряжений, полагая удельный вес продукта равен γ=10 кН/м3.
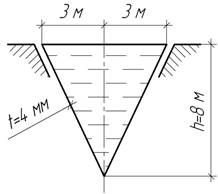
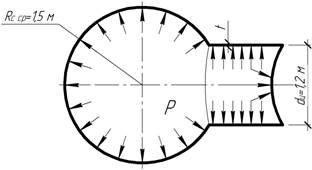
Задача 18.
Сосуд
подвергается давлению газа р=10 МПа. Найти толщину его
стенки, если [σ]=250
МПа.
Ответ:
t=30
мм.
Задача 19.
Вертикально
стоящий цилиндрический резервуар с полусферическим днищем доверху заполнен
водой. Толщина боковых стенок и днища t=2
мм. Определить наибольшие нормальные напряжения в цилиндрической и сферической частях конструкции.
Ответ:
Задача 20.
Резервуар
цилиндрической формы дополнен до глубины Н1=6
м жидкостью с удельным весом 
а поверх не – на толщину Н2=2 м –
водой. Определить толщину стенки резервуара у дна, если [σ]=60 МПа.
Ответ:
t=5
мм.
Задача 21.
Небольшой
газгольдер для светильного газа имеет толщину стенок t=5 мм. Найти наибольшие
напряжения ы стенках верхнего и нижнего сосудов.
Ответ:
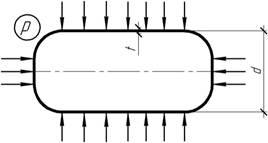
Задача 22.
Поплавок
клапана испытательной машины представляет собой замкнутый цилиндр из
алюминиевого сплава диаметром d=100
мм. Поплавок подвергается всестороннему сжатию давлением р=23
МПа. Определить толщину стенки поплавка, используя четвертую гипотезу
прочности, если [σ]=200 МПа.
Ответ:
t=5
мм.
Задача 23.
Тонкостенный
сферический сосуд с диаметром d=1
м и толщиной t=1
см находится под действием внутреннего давления и внешнего Каков запас прочности стенок сосуда 
если
Ответ:
.
Задача 24.
Определить
наибольшие меридиональные и окружные напряжения в торообразном баллоне, если р=1,8 МПа, t=3
мм, а=0,5 мм; d=0,4 м.
Ответ:
Задача 25.
Стальной
полусферический сосуд радиуса R=4
м заполнен жидкостью с удельным весом γ=7,5 кН/м3. Принимая припуск на коррозию 2 мм и пользуясь III гипотезой прочности,
определить необходимую толщину стенки сосуда, если [σ]=80 МПа.
Ответ:
t=3
мм.
Задача 26.
Определить,
на какой глубине находятся точки с наибольшими меридиональными и окружными
напряжениями и вычислить эти напряжения, если толщина стенки t=4 мм, удельный вес
жидкости γ=10 кН/м3.
Ответ:
на глубине 2 м; 
на глубине 4 м.
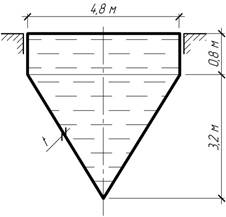
Задача 27.
Цилиндрический
сосуд с коническим днищем заполнен жидкостью с удельным весом γ=7 кН/м3.
Толщина стенок постоянна и равна t=5мм.
Определить наибольшие меридиональные и окружные напряжения.
Ответ:
Задача 28.
Цилиндрический
сосуд с полусферическим днищем заполнен жидкостью с удельным весом γ=10
кН/м3. Толщина стенок постоянна и равна t=5 мм. Определить наибольшее напряжение в
стенке сосуда. Во сколько раз увеличится это напряжение, если длину
цилиндрической части удвоить, сохранив неизменными все
остальные размеры?
Ответ:
увеличится в 1,6
раза.
Задача 29.
Для
хранения нефти с удельным весом γ=9,5 кН/м3 используется сосуд
в виде усеченного конуса с толщиной стенки t=10 мм. Определить наибольшие
меридиональные и окружные напряжения в стенке сосуда.
Ответ:
Задача 30.
Тонкостенный
конический колокол находится под слоем воды. Определить наибольшие
меридиональные и окружные напряжения, если давление воздуха на поверхность 
под колоколом 
толщина стенки t=10 мм.
Ответ:
Задача 31.
Оболочка
толщиной t=20
мм, имеющая форму эллипсоида вращения (Ох – ось вращения), нагружена внутренним
давлением р=1 МПа. Найти напряжения в продольном и
поперечном сечениях.
Ответ:
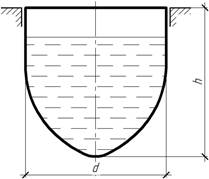
Задача 32.
Пользуясь
третьей гипотезой прочности, проверить прочность сосуда, имеющего форму
параболоида вращения с толщиной стенки t=2 мм, если удельные вес жидкости
γ=10 кН/м3, допускаемое напряжение [σ]=20 МПа, d=h=5 м. Прочность
проверить по высоте верхнего уровня жидкости.
Ответ:
т.е. прочность обеспечена.
Задача 33.
Цилиндрический
сосуд со сферическими днищами предназначен для хранения газа под давлением р=1 МПа. Под каким давлением можно будет хранить газ в
сферическом сосуде той же емкости при неизменном материале и толщине стенки?
Какая при этом достигается экономия материала?
Ответ:
экономия составит 36%.
Задача 34.
Цилиндрическая
оболочка с толщиной стенки t=5
мм сжимается силой F=31,4
кН. образующие оболочки из-за неточности изготовления
получили малое осесимметричное искривление. Пренебрегая влиянием этого
искривления на меридиональные напряжения, вычислить 
в середине высоты оболочки в предположении,
что образующие искривлены по одной полуволне синусоиды, а f=0,01l;
l=r.
Ответ:
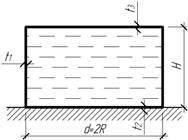
Задача 35.
Вертикальный цилиндрический сосуд предназначен для хранения
жидкости объема V
и удельного веса γ. Суммарная толщина верхнего и нижнего оснований,
назначаемая по конструктивным соображениям, равна 
Определить наивыгоднейшую высоту резервуара Нопт,
при которой масса конструкции будет минимальна.
Принимая высоту резервуара, равной Нопт,
найти толщину стенки цилиндрической части, полагая [σ]=180 МПа, Δ=9
мм, γ=10 кН/м3, V=1000
м3.
Ответ:
Нопт=9 м, 
мм.
Задача 36.
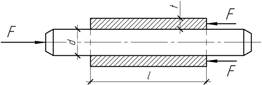
Длинная
тонкая трубка толщиной t=2
мм надета с натягом Δ на абсолютно жесткий стержень диаметра d=50 мм. Какую силу
необходимо приложить к трубке, чтобы снять ее со стержня, если Δ=0,0213
мм; f=0,1;
l=10
см, Е=100 ГПа, ν=0,35.
Ответ:
F=10
кН.
Задача 37.
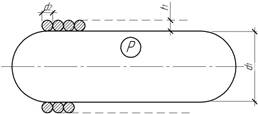
Тонкостенный
цилиндрический сосуд со сферическими днищами подвергается изнутри давлению газа
р=7 МПа. Путем навивки высокопрочной проволоки
диаметром 
,
уложенной виток к витку с начальным натяжением N02,
обеспечивается равнопрочность оболочки в окружном и
меридиональном направлениях. Определить толщину оболочки 
диаметр проволоки и начальное натяжение N02,
если 
Е1=Е2=200 ГПа.
Ответ:
N02=215
Н.
Задача 38.
Среди
прочих конструктивных элементов в авиационной и в ракетной технике используются
баллоны высокого давления. Обычно они имеют цилиндрическую или сферическую
форму и для них, как и для прочих конструктивных узлов, чрезвычайно важно
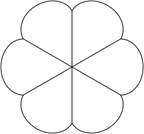
соблюсти требование минимального веса. Предлагается конструкция фасонного
цилиндра, показанная на рисунке. Стенки баллона состоят из нескольких
цилиндрических секций, связанных радиальными стенками. Поскольку цилиндрические
стенки имеют небольшой радиус, напряжения в них уменьшается, и можно надеяться,
что несмотря на увеличение веса за счет радиальных
стенок, общий вес конструкции окажется меньшим, чем для обыкновенного цилиндра,
имеющего тот же объем. Насколько оправданы эти надежды?
Задача 39.
Определить
форму меридиана тонкостенной оболочки равного сопротивления, содержащей
жидкость удельно веса γ.
Расчет толстостенных труб
Задача 1.
Какое
давление (внутреннее или наружное) опаснее для толстостенной трубы? Во сколько
раз наибольшие эквивалентные напряжения по III гипотезе прочности в одном случае больше
или меньше, чем в другом, если величины давления одинаковы? Будут ли равны
наибольшие радиальные перемещения в обоих случаях?
Задача 2.
Две
трубы отличаются только размерами поперечного сечения: 1-я труба – а=20 см, b=30 см; 2-я труба – а=10 см, b=15
см. Какая из труб обладает большей несущей способностью?
Задача 3.
Толстостенная
труба с размерами а=20
см и b=40
см не выдерживает заданное давление. С целью повышения несущей способности
предлагаются два варианта: 1) увеличить в П раз
наружный радиус b;
2) уменьшить в П раз внутренний радиус а.
Какой из вариантов дает больший рост несущей способности при одинаковом
значении П?
Задача 4.
Труба
с размерами а=10 см и b=20 см выдерживает
давление р=100 МПа. Насколько (в процентах) увеличится
несущая способность трубы, если наружный радиус увеличить в 2 раза?
Задача 5.
В
конце первой мировой войны (1918 г.) Германии была изготовлена
сверхдальнобойная пушка для обстрела Парижа с расстояния 115 км. Это была стальная труба 34 м длиной и толщиной стенок в казенной
части 40 см. Весило орудие 7,5 МН. Его 120-килограммовые снаряды имели метр в
длину при диаметре 21 см. Для заряда употреблялось 150 кг пороха, развивавшего
давление в 500 МПа, которое выбрасывало снаряд с начальной скоростью 2 км/с.
Каков должен быть предел текучести стали, использованной для изготовления
ствола орудия, при не менее чем полуторакратным запасе прочности?
Задача 6.
Во
сколько раз повысится несущая способность толстостенного сосуда, если цельную
трубу с размерами, а=10 см и b=40 см заменить
составным цилиндром из двух соединенных с натягом труб? Посадка труб выполнена
по соотношению Гадолина?
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
