Главная

Лекция 8. Расчет оболочек

Содержание

Основные положения теории оболочек

Тонкостенная осесимметричная оболочка

Сферическая оболочка

Цилиндрическая оболочка

Коническая оболочка

Толстостенный цилиндр

Составные цилиндры. Автофретирование. Общие положения

Пример расчета элемента тонкостенной оболочки вращения

Пример расчета толстостенной стальной трубы

Вопросы для самопроверки

Основные положения теории оболочек

Большинство элементов инженерных конструкций в расчетной схеме, подлежащих расчету на прочность, как это уже было отмечено, связаны с расчетом бруса, пластинок или оболочек.

Предыдущие разделы были достаточно подробно посвящены вопросам расчета стержней и стержневых систем. Настоящий раздел книги посвящен различным вопросам расчета пластинок и оболочек.

Под оболочкой понимается тело, одно из измерений которого (толщина) значительно меньше двух других. Геометрическое место точек, равноотстоящих от обеих поверхностей оболочки, носит название срединной поверхности.

Если срединная поверхность оболочки является плоскостью, то такую оболочку называют пластиной.

Геометрическая форма объектов, которые могут быть причислены к оболочкам или пластинам, чрезвычайно разнообразна: в машиностроении - это корпуса всевозможных машин; в гражданском и промышленном строительстве - покрытия и перекрытия, навесы, карнизы; в кораблестроении - корпуса судов, сухих и плавучих доков; в авиастроении - фюзеляжи и крылья самолетов; в подвижном составе железнодорожного транспорта, кузова вагонов, цистерны, несущие конструкции локомотивов; в атомной энергетике - защитная конструкция атомных станций, корпуса реакторов и т.д.

Если срединная поверхность оболочки образует поверхность вращения в форме цилиндра, то оболочку называют цилиндрической.

К схеме осесимметричной цилиндрической оболочки сводится очень много инженерных конструкций, в том числе: котлов, баков, нефтепроводов, газопроводов, деталей машин и др.

Задача о расчете тонкостенных оболочек вращения наиболее просто решается в том случае, когда возможно принять, что напряжения, возникающие в оболочке, постоянны по толщине и, следовательно, изгиб оболочки отсутствует.

Теория оболочек, построенная в этом предположении, называется безмоментной теорией оболочек.

Если оболочка имеет резкий переход и жесткие защемления и, кроме того, нагружена сосредоточенной силой и моментами, то в местах крепежа оболочки, резких изменений формы, и в местах действия сосредоточенных сил и моментов возникают интенсивные напряжения, обусловленные изгибным эффектом. Учет изгибных эффектов можно получить в рамках моментной теории оболочек.

Следует отметить, что чем меньше отношение толщины h оболочки к ее радиусу R, тем точнее выполняется предположение о постоянстве напряжений по толщине и тем более точнее выполняются расчеты по безмоментной теории.

Отметим, что оболочка считается тонкой, если h/R≤1/20.

Следовательно, при расчете на прочность тонких оболочек в зависимости от характера распределения внешних нагрузок, опорных закреплений, применяется или безмоментная или моментная теория. При этом предполагается равномерное распределение напряжений по продольным и поперечным сечениям оболочек (отсутствие в этих сечениях изгибающих, крутящих моментов и поперечных сил).

При осесимметричной нагрузке отсутствуют также сдвигающие силы. Определение усилий по безмоментной теории производится достаточно точно на расстоянии, превышающем величину (3÷5) от мест скачкообразного изменения формы или площади сечения, жестких контурных закреплений или от места приложения внешних сосредоточенных сил и моментов. Вблизи указанных мест возникают дополнительные напряжения от изгибного эффекта.

В моментной и безмоментной теории тонких оболочек или, так называемой технической теории оболочек, состоящей в резком различии их толщины и габаритных размеров, влечет за собой возможность упрощения теории путем некоторой схематизации действительной работы конструкций. Эта схематизация формируется в используемых гипотезах, аналогичных гипотезам в теории стержней, т.е. гипотезам плоских сечений и гипотезам “ненадавливания” слоев оболочки друг на друга.

Эти гипотезы позволяют свести трехмерную задачу механики сплошной среды к двумерной, подобно тому как в теории стержней трехмерная задача сведена к одномерной.

Далее в технической теории тонких оболочек пренебрегают членами h/R по сравнению с единицей.

Оболочки, к которым применимы упомянутые выше гипотезы, называются тонкими, а те, к которым эти гипотезы не применимы, называются толстыми.

Граница между тонкими и толстыми оболочками условны и определяются отношением h/R≈1/20.

В тех случаях, когда h/R≥1/20 для получения приемлемых результатов по точности применяется аппарат механики сплошной среды, в частности теории упругости или пластичности в зависимости от постановки задачи.

Тонкостенная осесимметричная оболочка

Тонкостенной осесимметричной называется оболочка, имеющая форму тела вращения толщина, которой мала по сравнению с радиусами кривизны ее поверхности (рис.8.1).

При расчете тонкостенных оболочек все нагрузки, действующие на них, прикладывают к срединной поверхности оболочки.

К тонким оболочкам могут быть отнесены такие часто встречающиеся элементы конструкций как резервуары, цистерны, газовые баллоны, корпуса аппаратов химических агрегатов и др.

При расчете таких элементов конструкций используется безмоментная теория оболочек, основные положения которой заключаются в следующем:

1. нагрузки, действующие на поверхности оболочки, могут считаться перпендикулярными им и симметричными относительно оси вращения оболочки;

2. вследствие малой толщины оболочки сопротивление изгибу отсутствует (изгибающий момент не возникает);

3. напряжения по толщине стенки оболочки распределены равномерно.

Из оболочки, изображенной на рис.8.1 выделим двумя меридиональными плоскостями nn₁n₂ и nn₃n₂, (т.е. плоскостями проходящими через ось симметрии оболочки), с углом dφ между ними и двумя плоскостями, перпендикулярными оси симметрии оболочки BC и AD, элемент ABCD.

Радиусы кривизны O₂A и O₂B элемента ABCD в меридиональной плоскости обозначим через R₂, а радиусы кривизны O₁B и O₁C в плоскости, перпендикулярной меридиану, обозначим через R₁. Нормальные напряжения, действующие по боковым граням AB и CD, соприкасающимся с меридиональными плоскостями, называются окружными напряжениями σ_t. Нормальные напряжения, действующие по боковым граням BС и AD, называются меридиональными напряжениями σ_s. Кроме напряжений σ_s и σ_t. на элемент оболочки действует нагрузка в виде давления q, перпендикулярного поверхности ABCD.

Рис.8.1

Основным уравнением безмоментной теории оболочек является уравнение Лапласа, которое имеет следующий вид

где δ - толщина оболочки.

Прежде чем перейдем к рассмотрению различных вариантов определения напряжений в оболочках остановимся на некоторых различиях, вызванных наличием газа или жидкости внутри оболочки.

В случае газового давления величина давления q постоянная во всех точках поверхности оболочки. Для резервуаров, наполненных жидкостью, значение q по их высоте переменно.

Для случая наполнения резервуара жидкостью необходимо учитывать, что если на какую-либо поверхность действует давление жидкости, то вертикальные составляющие сил давления равны весу жидкости в объеме, расположенном над поверхностью. Поэтому давление жидкости в различных сечениях оболочки будет различным, в отличие от давления газа.

Определим напряжения в сферических и цилиндрических оболочках т.к. они наиболее часто используются в промышленности.

Сферическая оболочка

Отсечем часть сферической оболочки нормальным коническим сечением с углом 2φ при вершине и рассмотрим равновесие этой части оболочки вместе с заключенной в ней жидкостью с удельным весом γ. Сферическую часть отделим от основной оболочки плоскостью, перпендикулярной оси симметрии.

Рис.8.2

На рис.8.2 изображена расчетная схема сферической оболочки радиусом R_s. Высота отсеченной поверхности . Давление q на отсеченную часть в этом и последующих случаях равно весу жидкости в объеме, расположенном над поверхностью, который равен

где - высота столба жидкости выше отсеченной части оболочки.

Уравнение равновесия отсеченной части может быть записано, как сумма проекций всех сил на вертикальную ось

В данном уравнении величина G – вес жидкости, заполняющей отсеченную часть сферической оболочки (см. рис.8.2).

где - объем нижней отсеченной части сферической оболочки.

Путем интегрирования объем сферического сегмента может быть определен по формуле

После подстановки уравнения (8.5) в выражение (8.4), и затем, в (8.3), получим конечное уравнение равновесия для сферической части сегмента

Из этого уравнения можно определить величину меридионального напряжения , и, после подстановки в уравнение Лапласа (16.1), найти величину окружного напряжения .

Цилиндрическая оболочка

Рассмотрим цилиндрическую оболочку радиусом , заполненную жидкостью с удельным весом γ (см. рис.8.3).

Рис.8.3

В данном случае цилиндрическая часть отделена от остальной части оболочки сечением, перпендикулярным оси симметрии.

Уравнение равновесия отсеченной части может быть получено, как сумма проекций всех сил на вертикальную ось.

где - вес жидкости, заполняющий отсеченную часть цилиндрической оболочки.

Объем цилиндра с высотой x и радиусом может быть определен по формуле

С учетом этого уравнение равновесия принимает вид

В этом уравнении, также как и в предыдущем случае, одна неизвестная

Для случая цилиндрической оболочки при подстановке в уравнение Лапласа необходимо учесть, что величина , значит

.

Коническая оболочка

Отсечем часть конической оболочки нормальным коническим сечением с углом 2φ при вершине и рассмотрим равновесие отсеченной части.

Рис.8.4

Как видно из рис.8.4 φ = π/2 - α.

Уравнение равновесия отсеченной части оболочки будет иметь вид

где - вес жидкости, заполняющий отсеченную часть конуса.

С учетом (8.11), выражение (8.10) имеет следующий вид

Из этого уравнения можно рассчитать величину меридионального напряжения и, подставив его в уравнение Лапласа, найти величину .

Возможно отделение сечением не нижней, а верхней части оболочки с последующей записью уравнения равновесия. Это делается для того, чтобы при составлении условий равновесия отсеченного элемента крепление оболочки не попадало в схему отсеченной части. В подобных вариантах во всех рассмотренных случаях изменится знак силы G, т.к. в этом случае ее направление будет совпадать с направлением вертикальной составляющей напряжения .

В этом случае, при расчете величины G, в качестве объема будет браться объем отсеченной верхней части , а при расчете величины q в формулу (8.2) во всех случаях войдет величина - высота столба жидкости в отсеченной нижней части оболочки. В остальном порядок расчета останется неизменным.

В случае, если жидкость находится в сосуде под давлением P, то при расчете величины q добавляется величина давления P. Формула (8.2) будет иметь следующий вид

В некоторых задачах отсеченная часть представляет собой не какой-то один элемент, а два или более состыкованных элемента. При этом вид уравнений равновесия остается неизменным, а изменяется только величина объема верхней или нижней части сосуда, однако, если известны зависимости, определяющие объемы элементов, то найти суммарный объем не представляет затруднения.

На рис.8.5, а показана схема оболочки вращения, состоящей из сферической, цилиндрической и конической оболочек. Крепление оболочки располагается на уровне стыка сферической и цилиндрической оболочек. Сосуд наполнен жидкостью, находящейся под давлением Р.

На рис.8.5, б показан пример построения эпюр напряжения. В левой половине оболочки расположена эпюра , а в правой .

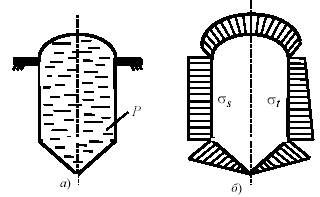
Рис.8.5

Полученные построения справедливы для участков, находящихся на некотором удалении от линии закрепления оболочки и точек сопряжения сфера-цилиндр и цилиндр-конус. В точках сопряжения возникают эффекты, которые не могут быть учтены теорией безмоментного напряженного состояния. Все это также относится и к точкам, непосредственно примыкающим к вершине конуса.

Толстостенный цилиндр

Толстостенным называется такой цилиндр, для которого отношение толщины стенки к внутреннему диаметру не менее 1/20.

Задача о расчете толстостенного цилиндра решается с учетом равномерно распределенного наружного давления и внутреннего давления . Мы исходим из того, что такая нагрузка не может вызвать деформации изгиба цилиндра.

Нормальные напряжения . в сечениях плоскостями, перпендикулярными оси симметрии О цилиндра нельзя считать равномерно распределенными по толщине стенки, как это делается при расчете тонкостенных оболочек вращения (рис.8.6).

Нормальные напряжения действующие по цилиндрической поверхности с радиусом r могут быть одного и того же порядка и даже превышать напряжение, что при тонкостенных цилиндрах невозможно.

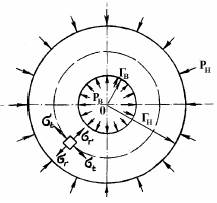
Рис.8.6

В поперечных сечениях цилиндра касательные напряжения также предполагаются равными нулю, однако, возможно существование нормальных осевых напряжений , которые возникают как следствие нагружения цилиндра силами, действующими вдоль оси. В дальнейшем мы будем рассматривать открытые цилиндры, т.е. не имеющие днищ. Напряжения в таких цилиндрах равны нулю. Вывод формул расчета напряжений в толстостенных цилиндрах основан на том, что для них соблюдается гипотеза плоских сечений, т.е. поперечные сечения цилиндра, плоские до нагружения, останутся плоскими и после нагружения.

Основными уравнениями для расчета напряжений в толстостенных цилиндрах являются формулы Ламе:

При действии на цилиндр только наружного или внутреннего давления знаки эпюр , во всех точках цилиндра одинаковы. Эпюры изменения радиального и окружного напряжения для случая действия только наружного давления показаны на рис.8.7. Эти напряжения во всех точках цилиндра отрицательны, что соответствует сжатию.

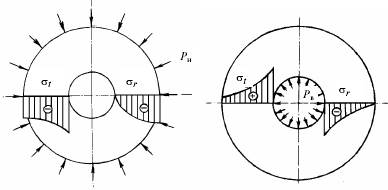
Рис.8.7 Рис.8.8

При нагружении внутренним давлением эпюры изменения радиального окружного напряжения показаны на рис.16.8. Окружное напряжение является расширяющим, а радиальное сжимающим.

Анализ формул Ламе показывает, что увеличение толщины не может во всех случаях обеспечить необходимой прочности цилиндра. Поэтому для сосудов высокого давления необходимо искать какие-то другие конструктивные решения. Одним из таких решений является создание составных, соединенных с натягом, цилиндров. Этот прием используется как в технике высоких давлений, так и в артиллерийской практике для упрочнения стволов мощных орудий.

В результате натяга в трубах возникают нормальные напряжения, которые частично компенсируют напряжения в трубе от действия высокого давления.

Составные цилиндры. Автофретирование. Общие положения

Из формул (8.14) и (8.15) следует, что при действии только внутреннего давления напряжения в любых точках цилиндра положительны и по абсолютной величине больше напряжений . Наибольшего значения напряжения достигают у точек внутренней поверхности цилиндра, где они равны

В остальных точках напряжения меньше этого значения.

Наибольшее значение можно уменьшить путем применения составных толстостенных цилиндров, состоящих из более тонких труб, надетых друг на друга. При этом наружная труба изготавливается с внутренним диаметром, несколько меньшим наружного диаметра внутренней трубы. Разница между этими диаметрами до сборки принимается до изготовления и называется натягом.

Чтобы соединить цилиндры наружный цилиндр обычно нагревают, он расширяется и появляется возможность одеть его на внутренний цилиндр. Возможно такое охлаждение внутреннего цилиндра в жидком азоте или запрессовка цилиндров друг в друга. После сборки выравнивается температура, наружный цилиндр плотно охватывает внутренний и получается надежное соединение.

В результате натяга в трубах возникают начальные напряжения, причем, чем больше величина натяга, тем больше начальные напряжения.

Способ уменьшения напряжений и, как следствие, повышение прочности толстостенных цилиндров путем замены сплошного цилиндра составным был предложен академиком А.В.Гадолиным.

Обозначим через b и c радиусы наружного цилиндра, через a и b+∆/2 радиусы внутреннего цилиндра, а ∆ - натяг (см. рис.8.9).

Рис.8.9

При одинаковой длине соединенных цилиндров контактное давление p_k равномерно распределено по посадочной поверхности.

Подставив в формулы (8.14) и (8.15) параметры, характеризующие напряжения в наружном цилиндре получим

Аналогично можно определить напряжения, возникающие на посадочной поверхности внутреннего цилиндра

Если внутренний и наружный цилиндры изготовлены из одного и того же материала, то контактное давление p_k определяется зависимостью

где Е – модуль упругости материала внутреннего и наружного цилиндров.

За счет натяга в составном цилиндре возникают начальные напряжения, характер изменения которых по наружному сечению показан на рис.8.10.

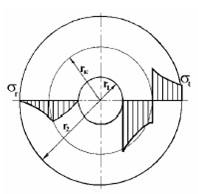
Рис.8.10 Рис.8.11

При приложении внутреннего рабочего давления на начальные напряжения накладываются рабочие напряжения (показываются на рис.8.11 пунктиром). Суммарные напряжения показаны на рис.8.11.

В точках, расположенных на внутренней поверхности составного цилиндра, суммарное окружное напряжение получается меньше, чем в тех же точках целого цилиндра.

Оптимальное значение натяга можно определить из условия равнопрочности внутреннего и наружного цилиндров, оптимальное значение радиуса контактной поверхности – из условия наибольшего снижения эквивалентного напряжения в опасной точке.

В соответствии с этим оптимальный радиус контактной поверхности:

Натяг соответствующий этому радиусу и внутреннему давлению p_в:

Необходимо отметить, что детали, предназначенные для соединения с натягом, должны изготавливаться с большой точностью, т.к. даже небольшое отклонение от номинальной величины натяга может привести к снижению прочности соединения.

В технике высоких давлений, кроме посадки, применяется так называемое автофретирование, которое заключается в предварительной нагрузке цилиндра внутренним давлением, больше рабочего, с таким расчетом, чтобы во внутренних слоях цилиндра возникали пластические деформации. После снятия давления во внешних слоях цилиндра сохраняются упругие напряжения растяжения, а во внутренних слоях возникают деформации сжатия (см. рис.8.12).

В дальнейшем при нагрузке цилиндра давлением остаточные напряжения суммируются с рабочим так, что во внутренних слоях имеет место чистая разгрузка. Материал цилиндра не получает пластических деформаций, если только рабочее давление не превышает давление предварительного обжатия.

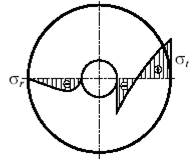
Рис.8.12

Пример расчета элемента тонкостенной оболочки вращения

Рассчитать коническую часть тонкостенной оболочки вращения (рис.8.13) с толщиной стенки δ = 0,02 м. Давление внутри оболочки P = 0,2 МПа, удельный вес жидкости γ = 1,5∙10⁴ н/м³.

Рис.8.13

Решение:

Рассмотрим отсеченную часть с действующими на нее силовыми факторами (см. рис.8.4).

Проводим через точку А первое сечение.

; ; ; .

Второе сечение проводим на расстоянии x = 0,15 м.

Высота столба жидкости над сечением v = 10 - 0,15 = 9,85 м.

Давление .

В соответствии с уравнением равновесия нижней отсеченной части оболочки (8.13) имеем

В соответствии с уравнением Лапласа имеем,

Радиус кривизны R₂ для конуса равен ∞

Третье сечение проведем через точку В (x = 0,25 м).

Высота столба жидкости над сечением v = 10 - 0,25 = 9,75 м.

Давление .

Решая уравнение равновесия (8.16) имеем

В соответствии с уравнением Лапласа имеем,

Радиус кривизны R₂ для конуса равен ∞

Пример расчета толстостенной стальной трубы

Для толстостенной стальной трубы, имеющей внутренний диаметр d = 0,03 м и наружный диаметр D = 0,18 м, и изготовленной из пластичного материала с σ_T = 250 МПа и с коэффициентом Пуассона μ = 0,5, требуется:

1. Определить давление p_T, при котором в материале трубы начнется пластическое деформирование;

2. Определить предельное внутреннее давление p_ПР, при котором весь материал будет находиться в пластическом состоянии;

3. Построить эпюры распределения напряжений σ_p, σ_φ, σ_z по толщине стенки для двух состояний трубы, рассмотрены в п. 1 и 2;

4. Определить допускаемое значение давления p_a = p_ДОП при коэффициенте запаса прочности n = 1,5.

Решение.

1. По формуле определяем давление, при котором на внутренней поверхности трубы появятся пластические деформации:

2. С учетом того, что p_a = p_T , из формул

определяем напряжения, соответствующие началу пластического течения:

Данные для числовых расчетов сводим в таблицу

1,5	148,5	-140,5
3	40,1	-32
6	13,0	-5,0
9,5	8,0	0

Эпюры напряжений σ_p, σ_φ, σ_z для упругого состояния материала трубы приведены на рис. 1, а.

Рассмотрим теперь предельное состояние трубы, когда весь материал трубы находится в пластическом состоянии. Предельное давление в этом случае определяется по формуле

Рис.1

3. Для определения напряжений σ_p, σ_φ, σ_z воспользуемся формулами

Данные для числовых расчетов сводим в таблицу

1,5	-517,8	-228,9	-373,4
3	-317,6	-28,6	-173,1
6	-117,5	-171,7	27,2
9	0	289,0	144,5

Для более точного построения эпюр и определим точки, в которых указанные напряжения равны нулю:

для эпюры

для эпюры

4. Эпюры напряжений σ_p, σ_φ, σ_z приведены на рис. 1, б. Допускаемое значение внутреннего давления определяется из условия p_ДОП = p_ПР/n : p_ДОП = 517,8/1,5 = 345,2 МПа.

Пример 3.

Для стальной составной трубы (рис. 1) заданы: внутренний радиус внутренней трубы а = 7см, внутреннее давление р = 100 МПа, расчетное сопротивление стали R_y = 240 МПа, коэффициент Пуассона ν = 0,3; модуль продольной упругости Е = 2∙10⁵ МПа.

Требуется:

1) определить внешний радиус внутренней трубы b, внешний радиус наружной трубы с, радиальный натяг δ;

2) проверить прочность сплошной трубы с внутренним радиусом а и внешним радиусом с, нагруженной внутренним давлением р, используя III теорию прочности;

3) проверить прочность в опасных точках составной трубы, нагруженной внутренним давлением р, используя III теорию прочности;

4) определить радиальные перемещения точек внутреннего канала.

Рис.1

Решение.

1) Определение геометрических параметров b, c и δ.

Внешний радиус с наружной трубы определяется на основе условия прочности:

Внешний радиус b внутренней трубы определяется по формуле:

Радиальный натяг рассчитываем по формуле:

2) Проверка прочности сплошной трубы с внутренним радиусом а и внешним радиусом с, нагруженной давлением р.

Из теории расчета толстостенных труб известно, что и при нагружении внутренним давлением, и при нагружении внешним давлением опасными являются точки на внутреннем канале трубы.

Рассчитываем напряжения в точках 1 (рис. 1), используя формулы

и полагая в них b = c, p_a = p, p_b = 0, r = a:

По аналогии определяем в точках 2 и 3:

и в точке 4:

Эпюра распределения напряжений по толщине сплошной трубы с внутренним радиусом a и внешним радиусом c показана на рис. 2.

Рис.2

Условие прочности по III теории прочности имеет вид

В нашем случае в точке 1 трубы будет

Таким образом, получаем

Условие прочности для сплошной трубы не выполняется.

3) Проверка прочности в опасных точках составной трубы, нагруженной внутренним давлением р.

Вначале рассчитываем давление от натяга р_к на поверхности контакта наружной и внутренней трубы, используя формулу

Рассчитываем напряжения и в точке 1 от действия натяга р_к, используя формулы

и полагая в них p_a = 0, p_b = p_k , r = a:

Рассчитаем суммарные напряжения и в точке 1 от действия р и p_k:

Проверяем прочность составной трубы в точке 1 по III теории прочности:

Условие прочности для составной трубы выполняется.

4) Определение радиальных перемещений точек 1 составной трубы.

Воспользуемся законом Гука для двухосного напряженного состояния

Вопросы для самопроверки

- Что называется оболочкой?

- Приведите примеры конструкций, которые могут быть отнесены к оболочкам?

- Какие элементы конструкций относятся к тонкостенным сосудам?

- Что является границей между тонкостенными и толстостенными сосудами?

- Какая теория используется при расчете тонкостенных сосудов?

- Какая поверхность называется срединной поверхностью оболочки?

- Какая оболочка называется осесимметричной?

- Сформулируйте основные положения безмоментной теории оболочек?

- В каких случаях можно использовать безмоментную теорию?

- Запишите уравнение Лапласа для тонкой оболочки.

- Запишите уравнение равновесия отсеченной части осесимметричной оболочки.

- Запишите условие четвертой теории прочности для оболочек.

- На чем основан расчет газгольдера?

- На чем основан расчет котла?

- Какая разница между меридиальным и окружным напряжениями?

- Почему при достижении предельного давления в трубе она разрушается по образующей?

- Чем принципиально отличается расчет тонкостенного и толстостенного сосудов?

- По каким формулам вычисляются напряжения в длинной круговой цилиндрической оболочке, нагруженной равномерным всесторонним внешним или внутренним давлением?

- По каким формулам вычисляются нормальные напряжения в сферической оболочке, нагруженной равномерным всесторонним внешним иили внутренним давлением?

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00