Главная
Лекция 13 (продолжение). Примеры решения
на вычисление перемещений методом Мора-Верещагина
Определение перемещений в рамах
Пример 1.
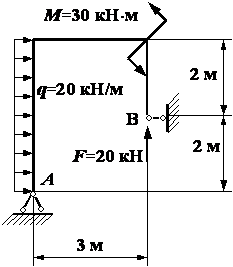
Для стальной рамы построить эпюры внутренних
силовых факторов, подобрать двутавровое поперечное сечение, определить
вертикальное перемещение и угол поворота сечения в точке С, если F = 10 кН, q =
4 кН/м, a = 2 м, b =
1м, 
= 120 МПа.
Решение.
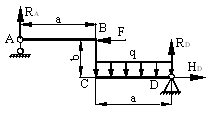
1) Определяем опорные реакции
; 
; 
; 
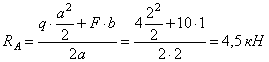
Проверка
; 
- верно
2) Строим эпюры внутренних силовых факторов
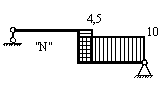
2.1) Эпюра нормальной силы
2.2) Эпюра поперечной силы
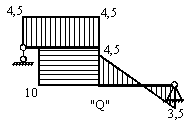
2.3) Эпюра изгибающего момента
Составляем уравнения изгибающих моментов для каждого участка рамы.
АВ
ВС
Найдем координату сечения, в котором эпюра изгибающего момента пересекает нулевую линию.
CD
Найдем координату сечения, в котором эпюра изгибающего момента пересекает нулевую линию.
Найдем координату сечения, в котором эпюра изгибающего момента имеет максимум. Для этого найдем производную от изгибающего момента и приравняв ее к нулю выразим z3 max.
Найдем максимум изгибающего момента.
Эпюра изгибающего момента
Максимальный изгибающий момент возникает в т. В, его величина составляет Mmax= 9 кНм. Нормальная сила в этом сечении N=4,5 кН.
3) Подбираем поперечное сечение
Поперечное сечение подбираем из условия прочности на изгиб:
По ГОСТ 8239 – 89 подбираем двутавр № 14: WX = 81,7 см3, IX = 572 см4.
4) Проверяем поперечное сечение по условию прочности
Условие прочности выполняется.
5) Строим единичные эпюры
5.1) Эпюра от единичного момента
Определяем опорные реакции от действия единичного момента.
; 
;
; 
Эпюра представлена на рисунке.
5.2) Эпюра от единичной силы
Определяем опорные реакции от действия единичной силы.
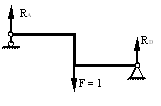
Эпюра представлена на рисунке.
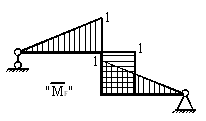
6) Определяем угол поворота т. С
Угол поворота определим по способу
Верещагина, перемножив эпюры 
и 
.
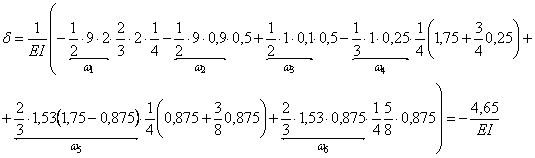
7) Определяем вертикальное перемещение т. С
Перемещение определим, перемножив эпюры и 
.
Пример 2.
Для рамы, показанной на рис.1, найти
вертикальное перемещение точки В и
угол поворота сечения А. Жесткость
стержней рамы будем считать одинаковой (
). Перемещения ищем методом Максвелла – Мора,
интегрируя формулу Максвелла – Мора аналитически и графически (с помощью
правила Верещагина).
Рис.1
Решение.
Будем искать
первое обобщенное перемещение – вертикальное перемещение точки В. В соответствии с методом Максвелла –
Мора для определения этого перемещения приложим в точке В единичную вертикальную сосредоточенную силу (рис. 2, а)
и найдем изгибающий момент, вызванный этой нагрузкой (координаты 
, 
, 
должны отсчитываться
так же, как при определении момента от заданной нагрузки):
участок 1:
м;
;
участок 2:
м;
;
участок 3:
м;
.
Рис.2
Аналогично для определения второго обобщенного перемещения – угла поворота сечения А – приложим в точке А сосредоточенную пару сил, равную единице (рис. б), и определим изгибающий момент от этой пары:
участок 1:
м;
;
участок 2:
м;
;
участок 3:
м;
.
Вариант 1. Аналитическое интегрирование формулы Максвелла – Мора
Подставим в формулу
Максвелла – Мора 
выражения для изгибающих
моментов от заданной нагрузки, найденные ранее при определении внутренних
усилий в рассматриваемой раме, умножим их на выражения для изгибающих моментов
от единичных обобщенных сил на всех трех участках и выполним интегрирование.
Тогда, учтя, что , проинтегрируем формулу :
;
В соответствии с правилом знаков метода Максвелла – Мора положительный знак вертикального перемещения говорит о том, что точка В перемещается по направлению обобщенной силы, то есть вверх. Сечение А поворачивается по часовой стрелке (в сторону, противоположную направлению единичной пары сил, так как знак угла поворота отрицательный).
Вариант 2. Интегрирование формулы Максвелла – Мора с помощью правила Верещагина
Построим эпюры моментов от заданной нагрузки М и от единичных обобщенных сил, соответствующих искомым перемещениям, М1 и М2 (рис. 3).
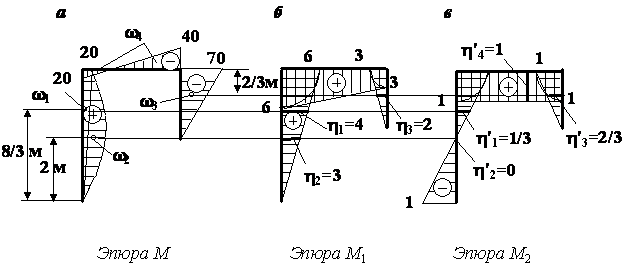
Рис.3
Для перемножения эпюр разобьем эпюру М на 4 простые фигуры: два треугольника 
и 
, сегмент 
и трапецию 
. Найдем ординаты под центрами тяжести этих фигур на эпюре М1 (
, 
и 
на
рис. 3, б). Эпюру М на ригеле,
имеющую форму трапеции с основаниями разного
знака, умножаем на трапецию эпюры М1 по правилу трапеций 
.
Согласно правилу Верещагина
.
Аналогично находим угол поворота сечения А, перемножая эпюры М и М2.
Ординаты под центрами тяжести площадей , и показаны на
рис. 3, в (, и ). Для перемножения трапеции на прямоугольник эпюры
М2
нет необходимости пользоваться правилом трапеций, так как, где бы ни
находился центр тяжести трапеции, значение 
известно (ординаты на
эпюре М2 на этом участке
постоянны).
.Результаты, полученные по двум вариантам использования формулы Максвелла – Мора, совпадают.
В заключение построим деформированную ось рамы так, чтобы она удовлетворяла эпюре изгибающих моментов и условиям закрепления рамы (рис. 4).
Рис.4
На рис. 4 показаны полученные
перемещения –
, 
в соответствии с их
направлениями. Точка перегиба (крестик) изогнутой оси ригеля имеет место в
сечении, где меняет знак изгибающий момент. Углы рамы в процессе деформации не
меняются.
Пример 3.
Определить горизонтальное и вертикальное перемещения точки А в раме (рис. а).
Решение.
Для решения задачи необходимо рассмотреть
три состояния рамы: грузовое и два единичных. Эпюра моментов MF , соответствующая первому
состоянию, представлена на рис. б. Для вычисления горизонтального перемещения
прикладываем в точке А по направлению
искомого перемещения (т.е. горизонтально) силу 
, а для вычисления вертикального перемещения силу прикладываем
вертикально (рис. в,д). Соответствующие эпюры 
и 
показаны на рис. г,е.
Горизонтальное перемещение точки А:
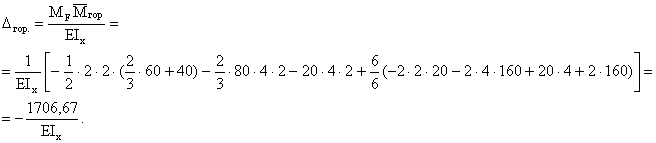
При вычислении 
на участке АВ трапеция (эпюра MF)
разбита на треугольник и прямоугольник, после чего треугольник с эпюры "умножен" на каждую из этих фигур. На участке ВС криволинейная трапеция разделена на криволинейный
треугольник и прямоугольник.
Знак "-", полученный при
вычислении , означает, что точка А перемещается по горизонтали не влево (в этом направлении
приложена сила ), а вправо.
Вертикальное перемещение точки А:
Здесь знак " - " означает, что точка А перемещается вниз, а не вверх.
Отметим, что единичные эпюры моментов,
построенные от силы , имеют размерность длины, а единичные эпюры моментов построенные от момента 
, являются безразмерными.
Пример
4.
Дано: 
Для рамы, показанной
на рис.1, а необходимо:
1. Построить эпюру изгибающих моментов.
2. Определить по правилу Верещагина линейные перемещения сечения А в вертикальном и горизонтальном направлениях.
3. Найти полное линейное перемещение сечения А.
4. Определить угол поворота сечения B.
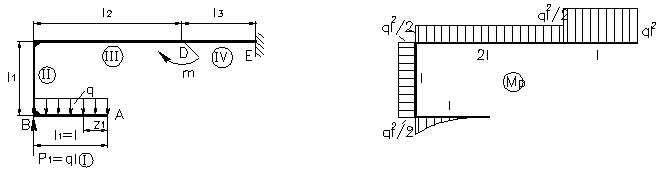
а) б)
Рис.1
Решение.
1) Строим эпюру изгибающих моментов 
по точкам на
участках I, II,III, IV, используя метод
сечений (рис.1, б). Построение эпюры ведем со свободного края А, т.к. рама является консольной.
На I участке: 
На II участке : 
.
Далее используя правило «циркуля» получаем:
На III участке : 
На IV участке : 
2) Линейные и угловые перемещения сечений рамы вычисляем по формуле для произвольного сечения К при помощи правила Верещагина
.
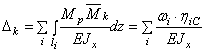Здесь
- площадь нелинейной эпюры изгибающих моментов на i –ом участке, 
- ордината линейной
эпюры моментов, соответствующая центру тяжести С нелинейной эпюры.
Для определения вертикальной и
горизонтальной составляющих перемещения сечения А прикладываем к сечению А соответственно вертикальную (рис.2) и
горизонтальную (рис.3) единичные силы и строим эпюры единичных моментов 
, используя правило «циркуля» в узлах.
Рис. 2
Рис.3
При
этом отметим, что внешние нагрузки 
отбрасываются.
Вычислим теперь вертикальное перемещение
сечения А путем «перемножения» по
правилу Верещагина эпюр 
и 
:
Знак «-«
говорит о том, что направление 
противоположно направлению вертикальной
единичной силы.
Вычислим теперь горизонтальное перемещение
сечения А
путем «перемножения» по правилу Верещагина эпюр
и 
:
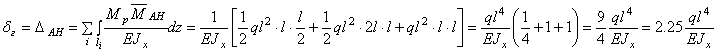
Горизонтальное перемещение сечения А совпадает по направлению с горизонтальной единичной силой.
3) Определим полное перемещение сечения А по формуле:
4) Найдем угол поворота сечения В.
Для этого «перемножим» по правилу Верещагина
эпюры и 
. Эту эпюру получаем, приложив в сечении В единичный момент (рис.4).
Рис. 4
Пример
5.
Определить горизонтальное смещение опорной точки В ломаного стержня (рамы), изображенного на рис. а. Жесткость на изгиб всех участков рамы постоянна и равна EI.
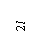
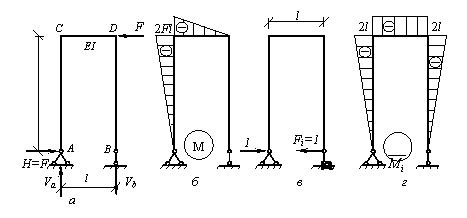
Решение.
Строим эпюру изгибающих моментов М от действия внешней силы F. Для этого предварительно определим опорные реакции:
откуда H=F; 
откуда Vb=2F;
тогда Va = 2F.
В этом случае для эпюры изгибающих моментов М получаем: МА = 0, 
МD = МВ
= 0 (рис. б).
По условию требуется определить
горизонтальное смещение хВ
опорной точки В
рамы, поэтому прикладываем единичную горизонтальную силу Fi = 1
в точке В (рис. в). Затем строим единичную эпюру изгибающих моментов 
(рис. г) от
единичной силы.
Перемножая эпюры М и на соответствующих участках
рамы окончательно находим
Пример 6.
Определить вертикальное перемещение точки А плоско-пространственной системы (рис. а).
Решение.
Как известно в поперечных сечениях стержней плоско-пространственной системы возникают три внутренних силовых фактора: поперечная сила Qy, изгибающий момент Mx и крутящий момент Mкр. Так как влияние поперечной силы на величину перемещения незначительно, то при вычислении перемещения методом Мора и Верещагина из шести слагаемых остаются только два.
Для решения задачи построим эпюры изгибающих
моментов Mx,q и крутящих
моментов Мкр,q от внешней
нагрузки (рис. б), а затем в точке А приложим силу по направлению
искомого перемещения, т.е. вертикального (рис. в), и построим единичные эпюры
изгибающих моментов 
и крутящих моментов 
(рис. г). Стрелками на эпюрах крутящих моментов показаны
направления закручивания соответствующих участков плоско-пространственной
системы.
Вертикальное перемещение точки А:
При перемножении эпюр крутящих моментов произведение берется со знаком "+", если стрелки, указывающие направление кручения, сонаправлены, и со знаком "-" – в противном случае.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
