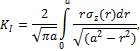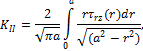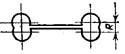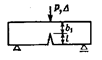Лекция 22. Понятие
о механике разрушения
Содержание
Предмет механики разрушения
Постановка вопроса о прочности
Виды и классификация разрушений
Хрупкое и пластическое разрушение
Условия пластичности и разрушения
материалов
Теория прочности Мора (1860г.)
Дефекты структуры тела, способствующие
разрушению
Типы трещин
Основные механизмы образования трещин
Механизмы, микромеханизмы,
карты разрушения
Классические схемы хрупкого, квазихрупкого, вязкого разрушения
Сингулярные задачи теории упругости для тел
с трещинами
Теоретическая и техническая прочности
Работа Гриффитса
«Явление разрушения и течения твердого тела»
Силовой критерий разрушения – K1c
Расчет на прочность материалов с трещинами
Использование коэффициента интенсивности
напряжений (КИН) в рамках линейной упругой механики разрушения (ЛУМР)
1) Критерий разрушения Kc
2) Ограничения линейной упругой механики
разрушения
Оценка коэффициента интенсивности
напряжений
1) Аналитические методы
2) Метод конечных элементов (МКЭ)
2.1) Прямой
метод
2.2) Энергетический метод
2.3) Использование специальных элементов
Управление поведением трещин на основе
линейной механики разрушения
Напряженное и деформированное состояние в
вершине трещины в упругопластической области. Раскрытие трещины
1) Модель Дагдейла
2) Модель Билби-Коттрелла-Суиндена
3) Критерий разрушения COD
4) Оценка раскрытия трещины
4.1) Определение раскрытия трещины на
основе центра поворота
4.2) Решение при помощи МКЭ
J-интеграл
1) Определение J-интеграла
2) Энергетическая трактовка J-интеграла
3) Применение J-интеграла
4) Оценка J-интеграла
4.1) Энергетические способы
4.2) Определение J-интеграла методом
конечных элементов
Связь силового, деформационного и
энергетического критериев механик разрушения
Вопросы для самопроверки
Предмет механики разрушения
Выбор метода изучения прочности и разрушения материалов
зависит от размера исследуемого объекта (рис. 22.1). Размер часто определяет
раздел науки или в пределах раздела уровни
исследования, которые могут развиваться практически независимо друг от друга.
Например: 1) на уровне физических теорий, или физика твердого тела; 2) на
уровне материаловедческих исследований для металлов – металловедение; 3) на уровне
механики материалов, или механические исследования конструкций. Для удобства в
дальнейшем будет использоваться эта классификация.
Чтобы проследить за развитием науки о прочности,
необходимо детально изучить каждую ее специальную область. В настоящее время,
несмотря на существенный прогресс в каждой из трех областей науки о прочности,
все же имеет место большое различие между исследованиями, проводимыми на
микро- и макроскопических уровнях, что связано с известными затруднениями.
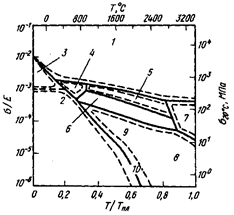
На рис. 22.1
представлены размеры изучаемых объектов. К объектам, равным 10-2-10-3
см, относятся, с одной стороны, зерна – основные объекты исследования металловедения
и физики металлов, с другой – трещины – объект, изучаемый механикой материалов.
В целом во всем интервале размеров могут содержаться объекты, начиная от
дислокации и вакансий – дефектов на атомном уровне – и кончая трещинами – макродефектами. Указанные дефекты можно объединить общим
названием «структурные дефекты материала».
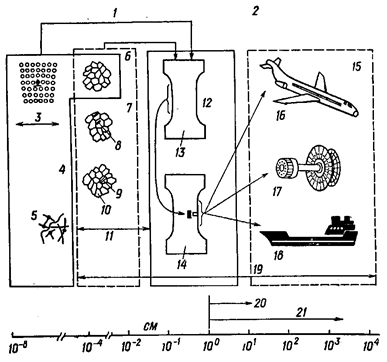
Рис. 22.1. Спектр объектов исследований, механизмы прочности и
разрушения.
Область микроисследований – физика твердого тела,
металлургия, металловедение; область макроисследований
– механика материалов, механика непрерывных сред, прочность конструкций. Все
эти направления исследований на рис.22.1 обозначены штриховыми и сплошными
линиями. Следует строго разграничивать микро- и макрообласти исследований, а внутри этих больших разделов –
области каждого научного направления. На схеме показан интервал размеров
твердых тел от 10-8 до 104 см. В настоящее время
серьезной проблемой является система, которая координировала бы взаимосвязь
между сферами исследований. Например, необходимо исследование
влияния надреза 100 – 101 см (раздел Механика
материалов) согласовать с прочностью
объектов 102 – 104 см – крупногабаритные турбины,
самолеты и т. д.: 1 – микроисследования; 2 – макроисследования;
3 – размер дислокаций; 4 – физика твердого тела; 5 – размер крупных молекул; 6 –
металлургия; 7 – материаловедение; 8 –
неметаллические включения; 9 – трещина; 10
– кристаллические зерна;
11 – размер зерен; 12 – механика
сплошных сред и механика материалов; 13 –
гладкие образцы; 14 – образцы с
трещиной или надрезом; 15 – прочность
конструкций; 16 – самолеты; 17 –
крупногабаритные турбины; 18 –
корабли; 19 — длина трещины; 20 –
толщина образца; 21 – ширина образца.
Может
показаться, что эти дефекты не могут рассматриваться совместно. Однако имеются
все основания для изучения микро- и макрообъектов, что имеет важное
практическое значение. Учет роли всевозможных дефектов структуры в формировании
макроскопических свойств материала невозможно выполнить простым суммированием
функций, которые линейно описывают закономерности влияния этих дефектов. Макроскопические
закономерности поведения сплошного тела, по-видимому, можно описать как
суперпозиции функций мультипликативного вида, комплексно описывающих влияние
структурных дефектов. При изучении этих проблем положены в основу следующие
принципы: 1) комплексность; 2) широкий охват исследуемых материалов; 3)
изучение разрушения в различных условиях нагружения
(течение, хрупкое и вязкое разрушение, разрушение в средах в условиях
усталости и ползучести).
В настоящее
время комплексный подход в области прочности материалов предполагает следующие
направления.
1. Атомистический подход (атомистическая
теория и теория дислокации)
2. Микроструктурный подход — изучение
структуры материалов (металловедение и физика металлов)
3. Подход с позиции механики сплошных сред
(механика разрушения)
4. Феноменологический подход (аналитические
методы расчета)
5. Подход, базирующийся на термодинамике и
статистической механике
6. Статистический (вероятностный) подход
7. Подход, учитывающий влияние окружающей
среды
8. Механические испытания материалов (анализ
напряжений и деформаций в материалах)
9. Подход с точки зрения прочности
конструкций (считается основным, так как именно здесь в полной мере можно
использовать принцип систематизации и новые методологические разработки).
Конструкционный подход
а) синтез микро- и макроисследований с позиций механики разрушения
б) связь микро- и макрообъектов с позиции
кинематики
в) вероятностные подходы
Постановка
вопроса о прочности
Основной областью применения сопротивления
материалов и в целом механики деформируемого твердого тела является оценка
прочности реальных материалов и элементов конструкций при их эксплуатации.
Определение напряжений, деформаций и перемещений в телах еще не дает ответа на
вопрос об их прочности. Термин «прочность» требует некоторого разъяснения. В
широком смысле слова под нарушением прочности (разрушением) понимается
достижение такого состояния, когда нарушается конструктивная функция тела и оно становится непригодным к эксплуатации. В прямом,
но более узком смысле слова, под нарушением прочности (разрушением) понимается
разделение тела на части. Для пластичных материалов под разрушением следует понимать
возможность появления недопустимо больших деформаций. Заметим, что для
пластичных материалов выполнение условия пластичности в одной точке тела еще не
означает потери его несущей способности. Например, в балке на рис. 22.2,а появление пластичности в точках А и В среднего опасного сечения не представляет реальной опасности.
Поэтому расчет по методу допускаемых напряжений для пластичного материала безусловно гарантирует прочность элемента
конструкции. В то же время перемещения в балке остаются ограниченными, и потому
обнаруживается значительный резерв прочности.
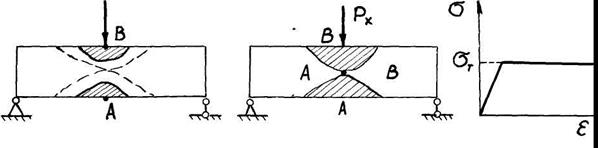
а)
б)
в)
Рис.
22.2
При увеличении внешней нагрузки
заштрихованные пластические зоны расширяются и, наконец, соединяются, отделяя
при этом жесткие части А и В друг от друга (рис. 22.2,
б). Эти части могут теперь свободно
перемещаться друг относительно друга, а тело балки получает неограниченно большие
деформации и перемещения (рис.22.2, в).
Поэтому расчет по методу допускаемых нагрузок представляет собой расчет на
прочность. С другой стороны, пластические материалы при низких температурах
разрушается без заметных пластических деформаций. Такое разрушение называют
хрупким в результате разрыва материала. Разрушение хрупкого материала
начинается локально с отдельной микротрещины путём её разрастания. Локальное
разрушение служит источником концентрации напряжений и потому может послужить
началом мгновенного разрушения тела в целом путем разделения на части. Поэтому
расчет хрупких материалов на прочность по допускаемым напряжениям в наиболее
напряженной точке тела оправдан.
Отметим, что деление материалов на пластические и хрупкие является условным. Например, хрупкие
материалы (бетон, гранит и др.) при высоких давлениях и температурах
обнаруживают значительные пластические деформации. Существенную роль в оценке
прочности играет время.
Разрушение является процессом, развертывающимся во времени, и потому может произойти
при разных уровнях напряжений. Так, в условиях ползучести мы ввели понятие о
времени разрушения, пределе длительной прочности (напряжении, приводящем к
разрушению через определенное время). Таким образом, проблема прочности и
разрушения зависит от многих факторов и очень сложна. Несмотря на сложность
проблемы, в сопротивлении материалов есть разделы, с помощью которых можно
прямо и непосредственно ответить на вопрос о возможности разрушения. Это
разделы об устойчивости и колебаниях упругих и упругопластических систем.
Достижение нагрузкой предельной величины
можно считать за момент разрушения. Если частота возмущающей силы совпадает с
частотой низших собственных колебаний, наступает резонанс с недопустимо
большими перемещениями, приводящими к разрушению. Отметим, что резонанс на
высоких гармониках, как правило, не страшен.
Виды
и классификация разрушений
Разрушение
представляет собой чрезвычайно сложный, многостадийный процесс, управляемый
большим количеством факторов. В зависимости от изменяющихся условий можно
получить весьма различные характеристики процесса разрушения. О сложности и
неоднозначности явления свидетельствует тот факт, что нет общепринятого
определения разрушения и общепринятой классификации видов разрушения.
В общем случае механическое
разрушение может быть определено как любое изменение размера, формы или
свойств материала конструкции, машины или отдельной детали, в результате которого она утрачивает способность
удовлетворительно выполнять свои функции. Основываясь на этом, вид разрушения можно определить как
физический процесс или несколько взаимосвязанных между собой процессов,
приводящих к разрушению.
Рассмотрим
наиболее известные попытки классификации видов и типов разрушения.
Проф. Старки
(W. L. Starkey) из Университета шт. Огайо предложил систему классификации всех
возможных видов разрушения. Эта система основана на учете трех факторов:
(1) характера разрушения, (2) причин разрушения и (3) места разрушения.
Подробно эти факторы определяются ниже. Каждый отдельный вид разрушения
характеризуется тем, как проявляйся разрушение, что его вызывает и где оно
происходит. Используя различные комбинации этих факторов, можно указать
буквально сотни видов разрушения. Чтобы подробнее пояснить суть этой системы
классификации, раскроем содержание каждого из этих трех факторов.
По характеру разрушения
можно выделить четыре класса (причем некоторые из них могут состоять из
подклассов):
1. Упругая деформация.
2. Пластическая деформация.
3. Разрыв, или
разделение на части.
4. Изменение материала: (А)
металлургическое; (В) химическое; (C) ядерное.
По причинам разрушения можно определить четыре класса:
1. Нагрузки: (А) установившиеся; (В) неустановившиеся; (С) циклические; (D)
случайные.
2. Время процесса: (А) очень
малое; (В) малое; (С) продолжительное.
3. Температуры: (А) низкие; (В) комнатные; (С) повышенные; (D) установившиеся;
(Е) неустановившиеся; (F) циклические; (G) случайные.
4. Воздействия окружающей среды:
(А) химические; (В) ядерные.
По месту разрушения существует
два типа разрушения: (А) объемное; (В) поверхностное.
Для точного описания какого-либо
вида разрушения необходимо выбрать характеристики процесса из указанного
перечня, не упуская из виду ни одного из трех основных факторов. Например, для
описания разрушения в качестве характерного проявления можно выбрать пластическую деформацию, в качестве
причин — установившуюся нагрузку и комнатную температуру, а в качестве
типа — объемный тип разрушения. Таким
образом, указанный вид разрушения можно определить как объемное пластическое деформирование
под действием установившейся нагрузки при комнатной температуре. Такой вид
разрушения обычно называется течением.
Отметим, однако, что термин течение
обычно определяет не только указанный вид разрушения: этот термин имеет более
общий смысл.
Используя перечисленные классы и
подклассы трех основных факторов, определяющих вид разрушения, можно дать
определение многих других видов разрушения. Приведенный перечень характеристик
процесса разрушения нуждается в дополнительном пояснении и конкретизации,
особенно применительно к наиболее опасным видам разрушения. Ниже перечислены
двадцать три таких вида разрушения.
Нижеследующий перечень содержит
наиболее часто встречающиеся на практике виды разрушения. Глядя на этот
перечень, можно заметить, что некоторые виды разрушения являются простым процессом,
в то время как другие представляют собой сложные явления. Например, в этом
перечне в качестве видов разрушения указаны коррозия и усталость, а наряду с
этим в качестве еще одного вида разрушения указана коррозионная усталость. Это
сделано потому, что и коррозия, и усталость часто оказывают существенное
влияние на поведение конструкций, причем механизмы их действия взаимосвязаны.
Это означает, например, что при коррозионной усталости коррозия ускоряет
процесс усталости, а действие циклических усталостных нагрузок в свою очередь
ускоряет процесс коррозии. В приведенном перечне содержатся все обычно наблюдаемые
виды механического разрушения.
1. Упругая деформация, вызванная
действием внешних нагрузок и (или) температуры.
2. Текучесть.
3. Бринелирование.
4. Вязкое разрушение.
5. Хрупкое разрушение.
6. Усталость: (А) многоцикловая; (В) малоцикловая; (С) термическая; (D)
поверхностная; (Е) ударная; (F) коррозионная; (Q) фреттинг-усталость.
7. Коррозия: (А)
химическая; (В) электрохимическая; (С) щелевая; (D) точечная (питтинговая); (Е) межкристаллическая; (F) избирательное
выщелачивание; (G) эрозионная; (Н) кавитационная; (I)
водородное повреждение; (J) биологическая; (К) коррозия под напряжением.
8. Износ: (А) адгезионный; (В)
абразивный; (С) коррозионный; (D) поверхностный усталостный; (Е)
деформационный; (F) ударный; (G) фреттинг-износ.
9. Разрушения при ударе: (А)
разрыв при ударе; (В) деформирование при ударе; (С) ударный износ; (D) ударный
фреттинг; (Е) усталость при ударе.
10. Фреттинг:
(А) фреттинг-усталость; (В) фреттинг-износ;
(С) фреттинг-коррозия.
11. Ползучесть.
12. Термическая релаксация.
13. Разрыв при кратковременной
ползучести.
14. Тепловой удар.
15. Заедание и схватывание.
16. Откол.
17. Радиационное повреждение.
18. Выпучивание.
19. Выпучивание при ползучести.
20. Коррозия под напряжением.
21. Коррозионный износ.
22. Коррозионная усталость.
23. Ползучесть с усталостью.
Ниже дается краткое определение
с соответствующими пояснениями видов механического разрушения.
Упругая деформация, вызванная действием внешних нагрузок и
(или) температур. Этот вид разрушения имеет место, когда упругая (обратимая)
деформация элемента, возникающая при действии эксплуатационных нагрузок и
температур, становится настолько большой, что элемент утрачивает способность
выполнять предназначенную ему функцию.
Текучесть имеет место,
когда пластическая (необратимая) деформация пластичного элемента, возникающая
при действии эксплуатационных нагрузок, становится настолько большой, что
элемент утрачивает способность выполнять предназначенные ему функции.
Бринелирование,
или разрушение вдавливанием, происходит, когда статические усилия в месте
контакта криволинейных поверхностей приводят к появлению локальных
пластических деформаций у одного или у обоих соприкасающихся элементов, в
результате чего происходит необратимое изменение формы поверхности. Например,
если шарикоподшипник статически нагружен так, что шарик вдавливается в обойму,
пластически деформируя ее, то поверхность обоймы становится волнистой. При
дальнейшем использовании подшипника могут возникнуть недопустимые вибрации,
шум и перегрев, т. е. налицо его разрушение.
Вязкое (пластическое) разрушение
наблюдается, когда пластическая деформация пластичного элемента достигает
такой величины, что он разделяется на две части. Разрушение происходит в
результате процесса зарождения, слияния и распространения внутренних пор,
поверхность разрушения при этом гладкая и волнистая. Примером пластического
разрушения может служить разрыв образца из отожженной меди после 100% сужения
шейки при растяжении, происходящий в результате утраты способности материала
сопротивляться пластической деформации.
Хрупкое
разрушение происходит,
когда упругая деформация элемента из хрупкого материала достигает такой
величины, что разрушаются первичные межатомные связи и элемент разделяется на
две или более части. Внутренние дефекты и образующиеся трещины быстро
распространяются до полного разрушения; поверхность разрушения при этом
неровная, зернистая.
Хрупкое разрушение подразделяется на идеально хрупкое и квазихрупкое
(как бы хрупкое).
Идеально хрупкое или хрупкое
разрушение происходит без пластической деформации. После разрушения можно
заново составить тело прежних размеров из осколков зазоров между ними.
Квазихрупкое разрушение предполагает наличие
пластической зоны перед краем трещины (локальная зона пластической деформации)
и наклепанного материала у поверхности трещины. Остальной, значительно больший
по величине, объем тела находится при этом в упругом состоянии.
Термин усталость
применяется для обозначения разрушения в виде неожиданного внезапного
разделения детали или элемента машины на две или более части в результате
действия в течение некоторого времени циклических нагрузок или деформаций. Разрушение
происходит путем зарождения и распространения трещины, которая после
достижения некоторого критического размера становится неустойчивой и быстро
увеличивается, вызывая разрушение. Нагрузки и деформации, при которых обычно
происходит усталостное разрушение, намного ниже тех, которые приводят к
разрушению в статических условиях. Когда величины нагрузок и перемещений таковы,
что разрушение происходит более чем через 10 000 циклов, явление обычно
называется многоцикловой
усталостью. Когда же величины нагрузок и перемещений таковы, что
разрушение происходит менее чем через 10 000 циклов, явление называется малоцикловой
усталостью.
Когда
циклические нагрузки и деформации возникают в детали в результате действия
циклически меняющегося температурного поля, явление обычно называется термической
усталостью. Разрушение,
называемое поверхностной усталостью, обычно происходит при наличии
вращающихся контактирующих поверхностей. Проявляется оно в виде питтинга, растрескивания и выкрашивания
контактирующих поверхностей в результате действия контактных напряжений, под
влиянием которых на небольшой глубине у поверхности возникают максимальные по
величине циклические касательные напряжения. Эти напряжения приводят к
возникновению трещин, которые выходят на поверхность, при этом некоторые
частицы материала отделяются. Это явление часто считается разновидностью
износа. Ударная усталость, коррозионная усталость и фреттинг-усталость
будут описаны ниже.
Коррозия — термин, используемый для обозначения
широкого класса видов разрушения, при которых деталь или элемент машины
утрачивает способность исполнять свою функцию из-за нежелательной порчи
материала в результате химического или электрохимического взаимодействия с
окружающей средой. Коррозионное разрушение часто проявляется во взаимодействии
с другими видами разрушения, такими, как износ или усталость. Среди многих
типов коррозии отметим следующие. Химическая коррозия представляет
собой, по-видимому, наиболее общий тип коррозии вследствие непосредственного
контакта поверхности детали с коррозионной средой. Химическая коррозия
происходит более или менее равномерно по всей открытой поверхности детали. Электрохимическая
коррозия происходит, когда два разнородных металла образуют
часть электрической цепи, замыкаемой раствором или пленкой электролита
или коррозионной средой.
Щелевая коррозия — в значительной степени локализованный
быстропротекающий процесс в щелях, трещинах или стыках, т. е. в местах, где
задерживаются малые количества раствора, соприкасающегося с корродирующим
металлом. Точечная (питтинговая) коррозия
представляет собой локализованные воздействия, в результате которых происходит
образование углублений и ямок на поверхности металла. Межкристаллическая коррозия
характеризуется локальными воздействиями на границах зерен некоторых медных,
хромовых, никелевых, алюминиевых, магниевых и цинковых сплавов после
неправильной термообработки или сварки. Образование локальных гальванических
ячеек, в которых осаждаются продукты коррозии, приводит к существенному
снижению прочности материала в результате межкристаллической коррозии.
Избирательное выщелачивание
представляет собой коррозионный процесс, в результате которого из сплава
удаляется какой-либо элемент. Примерами могут служить процессы обесцинкования латуни и графитизации
чугуна. Эрозионная коррозия —
это быстропротекающий химический процесс, при котором в результате воздействия
абразивных веществ или потоков вязких материалов на поверхности материала
постоянно в месте контакта с коррозионной средой обнажается свежий
незащищенный материал. Кавитационная
коррозия наблюдается, когда под влиянием давления пара пузырьки и
каверны в жидкости лопаются у поверхности сосуда давления, в результате чего
удаляются частицы материала и открывается доступ коррозионной среде к свежему,
незащищенному материалу.
Водородное повреждение, хотя
само и не является какой-либо разновидностью коррозии, вызывается ею. К этому
виду повреждения относятся насыщение водородом, водородное охрупчивание
и обезуглероживание. Биологическая коррозия представляет
собой процесс коррозии вследствие активности живых организмов, а именно
процессов поглощения ими пищи и выделения отходов. Отходами являются вызывающие
коррозию кислоты и гидроокиси. Коррозия под напряжением — очень важная разновидность коррозии
(она будет отдельно рассмотрена ниже).
Износ является
нежелательным процессом постепенного изменения размеров вследствие удаления
отдельных частиц с контактирующих поверхностей при их движении, обычно
скользящем, относительно друг друга. Износ является в основном результатом
механического действия. Это сложный процесс, точнее даже ряд различных
процессов, которые могут протекать как независимо, так и взаимосвязано.
Результатом этих процессов является удаление материала с контактирующих
поверхностей вследствие сложного взаимодействия локальных сдвигов, вдавливаний,
сваривания материала, разрывов и других механизмов.
Адгезионный износ
происходит в результате действия высоких локальных давлений, сваривания между
собой шероховатостей поверхностей, последующей пластической деформации,
возникающей при их относительном перемещении, разрушения локальных сцеплений
шероховатостей, удаления или переноса металла. При абразивном износе частицы
удаляются с поверхности в результате режущего или царапающего действия
неровностей более твердой из контактирующих поверхностей или твердых частиц,
задержавшихся между поверхностями. Когда одновременно возникают условия как
для адгезионного, так и для абразивного износа и коррозии, эти процессы
взаимодействуют между собой и происходит коррозионный
износ.
Поверхностный усталостный износ
представляет собой изнашивание вращающихся или скользящих относительно друг
друга криволинейных поверхностей. При этом в результате действия циклических
касательных напряжений на небольшой глубине у поверхности возникают
микротрещины, выходящие на поверхность, откалываются макрочастицы
материала и на поверхности образуются ямки. Деформационный износ
происходит в результате повторного пластического деформирования изнашиваемых
поверхностей, приводящего к образованию сетки трещин, при росте и объединении
которых образуются частицы износа. Деформационный износ часто наблюдается при
действии ударных нагрузок. Ударный износ имеет место при
повторном упругом деформировании в
процессе действия ударных нагрузок, образовании сетки трещин, которые растут
так же, как при поверхностной усталости. Фреттинг-износ
описан ниже.
Разрушение при
ударе происходит,
когда в результате действия неустановившихся нагрузок в детали возникают такие
напряжения или деформации, что деталь уже не в состоянии выполнить предназначенную
ей функцию. Разрушение происходит в результате взаимодействия волн напряжений
и деформаций, являющихся следствием динамического или внезапного приложения
нагрузок. Взаимодействие волн может приводить к
возникновению локальных напряжений и деформаций, во много раз превышающих возникающие
при статическом приложении тех же самых нагрузок. Если величины
напряжений и деформаций таковы, что происходит разделение детали на две или
более частей, то налицо разрыв при ударе.
Если удар приводит к возникновению недопустимых упругих или пластических
деформаций, такое разрушение называется деформированием
при ударе. Если при повторных ударах возникают циклические упругие
деформации, в результате чего появляется сетка усталостных трещин, при росте
которых наблюдается описанное ранее явление поверхностной усталости, то
процесс называется ударным износом.
Если в
результате малых относительных поперечных смещений двух поверхностей при ударе,
которые могут вызываться поперечными деформациями или действием случайных
малых боковых составляющих скоростей, происходит фреттинг,
то разрушение называется ударным фреттингом. Усталость
при ударе наблюдается, когда разрушение происходит при повторном
действии ударных нагрузок вследствие образования и распространения усталостных
трещин.
Фреттинг может происходить на поверхности контакта двух
твердых тел, прижатых друг к другу нормальной силой и совершающих относительно
друг друга циклические движения малой амплитуды. Фреттинг
обычно имеет место в местах соединений, там, где движения не должно быть, но в
результате действия вибрационных нагрузок или деформаций незначительные
циклические смещения все-таки есть. Обычно отколовшиеся при фреттинге
частицы материала задерживаются между контактирующими поверхностями, поскольку
относительные смещения их малы.
Фреттинг-усталость представляет собой преждевременное усталостное
разрушение детали машины, на которую действуют циклические нагрузки или
деформации в условиях, способствующих фреттингу.
Поверхностные повреждения и микротрещины, появляющиеся в результате фреттинга. играют роль зародышей усталостных трещин, в
результате роста которых усталостное разрушение происходит при таких нагрузках,
которые в других условиях не вызывали бы разрушения. Фреттинг-усталость
– очень опасный и коварный вид разрушения, поскольку фреттинг
обычно происходит в местах соединений, не доступных для наблюдения, и приводит
к преждевременному или даже неожиданному (внезапному) катастрофическому
усталостному разрушению.
Фреттинг-износ
наблюдается, когда изменения размеров контактирующих деталей в результате фреттинга становятся недопустимо большими или такими, что
появляются концентраторы напряжений и локальные напряжения превышают допустимый
уровень. Фреттинг-коррозия происходит,
когда в результате фреттинга свойства материала
детали ухудшаются настолько, что она не может выполнять своих функций.
Разрушение в результате ползучести происходит,
когда пластическая деформация элемента машины или конструкции, накопленная в
течение некоторого времени действия напряжений и температуры, приводит к
изменениям размеров, вследствие которых элемент не может удовлетворительно
выполнять предназначенную ему функцию. При достаточно высоких температурах в
поликристаллическом металле границы зерен становятся более слабыми, чем сами
зерна, и значительная часть деформации ползучести происходит за счет скольжения
зерен относительно друг друга. Это скольжение носит характер вязкого течения,
оно затруднено кинематически, т.к. зерна имеют
неправильную форму и каждое зерно встречает сопротивление со стороны соседних. Скольжение становится возможным за счет
пластической деформации зерен и сопровождается появлением межзеренных
трещин, приводящих к разрушению.
Процесс
ползучести, как правило, можно разделить на три стадии: (1) неустановившуюся,
или первичную, ползучесть, во время которой скорость деформации уменьшается;
(2) установившуюся, или вторичную, ползучесть, во время которой скорость
деформации практически постоянна, и (3) третичную ползучесть, при которой
скорость деформации ползучести увеличивается (часто довольно быстро) вплоть до
разрушения. Такой вид разрушения часто называется разрывом при ползучести.
Произойдет или нет такое разрушение — зависит от характера изменения во времени
напряжений и температуры.
Термическая релаксация
наблюдается, когда в процессе ползучести, приводящей к релаксации
предварительно напряженной или деформированной детали, ее размеры изменяются
так, что деталь уже не может выполнять предназначенной ей функции. Например,
если предварительно напряженные болты сосуда давления, работающего в условиях
высоких температур, релаксируют вследствие
ползучести так, что нагрузка от максимального давления превышает
предварительную нагрузку и герметичность соединения нарушается, говорят, что
болты разрушаются вследствие термической релаксации.
Разрыв при кратковременной
ползучести тесно связан с процессом ползучести, однако при этом
зависимость напряжений и температуры от времени такова, что элемент разделяется
на две части. При этом напряжения и температура, как правило, таковы, что
период установившейся ползучести очень непродолжителен или совсем отсутствует.
Тепловой удар происходит,
когда градиенты возникающего в детали температурного поля настолько велики, что
вследствие перепадов температурных деформаций начинается текучесть или разрушение.
Заедание
наблюдается в случае, когда на две скользящие друг по другу поверхности
действуют такие нагрузки и температуры, а скорость скольжения, смазка и условия
окружающей среды таковы, что в результате значительной пластической деформации
шероховатостей поверхностей, их сваривания, отламывания и царапающего действия
происходит существенная деструкция поверхности и перенос металла с одной
поверхности на другую. Заедание можно считать очень интенсивным
процессом адгезионного износа. Когда указанные процессы приводят к
значительному ослаблению соединения или, наоборот, к схватыванию, говорят, что
соединение разрушается в результате заедания. Схватывание является, по
существу, интенсивным процессом заедания, при котором контактирующие детали
практически свариваются и их относительное перемещение становится невозможным.
Разрушение
отколом происходит,
когда от поверхности детали самопроизвольно отделяется часть материала, в
результате чего нормальная работоспособность элемента машины утрачивается. Например,
бронеплита разрушается в результате откола, когда при ударе снаряда о наружную
поверхность бронезащиты в плите возникают волны
напряжений, приводящие к отколу с внутренней стороны части материала, которая
сама становится смертоносным снарядом. Другим примером разрушения отколом может
служить разрушение подшипников качения или зубьев шестерен вследствие
описанного ранее явления поверхностной усталости.
Разрушение
вследствие радиационного повреждения означает, что при радиационном облучении произошли
такие изменения свойств материала, что деталь уже не может выполнить своих функций.
Обычно эти изменения связаны с потерей пластичности в результате облучения и
служат причиной начала процесса разрушения того или иного вида. Эластомеры и
полимеры обычно более подвержены радиационному повреждению, чем металлы, причем
прочностные характеристики последних после
радиационного облучения иногда улучшаются, хотя пластичность, как правило,
уменьшается.
Разрушение
выпучиванием наблюдается,
когда при некоторой критической комбинации величины и (или) места приложения нагрузки,
а также формы и размеров детали ее перемещения или прогибы внезапно резко
увеличиваются при малом изменении нагрузки. Такое нелинейное поведение
приводит к разрушению выпучиванием, если потерявшая устойчивость деталь уже не
может выполнять своих функций.
Разрушение
вследствие выпучивания при ползучести происходит, когда по истечении некоторого времени
в результате процесса ползучести возникает неустойчивое состояние, т. е.
нагрузки и геометрические параметры детали становятся такими, что теряется
устойчивость и происходит разрушение.
Разрушение в
результате коррозии под напряжением наблюдается, когда действующие напряжения приводят
к возникновению локальных поверхностных трещин, располагающихся обычно вдоль
границ зерен, в детали, находящейся в коррозионной среде. Часто образование
трещин инициирует начало процессов разрушения других видов. Разрушение в
результате коррозии под напряжением представляет собой очень опасный вид
коррозионного разрушения, поскольку ему подвержены многие металлы: Например,
разнообразные чугуны, стали, нержавеющие стали, медные и алюминиевые сплавы
подвержены коррозионному растрескиванию под напряжением в некоторых
коррозионных средах.
Разрушение
вследствие коррозионного износа
является сложным видом разрушения, при котором неблагоприятные последствия
коррозии и износа приводят совместно к потере работоспособности детали. В
процессе коррозии часто образуются твердые абразивные частицы, которые ускоряют
изнашивание, а в процессе изнашивания в свою очередь с поверхности постоянно
удаляются защитные слои и обнажается свежий металл, что ускоряет коррозию.
Взаимное влияние этих процессов друг на друга существенно повышает опасность
разрушения.
Коррозионная
усталость представляет
собой сложный вид разрушения, при котором совместно сказываются
неблагоприятные эффекты коррозии и усталости, приводящие к разрушению. В процессе
коррозии на поверхности металла часто образуются ямки, служащие концентраторами
напряжений. В результате концентрации напряжений процесс усталостного
разрушения ускоряется. Кроме того, трещины в хрупком слое продуктов коррозии
служат зародышами усталостных трещин, распространяющихся в основной металл. С
другой стороны, в результате действия циклических напряжений или деформаций
происходит растрескивание и отслаивание продуктов коррозии, т. е. открывается
доступ коррозионной среде к свежему металлу. Таким образом, оба процесса ускоряют
друг друга, и опасность разрушения может быть очень большой.
Разрушение вследствие ползучести с
усталостью является видом разрушения, происходящего в условиях,
вызывающих одновременно и усталость, и ползучесть. Взаимодействие процессов
ползучести и усталости изучено пока недостаточно, но, по-видимому, оно синергично.
Еще одна
распространенная классификация – классификация Я.Б.Фридмана.
Первый классификационный признак в этой таблице – характер силового воздействия
– является наиболее формальным, но в то же время он достаточно четко делит
процессы разрушения на несколько видов, которые следует рассматривать
раздельно. В пределах каждого из этих видов разрушения, конечно, необходимо
подразделение по другим используемым в классификации признакам. Так,
кратковременное однократное статическое разрушение может быть хрупким и
пластическим (вязким), соответственно может изменяться ориентировка
макроскопической поверхности разрушения и размер зоны пластической деформации.
Трещина может проходить преимущественно по телу или, наоборот, по границам
зерен; могут быть зафиксированы различные стадии процесса (начальное, развитое,
полное разрушение), возможно одновременное воздействие среды и т.д.
Возможны и
другие классификации видов разрушения.
Таблица 22.1
|
Классификационный
признак
|
Разрушение
|
|
Характер
силового воздействия:
- нагрузка в основном монотонно изменяется, периода
постоянной нагрузки нет или, он мал относительно
периода разрушения
- период неменяющейся нагрузки соизмерим
с периодом разрушения
- нагрузка периодически и
многократно изменяется в процессе разрушения
|
Кратковременное
однократное статическое
Длительное однократное
статическое и замедленное
Усталостное
|
|
Ориентировка
макроскопической поверхности разрушения при разных способах. нагружения
(растяжение,
изгиб,
сжатие, кручение, вдавливание и т. п.):
-
макроскопическая поверхность разрушения перпендикулярна направлению +σmax или +εmax
при крайне
малом пластически деформированном объеме в зоне
разрушения
- поверхность наклонена под
углом примерно 45° к
направлению +σmax
|
Отрыв
Срез
|
|
Локальность разрушения,
оцениваемая по соотношению размеров разрушаемой зоны и
структурных элементов
|
Субмикроскопическое третьего рода;
микроскопическое второго рода;
макроскопическое первого
рода
|
|
Пластическая
деформация, предшествующая разрушению
|
Хрупкое; макрохрупкое, но
микропластическое; пластическое
|
|
Структурное расположение
поверхности разрушения
|
Внутрикристаллитное;
межкристаллитное; смешанное
|
|
Степень развития разрушения
|
Начальное –
поверхность трещины значительно меньше площади сечения тела;
развитое, в том
числе полное
|
|
Влияние внешней среды
|
Вызванное
понижением поверхностной энергии
(наличие
легкоплавких покрытий); вызванное
коррозией; связанное с облучением
|
Хрупкое
и пластическое разрушение
В начале мы ввели
понятия о двух простейших типах разрушения:
1) хрупком – путем
отрыва от наибольших растягивающих нормальных напряжений σmax=R;
2) пластичном –
путем сдвига от максимальных касательных напряжений τmax=τT.
Схематически эти условия показаны на рис.22.3
с помощью прямых 1-1 и 2-2.
Свойство материала разрушаться пластически
(вязко) или хрупко не является абсолютным. Каждое тело обладает тем и другим
свойством в большей или меньшей степени в зависимости от температуры, внешнего
давления, скорости нагружения, времени нагружения и др.

Рис.
22.3
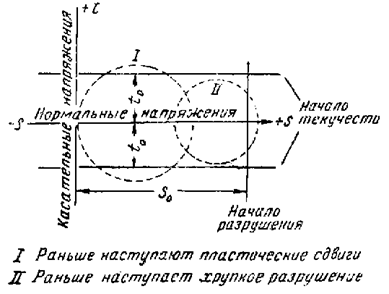
Пусть напряженное состояние в точке тела
описывается окружностью Мора 1 (рис. 22.3), которая касается вертикальной
прямой 1-1 и не пересекает прямой 2-2, в этом случае произойдет хрупкое
разрушение материала путем отрыва, и критерий разрушения запишется в виде:
σ1=R, (σ1>0). (22.1)
Сопротивление отрыву R считается постоянной величиной, не зависяшей
от вида напряженного состояния. Если окружность Мора II касается горизонтальной прямой 2-2, то
наступает текучесть материала при касательном напряжении τmax=τT, которая может привести, а может и не привести к большим
деформациям.
Изложенная простая схема разрушения носит
довольно грубый и приближённый характер в силу того, что разрушение является
смешанным. Однако представление о существовании двух видов разрушения
материалов путём сдвига и отрыва имело и имеет положительное методическое
значение для объяснения физической стороны вопроса о разрушении.
Ещё одним простейшим критерием хрупкого
разрушения материалов является критерий наибольших удлинений Сен-Венана,
согласно которому предельное состояние материала в частице тела достигается
тогда, когда максимальное растягивающее удлинение εmax=ε1 достигает
некоторого предельного постоянного значения, равного относительному удлинению ε0
при разрыве от растяжения, т.е.:
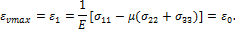
Для хрупкого материала 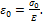 Поэтому получаем:
Поэтому получаем:

где величину σэкв
назовём эквивалентным удлинением.
Данный критерий не нашёл на практике должного
экспериментального подтверждения. Однако он в некоторых случаях даёт
качественное подтверждение характера разрушения материалов. Например, при
сжатии ряда горных пород возникают продольные трещины разрушения. При сжатии и
выпучивании цилиндрической оболочки из дюраля возникают продольные трещины от
окружного растяжения при отсутствии соответствующего растягивающего напряжения
и др.
Условия
пластичности и разрушения материалов
Условия (критерии) пластичности и разрушения
являются важными обобщениями понятий пределов текучести и прочности при
одноосном растяжении (сжатии) на случай
сложного напряжённого состояния (рис. 22.4).
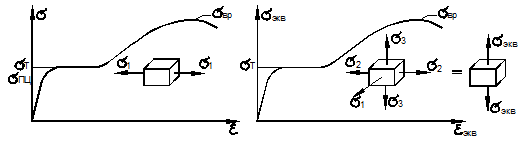
Рис.
22.4
При одноосном растяжении предельные условия
перехода в пластическое состояние и разрушение имеют соответственно вид (рис.
22.4)
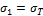 ,
, 
а условие прочности – 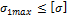
Предположим, что для любого сложного
напряжённого состояния можно найти ему равноопасное
одноосное напряжённое состояние, осуществляемое некоторым эквивалентным напряжением
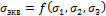
являющимся комбинацией главных
напряжений. Тогда предельные условия при сложном напряжённом состоянии
могут быть записаны в виде

а условие прочности –

Такая постановка задачи не является
безупречной, но в то же время она удобна для ведения практических расчётов на
прочность. Рассмотрим два критерия (условия) перехода тела из упругого
состояния в неупругое или пластическое.
Условие
пластичности Сен-Венана
Согласно этому критерию свойство пластичности
материала при сложном напряжённом состоянии начинает проявляться тогда, когда
максимальное касательное напряжение достигает некоторого предельного
постоянного значения k, т.е.

В случае простого растяжения предельное
условие имеет место при σ1 = σT, σ3 = 0 Поэтому
из (22.4) имеем  . Условие пластичности принимает вид
. Условие пластичности принимает вид

В случае чистого сдвига имеем σ1 = τ, σ3
= -τ, k = τT Следовательно, должно
выполняться условие:

Сравнивая (22.5) с (22.2) видим, что  . Условие прочности, согласно (22.3), запишем
в виде
. Условие прочности, согласно (22.3), запишем
в виде

Условие пластичности (22.5) Сен-Венана
достаточно хорошо подтверждается экспериментами. Его недостатком является то, что
не учитывает среднее главное напряжение σ2
Условие (критерий) пластичности
Мизеса
Согласно этому критерию материал переходит в
пластическое состояние тогда, когда октаэдрическое
касательное напряжение достигает некоторого предельного постоянного значения,
т.е.

При простом растяжении это условие
соответствует 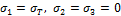 . Следовательно,
. Следовательно, 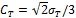 и
потому, согласно (22.2),
и
потому, согласно (22.2),
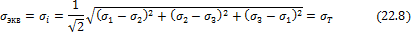
Следовательно,
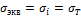
В случае чистого сдвига  Из (22.7) следует
Из (22.7) следует 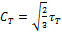 Сравнивая значения постоянных
Сравнивая значения постоянных  при
растяжении и чистом сдвиге, находим связь между пределами текучести:
при
растяжении и чистом сдвиге, находим связь между пределами текучести:
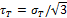
Условие пластичности Мизеса
(22.8) лучше соответствует экспериментальным данным, нежели условие
пластичности Сен-Венана (22.5). В отличие от последнего, условие пластичности Мизеса учитывает все три главных напряжения 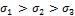 Отметим, что условие Сен-Венана и Мизеса
дают различные формулы, связывающие пределы текучести k и
Отметим, что условие Сен-Венана и Мизеса
дают различные формулы, связывающие пределы текучести k и  при
чистом плоском сдвиге и растяжении.
при
чистом плоском сдвиге и растяжении.
Теория
прочности Мора (1860г.)
Согласно этой теории нарушение прочности
происходит тогда, когда на некоторой площадке с нормалью v возникает наиболее
неблагоприятная комбинация нормального и касательного напряжений. Запишем это
условие в виде

Чтобы сформулировать условие Мора (22.9) в
терминах главных напряжений, воспользуемся кругами напряжений Мора.
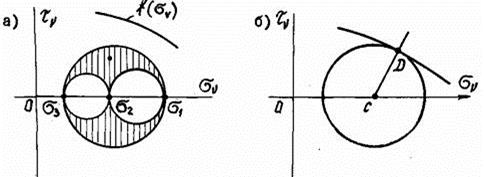
Если 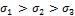 , то мы можем в одной плоскости построить три
окружности Мора (рис.22.5, а).
Условие (22.9) изображается в этой плоскости некоторой кривой.
, то мы можем в одной плоскости построить три
окружности Мора (рис.22.5, а).
Условие (22.9) изображается в этой плоскости некоторой кривой.
а)
б)
Рис.
22.5
Если окружность большого круга Мора не
касается предельной кривой, как показано на рис. 22.5, а, то разрушения не произойдет. Если круг Мора коснется предельной
кривой (рис.22.5, б), то произойдет
локальное разрушение. Следовательно, становится ясным, как построить предельную
кривую 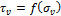 . Необходимо провести несколько испытаний до
разрушения при различных однородных напряженных состояниях, т.е. различных сотношениях
. Необходимо провести несколько испытаний до
разрушения при различных однородных напряженных состояниях, т.е. различных сотношениях  , а затем построить круги Мора. На рис. 22.6
построены три предельных круга Мора для случаев растяжения чистого сдвига и
сжатия. Огибающая этих предельных окружностей и будет предельной кривой.
Наиболее просто построить предельные окружности Мора при растяжении и сжатии
(рис. 22.7, а). Проведем к ним касательную и допустим, что эта касательная
служит предельной огибающей
, а затем построить круги Мора. На рис. 22.6
построены три предельных круга Мора для случаев растяжения чистого сдвига и
сжатия. Огибающая этих предельных окружностей и будет предельной кривой.
Наиболее просто построить предельные окружности Мора при растяжении и сжатии
(рис. 22.7, а). Проведем к ним касательную и допустим, что эта касательная
служит предельной огибающей 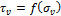 .
.
Это внесет некоторую погрешность в наши
рассуждения.
Рассмотрим теперь произвольную предельную
окружность Мора, касающуюся предельной прямой
огибающей (рис. 22.7, б). Из подобия
треугольников АОВ и CDB следует:  .
.
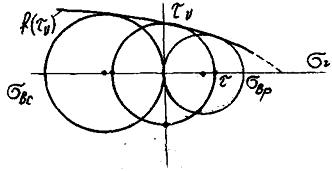
Рис.
22.6
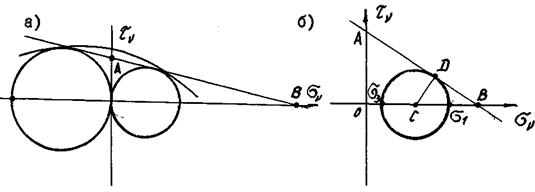
Рис.
22.7
Поскольку

то

Так как отрезки АО, ОВ, АВ - фиксированы, то получаем связь
между 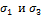 в
виде
в
виде
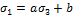
В случае растяжения в предельном состоянии 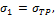
 и
потому b
и
потому b . В случае сжатия
. В случае сжатия  Следовательно,
Следовательно,  .
Таким образом, условие разрушения по Мору
.
Таким образом, условие разрушения по Мору
принимает
вид:

Условие прочности для хрупких материалов по
Мору принимает вид:

где  -
допустимое напряжение на растяжение.
-
допустимое напряжение на растяжение.
Для пластичных материалов ( ) условие (22.10)
превращается в условие прочности по Сен-Венану. Отметим, что у некоторых
пластичных материалов пределы текучести при растяжении и сжатии различны, т.е.
) условие (22.10)
превращается в условие прочности по Сен-Венану. Отметим, что у некоторых
пластичных материалов пределы текучести при растяжении и сжатии различны, т.е.  . В этом случае условие Мора (22.10)
преобразуется в условие пластичности для таких материалов:
. В этом случае условие Мора (22.10)
преобразуется в условие пластичности для таких материалов:

Недостатком теории Мора является то, что она
не учитывает среднего главного напряжения 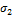 , т.е. по существу обоснована только для
плоского напряженного состояния.
, т.е. по существу обоснована только для
плоского напряженного состояния.
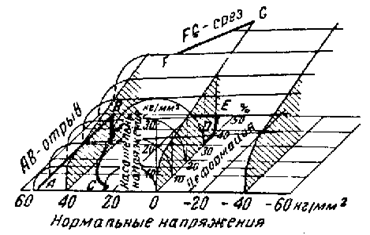
Чтобы устранить этот недостаток, Шлейхером (1926г.) было предложено считать, что предельное
состояние (разрушение) достигается тогда, когда возникает наиболее
неблагоприятная комбинация октаэдрических
касательного и нормального напряжений:
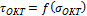
При 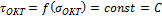 приходим к условию пластичности
Мизеса (прямая 1-1 на pис.22.8). В общем случае
предельная кривая
приходим к условию пластичности
Мизеса (прямая 1-1 на pис.22.8). В общем случае
предельная кривая 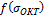 является гладкой. Прямая
2-2 соответствует хрупкому разрушению от всестороннего растяжения. Эта кривая
задается некоторым аналитическим выражением, соответствующим экспериментальным
данным.
является гладкой. Прямая
2-2 соответствует хрупкому разрушению от всестороннего растяжения. Эта кривая
задается некоторым аналитическим выражением, соответствующим экспериментальным
данным.

Рис.
22.8
В механике горных пород теория прочности Мора
нашла широкое применение.
На рис. 22.9,а изображён круг напряжений Мора радиусом  произвольного
предельного напряжённого состояния, а также круг Мора в предельном состоянии
для напряжённого состояния чистого сдвига.
произвольного
предельного напряжённого состояния, а также круг Мора в предельном состоянии
для напряжённого состояния чистого сдвига.

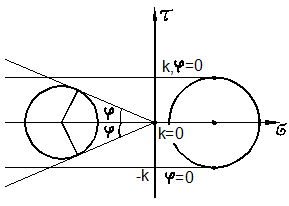
а)
б)
Рис.
22.9
Уравнение предельной прямой АВ представим в
виде
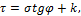
где k называют коэффициентом сцепления горных пород, величину σ – сопротивлением всестороннему
растяжению, φ - угол внутреннего
трения.
Если φ=0,
k = τT, то среду называют идеально связной (металлы, бетон,
гранит и др.). Если k =
0, то среду называют сыпучей (сухой песок). Последняя
совершенно не воспринимает растяжение (рис. 22.8,б).
Из подобия СДВ и OFB (рис. 22.9,а) находим:
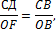
или, с учётом
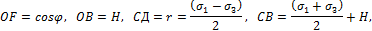

откуда

Величины
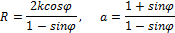
представляют собой параметры предельного
состояния горной породы. Величина R может быть названа
расчётным сопротивлением среды. Оба параметра R, a
выражены через два других параметра предельного состояния: сцепления среды k и угол внутреннего
трения φ.
Определяем главные напряжения по формуле:
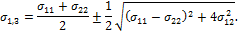
Дефекты структуры тела, способствующие
разрушению
Все основные физико-механические
характеристики материалов, такие, как сопротивление различным видам пластической
деформации и разрушению, развитие трещин, сопротивление усталости, относят к
структурно-чувствительным характеристикам. Структура материала определяет
уровень перечисленных свойств, но в разных областях нагружения
по-разному.
В области упругих деформаций, когда нагрузки
не превышают предел пропорциональности материала (область действия закона
Гука), структура материала в меньшей степени влияет на свойства металлов. В
области пластических деформаций это влияние более существенное. Условно
различают макро-, микро- и субмикроструктуру
металлов.
Макроструктура – это
то, что можно наблюдать на отшлифованных и протравленных образцах металла
невооруженным глазом или при 25-кратном увеличении. В большинстве случаев
макроструктура представляет собой направленные волокна, образующиеся после
отливки или проката металла. Поверхности изломов также могут характеризоваться
макроструктурными признаками. Даже длительное воздействие рабочих нагрузок не
оказывает заметного влияния на макроструктуру металлов. Она может видоизменяться
лишь при интенсивном силовом воздействии, заметно превышающем
характеристики устойчивости,
податливости, ударной стойкости и т. д.
Основным элементом микроструктуры металлов
является зерно (кристаллит), состоящее из блоков монокристаллов. Размеры этих
блоков колеблются от 10-5 до 10-1 см. К мелкозернистым
материалам относятся высокопрочные конструкционные стали, а наибольший размер
зерен имеют литые жаропрочные сплавы. К элементам микроструктуры, влияющим на
большинство характеристик прочности, относятся также межзеренные
границы металла.
Зерна, блоки монокристаллов, межзеренные границы большинства материалов способны
постепенно видоизменяться в процессе работы. Эти изменения можно наблюдать при
микроскопических исследованиях структуры (увеличение 100…400 крат). Например,
если металл испытывает длительное время постоянно приложенную растягивающую нагрузку
в пределах деформаций, близких к пределу пропорциональности, то можно наблюдать
постепенное увеличение размеров зерен, их ориентацию в направлении главного
вектора напряжений, а также некоторое расширение межзеренных
границ.
Длительное воздействие повторно-переменных
нагрузок в упругой области может приводить к уменьшению размеров зерен (к
увеличению плотности упаковки). Повышение температуры интенсифицирует отмеченные
процессы. В определенных условиях можно наблюдать рост новых "субзерен", проявление линий скольжения в кристаллите
(особенно типично для жаропрочных сплавов). Отмеченные процессы могут существенным
образом влиять на физико-механические характеристики. Причем, как будет
показано ниже, это влияние неоднозначно.
Наблюдать структуру моноблока можно лишь при
сравнительно больших увеличениях (500...1000 крат). Эту задачу решают с помощью
специальных металлографических или электронных микроскопов. При упомянутых
увеличениях структура монокристалла имеет вид твердого раствора (основной
металл) с вкраплением различной формы упрочняющих и разупрочняющих
компонент (фаз). Число и соотношение этих фаз в твердом растворе определяет склонность
металла к повреждению рабочими нагрузками.
Вид нагружения и
морфологические признаки элементов микроструктуры на электроннограммах
взаимосвязаны.
Число и соотношение упрочняющих и разупрочняющих фаз в работающем материале не остаются
постоянными. При расчетном уровне нагружения эти
фазы, имеющие, как правило, довольно сложный химический состав, претерпевают
изменения. Непрерывно идут процессы роста, а также коагуляции и растворения фаз
в твердом растворе, что отражается на прочностных свойствах материала
конструкций.
Особенно интенсивно фазовые трансформации
происходят в металлах при воздействии нерасчетных нагрузок.
На рис.22.10 схематически изображена
электроннограмма микроструктуры жаропрочного сплава ХН77ТЮР,
из которого изготавливают лопатки турбин ГТД, до и после воздействия повышенных
температур. Видно (рис. 22.10, б), что произошла коагуляция и частичное
растворение в основном металле интерметаллидной
упрочняющей фазы Ni3 (Al, Ti) или так называемой γ-фазы,
что существенно снизило жаропрочность сплава.
В то же время надо отметить, что фазовые
превращения в металлах могут иметь обратимый характер. Например, первоначальную
структуру (рис. 22.10, а) можно
получить последующим воздействием на поврежденный материал расчетных рабочих
температур, что восстановит сплав практически до уровня исходных свойств.
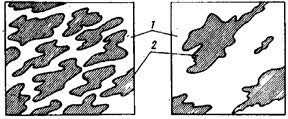
Рис. 22.10. Схематическое изображение микроструктуры (×750)
жаропрочного сплава в исходном состоянии (а) и в состоянии перегрева (б): 1 –
твердый раствор; 2 - γ-фаза
При увеличении свыше 103
крат проявляются фрагменты субмикроструктуры. Субмикроструктура отражает вид и форму кристаллических
решеток металла.
Непосредственно наблюдать
кристаллические решетки металла еще не приходилось. Это и неудивительно, ведь
кристаллическая решетка в известной мере схематична (рис. 22.11). Межузловые связи в том виде, как их отображают на рисунках, в природе отсутствуют. Линии, соединяющие
атомы, лишь символизируют наличие сил межатомного взаимодействия. С помощью
современных технических средств можно оценивать параметры кристаллических
решеток, а также степень их деформации.
Эти измерения выполняют методом просвечивающей электронной микроскопии.
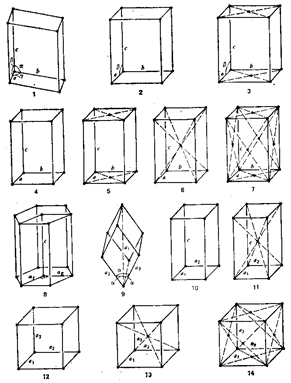
Рис. 22.11. Единичные ячейки 14 типов пространственных решеток: 1
– триклинная простая; 2 – моноклинная простая; 3 – моноклинная базоцентрированная;
4 – ромбическая простая; 5 –
ромбическая базоцентрированная; 6 – ромбическая объемноцентрированная; 7 – ромбическая гранецентрированная;
8 – гексагональная; 9 –
ромбоэдрическая; 10 – тетрагональная простая; 11 – тетрагональная объемноцентрированная;
12 – кубическая простая; 13 – кубическая
объемноцентрированная; 14 – кубическая
гранецентрированная
Существенное влияние на
повреждаемость оказывают несовершенства кристаллических решеток, называемые
дислокациями. Показано, что форма, число и плотность дислокации могут оказаться
не менее важными в механизме повреждаемости конструкций, чем макро- и
микроструктура.
Для оценки особенностей
трансформации субмикроструктур необходимо знать, что
такое "дефект кристаллической решетки". Примером дефекта решетки
является вакансия (рис. 22.12, а),
незанятое место решетки или межузельный
(внедренный) атом (рис. 22.12, б). Различают точечные, линейные,
поверхностные и объемные дефекты кристаллических решеток.

Рис.
22.12. Дефекты кристаллической решетки материала:
а – вакансия; б – межузловой
атом в кристалле
Пространственное расположение атомов
в узлах кристаллической решетки определяется следующим свойством: если О — некоторый узел решетки, то вектор OO1, связывающий О с произвольным узлом, определяется соотношением

где  - векторы трансляции, т.е. смещения, соединяющие
узел О с
ближайшими атомами по трем осям; ni – целые числа.
- векторы трансляции, т.е. смещения, соединяющие
узел О с
ближайшими атомами по трем осям; ni – целые числа.
Дислокация — это специфический
линейный дефект кристаллической решетки, нарушающий правильное чередование
атомных плоскостей (рис. 22.13). Если одна из плоскостей обрывается (рис. 22.13,
б),
то ее край образует линейный дефект, называемый краевой дислокацией. В природе
существуют также винтовые дислокации и всевозможные комбинации краевых и винтовых дислокации.

Рис. 22.13. Конфигурация атомных плоскостей:
а – идеальный кристалл;
; б – краевая дислокация
Важной характеристикой
дислокации является контур Бюргерса, косвенно
определяющий размеры и ориентировку дислокации в кристалле (рис.22.14 и
22.15). Звенья этого контура совпадают с так называемыми векторами трансляции.
Контур Бюргерса можно строить, начиная с произвольно
взятого узла последовательными шагами (от узла к узлу). Оказывается, что
контур, построенный вокруг дислокации, не замыкается. Вектор b называют невязкой, или вектором Бюргерса, который всегда постоянен вдоль линии дислокации.
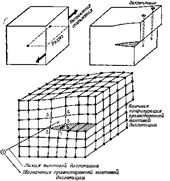
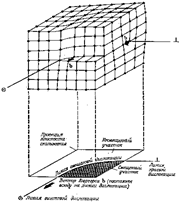
Рис. 22.14. Геометрическое представление винтовой и смешанной
дислокации
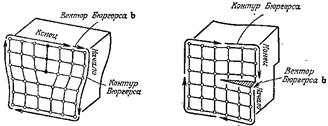
Рис. 22.15. Контуры Бюргерса для краевой
и винтовой дислокаций
Если материальное тело находится
под нагрузкой, то дислокации могут двигаться. Существует аналогия движения
дислокаций передвижению дождевого червя и змеи (рис. 22.16). Они скользят по
поверхности земли, перемещая свое тело частями, аналогично нашим представлениям
о движении дислокаций. У дождевого червя участок, с которого начинается
перемещение всего тела, находится у головы, у змеи – у хвоста, хотя оба
передвигаются в одну сторону. В обоих случаях участки, через которые прошла
волна возмущений, восстанавливают исходную форму.
Еще один пример – тяжелый ковер,
лежащий на полу, очень трудно сдвинуть, прикладывая к нему силу. Гораздо легче
образовать сначала складку и передвигать ее, пока складка не схлопнется, дойдя до другого края ковра. Окончательным
итогом в обоих случаях будет смещение всего ковра.
Скольжением дислокации
называется ее движение по атомной плоскости, параллельной вектору Бюргерса (рис. 22.17). Как правило, скольжение дислокации
всегда сопровождается пластической деформацией материала (рис. 22.18). Переползание дислокации — это перемещение краевой
дислокации по нормали к плоскости скольжения (рис. 22.19). Любое перемещение
дислокации в материале может быть сведено к скольжению или переползанию.
Этот процесс зависит от уровня действующих нагрузок и внутренней энергии
деформирования.
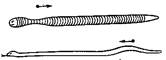
Рис. 22.16. Движение червя и змеи – аналогия перемещению дислокаций
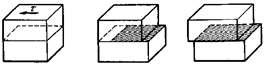
Рис.
22.17. Последовательное перемещение краевой дислокации при скольжении
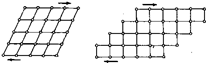
Рис. 22.18. Схематическое изображение
упругой (а) и пластической (б)
деформаций кристаллической решетки
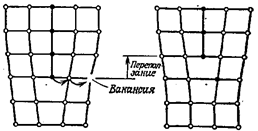
Рис. 22.19. Схематическое
изображение деформации кристалла при переползании
Важно отметить одно обстоятельство,
свидетельствующее о необязательности снижения, например, прочности материала с
увеличением числа дислокации. На рис. 22.20 изображен кристалл
с двумя краевыми дислокациями, развивающимися в противоположных
направлениях. В силу перечисленных свойств "положительная" и
"отрицательная" краевые дислокации, лежащие в одной плоскости
скольжения, могут встретиться и образовать полную атомную плоскость. При этом
обе дислокации исчезают, а прочность кристалла возрастает
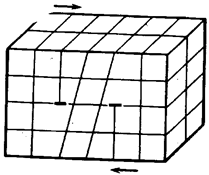
Рис. 22.20.
“Положительная” и “отрицательная”
краевые дислокации, способные к самоупорядочению
кристалла
Подвижность субмикроструктуры
обусловлена избыточностью энергии, заложенной в материал при силовом и температурном
воздействии в процессе изготовления. Освобождение этой энергии происходит под
воздействием эксплуатационного нагружения.
В процессе движения субмикроструктуры дефекты низшего
порядка притягиваются дефектами высшего порядка. Например, объемные дефекты
могут притягивать поверхностные, а они в свою очередь – линейные и точечные
дефекты.
Любой материал, какой бы технологической
обработке он ни подвергался, всегда обладает каким-либо несовершенствами:
большим количеством вакансий или межузельных атомов,
большой первоначальной плотностью дислокаций, микротрещинами, включениями,
дефектами изготовления. Каждое из этих несовершенств определенным образом
влияет на прочность детали, т.е. на развитие в ней трещины. До сороковых годов XX в. наличие дефектов в деталях машин или элементах конструкций
при расчетах на прочность не учитывалось. Считалось, что при достижении
предельного значения напряжения конструкция мгновенно разрушается, т.е. процесс
развития трещин во внимание не принимался. Однако анализ катастроф гражданских
и промышленных объектов в авиации, в морском судоходстве показал, что развитие
трещины занимает значительный период, предшествующий не только пластическому
разрушению, но и усталостному, и даже хрупкому. Во всех этих случаях разрушение
происходило без заметных остаточных деформаций. Наблюдения показали, что
развитие трещины – сложный процесс и знание его закономерностей имеет огромное
значение для практики.
Типы трещин
Большую роль в разрушении реальных материалов
имеют те или иные дефекты (неоднородность материала, поры, трещины, надрезы,
повреждения поверхности). Особая роль среди этих дефектов принадлежит
микротрещинам. При малых нагрузках эти трещины безопасны, так как не
обнаруживают тенденции к расширению. При больших нагрузках они могут оказаться
неустойчивыми, способными к быстрому росту, слиянию друг с другом и образованию
магистральных трещин, приводящих к разрушению конструкций. Есть много примеров
катастрофического разрушения газопроводов, корпусов судов, мостов, самолетов,
ракет в результате трещинообразования. Это свидетельствует о недостаточности
оценки прочности с помощью традиционных подходов по упругому или пластическому
состоянию конструкций.
Поэтому большое значение приобретает анализ
закономерностей развития трещины. Трещины начинают развиваться задолго до
полного разрушения при усталостном, пластическом и даже хрупком разрушении.
Длительность процесса разрушения, т.е. роста трещины до полного разрушения,
занимает значительную часть «жизни» детали, доходя до 90% и выше. Главное при
эксплуатации детали не наличие у нее трещины, а темп ее роста. Рассмотрим,
какие типы трещин встречаются на практике.
Раскрытие трещины в твердом теле может быть
осуществлено тремя различными путями (рис.22.21).
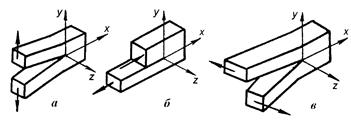
Рис.22.21
При нормальных напряжениях возникает трещина
типа «разрыв» (тип I) (рис.22.21, а), когда берега трещины перемещаются
перпендикулярно плоскости трещины. При плоском сдвиге образуется трещина типа
«сдвиг» (тип II) (рис.22.21,б): перемещения берегов трещины происходят в плоскости и
перпендикулярно ее фронтальной линии. Трещина типа «срез» (тип III) (рис.22.21, в)
образуется при антиплоском сдвиге: перемещения
берегов трещины совпадают с плоскостью трещины и параллельны ее направляющей
кромке. В общем случае трещину можно описать этими тремя типами. Чаще всего в
технике встречается трещина типа I, т.к. большая часть
элементов конструкций разрушается в случае, если берега трещины перпендикулярны
плоскости трещины.
Основные механизмы образования
трещин
Известно, что зарождение
микротрещин не может быть связано с упругим деформированием. В принципиальном
отношении существующие сегодня взгляды не претерпели изменений с того времени,
как А.В.Степанов (30-е гг.) выдвинул известное
положение об ответственности пластической деформации за возникновение
микротрещин. Однако развитие дислокационных представлений позволило
количественно их сформулировать. Суть вопроса состоит в том, что на самых ранних
стадиях пластического деформирования взаимодействие дислокаций приводит к
образованию микрощели атомного масштаба. Предложено довольно много
дислокационных механизмов и они весьма разнообразны. Идея модели слияния дислокаций основывается на представлениях о
возможности слияния головных дислокаций
в достаточно мощном скоплении, заторможенном у какого-либо прочного
барьера, например у границы зерна (рис.22.22). Расчеты, выполненные Стро, показали, что как только первые две дислокации
скопления сольются с образованием микротрещины атомного размера, она получает
возможность расти, и все остальные дислокации скопления сливаются в одну
микротрещину.

Рис. 22.22. Возникновение микротрещин
при слиянии дислокаций в вершине скопления.
Предложено большое количество
других механизмов (рис. 22.23). Все механизмы можно разделить на несколько
групп. Прежде всего это случаи, когда принудительное
слияние экстраплоскостей многих дислокаций ведет к
формированию полости. Далее следуют механизмы, связанные с заторможенным
сдвигом, при котором возникновение микротрещины обусловлено полями упругих
напряжений в голове скопления.
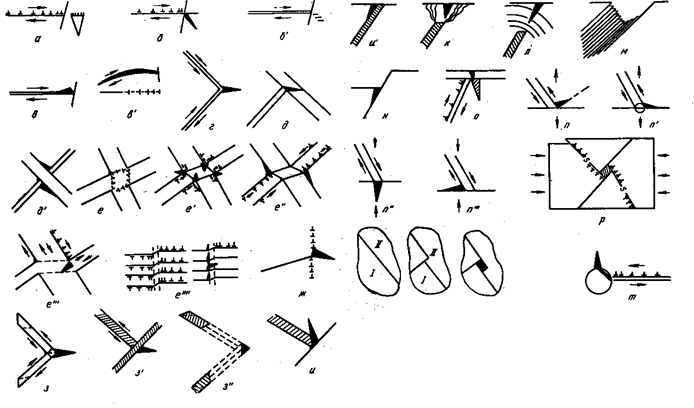
Рис. 22.23. Механизмы зарождения микротрещин: а – слияние
головных дислокаций; б – вскрытие трещины в вершине заторможенного сдвига под
действием нормальных напряжений; б’ – разрыв в плоскостях, параллельных
плоскости скольжения; в – вскрытие плоскости скольжения;
г – вскрытие искривленной плоскости скольжения; г’ – слияние дислокаций в
пересекающихся плоскостях скольжения; д, д’ – разрушение при пересечении
плоскостей скольжения; е-е’’’’ – различные варианты
возникновения микротрещин при пересечении плоскостей скольжения и образовании
сбросов; ж – разрыв дислокационной стенки; з-з’’ – варианты встречи двойников;
и – встреча двойник-граница с возникновением трещин по спайности; и’ – встреча
двойник-граница с образованием трещины по зоне аккомодации; к – двойник своими
дислокациями опережения стимулирует поверхностную микротрещину; л – двойник
вскрывает трещину на поверхности своей упругой волной; м – формирование
профиля микротрещины при локализованном скольжении; н – микротрещина в
основании ступеньки; о – полоса скольжения инициирует трещину в хрупкой пленке,
откуда она распространяется в матрицу; п-п’’’ – варианты возникновения
микротрещин на межзеренном сочленении, атакованном поллосой скольжения; р –
образование трещины на межзеренной границе, атакованной
двумя полосами скольжения; с – образование микропоры на границе за счет
проскальзывания; т – трещина возникает в хрупком неметаллическом включении и
распространяется в матрицу.
Может наблюдаться вскрытие самой
плоскости скольжения. Довольно четко объединяются схемы пересечения
двойник-двойник, полоса скольжения-полоса скольжения.
Существует вариант образования зародыша трещины при разрыве или частичном
смещении дислокационной стенки. Следует, однако, иметь в виду то
обстоятельство, что во многих случаях невозможно провести четкую грань между
различными вариантами и исключить существование еще серии механизмов, отличных от рассмотренных.
В результате движения дислокаций,
взаимодействия их с жесткими препятствиями и между собой возникают большие местные
концентрации напряжений, которые могут вызвать образование трещин размером в
несколько межатомных расстояний. Рассмотрим подробнее некоторые механизмы
образования дислокационных трещин.
Какой из механизмов можно считать
предпочтительным в случае технических поликристаллических материалов?
Эксперименты показывают, что основным можно считать механизм образования
микротрещин в карбидных частицах, действующих в ферритной матрице как мощные
концентраторы напряжений, способные создавать зародыши разрушения уже при
деформации 1%. Более 90% микротрещин возникает по этой причине.
Механизмы, микромеханизмы,
карты разрушения
Во всех случаях процессы
повреждения и разрушения определяются материалом, напряженно-деформированным
состоянием и средой. Необходимо идентифицировать микромеханизмы,
способные вызвать разрушение, и определить области температур и напряжений, в
которых эти механизмы действуют.
В макроскопических теориях
прочности различают два вида разрушения: 1) отрыв в результате действия
растягивающих напряжений и 2) срез под действием касательных напряжений.
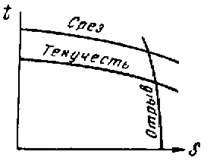
В таблице (рис. 22.24)
представлены соответствующие схемы для ряда испытаний.
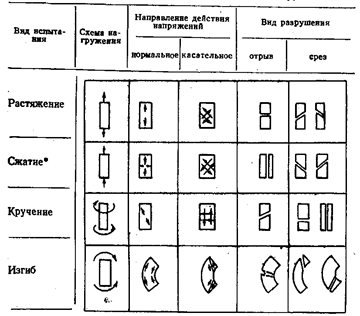
Рис. 22.24. Схемы разрушения путем отрыва и среза
при различных
механических испытаниях (по Я.Б.Фридману)
Для чистого
железа, ферритных и аустенитных сталей, тугоплавкой
керамики, а также льда можно выделить семь основных микромеханизмов
разрушения: 1) раскол (cleavage), тип 1; 2) раскол, тип 2; 3) раскол, тип 3;
4) вязкое разрушение; 5) разрушение в результате внутризеренной
ползучести (transgranular
creep fracture); 6)
разрушение в результате межзеренной ползучести (intergranular creep fracture); 7)
пластический разрыв (rupture).
При особых обстоятельствах
существуют еще два микромеханизма разрушения: динамический и диффузионный.
Важнейшей задачей является
установление доминирующего механизма при статическом или динамическом нагружении, особенно при одновременном воздействии
временных и циклических процессов, что, например, типично для суперпозиции
ползучести и усталости. Все детали и конструкции в целом содержат некоторые
геометрические дефекты, например, пустоты (поры), маркировочные знаки и т.д.
Все они вызывают концентрацию напряжений при нагружении.
В таких локальных областях
зарождаются и начинают расти микроскопические дефекты. С другой стороны,
большие трещины могут зарождаться уже в процессе обработки, например, при
сварке из-за непроваров или возникновения остаточных
напряжений. В результате, когда конструкция или деталь, содержащая такие
врожденные дефекты, подвергается нагружению,
материал в области вершины трещины испытывает значительные деформации и
трещины начинают распространяться по одному из микромеханизмов,
которые будут подробно рассмотрены ниже.
Следует отметить, что чистота
материала, вариации легирования, процесс изготовления, размер зерна, текстура
лишь незначительно влияют на границы областей разрушения, показанные на
прилагаемых картах механизмов. Конструкторы должны, помимо прочего, иметь в
виду, что при прогнозировании долговечности и поведения реальных деталей на
основе результатов лабораторных испытаний особое внимание следует удалять
информации о режимах, так как, например, при высоких напряжениях и температурах
активны одни механизмы, а при низких –
другие. Также необходимо учитывать возможность независимого накопления
двух видов повреждений в случае суперпозиции процессов, зависящих от времени и
циклического нагружения.
Механизмы
разрушения. Разрушение (Separation) материала происходит в результате зарождения
и роста (или увеличения числа) дефектов типа дислокации, пор и трещин. Эти
дефекты могут приводить к хрупкому или вязкому разрушению, усталости,
разрушению в процессе ползучести, причем в одних случаях разрушение носит межзеренный, а в других – внутризеренный
характер. Поэтому весьма важно уметь выделить доминирующий механизм.
На рис. 22.25
показан широкий спектр механизмов разрушения при низких и высоких температурах
– от чисто хрупкого до чисто пластического.
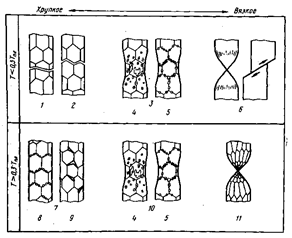
Рис. 22.25.
Классификационная схема механизмов разрушения:
1 - раскол; 2 - хрупкое межзеренное разрушение; 3
- вязкий рост пор; 4 -внутризеренный рост пор; 5 - межзеренный рост пор;
6 - разрыв в
результате пластического сужения или среза; 7 - межзеренная
ползучесть; 8 - порообразование;
9 -
клиновидные трещины; 10 - рост пор но механизму степенной ползучести;
11 -разрыв в результате сужения при
динамическом возврате или рекристаллизации.
В области
низких температур (Т < 0,25Тпл)
пластическое течение больше зависит от напряжения, чем от времени. При высоких
температурах на деформацию в основном влияют температура и время, доминируют
процессы ползучести.
Хрупкое поведение. Хрупкое разрушение может происходить либо по
телу зерна (раскол), либо по границам зерен. В этих случаях разрушающее
напряжение ниже предела текучести материала.
По мере повышения температуры и
снижения напряжения течения возникает пластическая деформация, но разрушение
может быть связано только с микропластическими явлениями – образованием пор
или клиновидных трещин, которые затем распространяются по границам зерен. Эти
процессы требуют для своего развития значительного времени, и поэтому такой
тип хрупкого поведения рассматривается как межзеренное
разрушение при ползучести.
Пластическое поведение. При низких температурах могут быть оперативны
несколько систем скольжения, что особенно характерно для металлов с г-ц.к.-решеткой – Ag, Au, Pt,
Al, Cu, Pb.
В этом случае раскол становится невозможным и
разрушение происходит за счет разрыва в результате сужения поперечного сечения
до нуля при образовании шейки (сужение до точки, necking) или сдвига (сужение до лезвия, shearing off). При высоких температурах могут
иметь место динамический возврат или рекристаллизация, которые приводят к
накоплению деформаций и окончательному разрушению в результате уменьшения
сечения, несущего нагрузку.
Переходная зона. Между двумя описанными крайними случаями хрупкого
и вязкого разрушения возможны различные случаи ограниченного пластического
течения, которое вызывает рост внутризеренных или межзеренных пор.
Микромеханизмы. На
представленных ниже картах показаны области, в которых доминирует тот или иной
микромеханизм. По осям этих карт откладывается
нормализованная (по Тпл
температура и нормализованные (по модулю нормальной упругости
Е, соответствующему
температуре) напряжения.
За верхнюю границу напряжения
принимается идеальная (теоретическая) прочность материала, примерно равная 0.1Е.
Рассматриваемые далее границы
действия механизмов являются довольно
условными, так как во многих случаях
одновременное действие нескольких механизмов приводит к разрушению по
смешанному типу.
Типы микромеханизмов
Раскол (тип 1). При
достаточно низкой температуре пластическое
течение снижается до минимума и разрушение
происходит в результате быстрого
развития врожденного (inherent)
дефекта размером 2а. Разрушающее
напряжение при этом

где Gс – вязкость
разрушения, 2а – размер
дефекта или наиболее длинной трещины.
Раскол (тип 2). Если ни один из дефектов не достигает критического
размера, то в результате микропластической деформации (скольжения или двойникования) могут образоваться мелкие трещины, и
разрушающее напряжение будет равно

где d – размер зерна. Отметим,
что здесь σf > σy (σy –
напряжение микротечения) и
деформация при разрушении εf
< 1%.
Раскол (тип 3). С
повышением температуры и снижением
напряжения текучести могут развиваться значительные пластическое деформации (до 1—10%), прежде чем произойдет
внезапное катастрофическое разрушение в результате раскола. Пластическая деформация в этом случае вызывает возрастание Gс, а следовательно и σf
, в результате чего трещина притупляется, что может привести к стабильному
росту трещины без катастрофического внезапного разрушения.
Весьма незначительные изменения
текстуры, содержания примесей и температуры могут способствовать развитию либо
внутри-, либо межзеренного
разрушения; в дальнейшем будем называть первый случай расколом (типы 1, 2, 3),
а второй – хрупким межзеренным
разрушением (BIF, Brittle intergranular fracture, 1, 2,
3).
Вязкое разрушение. Вязкое разрушение начинается с зарождения и
быстрого роста внутризеренных пор. Отсюда следует,
что оно определяется размером дефектов (поры, включения) и расстоянием между
ними. Их росту способствует концентрация напряжений; наблюдающееся при этом
слияние пор в области локального сужения ведет к разрушению.
Вязкое разрушение обычно идет по
телу зерна, но если включения выделяются преимущественно по границам зерен,
становится возможным волокнистое вязкое межзеренное
разрушение.
Твердые включения в мягкой
матрице вызывают искажения локальных полей напряжений, и создающиеся
концентрации напряжений могут привести к разрушению включения или к его
отделению (отрыву) от матрицы. Возникшая таким способом пора первоначально
удлиняется со скоростью примерно в 2 раза превышающей скорость удлинения образца,
но эта скорость постепенно уменьшается по мере того, как пора принимает
эллипсоидальную форму. Окончательное разрушение происходит, когда высота
эллипсоида 2h приближается к величине
расстояния между порами 2l в
результате локального сужения пластичной матрицы между порами. Исходя из этих
предпосылок, можно показать, что деформация при разрушении пластичного
материала равна

где fn – объемная доля
пор, α –
постоянная материала, близкая к 1, С –
разность скоростей деформации поры и матрицы.
Внутризеренное разрушение при ползучести. Если Т > 0,3Tпл, металл деформируется посредством ползучести,
развитие которой зависит от времени; напряжение течения зависит при этом от
деформации. Простейшее выражение для скорости деформации имеет вид 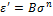 (степенная
ползучесть, power low creep), где В
и п — материальные постоянные; поры
зарождаются в этом случае внутри зерен. Однако вследствие того, что
пластическое течение при температурах Т > 0,3Тпл зависит от времени, оно может происходить при
весьма низких напряжениях, и процесс зарождения пор оказывается длительным.
Более того, может замедляться также и процесс слияния пор. В итоге разрушение
оказывается зависящим от времени.
(степенная
ползучесть, power low creep), где В
и п — материальные постоянные; поры
зарождаются в этом случае внутри зерен. Однако вследствие того, что
пластическое течение при температурах Т > 0,3Тпл зависит от времени, оно может происходить при
весьма низких напряжениях, и процесс зарождения пор оказывается длительным.
Более того, может замедляться также и процесс слияния пор. В итоге разрушение
оказывается зависящим от времени.
Межзеренное разрушение при ползучести. В условиях долговременного действия
низкого напряжения и, соответственно, при больших долговечностях может
развиваться межзеренное разрушение. В такой ситуации
проскальзывание по границам способствует зарождению пор и клиновидных трещин,
нормальных к направлению действия растягивающего напряжения. Поведение
материала в таком режиме с хорошим приближением может быть описано уравнением 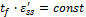 , где tf – долговечность (время до разрушения),
, где tf – долговечность (время до разрушения), 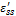 – скорость установившейся ползучести. В
основе этого соотношения лежит предположение о том, что разрушение происходит в
результате степенной ползучести, которая контролирует зернограничное
скольжение и, следовательно,
зарождение пор, которое при этом занимает основную долю жизни металла. Если же
основную долю жизни занимает процесс роста пор, то это контролируется
диффузионными процессами, которые в свою очередь определяются степенной
ползучестью окружающей матрицы.
– скорость установившейся ползучести. В
основе этого соотношения лежит предположение о том, что разрушение происходит в
результате степенной ползучести, которая контролирует зернограничное
скольжение и, следовательно,
зарождение пор, которое при этом занимает основную долю жизни металла. Если же
основную долю жизни занимает процесс роста пор, то это контролируется
диффузионными процессами, которые в свою очередь определяются степенной
ползучестью окружающей матрицы.
Разрыв. Если все другие моды разрушения исключены, возможно значительное пластическое сужение площади
поперечного сечения. Зарождение и слияние пор может оказаться подавленным
динамическим возвратом и рекристаллизацией. Деформация локализуется в шейке
или в полосах сдвига и продолжается до тех пор, пока площадь поперечного сечения
не приблизится к нулю.
Динамическое разрушение. Это –
мгновенное разрушение в результате быстрого приложения нагрузки, вызывающего
образование в материале упругих и пластических волн.
Чисто диффузионное разрушение. Это – предельный случай разрушения при межзеренной
ползучести, имеющий место при низких напряжениях и высоких температурах, когда
становится возможным долговременная диффузия дислокации. Этот случай
разрушения возможен лишь в определенных случаях.
Карты разрушения.
На рис. 22.26 и 22.27
представлены примеры карт механизмов разрушения для разных материалов.
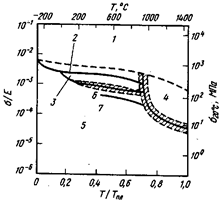
Рис.
22.26. Карта
механизмов разрушения никеля технической чистоты (г.ц.к.-решетка): 1 -
динамическое разрушение; 2 - вязкое внутризеренное разрушение;
3 - внутризеренная
ползучесть; 4 - разрыв (при
динамической рекристаллизации); 5 -разрушение в результате внутризеренной ползучести; б - клиновидные трещины; 7- поры
Области разрушения,
характеризуемые разными микромеханизмами,
определяются обычно путем фрактографических
исследований, но в некоторых случаях они могут быть найдены по резкому
изменению εf и tf.
Карты справедливы лишь для уровней напряжений, соответствующих скорости
деформации ~106 с-1,
т.е. для долговечностей порядка 10-6 с, так
как при более жестких условиях характерно разрушение
за счет динамической деформации, при которой через металл распространяются
упругие и пластические волны. Это не следует смешивать с быстрым разрушением
при низких напряжениях материалов, имеющих врожденные острые и крупные
дефекты.
Металлы г.ц,к.
Карта (рис. 22.26), построенная на основе испытаний на растяжение никеля
технической чистоты, является типичной для многих г.ц-к.-сплавов
и металлов.
На карте выделено четыре области
механизмов разрушения. При высоких
напряжениях и низких температурах разрушение носит вязкий характер. Повышение
температуры приводит к ползучести и
уменьшению разрушающего напряжения.
Быстрое разрушение происходит за счет внутризеренной
ползучести аналогично вязкому
разрушению, при этом мода пластической деформации
изменяется от скольжения до
степенной ползучести. Однако само разрушение происходит в результате роста и объединения пор. При
более низких напряжениях и,
следовательно, больших долговечностях
доминируют процессы межзеренной ползучести, причем
можно выделить две подобласти, в одной из
которых основной причиной разрушения является зарождение клиновидных трещин, а в другой –
преимущественное образование пор по границам зерен. Для обеих форм межзеренной ползучести характерна низкая пластичность и
разрушение после весьма малых деформаций. Зона перехода от внутризеренного разрушения к межзеренному на диаграмме заштрихована; здесь можно наблюдать разрушение
смешанного типа.
При дальнейшем повышении
температуры ползучести сопутствует динамическая рекристаллизация, и разрушение
происходит с образованием шейки или при сужении сдвигом до лезвия (chisel edge).
Легирование влияет на механизмы,
а значит и на области их действия.
Стабильные дисперсные выделения подавляют рекристаллизацию и тем самым сдерживают
разрушение, в то время как некоторые весьма чистые металлы могут разрушаться по
механизму разрыва при комнатной
температуре. При одновременном наличии
дисперсных выделений и твердого раствора
прочность возрастает и имеется тенденция к расширению зоны
разрушения по механизму межзеренной ползучести на области, в других ситуациях
свойственные иным механизмам
разрушения.
Металлы о. ц. к.
На рис. 22.27 представлены детализированные характеристики разрушения
вольфрама технической чистоты, который является типичным представителем о.ц.к.-металлов.
При наличии в образце внутренних
дефектов происходит низкотемпературный раскол типа 1 без пластической
деформации. Однако обычно трещины зарождаются в результате двойниковаиия
или скольжения; в дальнейшем они распространяются по механизму либо внутризереиного раскола типа 2, либо BIF2. Уже небольшое
повышение температуры делает возможным некоторое пластическое течение, так как предел текучести снижается при
этом быстро, однако разрушение происходит расколом по типу 3, несмотря на
повышение вязкости разрушения, о котором свидетельствует возрастание
пластичности при разрушении е у примерно да 10%. При Т > 0,3Тпл
наблюдается вязкое разрушение при повышенных напряжениях. И здесь снова
небольшое снижение напряжения делает доминирующим процесс ползучести, хотя
характер разрушения остается вязким.
При низких напряжениях
характерна межзеренная ползучесть. В области 0,5Тпл и 𝜎/Е = 10-4 типичны клиновидные трещины, а при более низких
напряжениях и одновременно высоких температурах разрушение связано с развитием
пор; в области температур, близких к точке плавления, и относительно высоких
напряжениях происходит разрушение разрывом.
Таким образом, как видно, процесс
разрушения является чрезвычайно сложным, многоступенчатым, зависящим от
условий, и это все проявляется как на субмикроскопическом и микроскопическом
уровнях (физика, материаловедение, металлургия), так и на макроуровне (механика
разрушения, конструкционная прочность). Механика разрушения преимущественно
рассматривает феноменологические модели на макроуровне и поэтому не оперирует
столь большим разнообразием физических механизмов и видов разрушения, а в
качестве основных рассматривает хрупкое, квазихрупкое,
упругопластическое и усталостное разрушения.
Классические схемы хрупкого, квазихрупкого, вязкого разрушения
Граница между различными видами
разрушения до сих пор размыта и не является четко очерченной. До сих пор нет
общепринятого определения хрупкого разрушения. Вот некоторые из них.
1. Разрушение является хрупким,
если для его протекания и завершения достаточно упругой энергии разрушаемой
конструкции.
2. Хрупким является разрушение,
при котором нестабильный рост трещины происходит при напряжениях, меньших
предела текучести.
3. Хрупким является разрушение
без заметных пластических деформаций.
4. Разрушение хрупкое, если
достаточно велика доля хрупкого составляющего в изломе
5. Качественное различие между
разрушениями связано со скоростью распространения трещины. При хрупком
разрушении эта скорость очень велика – достигает 0,4…0,5 скорости
распространения звука в материале образца. В случае же вязкого разрушения
трещина распространяется с относительно малой скоростью, соизмеримой со
скоростью деформации образца.
В зависимости от условий
состояние материала и характер разрушения меняется. Известны несколько
классических схем, связывающих характер разрушения с внешними условиями,
показывающих условия перехода материалов из
пластического в хрупкое состояние.
Схема П.Людвика
(1909 г.). Схема (рис.22.28) построена в координатах напряжение –
деформация, но в качестве фактора, влияющего на сопротивление пластической
деформации и на пластичность, принята скорость деформации.
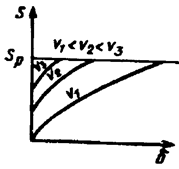
Рис. 22.28. Схема П.Людвика
Схема А.Ф.Иоффе
(1924 г.). Состояния материала были представлены Иоффе в виде удобной
схемы (рис. 22.29), носящей его имя.

Рис. 22.29. Схема А.Ф.Иоффе,
σт
– предел текучести; σот – сопротивление отрыву
Здесь кривая σт есть
изменение начального предела текучести в зависимости от абсолютной температуры.
Прямой σот
изображено сопротивление отрыву стали при низких
температурах при отсутствии общей пластической деформации. Рассмотрение причин
возникновения трещин показывает, что для достижения приложенным напряжением
величины сопротивления отрыву σот даже при отсутствии
общей пластической деформации необходима небольшая величина местной
пластической деформации. Эти две кривые (σт
и σот)
пересекаются при температуре хрупкого перехода ТR(1).
Ниже ТR(1) напряжение в образце
станет равным сопротивлению отрыву до достижения напряжения общей текучести и
поэтому произойдет хрупкое разрушение. Выше температуры ТR(1)
сначала будет достигнут предел текучести и поэтому
произойдет большая или меньшая пластическая деформация. Увеличение скорости
деформации, большая степень трехосности напряженного
состояния приводят к повышению предела текучести, в результате чего кривая σт смещается в
положение кривой σт’. Пересечение кривых σот и σт’ происходит при более
высокой температуре ТR(2), т.е.
температура изменения вида разрушения увеличивается от ТR(1)
до ТR(2). С другой стороны, предварительная пластическая
деформация при умеренных температурах увеличивает работу разрушения и,
следовательно, сопротивление отрыву от σот
до σот’,
уменьшая тем самым температуру хрупкого перехода при обычных изменениях σт.
Схема построена на основании
опытов, проводившихся на каменной соли, и относится либо к однородному
напряженному состоянию, либо к элементу объема. Такие важнейшие факторы, как
вид напряженного состояния и существование у одного и того же материала двух
физически различных сопротивлений разрушению, в этой схеме вовсе не отражены.
Хотя схема Иоффе построена в координатах напряжение – температура испытания, а
схема Людвика в координатах напряжение – деформация
(при различных скоростях деформации), по сути дела в обоих
схемах выражена одна и та же идея – материал имеет практически не изменяющееся
(от температуры в схеме Иоффе или от скорости в схеме Людвика)
сопротивление разрушению (отрыву) и сильно изменяющееся от тех же факторов
сопротивление пластической деформации, которое
характеризуется в схеме Иоффе пределом текучести, а в схеме Людвика
– текущими ординатами кривой деформации).
Схема А.Ф.Иоффе
сыграла важную роль в понимании механических свойств, в особенности при
изучении хладноломкости металлов в работах Н.Н.Давиденкова
и его школы. Применение и развитие этой схемы для металлов принадлежит Н.Н.Давиденкову. Он отмечал, что одни металлы являются
хладноломкими, т.е. разрушаются хрупко при понижении температуры, а другие нет.
Потеря пластичности и переход в хрупкое состояние при определенной критической
температуре (или в интервале температур) свойственны не всем металлам. С одной
стороны, малоуглеродистые стали, цинк, кадмий, магний, подвержены
хладноломкости, с другой стороны, медь, алюминий, никель, свинец, аустенитные стали даже при испытании на ударный изгиб с
надрезом при низких температурах не теряют своей пластичности. Можно предположить, что различное поведение зависит от типа
кристаллической решетки и что решетки объемноцентрированного
куба и гексагональная склонны к хладноломкости, а решетка гранецентрированного
куба ее не обнаруживает. Для металлов с решеткой объемноцентрированного
куба и гексагональной повышение диаграммы сжатия, главным образом, вызывается
одним охлаждением и проявляется в повышении предела текучести, тогда как для
металлов с решеткой гранецентрированного куба следствием понижения температуры
является повышение коэффициента упрочнения. При этом повышение предела
текучести у первых металлов при растяжении может привести к хрупкому
разрушению, если только предел текучести поднимется выше сопротивления отрыву
(по схеме А.Ф.Иоффе). Напротив, для второй группы
металлов сопротивление отрыву при наличии растягивающих напряжений могло бы
быть достигнуто (впрочем, никогда не достигается) только после определенной
степени пластической деформации, поэтому совершенно хрупкое разрушение
невозможно.
Схема Н.Н.Давиденкова
(1936 г.) (рис.22.30). Основываясь на
результатах исследования монокристаллов α-железа,
которые в зависимости от температуры и других условий опыта могут разрушаться
пластически, по плоскостям, проходящим через диагональ куба, и хрупко по граням
куба, было предложено учитывать не только два вида разрушения, но и два
сопротивления разрушению, названные Давиденковым
вязким и хрупким отрывом.
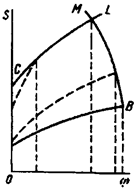
Рис.22.30.
Схема Н.Н.Давиденкова.
Кривая CL – сопротивление хрупкому
разрушению,
MB – сопротивление вязкому разрушению.
Введенные Давиденковым
в схему механического состояния две различные ветви разрушения положили начало
разграничению между характеристиками разрушения – сопротивлением отрыву и
сопротивлением срезу. В дальнейшем выяснилось, что каждая из
этих характеристик связана с различными по характеру напряжениями:
сопротивление отрыву с растягивающими, сопротивление срезу с касательными.
На схеме наносится семейство истинных кривых деформирования для различных
напряженных состояний. Концевые точки кривых (соответствующие разрушению)
располагаются на ветви CL – хрупких разрушений и ветви MB – вязких разрушений.
Схема перехода из вязкого в хрупкое состояние
(рис. 22.31), предложенная Е.М.Шевандиным (1953 г.), состоит из кривых истинных
напряжений s=f(ψ),
полученных при температуре испытания от +20 до –196°С для сталей, склонных к хрупкому разрушению. Схема похожа
на схему Н.Н.Давиденкова, однако кривая, огибающая
конечные точки кривых истинных напряжений, состоит не из двух ветвей, как у Давиденкова, а из трех. Ветвь DC определяет область вязких
разрушений с изломами волокнистого строения, ветвь CB – область полухрупких смешанных разрушений с изломами частично
кристаллического строения, ветвь BA – хрупкие разрушения с изломами
кристаллического строения.
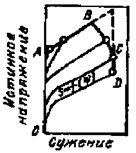
Рис.
22.31. Схема Е.М.Шевандина
Во всех этих схемах не отражено влияние
одного из наиболее важных (если не самого важного) факторов: напряженного
состояния, которое оказывает огромное влияние на механические свойства.
Различными авторами был предложен ряд схем
(рис. 22.32-22.37), в которых в отличие от описанных схем учтено также и
напряженное состояние, причем в большинстве этих схем принято, что разрушение путем
отрыва описывается I, а путем среза – III теорией прочности.
В качестве основы для расчетов прочности при
сложном напряженном состоянии предлагались различные принципы, обычно
называемые теориями прочности. Неоднократно делавшиеся попытки применить ко
всем материалам при различных напряженных состояниях какую-либо одну теорию
неизменно кончались неудачей, т.к. I теория оказывалась неудовлетворительной
для пластичных материалов, а III – для хрупких. Поэтому было предложено
разграничить выбор теорий прочности в зависимости от свойств материалов, а
именно: для хрупких материалов (чугун, бетон и т.п.) применять I и II, а для
пластичных (большинство металлов) – III и
IV теории.
Однако в настоящее время можно
считать установленным, что хрупкость и пластичность – состояния, в которые при
определенных условиях может быть переведено большинство материалов (например,
чугун может быть пластически деформирован при сжатии, а многие стали из пластичных становятся хрупкими при переходе от кручения к
растяжению). Отсюда, естественно, вытекает, что для одного и того же материала,
в зависимости от того, находится ли он в хрупком или в пластическом состоянии,
должны применяться разные теории прочности. Поэтому можно говорить о синтезе
теорий прочности, которые отражают различные виды нарушения прочности.
В качестве приближенного
графического отображения такого синтеза Я.Б.Фридманом
было предложено построение диаграммы механического состояния (рис. 22.38), оценивающей
поведение материала при однократных кратковременных
статических нагружениях.
Диаграмма механического состояния Фридмана.
Диаграмма учитывает (рис. 22.38)
1. Напряженное состояние,
приближенно характеризуемым отношением α=tmax/Snmax;
а) если tmax >> Snmax, т.е. касательные напряжения
создаются при очень малых удлинениях, то способ нагружения
является мягким (например, испытание на твердость при вдавливании, осевое
сжатие под гидростатическим давлением и т.п.);
б) если tmax << Snmax, т.е. создаются значительные
упругие удлинения при малых касательных напряжениях, то способ нагружения является жестким (например, трехосное
растяжение, возникающее во внутренних слоях растягиваемого надрезанного
образца, в меньшей мере изгиб и растяжение);
в) наконец, если tmax ≈
Snmax, то способ нагружения является средним по своей жесткости (например,
кручение цилиндрического стержня, при котором при μ=0.25tmax/Snmax
= 0.8).
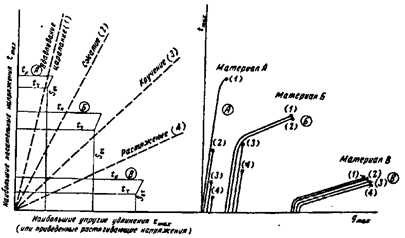
Рис.
22.38. Диаграмма механического состояния Я.Б.Фридмана
Величина α
не может исчерпывающе характеризовать вид нагружения.
Назначение этой величины в том, чтобы дать сравнительную оценку опасностей двух
видов нарушения прочности: от касательных напряжений (текучесть или срез) и от
растягивающих (отрыв). При этом предполагается, что эти нарушения прочности
определяются величинами tmax
и Smax.
2. Отношение сопротивления
отрыву Sот к сопротивлению срезу tк:
а) если Sот
<< tк, то материал при многих способах нагружения будет склонен к разрушению путем отрыва, как
правило, хрупкому (стекла, горные породы, чугуны, твердые сплавы, пластмассы);
такие материалы обычно значительно менее прочны при растяжении, чем при сжатии;
б) если Sот
>> tк, то материал при многих способах нагружения будет склонен к разрушению путем среза, как
правило, пластичному (алюминий, медь, свинец, многие железные сплавы);
в) если Sот
≈ tк,, то
материал при близких нормальных и касательных напряжениях будет примерно в
равной степени склонен к обоим видам разрушения.
3. Разное для разных способов нагружения положение сопротивления отрыву по отношению к
обобщенной кривой.
Диаграмма механического
состояния составляется из двух расположенных рядом частей. По оси ординат обеих
частей диаграммы отложены максимальные
касательные напряжения tmax.
По оси абсцисс отложены в левой части максимальные
приведенные растягивающие напряжения Snmax,
в правой – максимальные пластические сдвиги gmax. Левая
часть диаграммы характеризует условно жесткость или мягкость способа нагружения, в то время как правая часть диаграммы
представляет собой просто обобщенную кривую течения.
Какой-либо способ нагружения (в данной точке тела) изображен в левой части
диаграммы лучом, имеющим определенный угол наклона. Кроме того, в левой части
нанесены прямыми линиями: предел текучести tт,
сопротивление срезу tк,
выраженные в касательных напряжениях, и сопротивление отрыву Snот, - в приведенных напряжениях.
Если условия нагружения
таковы, что равенство tmax
= tк будет осуществлено раньше, чем Snmax = Snот, то произойдет разрушение путем
среза. В этом случае по мере повышения касательного напряжения от tmax
= tт (переход в пластическую
область) до tmax
= tк
(срез) будет полностью “использована” обобщенная кривая течения данного
материала. Если же еще до того, как будет достигнуто условие tmax
= tк, осуществится условие Snmax ≥
Snот, то материал разрушится
путем отрыва и кривая tmax=f(gmax) “преждевременно”
оборвется; пластичность gmax
и вязкость (пропорциональная площади кривой) окажутся пониженными, причем
степень этой “преждевременности” будет тем большей, чем больше Snmax/ tmax.
Конечно, если материал столь
хрупок, что tт = tк, то никаким
изменением способа нагружения (при данной скорости и
температуре деформации) его нельзя перевести в пластичное состояние и кривая tmax=f(gmax) у него
отсутствует.
Таким образом, на диаграмме
механического состояния прямые tт, tк и Sот ограничивают две замкнутые области (рис. 22.39):
а) упругую область, ограниченную
линиями tт (переход в пластическую область), и Sот (переход к хрупкому отрыву без пересечения
пластической области, т.е. при t <
tт).Нижняя часть вертикальной линии Sот
ограничивает хрупкое состояние, т.е. отрыв без предшествующей пластической
деформации;
б) пластическую область,
ограниченную линиями tк (разрушение путем среза) и Sот (не вполне хрупкое разрушение путем отрыва).
В последнем случае отрыв происходит уже после более или менее значительной
пластической деформации, которая оказывает сильное влияние на величину
сопротивления отрыву.

Рис.
22.39. Схема, показывающая области упругой
и пластической деформации на диаграмме механического
состояния
Широко известны температурные
зависимости механических свойств и характера разрушения (рис. 22.40).

Рис. 22.40. Зависимость механических свойств
от температуры
С понижением температур
большинство малоуглеродистых и низколегированных сталей изменяет свои
механические свойства. Точка пересечения кривых предела текучести и
сопротивления отрыву определяет критическую температуру хрупкости согласно
схеме Иоффе. С понижением температуры предел текучести и временное
сопротивление повышается, а пластичность ψ падает.
По температурным зависимостям характеристик
разрушения образца с трещиной можно выделить две критические температуры:
первую, при 50% вязкого составляющего в изломе, и вторую, характеризующуюся
точкой пересечения разрушающего напряжения и предела текучести. Принято
считать, что при температурах выше первой критической возникают вязкие
разрушения, при температурах ниже второй критической – хрупкие, в промежутке
между критическими температурами – квазихрупкие
разрушения.
Сингулярные
задачи теории упругости для тел с трещинами
Основным модельным
представлением в механике разрушения является пластина с нарушением сплошности, представляющим собой разрез (трещину) и
являющимся концентратором напряжений. Рассмотрение трещин в хрупких телах можно
рассматривать как предельный случай концентрации напряжений. Исторически первым
является решение задачи о концентрации напряжений возле кругового отверстия (Г.Кирш, 1898 г.). В современной интерпретации с
использованием функций напряжений Эри задача выглядит следующим образом.
Рассматривается бесконечная пластина с круглым отверстием радиусом а, находящаяся под воздействием
одноосного напряжения σ. Для плоского
напряженного состояния в полярных координатах зависимости компонентов
напряжений при θ=π/2
или θ=3π/2 имеют вид (рис. 22.41)

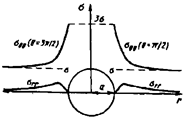
Рис. 22.41. Распределение напряжений у
круглого отверстия
в
бесконечной пластине
Дальнейшим развитием является
анализ напряжений вокруг овального отверстия в пластине в случае растяжения,
чистого изгиба, чистого сдвига (Г.В.Колосов, 1910 г.,
К.Инглис, 1913 г.), в соответствии с которым в
вершине отверстия возникает напряжение (рис. 22.42)

где ρ
- радиус кривизны в вершине отверстия.
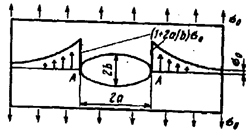
Рис. 22.42.
Графическая иллюстрация результатов Колосова и Инглиса
В дальнейшем был поставлен и
решен целый класс сингулярных краевых задач теории упругости, т.е. граничных
задач с особыми точками. Такими точками являются, например, бесконечно удаленная
точка, точка разрыва граничных условий точка приложения сосредоточенной силы и
т.д. При этом в линейных задачах решение (или его производные, начиная с
некоторого порядка) стремится к бесконечности при приближении к особой точке.
Поскольку граничная задача в особой точке не определена, встает вопрос о
формулировке физически осмысленного дополнительного условия в такой точке, т.е.
о постановке корректной сингулярной краевой задачи.
Наиболее успешно для решения
сингулярных задач используются мощные методы, развитые Г.В.Колосовым
и Н.И.Мусхелишвили для общего случая плоской задачи
теории упругости.
Допустим, что поле упругих
смещений и деформаций не зависит от одной из прямоугольных декартовых координат
x, y, z, например, от z. В этом весьма общем и
важном случае все смещения и напряжения можно представить через функции Ф(z), ψ (z) и f(z), являющиеся аналитическими
функциями комплексного переменного z=x+iy в области, занятой телом. Первые две из них часто
называют потенциалом Колосова-Мусхелишвили. Выражения для комплексного
представления смещений и напряжений имеют следующий вид


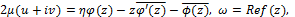
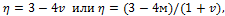
где μ
- модуль сдвига; v - коэффициент Пуассона.
Для механики разрушения большой
интерес представляет изучение асимптотического распределения напряжений,
деформаций и смещений вблизи фронта трещины. Рассмотрим малую окрестность
произвольно фиксированной точки на гладком контуре трещины (рис. 22.43).
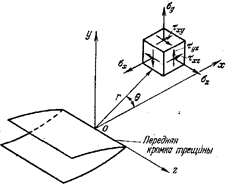
Рис. 22.43. Система координат и компоненты
напряжений у кончика трещины
Общее корректное решение зависит
от трех действительных параметров, которые участвуют в решении на основе
потенциалов Колосова-Мусхелишвили в качестве множителей при различных членах
асимптотики и которые определяются из
решения задачи. Каждый из указанных трех членов асимптотического разложения соответствует
одному из трех основных типов трещин (рис. 22.44).
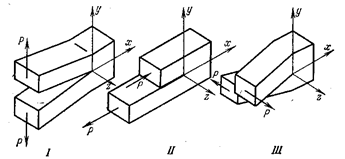
Рис. 22.44. Основные виды смещений
поверхности трещины
Окончательное решение дает распределение
напряжений и смещений вблизи края произвольной хрупкой трещины для указанных
основных типов разрывов:
– нормальный разрыв


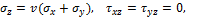


– поперечный сдвиг
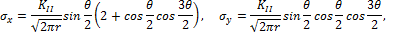

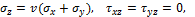
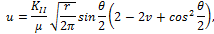

– продольный сдвиг

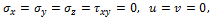

Эти формулы были получены для
случая плоской деформации; в случае плоского напряженного состояния нужно взять
в них σz=0 и
заменить v на v/(1+v). Формулы справедливы в
малой окрестности края трещины, т.е. r
должно быть малым по сравнению с характерным линейным размером тела, например,
длиной трещины или расстоянием ее конца от свободной границы.
Трем типам разрывов в теории дислокаций
соответствуют клиновые, краевые и винтовые дислокации. Для трещин произвольного
типа все величины KI, KII,
KIII отличны от нуля. Эти величины называются коэффициентами
интенсивности напряжений и имеют размерность силы, деленной на длину в степени
три вторых.
Теоретическая и техническая прочности.
Вопросы прочности и разрушения твердых тел
изучаются различными специалистами: теоретиками в области физики твердого тела,
физиками-экспериментаторами, металлургами и инженерами, изыскивающими пути
улучшения механических свойств конструкционных материалов.
Физиками-теоретиками было установлено, что
величина сил притяжения и отталкивания между атомами зависит от межатомного
расстояния.
На рис.22.45 показана зависимость сил
взаимодействия атомов от межатомного расстояния. Кривая 1 – сила
притяжения между атомами, кривая 2 – сила отталкивания, кривая 3
– результирующая сила. Через а
обозначено межатомное расстояние, λ/2- половина длины волны
аппроксимирующей синусоиды. При малых межатомных расстояниях наклон кривой силы
отталкивания больше, чем кривой притяжения, поэтому наклон кривой суммарного
взаимодействия положителен (для малых расстояний) и его значение становится
равным нулю при достижении межатомного расстояния а, соответствующего условию равновесия двух атомов при действии
силы сцепления. Притяжение атомов есть результат низкоэнергетического состояния
валентных электронов, тогда как причиной
отталкивания является перекрытие заполненных уровней, происходящее по мере уменьшения
расстояния между соседними атомами.
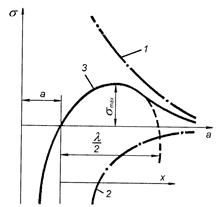
Рис.22.45
Для того чтобы увеличить расстояние между
атомами, находящимися в равновесии, на величину a, необходимо приложить
растягивающее напряжение. Считая силу взаимодействия равной этому напряжению,
его можно приближенно выразить в виде гармонической функции расстояния

где  -
теоретическая прочность сцепления атомов.
-
теоретическая прочность сцепления атомов.
Напряжению σ и перемещению x соответствует работа на единицу площади, равная при
разрушении площади под отрезком кривой напряжения в пределах от x =0
до 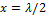 . Таким образом,
. Таким образом,
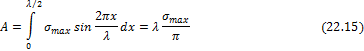
Если энергия на единицу площади, расходуемая
при создании новой поверхности, равная γ, связана исключительно с работой
разрушения, то

В случае малых перемещений x в области линейной
упругости справедливы уравнения (22.14), с одной стороны, и закон Гука, с
другой стороны, т.е.

Исключая σ/x, получим  , что в комбинации с уравнением (22.16) дает
выражение для теоретической прочности:
, что в комбинации с уравнением (22.16) дает
выражение для теоретической прочности:

Если из
рассчитываемого материала изготовить образец и разрушить его, то можно получить
значение технической или экспериментальной прочности. При
теоретическом расчете сил разрыва связи между атомами, отнесенных к единице
площади, получаем величину теоретической прочности примерно 1/10 модуля Юнга.
На самом деле фактическая прочность составляет 1…10% теоретической прочности.
Физики
предположили, что причина расхождения между теоретической и реальной
прочностью заключается в том, что в основе теоретического расчета лежит
гипотеза о преодолении сил связи атомов при отрыве одновременно по всему
сечению испытываемого образца. В действительности же силы связи преодолеваются
не одновременно. Причиной этого являются местные дефекты. Разрушение реальных
кристаллов происходит не одновременно по всему сечению, а в две стадии: 1)
возникновение трещин в дефектных местах; 2) распространение трещин по всему
сечению с разделением кристалла на две части.
Объяснение столь резкой разницы впервые было
дано в 1920 г. академиком А.Ф.Иоффе на следующем примере: им были испытаны
два кристалла поваренной соли, второй из которых он выдерживал некоторое время
в горячей воде. Если прочность первого кристалла равнялась нескольким мегапаскалям, то прочность второго была более высокой –
около 2000 МПа, что лишь в два раза меньше теоретического значения прочности
для поваренной соли.
Такое существенное различие в
экспериментальных прочностях объясняется тем, что первый образец имел большое
количество поверхностных дефектов (щербины, царапины, трещины), второй же
образец, лишившись поверхностного слоя, освободился от них. Отсюда вывод: чем
совершеннее структура материала, тем ближе его техническая прочность к теоретической.
Интенсивные исследования в области получения
чистых металлов позволили еще в 30-х гг. академикам С.Н.Журкову и
А.П.Александрову достигнуть
чрезвычайно высокой технической прочности на кварцевых нитях (σв=13∙103 МПа), а на
стеклянных нитях техническая прочность
равнялась σв =6∙103
МПа. Позднее в Физико-техническом институте им. А.Ф.Иоффе
профессором А.В.Степановым
были получены нитевидные монокристаллы («усы») некоторых металлов с прочностью
около 10000 МПа. Если учесть, что прочность конструкционных сталей колеблется в
пределах 300...800 МПа, то огромная разница в прочности налицо: исправление
дефектной структуры кристаллов увеличивает их прочность на несколько порядков и
приближает ее к теоретическому значению, которое можно приближенно считать
равным 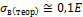 .
.
Другим доказательством и следствием
установленной роли дефектов являются статистические теории прочности, хорошо
согласующиеся с опытом. Статистические теории основаны на том, что прочность
реальных тел определяется дефектами. Появление дефектов разной степени
опасности и их распределение в материалах подчиняются законам случайности.
Разрушение, согласно этим теориям, происходит при достижении средним
напряжением предела местной прочности, т. е. прочности ослабленного дефектом
сечения образца.
Вероятность появления в теле наиболее
опасного дефекта увеличивается с увеличением объема тела. Вследствие этого
появляется зависимость средней прочности от объема нагруженного тела.
На рис. 22.46 показана зависимость прочности
стеклянных нитей от их диаметра d.
Зависимость получена опытным путем, но она согласуется с результатами,
полученными по статистическим теориям.
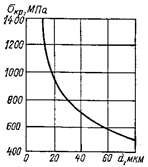
Рис. 22.46. Зависимость
прочности стеклянных нитей от диаметра
Эксперименты по упрочнению кристаллов, а
также многочисленные случаи преждевременного разрушения конструкций и сооружений
при напряжениях, значительно меньших расчетных, показали, недостаточность
развитых представлений о прочности как о постоянной
материала. Такое значительное различие между теоретической и реальной
прочностью материалов на современном уровне объясняется следующими факторами:
- значительными отклонениями от строгого,
регулярного расположения атомов в кристаллической решетке материала, т.е.
дефектностью структуры материала;
- технологическими нарушениями сплошности материала – трещинами.
Работа
Гриффитса «Явление разрушения и течения твердого
тела»
Существует широкий круг явлений
хрупкого разрушения, для которых представление о критериях разрушения (теориях
прочности) неприменимо. Открытый А.Ф.Иоффе
эффект увеличения прочности кристалла каменной соли при растворении его
поверхностных слоев, многочисленные случаи разрушения металлических конструкций
при напряжениях, меньших условного предела текучести, а также многие другие
явления разрушения, принципиально необъяснимые с точки зрения теорий прочности,
заставили ряд исследователей отказаться от галилеева
представления о прочности, как о некоторой константе материала. Это
направление в механике разрушения основано на изучении самого процесса
разрушения. Несоответствие между теоретической прочностью межатомных связей и
экспериментальной прочностью натолкнуло английского ученого А.Гриффитса на мысль, что
большое расхождение в прочностях объясняется наличием мелких трещин в
однородном материале, которые приводят к большой концентрации напряжений в
упругом состоянии. Появившиеся в 1921 и 1924 гг. работы Гриффитса
по теории трещин считаются основополагающими в области теоретических
исследований механики разрушения.
Рассмотрим бесконечную пластину единичной
толщины с центральной поперечной трещиной длиной 2l. Края трещины
неподвижны, а напряжение в ней равно σ (рис.22.47, а).
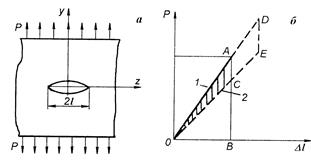
Рис.22.47
На рис.22.47, б приведена диаграмма «нагрузка-удлинение». Запасенная в пластине упругая
энергия представлена площадью ОАВ.
Если длина трещины увеличится на величину dl, то жесткость пластины уменьшится
(линия ОС); это означает, что
нагрузка несколько уменьшится, поскольку края пластины неподвижны.
Следовательно, упругая энергия, запасенная в пластине, уменьшится до величины,
равной ОСВ. Увеличение длины трещины
от l до l+dl приведет к
высвобождению упругой энергии, равной по величине площади ОАС.
Если пластина нагружена до более высокого
напряжения, то при увеличении длины трещины на величину dl освободится большая
энергия. Гриффитс предположил, что трещина будет
расти лишь в том случае, если освобождаемая при этом энергия достаточна для
обеспечения всех затрат энергии, связанных с этим ростом. В противном случае
необходимо увеличить напряжение. Треугольник ODE иллюстрирует энергию, выделяемую
при распространении трещины.
Условие, необходимое для роста трещины,
следующее:

где U - упругая энергия;
W - энергия,
необходимая для роста трещины.
Основываясь на расчетах, Гриффитс
получил выражение для  в виде
в виде

на единицу толщины пластины, где E- модуль упругости
первого рода.
Величину 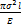 называют скоростью высвобождения упругой энергии,
или трещинодвижущей силой.
называют скоростью высвобождения упругой энергии,
или трещинодвижущей силой.
Поверхностная энергия пластины, связанная с
наличием в ней трещины:

где γ - удельное поверхностное
натяжение, вводимое для твердого тела по аналогии с таким же понятием для
жидкости.
Энергию, расходуемую на распространение
трещины, найдем как

Приравнивая правые части (22.20) и (22.22),
получим

Вследствие этого возникает хрупкое
разрушение, которое характеризуется коэффициентом интенсивности напряжений

Из анализа уравнений (22.20) и (22.22) видно,
что трещина, достигнув критической длины lk
при напряжении σk, становится
неустойчивой.
Этот коэффициент имеет размерность Н/мм3/2.
Графическое изображение критического
состояния представлено на рис.22.48. Из графика видно, что при напряжении
меньше критического трещина развиваться не будет. При достижении критического
напряжения трещина начинает развиваться неустойчиво.
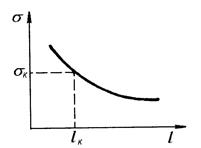
Рис.22.48
Энергетический метод Гриффитса
для идеально хрупких материалов позволяет отвлечься от детального анализа
механизма разрыва межатомных связей в конце трещины и установить
феноменологическую связь между внешними и внутренними силовыми факторами.
Примерно до 50-х годов считалось, что теория Гриффитса применима только к хрупким материалам типа
стекол; большинство же конструкционных материалов проявляет пластические
свойства при разрушении. Следующий значительный шаг в становлении механики
разрушения связан с экспериментальными исследованиями Дж.Ирвина (1948 г.) и Е.Орована
(1950 г.), предложившими использовать теорию Гриффитса
для разрушения пластичных металлов с учетом понятия энергии, затрачиваемой на
развитие пластических деформаций вблизи трещины.
Силовой критерий разрушения – K1c
Гриффитс вывел свое
уравнение для стекла – очень хрупкого материала. Он предполагал, что величина  , т.е. энергия, расходуемая на
распространение трещины, определяется только поверхностной энергией. В вязких
материалах, например, металлах, при вершине трещины образуются пластические
деформации. Для образования новой зоны пластических деформаций при вершине
трещины необходима большая энергия.
, т.е. энергия, расходуемая на
распространение трещины, определяется только поверхностной энергией. В вязких
материалах, например, металлах, при вершине трещины образуются пластические
деформации. Для образования новой зоны пластических деформаций при вершине
трещины необходима большая энергия.
Модель развития трещины для пластического
материала показана на рис.22.49.
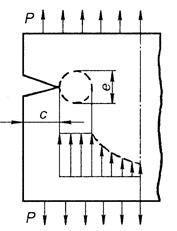
Рис.22.49
Предполагается, что при нагружении
пластины с надрезом в зоне надреза на расстоянии c от края пластины появляется
пластическая зона диаметром e, в которой действует постоянное напряжение. По мере
удаления от этой зоны напряжение падает. Поскольку пластическая зона должна
быть образована в процессе роста трещины, то энергию, необходимую для
распространения трещины, считают равной энергии, необходимой для образования
этой трещины. Это означает, что в металлах величина  определяется главным образом энергией
деформации в пластической зоне; поверхностная энергия в этом случае настолько
мала, что ею пренебрегают. Исходя из этих соображений, американский ученый Д.Ирвин, развивая идею Гриффитса,
предложил величину
определяется главным образом энергией
деформации в пластической зоне; поверхностная энергия в этом случае настолько
мала, что ею пренебрегают. Исходя из этих соображений, американский ученый Д.Ирвин, развивая идею Гриффитса,
предложил величину

назвать силой, необходимой для
распространения трещины на 1 см. Если сила распространения трещины G превысит
критическое значение 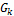 , то трещина будет распространяться
самопроизвольно. Таким образом, критерием разрушения является
, то трещина будет распространяться
самопроизвольно. Таким образом, критерием разрушения является

Для плоского напряженного состояния

а при плоском деформированном состоянии

где μ-
коэффициент Пуассона материала;
l - длина
трещины, мм;
σ
- действующее напряжение, МПа;
E - модуль
упругости первого рода материала, МПа.
Величина G достигает своего критического
значения при критическом значении 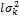 , т.е. опасность разрушения определяется
величиной
, т.е. опасность разрушения определяется
величиной 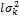 ,. Если в это произведение включить π, то получим ту же зависимость,
которая в свое время была получена Гриффитсом:
,. Если в это произведение включить π, то получим ту же зависимость,
которая в свое время была получена Гриффитсом:

Предельное значение коэффициента K Ирвин обозначил через  и
назвал коэффициентом вязкости разрушения.
и
назвал коэффициентом вязкости разрушения.
Величина  играет
в механике разрушения доминирующую роль, определяя вязкость разрушения
материала при достижении критической интенсивности напряжения. Коэффициент
играет
в механике разрушения доминирующую роль, определяя вязкость разрушения
материала при достижении критической интенсивности напряжения. Коэффициент  имеет
размерность Н/мм3/2.
имеет
размерность Н/мм3/2.
Важность данной характеристики общепризнанна. Сложность этого мероприятия состоит в
трудоемкости методов оценки  , особенно для пластических материалов и
сплавов, поскольку требуются испытания образцов чрезвычайно больших размеров.
Так, для стали с пределом прочности 500...700 МПа для создания плоской
деформации при комнатной температуре необходимо проводить испытания на образцах
толщиной 250 мм, высотой 610 мм, шириной 635 мм, для титановых сплавов
соответственно 120×400×80 мм.
, особенно для пластических материалов и
сплавов, поскольку требуются испытания образцов чрезвычайно больших размеров.
Так, для стали с пределом прочности 500...700 МПа для создания плоской
деформации при комнатной температуре необходимо проводить испытания на образцах
толщиной 250 мм, высотой 610 мм, шириной 635 мм, для титановых сплавов
соответственно 120×400×80 мм.
В настоящее время используются два метода
определения коэффициента вязкости разрушения  : статический и циклический.
: статический и циклический.
Статический метод определения  заключается в том, чтобы установить величину
нагрузки, вызывающей «лавинный» рост трещины. При этом каждому образцу и
характеру приложения напряжений соответствует критический размер трещины,
определяющий переход от медленного распространения к
быстрому. Расчетная формула для определения
заключается в том, чтобы установить величину
нагрузки, вызывающей «лавинный» рост трещины. При этом каждому образцу и
характеру приложения напряжений соответствует критический размер трещины,
определяющий переход от медленного распространения к
быстрому. Расчетная формула для определения  имеет
вид
имеет
вид

где y- калибровочный коэффициент, определяемый характером нагружения, размерами образца и надреза трещины;
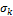 - напряжение в опасном сечении,
соответствующее началу разрушения образца;
- напряжение в опасном сечении,
соответствующее началу разрушения образца;
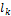 - критическая длина трещины.
- критическая длина трещины.
Исследованиями установлено, что чем больше
толщина образца, тем меньше зона пластической деформации и тем быстрее
происходит процесс хрупкого разрушения методом отрыва, т.е. вершина трещины
образца находится ближе к плоскому напряженному состоянию, чем к плоскому
деформированному состоянию.
Разрушение в условиях плоской деформации при
быстром распространении трещины ограничивает возможную минимальную зону
пластической деформации. Уменьшение пластической деформации в приповерхностных
слоях за счет увеличения толщины образца приводит к «прямому» излому без
боковых сколов. При этом  достигает некоторого предела, которым и
является
достигает некоторого предела, которым и
является  (рис.22.50).
(рис.22.50).
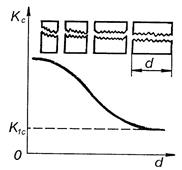
Рис.22.50
Поскольку значения  являются искомыми, толщина образца d предварительно
выбирается в зависимости от отношения
являются искомыми, толщина образца d предварительно
выбирается в зависимости от отношения 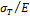 . В табл.22.2 представлены рекомендуемые
толщины образцов в зависимости от
. В табл.22.2 представлены рекомендуемые
толщины образцов в зависимости от 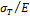 .
.
Таблица 22.2
|
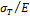
|
Толщина d, мм
|
|
До 0,005
|
100
|
|
0,005...0,0057
|
75
|
|
0,0057...0,0062
|
63
|
|
0,0062...0,0065
|
50
|
|
0,0065...0,0071
|
38
|
|
0,0071...0,0080
|
25
|
|
0,0080...0,0095
|
13
|
|
0,0095 и более
|
6,5
|
Во время проведения опыта при определенной
величине нагрузки на образец часто наблюдается предкритическое раскрытие трещины,
за которым при дальнейшем повышении нагрузки следует скачок трещины.
Циклический метод определения  заключается в том, что при одном или нескольких уровнях напряжений
испытывают на усталость цилиндрические или плоские образцы (гладкие или с надрезом)
до разрушения. Затем на измломе определяют длину (при
плоском образце со сквозной щелью) или
глубину (при цилиндрическом образце) критической усталостной трещины. Метод был
предложен профессором В.С.Ивановой.
заключается в том, что при одном или нескольких уровнях напряжений
испытывают на усталость цилиндрические или плоские образцы (гладкие или с надрезом)
до разрушения. Затем на измломе определяют длину (при
плоском образце со сквозной щелью) или
глубину (при цилиндрическом образце) критической усталостной трещины. Метод был
предложен профессором В.С.Ивановой.
Для цилиндрических образцов при испытании на
изгиб с вращением (обычная выносливость)

где σ
- действующее максимальное брутто-напряжение цикла;
lk -
критическая длина трещины.
На величину  , определяемую циклическим методом, форма
образцов и амплитуда нагружения не оказывают влияния.
Результаты идентичны при испытании на выносливость или на малоцикловую
усталость, что позволяет в сравнительно короткое время накопить по важнейшим
машиностроительным материалам необходимые данные по новым критериям разрушения
, определяемую циклическим методом, форма
образцов и амплитуда нагружения не оказывают влияния.
Результаты идентичны при испытании на выносливость или на малоцикловую
усталость, что позволяет в сравнительно короткое время накопить по важнейшим
машиностроительным материалам необходимые данные по новым критериям разрушения  ,
,  . Различия в значения
. Различия в значения  при
определении статическими и циклическими методами не превышают 6%.
при
определении статическими и циклическими методами не превышают 6%.
Для количественной оценки нового критерия
прочности  с основной
механической характеристикой
с основной
механической характеристикой  в
табл.22.3 приведены данные трех широко распространенных материалов.
в
табл.22.3 приведены данные трех широко распространенных материалов.
Таблица 22.3
|
Материал
|
 , МПа , МПа
|
 , Н/мм3/2 , Н/мм3/2
|
|
Сталь
|
1750
|
3550
|
|
Сплав
алюминия
|
600
|
1050
|
|
Сплав
титана
|
1000
|
2800
|
Доминирующую роль величины  в механике разрушения необходимо учитывать
при выборе материалов для создания той или иной конструкции.
в механике разрушения необходимо учитывать
при выборе материалов для создания той или иной конструкции.
Расчет на прочность материалов с
трещинами
При статическом нагружении
деталей машин или элементов конструкций, не имеющих дефектов в виде трещин,
условия разрушения и прочности при растяжении-сжатии записываются в напряжениях
в следующем виде:


По основному уравнению линейной механики
разрушения эти же условия записываются в коэффициентах интенсивности
напряжений:


В уравнениях (22.34) и (22.35)  является критическим значением интенсивности
напряжений, а
является критическим значением интенсивности
напряжений, а 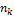 - коэффициентом
запаса прочности.
- коэффициентом
запаса прочности.
Согласно уравнениям (22.34) и (22.35) можно
решать четыре рода задач механики разрушения:
- определять критическое, или, иначе,
разрушающее напряжение:

- проверять прочность детали, или элемента
конструкции:

- определять допускаемые размеры трещины:

- определять допускаемые напряжения:

При расчетах на прочность материалов с
трещинами в первую очередь учитываются размеры трещины и напряжения. Для
определения размеров трещин на практике необходимо применять современные методы
дефектоскопического контроля: ультразвук, рентгеноскопию, акустическую эмиссию
и др., что позволяет прогнозировать наступление критического состояния
конструкции, обеспечивать своевременный ее ремонт и, следовательно, продление
ресурса работы.
На практике часто встречаются многократные
циклические нагрузки. Скорость распространения циклических трещин в миллионы
раз меньше, хрупких, и зависит только от коэффициента интенсивности напряжений:

где N- число циклов нагружения;
l -
длина трещины;
C- постоянная материала;
m -
показатель степени (для большинства материалов 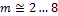 ).
).
Следовательно, при расчете на трещиностойкость деталей машин, работающих в циклическом режиме,
необходимо учитывать скорость распространения трещины.
В целом раздел сопротивления материалов о
хрупком разрушении (механика разрушения) бурно развивается и еще далек от
завершения.
Использование коэффициента интенсивности напряжений (КИН)
в рамках линейной упругой механики разрушения (ЛУМР)
1) Критерий
разрушения Kc
КИН используется в рамках ЛУМР
как силовой критерий разрушения, не требующий объяснений, связанных с
энергетическим балансом при распространении трещины, как в основополагающей
работе Гриффитса. В основе силового критерия лежит
предпосылка, согласно которой разрушение возникает тогда, когда у трещины в
пределах достаточно большой области напряжение превышает предельное значение.
Эту предпосылку можно непосредственно связать с КИН, характеризующим
поля напряжений в соответствии с асимптотическими формулами для компонент
напряжений и деформаций. КИН зависит от нагрузки и конфигурации образца. Даже в
том случае, когда схема приложения нагрузки и конфигурации образцов оказываются
различными, при одинаковых КИН поля напряжений
оказываются одинаковыми. Предельное значение К, при
котором возникает разрушение, можно обозначить символом Кс, который
отражает одну из характеристик материала, носящую название вязкости разрушения.
Расчет на прочность,
предлагаемый механикой хрупкого разрушения, включает в себя следующие основные
моменты:
а) выбор формы, размера и
местоположения наиболее опасного трещиноподобного
дефекта;
б) определение КИН на фронте
трещины с учетом внутренних напряжений металлургического, технологического или
эксплуатационного происхождения;
в) выбор критерия локального
разрушения на фронте трещины, изучение докритического развития трещины и
отыскание критического (предельного) состояния, которое соответствует выходу
конструкции на нерасчетный режим (например, разрушению).
Первый из этих вопросов решается
на основе натурных и лабораторных наблюдений и во многом пока зависит от
интуиции инженера.
Второй вопрос решается на основе
методов классической теории упругости.
На последнем этапе расчета на
прочность вычисленное значение наибольшего КI
(как определенной функции нагрузок, размеров тела и длины начальной трещины)
приравнивается некоторому критическому значению этого коэффициента,
характеризующему сопротивление материала отрыву на фронте трещины нормального
разрыва.
Практически наиболее важную роль
играют следующие критические КИН:
а) вязкость разрушения КIc (при монотонном нагружении до начала локально нестабильного разрушения в
условиях стесненной плоской деформации);
б) величина Кс (при монотонном нагружении пластин со
сквозными трещинами);
в) величина КY
(при циклическом нагружении);
г) величина КIscc (в условиях длительного нагружения постоянной нагрузкой в коррозионно-активной
среде).
Величина Кс
изменяется в пределах (1…3)КIc.
Величина КY представляет собой практический
предел усталости, она равна примерно (0.1…0.05)КIc.
Пороговый коэффициент интенсивности напряжений КIscc существенно зависит от
внешней среды, он может меняться в пределах (0.1…1) КIc.
Если КI меньше КY (или соответственно КIscc),
то трещина не растет. На самом деле это заключение справедливо только для
некоторой фиксированной базы испытания, играющей роль гарантийного срока (менее
108 – 109 циклов для КY
и менее года для КIscc).
Указанный метод расчета хрупкой
прочности по критическим КИН нельзя считать вполне
удовлетворительным, так как он не учитывает медленного докритического развития
усталостных и коррозионных трещин. Однако ясно, что этот фактор идет в запас
прочности, поэтому в ряде случаев бывает достаточно получаемых оценок.
Размерности КИН: напряжение× (длина)1/2 или сила/(длина)3/2.
К примеру, 0.825 кН/мм3/2
= 825 Н/мм3/2 = 825 H/(мм∙мм1/2)
= 825 H/мм2∙мм/мм1/2 =
825 МПа∙(0.001 м)1/2 = 26 МПа∙м1/2.
Таблица 22.4. Температурные
зависимости вязкости разрушения (МПа∙м1/2)
|
Сталь
|
Температура, К
|
|
213
|
233
|
253
|
273
|
293
|
|
Статическое нагружение
|
|
10ХСНД
|
70
|
71
|
71
|
70
|
68
|
|
09Г2С
|
65
|
61
|
59
|
58
|
57
|
|
Вст3сп
|
54
|
55
|
56
|
56
|
56
|
|
Ст20
|
51
|
52
|
53
|
55
|
58
|
|
15Х2НМФА
|
102
|
115
|
124
|
141
|
154
|
|
Динамическое нагружение
|
|
10ХСНД
|
23
|
28
|
38
|
50
|
60
|
|
09Г2С
|
39
|
43
|
48
|
60
|
68
|
|
Вст3сп
|
24
|
25
|
31
|
40
|
50
|
|
Ст20
|
20
|
22
|
27
|
33
|
43
|
|
15Х2НМФА
|
58
|
66
|
75
|
81
|
87
|
2) Ограничения
линейной упругой механики разрушения
Уравнения ЛУМР, являясь
приближенными, имеют верхний и нижний пределы применимости. Это
связано с тем, что решения с использованием КИН приводят к сингулярности
напряжения у вершины трещины при r=0,
и хотя они могут давать достаточно хорошую оценку величины пластической зоны,
они не применимы для описания поля деформации внутри пластической зоны и,
следовательно, не пригодны для описания процесса вязкого разрушения внутри
пластической зоны. Пределы применимости модели интенсивности упругих
напряжений становятся очевидными при высоком уровне напряжений. Тогда К-решения
фактически уже не описывают действительного поля напряжений, и, следовательно,
истинных размеров пластической зоны. Это может привести к неоправданно
консервативным результатам расчетов, так как перераспределение напряжений в
результате пластического течения и притупления вершины трещины, связанного с
ним, делают допустимыми более высокие эксплуатационные нагрузки, особенно для высокопластичных материалов.
Принято, что ЛУМР может быть
использована при соблюдении условий rp ≤ a/50, W/50, B/50, где W, B – ширина и толщина
пластины. При этом напряжения не должны превосходить σт/5. В конечном итоге
испытания на основе методов ЛУМР и применение концепции КIc для материалов с высокой вязкостью и
пластичностью (хрупкому разрушению предшествует развитие большой пластической
зоны у вершины трещины) требуют весьма крупных образцов, в которых трещины и их
пластические зоны не зависят от границ образца и достигается плоское
деформированное состояние, т.е. выполняется условие B ≥2.5(K/σт)2.
Также недоступна для описания
аппаратом ЛУМР трещина, возникшая у дна надреза, т.е. находящаяся в
пластической зоне. Здесь справедливо условие rp > a, и, очевидно, ЛУМР не может быть применена в такой ситуации.
За пределами указанных
ограничений применение ЛУМР дает ошибку, возрастающую с ростом отношения
размера пластической области к размеру упругой области. До какого момента можно
допускать существование указанной ошибки? Ответ на этот вопрос зависит от тех
требований, которые приняты при проектировании.
В случае разрушения хрупких
материалов в ЛУМР вводят соответствующую поправку на пластичность, что
позволяет уменьшить эту ошибку.
В заключение отметим, что нижний
предел размеров любой трещины, которая поддается описанию на основе законов
механики сплошной среды, можно найти, введя понятие размера минимальной
пластической зоны, например, субъячейки, т.е. ~10
мкм, что дает минимальную длину трещины ~0.5 мм. При меньших размерах
ЛУМР становится неприменимой, и трещины длиной менее 0.5 мм рассматриваются как
короткие.
Оценка коэффициента интенсивности напряжений
1) Аналитические
методы
В настоящее время аналитическими
методами теории упругости решено большое количество задач для различных
конфигураций твердого тела, трещины и условий нагружения.
Плоские статические задачи.
В задачах о плоской деформации и плоском напряженном состоянии КИН определяются
по асимптотике комплексного потенциала Ф(z) в конце разреза.
Разрезы вдоль одной и той же прямой или вдоль одной и той же
окружности в бесконечной упругой плоскости. Если совокупность
математических разрезов расположена вдоль одной и той же прямой или вдоль одной
и той же окружности и других границ упругое тело не имеет, то могут быть решены
следующие краевые задачи:
а) на разрезах произвольно
задана нормальная и касательная нагрузка;
б) на разрезах заданы
произвольные смещения;
в) на одном берегу разрезов
задаются смещения, а на другом берегу – нагрузки;
г) участки с произвольно
заданными смещениями или нагрузками чередуются любым образом вдоль нижнего и
верхнего берегов разрезов;
д) берега разрезов
взаимодействуют, причем касательное напряжение взаимодействия произвольным
образом зависит от нормального давления;
е) касательное напряжение на
разрезах обращается в нуль, участки с произвольно заданным нормальным
смещением или с нормальной нагрузкой
расположены произвольно на берегах разрезов.
Для указанных типов задач можно найти
КИН; некоторые случаи рассмотрены ниже.
Если в упругой плоскости имеется
один прямолинейный разрез и сосредоточенные сила и момент приложены симметрично
к верхнему и нижнему берегам щели (рис. 22.51), то
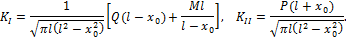
Для распределенных на некотором
участке верхнего берега щели нагрузок (рис. 22.52) имеем


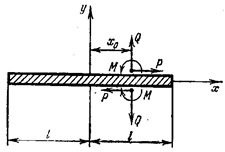
Рис. 22.51
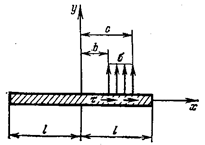
Рис. 22.52
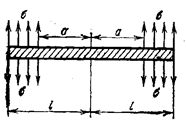
Рис. 22.53
В случае, изображенном на рис.
22.53, имеем

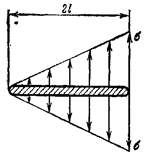
Рис. 22.54
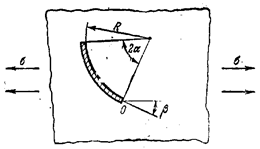
Рис. 22.55
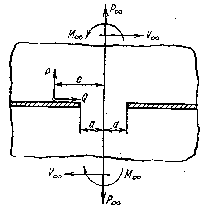
Рис. 22.56
Для примера на рис. 22.54 на
правом и левом конце соответственно
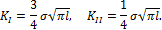
Для щели, располагающейся вдоль
длины окружности (рис. 22.55), КИН в наиболее опасной точке О
имеют вид

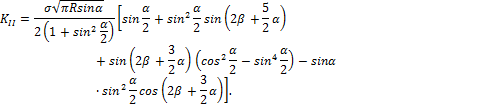
В случае перешейка между двумя полубесконечными щелями (рис.22.56) имеют место следующие
формулы
- у левого конца перешейка

- у правого конца перешейка
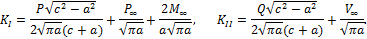
Разрез в полуплоскости. Задача о растяжении упругой
полуплоскости с краевой щелью (рис. 22.57) рассматривалась многими
авторами. Ее решение получено многими способами – как точными аналитическими
методами, так и приближенными:

Коэффициент 1.12 вычислен с
погрешностью 1%. Как видно, влияние свободной границы тела приводит к
увеличению КИН на 12%.
Для задачи на рис. 22.58
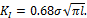
Коэффициент 0.68 вычислен с ошибкой
3%.
В случае полубесконечного
разреза, приближающегося к свободному краю полуплоскости (рис. 22.59) КИН равен
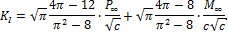
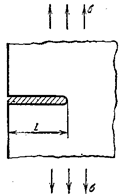
Рис. 22.57
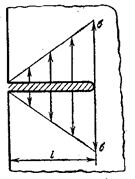
Рис. 22.58
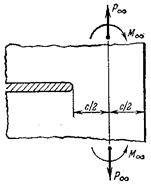
Рис. 22.59
Разрезы, исходящие из круглого отверстия. Решена задача о всестороннем
и одностороннем растяжении плоскости с одной и двумя щелями, исходящими из
кругового отверстия (рис. 22.60).
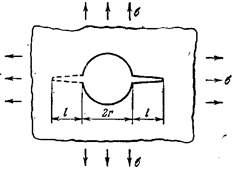
Рис. 22.60
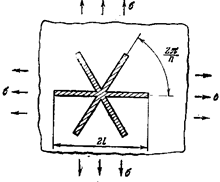
Рис. 22.61
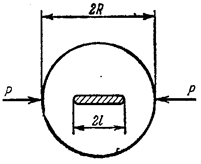
Рис. 22.62
Имеем

Решена задача о всестороннем
растяжении плоскости со звездообразной щелью (рис. 22.61). Окончательный результат имеет вид

где ξ(m) – коэффициент, зависящий от числа разрезов n.
Для круглого диска с внутренней
щелью, раздавливаемого двумя сосредоточенными силами (рис. 22.62),

Тела сложной формы. Изучены многие случаи различных
криволинейных отверстий со щелями. В случае всестороннего растяжения упругой
плоскости с гипоциклоидальным отверстием, контур
которого описывается уравнениями

где n – целое положительное число, КИН равен

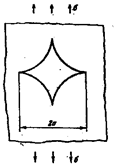
Рис. 22.63
Гипоциклоида имеет n+1 точку возврата, каждая из которых с
точки зрения концентрации напряжений эквивалентна концу трещины (на рис. 22.63
изображена астроида с n=3).
Пространственные задачи. В силу сложности решения пространственных задач
готовых решений накоплено значительно меньше, чем для плоского случая. Приведем
окончательные результаты вычисления КИН в пространственных задачах.
Дискообразная щель. В общем осесимметричном случае
дискообразного разреза вдоль z=0, x2+y2<a2
в безграничном пространстве (рис. 22.64) имеем
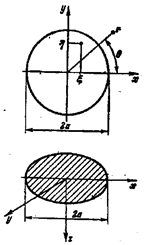
Рис. 22.64
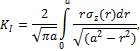
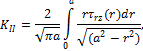

Здесь предполагается, что нагрузки
симметрично приложены к верхнему и нижнему берегам щели, а на бесконечности
напряжения исчезают.
При чистом изгибе стержня с
дискообразной щелью (рис. 22.65) КИН будет
следующим

Здесь Jy – соответствующий
момент инерции поперечного сечения стержня, b
– расстояние центра щели от нейтральной линии.
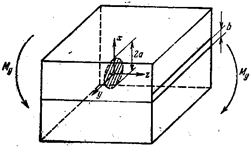
Рис.22.65
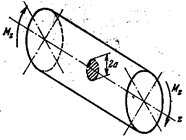
Рис.22.66
При скручивании круглого
цилиндрического стержня с дискообразной щелью (рис. 22.66) имеем (здесь
предполагается, что центр щели лежит на оси стержня, а плоскость щели
перпендикулярна этой оси)
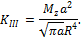
Итак, имеется большое количество
решенных аналитическим способом задач по определению КИН для тел с трещинами
различной конфигурации, но все же число этих задач ограничено.
2) Метод конечных
элементов (МКЭ)
В настоящее время известны
различные методы расчета коэффициента интенсивности напряжений (КИН),
использованные на использовании МКЭ. Они имеют свои преимущества и недостатки.
Рассмотрим некоторые из них.
2.1) Прямой метод
В этом случае для определения
КИН в асимптотические формулы для компонент напряжений и перемещений в вершине
трещины непосредственно подставляют возникающие в окрестности вершины трещины
напряжения или перемещения, полученные с помощью МКЭ. При использовании
напряжений этот способ называется прямым методом напряжений, а при
использовании перемещений – прямым методом перемещений. Значения напряжений или
перемещений, которые необходимо подставить в формулы, следует выбирать такими,
чтобы они были определяющими для рассматриваемого типа деформирования.
Например, в случае трещины типа I необходимо подставить компоненту напряжения sy, которая действует на оси х в направлении оси у. По сравнению с методом напряжений метод
перемещений дает более надежные результаты с точки зрения точности.
Расчет КИН прямым методом
требует, чтобы решение для напряжений и перемещений имело достаточно высокую
точность в окрестности вершины трещины. При использовании обычных элементов
нельзя отразить особенность при приближении непосредственно к вершине трещины.
Поэтому нельзя ожидать, что точность расчета напряжений и деформаций в
окрестности вершины трещины будет высокой. Следовательно, установленные по этим
параметрам КИН также будут иметь не слишком хорошую точность. Поэтому при
определении КИН с помощью обычных элементов необходимо предусмотреть меры,
позволяющие улучшить точность решения. К таким мерам можно отнести следующие.
(1) У вершины трещины, насколько
это возможно, желательно использовать разбиение на
малые элементы (мелкую дискретизацию).
(2) Часто могут возникать
ситуации, например при решении трехмерных задач, когда
разбиение на мелкие элементы оказывается нерациональным с точки зрения
вычислительных ресурсов. В таких случаях сначала находят решения для грубого
разбиения, а затем выделяют окрестность вершины трещины, выполняют мелкое
разбиение и решают задачу. При этом в качестве граничных условий используют
перемещения узлов и узловые силы, полученные в предыдущем решении. Такой способ
решения называют поэтапным.
(3) Используя асимптотические
формулы для компонент напряжений и перемещений в вершине трещины, в точках,
расположенных на различных расстояниях r
от вершины трещины, расчетным путем определяют значения К
и строят график зависимости К от r.
Искомое значение К, соответствующее рассматриваемой
трещине, принимают равным тому значению, которое получается в результате
экстраполяции при r → 0 (рис. 22.67).
Следует иметь в виду, что значения К, соответствующие
точкам, наиболее близко расположенным к трещине, обладают не очень хорошей
точностью. Поэтому при проведении экстраполяции эти значения исключают.
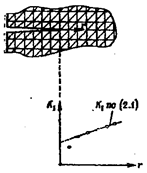
Рис.
22.67. Оценка КИН путем экстраполяции
(4) Используют всевозможные
разбиения от грубых до мелких и определяют значения К,
проводя так же, как в п. 3, экстраполяцию при r → 0.
В пп.
(1) и (3) дискретизация выполняется один раз, а в пп.
(2) и (4) – несколько раз, что затрудняет решение задачи. Пункты (1) и (3), а
также их сочетание можно отнести к таким методам оценки К,
когда необходимо, используя обычные элементы и не выделяя особенностей,
довольно быстро определить КИН. В других случаях необходимо использовать специальную
дискретизацию.
2.2) Энергетический
метод
Известно несколько
энергетических методов, наиболее распространенным из которых является метод
полной энергии. Интенсивность G
освобождения энергии, которое имеет место при распространении трещины в упругом
теле, связана с КИН зависимостью

При распространении трещины на
величину δА
изменение энергии деформации составляет δU.
Интенсивность освобождения энергии можно также представить как G=δU/δА. Таким образом, если в результате использования МКЭ
установить интенсивность освобождения энергии G, можно определить КИН. Однако видно, что найденный таким образом
КИН должен относиться к трещине одного из типов, т.е. для этих типов трещин
расчет К возможен только порознь.
При определении интенсивности
освобождения энергии можно воспользоваться изложенными ниже двумя способами.
А. Методом конечных элементов проводят численное решение для трещины площадью А. При этом
определяют энергию упругой деформации U(A). Затем рассматривают рост
трещины на один элемент. При тех же граничных условиях вновь МКЭ решают задачу
и определяют U(A+δА).
Тогда G=(U(A+δА) - U(A))/ δА. Энергию упругой деформации можно
установить путем интегрирования энергий деформации в отдельных точках по всей
рассматриваемой области. Полученное значение должно быть равно работе внешних
сил. Однако расчет работы внешних сил довольно прост и позволяет исключить
сложности, связанные с интегрированием.
Б. Можно не рассматривать рост
трещины на один элемент, а за счет соответствующего смещения координаты вершины
трещины задавать ее распространение (рис. 22.68). В результате такой операции
будет происходить изменение жесткости. При этом можно считать, что жесткость
меняется лишь у тех элементов, которые окружают вершину трещины. Если принять
это во внимание и путем исключения решать систему линейных уравнений, можно за
одно решение определить δU=
U(A+δА)
- U(A). При этом необходимо в процессе исключения вначале соответствующим
образом вводить указанную операцию распространения трещины.
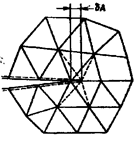
Рис. 22.68.
Виртуальный рост трещины
В случае использования метода А необходимо по отдельности дважды проводить решение. В
рассматриваемом же методе в этом нет необходимости. Его можно эффективно
использовать при большом числе уравнений, в частности при решении трехмерных
задач. Метод Б носит название метода виртуального
роста трещины, а метод А – метода податливости.
2.3) Использование специальных элементов
Методы, использующие аналитические решения. На рис. 22.69 изображен треугольный элемент с
трещиной, предложенный Бисковым. В качестве решения
вводится решение, полученное из функции напряжений Мусхелишвили. При этом
аналитическое решение имеет особенность напряжений, характерную для вершины
трещины. В случае такого элемента восьми степеням свободы узлов соответствует
восемь независимых переменных: три переменные, характеризующие перемещения
твердого тела, три средних напряжения и КИН КI и КII.
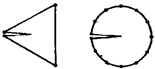
Рис.
22.69. Специальные элементы Бискова и Уилсона
Руководствуясь аналогичными соображениями,
Уилсон предложил круглый элемент с трещиной (рис. 22.69) и нашел решение,
используя до высоких порядков разложение функции перемещения в окрестностях
трещины.
Необходимо отметить, что при использовании
этих элементов в реальных условиях обычно их окружение составлено из
треугольных элементов. При этом обеспечиваются такие условия, при которых
перемещения смежных элементов в узлах совпадают, однако в общем случае не
выполняется условие неразрывности перемещений на границах элементов, за
исключением узлов. Поэтому не существует теоретического обоснования сходимости.
Тем не менее, численные эксперименты показали, что при этом не возникает
существенных проблем.
Методы, использующие простые
функции для описания особенностей. На рис. 22.70 показан предложенный
Уилсоном элемент, представляющий собой равнобедренный треугольник, вершина
которого находится в вершине трещины. Для этого элемента перемещение можно
представить таким образом
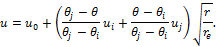
Аналогично
можно определить перемещение v. Такой
элемент для напряжений и деформаций имеет особенность в вершине трещины.
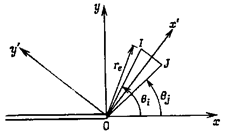
Рис. 22.70. Специальный элемент Уилсона
Деформированные изопараметрические элементы. У обычного восьмиузлового изопараметрического
элемента узлы находятся на серединах сторон. Если сместить узлы в точки,
соответствующие 1/4 длины стороны, то можно получить особенность в вершине
трещины (рис. 22.71). Однако в этом случае будет отсутствовать сходимость решения и энергия деформации будет иметь особенность в
вершине трещины. В связи с этим предложено считать длину одной из сторон
четырехугольника равной нулю. В результате объединения смежных узлов удалось
получить элемент, который одновременно обладал всеми необходимыми свойствами
(рис. 22.71).
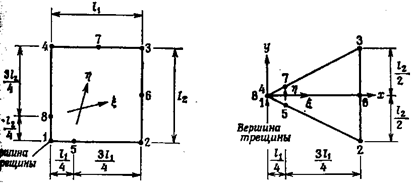
Рис. 22.71.
Деформированные элементы
Такой элемент может быть
использован как для упругого тела, так и для идеально пластического без
деформационного упрочнения.
Управление поведением трещин на основе линейной механики разрушения
Одно из наиболее важных для
инженерной практики применение методов механики разрушения – управление
поведением трещин. Здесь речь идет о том, что при обнаружении трещины есть
возможность тормозить и (или) останавливать ее развитие, а также принимать
меры, чтобы в данном месте конструкции трещина больше не возникала. Достижение
этих целей требует, как правило, некоторых конструктивных изменений в
поврежденный узел или элемент конструкции. И тогда необходимо вести речь о
проектировании модернизации. Другими словами, имея дело уже с возникшей при
эксплуатации трещиной, или предполагая, исходя из анализа
напряженно-деформированного состояния, возможность ее возникновения, необходимо
принятие соответствующих проектно-конструкторских решений. В большинстве
случаев они сводятся к конструкционному торможению трещин с помощью ребер
жесткости, ремонтных заплат, разгружающих отверстий и стопперов.
Конструкционное торможение
трещины ребрами жесткости. Одной из важнейших характеристик
сопротивления материала трещинообразованию является величина предельной
нагрузки, связанная с началом развития трещины. Однако это справедливо только в
случае лавинообразного неустойчивого распространения. Во многих случаях
взаимодействия трещин с препятствиями и границами, как показывают эксперименты
и расчеты, на значительном участке изменения нагрузки развитие трещины
протекает устойчиво. Очевидно, что наличие устойчивых трещин в конструкциях,
работающих зачастую в определенных режимах изменения внешних нагрузок, гораздо
менее опасно, а искусственное усиление таких конструкций (за счет постановки
заклепок, пластин и стрингеров, высверливания отверстий на пути распространения
трещин и т.д.) может значительно продлить их жизнь.
Для предотвращениия
катастрофического развития трещины и разрушения конструкции трещины подкрепляют
ребрами жесткости, препятствующими их распространению (рис. 22.72). Возможна следующая простейшая схематизация этой
задачи. Бесконечная пластина единичной толщины с трещиной растягивается на
бесконечности однородным напряжением (рис. 22.73); действие подкрепляющих ребер
заменяется четырьмя симметрично расположенными сосредоточенными силами,
приложенными в местах расположения ближайших к трещине заклепок; величина этих
сил считается заданной. Как показывают оценки, действием более удаленных
заклепок можно пренебречь.
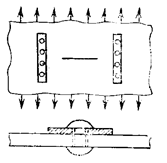
Рис. 22.72. Панель с приклепанными ребрами жесткости
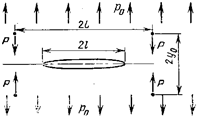
Рис. 22.73. Схематизация задачи о трещине в листе с ребрами
жесткости
На рис. 22.74 представлены
зависимости критического напряжения от длины трещины и местоположения заклепок.
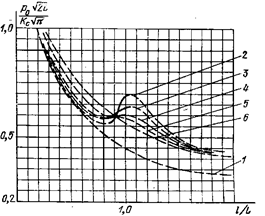
Рис. 22.74. Зависимость критического напряжения от длины трещины
для различных положений точек приложения сосредоточенных сил, имитирующих
действие заклепок.
Линия 1
соответствует отсутствию заклепок. Величина ε равна: для линий 2 – 0.15; 3 – 0.25; 4 – 0.4; 5 –
0.5; 6 – 0.75
Здесь же построена кривая 1,
соответствующая отсутствию подкрепляющих ребер. Очевидно, что трещина
устойчива, если напряжение, необходимое для ее поддержания в критическом
состоянии, возрастает с увеличением длины трещины. Как видно, существует
критическое значение ε0 безразмерного
параметра ε=y0/L такое, что
при ε > ε0 кривая не имеет участков возрастания, так что трещина
всегда неустойчива, а при ε < ε0 имеется участок возрастания, на котором трещина
устойчива.
В этом решении сила Р, характеризующая действие заклепок, считалась постоянной.
На самом деле величина этих сил вполне определяется упругими и геометрическими
характеристиками рассматриваемой задачи, а также величиной приложенной
нагрузки. При этом результаты количественно несколько отличаются от представленных.
Введение в рассмотрение нескольких
рядов заклепок действие подкрепляющих ребер сказывается в появлении нового
качественного эффекта – стабилизации трещин.
Конструкционное торможение трещин
ремонтными заплатами. Постановка ребер жесткости может производиться как
при создании конструкции, так и после непосредственного обнаружения трещин,
появившихся в процессе ее эксплуатации. В последнем случае в качестве ребра,
наряду с обычными стрингерами могут применяться и ребра в виде полос или
заплат-дублеров, приваренных, приклеенных или приклепанных к конструкции (рис.
22.75). В отдельных случаях такие ребра, помимо торможения трещин, могут
обеспечивать также герметичность, местную прочность конструкции, защиту от
коррозии и т.п., т.е. могут выполнять несколько функций.
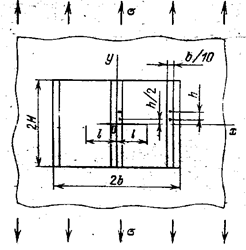
Рис. 22.75. Лист с трещиной и
приклепанной заплатой
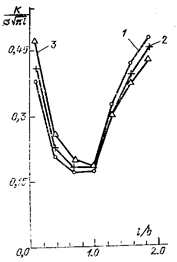
Рис. 22.76. КИН в листе с трещиной и заплатой: 1 – H/b=0.6; 2 – H/b=1; 3 – H/b=2
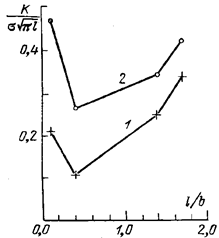
Рис. 22.77. КИН для двух разных жесткостей ремонтной заплаты: 1 –
S=0.5; 2 – S=2
Основными факторами, влияющими на
КИН в связи установкой ремонтных заплат, являются форма заплаты и ее жесткость.
На рис. 22.76 показано изменение коэффициента интенсивности напряжений в
функции отношения длины трещины к ширине заплаты для трех размеров заплаты.
Видно, что КИН сначала (по мере увеличения длины трещины) уменьшается, пока
вершины трещины не достигнут края заплаты. Когда вершины трещины находятся под
заплатой, КИН также уменьшается с уменьшением размера заплаты. Когда же трещина
выходит за пределы заплаты, КИН быстро увеличивается.
КИН рассчитаны также для двух
значений жесткости S=tE/tзEз. Видно
(рис. 22.77), что более жесткая заплата с меньшей S уменьшает КИН.
Результаты расчетов указывают, что
жесткость заплаты является основным фактором (по сравнению с размерами заплаты
и числом точек ее скрепления с пластиной), определяющим ее влияние на КИН.
Конструкционное торможение трещин
разгружающими отверстиями. Следует заметить, однако, что использование
приведенных выше результатов и выводов существенно ограничивается принятым при
решении предположением о возможности сноса сил взаимодействия пластин и ребер
жесткости в срединную плоскость пластин. Такой подход, строго говоря,
правомерен лишь для случая симметричного относительно срединной плоскости
пластин, расположения ребер. В противном случае изгибные напряжения,
действующие в пластине, могут не только уменьшить подкрепляющий эффект ребер
жесткости, но и привести к увеличению КИН в конце трещины. С этой точки зрения
наиболее достоверные результаты получены для методов конструкционного
торможения трещин, основанных на использовании разгружающих отверстий. Такие
отверстия не вносят нежелательный эксцентриситет, более просты в исполнении и
не требуют дополнительных затрат металла. На рис. 22.78 приведена зависимость
КИН для трещины, распространяющейся между двумя отверстиями, от геометрии
трещины и отверстий.
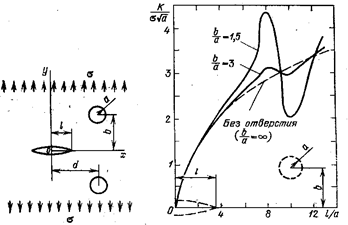
Рис. 22.78. Схема остановки трещины
Достигаемое в рассмотренном случае
значительное снижение КИН способствует переходу неравновесной трещины (или
трещины усталости) в равновесную. Однако увеличение
КИН при приближении трещины к отверстию приводит к разгону развивающейся трещины,
что не позволяет надежно использовать такую схему торможения.
При распространении реальных
трещин возможно также отклонение ее траектории от прямолинейной вплоть до
захвата трещины отверстием. При этом на первом этапе происходит постепенное
исчезновение сверхострого концентратора в вершине трещины при достижении
отверстия. Второй этап – вторичное появление зоны сверхконцентрации
напряжений и появление трещины на противоположной стороне отверстия. И хотя
вторая стадия значительно продолжительнее первой, полной остановки трещины не
наблюдается.
Влияние отверстий на развитие
усталостных трещин состоит в следующем. Если на пути
развивающейся усталостной трещины встречается круглое отверстие, то тормозящий
эффект этого отверстия, проявляющийся после входа в него трещины (независимо от
размера и местоположения отверстия), практически компенсируется ускорением
роста трещины при ее приближении к отверстию (за счет увеличения КИН) и
увеличением размера повреждения (за счет присоединения к повреждению самого отверстия).
Иначе обстоит дело, если
разгружающее отверстие просверлено в кончике трещины после ее обнаружения.
Эффективность такого приема определяется различного рода факторами: устранением
сверхконцентрации напряжений и наиболее поврежденного
материала в кончике трещины, появлением остаточных сжимающих напряжений в
процессе холодной обработки и уменьшением чувствительности материала к
концентрации напряжений и т.п. Количественная оценка столь многофакторного
явления очень сложна. Можно использовать следующий инженерный подход к оценке
эффективности торможения трещин с помощью засверливания ее концов, основанный
на принципе равнопрочности. Учитывая что элементы
конструкции содержат как правило, концентраторы
напряжений, представляется возможным выбрать из них те, которые работают в
условиях, аналогичных элементам, содержащим трещину. Тогда можно считать, что
достаточный эффект торможения засверленной по краям трещины достигнут, если
теоретический коэффициент концентрации для образовавшегося при засверловке концентратора не больше, чем для концентраторов
в элементах-аналогах (выполненных из одинакового материала), т.е., когда достигнута равнопрочность
элементов. Такой подход дает ошибку в безопасную сторону для большинства
практически реализуемых случаев, когда эффективный коэффициент концентрации
напряжений не больше теоретического. И хотя оценка получается относительной, и
на вопрос о времени появления вторичной трещины следует ответ: “Практически не
раньше, чем у концентратора-аналога”, данный подход представляется наиболее
целесообразным на сегодняшний день. Таким образом, в первом приближении задача
может быть сведена к определению концентрации напряжений при
статическом нагружении.
Известно, что коэффициент
концентрации напряжений определяется в основном длиной концентратора и радиусом
кривизны его контура в точке действия максимальных напряжений. Это позволяет в ряде случаев при определении концентрации
напряжений изучаемый концентратор
заменить на эквивалентный, решение для которого имеется. Можно
ввести понятие эквивалентного эллипса, позволяющее определить максимальный
коэффициент концентрации напряжений для концентратора в виде трещины с
отверстиями в ее концах в пластине при растяжении. Около концентратора
описывается эллипс (полуэллипс) с большой осью (полуосью),
равной длине концентратора, и минимальным радиусом в вершине, равным радиусу
отверстия. В таблице представлены теоретические коэффициенты концентрации
напряжений эквивалентного эллипса для различных случаев засверловки
отверстия.
Четвертая схема в таблице
соответствует взаимодействию круглого отверстия – инициатора трещины и
разгружающего отверстия. Из формулы видно, что при больших отношениях l/R засверливание концов трещины малоэффективно, т.к.
коэффициент концентрации напряжений может принимать достаточно большое
значение. Его уменьшение может быть достигнуто за счет замены формы
разгружающих отверстий, например, на эллиптические.
Однако изготовление такого отверстия трудоемко. Поэтому более целесообразным
представляется использование системы основных и дополнительных (деконцентраторов) разгружающих отверстий, эквивалентных
заменяемому эллиптическому отверстию. Некоторые такие возможные схемы приведены
в таблице. Значение N указывает долю коэффициента концентрации напряжений
при наличии дополнительных разгружающих отверстий в сравнении с их отсутствием.
Практически в среднем тридцатипятипроцентное уменьшение коэффициента
концентрации засверленной по концам трещины определяется сглаживанием
траектории главных напряжений растяжения в районе разгружающих отверстий.
Очевидно, что эффективное
использование систем разгружающих отверстий и ребер жесткости возможно лишь для
торможения равновесных трещин. Для торможения же быстроразвивающихся хрупких
трещин наиболее перспективным является применение стопперов в виде пластин или
полос из стали с повышенными вязкостными характеристиками, вваренными в
основную конструкцию. Способность стоппера тормозить трещину зависит как от
характеристик его материала, так и от размеров стоппера, его расположения
относительно места зарождения трещины и направления ее распространения. Отметим
лишь, что использование стопперов предполагает знание слабых мест конструкции,
подверженных трещинообразованию, и предусматривается, как правило, еще на
стадии проектирования конструкции или в проектах модернизации.
Таблица 22.5. Теоретические
коэффициенты концентрации напряжений
|
Конструктивная
схема
|
Выражение
для коэффициента концентрации
|
|
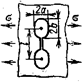 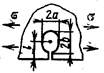
|

|
|
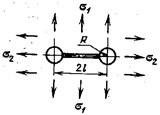
|
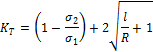
|
|
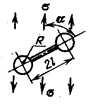
|
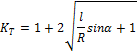
|
|
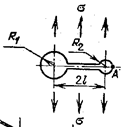
|
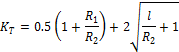
|
Таблица 22.6. Варианты
разгружающих отверстий у вершины трещины
|
Номер схемы
|
Геометрические
параметры (R/r=2)
|
N
|
|
1
|
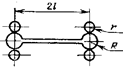
|
0.775
|
|
2
|
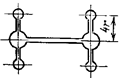
|
0.89
|
|
3
|
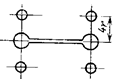
|
0.775
|
|
4
|
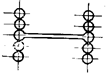
|
0.66
|
|
5
|
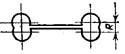
|
0.775
|
|
6
|
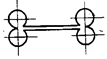
|
0.89
|
|
7
|
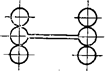
|
0.66
|
Напряженное и деформированное состояние в вершине трещины в
упругопластической области. Раскрытие трещины
В области, где не удовлетворяется условие маломасштабной
текучести, нельзя использовать коэффициент интенсивности напряжений. Подход,
связанный с использованием поправки Ирвина на пластичность здесь дает
существенную погрешность и необходимы другие критерии и подходы. Из
рассмотрения деформаций в вершине трещины непосредственно вытекает критерий
раскрытия трещины (COD).
1) Модель Дагдейла
Одним из методов, который
позволяет при плоском напряженном состоянии определить длину пластической
области перед трещиной. На рис. 22.79,а показана трещина длиной 2l.
Трещина находится в пластине, в которой на значительном удлинении от нее
действует растягивающее напряжение σ. У вершин трещины
образуются пластические области rp. При
составлении своей модели Дагдейл поступил
как показано на рис. 22.79,б, в. Он
предположил, что существует некоторая фиктивная упругая трещина, которая
состоит из действительной трещины и дополнительной вместо пластической зоны.
Участок действительной трещины имеет свободные поверхности, а участок вместо
пластической зоны представляет собой область, где действуют растягивающие
напряжения σт.
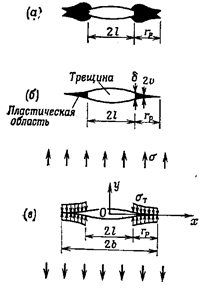
Рис.
22.79. Пояснение к модели Дагдейла
Таким подходом можно
пользоваться и при анализе напряжений упругости, возникающих в растягиваемых
телах, часть берегов трещины в которых подвержена действию напряжения σт. Для определения длины
пластической зоны rp
Дагдейл рассмотрел следующее. В вершинах пластических
зон напряжение равно σт
и особенность напряжений отсутствует. Поэтому в таких точках КИН обращается в
нуль. Используя КИН К1 рассматриваемой
трещины, обусловленный удаленными напряжениями, и КИН К2 из-за
напряжений σт,
действующих на берегах трещины, можно записать условие К1+К2=0.
Для бесконечной пластины с трещиной К1=σ(πb)1/2
(рис. 22.80). Таким образом, осталось найти КИН К2. Это можно сделать следующим образом. Как
показано на рис. 22.80, в точке с координатой х на берегах трещины действуют две сосредоточенные силы Р. В этом
случае для точек А и В КИН можно представить зависимостями

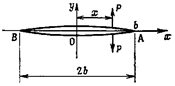
Рис. 22.80. Действие на трещину сосредоточенной раскрывающей нагрузки
Когда при l ≤|x|≤ b действуют равномерно распределенные растягивающие напряжения, в
предположении, что Р=
–σтdx, можно установить следующее

Интегрируя, получим

Следовательно

Полученную зависимость можно
преобразовать к виду
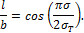
Отсюда для длины пластической
зоны можно получить выражение

При маломасштабной текучести,
т.е. в случае σ
<< σТ,
разлагая в ряд последнее выражение и отбрасывая члены более высокого порядка,
получаем

Представляет интерес сопоставить
полученный результат с поправкой Ирвина, т.е. с

Приходим к выводу, что сравниваемые
зависимости хорошо совпадают, если не принимать во внимание небольшое различие
в коэффициентах.
Перейдем теперь к определению
раскрытия трещины, основанному на модели Дагдейла.
Окончательный результат имеет вид
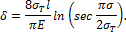
При маломасштабной текучести

На рис. 22.81 приведены
зависимости безразмерных длины пластической области и
раскрытия трещины от относительного напряжения, полученные из модели Дагдейла. Эти зависимости сопоставлены с результатами, установленными
при маломасштабной текучести. Факты свидетельствуют, что если относительное
напряжение не превышает 0.4…0.5, то можно считать, что допущение о
маломасштабной текучести справедливо.
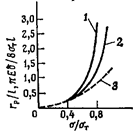
Рис. 22.81. Раскрытие трещины в вершине и длина пластической области
по модели Дагдейла:
1 – безразмерная длина
пластической области; 2 – безразмерное раскрытие трещины;
3 – результаты при
маломасштабной текучести
2) Модель Билби-Коттрелла-Суиндена
Билби,
Коттрелл и Суинден, не
используя модель Дагдейла, проанализировали
рассматриваемую задачу, полагая, что приемлемой является теория непрерывно
распределенных дислокаций. Они применили приведенную на рис. 22.82 модель,
согласно которой сама трещина и пластические области, расположенные по ее
концам, могут быть заменены некоторым фиктивным распределением дислокаций. В
такой модели трещина типа III (продольный сдвиг) может быть представлена
винтовыми дислокациями, а трещина типа II (поперечный сдвиг) – краевыми
дислокациями.
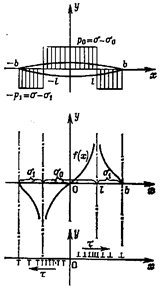
Рис. 22.82. Модель Билби-Коттрелла-Суиндена
(трещина типа II)
Из рассматриваемой модели
вытекает следующая зависимость для раскрытия трещины
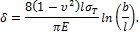
Моделями Дагдейла
и Билби-Коттрелла-Суиндена удобно пользоваться для
оценки COD в диапазоне полномасштабной текучести. Однако при равенстве
напряжений пределу текучести вдали от трещины пластические области становятся
бесконечно большими. При этом указанные модели теряют смысл и не могут быть
использованы для полной текучести. Чтобы обойти эти трудности, следует принять
во внимание, что в реальных материалах происходит деформационное упрочнение.
При этом в формулах предел текучести можно заменить пределом прочности.
3) Критерий
разрушения COD
Как и в случае ЛУМР,
использование критерия разрушения COD основано на допущении, что разрушение
наступает, когда раскрытие трещины в вершине δ
достигает некоторого критического значения δс, характерного для рассматриваемого
материала. Необходимо иметь в виду, что на настоящем этапе обоснование такого
допущения является еще несовершенным. Тем не менее, измерение δс материалов,
разрушающихся после общей текучести, представляет определенную ценность, так
как позволяет оценивать их относительную вязкость при данной температуре.
При этом должно быть ясное
представление о том, что значение δс относится
только к началу движения трещины, и в отличие от параметра КIc не характеризует точку полной нестабильности
разрушения, полученную из энергетических соотношений. Разница между δс при начале
роста трещины и при наступлении полной нестабильности ее развития может быть
существенной.
Таким образом, можно считать, что
среди критериев разрушения, основанных на использовании COD, можно выделить
величину δi появления
устойчивой трещины у затупившейся ее вершины, являющуюся параметром, который
можно рассматривать в большей степени как константу материала. Если говорить о
применимости δi для оценки
материала, то не обязательно следует иметь в виду проверку в широком диапазоне
толщин и форм образцов. Важными являются случаи, при которых используют
глубокие исходные разрезы. Это позволяет добиться значительной степени
стеснения, с которой приходится иметь дело на практике. Полученная для таких
случаев величина δi по крайней мере может служить критерием безопасности
для низкопрочных конструкционных материалов,
обладающих высокой пластичностью, у которых перед окончательным разрушением
происходит окончательный рост трещины. Следует также отметить, что
использование при проектировании величины δi идет в запас
прочности.
4) Оценка раскрытия
трещины
4.1) Определение раскрытия трещины на основе
центра поворота
При помощи представленного на рис.
22.83 центра поворота можно описать COD у образца, в котором под действием
изгибной нагрузки возникает полная текучесть.
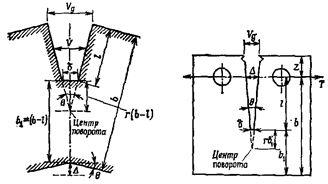
Рис. 22.83. Центр поворота образца для испытаний на трехточечный
изгиб
и компактного
образца
Полагают, что относительно этого
центра происходит поворот половинок образца как твердых тел. Здесь b1 – остаточная длина
сечения. Расстояние от вершины трещины до центра поворота можно представить как
rb1=r(b-l), где r –
коэффициент поворота. Раскрытие трещины на поверхности образца равно Vg и определяется датчиками раскрытия. Исходя из
простых геометрических соображений, можно найти раскрытие трещины в вершине
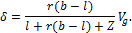
Образцы для изгиба приняты за стандартные для определения предельных значений COD в
лабораторных условиях. При этом по результатам измерения перемещений с помощью
датчиков раскрытия оценивают COD по специальным формулам. При составлении таких
формул принимали во внимание также эффект, который вносит упругая деформация как в области маломасштабной текучести, так и в
области полномасштабной текучести.
4.2) Решение при
помощи МКЭ
Точное определение COD при помощи
МКЭ оказывается затруднительным. COD представляет собой раскрытие трещины в
вершине. Для его точного определения необходимо использовать решение,
учитывающее большие деформации. В обычных программах МКЭ полагают, что
деформации являются малыми. При этом считают, что узлы в вершине трещины
фиксированы. Поэтому в месте расположения таких узлов раскрытие трещины
оказывается равным нулю. Чтобы по результатам такого решения оценить COD,
приходится использовать различные приемы.
Экстраполяция. Предположим, что можно исключить из рассмотрения
один-два узла, которые располагаются в окрестности вершины трещины. При этом
перемещения других узлов, расположенных на трещине, укладываются почти на одну
прямую линию. Если для такой линии выполнить экстраполяцию до вершины трещины,
то можно получить соответствующую оценку для COD (рис. 22.84).
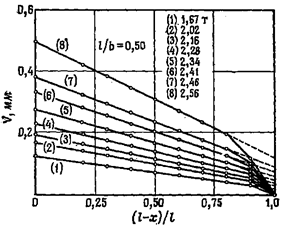
Рис. 22.84. Раскрытие трещины в вершине при трехточечном изгибе
при полной текучести
Такой подход оказывается возможным для образцов,
величина COD которых может быть выражена при помощи центра поворота. Это обычно
образцы для испытаний на трехточечный изгиб, компактные образцы, а также
образцы с одним краевым надрезом. При дальнейшей экстраполяции прямая линия
пересечется с осью, содержащей трещину. Можно считать, что точка пересечения
является центром поворота.
На рис.22.84 показаны перемещения
поверхности трещины у образца на трехточечный изгиб. По оси абсцисс отложен
параметр (l-x)/l. Нулевое значение
этого параметра соответствует поверхности образца, а единичное – вершине
трещины. Из рисунка видно, что если исключить два узла, считая от вершины
трещины, то раскрытия трещины будут укладываться почти на прямые линии. Если
для этих прямых провести экстраполяцию, показанную штриховыми линиями, то при (l-x)/l=1 можно определить
соответствующие значения COD. Продолжение этих линий до пересечения с осью
абсцисс позволит найти коэффициенты поворота. Полученные таким образом
коэффициенты поворота r в диапазоне
маломасштабной текучести принимают малые значения, а с ростом деформации
коэффициент поворота становится почти постоянным и равен 0.3.
Использование специальных элементов. В окрестности вершины трещины могут быть использованы
показанные на рис. 22.85 секторные элементы. Функцию перемещения для этих
элементов можно записать в виде

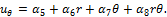
Рис. 22.85. Секторные элементы
Когда узлы i и
1 в вершине трещины совпадают, деформация внутри элемента имеет особенность
вида 1/r. С развитием деформации
складывается такая ситуация, при которой перемещение узла i отличается от перемещения узла 1. Ранее совпадавшие узлы
расходятся. Тогда перемещение в вершине трещины можно представить как функцию
параметра θ.
J-интеграл
1) Определение J-интеграла
Понятие J-интеграла было введено с целью исследования свойств концентрации
деформаций, которые происходят в окрестности вершины трещины в материале,
поведение которого носит нелинейный характер.
Рассмотрим однородное тело,
которое может обладать линейным и нелинейным поведением, и не имеет массовых
сил (рис. 22.86).

Рис. 22.86. Щелевой надрез и произвольный
контур,
охватывающий
его вершину
Положим, что в таком теле имеется
двумерное деформационное поле, все компоненты напряжений которого определяются
только двумя декартовыми координатами x=x1 и y=x2. Это
может быть плоская деформация, плоское напряженное состояние. Рассматриваемое
тело имеет надрез, который состоит из свободных поверхностей, параллельных оси
х, и дуги Гt.
Прямую трещину можно отнести к предельному случаю, при котором радиус кривизны
дуги обращается в нуль. Для этого тела плотность энергии деформации можно
определить как

Тогда J-интеграл можно определить в виде

где Г – контур, окружающий вершину
разреза. Интегрирование начинается с нижней поверхности надреза вдоль контура Г
против часовой стрелки и заканчивается на верхней поверхности надреза. Здесь Т – поверхностный
вектор силы, и – вектор перемещения
на контуре Г, а ds
– малый его элемент.
Доказано, что для произвольной
замкнутой кривой Г* справедливо

Рассмотрим два контура Г1 и Г2 (рис. 22.87).
Рис. 22.87. Два контура
интегрирования,
охватывающие вершину надреза
Начнем перемещаться вдоль контура
Г1 от нижней поверхности надреза против
часовой стрелки к верхней поверхности. Затем перейдем ко второму контуру Г2 и от верхней поверхности надреза переместимся к
нижней поверхности, двигаясь по часовой стрелке. По нижней поверхности надреза
вернемся в начальную точку контура Г1,
пройдя замкнутый путь. Поскольку в рассматриваемом случае образуется один
замкнутый контур, интеграл по этому контуру обращается в нуль. На участках,
которые расположены на поверхностях надреза и являются параллельными оси х, Т=0 и dy=0. На основании этого можно
записать

Это означает, что сумма интегралов: интеграла по
контуру Г1 (интегрирование против часовой стрелки)
и интеграла по контуру Г2 (интегрирование по часовой стрелке) равна
нулю. Если провести интегрирование по контурам Г1
и Г2, обходя контуры против часовой стрелки, то значения интегралов,
соответствующих этим контурам, будут равны. Следовательно, можно считать, что J-интеграл не зависит от пути
интегрирования.
2) Энергетическая трактовка J-интеграла
Два частных случая. Для двух приведенных на рис. 22.88
конфигураций можно весьма просто найти J-интеграл.

Рис.
22.88. Бесконечные полосы с полубесконечными
надрезами
Такие конфигурации не особо важны в реальных
задачах. Однако ими удобно пользоваться для объяснения зависимости, связывающей
J-интеграл с интенсивностью изменения потенциальной энергии. На рис. 22.52,а показана полубесконечная
полоса шириной h с разрезом, параллельным оси x. На верхнюю и нижнюю поверхности
полосы действуют внешние силы таким образом, что вектор перемещений u является постоянным
(поворот отсутствует). Остановимся на рассмотрении
показанного штриховой линией контура Г. Положим, что в направлении оси х
этот контур распространяется до бесконечности. Для частей контура,
расположенных на верхней и нижней поверхностях, можно считать, что dy=0
и ∂u/𝜕x=0. Поэтому вклад этих
частей в J-интеграл оказывается нулевым. Помимо этого следует иметь в виду, что
W=0 и ∂u/𝜕x=0 при х= -∞.
Поэтому вклад в J-интеграл на таком участке также отсутствует. Следовательно,
можно считать, что значение J-интеграла определяется вкладом, который имеет
место при х= +∞. Если принять во
внимание, что на этом участке ∂u/𝜕x=0, то
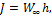
где W∞
- постоянная плотность энергии
деформации при х= +∞.
На рис. 22.88,б представлен случай, при котором рассматривается такая же
конфигурация, но с другими внешними нагрузками. При х= -∞
действуют моменты М, отнесенные к единице толщины. Таким образом, можно
считать, что при х= -∞ возникает чистый
изгиб. При этом все компоненты напряжений за исключением sх, можно положить равными нулю. Рассмотрим
показанный штриховой линией контур Г. Ввиду того, что при х= +∞
параметры W и Т обращаются в нуль, вклад в J-интеграл отсутствует.
Как и в предыдущем примере, на верхней и нижней поверхностях надреза dy и Т равны нулю и вклада в J-интеграл нет. Следовательно, в
рассматриваемом случае величина J может быть получена при х=
-∞
в результате интегрирования в направлении высоты балочного участка. На этом
участке dy= -ds, Ty = 0 и Tx = -𝜎x. Если учесть этот вклад для верхней и нижней балок, то можно
установить следующее

Величина Ω характеризует
плотность дополнительной энергии. Таким образом, при чистом изгибе, когда на
единицу толщины действует момент М, величину J можно
записать в виде
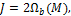
где Ωb(М) – дополнительная энергия, отнесенная к единицам длины
и толщины балок.
J-интеграл при маломасштабной текучести.
Положим, что в теле имеется узкий надрез или трещина, которая представляет
собой предельный случай надреза. Под действием внешних сил в окрестности
вершины надреза возникает маломасштабная текучесть (рис. 22.89).
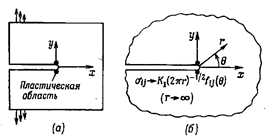
Рис. 22.89.
(а) маломасштабная текучесть у вершины трещины или надреза
в упругопластическом теле; (б) асимптотическая
аппроксимация при замене
конечного тела на бесконечное
с полубесконечным надрезом
Под действием симметричной нагрузки,
приложенной к участку, где расположена трещина или надрез, в материале
возникают деформации, которые носят плоский характер. Остановимся сначала на
решении задачи линейной упругости в предположении, что надрез представляет
собой острую трещину (или разрез). Воспользуемся полярными координатами r и
q, начало которых находится
в вершине трещины. Напряжение, действующее в вершине трещины, можно представить
так
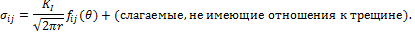
Положим, что в рассматриваемом материале
могут возникать упругопластические деформации. При действии достаточно малых
внешних сил у вершины трещины возникает пластическая область, которая
достаточно мала по сравнению с длиной разреза и другими размерами образца.
Таким образом, остановимся на случае маломасштабной текучести (рис. 22.89,а). Можно
предположить, что особенность напряжений вида r-1/2 является
определяющей с внешней стороны пластической области и располагается на
некотором удалении от вершины надреза, причем на таком участке, который
достаточно близок к вершине сравнительно с длиной разреза. Рисунок 22.89,а соответствует конфигурации, с которой
приходится иметь дело в действительности. Такую конфигурацию можно заменить
более простой (рис.22.89,б),
представляющей собой бесконечное тело, имеющее разрез полубесконечной
длины. В таком случае вместо граничных условий, характеризующих рис.22.89,а, используют асимптотическое граничное
условие

Полученное решение оказывается справедливым с
математической точки зрения только при очень низких внешних силах. Если
провести сопоставление с полным решением, при котором учитывается пластичность,
то можно, однако, установить, что решение, основанное на использовании
изложенного выше подхода, оказывается приемлемым до нагрузок, составляющих
значительную часть (примерно половину в обычных условиях) нагрузки, при которой
возникает полная текучесть. Воспользуемся таким подходом и проведем оценку
J-интеграла. С этой целью для случая рис.22.89,б примем, что контур Г представляет собой большую окружность
радиуса r. Тогда
можно записать следующее:
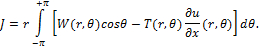
Согласно инвариантности, можно считать, что
при любом радиусе r величина J не изменяется. Это
позволяет считать, что возможен предельный переход при r →∞.
Зависимость W от деформации является зависимостью
второго порядка. В таком случае члены в
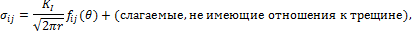
имеющие особенность r-1/2, в основном и определяют величину J. Вклад, который вносят другие члены, можно при переходе к
пределу не принимать во внимание. Если выполнить операцию интегрирования
предпоследнего уравнения, полагая, что существует поле плоской деформации, то
для маломасштабной текучести можно установить следующее соотношение:
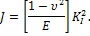
Для бесконечной пластины, имеющей разрез
длиной 2l, в
которой на значительном удалении от разреза действуют равномерно распределенные
растягивающие напряжения σ∞,
можно установить, что KI = σ∞(πl)-1/2. Следовательно, в
случае маломасштабной текучести
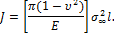
Для плоского напряженного состояния вместо
(1-n2) следует
подставить единицу. Аналогично можно поступить и при нагрузке общего вида.
Можно воспользоваться коэффициентами KI, KII, KIII, которые
представляют соответственно отрыв, поперечный и продольный сдвиг. Если
существует поле, в котором сосуществуют эти три параметра, то при
маломасштабной текучести получим
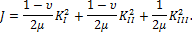
Таким образом, J-интеграл эквивалентен
интенсивности освобождения упругой энергии G в
области маломасштабной текучести.
Связь J-интеграла с интенсивностью
освобождения упругой энергии. Рассмотрим двумерное упругое тело с
надрезом (рис. 22.90).
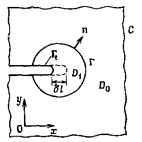
Рис. 22.90.
Контур интегрирования, охватывающий вершину надреза
Это тело занимает область D, имеющую границу С. Приходящаяся на единицу толщины
потенциальная энергия

где СТ – часть границы С, на которой задана поверхностная сила Т. Положим, что
происходит переход от одного состояния к другому, который сопровождается
увеличением надреза на величину δl. При этом конфигурация
контура Гt у вершины
надреза остается прежней. В результате изменения длины надреза на dl происходит
изменение потенциальной энергии. После проведения всех выкладок оказывается,
что J = - ∂П/∂l.
Таким образом, J-интеграл может быть представлен через интенсивность освобождения упругой
потенциальной энергии при изменении длины надреза. Можно считать, что
J-интеграл, с одной стороны, имеет смысл интенсивности освобождения упругой
энергии, а с другой – представляет собой параметр, который характеризует
местное поле деформаций, возникающее в окрестности вершины разреза.
3) Применение J-интеграла
Определение концентрации деформации у
вершины трещины. Понятие
J-интеграла впервые было введено Райсом и Черепановым с целью исследования
свойств концентрации деформаций, которые происходят в окрестности вершины
трещины в материале, поведение которого носит нелинейный характер. Примерно
одновременно были опубликованы работы Хатчинсона, а также Райса и Розенгрена, в которых были рассмотрены особенности
деформаций у вершин трещин, возникающих в материалах, следующих деформационной
теории пластичности. Полученное решение назвали ХРР-решением, используя
начальные буквы фамилий указанных авторов. Основные результаты здесь
заключаются в следующем.
Связь между напряжениями и деформациями может
быть представлена степенным законом упрочнения в следующем виде

где εП
– пластическая составляющая деформации; σТ
– предел текучести при растяжении; εТ
=σТ/E; α и n – постоянные материала. В случае ХРР-решения считают, что для
указанного выше уравнения связи в окрестности вершины трещины имеет место
асимптотическое решение и что напряжение, деформация и энергия деформации имеют
особенности вида r-1/(n+1), r—n/(n+1), r-1 соответственно. При этом имеет место
зависимость J=IKσKε, где I – безразмерный
коэффициент; Kσ - пластический коэффициент
интенсивности напряжений; K𝜀 -
коэффициент интенсивности деформаций. При n = 1

имеет место линейно-упругое состояние.
Критерий разрушения Jc. Для использования J-интеграла как
параметра, описывающего условия разрушения пластического тела, теоретических
обоснований недостаточно. Тем не менее, эксперименты и численные расчеты
показывают, что J-интеграл может быть использован в
такой роли при проектировании с учетом того, что разрушение не должно
произойти.
Положим, что существуют две трещины: одна в
компактном образце, предназначенном для проведения испытаний в лабораторных
условиях, а вторая – в крупном элементе реальной конструкции. И образец, и
элемент изготовлены из одного и того же материала,
обладающего высокой пластичностью. Полученные расчетным путем значения
J-интеграла в случае их равенства некоторому постоянному значению JIc свидетельствуют о том, что начинается рост
трещины. Следует иметь в виду, что при высокой пластичности материала, прежде
чем будет достигнуто значение JIc, в компактном
образце возникнет значительная пластическая деформация и уменьшится стеснение
деформаций. При этом может случиться, что даже после достижения значения JIc будет происходить устойчивое распространение
трещины. В крупном элементе конструкции при достижении значения JIc еще будет маломасштабная
текучесть, а за пределами этого значения произойдет неустойчивое разрушение.
Результаты экспериментальных исследований,
полученные для различных материалов, показывают, что существует предельное
значение J, соответствующее возникновению разрушения и не зависящее от
конфигурации образца. Средние значения для наиболее распространенных
легированных сталей составляют 170…190 кДж/м2.
Итак, измерения COD и JIc являются попыткой охарактеризовать вязкое разрушение
однозначным параметром, который может быть связан с критической величиной
высвобождения энергии при разрушении массивного образца перед наступлением
общей текучести. Критерий раскрытия трещины сосредоточивает внимание на области
вершины трещины, и его можно прямо связать с микромеханизмами
разрушения на площади около 0.01 мм2;
J-интеграл связан с макроскопической работой или условиями у вершины трещины в
зависимости от выбранного Г-контура. Основным недостатком, как и в случае с КIc,
является то, что критическая величина параметра JIc не имеет физического обоснования.
4) Оценка J-интеграла
4.1) Энергетические способы
Из приведенных выше рассуждений об
энергетической трактовке J-интеграла следует, что J-интеграл представляет собой
разность потенциальных энергий двух напряженных тел, у которых длины трещин
отличаются на небольшую величину, а в остальном конфигурации идентичны.
Следовательно, для линейно упругих тел, обладающих маломасштабной текучестью,
J-интеграл эквивалентен силе G, движущей трещину. При
анализе нелинейно-упругих тел J-интеграл можно трактовать как энергию,
необходимую для роста трещины.
На рис. 22.91,а показана диаграмма нагрузка – перемещение точки приложения
нагрузки (здесь имеется в виду нагрузка, отнесенная к толщине, т.е. Р/t).
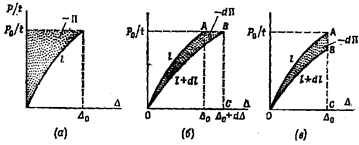
Рис. 22.91. Связь потенциальной энергии
системы
с диаграммами
нагрузка – перемещение точки приложения нагрузки
В этом случае потенциальной
энергии системы П, приходящейся на единицу толщины
образца, соответствует на рисунке отрицательная величина, показанная
затемненной областью. Эта величина равна дополнительной энергии с отрицательным
знаком. При фиксированном перемещении можно считать, что потенциальная энергия
равна энергии деформации, т.е. площади, расположенной под диаграммой нагрузка –
перемещение точки приложения нагрузки.
Остановимся на случае, когда в
нелинейно-упругом теле распространяется трещина длиной l. Такому случаю соответствует диаграмма на рис. 22.91,б. Под действием постоянной нагрузки Р0 произойдет распространение трещины – длина
трещины возрастет от l до l+dl. При
этом произведенная работа представлена площадью ОАВСО. Исходя из обратимости
нелинейно-упругого тела, можно считать, что кривая, соответствующая разгрузке
из точки В, совпадает с кривой ОВ, при которой тело
имеет трещину l+dl.
При нагружении такого тела до Р0
энергия деформации представлена площадью ОВСО. При этом затемненная площадь
ОАВО равна работе, затраченной на распространение трещины на dl, т.е. энергии,
необходимой для того, чтобы трещина выросла на dl. Эта площадь представляет собой приходящуюся на единицу толщины
разность потенциальных энергий тел с трещинами длиной l и l+dl,
находящихся под действием внешней силы Р0.
Применяя свойства обратимости упругого тела, можно считать, что J-интеграл, J= -∂П/∂l, является
энергией, затрачиваемой на то, чтобы трещина распространилась на единицу длины.
Если развитие трещины происходит
при постоянном перемещении (рис. 22.91,б),
то, ввиду того, что потенциальная энергия системы равна энергии деформации,
связанная с распространением трещины интенсивность освобождения энергии
оказывается равной -∂П/∂l. Исключая из
рассмотрения величины более высоких порядков, вызванные малыми приращениями d∆, считаем, что затемненные площади на рис. 22.91,б, в равны и
могут быть представлены как – dП.
Этими рассуждениями, а именно,
соотношением J = -∂П/∂l, пользуются,
когда необходимо теоретически или экспериментально определить J-интеграл.
Экспериментальная методика Бигли-Лэндеса. На рис.22.92 даны установленные экспериментально
диаграммы нагрузка-перемещение для образцов одинаковой формы, изготовленных из
одного материала.
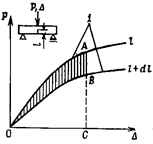
Рис. 22.92. Экспериментальная оценка
параметра J:
1 –
экспериментальные диаграммы
Образцы имели трещины длиной l и
l+dl. Следует обратить внимание на область,
ограниченную кривыми ОА и ОВ. Площадь этой области равна Jdl. Таким образом, можно экспериментально
найти величину J. В рассматриваемой методике для оценки величины J необходимо
иметь несколько образцов. Вследствие этого затраты на проведение
экспериментальных исследований возрастают. Поскольку результаты эксперимента
обрабатываются графически, трудоемкость оказывается значительной, а точность
результатов невысока.
Теоретическая методика Буччи. Буччи воспользовался упругим решением, а также анализом
предельного состояния, в котором после полной текучести не учитываются упругие деформации
и деформационное упрочнение.
По этим данным построены диаграммы
нагрузка – перемещение (рис.22.93).
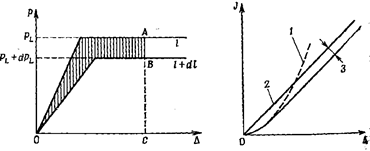
Рис. 22.93. Определение J с помощью упругопластического решения методом Буччи.
Зависимость J от ∆: 1 – упругое
решение; 2 – жесткопластическое решение;
3 – смещение диаграммы (суммарное решение)
При помощи зависимости J=-∂П/∂l, и этой диаграммы проведен расчет величины J. Следует отметить, что при такой оценке J-интеграла
считают, что можно не учитывать упругопластические деформации перед полной
текучестью и не состыковывать плавно-упругое решение J=f(∆2) c
жесткопластическим решением J=f(∆), а положить, что график J лишь смещается в области полной текучести. Это
смещение показано на рисунке. Для учета упругопластической области Буччи предложил использовать обычные поправки на
пластичность, в основе которых лежит коэффициент интенсивности напряжений:
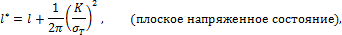
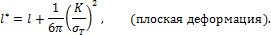
При таком подходе установлено, что
полученная расчетным путем диаграмма J-∆, для которой
с помощью последних формул введены поправки при плоском напряженном состоянии,
совпала с результатами экспериментальных исследований. Однако Буччи указал, что толщина образца может вносить
свои эффекты и поправка при плоском напряженном состоянии не всегда приемлема.
Предложенная методика позволяет
теоретически сравнительно просто оценить J-интеграл. Поэтому, когда необходимо
проанализировать основные свойства J-интеграла, пользуются такой методикой.
Упрощенные зависимости Райса. Райс предложил
способ оценки J-интеграла, при котором диаграмма нагрузка – перемещение зависит
только от остаточной длины сечения, обозначенной на рис. 22.94 через b1.
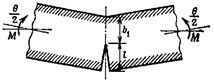
Рис. 22.94. Изгиб образца
В рассматриваемом случае получены
соответствующие выражения J для образцов
на растяжение с двумя боковыми трещинами, одной центральной или кольцевой, а
также для образцов на изгиб с односторонней трещиной. Без вывода эти выражения
приведены в таблице 22.7.
Таблица 22.7
|
Образец
|
Расчетная
зависимость
|
|
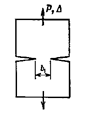 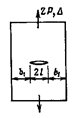
|

∆p – перемещение точки перемещения
нагрузки,
обусловленное
пластичностью
|
|
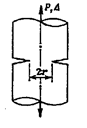
|

∆с – вклад в ∆, вносимый
трещиной
|
|
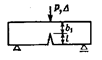 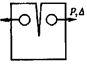
|

|
Эти зависимости позволяют довольно
просто определить J-интеграл. Такая методика при экспериментальной оценке
обладает следующими преимуществами:
1) Можно непосредственно
использовать диаграмму P - ∆, полученную экспериментально.
2) В отличие от методики Бигли и Лэндеса можно
воспользоваться лишь одной кривой P - ∆.
4.2) Определение J-интеграла методом конечных элементов
Чтобы с помощью МКЭ вычислить
J-интеграл, необходимо сначала разбить рассматриваемое тело на элементы и
определить соответствующие константы материала. Затем, постепенно увеличивая
нагрузку и удовлетворяя заданным граничным условиям, можно провести
упругопластическое решение. Для каждого шага нагрузки
определяют различные параметры (перемещение, деформацию, напряжение, энергию
деформации и т.п. (далее с помощью этих параметров вычисляется J-интеграл
различными способами.
Используя определение J-интеграла,
и интегрируя по контуру, можно непосредственно найти J-интеграл.
То, что Бигли
и Лэндес выполняли экспериментально, можно выполнить
МКЭ. С этой целью удобно воспользоваться способом, приведенным на рис. 22.92.
При этом следует найти площадь, заключенную между кривыми P - ∆, построенными
для двух образцов, у которых длины трещин отличаются лишь на ∆l. Используя эту
площадь, можно вычислить J-интеграл.
J-интеграл можно найти по
упрощенным зависимостям, например, по зависимостям Райса. При этом можно
обойтись одной кривой P - ∆.
Связь силового, деформационного и энергетического критериев
механик разрушения
Итак, мы рассмотрели три
классических параметра, характеризующих условия наступления разрушения в
различных условиях. Выше было показано, что в упругой области коэффициент
интенсивности напряжений и J-интеграл однозначно связаны с интенсивностью
высвобождения упругой энергии. При этом выявлена непосредственная связь между
КИН и J-интегралом вида
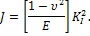
Между J-интегралом и раскрытием
трещины также существуют простые зависимости.
В случае маломасштабной текучести
можно использовать зависимость J=m𝜎T𝛿. Здесь m – параметр,
зависящий от пластического стеснения. При плоском напряженном состоянии m=1, а при
плоской деформации 1<m<3.
В диапазоне полномасштабной
текучести зависимость между J и COD
вытекает из модели Дагдейла и имеет вид J=𝛿𝜎T.
Таким образом, как видно, в
упругой области имеется однозначная связь между тремя основными параметрами
механики разрушения. Зная один из них, всегда можно вычислить два других.
Вопросы
для самопроверки
1. Какие виды разрушения и типы трещин вы
знаете?
2. Что понимается под линейным дефектом
структуры материала?
3. Что такое двумерный дефект?
4. Приведите примеры объемных дефектов в
структуре материала.
5. Как определяется теоретическая прочность
материала?
6. В чем заключается разница между
теоретической и технической прочностями материала?
7. Объясните смысл теории Гриффитса.
8. Напишите формулу, по которой определяется
коэффициент интенсивности напряжения.
9. Какая принципиальная разница между
коэффициентом интенсивности напряжения и коэффициентом вязкости разрушения?
10. Как определяется коэффициент вязкости
разрушения?
11. Каков принцип расчета на прочность
материалов с трещиной?
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин
Теория машин и механизмов



![]()
![]() Поэтому получаем:
Поэтому получаем:![]()
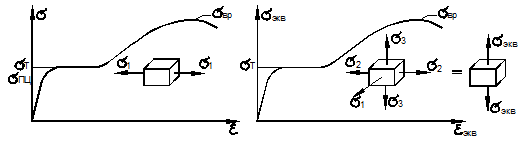
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Условие пластичности принимает вид
. Условие пластичности принимает вид![]()
![]()
![]() . Условие прочности, согласно (22.3), запишем
в виде
. Условие прочности, согласно (22.3), запишем
в виде![]()
![]()
![]() . Следовательно,
. Следовательно, ![]() и
потому, согласно (22.2),
и
потому, согласно (22.2),![]()
![]()
![]() Из (22.7) следует
Из (22.7) следует ![]() Сравнивая значения постоянных
Сравнивая значения постоянных ![]() при
растяжении и чистом сдвиге, находим связь между пределами текучести:
при
растяжении и чистом сдвиге, находим связь между пределами текучести:![]()
![]() Отметим, что условие Сен-Венана и Мизеса
дают различные формулы, связывающие пределы текучести k и
Отметим, что условие Сен-Венана и Мизеса
дают различные формулы, связывающие пределы текучести k и ![]() при
чистом плоском сдвиге и растяжении.
при
чистом плоском сдвиге и растяжении.![]()
![]() , то мы можем в одной плоскости построить три
окружности Мора (рис.22.5, а).
Условие (22.9) изображается в этой плоскости некоторой кривой.
, то мы можем в одной плоскости построить три
окружности Мора (рис.22.5, а).
Условие (22.9) изображается в этой плоскости некоторой кривой.
![]() . Необходимо провести несколько испытаний до
разрушения при различных однородных напряженных состояниях, т.е. различных сотношениях
. Необходимо провести несколько испытаний до
разрушения при различных однородных напряженных состояниях, т.е. различных сотношениях ![]() , а затем построить круги Мора. На рис. 22.6
построены три предельных круга Мора для случаев растяжения чистого сдвига и
сжатия. Огибающая этих предельных окружностей и будет предельной кривой.
Наиболее просто построить предельные окружности Мора при растяжении и сжатии
(рис. 22.7, а). Проведем к ним касательную и допустим, что эта касательная
служит предельной огибающей
, а затем построить круги Мора. На рис. 22.6
построены три предельных круга Мора для случаев растяжения чистого сдвига и
сжатия. Огибающая этих предельных окружностей и будет предельной кривой.
Наиболее просто построить предельные окружности Мора при растяжении и сжатии
(рис. 22.7, а). Проведем к ним касательную и допустим, что эта касательная
служит предельной огибающей ![]() .
.![]() .
.

![]()
![]()
![]() в
виде
в
виде![]()
![]()
![]() и
потому b
и
потому b![]() . В случае сжатия
. В случае сжатия ![]() Следовательно,
Следовательно, ![]() .
Таким образом, условие разрушения по Мору
.
Таким образом, условие разрушения по Мору ![]()
![]()
![]() -
допустимое напряжение на растяжение.
-
допустимое напряжение на растяжение.![]() ) условие (22.10)
превращается в условие прочности по Сен-Венану. Отметим, что у некоторых
пластичных материалов пределы текучести при растяжении и сжатии различны, т.е.
) условие (22.10)
превращается в условие прочности по Сен-Венану. Отметим, что у некоторых
пластичных материалов пределы текучести при растяжении и сжатии различны, т.е. ![]() . В этом случае условие Мора (22.10)
преобразуется в условие пластичности для таких материалов:
. В этом случае условие Мора (22.10)
преобразуется в условие пластичности для таких материалов:![]()
![]() , т.е. по существу обоснована только для
плоского напряженного состояния.
, т.е. по существу обоснована только для
плоского напряженного состояния.![]()
![]() приходим к условию пластичности
Мизеса (прямая 1-1 на pис.22.8). В общем случае
предельная кривая
приходим к условию пластичности
Мизеса (прямая 1-1 на pис.22.8). В общем случае
предельная кривая ![]() является гладкой. Прямая
2-2 соответствует хрупкому разрушению от всестороннего растяжения. Эта кривая
задается некоторым аналитическим выражением, соответствующим экспериментальным
данным.
является гладкой. Прямая
2-2 соответствует хрупкому разрушению от всестороннего растяжения. Эта кривая
задается некоторым аналитическим выражением, соответствующим экспериментальным
данным.
![]() произвольного
предельного напряжённого состояния, а также круг Мора в предельном состоянии
для напряжённого состояния чистого сдвига.
произвольного
предельного напряжённого состояния, а также круг Мора в предельном состоянии
для напряжённого состояния чистого сдвига.
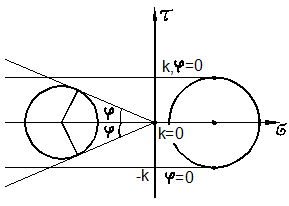
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]() - векторы трансляции, т.е. смещения, соединяющие
узел О с
ближайшими атомами по трем осям; ni – целые числа.
- векторы трансляции, т.е. смещения, соединяющие
узел О с
ближайшими атомами по трем осям; ni – целые числа. 













![]()
![]()
![]()
![]() (степенная
ползучесть, power low creep), где В
и п — материальные постоянные; поры
зарождаются в этом случае внутри зерен. Однако вследствие того, что
пластическое течение при температурах Т > 0,3Тпл зависит от времени, оно может происходить при
весьма низких напряжениях, и процесс зарождения пор оказывается длительным.
Более того, может замедляться также и процесс слияния пор. В итоге разрушение
оказывается зависящим от времени.
(степенная
ползучесть, power low creep), где В
и п — материальные постоянные; поры
зарождаются в этом случае внутри зерен. Однако вследствие того, что
пластическое течение при температурах Т > 0,3Тпл зависит от времени, оно может происходить при
весьма низких напряжениях, и процесс зарождения пор оказывается длительным.
Более того, может замедляться также и процесс слияния пор. В итоге разрушение
оказывается зависящим от времени.![]() , где tf – долговечность (время до разрушения),
, где tf – долговечность (время до разрушения), ![]() – скорость установившейся ползучести. В
основе этого соотношения лежит предположение о том, что разрушение происходит в
результате степенной ползучести, которая контролирует зернограничное
скольжение и, следовательно,
зарождение пор, которое при этом занимает основную долю жизни металла. Если же
основную долю жизни занимает процесс роста пор, то это контролируется
диффузионными процессами, которые в свою очередь определяются степенной
ползучестью окружающей матрицы.
– скорость установившейся ползучести. В
основе этого соотношения лежит предположение о том, что разрушение происходит в
результате степенной ползучести, которая контролирует зернограничное
скольжение и, следовательно,
зарождение пор, которое при этом занимает основную долю жизни металла. Если же
основную долю жизни занимает процесс роста пор, то это контролируется
диффузионными процессами, которые в свою очередь определяются степенной
ползучестью окружающей матрицы.