6. ТОЧНОСТЬ

Числовое моделирование требует упрощений и приближений. Результаты анализа FEA не дают 100%-ную гарантию от ошибок. Использование такого мощного инструмента, как "черного ящика", без надлежащего понимания его основных особенностей, может привести пользователей к серьезным ошибкам. К сожалению, человеческие ошибки неизбежны.

Проектировщик должен понимать:

-   Какой FE анализ является соответствующим для данной задачи;
-   Какая часть структуры, должна быть изучена детально;
-   Какие упрощения можно применить для частной ситуации.



Успех решения FEA зависит от того, как близко отвечают действительности граничные условия, геометрия и поведение материала модели. Ошибки формулировки имеют место, если конечные элементы неточно описывают поведение физической задачи.

Отбор походящего типа элемента и сетки уменьшают ошибки формулировки. Формулировка граничных условий – наиболее критический шаг анализа. Успех решения FEA зависит от того, как близко отвечают действительности граничные условия, геометрия и поведение материала модели.

FEM приближение реальной инженерной структуры с конечным количеством конечных элементов, также как размер и форма элементов, может вызвать ошибку дискретизации.

Числовые ошибки обычно более редки, по сравнению с ошибками формулировки и дискретизации.

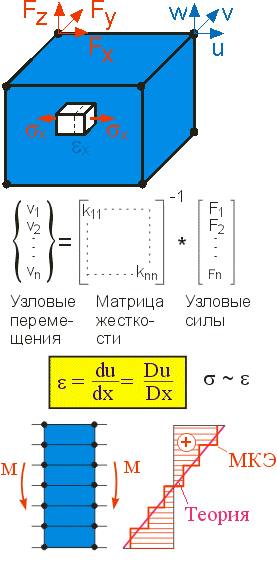
Перемещения сначала являются неизвестными величинами. FEM решение обычно получают в виде вектора узловых перемещений {v}. Решение во всех других областях элемента получается интерполяцией. После получения поля перемещений с функциями формы могут быть рассчитаны деформация и напряжение. Это означает, что точность для узловых перемещений должна быть максимальная. Деформация рассчитывается как разница между перемещениями соответствующих точек. Это является доказательством того, почему точность величин деформаций и напряжений максимальна в центральной части конечных элементов. Рисунок показывает распределение напряжений при изгибе. Теоретические и численные решения совпадают в центре элементов.

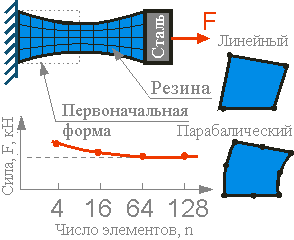
Тип и количество конечных элементов влияют на точность моделирования. Тип и количество конечных элементов влияют на точность моделирования. Для нелинейного анализа, где рассчитывается сила, количество конечных элементов в модели влияет на величину силы только при небольшом количестве. Сила становится стабильной с увеличением количества элементов.

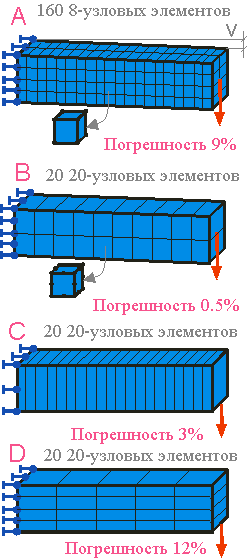
Существуют два метода для увеличения точности существующего решения: H-метод требует увеличить количество элементов (h длина стороны конечного элемента); В P-методе увеличивается полиномиальный порядок конечных элементов. Элементы второго порядка B демонстрируют более высокую точность. Для изгиба консольной балки одного элемента на всю высоту балки не достаточно. Чем больше количество параболических элементов по длине, тем лучше.

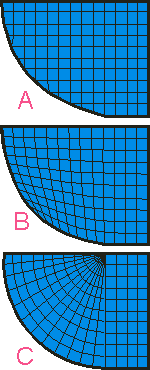
Сетка A предпочтительна для решения задач вычислительной динамики текучей среды (CFD). A. Структурная прямоугольная сетка.   Числовые аппроксимации сосредоточены в центре тяжести прямоугольного элемента. B. Структурная деформированная сетка.   Имеются много элементов, где числовые аппроксимации не центрированы (или симметричны). C. Структурная блочная сетка.   Элементы уплотнены в одной точке вдоль границы прямого участка.

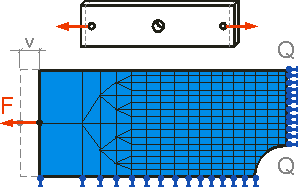
Нелинейный структурный анализ прогнозирует поведение образца из мягкой стали. Редкая сетка на левом конце не оказывает существенного влияния на результаты, чем область с более плотной сеткой, так как в этой области находятся величина максимального напряжения, деформации в области Q-Q и деформированная форма центрального отверстия. Условие приложения силы к левой стороне модели грубо совпадает с реальной ситуацией. Возможны ошибки на диаграмме " Сила - Перемещение F-v ".

Ошибки из-за численного анализа увеличиваются, если небольшие значения объемной деформации eV умножаются на большие значения объемного модуля K. Такой анализ требует дополнительных испытаний. Данная ситуация происходит, если коэффициент Пуассона приближается к значению 0.5.