5. ДЕФОРМАЦИЯ

Более всего процедуры метода конечных элементов базируются на "методе перемещений". Из условия равновесия, сумма сил (внутренних и внешних) в узле должна равняться нулю. Неизвестные переменные - перемещения. Далее представление уравнений равновесия в матричной форме:

[K] {D} = {F}

[K] = глобальная матрица жесткости;
{D}= вектор перемещения;
{R} = вектор сил.

Матрица жесткости [K] симметрична относительно диагонали. Имеются два главных типа методов решения: прямой и итерационный. Прямые методы решения обычно базируются на Гауссовском методе исключения. Прямые методы более четкие, но могут быть медленными и требуют больше места на диске для решения больших задач. Итерационные методы более быстрые и требуют немного места на диске.

Решением матричного уравнения является вектор перемещений {D}. По результатам перемещений вычисляются деформации.

Рисунок показывает, как деформация зависит от узловых перемещений. При перемещении жесткого тела по оси b>x на 5 мм, то деформация ex = 0. Если перемещение v увеличивается по оси y, то деформация ey положительна.

Для элементов первого порядка деформация растяжения определяется разницей соответствующих перемещений.

Имеется линейная функция для перемещений внутри элемента с 4 узлами. Это означает, что максимальное перемещение может быть только в узлах. Деформация постоянна для элемента. Для показанного элемента второго порядка функция деформации квадратичная.

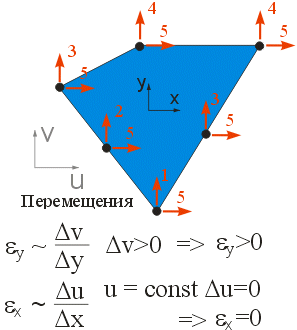
Рисунок показывает начальную и деформированную форму тонкой пластины. Фактор увеличения k=1. Можно получить большую деформацию, даже если свойства материала остаются линейными (упругими). Проблема была решена в соответствии с (геометрически) нелинейной структурной процедурой. В этом случае применено постепенное приложение нагрузки. Небольшая изгибная жесткость позволяет осуществить большую линейную деформацию. Изгибная жесткость небольшая, если модуль упругости или толщина t тоже небольшие. Теоретически, размеры конечных элементов не влияют на жесткость.

Деформированная форма помогает пользователю решать, правильно ли установлены граничные условия. Нет вращений по граням 1 и 2, а только вращения по граням 3 и 4.

Все перемещения линейны для плоского элемента с четырьмя узлами. Между конечными элементами нет промежутков. Грани могут быть полигональными линиями, если количество конечных элементов в модели большое.

На рисунке показаны деформированные структуры для различных схем нагружения. Однородные напряжения и деформации могут быть получены для первой схемы. Лучше, если нагрузка вдвое меньше на гранях, чем в центре.

Максимальная деформация находится в точке, где приложена сила. Максимальное напряжение среза в теле действует на поверхности элемента под силой. Жесткая пластина перераспределяет силу в теле. Контактное напряжение в теле меньше для второго примера. Расчетное значение максимального напряжения среза зависит от размера конечных элементов.

Левый конец вала был зафиксирован во всех узлах. На правом конце два узла были перемещены на 2 мм. Нагрузка соответствует кручению. На правом конце напряжение неоднородно. Если концы вала выполнены из относительно жесткого материала, то локальная деформация будет распределяться на весь вал. Поле напряжений более однородно для второго случая.