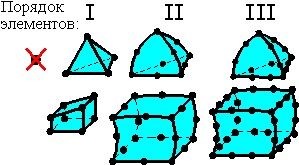
|
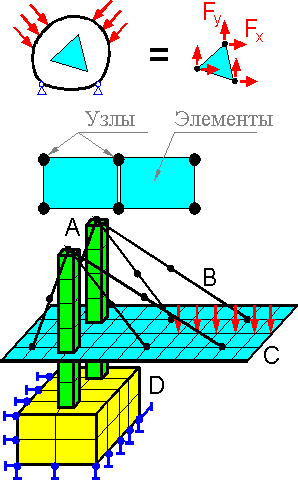
Обычно используются несколько типов конечных элементов: балка A, связка B, тонкая оболочка C, 2D или 3D среда (D). В модели можно использовать несколько типов элементов.
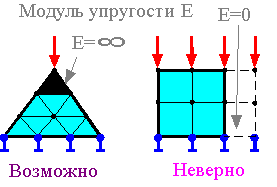
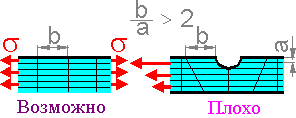
Надежность результатов метода конечных элементов зависит от количества конечных элементов. Если внутренние напряжения не изменяются в больших пределах, то количество конечных элементов не имеет значения для точности.