1. КРИСТАЛЛИЧЕСКИЕ ТЕЛА

Самая малая повторяющаяся единица структуры в кристалле называется элементарной ячейкой. Геометрия и положение атомов в пределах элементарной ячейки определяют структуру кристаллических материалов. Три длины ребер (a, b, c) и внутренние углы (a, b, g) используются для описания геометрии единичной ячейки. В зависимости от величины a, b, c и a, b, g определяют семь кристаллических систем координат и четырнадцать возможных элементарных ячеек (решетки Бравэ). 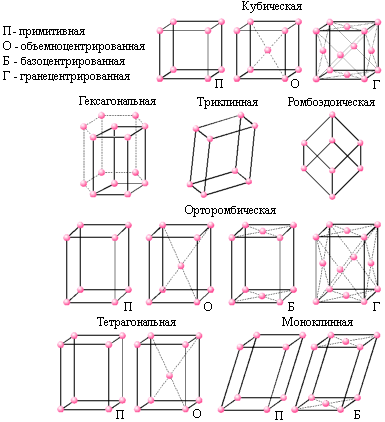Система Длины Углы Кубическая a=b=c a=b=g=90o Тетрагональная a=b№c a=b=g=90o Моноклинная a№b№c a=g=90o№b Орторомбическая a№b№c a=b=g№90o Ромбоэдрическая a=b=c a=b=g№90o Гексагональная a=b№c a=b=90o, g=120o Триклинная a№b№c a№b№g№90o

Некоторые из атомов в пределах элементарной ячейки могут принадлежать нескольким смежным ячейкам. Поэтому, для вычисления числа атомов в элементарной ячейке мы должны рассмотреть следующие вклады для частицы согласно ее положению: - Атомы, расположенные в центре грани, считают как 1/2; - Атомы, расположенные в центре ребер, считают как 1/4; - Атомы, расположенные в углах, считают как 1/8 В примитивной кубической ячейке число атомов в элементарной ячейке = 1; в объемноцентрированной кубической = 2; в гранецентрированной кубической = 4. Коэффициент заполнения = (Объем атомов)/(Объем элементарной ячейки). Для примитивной кубической ячейки – коэффициент заполнения = 0.52; для объемноцентрированной кубической (ОЦК) - 0.68; для гранецентрированной кубической ячейки (ГЦС)- 0.74

Для определения кристаллографических направлений (индексов направлений) по осям [uvw] в элементарной ячейке необходимо: 1. Найти проекции вектора на три оси в единицах элементарной ячейки. A - 1,0,1;   B - 0,1/2,1;   C - 0,1,1/2; D - 1/2,1,0;   E - 1,1,0;   F - 1,1/2,0. 2. Привести отношение этих координат к отношению трех наименьших целых чисел. A - [101];   B - [012];   C - [021]; D - [120];   E - [110];   F - [210].

Плоскость в пределах кристалла определяется индексами Миллера (кристаллографические индексы). Для определения кристаллографических индексов (hkl) плоскости необходимо: 1. Найти координаты пересечения плоскости по трем осям в единицах элементарной ячейки. 2. Определить обратные величины этих значений. 3. Привести их к наименьшему целому, кратному каждому из полученных чисел.

Существует два главных типа плоскостных (двухмерных) дефектов реальных кристаллов, которые называются дислокациями – краевая дислокация и винтовая дислокация. Дислокация - резкое изменение порядка атомов вдоль линии. Дислокации перемещаются по плоскости скольжения. Величина и направление скольжения определяются вектором Бюргерса, b. Для краевой дислокации направление скольжения перпендикулярно направлению дислокации. Для винтовой дислокации направление скольжения параллельно направлению дислокации.

При пластической деформации металла смещение атомов происходит по плоскостям (как показано на рисунке) в направлении максимальной плотности атомов. Плоскости и направления скольжения образуют системы скольжения. Если существует много систем скольжения, тогда деформирование кристалла может происходить относительно легко и, такой металл является пластичным. ОЦК кристаллические структуры имеет до 48 систем скольжения. ГЦК кристаллические структуры имеет 12 систем скольжения. Кристаллические структуры, имеющие гексагональную плотную упаковку (ГПУ), имеют только 3 системы скольжения. Соответственно, большинство металлов с ГПУ кристаллической структурой (Мг, Zn, Be) менее податливы, чем металлы с ОЦК (W, Fe, K) или ГЦК (Cu, Al, Ni) структурой.

Кристалл Структура Модуль упругости, ГПа [100] [111] Real Свинец ГЦК 7 28 14 Алюминий ГЦК 63 77 70 Медь ГЦК 70 196 112 Железо ОЦК 133 287 210 Расстояние между атомами меняется в зависимости от кристаллографических направлений. Это определяет анизотропию механических и физических свойств кристалла. Поэтому образцы, вырезанные из монокристалла в различных направлениях, будут иметь различные значения модуля упругости. ГЦК и ОЦК металлы имеют наибольший модуль упругости в направлении [111], в то время как наименьший - в направлении [100]. Реальные материалы состоят из множества хаотично ориентированных монокристаллов, что приводит к изотропии их свойств.

Некоторые материалы могут существовать в формах с различной кристаллической структурой при одном и том же химическом составе (полиморфизм). Это можно продемонстрировать на примере чистого железа, которое имеет объемноцентрированную кубическую (ОЦК) ячейку при комнатной температуре и гранецентрированную кубическую (ГЦК) структуру при 911 oC. Это изменение сопровождается уменьшением объема, так как структура ГЦК более плотно упакована, чем ОЦК решетка. Вторичная трансформация от ГЦК к ОЦК происходит при температуре 1392 oC.