Главная

Лабораторная работа

Тема: Опытная проверка теории внецентренного растяжения-сжатия

Цель работы:

1. Определить опытным путем нормальные напряжения в крайних волокнах поперечного сечения бруса при внецентренном растяжении

2. Сравнить их с напряжениями, вычисленными теоретически.

I. НЕОБХОДИМЫЕ ПРИБОРЫ И ОБОРУДОВАНИЕ

1. Разрывная машина с силоизмерительным устройством ДМ-30 М.

2. Рычажные тензометры.

II. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

Внецентренным растяжением называют такой вид деформации, при котором внешние продольные силы F приложены с некоторым эксцентриситетом e относительно центра тяжести поперечного сечения бруса (рис.1).

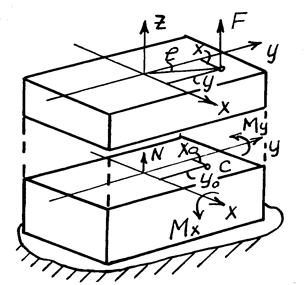
Рис.1. Схема для определения внутренних силовых факторов

На основании принципа независимости действия сил нормальные напряжения в любой произвольной точке C поперечного сечения бруса (рис. 1), имеющей координаты X и Y будут складываться из напряжений от продольной силы N и напряжений от чистого изгиба моментами M_x и M_y:

или

Для сечения в виде прямоугольника напряжения в крайних волокнах можно рассчитать по формуле:

При этом знаки в формуле выбирают на основании анализа расчетной схемы. Если в брусе прямоугольного поперечного сечения (рис.2) точка приложения растягивающей силы F будет находиться на одной из главных осей поперечного сечения, например, на оси X, то напряжения в крайних волокнах (в точках A и B) на основании (2) от продольной силы N=F будут одинаковы, т. е.

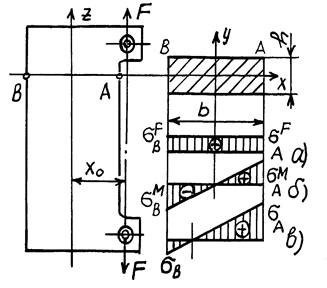
Рис.2. Схема плоского внецентренного растяжения

От изгибающего момента в точке возникают растягивающие напряжения, а в точке - сжимающие. Тогда получают

где

Суммарные напряжения в точках A и B с учетом формул (3) и (4) будут равны

В итоге получают: наибольшие напряжения возникают, как и при изгибе, в наиболее удаленных от нейтральной оси точках. На рис. 2, а, показана эпюра напряжений от растяжения, на рис. 2, б – от изгиба, а на рис. 2, в – суммарная эпюра напряжений.

Наибольшую нагрузку F_max, которую можно приложить к образцу, определяют из (5), учитывая, что максимальные напряжения не должны вызывать пластических деформаций, т. е. . Тогда с учетом формулы (5) получают

Работа выполняется на машине ДМ-30 М. Схема машины с установленным на ней образцом показана на рис. 3.

Рама машины состоит из основания 1, двух колонн 2 и поперечины 3. На поперечине смонтирован установочный узел, включающий маховик 4 и винтовую пару 5, 6, с помощью которого можно менять по высоте расстояние между захватами машины 9 и 12. Силоизмерительное устройство состоит из динамометрического кольца 7 и индикатора часового типа 8 с ценой деления K= 0,002 мм.

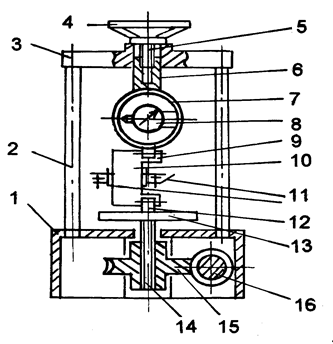
Рис. 3. Схема испытательной машины ДМ-30 М

Индикатор 8 установлен по горизонтальной оси симметрии кольца 7. Кольцо прикреплено к винтовой паре 5, 6, а снизу к нему присоединен захват 9. При приложении нагрузки к захвату 9 кольцо 7 деформируется. Зная величину этой деформации, зафиксированную индикатором 8, по тарировочному графику (рис. 4) определяют приложенную нагрузку.

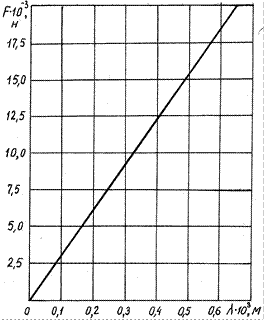
Рис. 4. Тарировочный график динамометрического кольца силоизмерителя

Нагружающее устройство смонтировано на станине 1 и состоит из стола 13, установленного на вертикально перемещающемся грузовом винте 14, который входит в резьбовую втулку червячного колеса 15, приводимого во вращение червяком 16 вручную (маховик привода червяка условно не показан).

Образец для испытания 10, установленный в захватах 9 и 12, представляет собой брус прямоугольного поперечного сечения b x h (рис. 3). Растягивающая нагрузка прикладывается с эксцентриситетом X₀, взятым вне ядра сечения, чтобы получить в крайних волокнах напряжения разных знаков.

Для измерения деформаций в крайних волокнах на образце установлены два рычажных тензометра 11, например, типа ТА-2 конструкции Н.Н. Аристова, схема которого показана на рис. 5.

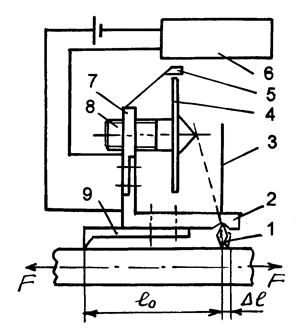
Рис.5. Схема тензометра ТА-2 конструкции Н.Н. Аристова

Тензометр имеет основание, состоящее из планки 2 и опорного ножа 9. В вырезе планки 2 установлена призма 1 с пластиной 3, снабженной на верхнем конце контактной площадкой. В стойке 7, изолированной от планки 2, установлен микрометрический винт 8, снабженный лимбом 4 с делениями и оканчивающийся острием. Напротив лимба закреплена визирка 5 для отсчета деформации. К планке 2 и стойке 7 подсоединен звуковой индикатор 6, включающийся при замыкании острия винта 8 и контакта пластины 3, которая получает перемещение при повороте призмы 1 вследствие деформации образца .

Соотношение элементов рычажной системы таково, что цена одного деления шкалы лимба 4 равна C=0,001 мм. Расстояние l₀ между ножом 9 и призмой 1 называют базой тензометра.

III. ВЫПОЛНЕНИЕ ЭКСПЕРИМЕНТА И ОБРАБОТКА РЕЗУЛЬТАТОВ ИСПЫТАНИЙ

1. Штангенциркулем с точностью 0,1 мм измеряют размеры поперечного сечения образца b и h, а также эксцентриситет X₀ приложения нагрузки. Эти величины, а также значения модуля продольной упругости E и базы тензометров l_OA и l_OB заносят в журнал наблюдений.

2. Из формулы (6) для материала образца определяют максимальную нагрузку F_max и, приняв начальную нагрузку F₀, определяют величину ступени нагружения такой, чтобы можно было выполнить 3 – 4 нагружения образца. Затем, вращая маховик червячного винта 16 (рис. 3) нагружающего устройства, прикладывают начальную нагрузку F₀ для выбора всех зазоров. Снимают показания тензометров 11. Для этого вращают лимб 4 до момента появления сигнала звукового индикатора при замыкании острия винта 4 с пластиной 3 и делают отсчет напротив визирки 5 на лимбе 4 (рис. 5). Затем прерывают контакт, отводя винт 4 обратно. При этом лимб правого тензометра, установленного на растянутых волокнах, необходимо отвести на 15-20 делений, т. к. при растяжении образца пластина 3 приближается к винту 4 и необходимо исключить преждевременное включение звукового индикатора 6. Винт левого тензометра, установленного на сжатых волокнах, достаточно отвести на 2 – 3 деления.

Величину начальной нагрузки и показания обоих тензометров принимают за исходные и записывают в таблицу журнала наблюдений.

3. Увеличивают нагрузку равными ступенями 3 – 4 раза, снимают показания тензометров и заносят в таблицу.

4. Согласно требованиям раздела 4 обрабатывают результаты исследований и вычисляют опытные значения напряжений, используя закон Гука:

5. Вычисляют теоретические значения напряжений в точках A и B ( и ) по формулам (5) при ступени нагружения , строят совмещенные эпюры нормальных напряжений по опытным и теоретическим данным (см. рис. 2, в) и сравнивают полученные значения напряжений.

Форма отчета по лабораторной работе

1. Название лабораторной работы.

2. Цель работы.

3. Испытательная машина.

4. Измерительные приборы.

5. Схема установки.

6. Исходные данные.

- Модуль продольной упругости E.

- Размеры поперечного сечения образца h и b.

- База тензометров l_A, l_B.

- Цена деления шкалы тензометров C.

- Координаты приложения силы x₀, y₀.

- Площадь поперечного сечения образца A.

- Осевой момент сопротивления сечения W_y.

7. Результаты эксперимента.

№ п/п	Нагрузка F	Приращение нагрузки,	Показания тензометров		Приращение показаний тензометров
Средние значения приращений

8. Опытное определение напряжений и .

9. Теоретическое определение напряжений и .

10. Сравнение опытных и теоретических значений.

Вопросы для подготовки к защите работы

- Какова цель данной лабораторной работы?

- На какой машине выполняется работа? Каково её устройство?

- Как устроено силоизмерительное устройство? Как пользоваться тарировочным графиком?

- Какой образец применяют в работе?

- Какой случай сложного сопротивления называют внецентренным растяжением (сжатием)?

- Как нагружен стержень при внецентренном сжатии?

- По какой формуле вычисляют нормальное напряжение при внецентренном сжатии?

- Как записывают уравнение плоскости напряжений при внецентренном сжатии?

- Чем отличается частный случай внецентренного растяжения (сжатия) от общего? Приведите примеры.

- Какие внутренние силовые факторы возникают в поперечном сечении бруса при внецентренном растяжении (сжатии)?

- По какой формуле можно теоретически определить напряжения в любой точке сечения при внецентренном растяжении (сжатии)?

- По какой формуле можно вычислить наибольшие напряжения при внецентренном растяжении для сечений, имеющих выступающие углы?

- Какая линия называется нейтральной и как она располагается?

- Каким свойством обладает нейтральная линия?

- Как вычисляют осевую относительную деформацию при внецентренном сжатии?

- Как находят напряжение при осевом действии сил?

- Как определяют значение модуля Юнга при внецентренном сжатии?

- Какое напряженное состояние возникает в любой точке бруса при внецентренном растяжении?

- Как определить опытным путем напряжения в крайних волокнах сечения бруса?

- Как устроен рычажный тензометр Аристова типа ТА-2?

- Почему брус нагружают равными ступенями? С какой целью прикладывается начальная нагрузка?

- В каких точках поперечного сечения бруса возникают наибольшие напряжения при внецентренном растяжении (сжатии)?

- Как строят эпюру нормальных напряжений при внецентренном сжатии?

- Как определяют положение опытной нейтральной линии при внецентренном сжатии?

- Как проверяют справедливость гипотезы плоских сечений при внецентренном сжатии?

- Как вычисляют радиусы инерции сечения?

- Как определяют положение теоретической нейтральной линии при внецентренном сжатии?

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00