Главная
Лабораторная работа
Тема: Опытная проверка
теории косого изгиба
Цель работы:
Определить опытным путем величину и направление прогиба свободного конца консоли и нормальное напряжение при косом изгибе и сравнить полученные результаты с величинами, вычисленными теоретически.
I. НЕОБХОДИМЫЕ ПРИБОРЫ И ОБОРУДОВАНИЕ
1. Данная лабораторная работа выполняется на специальных установках. В частности, может быть использована консольная балка прямоугольного сечения. Для создания условий косого изгиба на этой установке должна быть предусмотрена возможность поворота жесткой заделки вокруг продольной оси испытываемой балки. Нагружение балки, как и ранее, осуществляется приложением сосредоточенного груза к центру тяжести поперечного сечения свободного конца консоли (рис. 1).
2. Штангенциркуль,
3. Тензометры и стрелочные индикаторы.
II. СОДЕРЖАНИЕ РАБОТЫ
В этом опыте внешняя нагрузка направлена перпендикулярно оси балки и приложена к центру тяжести ее поперечного сечения, но данная деформация является косым изгибом, поскольку плоскость действия нагрузки не совпадает ни с одной из главных плоскостей сечения балки.
Для определения продольных деформаций крайних волокон сечений на балку в соответствующих местах устанавливаются тензометры рычажного типа.
Нормальные
напряжения на основании опытных данных определяются с помощью закона Гука по
соотношению 
При коэффициенте увеличения k и базе Б относительная деформация определяется по известной формуле
где 
– средняя разность отсчетов по шкале
тензометра, полученных при загружении балки одинаковыми приращениями нагрузки.
Теоретически нормальные напряжения при косом изгибе определяются по формуле
где Mz и My – изгибающие моменты относительно главных осей z и y сечения; Iz и Iy – осевые моменты инерции поперечного сечения балки относительно тех же осей; z и y – координаты точки поперечного сечения балки, в которой определяется нормальное напряжение.
Для точек сечения, наиболее удаленных от главных осей y и z, формула для нормальных напряжений имеет вид
где Wy и Wz – осевые моменты сопротивления.
Для определения изгибающих моментов Мz и My вертикально приложенную нагрузку (силу F) заменяют ее составляющими Fz и Fy:
откуда 
где l –
расстояние от места установки тензометра до точки приложения силы F.
Полученные из опыта величины приращений напряжений сравниваются с подсчитанными теоретически и определяется расхождение в процентах к теоретическим величинам по формуле
Опытное определение прогиба конца консоли производится при помощи стрелочных индикаторов, один из которых измеряет вертикальную составляющую прогиба, а второй – горизонтальную (рис. 2). Величина полного прогиба может быть определена по формуле
где fверт и fгор – вертикальная и горизонтальная составляющие прогиба.
Теоретическое значение прогиба, т.е. перемещения центра тяжести сечения, определяется по формуле
где fz и fy – составляющие прогиба по главным центральным осям z и y поперечного сечения (рис. 3).
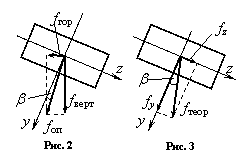
Составляющие fz и fy полного прогиба fтеор соответствуют прогибам от раздельного действия на балку составляющих Fz и Fy полной нагрузки F и определяются по формулам
Угол наклона 
линии прогиба f с главной
центральной осью y определяется
по формуле
Так как 
,
из последней формулы следует, что 
,
т.е. направление прогиба не совпадает с направлением силы F, что
является особенностью косого изгиба.
Полученное в опыте среднее значение приращения прогиба сравнивается с рассчитанным теоретически и определяется расхождение в процентах к теоретическому значению по формуле
III.ПОРЯДОК ВыполнениЯ РАБОТЫ
-
Ознакомиться с установкой и занести в журнал работ размеры испытываемой балки,
места расположения тензометров и прогибомеров, угол
наклона 
главной оси
y к горизонтали.
- После предварительного нагружения балки записать начальные отсчеты приборов.
- Равными ступенями увеличивать нагрузку, записывая при этом отсчеты приборов. Снять нагрузку до начальной и сверить показания всех приборов с первоначальными. При значительном расхождении опыт повторить.
- Определить разности отсчетов по приборам и найти их средние значения. Определить средние приращения по каждому прибору и вычислить средние опытные приращения напряжений и прогибов.
- Вычислить приращения напряжений и прогибов для тех же точек по формулам сопротивления материалов.
- Вычислить расхождения между теоретическими значениями напряжений и прогибов и полученными опытным путем.
Вопросы
для подготовки к защите работы
- Какова цель данной лабораторной работы?
- Как устроена лабораторная установка?
- Какой изгиб называют косым? Какие виды изгибов Вы еще знаете?
- Какие силовые факторы действуют в поперечных сечениях балки при косом изгибе?
- Что называют плоскостью изгиба? Силовой плоскостью?
- Какое нагружение создаёт косой изгиб балки?
- На какие простые виды нагружения раскладывают косой изгиб?
- Что называют нейтральной (нулевой) линией при косом изгибе балки и как она расположена относительно плоскости действия изгибающего момента (силовой плоскости)?
- Как расположена линия полного прогиба по отношению к плоскости действия изгибающего момента? По отношению к нулевой линии сечения?
- Как вычисляют нормальное напряжение при косом изгибе?
- Как вычислить теоретически составляющие и суммарный прогиб конца консольной балки при косом изгибе?
- Как будет изменяться суммарный
прогиб конца консоли от действия постоянной нагрузки при увеличении угла ?
При его уменьшении?
- Как определяют положение нулевой линии?
- Как определяют угол между суммарным прогибом и силовой плоскостью?
- Как опытным путём определяют нормальное напряжение?
- Как опытным путём определяют полный прогиб балки?
- Почему составляющие нормального напряжения суммируют алгебраически, а составляющие прогиба – геометрически?
- Как изменится соотношение величин прогибов, если прямоугольное сечение балки заменить круглым, квадратным?
- Назовите формы поперечных сечений балок, для которых невозможен косой изгиб.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
