Главная

Лабораторная работа

Тема: Определение нормальных напряжений при изгибе.

Видеоролик по лабораторной работе №5

Цель работы:

Экспериментальная проверка формул для нормального напряжения и перемещения при плоском изгибе балки. Ознакомление с методом электротензометрирования.

I. НЕОБХОДИМЫЕ ПРИБОРЫ И ОБОРУДОВАНИЕ

1. Экспериментальная установка СМ-4М,

2. Тензостанция ЦТМ-3,

3. Индикаторы часового типа,

4. Штангенциркуль.

II. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ.

В основе теории чистого изгиба, когда во всех сечениях балки поперечная сила равна нулю, лежит гипотеза плоских сечений: поперечные сечения балки, будучи плоскими до нагружения, остаются плоскими и после нагружения, поворачиваясь относительно нейтральной линии, разделяющей сжатую и растянутую области сечения. С использованием этой гипотезы получена теоретическая формула для нормального напряжения :

где M - изгибающий момент в поперечном сечении; осевой момент инерции сечения балки; y – расстояние от точки, в которой определяется напряжение, до оси X, проходящей через центр тяжести сечения.

Чистый изгиб в инженерной практике встречается редко, гораздо чаще балки испытывают поперечный изгиб (), при котором гипотеза плоских сечений нарушается вследствие сдвиговых деформаций, вызванных касательными напряжениями. Теоретические оценки погрешности формулы (1), распространяемой на случай поперечного изгиба, показывают, что ошибки редко превышают 5%. В данной работе необходимо опытным путём убедиться в приемлемости формулы (1) для инженерных расчётов.

Перемещения поперечных сечений балок определяют путём решения приближённого дифференциального уравнения изогнутой оси

где v(z) - прогиб балки, т.е. линейное перемещение центра тяжести сечения по перпендикуляру к геометрической оси; M(z) - изгибающий момент в сечении z балки; E – модуль Юнга; - осевой момент инерции поперечного сечения.

После интегрирования уравнения (1) получают выражения для угла поворота сечения относительно нейтральной линии и прогиба:

Здесь C и D – постоянные интегрирования, которые определяют из граничных условий, зависящих от способа опирания балки.

Учёные разработали упрощённые методы определения перемещений, к которым можно отнести метод начальных параметров и метод Мора. Эти методы подробно рассматривают на лекциях и используют при выполнении домашних заданий. В данной работе необходимо проверить справедливость формул для прогибов и углов поворота при частном случае нагружения балки с помощью тензометрирования.

На рис. 1 показана конструктивная схема установки СМ-4М для исследования напряжений и перемещений двухопорной балки.

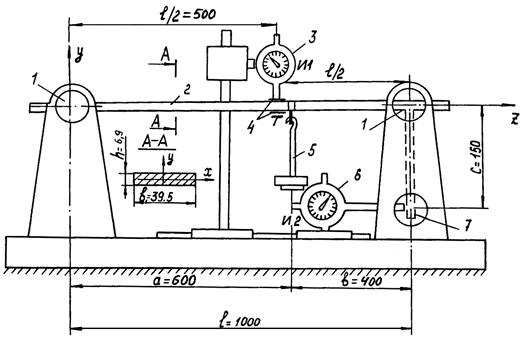
Рис.1. Конструктивная схема установки СМ-4М:

1 – шарнирные опоры; 2 – балка; 3, 6 – индикаторы часового типа;

4 – тензодатчики; 5 – грузовая платформа; 7 – рычаг

Стержень 2 прямоугольного поперечного сечения установлен на шарнирных опорах 1. Нагружение балки осуществляют с помощью платформы с грузом 5. Для определения нормального напряжения на горизонтальных гранях среднего сечения наклеены два тензодатчика 4, подключённые в смежные плечи полумоста Уинстона. Так как они фиксируют деформации разных знаков (верхний – сжатие, нижний – растяжение), то тензостанция регистрирует удвоенную относительную деформацию, что необходимо учитывать при обработке результатов опыта.

Для определения прогиба среднего сечения балки используют индикатор часового типа 3. Принцип их действия заключается в преобразовании поступательного движения штока, находящегося в соприкосновении с исследуемым объектом, во вращательное движение стрелки с помощью системы зубчатых колёс.

Поскольку угол поворота опорного сечения достаточно мал, его определяют косвенным путём с помощью индикатора 6, регистрирующего горизонтальное перемещение конца рычага 7, жёстко соединённого с балкой. Угол поворота находят как отношение перемещения рычага w к его длине с:

На рис. 2 изображена расчётная схема балки, пользуясь которой определяют опорные реакции и строят эпюру изгибающих моментов. Формулы для прогиба и угла поворота выписывают из справочника.

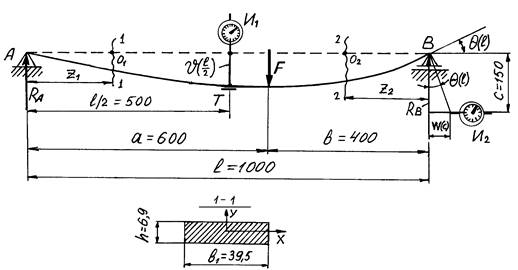
Рис. 2. Расчётная схема балки: A – шарнирно-неподвижная опора; B – шарнирно-подвижная опора;

F – внешняя активная нагрузка; Т – тензодатчики; И – индикаторы часового типа; v(l/2) - прогиб среднего сечения балки;

Q(l) - угол поворота правого опорного сечения балки; w(c) - перемещение свободного конца рычага;

(1-1) – поперечное сечение балки

При опытном определении напряжений в заданной точке балки измеряют упругие линейные деформации , а затем, воспользовавшись законом Гука (), определяют искомые напряжения. Определение напряжений по измеренной деформации называют тензометрированием.

Электротензометрический метод измерения линейных деформаций основан на том, что деформация проводника вызывает изменение некоторых его электрических параметров (сопротивления, емкости, индуктивности). Элемент, воспринимающий деформацию тела, называют датчиком. Изменение электрического параметра передается на регистрирующее устройство. Наиболее широко используют в качестве электротензометров проволочные датчики омического сопротивления.

Основными преимуществами электротензометров являются: высокая точность измерения, малые размеры тензометров, возможность передачи показаний на расстояние и выдачи результатов на ЭВМ, возможность измерять деформации на поверхностях сложной конфигурации и в труднодоступных местах, практически полная безинерционность аппаратуры, возможность регистрации быстроизменяющихся процессов. Эти преимущества компенсируют недостатки электротензомерирования: сложность и значительную стоимость измерительной аппаратуры, необходимость высокой квалификации персонала.

Точность измерения деформации при помощи проволочных тензодатчиков несколько меньше, чем при измерении механическим или оптическим тензометром, но практически она вполне достаточна для надежного вычисления напряжений.

В основе метода лежит зависимость омического сопротивления R проводника от его геометрических размеров – длины l и площади поперечного сечения A

где - удельное сопротивление проводника.

Чем длиннее проводник датчика, тем больше изменение омического сопротивления при деформации, а следовательно, тем точнее результаты измерений. В тоже время при неравномерной деформации исследуемого тела возникает необходимость проводить измерения на возможно меньшей длине (базе измерений). Конструктивно эта задача была решена путем укладки длинного проводника в виде петель на малой базе.

Тензодатчик представляет собой плоский элемент (рис. 3), состоящий из тонкой (0,015 – 0,03 мм) проволоки (или фольги) 1, материал которой обладает высоким омическим сопротивлением (константан, нихром), уложенной зигзагообразно между двумя полосками специальной тонкой (0,002 – 0,005 мм) бумаги или полимерной пленки 2.

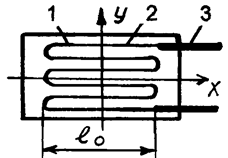
Рис. 3. Схема тензодатчика

К концам проволоки сваркой либо пайкой, что менее предпочтительно, присоединены латунные выводы 3, служащие для соединения тензодатчика с регистрирующей аппаратурой. Применение константановой проволоки обусловлено двумя существенными факторами: а) высоким омическим сопротивлением проводника; б) постоянством удельного сопротивления при повышении температуры до 500 ⁰С. Например, у железа в этом же диапазоне температур удельное сопротивление увеличивается почти в восемь раз. Датчик вследствие зигзагообразной укладки проволоки реагирует только в направлении оси X и не чувствителен в направлении оси У.

Базой тензодатчика называют длину l₀ прямолинейных участков проводника, из которого он изготовлен. Отношение относительного изменения сопротивления к относительной продольной деформации называют коэффициентом тензочувствительности K. Для большинства применяемых материалов он приблизительно равен 2:

Промышленность выпускает проволочные, а также фольговые датчики с базой l₀= 5, 10, 20, 30 мм и сопротивлением R= 50, 100, 200, 300 Ом. Следует однако учитывать, что с уменьшением базы датчика снижается его тензочувствительность из-за увеличения влияния криволинейных участков (петель датчика). Поэтому без необходимости применять датчики с малой базой не рекомендуется.

Место установки тензодатчика тщательно зачищается и обезжиривается спиртом или ацетоном. Тензодатчик наклеивают на поверхность балки при помощи специальных клеев (БФ-2 и др.) так, чтобы направление его базы l₀ совпадало с направлением измеряемой деформации. При нагружении балки деформируется вместе с ней и тензодатчик, сопротивление которого изменится и его величина будет зарегистрирована измерительной схемой, состоящей из моста Уинстона, усилителя и регистрирующего прибора (миллиамперметра или осциллографа).

На рис. 4 показана принципиальная упрощённая схема тензостанции ЦТМ-3 (цифровой тензометрический мост).

Четыре сопротивления соединены последовательно, образуя мост Уинстона. Пассивное плечо моста, состоящее из двух регулируемых балансировочных сопротивлений и , находится внутри прибора. Активное плечо моста образуется двумя тензодатчиками равного сопротивления. Активный датчик наклеен на исследуемый объект, компенсационный датчик наклеен на ненагруженную пластинку из того же материала, что и объект. Он служит для компенсации тех изменений сопротивления активного датчика, которые вызваны температурными деформациями.

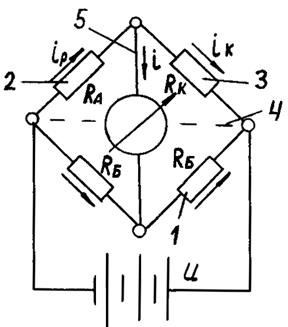
Рис. 4. Схема тензостанции:

1 – балансировочные сопротивления; 2 – активный датчик;

3 – компенсационный датчик; 4 – рабочая диагональ моста;

5 – измерительная диагональ моста

При подаче напряжения U на рабочую диагональ моста в измерительной диагонали появляется ток i, который усиливается и регистрируется на цифровом табло тензостанции. Ток будет равен нулю только в том случае, если

Выполнив предварительную тарировку, устанавливают цену единицы младшего разряда цифрового табло . Относительную деформацию, вызванную нагружением объекта исследования, находят по формуле

где - разность показаний цифрового табло после и до нагружения.

III. ВЫПОЛНЕНИЕ ЭКСПЕРИМЕНТА И СРАВНИТЕЛЬНЫЙ АНАЛИЗ ТЕОРЕТИЧЕСКИХ И ОПЫТНЫХ ДАННЫХ

Лабораторную работу выполняют в следующем порядке:

- измеряют штангенциркулем геометрические параметры балки: b₁, h, l, a, b, c;

- включают тензостанцию для прогрева в течение 10 мин;

- нагружают балку начальной силой кгс для устранения зазоров и люфтов. Записывают в протокол испытания (табл. 1) показания тензодатчика и индикаторов часового типа

- дают приращение нагрузки кгс и записывают в протокол испытания изменившиеся показания

- находят разность показаний приборов:

- вычисляют значение относительной деформации при

- находят опытное значение напряжения, принимая МПа:

- находят опытное значение прогиба среднего сечения

- вычисляют опытное значение угла поворота опорного сечения

- определяют для расчётной схемы балки опорные реакции, соответствующие нагрузке кгс=19,6 Н. Строят эпюру изгибающих моментов и находят значение момента M в месте наклейки тензодатчика при

- вычисляют осевой момент инерции поперечного сечения балки

- находят теоретическое значение напряжения

- сравнивают теоретическое и экспериментальное значения напряжения

- вычисляют теоретическое значение прогиба среднего сечения

- сравнивают теоретическое и экспериментальное значения прогиба

- вычисляют теоретическое значение угла поворота опорного сечения

- сравнивают теоретическое и экспериментальное значения угла поворота

- делают выводы по работе.

Таблица 1. Протокол испытания балки на изгиб

Нагрузка F, кгс	Показания приборов			Приращение нагрузки		Приращения показаний
	Т	И1, мм	И2, мм	кгс	Н		, мм	, мм
0,5				2,0	19,6
2,5

Вопросы для подготовки к защите работы

- Какова цель данной лабораторной работы?

- В каком случае балка испытывает чистый изгиб?

- Как формулируют гипотезу плоских сечений?

- Как определяют нормальное напряжение при чистом изгибе?

- Какой изгиб балки называют поперечным изгибом?

- Почему при поперечном изгибе гипотеза плоских сечений несправедлива?

- Как записывается условие прочности при изгибе?

- Каково устройство лабораторной установки?

- Какой изгиб называют поперечным? Плоским?

- Как теоретически определяют нормальные напряжения при плоском изгибе в любом слое поперечного сечения балки?

- Как определяют максимальные нормальные напряжения в сечении балки при плоском изгибе?

- Как распределяются нормальные напряжения по высоте сечения балки при плоском изгибе? Покажите эпюру?

- Как записывают приближённое дифференциальное уравнение изогнутой оси балки?

- Как записывают общее выражение для угла поворота сечения балки?

- Как записывают общее выражение для прогиба балки?

- Из каких условий определяют постоянные интегрирования в общих выражениях для перемещений?

- Как определяют нормальное напряжение опытным путём?

- Как определяют прогиб балки опытным путём?

- Как определяют угол поворота балки опытным путём?

- Как определяют опорные реакции в балке?

- Как строят эпюру изгибающих моментов в балке?

- Как вычисляют осевой момент инерции сечения?

- Как определяют теоретическое значение напряжения?

- Что называют тензометрированием?

- На чем основан метод электротензометрирования?

- Какие преимущества и недостатки электротензометрирования Вы знаете?

- Почему тензостанция регистрирует удвоенную относительную деформацию на поверхности балки?

- Как устроен тензодатчик?

- Что называют базой тензодатчика?

- Какие соображения должны учитываться при обосновании выбора базы тензодатчика?

- Как подключается тензодатчик в измерительную систему? Опишите её?

- Что понимают под балансом моста?

- Как определяют тарировочные коэффициенты?

- Как проводят определение напряжений при помощи тензодатчиков в исследуемой балке?

- Для чего применяют компенсационный датчик и где и как он должен быть расположен?

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00