Главная
Лабораторная работа
Тема: Расчет толстостенных цилиндров и труб
Цель работы:
Исследование влияния ряда
параметров на прочность толстостенных цилиндров и труб.
I. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ.
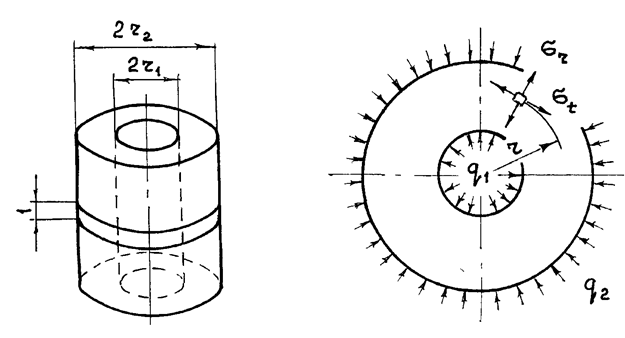
Рис. 1 Рис. 2
Если на достаточном удалении от днищ цилиндра или торцов трубы, где не обнаруживается влияние этих днищ и торцов, двумя параллельными поперечными сечениями выделить объект единичной длины (рис. 1), то для такого объекта, расчетная схема которого показана на рис. 2, справедливы будут следующие зависимости:
![]()
В этих формулах: σr,t - соответственно
радиальное (r) и тангенциальное (t) напряжение в точках поперечного сечения, расположенных на
окружности радиуса r; r1
и r2 - внутренний и наружный радиусы (габариты)
объекта; q1 и q2
- равномерное по длине внутреннее и наружное давление.
Данные формулы для случая
упругого состояния материала объекта выведены Г. Ламэ
и опубликованы в
Правило знаков: указанным
направлениям векторов на расчетной схеме рис. 2 соответствуют положительные
численные значения величин в формуле Ламэ.
II. ПОСТАНОВКА ЗАДАЧ ИССЛЕДОВАНИЯ.
Согласно формуле Ламэ радиальные и окружные напряжения распределяются
нелинейно по толщине стенки. Кроме того, сама величина напряжений σr и
σt сложным образом зависит от внешнего давления q1 и q2, габаритных
размеров r1 и r2
и их соотношений: q1/q2
и r1/r2. Очевидно,
что при проектировании можно установить такой набор конструктивных параметров и
внешних факторов, при которых прочность и экономичность конструкции будут оптимальными.
Для этого следует установить характер и особенности влияния конструктивных
параметров и внешних нагрузок на величину напряжений в опасных точках объекта.
Задача 1. Исследование влияния
внешнего давления q2 на прочность, если
известны: предел текучести материала σT; габаритные размеры r1 и r2; внутреннее
давление q1 (рис. 3).
В данном случае целесообразно
рассматривать ряд дискретных значений q2 на
интервале от q2=0 до q2=2q1 с шагом,
зависящим от числа подгрупп в учебной группе и удобства выполнения
арифметических операций. Такой диапазон q2 позволяет
графически легко установить экстремальный характер зависимости коэффициента
запаса прочности.
Задача 2. Исследование влияния
внешнего размера r2 на прочность, если
известны: предел текучести материала σT; давление внутреннее q1 и внешнее q2; внутренний
размер r1 (рис. 4).
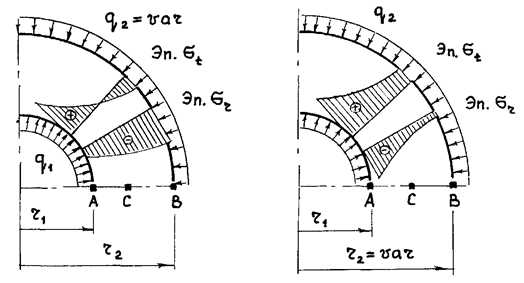
Рис. 3 Рис. 4
При решении этой задачи
целесообразно рассматривать ряд дискретных значений r2
на интервале от r2≈1,1r1 до r2≈10r1 с
увеличивающимся шагом при увеличении текущего размера r2.
Такое варьирование толщины стенки цилиндра позволяет графически приближенно
установить предельное значение запаса прочности рассматриваемого объекта. При
этом значение внешнего давления q2 следует
задать меньше внутреннего q1, исходя из
выводов, полученных ранее.
III. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ
1. Для каждой совокупности
исходных данных вычислить константы C1 и C2 формулы Ламэ и получить
уравнения распределения напряжений и по толщине стенки в численном виде:
![]()
![]()
где ![]()
![]() .
.
2. Построить эпюры распределения
напряжений по толщине стенки (рис. 3 и 4). Следует обратить внимание на то, что
при правильном вычислении коэффициентов C1 и C2 ординаты эпюры радиальных напряжений для точек
внутренней и внешней поверхности цилиндра совпадают по величине с приложенным
давлением: σrA =-q1; σrB =-q2. Допустимая
погрешность – в пределах 2 процентов. Если это условие не выполняется и
погрешность составляет больше 2 процентов, то следует повысить точность
выполнения всех промежуточных вычислений. Если величины радиальных напряжений σr в точках поверхностей существенно отличаются
от давлений q1 и q2,
то следует искать ошибку в расчетах, сравнивая значения C1
и C2, вычисленные для ближайших значений варьируемого
в задаче параметра. Ряды дискретных значений C1
и C2 образуют плавные закономерности.
3. Определить положение опасных
точек трубы, вычислить для них эквивалентное напряжение по третьей классической
гипотезе прочности ![]() и коэффициент запаса
и коэффициент запаса ![]()
В случае, когда напряжения σt во
всех точках сечения трубы растягивающие, нет сомнения, что опасными точками
являются точки внутренней поверхности трубы (т. А на рис. 4). В случаях, когда
эпюра σt двухзначная
(рис. 3), следует вычислить значения эквивалентных напряжений в точках
внутренней (А) и внешней (В) поверхности. При правильном выполнении расчетов
опасное состояние всегда будет во внутренних точках трубы.

σ1=σt;
σ2=0;
σ3=σr.
σ1=0;
σ2=σr;
σ3=σt при ![]()
4. Вычисленные напряжения
занести в сводные табл.1 и 2.
Таблица 1. Напряжения
в опасных точках трубы и оценка прочности
|
q2, Н/мм2 |
|
|
|
|
|
|
|
|
σr, Н/мм2 |
|
|
|
|
|
|
|
|
σt, Н/мм2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
Таблица 2. Напряжения
в опасных точках трубы и оценка прочности
|
r2, мм |
|
|
|
|
|
|
|
|
σr, Н/мм2 |
|
|
|
|
|
|
|
|
σt, Н/мм2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
Колонки табл. 1 и 2 заполняются
по мере завершения расчетов подгруппами студентов. По мере заполнения таблиц
анализируется плавность изменения расчетных параметров по строкам. При
выявлении допущенных отдельных ошибок они исправляются так, чтобы общая функциональная
зависимость нигде не нарушалась.
IV. АНАЛИЗ ТЕОРЕТИЧЕСКИХ ДАННЫХ
1. Проанализировать совокупность
данных табл. 1 и 2 и сделать первый общий вывод: при любых внешних воздействиях
и конструктивных параметрах опасные точки всегда внутренние.
2. Построить графики, отражающие
зависимость прочности от внешнего давления (рис. 5) и внешнего радиуса (рис. 6).
Обратить внимание на то, что характер влияния разный. Зависимость прочности от
внешнего давления имеет экстремальный характер; максимальная прочность достигается,
если q1= q2. Изменение прочности при увеличении внешнего
радиуса (толщины стенки) носит предельный характер.
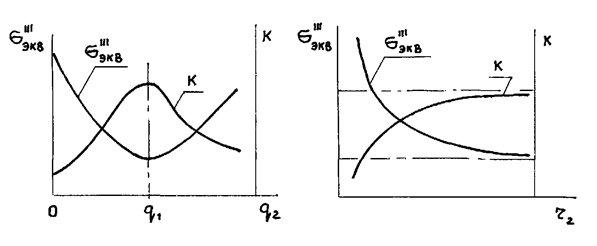
Рис. 5 Рис. 6
Каждой подгруппе студентов
следует самостоятельно описать полученные графические зависимости в выводах.
3. Обсудить теоретические
значения предельных напряжений для частных видов конструкций.
Случай 1. Деталь типа пластины с
круглым отверстием (r2→∞), внешнее давление отсутствует (q2=0).
При отсутствии внешнего давления
![]()
Для r2→∞ ![]()
В опасной точке при r=r1 напряжение σr,t =±q1.
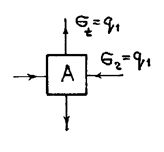
σ1=q1;
σ2=0;
σ3=-q1.
Тогда ![]()
Случай 2. Деталь типа стержня
под внешним давлением; внутреннее давление отсутствует (q1=0).
![]()
Если r1=0, σr,t =-q2.
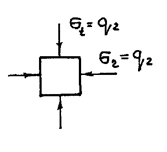
В этом случае во всех точках
детали двухосное равностороннее сжатие. Эквивалентное напряжение ![]()
Если в центре имеется отверстие,
но бесконечно малого размера, то есть r1→0, но не равен нулю, тогда
в опасной точке при r=r1 будут следующие
напряжения: σr =0; σt =-2q2.
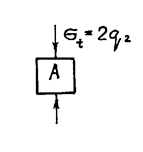
Эквивалентное напряжение ![]() Следовательно, отверстия малого размера
создают концентрацию напряжений с коэффициентом kσ=2.
Следовательно, отверстия малого размера
создают концентрацию напряжений с коэффициентом kσ=2.
Вопросы для подготовки к защите работы
- Укажите цель лабораторной
работы.
- Какие напряжения возникают в
точках поперечного сечения трубы, находящейся под давлением?
- Какие точки трубы будут
наиболее напряженными под действием внутреннего (внешнего) давления?
- Какому закону подчинено
распределение тангенциальных (радиальных) напряжений?
- Какие напряжения называют
главными? Какими свойствами обладают главные напряжения?
- Как обозначают главные
напряжения в случае объемного напряженного состояния?
- Как оценивают прочность при
плоском напряженном состоянии?
- Какие выводы сделаны в
результате выполнения расчетно-исследовательской работы?
- Как можно повысить прочность
трубы при неизменном внутреннем давлении?
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов