Главная

Лабораторная работа

Тема: Определение реакции "лишней" связи в статически неопределимой балке

Цель работы:

Проверка применимости метода сил для раскрытия статической неопределимости балки.

I. НЕОБХОДИМЫЕ ПРИБОРЫ И ОБОРУДОВАНИЕ

1. Экспериментальная установка – балка прямоугольного сечения, свободно лежащая на опорах,

2. Индикатор часового типа,

3. Грузы.

II. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ.

Объектом лабораторного исследования является балка с тремя симметрично расположенными опорами, нагруженная сосредоточенной силой P (рис. 1).

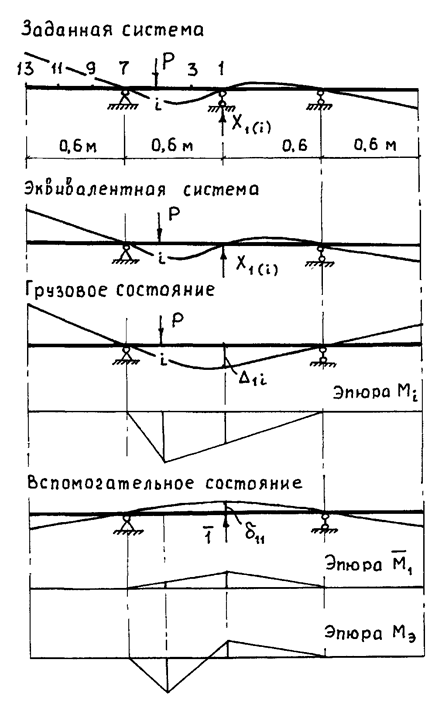
Рис. 1

Одним из методов раскрытия статической неопределимости, то есть определения реакций "лишних" связей, является метод сил. Если для исследуемого объекта реакцию средней "лишней" опоры обозначить X₁, то каноническим уравнением, которое позволит вычислить это неизвестное, будет уравнение суммарного перемещения сечения 1 в эквивалентной системе (рис. 1):

где δ₁₁ - перемещение сечения 1 по направлению силы X₁₍_i₎ от силы (см. вспомогательное единичное состояние); ∆₁_i - перемещение сечения 1 от внешней силы, приложенной в сечении i (см. грузовое состояние).

Коэффициенты канонического уравнения имеют смысл перемещений и могут быть найдены по формуле Мора:

Таким образом, каноническое уравнение метода сил основано на двух гипотезах сопротивления материалов: принципе независимости действия сил (принцип суперпозиции) и гипотезе о пропорциональности перемещений силам, их вызывающим (закон Гука).

Проверку применимости метода сил для раскрытия статической неопределимости балки можно выполнить решением следующих задач.

1. Для балки простого вида (рис. 1) вычислить ряд значений при различном положении внешней силы (i=2,3,4…,10). На опытной установке выполнить соответствующие измерения . Проанализировать полученные совокупности расчетных и экспериментальных значений, проверив равенство . Сделать вывод о применимости метода сил для балки простого типа.

Каждая совокупность дискретных значений составит линию влияния положения груза на величину реакции "лишней" связи.

2. Проверить справедливость принципа суперпозиции.

Для этого на опытной установке замерить величину реакции "лишней" связи при нагружении балки двумя силами P одновременно в двух сечениях, например, в i=3 и i=10 (рис. 2). Проверить, будет ли выполняться равенство .

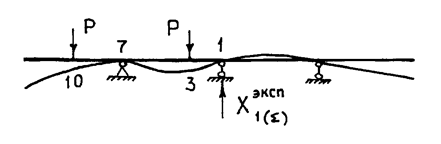
Рис. 2

3. Проверить справедливость закона пропорциональности.

Для этого выполнить измерение реакции "лишней" связи на опытной установке, приложив к двум сечениям силы, одна из которых будет кратна силе P, например, так, как показано на рис. 3. Проверить, будет ли выполняться равенство .

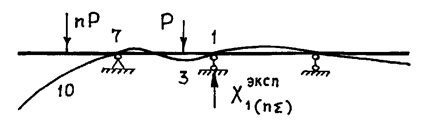
Рис. 3

При выполнении всех равенств с небольшими погрешностями (в пределах 1-2 процентов) сделать вывод о применимости метода сил для любой упругой балки при изгибе.

III. ПОСТАНОВКА ОПЫТА.

Установка напольного типа для выполнения лабораторных опытов (рис. 4) представляет собой стальную полосу 1 прямоугольного сечения длиной 2,4 м, свободно лежащую на опорах 2. Конструктивно через жесткую раму они связаны с массивным основанием 3. При таком свободном опирании балки с малыми контактными поверхностями легко обеспечивается поворот опорных сечений балки относительно поперечной оси; опирание соответствует идеальному шарнирному. Расстояние между опорами 1,2 м. На поверхности стальной полосы нанесены деления через каждые 10 см.

Нагружение опытной балки осуществляют с помощью набора грузов, устанавливаемых на подвесе 4. Подвес 4 можно поместить в любое сечение балки, как на консольном участке, так и в пролете.

Посередине пролета установлен микрометр часового типа 7, который обеспечивает измерение перемещения среднего сечения балки.

В среднем сечении балки установлен подвес 5 с емкостью 6, в которую при выполнении опыта засыпают груз (дробь).

Таким образом, стальная полоса является статически определимой балкой – физической моделью эквивалентной системы с рис. 1.

Опыт проводят следующим образом.

1. Устанавливают подвес 4 в заданное сечение i, подвес 5 – в среднее сечение балки 1. Выставляют нулевое положение шкалы индикатора 7 поворотом ее до совмещения со стрелкой.

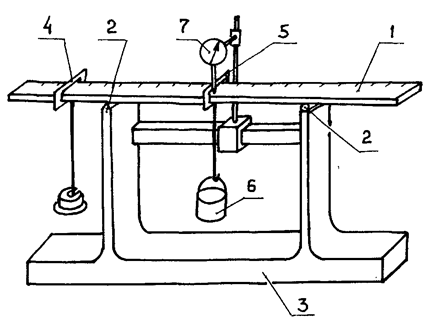
Рис. 4

2. На подвес 4 устанавливают груз P и замеряют прогиб среднего сечения .

3. Если среднее сечение балки переместилось вниз (см. рис. 1), то груз снимают. Затем на подвес 5 закрепляют емкость 6 и насыпают дробь в количестве, которое создаст точно такой же прогиб, как измеренный в п. 2. Емкость 6 снимают и взвешивают на весах. Вес емкости с дробью численно будет равен . Это значение заносят в таблицу опытных данных с положительным значением.

Если среднее сечение балки от груза P переместится вверх (такое будет для i=8,9,10,11), то в этом случае к подвесу 5 крепят емкость 6 и насыпают дробь в таком количестве, чтобы стрелка индикатора 7 вернулась в первоначальное нулевое положение. Емкость с дробью снимают и взвешивают на весах. Этот вес численно будет равен . Значение заносят в таблицу с отрицательным знаком, так как в опыте сила тяжести емкости 6 с грузом направлена вниз, а на расчетной схеме эквивалентного состояния (см. рис. 1) реакция "лишней" связи направлена вверх.

IV. ВЫПОЛНЕНИЕ ЭКСПЕРИМЕНТА

Лабораторную работу выполняют в следующем порядке:

Величину силы P задает преподаватель. Каждой подгруппе студентов преподаватель указывает номер сечения i, к которому будет приложена сила P.

1. Составить расчетные схемы заданного, эквивалентного грузового и вспомогательного единичного состояния. Записать каноническое уравнение метода сил.

2. Построить эпюру и вычислить коэффициент δ₁₁. Эта часть работы – общая для всей группы. Последующая работа – индивидуальная.

3. Построить эпюру M_i и вычислить грузовой коэффициент ∆₁_i.

4. Решить каноническое уравнение, вычислив .

5. Выполнить деформационную проверку, построив эпюру изгибающих моментов для эквивалентного состояния M_э (см. рис. 1):

При условии выполнения проверки полученное значение реакции "лишней" связи записать в табл. 1.

Таблица 1. Ординаты линии влияния

i	1	2	3	4	5	6	7	9	11	13
, Н							0
, Н							0
δ, %	-						-

По мере заполнения табл. 1 проверить соответствие полученного расчетного значения всей совокупности значений, внесенных в одну строку. Если значение не отвечает единой плавной функциональной зависимости, то проверить результаты вычислений на всех этапах расчета, сверив их с соответствующими численными значениями, которые получены в других подгруппах для "смежных" значений реакций табл. 1.

6. Измерить значение на опытной установке, выполнив действия по алгоритму III.1.-III.3.

7. Вычислить погрешность – процент расхождения между расчетным и опытным значением:

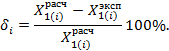
При правильном выполнении лабораторной работы расхождение, как правило, не превышает 2 процентов.

Последующие испытания являются общими для всей группы.

8. Выполнить измерение на экспериментальной установке, приложив к балке грузы в двух сечениях, например (см. рис. 2) в сечениях 3 и 10 (номера сечений могут быть заданы преподавателем произвольно). В этом случае это будет значение .

9. Выполнить измерение на опытной установке, приложив к одному сечению груз P, а ко второму кратный груз nP (кратность задает преподаватель).

V. СРАВНИТЕЛЬНЫЙ АНАЛИЗ ТЕОРЕТИЧЕСКИХ И ОПЫТНЫХ ДАННЫХ

1. Построить линии влияния положения груза на величину реакции "лишней" связи, отложив в масштабе расчетные и экспериментальные значения.

Проанализировать величину и характер погрешности по совокупности значений δ_i (случайная или систематическая, значительная или малая).

2. Проверить равенство

Сделать вывод о справедливости принципа суперпозиции.

3. Проверить равенство

Сделать вывод о применимости принципа пропорциональности.

4. На основании результатов всех проверок сделать общий вывод о применимости метода сил для расчета статически неопределимых балок.

Вопросы для подготовки к защите работы

- Укажите цель лабораторной работы.

- Какую систему называют статически неопределимой?

- Какой смысл имеет каноническое уравнение метода сил?

- Какой смысл имеют коэффициенты канонического уравнения?

- Какие задачи решены в лабораторной работе?

- Каким способом вычисляли коэффициенты канонического уравнения?

- В чем смысл деформационной проверки?

- Как опытным путем определяют перемещения?

- Для какой цели служат тензометры?

- Как устроен индикатор часового типа?

- Какое перемещение называют упругим?

- Как построена линия влияния?

- Как, используя линию влияния, определить реакцию "лишней" связи от совокупности сосредоточенных сил?

- Какие выводы сделаны в результате выполнения лабораторной работы?

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00