Главная

Лабораторная работа

Тема: Опытная проверка закона Гука. Определение модуля упругости первого рода и коэффициента Пуассона.

Цель работы:

1. Проверить в пределах упругости линейность связи деформации и нагрузки.

2. Определить числовые значения упругих постоянных E (модуля упругости первого рода) и (коэффициента Пуассона) для стали.

3. Выяснить при этом физический смысл этих постоянных.

I. НЕОБХОДИМыЕ ПРИБОРЫ И ОБОРУДОВАНИЕ:

1. Стальной образец прямоугольного поперечного сечения.

2. Разрывная машина с силоизмерительным устройством УМ-5.

3. Тензометр – прибор для измерения упругих удлинений.

4. Штангенциркуль.

П. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

Упругие постоянные материалов используются при решении большого числа задач прочности и всех задач жёсткости и устойчивости. Они характеризуют способность материала сопротивляться различным видам деформаций при воздействии на них внешних нагрузок. Значения упругих характеристик, равно как и всех известных физических постоянных, не могут быть постулированы или найдены на основе логических и математических рассуждений, а могут быть получены только экспериментальным путём при испытании образцов на растяжение (сжатие), изгиб и кручение.

Различают материалы изотропные и анизотропные. Изотропия означает независимость свойств материала от направления воздействия нагрузки. Изотропные материалы характеризуются тремя упругими постоянными: модулем Юнга, коэффициентом Пуассона и модулем сдвига. При этом, как показывает теория, только две из них являются линейно независимыми. Анизотропные материалы могут иметь до 18 различных характеристик.

Монокристаллы и отдельные зёрна сталей анизотропны. Однако, благодаря их малости и хаотическому расположению в пространстве сталь приобретает статистически обоснованную изотропность и нуждается в экспериментальном определении, как минимум, двух упругих постоянных (например, модуля Юнга и коэффициента Пуассона).

Модуль Юнга или модуль упругости первого рода E характеризует сопротивляемость материала деформированию в направлении воздействия растягивающих или сжимающих нагрузок. Чем больше модуль Юнга, тем меньше удлинение или укорочение стержня при прочих равных условиях (длине, площади, нагрузке). Модуль Юнга является коэффициентом пропорциональности между нормальным напряжением и относительной линейной деформацией в законе Гука, записанном в дифференциальной форме: . На основе этой формулы находят опытным путём значение модуля упругости

где - формула для напряжения при растяжении, подтверждённая теорией упругости (эталоном точности для сопротивления материалов) и опытными данными; F – сила, растягивающая образец и определяемая по силоизмерительному устройству; A – площадь поперечного сечения, определяемая путём измерения размеров; - относительная продольная деформация, определяемая методом тензометрирования.

На основании закона Гука (1) абсолютная продольная деформация бруса прямо пропорциональна внутренней продольной силе N, вызвавшей эту деформацию:

Измерив опытным путем величину осевой нагрузки F и вызванную ею продольную деформацию и зная размеры испытуемого бруса, вычисляют модуль продольной упругости по формуле, полученной из (2)

Геометрические параметры образца l и A находятся до нагружения, а нагрузка и соответствующее ей удлинение берутся из опыта.

Коэффициент Пуассона характеризует способность материала сопротивляться поперечному деформированию, т.е. изменению размеров в направлении, перпендикулярном воздействию силы. Это сопротивление французский академик Пуассон предложил характеризовать в безразмерной форме как модуль отношения поперечной и продольной относительных деформаций, определяемых опытным путём:

b и l - начальные поперечные и продольные размеры бруса, соответственно.

Для нахождения и достаточно при одной и той же нагрузке измерить абсолютное сужение и абсолютное удлинение , а также знать необходимые первоначальные размеры.

Изменение формы образца при испытаниях на растяжение

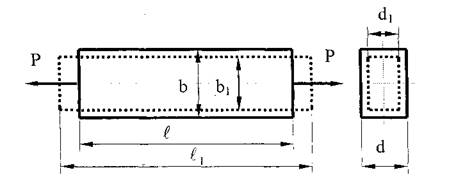
Модуль сдвига или модуль упругости второго рода G характеризует сопротивляемость материала угловым деформациям при воздействии пары сил. Он является коэффициентом пропорциональности между касательным напряжением и углом сдвига в законе Гука при сдвиге, записанном в дифференциальной форме: На основе этой формулы можно экспериментально определить модуль сдвига, например, при кручении образца круглого сечения. В данной работе модуль сдвига определяют косвенным путём, исходя из теоретической зависимости между тремя упругими постоянными:

Упругие постоянные материала имеют более стабильные значения по сравнению с механическими характеристиками. Например, для различных марок сталей временное сопротивление может отличаться в несколько раз (от 400 до 4000 МПа и выше), в то время как среднестатистические значения упругих постоянных для всех марок сталей изменяются в узких пределах:

МПа; МПа.

В лабораторной работе необходимо произвести сравнение полученных значений постоянных со средними справочными данными для стали:

МПа; МПа.

III. ВЫПОЛНЕНИЕ ЭКСПЕРИМЕНТА И ОБРАБОТКА РЕЗУЛЬТАТОВ ИСПЫТАНИЙ

1) Измерить ширину и толщину образца, подсчитать площадь поперечного сечения.

2) Ознакомиться со схемой разрывной машины, разобраться в принципе ее работы.

УНИВЕРСАЛЬНАЯ МАШИНА УМ-5

Универсальной машина УМ-5 называется потому, что позволяет проводить испытания на растяжение, сжатие, изгиб и срез. Максимальное усилие, развиваемое машиной – 5 тонн.

Кинематическая схема машины показана ниже.

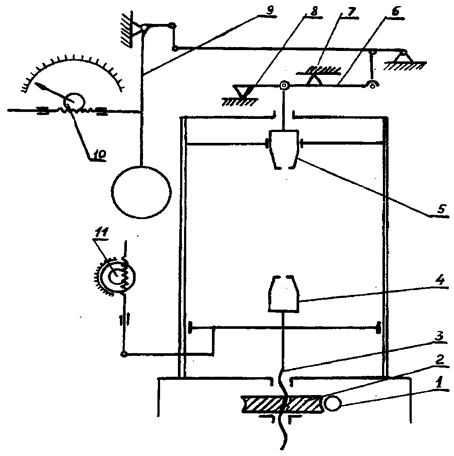
Рис.1. 1,2 - червячный механизм; 3 - винт; 4,5 - нижний и верхний захваты образца; 6 - рычаг силоизмерительного устройства;

7,8 - верхняя и нижняя опора рычага; 9 - маятник; 10 - колесико шкалы нагрузок; 11 - колесико шкалы деформаций.

Машина УМ-5 состоит из следующих узлов: станины, нагружающего механизма с коробкой скоростей, силоизмерительного механизма, измерителя деформаций и самопишущего диаграммного устройства.

Станина представляет собой жесткую раму, образованную чугунными коробками (верхней и нижней), соединенными между собой двумя колоннами.

В нижней коробке помещается червячный механизм (1-2). При вращении червячной шестерни (2) нагружающий винт (3) получает поступательное движение вниз или вверх. Реверсирование осуществляется переключением электродвигателя. Вращение от электродвигателя передается через коробку скоростей (на схеме не показана), позволяющей установить четыре скорости нагружения - 2, 4, 10, 60 мм/мин.

На конце нагружающего винта установлен нижний захват (4). Верхний захват (5) через промежуточную тягу подвешен к рычагу (6) силоизмерителъного механизма.

Рычаг (6) имеет две опоры: нижнюю – (8) и верхнюю – (7). Благодаря этому рычаг может воспринимать как нагрузку направленную вниз (растяжение), так и вверх (сжатие). От рычага через промежуточные звенья усилие передается на короткий рычаг двуплечего маятника (9), вызывая отклонение его, пропорционально приложенной нагрузке. Груз на конце маятника составной, что позволяет получить три диапазона максимальных нагрузок - 1000, 2000 и 5000 кгс (10, 20, 50 кн). При отклонении маятника перемещается рейка, поворачивая колесико со стрелкой. Так измеряется нагрузка.

Измеритель деформаций состоит также из рейки, связанннной одним концом с нижним захватом, а другим концом входящей в зацепление с колесиком (11). На оси с колесиком укрепляется стрелка, показывающая величину перемещения нижнего захвата, а, следовательно, и деформацию образца.

3) Разобраться со схемой рычажного тензометра и ознакомиться с реальным прибором (узнать, как он крепиться на деталь, как производится отсчет и т.п.).

ТЕНЗОМЕТР ГУГГЕНБЕРГЕРА РЫЧАЖНЫЙ

На стальном образце 1 прямоугольного поперечного сечения (рис. 2), закрепленном в захватах 2 машины УМ-5, установлены попарно (для увеличения точности измерений) рычажные тензометры Гуггенбергера: 3 – для измерения продольных деформаций, 4 – для измерения поперечных деформаций.

Рычажный тензометр (рис. 3) устанавливается на образец 1 с помощью специальной струбцины и опирается на него двумя ножами – неподвижным 2 и подвижным 3, выполненными в виде призмы.

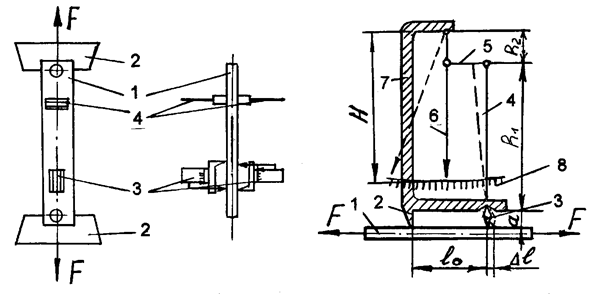
Рис. 2. Схема закрепления тензометров на образце Рис. 3. Схема рычажного тензометра

Расстояние l₀ между ножами называется базой тензометра (минимальная - 20 мм, но с помощью удлинителей база может быть увеличена до 100 мм). При деформации образца расстояние между ножами изменяется. Подвижный нож 3 повернется и отклонит рычаг 4. Отклонение рычага 4 через тягу 5 передается на стрелку 6, которая повернется вокруг оси, закрепленной на рамке 7. Перемещение стрелки по шкале 8 пропорционально изменению расстояния между ножами.

Шкала 8 тензометра проградуирована в миллиметрах. Отношение отсчета по шкале к изменению расстояния между ножами называют коэффициентом увеличения тензометра K, величина которого определяется соотношением

где - размеры плеч рычагов тензометра (рис. 3).

Значение его для каждого тензометра указывается в паспорте.

Для повышения точности определения искомых упругих характеристик образец необходимо нагрузить ступенями 3-4 раза. Наибольшую нагрузку на образец можно определить по величине предела пропорциональности или предела текучести материала по формуле:

Тогда при числе ступеней нагружений m величина ступени нагружения

III. ВЫПОЛНЕНИЕ ЭКСПЕРИМЕНТА И ОБРАБОТКА РЕЗУЛЬТАТОВ ИСПЫТАНИЙ

1. Штангенциркулем измеряют поперечные размеры образца b и h с точностью 0,1 мм. По формулам (4) и (5) определяют величину ступени нагружения и число опытов m и записывают эти данные в журнал наблюдений.

2. Нагружают образец предварительной нагрузкой и устанавливают стрелки 6 (рис. 2) всех четырех тензометров в исходное положение. Величину этой нагрузки и показания тензометров принимают за исходные и записывают в журнал наблюдений.

3. Нагружают образец равными ступенями и записывают соответствующие показания всех тензометров . Вычисляют среднее значение приращений показаний двух тензометров 3 для измерения продольных деформаций и двух тензометров 4 – для измерения поперечных деформаций по формулам соответственно:

где m - число ступеней нагружения.

После этого вычисляют опытные значения абсолютных продольных и поперечных деформаций

где K - коэффициент увеличения тензометра.

4. Подставив значение в формулу (3), определяют опытное значение модуля продольной упругости E. Затем, подставив значения и в формулу с учетом формулы , получают опытное значение коэффициента Пуассона .

5. Проводят анализ результатов опыта.

Форма отчета по лабораторной работе

1. Название лабораторной работы.

2. Цель лабораторной работы.

3. Испытательная машина.

4. Исходные данные.

4.1. Поперечное сечение образца: ширина b, высота h, площадь поперечного сечения A.

4.2. База тензометров:

для измерения продольных деформаций l₀;

для измерения поперечных деформаций b₀.

4.3. Коэффициент увеличения тензометра K.

4.4. Табличные значения:

- модуль продольной упругости для стали E;

- коэффициент Пуассона для стали .

№ п/п	Нагрузка F	Приращение нагрузки	Продольная деформация				Поперечная деформация
			I тензом.		II тензом.		I тензом.		II тензом.
Средние значения приращений

5. Обработка результатов опыта.

Расчёт опытных значений абсолютной продольной и абсолютной поперечной деформаций.

Расчёт опытных значений относительной продольной и относительной поперечной деформаций.

Расчёт опытных значений модуля продольной упругости E и коэффициента Пуассона .

6. Сравнение опытных и теоретических значений.

Вопросы для подготовки к защите работы

- Какова цель лабораторной работы?

- На какой машине выполняется лабораторная работа? Какой используется образец?

- Как устроен рычажный тензометр? Что им измеряют? Что такое коэффициент увеличения тензометра?

- Что называют базой рычажного тензометра?

- С какой целью к образцу прикладывают начальную нагрузку?

- Что такое ступень нагружения?

- Как вычисляют коэффициент увеличения тензометра?

- Как определяется наибольшая нагрузка, прикладываемая к образцу?

- Что собой представляет центральное растяжение - сжатие?

- Напишите формулу для определения нормальных напряжений при центральном растяжении.

- Как записывается формула абсолютного удлинения бруса при растяжении? Что такое жесткость сечения бруса при растяжении?

- Что происходит с поперечными размерами бруса при его растяжении в продольном направлении?

- Что собой представляет относительная линейная деформация?

- Что представляют собой относительная продольная и поперечная деформации?

- Что такое коэффициент Пуассона? Каковы пределы его изменения?

- Какие свойства материала характеризует коэффициент Пуассона?

- Напишите закон Гука при растяжении (сжатии). Связь каких величин отражает закон Гука?

- Что такое изотропия материалов?

- Какие упругие постоянные характеризуют изотропные материалы?

- Сколько линейно независимых упругих постоянных имеют изотропные материалы?

- Как можно характеризовать сталь по её монокристаллическому и поликристаллическому строению?

- Какие свойства материала характеризует модуль Юнга?

- Как записывают закон Гука при растяжении или сжатии в дифференциальной форме?

- Как находят модуль Юнга?

- Как вычисляют напряжение при растяжении?

- Как определяют относительную продольную деформацию опытным путём?

- Что представляют собой модуль упругости Е? Каков его физический смысл?

- Какие размерности имеют упругие постоянные Е и ?

- Как найти из эксперимента величины относительных линейных деформаций в продольном и поперечном направлениях?

- Можно ли определить из проведенных испытаний величину абсолютной линейной деформации в продольном направлении?

- Можно ли определить из проведенных испытаний величину абсолютной линейной деформации в поперечном направлении?

- Какие свойства материала характеризует модуль сдвига?

- Как записывают закон Гука при сдвиге в дифференциальной форме?

- Какая зависимость существует между упругими постоянными изотропного материала?

- Какие средние значения имеют упругие постоянные стали?

- С какой целью соединяют последовательно датчики, наклеенные на противоположных гранях образца?

- Какие деформации могут внести существенные погрешности в результате опыта?

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00