Главная
Лабораторная работа
Тема: Определение перемещений в балке
при изгибе по формуле Мора
Цель работы:
Опытная проверка применимости
формулы Мора для определения перемещений при изгибе и справедливости теоремы
Максвелла о равенстве взаимных перемещений.
Для проверки применимости
формулы Мора необходимо вычислить перемещения нескольких сечений балки при неизменном
положении груза P в сечении j, замерить соответствующие перемещения на опытной установке
и сравнить полученные совокупности расчетных и экспериментальных значений. Каждая
из этих совокупностей дискретных значений образует график изогнутой оси бруса.
Для проверки теоремы Максвелла о
взаимности перемещений необходимо вычислить ряд значений прогибов одного и того
же сечения j при перемещении
груза вдоль оси бруса для отдельных конкретных положений его на этой оси.
Измерить соответствующие прогибы на опытной установке и сравнить полученные совокупности
расчетных и экспериментальных значений. Каждая из этих совокупностей отражает
влияние положения груза P
на величину перемещения сечения j. Затем сравнить отдельно
ординаты графиков изогнутой оси и линии влияния.
Таким образом, необходимо решить
две задачи.
Задача 1: построение изогнутой
оси бруса от силы P, приложенной в сечении j.
Задача 2: построение линии
влияния положения груза на прогиб сечения
j.
I. НЕОБХОДИМЫЕ ПРИБОРЫ И ОБОРУДОВАНИЕ
1. Экспериментальная установка – балка прямоугольного сечения, закрепленная с обоих концов,
2. Индикатор часового типа,
3. Грузы.
II. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ.
Метод определения перемещений по
формуле О. Мора (1874) является энергетическим методом, универсальным для
линейных стержневых систем. Может быть применен для
определения углового или линейного перемещения сечений балки, выполненной из упругого
материала.
Изучаемый объект (рис. 1)
представляет собой балку постоянного сечения по всей длине l, установленную
на шарнирные опоры и нагруженную в сечении j сосредоточенной
силой P.
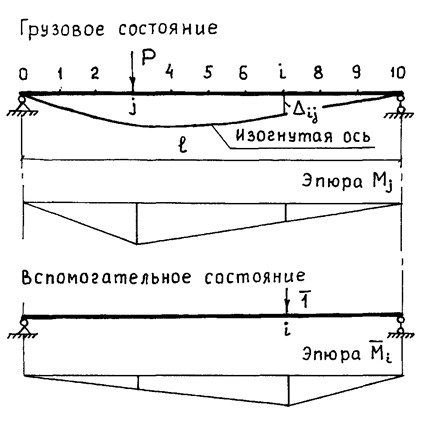
Рис. 1
Для рассматриваемого объекта
формула Мора для вычисления прогиба любого сечения (i =1,2,3,…10), если пренебречь
влиянием поперечных сил, представляет собой интеграл определенного вида:
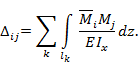
В формуле
Мора: 
- функция изгибающего момента
относительно поперечной оси x
от единичной силы вспомогательного состояния; 
- функция изгибающего момента
относительно поперечной оси х от внешней
нагрузки; k - количество
участков, на которые делят схемы грузового и единичного состояния для выполнения
расчета; lk - длина отдельного
участка; E - модуль
упругости материала; Ix - момент инерции поперечного сечения.
Интеграл Мора может быть
вычислен как аналитически, так и численным методом. Большое распространение в
инженерной практике получили формула Симпсона и правило Верещагина.
Положительное число, полученное
в результате вычисления интеграла Мора, означает, что реальное направление прогиба
совпадает с направлением вектора обобщенной силы, а отрицательное – что прогиб
сечения противоположен направлению единичного вектора. Линейные перемещения
сечений балки, совпадающие с опорами, равны нулю, в то время как угловые перемещения
могут быть любыми (см. рис. 1) – важное обстоятельство, которое будет использовано
в следующей лабораторной работе при исследовании статически неопределимой
балки.
Особенности:
1) схема вспомогательного
единичного состояния метода Мора представляет собой балку, нагруженную
обобщенной силой по направлению искомого перемещения;
2) k -
минимальное число участков, на которые делят схемы грузового и вспомогательного
единичного состояния;
3) в формуле Мора и - это функции одной и той же координаты
произвольного сечения, составленные с одним и тем же правилом знаков.
При линейно упругом
деформировании балки все перемещения будут пропорциональны силе P, вызывающей эти перемещения:
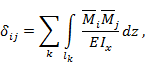
где 
- изгибающий момент от единичной внешней силы 
,
приложенной к сечению j.
Если сила P будет
приложена к сечению i (рис. 2), то тогда формула
Мора для прогиба сечения j будет иметь вид
где - изгибающий момент от обобщенной единичной силы
вспомогательного состояния; 
- изгибающий момент от внешней нагрузки.
Согласно закону Гука перемещение
∆ji
также пропорционально силе P:
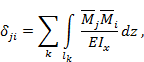
где - изгибающий момент от единичной внешней силы ,
приложенной к сечению i.
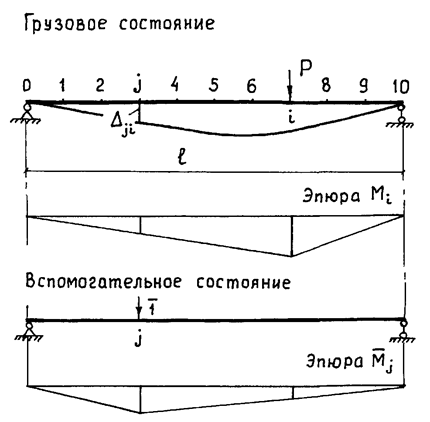
Рис. 2
Поскольку полученные
интегральные выражения одинаковые, то
.
Эта зависимость аналитически
выражает теорему Д. К. Максвелла (1864) о взаимности перемещений.
III. ПОСТАНОВКА ОПЫТА.
Установка для выполнения
лабораторных опытов (рис. 3) представляет собой балку в виде стальной линейки 1
длиной
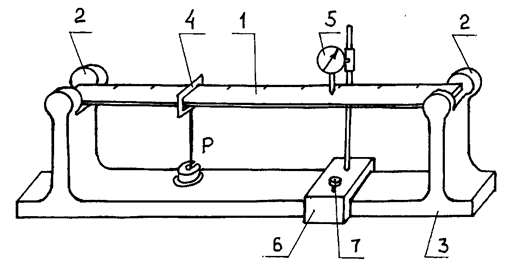
Рис. 3
Прогибы сечений, обозначенных
рисками, измеряют индикатором часового типа 5, закрепленным на штативе 6.
Корпус штатива 6 перемещается вдоль станины 3 как вдоль направляющей. Для
снижения погрешности измерения от зазора в паре скольжения 6-3 корпус штатива
притягивают стопорным винтом 7 после установки индикатора 5 к нужному сечению.
Для построения опытной кривой
изогнутой оси подвес 4 помещают в сечение j бруса. Балку нагружают
грузами. Производят замер перемещения сечений i =1,2,3,…9 бруса, для каждого
замера перемещая штатив 6 индикатора 5 вдоль направляющей станины 3. По
замеренным дискретным значениям ∆ij
строят график изогнутой оси.
Для построения линии влияния
положения груза на прогиб сечения j балки замер перемещений
выполняют при неизменном положении штатива индикатора в сечении j, а подвес 4 перемещают вдоль балки 1, совмещая с рисками сечений
i =1,2,3,…9.
Балку нагружают. По замеренным дискретным значениям строят линию влияния.
IV. ВЫПОЛНЕНИЕ ЭКСПЕРИМЕНТА
Лабораторную работу выполняют в
следующем порядке:
1. Построение изогнутой оси
Величина силы P и номер сечения j, к которому приложена
сила, задается преподавателем. Таким образом, конкретизируется заданное
грузовое состояние балки. Группа делится на подгруппы; каждая подгруппа выполняет
расчет для одного из номеров сечений балки i =1,2,3,…9 (номер определяет
преподаватель).
1.1. Для заданной расчетной
схемы грузового состояния построить эпюру изгибающих моментов Mj. Эта часть вычислительной
работы – общая для всей группы. Дальнейшая работа индивидуально выполняется каждой
подгруппой.
1.2. Составить схему
вспомогательного единичного состояния и построить для него эпюру .
1.3. Вычислить перемещение 
по формуле Мора численным методом, используя
формулу Симпсона или прием Верещагина. Для этого следует выделить одинаковые
участки на эпюрах грузового и единичного состояний (как правило, таких участков
для вычисления интеграла k=3) и вычислить значения
дополнительных граничных ординат.
Вычисленное значение занести в
табл. 1.
Проверить соответствие
расчетного значения всей совокупности значений, внесенных в одну строку. Если
расчетное значение не отвечает единой плавной функциональной зависимости, то подгруппе, выполнявшей этот расчет следует сверить все
промежуточные результаты вычислений с соответствующими численными значениями,
полученными студенческими подгруппами для смежных сечений.
Таблица 1. Ординаты
изогнутой оси бруса
|
i |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
δi,
% |
- |
|
|
|
|
|
|
|
|
|
- |
1.4. Измерить на опытной
установке перемещение того же сечения, для которого выше был выполнен расчет.
Для этого: подвеску 4 поместить в сечение j; штатив 6 индикатора 5
подвести к сечению i и закрепить стопорным
винтом 7; установить шкалу индикатора, совместив нулевое значение со стрелкой;
приложить груз P в виде набора тарированных стандартных
грузов; замерить перемещение по шкале (цена деления указана на шкале).
Полученное экспериментальное
значение 
занести в табл. 1. Проверить соответствие
результата замера всей совокупности опытных значений, внесенных в одну строку.
1.5. Вычислить погрешность –
процент расхождения между расчетным и опытным значением перемещения сечения i:
Результат занести в табл. 1.
2. Построение линии влияния.
Для всей группы номер j и величина внешней силы P остаются такими же, как
и в первой задаче. Номер для каждой подгруппы также остается прежним.
2.1. Показать вспомогательное состояние
метода Мора для определения перемещения сечения j и построить
эпюру .
Эта часть работы – общая для всей группы; последующая – индивидуальная.
2.2. Составить расчетную схему
грузового состояния. Она представляет собой двухопорную
балку с сосредоточенной силой P, приложенной к сечению i. Построить для нее эпюру
изгибающих моментов Mi.
2.3. Вычислить перемещение 
по формуле Мора численным методом, аналогичным
вычислению перемещения в предыдущей задаче. Результат расчета должен повторить
результат предыдущей задачи. При несовпадении найти ошибку, поэтапно
проанализировав промежуточные операции двух расчетов.
Полученное значение занести в
табл. 2.
Таблица 2. Ординаты
линии влияния
|
i |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
δi,
% |
- |
|
|
|
|
|
|
|
|
|
- |
2.4. Измерить на опытной
установке перемещение сечения j при нагружении
балки силой в сечении i. Для этого:
индикатор 5 установить в сечении j, а подвес 4 в сечении i; выставить нулевое значение
на шкале индикатора поворотом лимба; приложить грузы; снять показания со шкалы
микрометра. Показание должно с небольшой погрешностью повторить измерение в
предыдущей задаче. При несовпадении опыт повторить.
Измеренное значение 
записать в табл. 2.
2.5. Вычислить погрешность –
процент расхождения между расчетным и опытным значением перемещения сечения j:
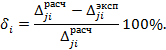
При правильном выполнении работы
величины погрешностей, полученные при решении двух задач, будут одинаковыми.
Результат занести в табл. 2.
V. СРАВНИТЕЛЬНЫЙ АНАЛИЗ ТЕОРЕТИЧЕСКИХ И
ОПЫТНЫХ ДАННЫХ
1. Построить графики изогнутой
оси бруса по расчетным и экспериментальным данным табл. 1. Проанализировать
графики и сделать вывод о применимости формулы Мора.
Если линии графиков много раз пересекаются и погрешности δi
принимают разные значения по величине и знаку, то ошибки опытов и расчетов
имеют случайный характер. По средней величине погрешности можно судить о
точности метода.
Если линии графиков не
пересекаются (заведомо неверные результаты при этом следует отбросить) и
погрешности δi по величине и
знаку одинаковые, то в таком случае ошибки имеют систематический характер и следует
выявить возможные причины.
Во-первых, неучет
влияния поперечной силы в формуле Мора может привести к небольшому снижению
расчетных значений.
Во-вторых, следует обратить
внимание на конструкцию опор, насколько они обеспечивают идеальное шарнирное опирание и соответствие расчетной схеме: отсутствие линейных
перемещений и свободный поворот относительно оси x. Как правило, на больших контактных поверхностях в узлах трения при
плохой смазке и низкой температуре создаются дополнительные усилия, уменьшающие
угол поворота и, следовательно, систематически снижающие экспериментальные
значения прогибов.
В-третьих, погрешность опытных
значений может создавать и измерительное устройство, так как при каждом
измерении осуществляется его переустановка. Кроме того, в нем также имеется
пара трения. Поэтому погрешность измерения может иметь как случайный, так и
систематический характер.
2. Построить линии влияния
положения груза на прогиб сечения по расчетным и опытным значениям.
Проанализировать отдельно
значения одинаковых строк двух таблиц: 
.
Сделать вывод о взаимности перемещений.
При равенстве совокупностей
значений перемещений по строкам и при одинаковых совокупностях δi
теорему Максвелла можно считать доказанной опытным путем.
Вопросы для подготовки к защите работы
- Укажите цель лабораторной
работы.
- Какие задачи решались в
лабораторной работе?
- Какие перемещения совершают
сечения при изгибе балки?
- Что называют прогибом?
- Какое перемещение можно
определить по формуле Мора?
- Что означают индексы в
обозначении перемещения?
- Каков порядок определения
перемещения при использовании формулы Мора?
- Как выбирают вспомогательное
состояние?
- Как вычисляют интеграл Мора?
- Каким численным приемом можно
воспользоваться для вычисления интеграла Мора?
- Как строят график изогнутой
оси бруса?
- Сформулируйте теорему
Максвелла.
- Какие выводы сделаны в
результате выполнения лабораторной работы?
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
