Главная
Лабораторная работа
Тема: Проверка теории
изгибающего удара
Цель работы:
Опытное определение динамического коэффициента при изгибающем ударе по середине пролета двухопорной балки и сравнение его с динамическим коэффициентом, полученным расчетом.
I. НЕОБХОДИМЫЕ ПРИБОРЫ И ОБОРУДОВАНИЕ
1. Лабораторная установка СМ-21М
2. Индикатор часового типа ИЧ-10.
II. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Явление удара возникает в том случае, когда скорость рассматриваемой части конструкции или соприкасающихся с ней тел изменяется в очень короткий период времени. При ударе груза F, падающего на балку с высоты H, балка прогнется. Изогнутая ось балки (эпюра динамического прогиба) будет иметь вид, показанный на рис.1,а. Изогнутая ось балки от статически приложенной силы F (эпюра статических прогибов) – вид, изображенный на рис.1,б.
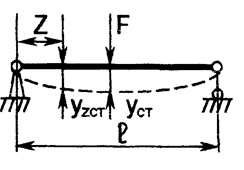
а)
б)
Рис.1. Эпюры динамического и статического прогибов
В основе приближенной теории удара, рассматриваемой в курсе сопротивления материалов, лежит гипотеза о том, что эпюра перемещений системы от груза F при ударе (в любой момент времени) подобна эпюре перемещений, возникающей от этого груза, но действующего статически. На основании указанной гипотезы и рис.1,а для динамического коэффициента получают зависимость
где 
и 
- динамический (статический) прогибы в
продольном сечении Z балки и в сечении, где приложена внешняя нагрузка F, соответственно.
При расчетах без учета массы балки динамический коэффициент КД при падении груза с высоты Н определяют по формуле:
Если высота падения груза H во много раз больше статического перемещения УСТ, то в формуле (1) можно пренебречь единицами и принять:
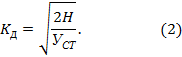
При расчете на удар с учетом массы балки Q/g динамический коэффициент определяют по формуле:
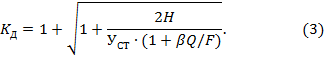
При этом
упругая система с распределенной массой мысленно заменяется системой,
обладающей такими же упругими свойствами, но с приведенной массой 
,
сосредоточенной в точке удара (
- коэффициент
приведения массы, g- ускорение
свободного падения). В случае изгибающего удара посередине балки, лежащей на
двух опорах, принимают = 17/35.
Работа выполняется на установке типа СМ-21М (рис.2).
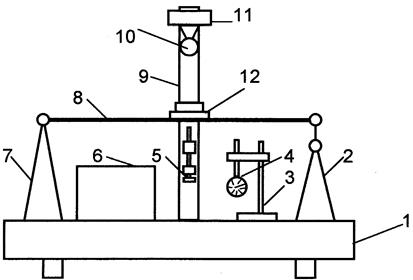
Рис.2. Схема лабораторной установки типа СМ-21М
Установка состоит из следующих основных частей: основания 1, на котором установлен исследуемый образец – балка 8 прямоугольного поперечного сечения, опирающаяся на шарнирно-подвижную 2 и шарнирно-неподвижную 7 опоры, индикатора 4 часового типа ИЧ-10 с ценой деления 0,01 мм, закрепленного на стойке 3, штанги 9 с электромагнитом 11и микрометрическим винтом 5 с ценой деления 0,01 мм, установленной по середине пролета балки 8; пульта управления 6. Электромагнит 11 предназначен для удержания падающего шарика 10 на требуемой высоте Н над исследуемой балкой 8. Для предупреждения возможного отскока шарика балка снабжена специальным ловителем 12, внутренняя поверхность которого выполнена конусной. Определение статического прогиба балки производят индикатором часового типа 4 с учетом веса ловителя 12 и соединенных с ним деталей. В процессе удара индикатор отводится в сторону. Величина динамического прогиба определяется с помощью микрометрического винта 5 в момент контакта его торца с колеблющейся балкой.
III. ВЫПОЛНЕНИЕ ЭКСПЕРИМЕНТА И ОБРАБОТКА РЕЗУЛЬТАТОВ ИСПЫТАНИЙ
1. Штангенциркулем измеряют размеры поперечного сечения балки b и h с точностью 0,1 мм, линейкой определяют длину пролета l, устанавливают электромагнит 11 на заданную высоту H и заносят данные в журнал наблюдений.
2. Определяют статический прогиб балки УСТ от веса шарика 10, веса ловителя 12 и веса балки 8. Для этого при помощи индикатора 4 замеряют прогиб балки УСТ от груза массой 1 кг после его установки на ловитель 12. Затем индикатор 4 снимают и вычисляют
где: вес
шарика F= 0,0665 кг; вес ловителя Q1=
0,0875 кг; вес балки 
кг (размеры b, h и l в см); 
- статический прогиб балки от груза, весом 1
кг.
3. Определяют
максимальный динамический прогиб 
.
Для этого подключают установку к сети и включают тумблер “220B”. При этом загорается лампа “Сеть”.
Тумблером “Электромагнит” подают напряжение на электромагнит 11.
С помощью микрометрического винта 5 определяют положение балки 8 до удара, а затем выворачивают вниз микрометрический винт 5 до упора. Устанавливают шарик 10 на острие сердечника электромагнита 11 и выключают тумблер “Электромагнит”. Шарик 10 нанесет удар по балке. Постепенно, ввинчивая винт 5 и нанося удары шариком по балке, добиваются касания балкой винта 5. Момент касания балки с винтом при ударе фиксируется загоранием лампы “Контакт” на пульте 6 установки. Динамический прогиб определяют не менее трех раз при одинаковой высоте падения шара H. Затем отключают установку от сети.
Максимальный динамический прогиб определяют как разность отсчетов по лимбу в начальном (до удара) и конечном (при ударе) положении винта 5 в момент касания его с балкой 8. Все данные измерений и показания приборов заносят в журнал наблюдений.
4. Обрабатывают результаты опыта и по формуле (3) определяют расчетное значение динамического коэффициента КД и производят сравнение теоретических и опытных значений.
Форма отчета по лабораторной работе
1. Название лабораторной работы.
2. Цель работы.
3. Лабораторная установка. Расчетная схема.
4. Измерительные приборы.
5. Исходные данные.
- Ширина поперечного сечения балки b.
- Высота поперечного сечения балки h.
- Длина пролета l.
- Высота, с которой падает шарик H.
6. Теоретические расчеты.
- Определение статического прогиба балки УСТ.
- Определение
динамического коэффициента 
- Определение
динамического коэффициента 
,
если высота во много раз превышает статический прогиб.
- Определение
коэффициента 
с
учетом массы балки.
7. Результаты испытаний.
- Статический
прогиб балки от груза в 1 кг .
- Статический прогиб балки УСТ от веса шарика F, веса ловителя Q1 и веса балки Q.
-
Максимальный динамический прогиб при падении шарика с высоты H (отсчет по лимбу) 
- Среднее
значение прогиба для трех величин 
-
Динамический коэффициент 
8. Сравнение опытных и теоретических значений.
Вопросы для подготовки к защите работы
- Какова цель лабораторной работы?
- Каково устройство лабораторной установки?
- Какое явление называется ударом и результатом чего он является?
- Какая гипотеза лежит в основе теории удара, рассматриваемой в курсе сопротивления материалов?
- Что называют динамическим коэффициентом при ударе?
- Как учитывают в выражении динамического коэффициента массу упругой системы, подвергающейся удару?
- Что такое “внезапное действие нагрузки” и чему равен динамический коэффициент при таком ее действии?
- Как определяют перемещения и напряжения при ударе?
- Применением каких конструктивных мероприятий можно уменьшить напряжения при ударном действии нагрузки?
- Зависят ли напряжения при ударе от модуля упругости материала системы, подвергающейся удару?
- Как определяют статический прогиб балки от собственного веса?
- Как определяют динамический прогиб балки при ударе в опыте?
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
