Главная

Лабораторная работа

Тема: Испытание стальной трубы на изгиб с кручением

Цель работы: Определение опытным путем величины и направления главных напряжений в поверхностном слое тонкостенной трубы при кручении, а также при одновременном изгибе и кручении, и сравнение их с данными, полученными теоретическим расчетом.

I. НЕОБХОДИМЫЕ ПРИБОРЫ И ОБОРУДОВАНИЕ

Для выполнения работы используется установка типа СМ-18А (рис. 1). На литой станине 1 закреплена консольная тонкостенная труба 2 из дюралюминия марки Д16Т с наружным диаметром D и внутренним – d. На свободном конце трубы горизонтально установлен равноплечий нагрузочный рычаг 3. К правому плечу рычага 3 на расстоянии a подвешен грузовой подвес 4, а к его левому плечу также на расстоянии a прикреплен тросик 5, перекинутый через блок 7, к концу которого подвешен грузовой подвес 6. Блок 7 установлен на кронштейне 8, прикрепленном к станине 1. При различных величинах грузов на концах поперечины трубчатый образец испытывает деформацию изгиба с кручением.

На расстоянии l от свободного конца трубы 2 наклеена розетка тензодатчиков 9 (в сечении K) согласно схемы их расположения, показанной на рис. 3. Компенсационные тензодатчики 10 наклеены на трубе 2 перпендикулярно ее продольной оси.

Для подсоединения выводов рабочих и компесационных тензодатчиков предусмотрена клеммная колодка 11.

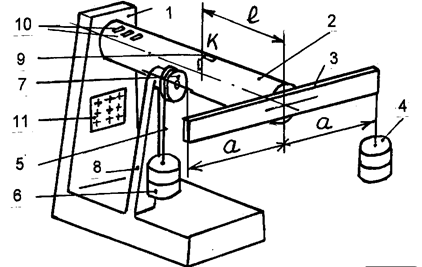
Рис.1. Схема лабораторной установки СМ-18А

II. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

В практике машиностроения часто возникает необходимость расчета тонкостенных стержней замкнутого профиля, например, труб, работающих при кручении, а также при совместном действии изгиба и кручения.

В этом случае в любой точке на поверхности трубы возникает плоское напряженное состояние.

При плоском напряженном состоянии величину и направления главных деформаций (совпадающие с направлениями главных напряжений) можно определить, если измерить линейные деформации на поверхности трубы по трем произвольно выбранным направлениям, используя для этого розетку тензодатчиков, т.е. три тензодатчика 1, 2 и 3 (рис. 3), наклеенные на трубу в исследуемом сечении K (на расстоянии l от конца трубы) так, чтобы, например, датчик 2 был параллелен образующей трубы (оси Z), а два других расположены к ней под углом 45º.

При изгибе с кручением (рис. 2, б) по деформациям , измеренным в направлении трех тензодатчиков, вычисляют главные деформации по формулам:

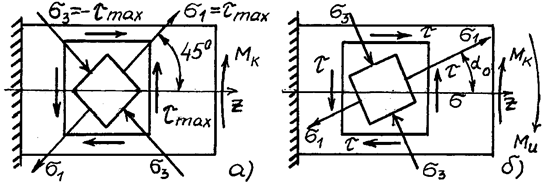
Рис.2. Напряженное состояние в произвольной точке тонкостенной трубы:

а) при кручении; б) при кручении с изгибом.

Затем, используя обобщенный закон Гука, по найденным значениям и вычисляют величину главных напряжений

где - коэффициент Пуассона; E - модуль продольной упругости

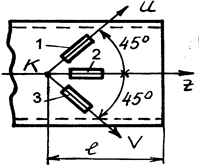
Рис.3. Розетка тензодатчиков материала трубы.

Угол между осью трубы Z и главным напряжением определяют по формуле:

Теоретическим расчетом величину главных напряжений при изгибе с кручением определяют по формуле

При этом для вычисления нормальных напряжений от изгиба и касательных напряжений от кручения используют известные формулы

где - осевой момент сопротивления сечения (C=d/D, где D и d - наружный и внутренний диаметры трубы, соответственно);

- полярный момент сопротивления сечения.

Положение главных площадок теоретически определяют по углу между направлением (осью Z) и направлением (рис. 2, б) по формуле

При кручении во всех точках на поверхности тонкостенной трубы возникает плоское напряженное состояние – чистый сдвиг (рис.2, а). В этом случае известно, что главные напряжения направлены под углом к продольной оси Z трубы.

Так как тензодатчики 1 и 3 (рис. 3) наклеены на трубу под углом 45° к ее продольной оси Z, (по направлениям главных напряжений), то для определения последних достаточно измерить значения главных деформаций и по этим же направлениям. Тогда, учитывая, что главные напряжения при чистом сдвиге равны по величине, но противоположны по знаку, формулы (2) упрощаются

где - главные деформации, измеренные датчиками 1 и 3, соответственно.

Теоретическим расчетом определяют величину главных напряжений из выражения

III. ВЫПОЛНЕНИЕ ЭКСПЕРИМЕНТА И ОБРАБОТКА РЕЗУЛЬТАТОВ ИСПЫТАНИЙ

1. Штангенциркулем измеряют наружный D и внутренний d диаметры трубы с точностью 0,1 мм. Линейкой измеряют с точностью 1 мм плечи a рычага 3 и расстояние l от свободного конца трубы 2 до сечения, в котором определяют главные напряжения (до точки K).

2. Определяют ступень нагружения , руководствуясь тем, чтобы после опытов (число нагружений m=3 – 4) величина эквивалентных напряжений в поверхностном слое трубы была несколько меньше предела пропорциональности материала трубы, т. е.

Если нагрузку F приложить только на подвес 4, то после приведения ее к центру трубы, получают совместное действие изгиба и кручения. Тогда, например, по третьей гипотезе прочности получают

где - наибольший изгибающий момент в сечении K;

- наибольший крутящий момент; С= d/D.

Отсюда наибольшая нагрузка, которая может быть приложена к трубе

Тогда ступень нагружения при числе опытов m будет равна

Если значение неизвестно, то его определяют по приближенной формуле (для материала трубы: дюралюминия марки Д 16Т, предел текучести МПа).

При кручении ступень нагружения определяют учитывая, что крутящий момент T=2Fa получают приложением к подвесам 4 и 6 одинаковых грузов.

3. Из справочника выписывают значения модуля продольной упругости материала трубы E и коэффициент Пуассона . Все эти данные заносят в журнал наблюдений.

4. Балансируют мостовые схемы тензоусилителя, предварительно включенного в сеть для прогрева в течение не менее 20 минут.

5. При изгибе с кручением трубу нагружают, последовательно прибавляя к грузовому подвесу 4 m раз внешнюю нагрузку , и заносят после каждого опыта в журнал наблюдений показания тензодатчиков . Затем вычисляют приращения показаний каждого тензодатчика и среднее значение этих показаний Определяют линейные деформации

где K_U, K_Z и K_V - тарировочные коэффициенты измерительных каналов тензоусилителя.

Вычисляют опытные значения: по формуле (1) главные деформации и ; по формуле (2) главные напряжения и , а по формуле (3) положение главных площадок – угол .

Рассчитывают теоретические значения: с учетом формулы (5) по формуле (4) – главные напряжения и , а по формуле (6) – положение главных площадок (угол ).

6. При кручении трубы прикладывают равными ступенями (3-4 раза) нагрузку к подвесам 4 и 5 и снимают показания тензодатчиков 1 и 3 – и . Определив средние значения приращений показаний и , вычисляют опытные значения главных деформаций

Вычисляют опытные значения главных напряжений и по формулам (8) и (9) по найденным выше и Положение главных площадок известно -

Рассчитывают теоретические значения главных напряжений и по формуле (10).

Обработку всех опытных данных проводят, руководствуясь разделом 4. В заключение выполняют анализ и сравнение полученных данных.

Форма отчета по лабораторной работе

1. Название лабораторной работы.

2. Цель работы.

3. Схема лабораторной установки.

4. Основные расчетные данные:

- Расстояние от свободного конца трубы до сечения l.

- Диаметры трубы: внутренний d и наружный D.

- Плечо внешней нагрузки a.

- Модуль продольной упругости материала E.

- Коэффициент Пуассона .

- Тарировочные коэффициенты тензометров K_U, K_Z, K_V.

- Осевой момент сопротивления сечения W_x.

- Полярный момент сопротивления сечения W_P.

- Изгибающий момент в заданном сечении M_x.

- Крутящий момент в заданном сечении T_Z.

5. Результаты эксперимента.

№ п/п	Нагрузка F	Приращение нагрузки	Показания тензометров			Приращение показаний тензометров
Средние значения приращений

6. Теоретическое определение главных напряжений при кручении с изгибом.

- Нормальные напряжения .

- Касательные напряжения .

- Главные напряжения и , положение главных площадок - .

7. Экспериментальное определение главных напряжений.

- Деформации, измеренные в направлениях трех тензодатчиков

- Главные деформации и .

- Главные напряжения и .

8. Определение угла наклона между осью трубы и направлением главного напряжения .

9. Сравнение опытных и теоретических значений.

Вопросы для подготовки к защите работы

- Какова цель данной лабораторной работы?

- Как устроена лабораторная установка СМ-18А?

- Как устроен проволочный тензодатчик? Объясните принцип его работы?

- Что называют «розеткой» тензодатчиков?

- Из каких простых видов нагружения состоит изгиб с кручением?

- Как определяют нормальные напряжения при чистом изгибе?

- Как определяют касательные напряжения при кручении?

- Что собой представляет напряжённое состояние в точке при изгибе с кручением?

- Какие напряжения возникают в поперечном сечении трубы при изгибе с кручением? – при кручении?

- По каким формулам определяют теоретические напряжения на поверхности трубы при изгибе и при кручении?

- Какие виды напряженных состояний Вы знаете? Какое напряженное состояние называют плоским?

- Какое напряженное состояние называют чистым сдвигом?

- Какие линейные деформации называют главными деформациями?

- Как записывается обобщенный закон Гука?

- Почему линейные деформации при кручении определяют с помощью датчиков наклеенных под углом 45º к оси трубы?

- Какие напряжения называют главными?

- Какая зависимость существует между касательными напряжениями в поперечном сечении бруса при кручении и главными напряжениями?

- Как нагрузить установку, чтобы труба испытывала изгиб и кручение? – только кручение?

- Как теоретически определить главные напряжения при изгибе с кручением?

- По каким формулам определяют опытным путем величину главных напряжений при изгибе с кручением?

- Какова размерность крутящего и изгибающего моментов?

- Как находят опасное сечение круглого бруса при изгибе с кручением?

- Как вычисляют главные напряжения при изгибе с кручением?

- Как определяют положение главных площадок при изгибе с кручением?

- Как вычисляют главные деформации при плоском напряжённом состоянии с использованием прямоугольной тензорозетки?

- Как вычисляют положение главных площадок для случая прямоугольной тензорозетки?

- Как определяют главные напряжения по формулам обобщённого закона Гука?

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00