Главная
Лекция 5 (продолжение). Примеры решения задач по кручению
Статически неопределимые задачи на кручение
Как известно, статически неопределимыми называют задачи, в которых
число неизвестных опорных реакций или число внутренних усилий превышает число
возможных уравнений статики. Один из методов решения статически неопределимых
задач сводится к следующему:
а) составляются все возможные в данной задаче уравнения статики;
б) представляется картина деформации, происходящей в
данной конструкции, и записываются деформационные уравнения, число которых
должно быть равно степени статической неопределимости задачи;
в) решается совместная система уравнений статики и
деформационных уравнений.
Рассмотрим решение статически неопределимой задачи на
кручение.
Пример № 1
Построить эпюру крутящих моментов для вала постоянного по длине поперечного сечения, жестко защемленного обоими торцами и нагруженного скручивающим сосредоточенным моментом М (см. рис.), расположенным на расстоянии а от левого закрепления.

Решение.
Так как вал
защемлен с двух торцов, то в обоих защемлениях возникнут реактивные опорные
моменты МА и МВ. Для их определения
используем вначале уравнения статики. В данном случае можно составить только
одно уравнение равновесия: ![]() , или
, или
МА+ МВ + М = 0. (1)
Уравнение содержит две неизвестные величины: МА и МВ. Следовательно, данная задача является один раз статически неопределимой.
Рассматриваем картину деформации вала (рис. б). Видно, что взаимный угол закручивания правого торца относительно левого равен нулю. Угол поворота правого торца относительно левого может быть представлен в виде суммы углов закручивания отдельных участков вала.
Согласно
формуле ![]() , углы закручивания по участкам определятся следующим
образом: для участка длиной а
, углы закручивания по участкам определятся следующим
образом: для участка длиной а ![]() для участка длиной b
для участка длиной b ![]() где Ta и Tb – крутящие
моменты на соответствующих участках вала. Суммарный угол закручивания по
условию закрепления концов равен нулю, т.е.
где Ta и Tb – крутящие
моменты на соответствующих участках вала. Суммарный угол закручивания по
условию закрепления концов равен нулю, т.е.
![]() (2)
(2)
Это и есть деформационное уравнение задачи.
Преобразуем его. Применяя метод сечений, выразим крутящие моменты Та и Тb:
Та = МА , Тb = МВ.
Подставив эти
значения моментов в уравнение (2), и сократив полученное уравнение на
постоянный множитель ![]() , получим
, получим
![]() . (3)
. (3)
Решая совместно уравнения (1) и (3), найдем
![]()
Знак «–» указывает на то, что истинное направление реактивных моментов противоположно выбранному первоначально. Вычислив реактивные моменты, строим эпюру крутящих моментов по известным правилам (рис. в).
Можно отметить
следующую особенность эпюр крутящих моментов в статически неопределимых валах с
![]() = const: суммарная площадь эпюры крутящих
моментов равна нулю, что по существу предопределено уравнением (3). Если вал
ступенчатый, то нулю должна быть равна сумма площадей эпюры крутящих моментов,
отнесенных к моментам инерции сечений на соответствующих участках.
= const: суммарная площадь эпюры крутящих
моментов равна нулю, что по существу предопределено уравнением (3). Если вал
ступенчатый, то нулю должна быть равна сумма площадей эпюры крутящих моментов,
отнесенных к моментам инерции сечений на соответствующих участках.
Пример № 2
Построить
эпюры крутящих моментов Т, абсолютных
![]() и относительных
и относительных ![]() углов закручивания
круглого сплошного ступенчатого стержня, защемленного с двух торцов и
нагруженного внешним крутящим моментом М
(см. рис.).
углов закручивания
круглого сплошного ступенчатого стержня, защемленного с двух торцов и
нагруженного внешним крутящим моментом М
(см. рис.).

Решение.
Задача один раз статически неопределима. Решим задачу следующим способом. Отбросим мысленно правое защемление, т.е. рассмотрим статически определимый стержень, показанный на рис. б. Эпюра крутящих моментов для него от действия внешнего крутящего момента М имеет вид, показанный на рис. в. Определим угол закручивания правого торца В статически определимого стержня:
![]()
Ответ
получился со знаком «+», следовательно, сечение В повернется вокруг оси х в направлении внешнего момента М. Но на самом деле сечение 4 статически неопределимого стержня
(рис. а) не поворачивается ![]() . Приложим к статически определимому стержню крутящий момент МВ (рис. г) и определим угол поворота
. Приложим к статически определимому стержню крутящий момент МВ (рис. г) и определим угол поворота ![]() правого торца только от действия момента МВ, используя эпюру крутящего момента
правого торца только от действия момента МВ, используя эпюру крутящего момента ![]() (рис. д),
(рис. д),
![]()
Теперь можно записать деформационное условие, показывающее, что угол поворота в сечении 4 статически неопределимого стержня должен быть равен нулю:
![]()
Из этого условия находим МВ = М/6. Крутящий момент МВ будет являться опорной реакцией для статически неопределимого стержня,
МВ = М4.
Окончательная
эпюра крутящих моментов получается сложением двух эпюр ![]() и
и ![]() (рис. е).
(рис. е).
Приступаем к
построению эпюры углов закручивания ![]() , для чего вычисляем по формуле
, для чего вычисляем по формуле ![]() углы закручивания для
каждого участка
углы закручивания для
каждого участка
![]()
![]()
![]()
а затем находим значения углов закручивания в характерных сечениях:
![]()
![]()
![]()
![]()
Последний
результат подтверждает правильность проведенных вычислений. Введя для
сокращения новое обозначение ![]() , окончательно получаем:
, окончательно получаем:
![]()
![]()
![]() .
.
Затем строим эпюру абсолютных углов закручивания (рис. ж).
Для построения эпюры относительных углов закручивания (рис. з) необходимо предварительно вычислить
![]() где принято
где принято
![]() следовательно,
следовательно, ![]()
![]()
Определим
необходимые диаметры стержня. Примем, что внешний крутящий момент М = 20 кНм, расчетное сопротивление материала стержня на срез Rs = 100 МПа, допустимый относительный угол закручивания ![]() , а модуль сдвига G = 8·104 МПа.
, а модуль сдвига G = 8·104 МПа.
Диаметр
стержня в пределах I и II участков будем обозначать d1, а в
пределах участка III – d4.
Согласно условию задачи между d1 и d4, существует соотношение (рис. а):
![]() и
и ![]() , тогда
, тогда ![]() откуда
откуда ![]()
Кроме
того, ![]()
Необходимый
диаметр d1 при условии
обеспечения прочности стержня определяем по формуле ![]() , взяв значение крутящего момента из эпюры Т, представленной на рис. е:
, взяв значение крутящего момента из эпюры Т, представленной на рис. е:
![]()
![]()
Определим максимальное касательное напряжение, которое возникнет в стержне на участке III:
![]()
Необходимый
диаметр при условии обеспечения жесткости стержня находим по формуле ![]() :
:
![]()
![]()
Сравнивая
результаты, принимаем окончательно d1
=13 см, d4 =11 см,
определенные из условия жесткости.
Диаметр
d4,жестк можно определить также, используя эпюру ![]() (рис. з),
из которой видно, что
(рис. з),
из которой видно, что ![]() на участке I, поэтому
приравнивая
на участке I, поэтому
приравнивая
![]()
находим ![]() и, наконец, определяем
и, наконец, определяем
![]()
а
![]()
Пример № 3
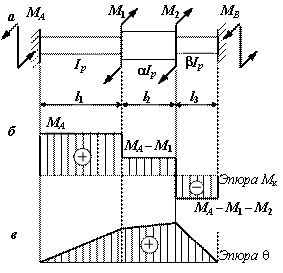
Стальной вал
круглого поперечного сечения состоит из трех участков с различными полярными
моментами инерции (рис. а). Концы вала жестко закреплены от поворота
относительно продольной оси вала. Заданы нагрузки: пары сил M1 и M2,
действующие в плоскости поперечного сечения вала; отношения полярных моментов
инерции участков вала ![]() и
и ![]() ; длины участков l1, l2, l3.
; длины участков l1, l2, l3.
Требуется:
1) построить эпюру крутящих моментов;
2) подобрать размеры поперечных сечений из условия прочности;
3) построить эпюру углов закручивания.
Решение.
Ввиду наличия
двух жестких опорных закреплений под действием нагрузки в каждом из них
возникают реактивные пары ![]() и
и ![]() . Составив условие равновесия вала
. Составив условие равновесия вала
![]() ,
,
убеждаемся в том, что записанное уравнение не может быть
решено однозначно, поскольку содержит две неизвестные величины: ![]() и
и ![]() . Остальные уравнения равновесия при данной нагрузке
выполняются тождественно. Следовательно, задача является один раз статически
неопределимой.
. Остальные уравнения равновесия при данной нагрузке
выполняются тождественно. Следовательно, задача является один раз статически
неопределимой.
Для раскрытия
статической неопределимости составим условие совместности деформаций.
Вследствие жесткости опорных закреплений концевые сечения вала не
поворачиваются. Это равносильно тому, что полный угол закручивания вала на
участке А–В равен нулю: ![]() , или
, или ![]() .
.
Последнее уравнение и есть условие совместности деформаций. Для его связи с уравнением равновесия запишем физические уравнения, связывающие крутящие моменты и углы закручивания (закон Гука при кручении), для каждого участка стержня:
![]() ,
, ![]() ,
, ![]() .
.
Подставив
физические соотношения в условие совместности деформаций, находим реактивный
момент ![]() , а затем из уравнения равновесия определяем
, а затем из уравнения равновесия определяем ![]() . Эпюра крутящих моментов показана на
рис. б.
. Эпюра крутящих моментов показана на
рис. б.
Для решения задачи о подборе сечения запишем формулы для определения максимальных касательных напряжений на каждом участке вала:
![]() ;
; ![]() ;
; ![]() .
.
Коэффициенты ![]() и
и ![]() , представляющие собой отношения полярных моментов
сопротивления сечений второго и третьего участков вала к полярному моменту
сопротивления сечения первого участка
, представляющие собой отношения полярных моментов
сопротивления сечений второго и третьего участков вала к полярному моменту
сопротивления сечения первого участка ![]() , определим через известные параметры
, определим через известные параметры ![]() и
и ![]() .
.
Полярный
момент инерции ![]() может быть записан
двояким образом:
может быть записан
двояким образом:
![]() ;
; ![]() ,
,
где ![]() ,
, ![]() -
радиусы первого и второго участков стержня. Отсюда выразим радиус
-
радиусы первого и второго участков стержня. Отсюда выразим радиус ![]() через
через
![]() :
:
![]() .
.
Тогда полярный момент сопротивления второго участка
![]() ,
,
то есть ![]() . Аналогично
. Аналогично ![]() .
.
Теперь можно
сравнить между собой максимальные касательные напряжения на отдельных участках
и для наибольшего из них записать
условие прочности ![]() . Из этого условия находим требуемый полярный момент
сопротивления
. Из этого условия находим требуемый полярный момент
сопротивления ![]() , и затем, используя формулу
, и затем, используя формулу ![]() ,
радиусы вала на каждом участке.
,
радиусы вала на каждом участке.
 ;
; ![]() ;
; ![]() .
.
Для построения
эпюры углов закручивания вычислим углы закручивания на каждом участке стержня
по формуле ![]() . Ординаты эпюры получаются последовательным суммированием
результатов для отдельных участков, начиная с одного из концов вала. Контролем
правильности решения является равенство нулю угла закручивания на другом конце
вала Вид эпюры углов закручивания
показан на рис. в.
. Ординаты эпюры получаются последовательным суммированием
результатов для отдельных участков, начиная с одного из концов вала. Контролем
правильности решения является равенство нулю угла закручивания на другом конце
вала Вид эпюры углов закручивания
показан на рис. в.
Пример № 4
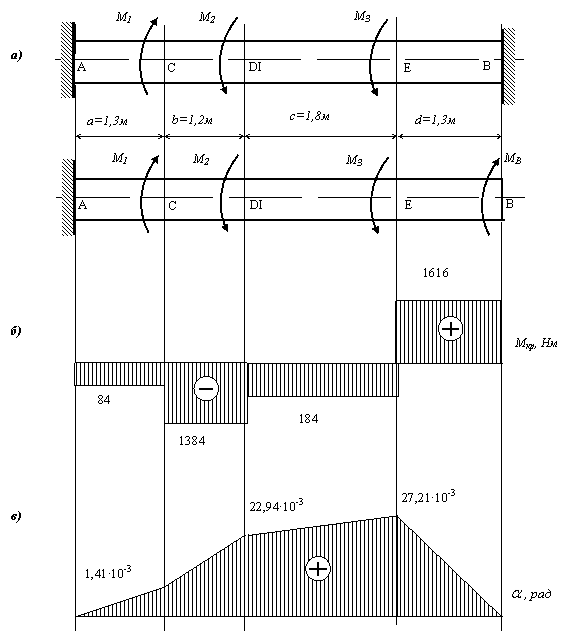
Круглый стальной брус, защемленный обоими концами, нагружен тремя моментами М1, М2, М3 (см. рис.).
а = ![]() = 55 МПа.
= 55 МПа.
Требуется:
1) определить реактивные моменты, возникающие в заделках бруса;
2) построить эпюру крутящих моментов;
3) определить из расчёта на прочность диаметр бруса и округлить его значение до ближайшего стандартного размера ГОСТ 6636-69;
4) построить эпюру углов поворота;
5) найти
наибольший относительный угол закручивания.
Решение.
1. Составляем
уравнение совместности деформаций, выражающее мысль о том, что угол поворота
правого концевого сечения равен нулю.
![]()
Подставив
цифровые значения, получим
![]()
![]()
отсюда МВ = 1616 Нм.
2. Построение
эпюры Мкр. На основании метода сечений имеем, что
крутящий момент в сечении численно равен алгебраической сумме внешних
(скручивающих) моментов, действующих по одну сторону от сечения.
![]()
![]()
![]()
![]()
![]()
3. По
полученным значениям строим эпюру Мкр (см. рис. б).
Условие
прочности:
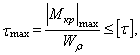
где ![]() = 1616 Нм,
= 1616 Нм, ![]() .
.
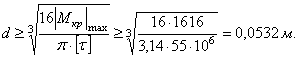
Отсюда
Принимаем по
ГОСТ 6636-69 d =
4. Строим
эпюру углов поворота. Угол закручивания на участке l:
![]()
![]()
где G = 8×104 МПа –
модуль упругости при сдвиге.
![]()
![]()
![]()
![]()
Находим углы
поворота характерных сечений:
![]() ,
,
![]()
![]()
![]()
![]()
![]()
По данным
значениям строим эпюру ![]() (см. рис. в)
(см. рис. в)
5. Находим
наибольший относительный угол закручивания
![]()
Следовательно,
наибольший угол закручивания будет на участке, где момент будет максимальным.
Участок ВЕ: Мкр =1616 Нм,
![]()
Онлайн-калькулятор "Подбор диаметра вала при кручении"
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
