Главная

Лекция 5. Кручение, сдвиг, срез

Содержание

Основные понятия. Крутящий момент

Построение эпюр крутящих моментов

Напряжения в поперечном сечении

Условие прочности при кручении вала круглого и кольцевого сечения

Рациональная форма сечения вала

Деформации при кручении и условие жесткости вала

Расчеты на прочность и жесткость валов круглого и кольцевого сечений

Потенциальная энергия деформации при кручении

Статически неопределимые задачи на кручение

Кручение бруса с некруглым поперечным сечением

Сдвиг

Расчет заклепок на срез

Расчет заклепок на смятие и листов на разрыв

Дополнительные задачи на сдвиг

Расчет сварных соединений

Расчет сварных соединений при проектировании строительных конструкций

Расчет винтовых пружин с малым шагом витков

Вопросы для самопроверки

Основные понятия. Крутящий момент

Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент M_k, (другое обозначение T, M_z), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют.

Или другое определение кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис. 5.1).

Кручение возникает в валах, винтовых пружинах, в элементах пространственных конструкций и т.п.

Деформация кручения наблюдается если прямой брус нагружен внешними моментами (парами сил M), плоскости действия которых перпендикулярны к его продольной оси

В чистом виде деформация кручения встречается редко, обычно присутствуют и другие внутренние силовые факторы (изгибающие моменты, продольные силы).

Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.

Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала.

Мы будем рассматривать прямой брус только в состоянии покоя или равномерного вращения. В этом случае алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, будет равна нулю.

При расчете брусьев, испытывающий деформацию кручения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от M_k), возникающих в брусе, и нахождение угловых перемещений в зависимости от внешних скручивающих моментов.

При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.

В ряде случаев величины внешних крутящих моментов определяются по величине потребляемой мощности и по скорости вращения вала. Если вал делает в минуту n оборотов, то угол поворота вала за 1 сек, выраженный в радианах, равен Работа крутящего момента M_k за 1 сек, т. е. мощность N, передаваемая валом, равна произведению величины момента на угол поворота вала (в радианах) за 1 сек:

где мощность N выражена в кГ∙м/сек.

Если мощность N задана в лошадиных силах (л.с.), то

Если мощность N задана в киловаттах, то, учитывая, что 1 л.с. равна 0,736 кВт, получаем

Построение эпюр крутящих моментов

Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов M_k (M_z) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.

В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣM_z=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 5.1, крутящий момент M_z в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M₁|=|M₂|.

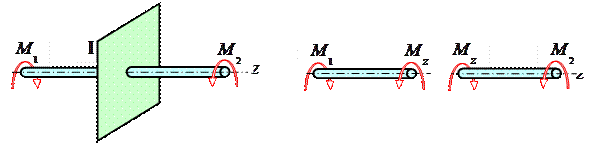
Рис. 5.1

В более сложных случаях, когда к валу приложено несколько внешних моментов, крутящие моменты M_k в поперечных сечениях различных участков вала неодинаковы.

На основании метода сечений крутящий момент в произвольном поперечном сечении вала численно равен алгебраической сумме внешних скручивающих моментов, приложенных к валу по одну сторону от рассматриваемого сечения.

При расчетах на прочность и жесткость знак крутящего момента не имеет никакого значения, но для удобства построения эп. M_k примем следующее правило знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части вала действующий на него момент представляется направленным по ходу часовой стрелки (рис.5.2).

В технике употребляется терминология « винт с правой нарезкой» или «…с левой нарезкой…», причем правый винт наиболее распространен, являясь стандартом. Полезно заметить, что при навинчивании гайки на правый винт мы прикладываем положительный момент M_кр , а при свинчивании гайки – отрицательный.

Рис. 5.2

При наличии распределенной моментной нагрузки m (рис.5.3) крутящие моменты М_К связаны дифференциальной зависимостью

из которой вытекает следующая формула:

где – крутящий момент в начале участка.

Согласно формуле (5.2) на участках с равномерно распределенной нагрузкой m крутящий момент изменяется по линейному закону. При отсутствии погонной нагрузки (m = 0) крутящий момент сохраняет постоянное значение (М_К = М_Ко = const). В сечениях, где к валу приложены сосредоточенные скручивающие моменты, на эпюре М_К возникают скачки, направленные вверх, если моменты направлены против часовой стрелки, либо вниз – при обратном направлении моментов.

Рис. 5.3

На рис. 5.4, а изображен стержень, жестко защемленный в правом концевом сечении, к которому приложены три внешних скручивающих момента.

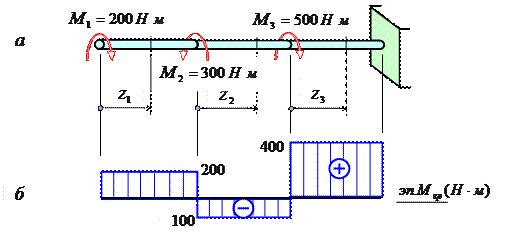
Рис. 5.4

В нашем случае крутящие моменты в их поперечных сечениях удобно выражать через внешние моменты, приложенные со стороны свободного конца бруса.

Это позволяет определять крутящие моменты, не вычисляя реактивного момента, возникающего в заделке.

Крутящий момент M_z1 в сечении I численно равен M₁=200 нм и, согласно принятому правилу знаков, положителен.

Крутящий момент M_z2 в сечении II численно равен алгебраической сумме моментов M₁ и M₁, т.е. M_z2 =200-300=-100 нм, а его знак зависит от соотношения этих моментов.

Аналогичным образом вычисляется крутящий момент M_z3 в сечении III: M_z3 =200-300+500=400 нм.

Изменение крутящих моментов по длине вала покажем с помощью эпюры крутящих моментов. На рис. 5.4, б показана такая эпюра для стержня, изображенного на рис. 5.4, а.

Каждая ордината эп. M_k в принятом масштабе равна величине крутящего момента, действующего в том поперечном сечении бруса, которому соответствует эта ордината.

В сечении, в котором к брусу приложен внешний скручивающий момент, ордината эпюры изменяется скачкообразно на величину, равную значению этого момента.

Следует учитывать, что наибольший внешний скручивающий момент, приложенный к брусу, не всегда равен наибольшему крутящему моменту, по которому ведется расчет бруса на прочность и жесткость.

Пример 1.

Построить эпюру крутящих моментов для жестко защемленного стержня (рис.5.4.1, а).

Рис.5.4.1

Решение.

Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.

1. Намечаем характерные сечения.

2. Определяем крутящий момент в каждом характерном сечении.

3. По найденным значениям строим эпюру (рис.5.4.1, б).

Пример 2.

Рассмотрим расчетную схему вала, нагруженного двумя сосредоточенными моментами М и 2М и распределенными по длине: т (рис. 5.4.2).

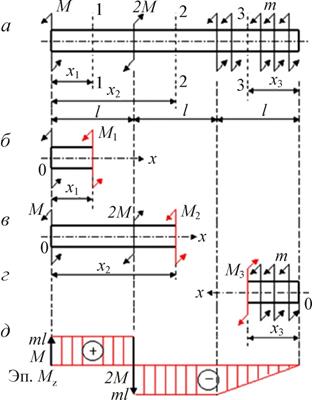
Рис. 5.4.2. Построение эпюры внутренних крутящих моментов:

а – расчетная схема; б – первый участок, левая часть; в – второй участок, левая часть;

г – третий участок, правая часть; д – эпюра внутренних крутящих моментов

Решение.

В исходных сечениях 1–1; 2–2; 3–3 задаются положительными значениями внутренних крутящих моментов М₁, М₂, М₃. Пусть .

Для первого участка (рис. 5.4.2, б):

ΣM_k = M₁ + M = 0;

M₁ = –M = ml = const.

Для второго участка (рис. 5.4.2, в):

Для третьего участка (рис. 5.4.2, г):

Границы измерения параметра х₃ в следующей системе координат:

Тогда

Отмеченные значения ординат откладываются на эпюре внутренних крутящих моментов (рис. 5.4.2, д).

Пример 3.

На рис. 5.4.3 дан пример определения по методу сечений внутренних крутящих моментов по участкам и внизу (ри.5.4.3, с) изображена суммарная эпюра М_кр.

Рис.5.4.3. a) заданный стержень с нагрузкой; b) отсеченные части стержня;

с) эпюра крутящих моментов.

Решение.

В данном случае для консольного стержня вести вычисления удобно, идя справа налево, начав их с 3–го участка.

Участок 3 (рис. 5.4.3, b). Неизвестный момент M_кр3 прикладываем к отсеченной части как положительный, после чего пишем условие равновесия отсеченной части:

Σ^отсеч m_z3=M_кр3 +5=0; → M_кр3 = -5 тм, (0≤z₃ ≤2).

Участок 2 (рис. 5.4.3, b). Положение сечения фиксируем с помощью местной координаты z_{2 :}

Σ^отсеч m_z2= M_кр2 +3(4-z_{2 )} -15 +5=0; → M_кр2 =10 – 3(4-z₂), (0≤z₂≤2).

Точка z₂ =0, M_кр2 =10 – 12= -2 тм.

Точка z₂ =4, M_кр2 =10 – 0= 10 тм.

Участок 1 (рис. 5.4.3, b):

Σ^отсеч m_z1= M_кр1 +3∙4+5+5-15=0; → M_кр1 = -7 тм, (0≤z₁ ≤2).

Найдем реактивный момент в заделке M₀ из условия равновесия всего стержня Σm_z =0, это дает M₀ +3∙4+5+5-15=0 и M₀ = -7 тм, что совпадает с M_кр1 , найденным на участке 1 по методу сечений. Этого конечно следовало ожидать, так как по существу реактивный момент – это внутреннее усилие, действующее в поперечном сечении, где соединены торец стержня и заделка.

Напряжения в поперечном сечении

Опыты показывают, что если на поверхности бруса круглого сечения нанести прямоугольную сетку, а на торцевой поверхности нанести радиальные линии (рис.5.5), то после деформации кручение окажется что:

- все образующие поворачиваются на один и тот же угол , а прямоугольники, нанесенные на поверхности, превращаются в параллелограммы;

- торцевые сечения остаются круглыми, плоскими, расстояния между ними не меняются;

- каждое сечение поворачивается относительно другого на некоторый угол , называемый углом закручивания;

- радиальные линии на торцевой поверхности остаются прямыми.

На основании этих наблюдений можно заключить, что может быть принята гипотеза Бернулли (гипотеза плоских сечений), а в вале возникают условия чистого сдвига, в поперечных сечениях действуют только касательные напряжения, нормальные напряжения равны нулю.

Рассмотрим поперечное сечение вала, расположенное на некотором расстоянии z от торцевого, где М_к=T (рис.5.5). На элементарной площадке dF будет действовать элементарная сила , момент который относительно оси вала равен . Крутящий момент М_к, в сечении равен

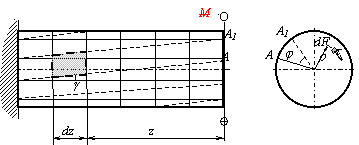
Рис.5.5

Для того чтобы проинтегрировать это выражение необходимо знать закон распределения напряжений в сечении. Выделим из вала элементарное кольцо длиной dz и толщиной (рис.5.6).

Правый торец элемента повернется относительно левого на угол , образующая СВ повернется на угол и займет положение СВ₁. Угол - относительный сдвиг. Из треугольника ОВВ₁ найдем:

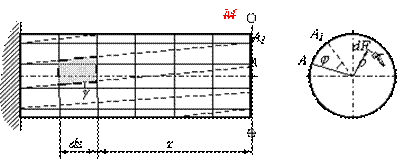
Рис.5.6 Рис.5.7

Из треугольника СВВ₁: . Откуда, приравнивая правые части, получим

На основании закона Гука при сдвиге:

Подставим выражение (5.2) в (5.1):

Откуда

Подставим значение в выражение (5.4) получим:

Таким образом, касательные напряжения при кручении прямо пропорциональны расстоянию от центра тяжести сечения до рассматриваемой точки и одинаковы в точках, одинаково удаленных от центра тяжести сечения (рис. 5.7). При получим . Наибольшие напряжения возникают в точках контура сечения при :

Величина отношения полярного момента инерции к радиусу вала называется моментом сопротивления сечения при кручении или полярным моментом сопротивления

Для сплошного круглого сечения

Для кольцевого сечения

где

Тогда максимальные касательные напряжения равны

Условие прочности при кручении вала круглого и кольцевого сечения

Условие прочности при кручении с учетом принятых обозначений формулируется следующим образом: максимальные касательные напряжения, возникающие в опасном сечении вала, не должны превышать допускаемых напряжений и записывается в виде

где - берется либо на основании опытных данных, либо (при отсутствии нужных опытных характеристик) по теориям прочности, соответствующим материалу. Например, из теорий прочности для хрупких материалов, примененных для чистого сдвига, следуют такие результаты:

- из второй теории прочности

- из теории Мора

Из теорий прочности для пластичных материалов при чистом сдвиге получим:

- по третьей теории прочности

- по четвертой теории прочности

Как следует из закона парности касательных напряжений, одновременно с касательными напряжениями, действующими в плоскости поперечного сечения вала, имеют место касательные напряжения в продольных плоскостях. Они равны по величине парным напряжениям, но имеют противоположный знак. Таким образом, все элементы бруса при кручении находятся в состоянии чистого сдвига. Так как чистый сдвиг является частным случаем плоского напряженного состояния, при котором , то при повороте граней элемента на 45⁰ в новых площадках обнаруживаются только нормальные напряжения, равные по величине (рис.5.8).

Рассмотрим возможные виды разрушения валов, изготовленных из различных материалов при кручении. Валы из пластичных материалов чаще всего разрушаются по сечению, перпендикулярному к оси вала, под действием касательных напряжений, действующих в этом сечении (рис.5.9,а). Валы из хрупких материалов, разрушаются по винтовой поверхности наклоненной к оси вала под углом 45⁰, т.е. по направлению действия максимальных растягивающих напряжений (рис.5.9,б). У деревянных валов первые трещины возникают по образующим цилиндра, так как древесина плохо сопротивляется действию касательных напряжений, направленных вдоль волокон (рис.5.9,в).

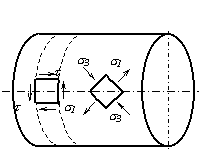
Рис.5.8 Рис.5.9

Таким образом, характер разрушения зависит от способности материала вала сопротивляться воздействию нормальных и касательных напряжений. В соответствии с этим, допускаемые касательные напряжения принимаются равным - для хрупких материалов и - для пластичных материалов.

Рациональная форма сечения вала

Анализируя эпюру касательных напряжений (рис.5.7) можно отметить, что наибольшие напряжения возникают на поверхности вала, в центральной части они значительно меньше и на продольной оси равны нулю. Следовательно, в сплошном валу материал, находящийся в центральной части в значительной степени недогружен, его вклад в прочность вала мал. Поэтому рациональным для валов считается кольцевое сечение.

Деформации при кручении и условие жесткости вала

Из выражения (5.5) следует, что

интегрируя которое по длине вала, получим:

Если М_к = const и по всей длине вала, то абсолютный угол закручивания

где - жесткость вала при кручении.

При скачкообразном изменении по длине бруса крутящего момента угол закручивания между его начальным и конечным сечениями определяется как сумма углов закручивания по участкам с постоянным M_k

Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания

Для обеспечения требуемой жесткости вала необходимо, чтобы наибольший относительный угол закручивания не превосходил допускаемого:

Эта формула выражает условие жесткости вала при кручении. Обычно принимается на 1 м длины вала.

Расчеты на прочность и жесткость валов круглого и кольцевого сечений

При расчетах на прочность при кручении (также как и при растяжении) могут решаться три задачи:

а) проверочный расчет – проверить, выдержит ли вал приложенную нагрузку;

б) проектировочный расчет - определить размеры вала из условия его прочности;

в) расчет по несущей способности - определить максимально допустимый крутящий момент.

- При проверочном расчете на прочность рекомендуется следующий порядок расчета валов при кручении:

1) по схеме вала и действующим на него скручивающим моментам строят эпюру внутренних крутящих моментов по отдельным участкам;

2) выбирают материал для рассчитываемого вала и определяют для этого материала допускаемое напряжение, например по формуле (5.9), ;

3) для участка вала с максимальным по модулю значением крутящего момента записывают условие прочности при кручении

- Проектировочный расчет проводится, исходя из условия прочности на основе следующего соотношения:

Для сплошного круглого сечения , отсюда можем записать выражение для определения диаметра вала из условия его прочности:

Для кольцевого сечения

Определив размеры вала из условия прочности, проверяют вал на жесткость.

Условие жесткости требует, чтобы максимальный относительный угол закручивания , был меньше или в предельном случае равен допускаемому углу закручивания единицы длины вала, т.е.

Из условия прочности можно найти необходимый для обеспечения прочности полярный момент сопротивления сечения, а по нему и диаметр вала:

но Wp = 0,2d³, поэтому

Из формулы (5.11) можно найти необходимый полярный момент инерции сечения, а по нему и диаметр вала

В этой формуле допускаемый относительный угол закручивания должен быть выражен в радианах; если этот угол дан в градусах, то соотношение для определения I_p будет выглядеть следующим образом:

но I_p = 0,1d ⁴ , поэтому

Из двух диаметров, рассчитанных по формулам (5.12) и (5.13), в качестве окончательного диаметра выбирается больший, который обычно округляется до целых миллиметров.

В случае расчета размеров вала кольцевого поперечного сечения при заданном соотношении внутреннего d_вн и наружного диаметров d, т.е. при заданном параметре k = d_вн /d, формулы (5.12) и (5.13) принимают вид:

Пример 4.

Подобрать диаметр сплошного вала, передающего мощность N=450 л.с. при частоте вращения n=300 об/мин. Угол закручивания не должен превышать одного градуса на 2 метра длины вала; МПа, МПа.

Решение.

Крутящий момент определяем из уравнения

Диаметр вала по условию прочности определяется из уравнения

Диаметр вала по условию жесткости определяется из уравнения

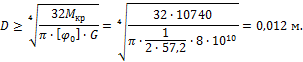
Выбираем больший размер 0,112 м.

Пример 5.

Имеются два равнопрочных вала из одного материала, одинаковой длины, передающих одинаковый крутящий момент; один из них сплошной, а другой полый с коэффициентом полости . Во сколько раз сплошной вал тяжелее полого?

Решение.

Равнопрочными валами из одинакового материала считаются такие валы, у которых при одинаковых крутящих моментах, возникают одинаковые максимальные касательные напряжения, то есть

Условие равной прочности переходит в условие равенства моментов сопротивления:

Откуда получаем:

Отношение весов двух валов равно отношению площадей их поперечных сечений:

Подставляя в это уравнение отношение диаметров из условия равной прочности, получим

Как показывает этот результат, полый вал, будучи одинаковым по прочности, вдвое легче сплошного. Это объясняется тем, что в силу линейного закона распределения касательных напряжений по радиусу вала, внутренние слои относительно мало нагружены.

Пример 6.

Найти мощность в квт, передаваемую валом, если диаметр сплошного вала d=0,15 м, число оборотов вала в минуту n=120, модуль сдвига и угол закручивания участка вала длиной 7,5 м равен 1/15 радиан.

Решение.

Из формулы

Определим передаваемую мощность

Пример 7.

Определить, на сколько процентов увеличится наибольшее напряжение вала при кручении, если в валу сделано центральное отверстие (С=0,4).

Решение.

Полагая , получим следующие выражения для напряжений сплошного и полого валов:

Искомая разница в напряжениях

Пример 8.

Заменить сплошной вал диаметра d=300 мм полым равнопрочным валом с наружным диаметром =350 мм. Найти внутренний диаметр полого вала и сравнить веса этих валов.

Решение.

Наибольшие касательные напряжения в обоих валах должны быть равными между собой:

Отсюда определим коэффициент С

Внутренний диаметр полого вала

Отношение весов равно отношению площадей поперечных сечений:

Из приведенных примеров 5 и 6 видно, что изготовление пустотелых валов, т.е. валов, у которых малонагруженная внутренняя часть удаляется, является весьма эффективным средством снижения затраты материала, а следовательно, и облегчения веса валов. При этом наибольшие напряжения, возникающие в пустотелом валу, мало отличаются от максимальных напряжений в валу сплошного сечения при том же наружном диаметре.

Так в примере 5 за счет сверления при , дающем облегчение вала на 16%, максимальные напряжения в наружных волокнах полого вала возросли всего на 2,6%. В примере 6 равнопрочный пустотелый вал, но с несколько большим наружным диаметром по сравнению со сплошным валом, оказался легче сплошного на 53,4%. Эти примеры наглядно свидетельствуют о рациональности применения пустотелых валов, что широко используется в некоторых областях современного машиностроения, в частности, в моторостроении.

Пример 9.

На участке сплошного круглого вала D=10 см действует крутящий момент Т=8 кHм. Проверить прочность и жёсткость вала, если τ_adm=50 МПа, К_{t adm}=0,5 град/м и модуль сдвига G=0,8∙10⁵ МПа.

Решение.

Условие безопасной прочности

Выразив K_t в размерности град/м, получим

что превышает величину допускаемого относительного угла закручивания K_{t adm}=0,5 град/м на 16%.

Следовательно – прочность вала обеспечена τ_мax=40,75 МПа < 50 МПа, а жёсткость не обеспечена.

Пример 10.

Стальной вал кольцевого сечения D=10 см, d=8 см нагружен моментом, вызвавшим τ_мах=τ_adm=70 МПа. Что произойдёт, если этот вал заменить сплошным круглым валом диаметром 8 см (материал сохранён).

Решение.

Максимальные касательные напряжения в вале

Для кольцевого сечения а для вала сплошного сечения . По условию для вала кольцевого сечения τ_мах=70 МПа, очевидно, что для вала сплошного сечения максимальные напряжения будут больше во столько раз, во сколько его момент сопротивления меньше.

Пример 11.

Для сплошного вала (пример 10) определить появились ли пластические деформации, если известно, что n_adm=1,8?

Решение.

Для пластичных материалов n_adm=τ_max/τ_adm, следовательно τ_у =70∙1,8=126 Мпа.

Действующие напряжения превысили предел текучести, следовательно появились пластические деформации.

Пример 12.

К стальному валу (см.рис.5.10) приложены скручивающие моменты: М₁, M₂, M₃, M₄. Требуется:

1) построить эпюру крутящих моментов;

2) при заданном значении определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей, соответственно равной: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм;

3) построить эпюру углов закручивания;

4) найти наибольший относительный угол закручивания.

Дано: М₁ = М₃ = 2 кНм, М₂ = М₄ = 1,6 кНм, а = b = с = 1,2 м, = 80 МПа.

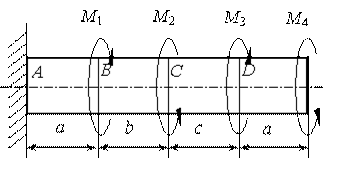
Рис.5.10

Решение.

1. Построить эпюру крутящих моментов.

При построений эпюр М_кр примем следующее правило знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части бруса действующий на него момент представляется направленным по движению часовой стрелки.

Крутящие моменты, возникающие в поперечных сечениях брусьев, определяются по внешним окручивающим моментам с помощью метода сечений. На основании метода сечения крутящий момент в произвольном поперечном сечении бруса численно равен алгебраической сумме внешних скручивающих моментов, приложенных к брусу по одну сторону от рассматриваемого сечения.

Для брусьев, имеющих один неподвижно закрепленный (заделанный) и один свободный конец, крутящие моменты всех поперечных сечений удобно выражать через внешние моменты, приложенные с той стороны от рассматриваемого сечения, с которой расположен свободный конец. Это позволяет определять крутящие моменты, не вычисляя реактивного момента, возникающего в заделке.

Для построения эпюры крутящих моментов необходимо найти величины крутящих моментов на каждом участке вала.

I участок (КД):

II участок (СД):

III участок (СВ):

IV участок (ВА):

По значению этих моментов строим эпюру М_кр в выбранном масштабе. Положительные значения М_кр откладываем вверх, отрицательные - вниз от нулевой линии эпюры (см. рис.5.11).

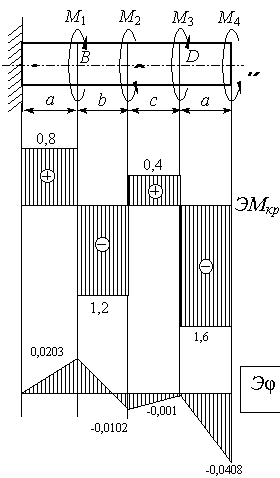
Рис.5.11

2. При заданном значении определим диаметр вала из расчета на прочность.

Условие прочности при кручении имеет вид

- максимальный крутящий момент, взятый по абсолютной величине. Определяется из эпюры М_кр (рис.5.11).

кНм;

- полярный момент сопротивления для сплошного круглого вала.

Диаметр вала определяется по формуле

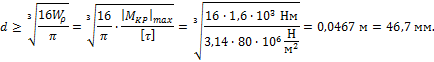
Принимаем d = 50 мм = 0,05 м.

3. Построим эпюру углов закручивания.

Угол закручивания участка вала длиной l постоянного поперечного сечения определяется по формуле

где - жесткость сечения вала при кручении.

- полярный момент инерции круглого вала

Вычислим углы закручивания сечений В, С, D и К относительно закрепленного конца вала (сечения А)

Строим эпюру углов закручивания (рис.5.11).

4. Найдем наибольший относительный угол закручивания

Пример 13.

Определить напряжения и погонный угол закручивания стальной разрезной трубы (рис.5.12), имеющей диаметр средней линии d=97,5 мм и толщину мм. Крутящий момент – 40 Нм. Модуль сдвига материала трубы МПа. Сравнить полученные напряжения и угол закручивания с напряжением и углом закручивания для сплошной трубы.

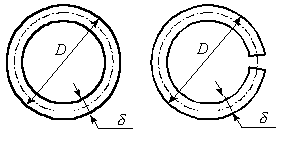
Рис.5.12

Решение.

Касательные напряжения в разрезной трубе, представляющей собой тонкостенный стержень, определим по формуле

где - развернутая длина осевой линии трубы.

Напряжение в сплошной трубе определяется по формуле

Угол закручивания на метр длины для разрезной трубы определяется по формуле

Погонный угол закручивания для сплошной трубы определяется по формуле

Таким образом, в сплошной трубе по сравнению с разрезанной вдоль образующей при кручении напряжения меньше в 58,3 раза, а угол закручивания – в 1136 раз.

Потенциальная энергия деформации при кручении

Элементарная работа статически приложенного внешнего момента Т на перемещении равна:

При чистом кручении М_к = Т и

Потенциальная энергия деформации

интегрируя выражение для элементарной работы по всей длине l стержня, получим

При М_к = const и = const, получим

Статически неопределимые задачи на кручение

Как известно, статически неопределимыми называют задачи, в которых число неизвестных опорных реакций или число внутренних усилий превышает число возможных уравнений статики. Один из методов решения статически неопределимых задач сводится к следующему:

а) составляются все возможные в данной задаче уравнения статики;

б) представляется картина деформации, происходящей в данной конструкции, и записываются деформационные уравнения, число которых должно быть равно степени статической неопределимости задачи;

в) решается совместная система уравнений статики и деформационных уравнений.

Кручение бруса с некруглым поперечным сечением

Определение напряжений в брусе с некруглым поперечным сечением представляет собой сложную задачу, которая не может быть решена методами сопротивления материалов. Причина заключается в том, что для некруглого поперечного сечения упрощающая гипотеза плоских сечений, оказывается неприемлемой. В данном случае поперечные сечения существенно искривляются, в результате чего заметно меняется картина распределения напряжений.

Таким образом, при определении углов сдвига, в данном случае, необходимо учитывать не только взаимный поворот сечений, но и деформации сечений в своей плоскости, связанная с искривлением сечений.

Задача резко усложняется тем, что для некруглого сечения, напряжения должны определяться как функции уже не одного независимого переменного , а двух - x и y.

Отметим некоторые особенности законов распределения напряжений в поперечных сечениях некруглой формы. Если поперечное сечение имеет внешние углы, то в них касательные напряжения должны обращаться в нуль. Если наружная поверхность бруса при кручении свободна, то касательные напряжения в поперечном сечении, направленные по нормали к контуру также будут равны нулю.

На рис. 4.3 показана, полученная методом теории упругости, эпюра касательных напряжений для бруса прямоугольного сечения. В углах, как видно, напряжения равны нулю, а наибольшие их значения возникают по серединам больших сторон:

в точке А

где - момент сопротивления при кручении, аналог полярного момента сопротивления поперечного сечения прямоугольного бруса;

Рис. 5.13

в точке В

здесь необходимо учесть, что b - малая сторона прямоугольника.

Значения угла закручивания определяется по формуле:

где - момент инерции при кручении, аналог полярного момента инерции поперечного сечения бруса.

Коэффициенты и зависят от отношения сторон h/b, и их значения приведены в табл. 4.1.

Таблица 4.1. Значения коэффициентов

для прямоугольных сечений

h/b
1,0	0,208	0,140	1,0
1,2	0,219	0,166	-
1,4	0,228	0,187	0,865
1,6	0,234	0,204	0,845
1,8	0,240	0,217	-
2,0	0,246	0,229	0,796
2,5	0,258	0,249	-
3,0	0,267	0,263	0,753
4,0	0,282	0,281	0,745
6,0	0,299	0,299	0,743
8,0	0,307	0,307	0,743
10,0	0,313	0,313	0,743
Более 10	0,333	0,333	0,743

Значения и для различных сечений приведены в табл.4.2.

Таблица 4.2. Геометрические характеристики жесткости и прочности для

некоторых сечений при кручении прямого бруса

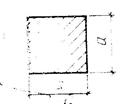
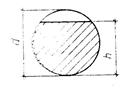
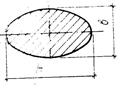
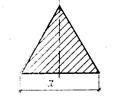
Форма поперечного сечения	Момент инерции при кручении	Момент сопротивления при кручении	Наибольшие касательные напряжения
Квадрат			В серединах сторон В углах
Круг с лыской h/d>0,5			В середине плоского среза
Эллипс h/b>1			В конце малой полуоси большой
Равносторонний треугольник			В серединах сторон в углах
Правильный шести- или восьмиугольник	(для шестиугольника k=0,133, для восьмиугольника k=0,130)	(для шестиугольника , для восьмиугольника )	В серединах сторон в углах
Форма клина			В точках длинных сторон ближе к широкому основанию
Полое эллиптическое сечение	(m>1); ()		В конце малой полуоси , большой , при малой толщине (равномерно по сечению)
Незамкнутое кольцевое сечение			В точках внутреннего и наружного сечения

Пример 14.

Имеются два равнопрочных вала из одного материала, одинаковой длины, передающие одинаковый крутящий момент; один из них круглого поперечного сечения, а другой - квадратного. Во сколько раз квадратный вал тяжелее круглого?

Решение.

Условие равной прочности имеет следующий вид:

где ; значение коэффициента определяется по таблице 4.1 и составляет для квадратного сечения (b=h) .

Из условия равной прочности получаем:

Отношение весов двух валов равно отношению площадей их поперечных сечений:

Подставляя в это уравнение отношение b/D из условия равной прочности, получим

Сдвиг

Сдвигом называют деформацию, представляющую собой искажение первоначально прямого угла малого элемента бруса (рис.5.14) под действием касательных напряжений . Развитие этой деформации приводит к разрушению, называемому срезом или, применительно к древесине, скалыванием. Примером сдвига является резка полосы ножницами. На сдвиг работают жесткие соединения конструкций – сварные, заклепочные и так далее.

Напряженное состояние, при котором на гранях выделенного элемента возникают только касательные напряжения τ_, называется чистым сдвигом.

Деформация сдвига оценивается взаимным смещением граней 1 – 1 и 2 – 2 малого элемента (рис. 5.15), называемым абсолютным сдвигом и более полно – относительным сдвигом (углом сдвига)

являющимся безразмерной величиной.

В предположении равномерного распределения касательных напряжений по сечению площадью А, они определяются по формуле

где Q – поперечная сила в данном сечении.

Условие прочности записывается по минимальной площади среза S_min, отражающей минимальное число соединяющих элементов (заклепок, болтов, штифтов и т.д.) или минимальную длину сварного шва.

Величина допускаемых напряжений зависит от свойств материала, характера нагрузки и может быть определена по 3-ей теории прочности: а так как при чистом сдвиге , то

При расчете болтовых или заклепочных соединений учитывается смятие контактирующих поверхностей, то есть пластическую деформацию, возникающую на поверхности контакта.

где A_см – площадь проекции поверхности контакта на диаметральную плоскость.

При выполнении проектного расчета, то есть при определении необходимого диаметра заклепки, болта или при определении их количества необходимо учитывать условие прочности на срез и на смятие, из двух значений следует взять большее число, округлив его до ближайшего целого в меньшую сторону.

Примечания: 1. Так как болты и заклепки ослабляют соединяемые листы, последние проверяют на разрыв в ослабленных сечениях

При расчетах сварных швов наплывы не учитывают, а считают, что в разрезе угловой шов имеет форму прямоугольного равнобедренного треугольника и разрушение шва происходит по его минимальному сечению, высота которого

где – минимальная толщина соединяемых листов.

В пределах упругости касательное напряжение прямо пропорционально относительному сдвигу

– это закон Гука при сдвиге; G – модуль сдвига, Н/м², характеризующий жесткость материала при сдвиге.

Закон Гука при сдвиге через абсолютные деформации:

где а – расстояние между сдвигаемыми гранями; А – площадь грани.

Модуль сдвига G, модуль продольной упругости Е и коэффициент Пуассона материала связаны зависимостью

Удельная потенциальная энергия деформации сдвига равна

На практике чаще всего теория сдвига применяется к расчету болтов, заклепок, шпонок, сварных швов и других элементов соединений.

Расчет заклепок на срез

Мы изучали, что при простом растяжении или простом сжатии две части стержня, разделенные наклонным сечением, стремятся не только оторваться друг от друга, но и сдвинуться одна относительно другой. Растяжению сопротивляются нормальные, а сдвигу — касательные напряжения.

На практике целый ряд деталей и элементов конструкций работает в таких условиях, что внешние силы стремятся их разрушить именно путем сдвига.

В соответствии с этим при проверке прочности таких элементов на первый план выступают касательные напряжения. Простейшими примерами подобных деталей являются болтовые и заклепочные соединения. Заклепки во многих случаях уже вытеснены сваркой; однако они имеют еще очень большое применение для соединения частей всякого рода металлических конструкций: стропил, ферм мостов, кранов, для соединения листов в котлах, судах, резервуарах и т. п. Для образования заклепочного соединения в обоих листах просверливают или продавливают отверстия. В них закладывается нагретый до красного каления стержень заклепки с одной головкой; другой конец заклепки расклепывается ударами специального молотка или давлением гидравлического пресса (клепальной машины) для образования второй головки. Мелкие заклепки (малого диаметра — меньше 8 мм) ставятся в холодном состоянии (авиационные конструкции).

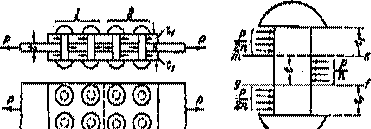
   Для изучения работы заклепок рассмотрим простейший пример заклепочного соединения (рис.5.16). Шесть заклепок, расположенных в два ряда, соединяют два листа внахлестку. Под действием сил Р эти листы стремятся сдвинуться один по другому, чему препятствуют заклепки, на которые и будет передаваться действие сил P).

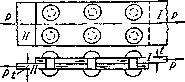
Рис.5.16

Для проверки прочности заклепок применим общий порядок решения задач сопротивления материалов.

На каждую заклепку передаются по две равные и прямо противоположные силы: одна—от первого листа, другая — от второго. Опытные исследования показывают, что одни из заклепок ряда нагружаются больше, другие — меньше. Однако к моменту разрушения усилия, передающиеся на различные заклепки, более или менее выравниваются за счет пластических деформаций. Поэтому принято считать, что все заклепки работают одинаково. Таким образом, при n заклепках в соединении, изображенном на рис.5.16, на каждую из них действуют по две равные и противоположные силы (рис.5.17); эти силы передаются на заклепку путем нажима соответствующего листа на боковую полуцилиндрическую поверхность стержня. Силы стремятся перерезать заклепку по плоскости mk раздела обоих листов.

Рис.5.17

Для вычисления напряжений, действующих по этой плоскости, разделим мысленно заклепочный стержень сечением mk и отбросим нижнюю часть (рис.5.17). Внутренние усилия, передающиеся по этому сечению от нижней части на верхнюю, будут уравновешивать силу т. е. будут действовать параллельно ей в плоскости сечения, и в сумме дадут равнодействующую, равную . Следовательно, напряжения, возникающие в этом сечении и действующие касательно к плоскости сечения, это — касательные напряжения . Обычно принимают равномерное распределение этих напряжений по сечению. Тогда при диаметре заклепки d на единицу площади сечения будет приходиться напряжение:

Величина допускаемого касательного напряжения , или, как говорят, допускаемого напряжения на срез, принято определять в виде: . Зная , мы напишем условие прочности заклепки на перерезывание в таком виде:

т. е. действительное касательное напряжение в материале заклепки должно быть равно допускаемому , или меньше его.

Из этого условия можно определить необходимый диаметр заклепок, если задаться их числом, и наоборот. Обычно задаются диаметром заклепочных стержней d в соответствии с толщиной t склепываемых частей (обычно ) и определяют необходимое число заклепок n:

Знаменатель этой формулы представляет собой ту силу, которую безопасно может взять на себя каждая заклепка.

Пусть ; тогда

Рис.5.18

При выводе формулы расчета заклепки на перерезывание, помимо оговоренных, допущена еще одна неточность. Дело в том, что силы действующие на заклепку, не направлены по одной прямой, а образуют пару. Эта пара уравновешивается другой парой, образующейся из реакций соединенных листов на головку заклепки (рис.5.18) и ведет к появлению нормальных напряжений, действующих по сечению mk.

Кроме этих нормальных напряжений, по сечению mk действуют еще нормальные напряжения, вызванные тем, что при охлаждении заклепочный стержень стремится сократить свою длину, чему мешает упор головок заклепки в листы. Это обстоятельство, с одной стороны, обеспечивает стягивание заклепками листов и возникновение между ними сил трения, с другой — вызывает значительные нормальные напряжения по сечениям стержня заклепки. Особых неприятностей эти напряжения принести не могут. На заклепки идет сталь, обладающая значительной пластичностью; поэтому даже если бы нормальные напряжения достигли предела текучести, можно ожидать некоторого пластического удлинения стержня заклепки, что вызовет лишь уменьшение сил трения между листами и осуществление в действительности той схемы работы заклепки на перерезывание, на которую она и рассчитывается. Поэтому эти нормальные напряжения расчетом не учитываются.

При проектировании строительных конструкций применяется следующее условие прочности на срез для заклепок и болтовых соединений

где Q – поперечная сила, равная внешней силе F, действующей на соединение; R_bs – расчетное сопротивление на срез; – расчетная площадь сечения болта или заклепки; d – диаметр заклепки или наружный диаметр болта; n_s – число срезов одного болта или заклепки; – коэффициент условий работы соединения, имеющий значения в интервале ; n – число болтов или заклепок.

Рис.5.19

Если величины F, R_bs, , n_s известны, то задаваясь числом заклепок или болтов n, можно найти необходимый для обеспечения прочности на срез диаметр

А зная d, F, R_bs, , n_s, можно определить потребное число заклепок или болтов

Расчет заклепок на смятие и листов на разрыв

Помимо среза заклепкам и соединяемым листам в конструкции угрожают и иные опасности.

Так как передача сил на заклепочный стержень происходит путем нажатия стенок заклепочного отверстия на заклепку, то необходимо установить, не произойдет ли наружное обмятие этого стержня или стенок отверстия, — произвести проверку на смятие.

Под смятием понимают пластическую деформацию, возникающую в соединениях на поверхностях контакта. Возникающие при этом напряжения являются нормальными, закон распределения которых по поверхности контакта достаточно сложен.

На рис.5.20 указана примерная схема передачи давлений на стержень заклепки. Закон распределения этих давлений по цилиндрической поверхности нам неизвестен; он во многом зависит от неправильностей формы заклепочного отверстиями стержня, вызванных условиями изготовления конструкции. Поэтому расчет производится условно. Принято считать, что неравномерное давление, передающееся на поверхность заклепки от листа, распределяется равномерно по диаметральной плоскости сечения заклепки. При этом напряжение по этой диаметральной плоскости оказывается примерно равным наибольшему сминающему напряжению в точке А поверхности заклепки.

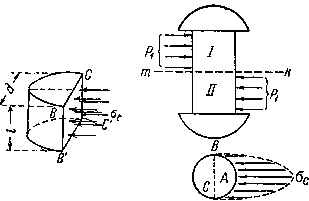
Рис.5.20

Чтобы вычислить это условное напряжение смятия, необходимо разделить силу, приходящуюся на заклепку, на площадь диаметрального сечения ВСС'В'. Эта площадь представляет собой прямоугольник, одной стороной которого служит диаметр заклепки, другая же равна толщине листа, передающего давление на стержень заклепки.

Так как давление на одну заклепку равно P/n, то

условие прочности на смятие будет иметь вид:

где — допускаемое напряжение на смятие. Отсюда необходимое число заклепок

Допускаемое напряжение на смятие принимают обычно в 2 - 2,5 раза больше основного допускаемого напряжения на растяжение и сжатие [], так как расчет на смятие по существу является упрощенной проверкой прочности по контактным напряжениям.

Таким образом, определяется число заклепок, необходимое для прочного соединения листов. Из двух полученных значений n, конечно, надо взять большее.

Если мы вернемся к рассмотренному ранее примеру и примем , то получим:

Таким образом, условие прочности заклепок на перерезывание требует постановки двадцати четырех заклепок; условие же прочности на смятие — пятнадцати заклепок. Очевидно, необходимо поставить двадцать четыре заклепки. В этом примере работа заклепок на срез оказывается опаснее работы их на смятие. Это обычно бывает в соединениях с так называемыми односрезными заклепками, в которых каждая заклепка перерезывается в одной плоскости.

а) расчетная схема, б) действующие усилия

Рис.5.21

В несколько других условиях будут работать заклепки соединения, показанного на рис.5.21,а. Здесь стык двух листов осуществлен при помощи двух накладок. Сила Р при помощи первой группы заклепок передается от левого листа обеим накладкам, а от последних при помощи второй группы заклепок передается правому листу.

Называя через n число заклепок, необходимое для передачи усилия Р от листа на накладки и от накладок на другой лист, получаем, что на каждую заклепку передается усилие от основного листа P/n. Оно уравновешивается усилиями P/2n, передающимися на заклепку от накладок (рис.5.21, б).

Стержень заклепки теперь подвергается перерезыванию уже в двух плоскостях; средняя часть заклепки сдвигается влево. Допускают, что срезывающая сила P/n равномерно распределяется по двум сечениям, mk и gf. Напряжение и условие прочности для двухсрезной заклепки принимает вид:

Таким образом, при двойном перерезывании число заклепок по срезыванию оказывается в два раза меньше, чем при одиночном перерезывании.

Переходим к проверке на смятие. Толщина склепываемых листов t; толщина накладок не должна быть меньше 0,5t, так как две накладки должны взять от основного листа всю силу Р. Поэтому:

Сила P/n сминает и среднюю часть заклепки и верхнюю с нижней. Опаснее будет смятие той части, где площадь смятия меньше.

Так как толщина среднего листа не больше суммы толщин обеих накладок, то в худших условиях по смятию будет средняя часть заклепки. Условие прочности на смятие останется таким же, как и при односрезных заклепках:

Таким образом, для рассматриваемой конструкции число заклепок в первой и во второй группах определится из полученных условий.

Пусть

Тогда:

В этом случае при двухсрезных заклепках условия их работы на смятие тяжелее, чем на срезывание; следует принять n=15.

На двух рассмотренных примерах мы установили общие методы проверки прочности заклепочных соединений. В металлических конструкциях иногда приходится склепывать целые пакеты соединяемых элементов. В таких пакетах заклепки могут работать и на большее число срезов. Однако методы расчета многосрезных заклепок не отличаются от изложенных. Для вычисления касательных напряжений следует разделить силу, относящуюся к одной заклепке, на суммарную площадь среза, воспринимающую эту силу. Для вычисления же напряжений смятия следует найти ту часть заклепки, которая находится в наиболее опасных условиях, т. е. воспринимает наибольшую силу на наименьшем протяжении. Напряжения смятия получаются делением этой силы на площадь диаметрального сечения наиболее напряженной части заклепки. Затем останется написать два условия прочности и получить n.

Наличие заклепок вносит некоторые изменения и в проверку прочности на растяжение или сжатие самих склепанных листов. Опасным сечением каждого листа (рис.5.22) будет теперь сечение, проходящее через заклепочные отверстия; здесь рабочая ширина листа будет наименьшей; принято говорить, что это сечение ослаблено заклепочным отверстием. Называя полную ширину листа b, получаем для него такое условие прочности:

где m — число отверстий, попадающих в сечение (в нашем случае — два).

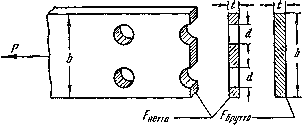
Рис.5.22

Отсюда можно найти величину b, задавшись толщиной листа t. Площадь (b-md)t ослабленного сечения называется площадью нетто, площадь же полного сечения листа bt называется площадью брутто.

Этот учет влияния заклепочных отверстий на прочность склепываемых листов общепринят, но является весьма условным. На самом деле, влияние отверстия в листе вызывает у его краев, на концах диаметра, перпендикулярного к направлению растяжения, значительные местные напряжения, которые могут достичь предела текучести материала и вызвать остаточные деформации, захватывающие, однако, весьма небольшой объем материала листа.

Некоторую опасность в отношении образования трещин эти местные напряжения могут представить лишь при действии переменных нагрузок в материале, имеющем низкий предел усталости. Однако в обычных условиях работы заклепочных соединений эта опасность может считаться исключенной. Во избежание возможности разрушения листов заклепками заклепки размещаются на определенных расстояниях друг от друга и от края листа.

Расположение заклепок в плане производится как по условиям обеспечения прочности и плотности соединения, так и по чисто производственным соображениям. Расстояния между центрами заклепок принимаются не менее 3d и не более 7d. Расстояния до края листов должны быть не менее (рис.5.23). Чтобы длина стыка была возможно меньше, берут , а в целях меньшего ослабления сечения расстояние е берут возможно большим (до 7d), что позволяет уменьшить число рядов, а следовательно, и ослабление.

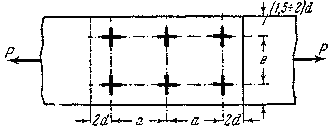
Рис.5.23. Практические рекомендации по расположению заклепок в соединении.

При проектировании заклепочных соединений для котлов и резервуаров, где добиваются плотных швов, помимо расчета на срез производят проверку сопротивления скольжению за счет трения. Однако допускаемое напряжение по скольжению дается в МПа поперечного сечения заклепки; таким образом, проверка на трение при односрезных заклепках сводится к проверке на срез лишь с другим допускаемым напряжением. При двухсрезных заклепках в расчет на трение вводится, конечно, одна площадь сечения заклепки, но зато повышается почти вдвое допускаемое напряжение на трение за счет двух накладок.

Поэтому так называемый расчет заклепок на трение является, по существу, проверкой прочности на срез с другими лишь допускаемыми напряжениями на квадратный сантиметр площади поперечного сечения заклепки.

Правильнее было бы сохранить лишь один метод проверки заклепочных соединений на смятие и срез, учитывая влияние сил трения при назначении допускаемых напряжений в зависимости от способа клепки, качества отверстий и требований, предъявляемых ко шву в отношении плотности.

В заклепочных соединениях для котлов принимают обычно допускаемое напряжение на скольжение (на 1 см² площади заклепки):

- от 50 до 70 МПа при швах внахлестку,

- от 90 до 120 с двумя накладками.

При проверке по этим данным, очевидно, надо вести расчет, как при заклепках одиночного перерезывания, с допускаемым напряжением от 50 до 70 или от 90 до 120 МПа.

При проектировании строительных конструкций применяется следующий алгоритм расчета болтовых и заклепочных соединений на смятие.

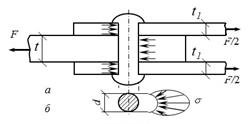
Рис.5.24

Упрощая расчет, площадь, подвергающуюся смятию, принимают равной

где d – диаметр заклепки (болта); n – их число; – наименьшая суммарная толщина элементов, сминаемых в одном направлении. Сминающей будет та же сила F, которая производит и срез. Таким образом, условие прочности на смятие имеет вид:

где R_bp – расчетное сопротивление на смятие.

Из условия (5.27) можно найти либо необходимый диаметр d по известным величинам F, t, n, R_bp,:

либо определить потребное число заклепок n

Из двух значений диаметров, рассчитанных по формулам (5.25) и (5.28), берут больший, округляя его до стандартного значения. Точно так же из двух значений n, рассчитанных по формулам (5.26) и (5.29), выбирают большее число, естественно, округленное до большего целого.

У к а з а н и я

1. В заклепочных и болтовых соединениях при действии поперечной силы Q , проходящей через центр тяжести соединения, распределение этой силы между заклепками или болтами принимают равномерным.

2. При действии на соединение момента, вызывающего сдвиг соединяемых элементов, распределение усилий на болты или заклепки следует принимать пропорционально расстояниям от центра тяжести соединения до рассматриваемого болта или заклепки.

3. Болты или заклепки, работающие одновременно на срез и растяжение, следует проверять отдельно на срез и на растяжение.

Дополнительные задачи на сдвиг

Задачи на сдвиг встречаются не только при расчете заклепочных и болтовых соединений. Имеются и другие элементы конструкций, испытывающие деформацию сдвига, и поэтому при их расчете необходимо всякий раз удовлетворять условию прочности на срез

и условию прочности на смятие

Например, при расчете соединения деревянных элементов в качестве условия (5.30) применяется условие прочности на скалывание вдоль волокон

где R_ск – расчетное сопротивление скалыванию.

Условие прочности на смятие в деревянных конструкциях вдоль волокон имеет вид соотношения (5.31).

Пример 15.

Определить необходимое число заклёпок диаметром 1,2 см для соединения “внахлёст” двух пластин толщиной 0,8 см и шириной 10 см, если известно, что нормальные напряжения в растянутой полосе σ =150 МПа и τ_adm=100 МПа.

Решение.

Если в растянутой пластине напряжения известны, то вызывавшая их сила P=σ∙A_пл=150 МПа∙(10∙0,8) см² =1,5∙10⁴ Н/см² ∙8 см² = 120 кН.

Эта сила будет срезающей для односрезных заклёпок, число которых:

Число заклёпок для обеспечения безопасной прочности соединения должно быть не менее 11 шт.

Пример 16.

Две тяги соединены штырём (рис.5.25) , вставленным в проушины, и нагружены силой F=150 кH. Определить действительный запас прочности, если: σ_у=230 МПа; τ_у=180 МПа.

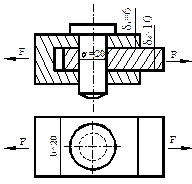
Рис.5.25

Решение.

Определим действующие напряжения среза в штыре

Запас прочности по касательным напряжениям

Определим действующие нормальные напряжения в ослабленном сечении правой пластины (т.к. суммарная толщина двух левых больше и там напряжения меньше)

Запас прочности по нормальным напряжениям

Решением является 1,53 - меньший из двух.

Пример 17.

Пуансон диаметром 2 см прошивает отверстие в стальной пластине толщиной 0,6 см с усилием 130 кН. Определить касательные напряжения в пластине и нормальные сжимающие напряжения в пуансоне.

Решение.

Площадь среза представляет собой цилиндрическую поверхность диаметром 2 см и высотой 0,6 см.

Напряжение в пуансоне

Пример 18.

Определить из условия прочности размеры стержня (рис.5.25.1) при допускаемых напряжениях при растяжении МПа, срезе МПа и смятии МПа.

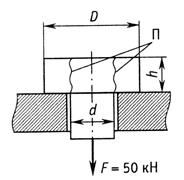
Рис.5.25.1

Решение.

Диаметр d стержня определим из условия прочности при растяжении

откуда

Принимаем d=20 мм.

Высоту головки стержня определяем из условия ее прочности при срезе

где Q=P.

Если прочность головки стержня окажется недостаточной, она срежется по поверхности цилиндра диаметром d и высотой h. Образующие поверхности среза П показаны на рисунке 5.25 волнистыми линиями. Подставив в условие прочности выражение для площади среза, получим

откуда

Принимаем h=10 мм.

Действующую силу P воспринимает опорная кольцевая поверхность головки стержня. Диаметр D головки стержня определяем из условия прочности опорной поверхности головки при смятии

откуда

Принимаем =28 мм.

Пример 19.

Обосновать соотношение между диаметром d и высотой головки h болта (рис. 5.26), если

Рис. 5.26

Решение.

Срез головки болта происходит по цилиндрической поверхности

Условие прочности на срез имеет вид:

Условие прочности на растяжение стержня болта имеет вид:

Предельное отношение касательных и нормальных напряжений определяет искомое соотношение между высотой головки болта и его диаметром:

Расчет сварных соединений

При изготовлении металлических конструкций часто применяется сварка с помощью электрической дуги.

Впервые электрическая дуга была открыта русским ученым проф. В. В. Петровым в 1802 г. Обнаружив плавление металла в пламени полученной им электрической дуги, проф. Петров указал на возможность использования этого явления в технике. Однако электрическая дуговая сварка была изобретена лишь в конце XIX века русскими инженерами Н. Н. Бенардосом (1882 г.) нашим земляком и Н. Г. Славяновым (1888 г.) и получила впоследствии широкое распространение во всем мире.

Сущность электросварки по методу Славянова заключается в том, что, расплавляя электрической дугой материал электрода (сталь), заполняют им стык соединяемых элементов, также прогреваемых дугой до температуры плавления. В результате, после остывания расплавленного металла, образуется шов, прочно соединяющий стыкуемые элементы. Схема сварки показана на рис.5.27. Электрическая дуга горит между металлическим электродом и свариваемым металлом, расплавляя электрод и кромки соединяемых элементов металла, между которыми образуется так называемая сварочная ванна.

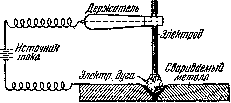
Рис.5.27. Технологическая схема сварки

Для защиты плавящегося металла от попадания вредных включений из окружающего воздуха на поверхность электрода наносится толстая защитная обмазка, выделяющая при плавлении электрода большое количество шлака и газов, благодаря чему плавящийся металл изолируется от окружающего воздуха.

Этим обеспечивается высокое качество металла сварного шва, механические свойства которого могут резко ухудшиться под влиянием кислорода и азота воздуха (при отсутствии обмазки или при тонкой обмазке). С той же целью автоматическая сварка производится под слоем флюса, защищающим плавящийся металл от попадания кислорода и азота воздуха.

При правильном выборе конструкции соединений, материалов и технологии сварки сварные соединения по надежности не уступают заклепочным при действии как статических, так и динамических нагрузок (в том числе ударных и знакопеременных). В то же время электросварка имеет ряд преимуществ перед клепкой, из которых важнейшими являются меньшая трудоемкость сварочных работ и отсутствие ослабления сечений соединяемых элементов отверстиями. Это дает значительную экономию средств и металла, помимо экономии, получаемой за счет большей компактности соединений. Большие экономические выгоды, приносимые электросваркой, и даваемое ею упрощение конструкций привели в последнее время к постепенному вытеснению заклепочных соединений сварными.

Значительное развитие электросварка получила в СССР благодаря трудам советских ученых Патона, Вологдина, Никитина, Хренова и др., разработавших новые методы сварки, обеспечивающие высокую прочность соединений.

Методы расчета сварных соединений тесно связаны с технологией сварки, причем для многих видов соединений расчет носит весьма условный характер. Вообще методику расчета сварных соединений нельзя еще считать установившейся.

Что касается норм допускаемых напряжений для материала швов, то они принимаются различными в зависимости от способа сварки (ручная и автоматическая), а также от состава и толщины защитной обмазки электродов.

В таблице 4.3. приведены допускаемые напряжения для сварных швов в конструкциях из стали марки ст. 3 по существующим нормам.

Таблица 4.3. Допускаемые напряжения при сварке.

Вид напряжения	Обозначение	Ручная сварка		Автоматическая сварка
		Электроды с тонкой обмазкой	Электроды с толстой обмазкой
Растяжение Сжатие Срез		1000 кг/см^2 1100 кг/см^2 800 кг/см^2	1800 кг/см^2 1450 кг/см^2 1100 кг/см^2	1300 кг/см^2 1450 кг/см^2 1100 кг/см^2

При проверке прочности сварных швов учитывается возможный непровар в начале шва и образование кратера в конце. Поэтому расчетная длина шва принимается меньшей, чем действительная или проектная на 10 мм.

Существует несколько типов сварных соединений. При соединении встык зазор между соединяемыми элементами заполняется наплавленным металлом. Типы сечений стыковых швов в зависимости от толщины соединяемых элементов показаны на рис. 5.28. В зависимости от направления действующего усилия F по отношению к шву их подразделяют на прямые и косые (рис. 5.29).

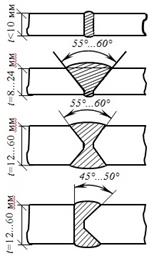
Рис. 5.28

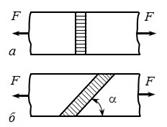
Рис. 5.29

Необходимо отметить, что наиболее простым и надежным видом соединения является соединение встык, образуемое путем заполнения зазора между торцами соединяемых элементов наплавленным металлом. Соединение встык осуществляется, в зависимости от толщины соединяемых элементов, по одному из типов, показанных на рис.5.30. Проверка прочности производится на растяжение или сжатие по формуле:

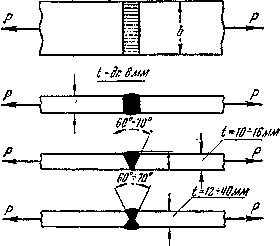
Рис.5.30. Расчетная схема сварного соединения.

Здесь — условная рабочая площадь сечения шва, где расчетная длина шва l=b-10 мм, а высота шва h принимается равной толщине свариваемых элементов t.

Поскольку допускаемое напряжение для сварного шва ниже, чем для основного металла, стремятся к увеличению длины стыкового шва. С этой целью применяют соединение встык с косым швом (рис.5.31). Исследования таких соединений, произведенные Институтом электросварки Академии наук УССР, показали, что равнопрочность их с основным металлом всегда обеспечивается.

Проверка прочности косых швов производится и по нормальным и по касательным напряжениям, возникающим по сечению шва mn:

Рис.5.31. Расчетная схема косого сварного соединения.

Имея в виду, что получим:

Здесь расчетная длина шва по техническим условиям принимается равной .

Как установлено опытом, наиболее рациональным углом наклона шва к линии действия сил является . Недостатком соединения косым швом является неудобство центрировки стыкуемых элементов при сварке, поэтому его применяют редко.

Иногда соединение листов производится внахлестку или встык с перекрытием накладками. Это вызывает необходимость сваривать листы, не лежащие в одной плоскости, что осуществляется при помощи так называемых валиковых (или угловых) швов — лобовых или торцевых (перпендикулярных к направлению действующей силы) и боковых или фланговых (параллельных ей).

Валиковый шов в сечении имеет довольно неопределенную форму (рис.5.32). В теоретических расчетах на прочность сечение шва принимается в виде равнобедренного треугольника (очерченного пунктиром) с расчетной высотой ).

Рис.5.32. Сварное соединение внахлестку: а) технология, б) расчетная схема

Соединения торцевыми (лобовыми) швами показаны на рис.5.33. Разрушение таких швов происходит по наиболее слабому сечению AB, как это установлено опытами.

Рис.5.33. Сварное соединение торцевыми швами

Как это видно из рис.5.32, б, полное напряжение, возникающее в сечении АВ, может быть разложено на нормальную и касательную составляющие. Поскольку сопротивление стали сдвигу ниже, чем при растяжении, расчет лобовых швов производится условно на срез в предположении равномерного распределения касательных напряжений по площади сечения АВ. Имея в виду, что на восприятие силы Р в этих соединениях (рис.5.33) работают два лобовых шва, верхний и нижний, получим:

Так как площадь сечения шва , а расчетная длина , то условие прочности примет вид:

В действительности, материал шва испытывает сложное напряженное состояние, причем напряжения по сечению АВ распределяются неравномерно. Исследования, произведенные методами теории упругости и подтвержденные экспериментально, показали, что в углах шва имеет место высокая концентрация напряжений.

Если учесть, что, вследствие укорочения швов при остывании, в зоне сварки возникают дополнительные напряжения и в основном металле, ведущие к переходу его в хрупкое состояние, то следует иметь в виду, что концентрация напряжений может явиться причиной появления трещин в основном металле соединения.

Поэтому такое соединение не может быть рекомендовано, особенно при переменной или ударной нагрузке. Значительно надежнее работа соединения встык без накладок.

Соединение фланговыми (или боковыми) швами показано на рис.5.34, а. Разрушение шва, показанное на рис.5.34, б, происходит на значительном его протяжении путем срезывания наплавленного металла в направлении, параллельном шву по наиболее слабой плоскости АВ.

Рис.5.34. Соединение фланговыми швами а) и его разрушение б)

Условие прочности для двух симметрично расположенных швов имеет вид:

Если стык перекрыт двухсторонними накладками, число швов удвоится и условие прочности примет вид:

Отсюда обычно определяют необходимую расчетную длину l фланговых швов. Проектная же длина каждого шва принимается равной .

Как показали опыты, разрушение фланговых швов происходит по типу разрушений пластичных материалов со значительными остаточными деформациями. Это делает работу фланговых швов более благоприятной, чем работу лобовых швов. Однако следует иметь в виду, что у концов фланговых швов также имеет место высокая концентрация напряжений.

При проектировании часто стремятся обеспечить большую надежность соединения, применяя вместо сварки встык, или в дополнение к ней, перекрытие стыка накладками, которые привариваются фланговыми или торцевыми швами, а иногда и теми и другими вместе. Как уже указывалось, при переменных и ударных нагрузках такое «усиление» стыка может принести больше вреда, чем пользы.

Что касается расчета такого комбинированного стыка, то при одновременном применении лобовых и фланговых швов считают, что сопротивление соединения равно сумме сопротивлений всех швов, т. е. , где сопротивление торцевого шва при расчетной длине равно , а сопротивление двух фланговых швов , причем , где b — ширина накладки. В результате подстановки получаем:

Зная длину торцевого шва, определяют длину фланговых швов .При двухсторонних накладках число швов удваивается, т. е. правую часть полученного соотношения следует удвоить.

Так как торцевые швы более жестки, то при совместной работе с фланговыми они перегружаются, что ведет к неравномерной работе соединения. Если учесть, что в таком соединении и термические напряжения достигают больших значений, то устройства такого стыка следует избегать.

Иногда при соединении внахлестку, в дополнение к фланговым швам, применяют прорезные швы, осуществляемые путем наплавки металла в узкую прорезь, сделанную в одном из соединяемых элементов параллельно действующему на соединение усилию.

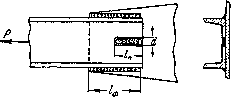
Рис.5.35. Комбинация фланговых и прорезных швов

При длине прорезного шва и ширине прорези d сопротивление такого шва срезу равно:

где — усилие, приходящееся на прорезной шов.

В комбинированном соединении с фланговыми швами для записи расчетного условия принимают, что или

Задавшись размерами одного из швов (обычно флангового), находят необходимую длину другого. При этом ширина прорези d принимается равной двойной толщине прорезанного металла, длина — не более двадцати толщин.

Недостатками соединения с прорезными швами являются: 1) ослабление сечения прорезями вследствие неизбежного непровара и 2) высокая концентрация напряжений в основном металле в зоне сварки, ведущая к появлению трещин около углов прорезного шва; поэтому такое соединение может применяться лишь в крайних случаях, при условии хорошо продуманной технологии сварочных работ.

В заключение заметим, что в том случае, когда приходится прибегать к соединению внахлестку, лучше всего ограничиться одними фланговыми швами, избегая комбинированных соединений.

Расчет сварных соединений при проектировании строительных конструкций

Прочность сварных швов характеризуется их расчетным сопротивлением. В основе расчета прямых стыковых швов лежит условие прочности на растяжение или сжатие:

где – расчетная длина сварного шва; t – наименьшая толщина соединяемых элементов; – расчетное сопротивление сварного соединения на растяжение или сжатие по пределу текучести (иногда берут – то же – по пределу прочности); – коэффициент условий работы ().

Необходимо иметь в виду, что вследствие дефектов сварного шва на его концах, окончательную длину назначают, прибавляя к рассчитанной по формуле (5.33) длине по 1 см на каждом конце.

В основе расчета косых стыковых швов лежат:

– условие прочности на растяжение (сжатие) в направлении, перпендикулярном шву:

– условие прочности на срез в направлении вдоль шва:

где – расчетное сопротивление сварного соединения на срез.

Соединение внахлестку выполняется при помощи угловых швов, которые могут быть лобовыми (рис. 5.36, а) и фланговыми (рис. 5.36, б).

Рис.5.36

При соединении внахлестку расчет угловых швов производится на срез (условный) по двум сечениям (рис. 5.37): по металлу шва (сечение 1) и по металлу границы сплавления (сечение 2). При рассмотрении сечения 1 условие прочности записывается в виде

а для сечения 2 в виде

Рис.5.37

В этих формулах: – расчетная длина шва, принимаемая меньше его полной длины на 1 см; и – коэффициенты, зависящие от прочности материала свариваемых элементов, вида сварки и принимаемые от 0,7 до 1,15; и – коэффициенты условий работы шва, принимающие значения от 0,85 до 1,0 в зависимости от районов эксплуатации конструкции; и – расчетные сопротивления сварных соединений при срезе соответственно по металлу шва и металлу границы сплавления; – коэффициент условий работы шва и назначения конструкции (); k_f – длина катета сварного шва.

Из двух длин , рассчитанных по формулам (5.36) и (5.37), выбирается наибольшая. Расчетная длина может быть разделена на несколько частей в зависимости от конструктивных особенностей соединения. В таких случаях с учетом непровара к длине каждой части добавляется по 1 см на каждый конец.

Пример 20.

Найти необходимую длину фланговых швов, соединяющих равнополочный уголок 63×63×5 с пластиной (рис.5.37.1), если действующее срезающее усилие F=65 кН, приняв R_ср=96 МПа.

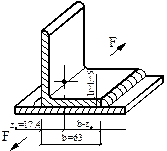
Рис.5.37.1

Решение.

Условия безопасной прочности имеет вид:

где h = 0,5 см - толщина полки уголка.

Для обеспечения одинаковой работы левого и правого швов длины провара следует выбрать обратными расстояниям до центра тяжести сечения уголка от левого и правого шва

Тогда l_лев=14 см, l_пр=5,5 см.

Расчет винтовых пружин с малым шагом витков

Винтовая пружина представляет собой тонкий стержень, чаще всего круглого сечения, ось которого является винтовой линией. Винтовые пружины применяются в вагонных рессорах и различных деталях машин и механизмов. Для пружин с малым шагом витков (рис.5.38, а) соблюдается условие

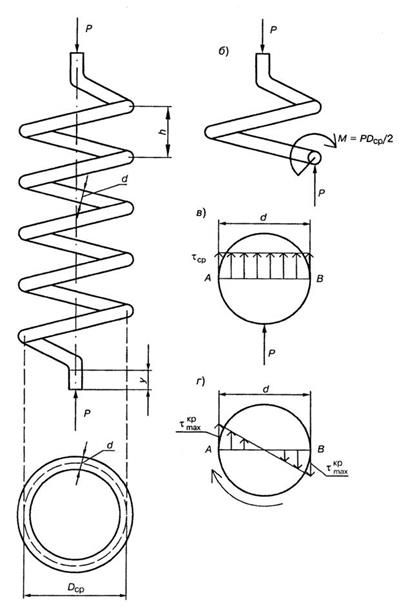
Рис. 5.38

Здесь - средний диаметр пружины, т.е. диаметр цилиндра, на котором лежит винтовая ось пружины. Таким образом, в этом случае, можно приближенно считать, что плоскость витка горизонтальна. Несмотря на сравнительную сложность формы оси, нетрудно вывести формулы для приближенного расчета пружин с малым шагом. При действии сил, направленных по оси пружины и растягивающих или сжимающих ее, стержень пружины в основном испытывает кручение.

Проведем в каком-либо месте разрез стержня пружины вертикальной плоскостью, проходящей через ось пружины (рис.5.38, б) и отбросим нижнюю часть. При условии (5.38) сечение приближенно можно считать не эллипсом, а кругом.

Действие отброшенной части на верхнюю сводится к силе Р, направленной вверх по оси пружины. При параллельном переносе силы Р в центр сечения стержня (рис.5.38, б) присоединится крутящая пара . Таким образом, в сечении пружины возникают два внутренних силовых фактора: поперечная сила Q=Р и крутящий момент . Оба эти фактора вызывают в сечении касательные напряжения. Наибольшие напряжения от кручения (у контура сечения) будут равны (рис.5.38, г)

где d – диаметр стержня пружины.

Напряжения от поперечной силы имеют наибольшую величину вдоль горизонтального диаметра АВ сечения, где они направлены вертикально. По формуле Журавского (рис.5.38, в)

Внутренняя точка А диаметра является опасной точкой сечения, так как здесь напряжения и совпадают по направлению и складываются. Расчетное напряжение будет

При малом отношении d/D можно вторым членом в скобках пренебречь по сравнению с единицей, т.е. рассчитывать пружину на одно кручение.

Если же отношение d/D не мало (например, в вагонных рессорах и других тяжелых пружинах), то влияние поперечной силы на напряжения значительно и должно учитываться. Кроме того, в этом случае существенно сказывается влияние кривизны стержня пружины, вследствие которой напряжение от кручения у внутренней точки А сечения оказывается больше, чем у наружной точки В. Ввиду этого в правую часть формулы (5.41) вместо выражения, стоящего в скобках, лучше ввести коэффициент К, учитывающий одновременно влияние поперечной силы и кривизны стержня:

Этот коэффициент можно вычислять по формуле

где - геометрический параметр пружины.

На практике нужно уметь вычислять удлинение или осадку пружины от растягивающих или сжимающих ее сил. Влияние поперечной силы на удлинение невелико, поэтому обычно принимается в расчет влияние кручения витков.

На рис.5.39 показан бесконечно малый элемент проволоки пружины dS, находящейся в условиях кручения. Правое сечение поворачивается на угол

а все точки на оси перемещаются на величину

Суммируя эти перемещения за счет закручивания длины проволоки, получим полное сокращение расстояния между торцами пружины

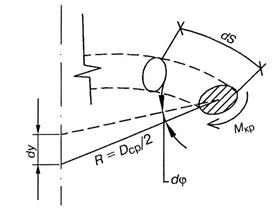
Рис. 5.39

Условие прочности пружины

Так как пружины должны давать достаточно большие упругие удлинения, то они изготовляются из закаленной стали с очень высоким пределом пропорциональности. Допускаемое касательное напряжение колеблется при статической нагрузке от 350 МПа до 500 МПа, а для особо прочных специальных сталей – и выше. При переменной нагрузке допускаемое напряжение значительно снижается (на 30-65%).

Вопросы для самопроверки

- Какой вид нагружения называется кручением?

- Что называется полярным моментом сопротивления и чему он равен для круга и кольца?

- Равен ли полярный момент сопротивления кольцевого сечения разности полярных моментов сопротивления наружного и внутреннего кругов?

- В каких площадках, проходящих через данную точку стержня круглого сечения, при кручении возникают экстремальные касательные напряжения и чему они равны?

- В каких площадках, проходящих через данную точку стержня круглого сечения, при кручении возникают экстремальные нормальные напряжения и чему они равны?

- Как разрушаются при кручении деревяные и чугунные брусья? Как объясниить характер разрушения для каждого из этих материалов?

- При каком нагружении возникает кручение бруса (вала)?

- Какой силовой фактор вызывает закручивание бруса?

- Что такое крутящий момент?

- Что называется валом?

- Когда в брусе возникают деформации кручения?

- Как определяют величину крутящего момента, действующего в сечении?

- Какое правило знаков для Т принято при построении эпюр?

- Как строятся эпюры крутящих моментов?

- Какой вид имеет эпюра крутящего момента на прямолинейном участке, свободном от распределенной нагрузки?

- Какова особенность эпюры крутящего момента в месте действия сосредоточенного момента, действующего вокруг продольной оси стержня?

- Какой вид имеет эпюра крутящего момента на участке, подверженном равномерно распределенной крутящей нагрузки?

- Какова размерность интенсивности распределенного крутящего момента?

- Как определяют угол закручивания на участке вала?

- Что называют относительным углом закручивания θ (или кривизной кручения k_t)?

- Какие напряжения возникают в поперечном сечении круглого вала при кручении и как они направлены?

- Какое напряженное состояние возникает в каждой точке вала круглого сечения при кручении?

- В каких площадках, проходящих через рассматриваемую точку, возникают максимальные нормальные напряжения при кручении стержня?

- В каких площадках, проходящих через рассматриваемую точку, возникают максимальные касательные напряжения при кручении стержня?

- Каково соотношение между наибольшими нормальными и наибольшими касательными напряжениями в точке при кручении?

- В каких точках и площадках возникают максимальные касательные напряжения при кручении стержня круглого сечения?

- Какой модуль упругости больше: E или G?

- Что называется жесткостью сечения при кручении?

- Что выражает условие жесткости при кручении?

- Чем объясняется, что вал кольцевого сечения при кручении экономичнее вала сплошного сечения?

- Как выполняют расчет вала на прочность?

- Какая зависимость существует между крутящим моментом, мощностью, передаваемой валом, и числом оборотов вала?

- Каким следует проектировать вал, если величины крутящих моментов существенно отличаются на его участках?

- Равен ли полярный момент сопротивления кольцевого сечения разности полярных моментов сопротивления наружного и внутреннего кругов?

- Как называется напряженное состояние, возникающее при кручении круглого бруса (вала)?

- Какие деформации возникают при кручении?

- Какие гипотезы выполняются при деформации кручения?

- Изменяются ли длина и диаметр вала после скручивания?

- Какие внутренние силовые факторы возникают при кручении?

- Что такое рациональное расположение колес на валу?

- Вывести формулу для определения напряжений в поперечном сечении скручиваемого круглого бруса.

- Вывести формулы для определения относительного и полного угла закручивания круглого бруса.

- Какая теоретическая зависимость существует между внешним крутящим моментом, поступающим на вал, и передаваемой мощностью?

- Как вычисляется скручивающий момент, передаваемый шкивом, по заданной мощности и числу оборотов в минуту?

- Как вычисляют значение крутящего момента в поперечном сечении вала?

- Что такое эпюра крутящего момента и как она строится?

- Для чего строится эпюра крутящих моментов?

- Опишите технику построения эпюры крутящих моментов?

- Как выглядит правило знаков для крутящего момента?

- В каком случае возникают скачки на эпюре крутящего момента?

- В каком случае график функции крутящего момента представляет собой постоянную функцию?

- Какие внутренние силовые факторы возникают в поперечном сечении стержня при кручении?

- Какие предпосылки используются в теории кручения круговых брусьев?

- Перечислите гипотезы, принимаемые в теории кручения прямого вала круглого поперечного сечения.

- Какие напряжения возникают в поперечном сечении круглого вала при кручении и как они направлены?

- По какой формуле определяется касательное напряжение при кручении?

- Напишите формулу для определения напряжений в поперечном сечении скручиваемого круглого вала.

- Получите формулу касательных напряжений при кручении кругового бруса? Охарактеризуйте эпюру напряжений? Каким выражением определяются наибольшие касательные напряжения, как записывается условие прочности при кручении?

- Как распределяется касательное напряжение при кручении? Чему равно напряжение в центре круглого поперечного сечения?

- Какое напряженное состояние возникает в каждой точке круглого вала при кручении?

- По каким напряжениям ведется расчет на прочность при кручении?

- Напишите формулу для расчета напряжения в любой точке поперечного сечения?

- Какой вид имеет формула максимального касательного напряжения при кручении стержня круглого сечения?

- Какой вид имеют формулы полярных моментов сопротивления круга и кольца?

- Напишите формулу для расчета напряжения на поверхности вала при кручении? Как изменится напряжение, если диаметр вала увеличится в два раза?

- Как должен изменяться диаметр вала, если передаваемая им мощность остается без изменения, а число оборотов увеличивается?

- Почему для деталей, работающих на кручение, выбирают круглое поперечное сечение?

- Какая выгода достигается при высверливании валов?

- В чем заключается расчет на прочность при кручении?

- В чем заключается расчет на жесткость при кручении?

- Напишите формулу для определения относительного и полного угла закручивания круглого вала.

- Почему при одинаковой прочности и жесткости вал кольцевого поперечного сечения легче, чем вал сплошного круглого сечения?

- Как разрушаются при кручении стержни из пластического материала? Как объяснить такой тип разрушения?

- Как разрушаются при кручении стержни из хрупкого материала? Как объясняется такой тип разрушения?

- Охарактеризуйте особенности деформации брусьев не кругового сечения. В чем сущность гидродинамической аналогии?

- Как вычислить потенциальную энергию деформации, накапливаемую валом при кручении?

- Почему нельзя для бруса некруглого поперечного сечения вывести методами сопротивления материалов формулу для определения напряжения и угла закручивания?

- В каких точках сечения получаются наибольшие напряжения при кручении бруса прямоугольного сечения?

- Какой из брусьев тонкостенного сечения имеет большее сопротивления кручению: с замкнутым или незамкнутым профилем?

- Какие допущения положены в основу вывода формулы для касательных напряжений, возникающих в поперечном сечении вала при кручении?

- Какое напряженное состояние возникает в каждой точке бруса круглого сечения при кручении?

- В каких точках бруса круглого сечения возникают наибольшее касательное напряжение? Как их вычисляют?

- Что такое полярный момент инерции? Какой физический смысл имеет эта величина? В каких единицах измеряется?

- По каким формулам вычисляют полярные моменты инерции и сопротивления для круглого и кольцевого сечения?

- Что такое полярный момент сопротивления сечения бруса ()? Получите выражение для кругового сечения?

- Напишите выражение для кольцевого сечения? Почему его нельзя вычислять как разность моментов сопротивления наружного и внутреннего кругов?

- Вычислите полярный момент сопротивления сечения круглого сплошного вала d=30 мм?

- Как распределяются касательные напряжения по поперечному сечению вала?

- Как проявляется закон парности касательное напряжение при кручении?

- Как определяется диаметр вала из условия прочности?

- Как определяется диаметр вала из условия жесткости?

- Как изменится напряжение в сечении, если диаметр вала уменьшить в два раза?

- Проведены расчеты вала на прочность и жесткость. Получено: диаметр вала из расчета на прочность 65 мм, диаметр вала из расчета на жесткость 70 мм. Каким должен быть вал?

- Как изменится угол закручивания вала, если крутящий момент увеличить в 4 раза, а диаметр уменьшить в 2 раза?

- Как определяется потенциальная энергия при кручении?

- Что называется жесткостью сечения при кручении?

- Что называется полярным моментом сопротивления, в каких единицах он выражается и чему равен (для круга и кольца)?

- Чем объясняется, что вал кольцевого сечения при кручении экономичнее вала сплошного сечения?

- Чему равны наибольшие касательные напряжения и наибольшие главные напряжения в скручиваемом вале круглого сечения? В каких точках они возникают?

- Как разрушаются при кручении стальные чугунные и деревянные валы? Как объяснить характер разрушения для каждого из этих материалов?

- Чему равна потенциальная энергия деформации кручения вала круглого сечения? Запишите соответствующую формулу.

- Как производится расчет вала на прочность при кручении?

- Как выбираются допускаемые напряжения при расчете на кручение?

- Как производится расчет вала на жесткость при кручении?

- Охарактеризуйте расчет статически неопределимых валов.

- Как оценивается рациональность поперечного сечения при кручении?

- Как формулируется закон Гука при сдвиге?

- Какой физический смысл у модуля упругости?

- Какой случай плоского напряженного состояния называется чистым сдвигом?

- Чему равен модуль упругости материала при кручении для стали? В каких единицах он измеряется?

- Что представляет собой деформация сдвига?

- Как обозначается деформация при сдвиге?

- Укажите единицы измерения напряжений сдвига и смятия и модуля упругости.

- Какой вид напряженного состояния называют чистым сдвигом?

- Что понимается под абсолютным сдвигом?

- Определите понятие относительного сдвига?

- Как записывается условие прочности при сдвиге?

- Какие внутренние силовые факторы возникают при сдвиге?

- Какая связь между углом сдвига и углом закручивания?

- Сформулируйте закон парности касательных напряжений?

- Что такое срез?

- Что такое смятие?

- Какие допущения проложены в основу практических расчетов элементов конструкции на срез и смятие?

- Опишите процесс разрушения при срезе?

- Чем отличается деформация сдвига от деформации среза?

- Как определяется потенциальная энергия при сдвиге?

- Как выбирается допускаемое напряжение при сдвиге?

- Что понимается под деформацией смятия?

- В чем заключается явление смятия и в каких местах оно наблюдается?

- Как записывается условие прочности на срез и на смятие?

- Как находится площадь смятия при соприкосновении цилиндрических поверхностей?

- Как определяется площадь смятия, если поверхность смятия плоская и если поверхность смятия цилиндрическая?

- Как определяется расчетная величина площади на срез и на смятие при болтовых соединениях листовых элементов внахлестку и с помощью накладок?

- Какие виды деформации испытывает нагруженное заклепочное соединение?

- Как учесть количество деталей, использованных для передачи нагрузки при расчетах на сдвиг и смятие?

- Почему при расчете на смятие цилиндрических деталей вместо боковой цилиндрической поверхности подставляют плоскость, проходящую через диаметр?

- Чем отличается расчет на прочность при сдвиге односрезной заклепки от двухсрезной?

- Какие упрощающие гипотезы используют при расчёте на срез?

- Как связаны поперечная сила Q и касательные напряжения в площадке среза?

- Как вычисляются действующие касательные напряжения в предположении их равномерного распределения в сечении?

- Запишите условие безопасной прочности при срезе.

- Как определить действительный запас прочности, если известны действующие касательные напряжения и прочностные характеристики материала?

- Как рассчитываются заклепочные и сварные соединения на срез?

- Как определить необходимое количество заклёпок, обеспечивающее безопасную прочность соединения?

- Почему в условии прочности для сварного шва содержится множитель 0,7 катета шва?

- Какие дополнительные проверки на прочность выполняют при расчёте заклёпочного соединения?

- Как определяют число срезов заклёпки, соединяющих пакет из m листов?

- Почему при расчёте сварного соединения можно суммировать длины продольных и поперечных швов?

- Какие виды сварных швов используются на практике?

- Как рассчитывается сварной шов встык?

- Как рассчитывается сварной шов внакладку?

- Какие напряжения возникают в сечение витка цилиндрической винтовой пружины, нагруженной осевой силой? Как они определяются?

- Как вычислить осадку цилиндрической винтовой пружины?

- Из каких сталей изготавливаются пружины с малым шагом?

- На какую деформацию ведется расчет пружин с малым шагом?

- Как ведется конструктивный расчет пружины?

- При кручении в поперечных сечениях стержня возникает внутреннее усилие …

- Величина касательного напряжения в любой точке поперечного сечения определяется по формуле…

- Величина наибольшего касательного напряжения в поперечном сечении равна…

- Полярный момент сопротивления сплошного круглого вала определяется по формуле…

- Касательные напряжения в точках на оси скручиваемого стержня равны…

- При кручении в поперечных сечениях вала возникают … деформации.

- Диаметр вала сплошного сечения при кручении, определяемый из условия прочности, должен быть не менее …

- Жесткостью сечения вала называют произведение …

- Главные площадки при кручении ориентированы относительно поперечного сечения под углом α, равным …

- Величина главных напряжений при кручении равна …

- Диаметр вала сплошного сечения, определяемый из условия жесткости при кручении, не должен быть менее величины …

- Полярный момент сопротивления вала кольцевого сечения равен …

- Относительный угол закручивания (кривизна кручения) определяется выражением …

- Брус кольцевого сечения более рационален, чем сплошной круглый брус потому, что …

- Условие жесткости при кручении имеет вид …

- Угол закручивания вала на участке определяют по формуле …

- Угол закручивания вала будет тем больше, чем … будет его жесткость.

- В качестве вала использовать чрезмерно тонкостенную трубу невозможно, потому что …

- Если известны материал и диаметр сплошного вала, то величина допускаемого крутящего момента не должна превышать …

- Если диаметр вала подобран и из условия безопасной прочности и из условия обеспечения жесткости, то необходимо назначить (больший?, меньший?) из полученных размеров?

- Отношение абсолютного сдвига ∆S к расстоянию между сдвигающимися плоскостями a называется…

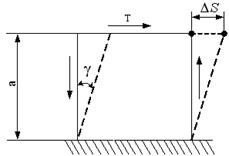
1. относительным сдвигом;

2. модулем Юнга;

3. модулем сдвига;

4. законом Гука при сдвиге.

- [τ] – допускаемое напряжение на срез для заклепки. Площадь поперечного сечения тела заклепки определяется по формуле…

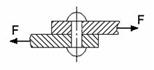
1.

2.

3.

4.

- Каков физический смысл модуля сдвига?

1. коэффициент пропорциональности между поперечной и продольной деформацией;

2. коэффициент пропорциональности между нормальным напряжением и линейной деформацией;

3. коэффициент пропорциональности между касательным напряжением и угловой деформацией.

- Почему продольные (фланговые) швы предпочтительнее торцевых (лобовых) при ударных нагрузках?

1. их можно выполнить более качественно;

2. протяжённость таких швов неограниченна шириной полосы;

3. потому что фланговые швы разрушаются без значительных пластических деформаций;

4. фланговые швы разрушаются с образованием значительных пластических деформаций.

Ответ: (4), предшествующие разрушению значительные пластические деформации могут поглощать значительно большую энергию удара, а при разрушении лобовых швов абсолютные сдвиговые деформации малы.

- Почему в заклёпочном соединении при большом количестве заклёпок их располагают несколькими рядами, а не в один ряд?

1. заклёпки более равномерно нагружены;

2. ослабление ”живого сечения” полосы меньше;

3. все заклёпки не помещаются в один ряд;

4. на каждую заклёпку в этом случае придётся большая часть нагрузки.

Ответ: (2), поскольку в этом случае ослабленная большим количеством отверстий под заклёпки полоса может не обеспечить прочность.

- Если две пластины соединяются сваркой встык, а толщина пластины t и ширина b, то каким будет правильное условие прочности:

1)

2)

3)

4)

Ответ: (3), поскольку в таком сварном шве площадка разрушения (b×t) и в ней действуют нормальные напряжения σ.

- Две пластины соединены с помощью двух накладок и растянуты силой F. Катет шва h. Какая из формул будет верной при проверке на прочность?

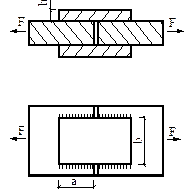
1)

2)

3)

4)

Ответ: (2), поскольку при разрушении соединения образуются две части и общая длина разрушенного шва будет составлять 4а, и площадь среза – 0,7h∙4a.

Онлайн-калькулятор "Расчет прочности при кручении вала круглого сечения"

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00