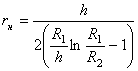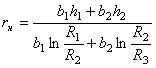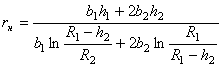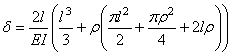Главная
Лекция 16. Расчет кривых брусьев
Понятие о кривых брусьях
Кривой брус в сопротивлении материалов и в теории упругости это тело, геометрическая форма которого образуется движением в пространстве плоской фигуры (называемом поперечным сечением кривого бруса), при этом центр её тяжести всегда остаётся на некоторой кривой (оси кривого бруса), а плоскость фигуры нормальна этой кривой. В зависимости от вида поперечного сечения различают: кривой брус постоянного сечения (пример - звено цепи, составленной из овальных или круглых колец) и кривой брус переменного сечения (пример - крюк подъёмного крана). По виду оси кривой брус может быть плоским (если его ось - плоская кривая) и пространственным (ось - пространственная кривая). Разновидностью кривого бруса является естественно закрученный кривой брус, отличающийся тем, что плоская фигура поперечного сечения при своём движении по оси кривого бруса одновременно вращается вокруг касательной к ней (пример - лопасть воздушного винта самолёта или вентилятора).
Рассмотрим расчет кривых брусьев, т. е. брусьев, имеющих криволинейные оси. К кривым брусьям относятся крюки (рис. 1, а), проушины (рис.1, 6), звенья цепей (рис.1, в), арки мостов (рис.1, г) и др. Наибольшее практическое значение имеют кривые брусья, оси которых расположены в одной плоскости, - плоские кривые брусья.
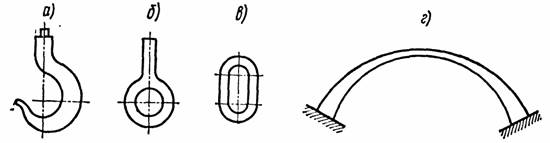
Рис.1
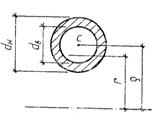
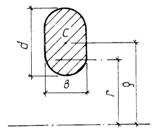
Определение напряжений в кривом брусе производится различно в зависимости от того, является он брусом малой кривизны или большой кривизны. Высота h поперечного сечения брус малой кривизны мала по сравнению радиусом r кривизны оси бруса он составляет менее 0,2r - 0,25r; высота h бруса большой кривизны составляет более 0,2r - 0,25r. При этом под высотой понимается наибольший размер поперечного сечения в плоскости кривизны оси бруса (рис.2).
Рис.2
Напряжения в брусьях малой кривизны с достаточной для практики точностью можно определять по формулам, полученным для прямых брусьев. Аналогично по формулам расчета прямых брусьев можно определять касательные напряжения в брусьях большой кривизны.
Распределение же нормальных напряжений в поперечных сечениях таких брусьев существенно отличается от распределения их в прямых брусьях, а потому эти напряжения в брусьях большой кривизны определяются по специальным формулам, приведенным ниже.
Построение эпюр внутренних усилий в кривых брусьях
В плоском криволинейном стержне так же, как в плоской раме, состоящей из прямолинейных стержней, возникает три внутренних усилия: N, Q и М. Процесс определения внутренних усилий в криволинейном стержне тот же, что и в раме. Особенность состоит в новом правиле знаков для изгибающего момента: изгибающий момент считается положительным, если он увеличивает кривизну стержня (Если рассматриваемый стержень имеет и прямолинейный, и криволинейный участки, то для того, чтобы не было противоречия из-за разного правила знаков для изгибающего момента в прямолинейной и криволинейной частях стержня, принято строить эпюру изгибающего момента со стороны растянутых волокон без определения знака). Правила знаков для продольной и поперечной сил те же, что и при их определении в плоских рамах.
Построение эпюр внутренних усилий рассмотрим на конкретном примере плоской круговой балки (т. е. балки с осью, очерченной по дуге окружности), изображенной на рис. 3, а.
Рис. 3
Для определения опорных реакций составим уравнения равновесия:
,
откуда
;
,
откуда
;
,
откуда
В этих выражениях величины 
и 
представляют собой
соответственно вертикальную и горизонтальную составляющие силы Р; ось 
горизонтальна.
Определяем значение радиуса r оси балки и центрального угла 
. Из рис. 3, а:
следовательно,
,
откуда
и
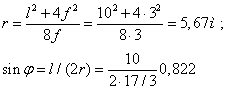
и 
Проведем через произвольную точку О участка 1 балки поперечное сечение n-n. Положение этого сечения определяется углом 
(рис.3, а). С сечением n-n совместим ось у подвижной системы координат; ось х перпендикулярна ей и касательна к
оси балки в точке О. Координаты точки
О в
неподвижной системе координат х0у0 равны:
;
.
Составим выражения изгибающего момента 
, поперечной силы 
и продольной силы 
в поперечных сечениях
участка I балки:
;
;
.
Аналогично составим выражения 
для участка II балки:
;
.
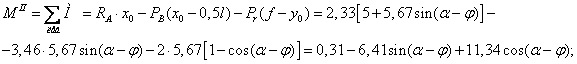
По полученным значениям усилий в поперечных сечениях балки на рис. 3, б, в, г построены эпюры М, Q и N.
Связь
между усилиями М, Q и N, действующими
в поперечных сечениях кривого бруса, определяется следующими дифференциальными
зависимостями:
;
(1)
; (2)
. (3)
где q и t — интенсивности распределенных нагрузок соответственно перпендикулярной и параллельной оси бруса; ds - длина элементарного отрезка оси кривого бруса.
Формула (1) аналогична формуле Журавского для прямых брусьев.
Зависимости (1) - (3) могут использоваться для проверки построенных эпюр М, Q и N. Проверим с их помощью эпюры, изображенные на рис. 3.
На участке I балки (см. рис. 3, а) ординаты эпюры Q положительны, а на участке II — отрицательны. Поэтому в соответствии с зависимостями (1) и (3) значения М и N на участке I возрастают слева направо (т.е. с увеличением криволинейной координаты s), а на участке II — убывают. Ординаты эпюры N на участке I отрицательны, а на участке II — положительны; в соответствии с зависимостью (2) значения Q на участке I возрастают, а на участке II — убывают.
Производная 
на отрезке, например, 2-3 оси балки (см. рис. 3, а) имеет среднее значение, равное (см.
рис.3, 6)
,
где длина участка
.
Этому
среднему значению производной в соответствии с зависимостью (1) примерно равна
средняя величина Q на отрезке 2-3 (см. рис.
3, в). Производная 
на участке, например, 3-4 балки имеет среднее значение
.
В соответствии с
зависимостью (2) такое же примерно значение на отрезке 3-4 имеет среднее
отношение 
, равное
.
Аналогично можно проверить выполнение условий (1)-(3) и на других отрезках оси балки.
Пример
1.
Построить эпюры изгибающих моментов, поперечных и продольных сил для бруса, изображенного на рис. 4.
Рис.4
Решение.
Для определения положения сечения используем
полярные координаты 
и . Общие выражения для изгибающего момента, продольной и
поперечной сил в произвольном сечении бруса записываются в виде
;
;
.
Давая определенные числовые
значения в пределах от 0 до 900, например, с шагом 100,
находим 
в этих сечениях.
Откладываем их в выбранном масштабе, соединяя ординаты плавными кривыми,
получаем искомые эпюры (рис.4).
Определение напряжений в брусьях
большой кривизны
Выведем формулы для определения нормальных напряжений в брусьях большой кривизны.
При выводе этих формул предполагается, что:
1) кривой брус является плоским (т.е. ось его представляет собой плоскую кривую);
2) брус симметричен относительно плоскости, в которой расположена его ось, а внешние силы действуют в этой плоскости;
3) поперечные сечения бруса, плоские до его деформации, остаются плоскими и после деформации (гипотеза плоских сечений);
4) давление продольных волокон бруса друг на друга не влияет существенно на распределение напряжений в брусе, а потому его можно не учитывать.
При изгибе брусьев малой кривизны нормальные
напряжения с достаточной степенью
точности можно определять по
формуле Навье для балок с прямой осью.
Максимальные напряжения, подсчитанные по формуле Навье
для бруса прямоугольного сечения с отношением 
, отличаются на 2% от
напряжений, вычисленных по формулам для бруса
большой кривизны; при 
- на 3,5%, при 
- на 7%.
Рассмотрим случай чистого изгиба бруса
большой кривизны (
) (рис.5). Предполагаем, что радиус 
нейтрального слоя
неизвестен и не совпадает с радиусом R оси стержня.
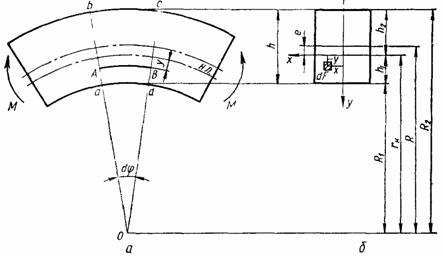
Рис.5
При выводе формулы для определения нормальных напряжений в брусе большой кривизны исходят из тех же гипотез, что и при выводе формулы Навье, т. е пользуются гипотезой плоских сечений и гипотезой о том, что продольные волокна материала не давят одно на другое. Выбираем направление осей сечения х и у, как показано на рис.6 (при этом ось х считается совпадающей с нейтральной линией, положение которой пока неизвестно). Направление у к центру кривизны принято за положительное.
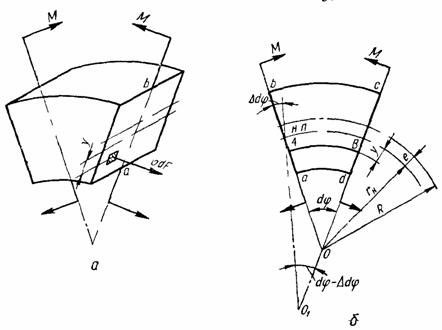
Рис.6
Рассмотрим статическую сторону задачи и запишем условие равновесия
применительно к элементу бруса (рис. 6, а), оставшемся после удаления отсеченных частей. Для нашего
случая, когда в сечении действует один силовой фактор 
, будем иметь
;
(4)
.
(5)
В силу симметрии F
.
Рассмотрим геометрическую сторону задачи. Относительное
удлинение произвольно выделенного элементарного участка АВ, находящегося на расстоянии у от нейтральной линии (рис. 6, б) и получившего в результате деформации
удлинение 
, равно
,
(6)
где
– длина элемента до деформации.
Из рассмотрения физической стороны задачи, определяемой законом Гука
,
(7)
условие (4) перепишем в виде
Так как
,
то
.
(8)
Из (5) находим
(9)
Так как
,
или
, (10)
Можем представить (9) так:
.
Отсюда
,
(11)
где 
— расстояние от нейтральной линии до
центра тяжести (эксцентриситет); F - площадь поперечного сечения.
Подставив (11) в (7), найдем формулу для определения нормальных напряжений при изгибе
, (12)
.
(13)
Здесь М — изгибающий момент в сечении; Sx — статический момент площади сечения кривого бруса относительно нейтральной линии.
Из анализа (12) или (13) видно, что
нормальные напряжения по высоте распределяются по
гиперболическому закону (рис. 7, б).
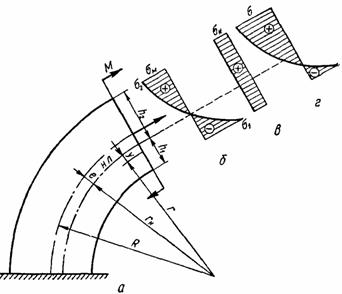
Рис. 7
Абсолютные величины напряжений в крайних волокнах сечения бруса согласно (12) определяются по формулам
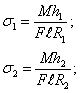(14)
где R1 и R2 — соответственно радиусы кривизны внутренних и внешних волокон кривого бруса; h1 и h2 — расстояния от нейтральной линии до этих волокон. Знак напряжения определяется по направлению изгибающего момента в сечении.
Формулы (12) - (14) могут быть использованы,
если известна входящая в эти формулы величина или радиус
нейтрального слоя 
поскольку
,
(15)
где R — радиус слоя, в котором расположены центры тяжести сечения
бруса. Радиус определим из уравнения
(8).
Произведя замену переменных 
или 
, перепишем уравнение (8) в следующем виде:
.
или
.
Отсюда
.
(16)
Так
как для прямоугольного сечения 
(h -
высота сечения; b - ширина сечения); 
, формула (16) может быть описана в виде
(17)
Воспользовавшись рядом
,
получим
.
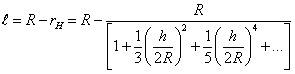В первом приближении
.
(18)
Во втором приближении
.
(19)
На основании (16) аналогичным путем можно
получить приближение для в
случае других форм поперечного сечения. Из (15) по известным могут быть определены величины .
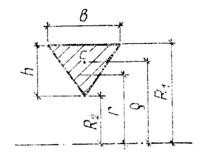
Значения
для часто
встречающихся сечений различной формы приведены в таблице 1.
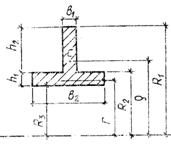
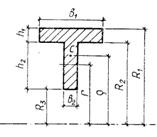
Таблица 1. Значения радиуса кривизны нейтрального слоя
|
Форма сечения |
Радиус кривизны нейтрального слоя |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; 
Радиус
кривизны нейтральной оси для сложных форм поперечных сечений может быть определен
приближенно с помощью замены интегрирования в выражении (16) на численное
суммирование. В этом случае вычерчивают в масштабе сечение и разбивают его
линиями, параллельными нейтральной оси, на достаточное число полосок. Площади
полосок и их радиусы кривизны измеряются в масштабе чертежа, тогда
,
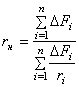где 
- площадь полоски; 
-радиус кривизны; 
- число полосок.
Эксцентриситет нейтральной оси для некоторых форм поперечного сечения кривого бруса можно
также вычислить следующим образом:
,
где 
- коэффициент, принимаемый по таблице 2 в зависимости от
отношения 
; 
- расстояние от центра тяжести сечения до внутренних волокон.
Если поперечные сечения кривых брусьев имеют две оси симметрии, то для
определения эксцентриситета нейтральной оси при небольшой кривизне брусьев
можно воспользоваться приближенной формулой Н.Н.Давиденкова
,
где 
- момент инерции сечения относительно центральной оси, параллельной нейтральной линии;
Формула
Н.Н.Давиденкова нередко с несколько меньшей, но достаточной для практики
точностью используют для вычисления эксцентриситета нейтральной оси и для
расчета сечений с одной осью симметрии.
Таблица
2. Значения коэффициента
|
|
|
|
|
1,2 |
0,224 |
0,305 |
|
1,4 |
0,151 |
0,204 |
|
1,6 |
0,108 |
0,149 |
|
1,8 |
0,084 |
0,112 |
|
2,0 |
0,069 |
0,090 |
|
2,2 |
0,058 |
0,077 |
|
2,4 |
0,049 |
0,065 |
|
2,6 |
0,042 |
0,055 |
|
2,8 |
0,036 |
0,047 |
|
3,0 |
0,030 |
0,041 |
|
3,5 |
0,022 |
0,028 |
|
4,0 |
0,016 |
0,021 |
|
6,0 |
0,0070 |
0,0093 |
|
8,0 |
0,0039 |
0,0052 |
|
10,0 |
0,025 |
0,0033 |
|
|
|
|
|
1,2 |
0,336 |
0,352 |
|
1,4 |
0,229 |
0,243 |
|
1,6 |
0,168 |
0,179 |
|
1,8 |
0,128 |
0,138 |
|
2,0 |
0,102 |
0,110 |
|
2,2 |
0,084 |
0,092 |
|
2,4 |
0,071 |
0,078 |
|
2,6 |
0,061 |
0,067 |
|
2,8 |
0,063 |
0,058 |
|
3,0 |
0,046 |
0,050 |
|
4,0 |
0,024 |
0,028 |
|
6,0 |
0,011 |
0,012 |
|
8,0 |
0,0060 |
0,0060 |
|
10,0 |
0,0039 |
0,0039 |
|
|
|
|
|
1,2 |
0,361 |
0,418 |
|
1,4 |
0,251 |
0,299 |
|
1,6 |
0,186 |
0,229 |
|
1,8 |
0,144 |
0,183 |
|
2,0 |
0,116 |
0,149 |
|
2,2 |
0,096 |
0,125 |
|
2,4 |
0,082 |
0,106 |
|
2,6 |
0,070 |
0,091 |
|
2,8 |
0,060 |
0,089 |
|
3,0 |
0,052 |
0,079 |
|
3,5 |
0,038 |
0,052 |
|
4,0 |
0,029 |
0,040 |
|
6,0 |
0,013 |
0,018 |
|
8,0 |
0,0060 |
0,010 |
|
10,0 |
0,0039 |
0,0065 |
|
|
|
|
|
1,2 |
0,409 |
0,408 |
|
1,4 |
0,292 |
0,285 |
|
1,6 |
0,224 |
0,208 |
|
1,8 |
0,178 |
0,160 |
|
2,0 |
0,144 |
0,127 |
|
2,2 |
0,120 |
0,104 |
|
2,4 |
0,103 |
0,088 |
|
2,6 |
0,089 |
0,077 |
|
2,8 |
0,077 |
0,067 |
|
3,0 |
0,067 |
0,058 |
|
3,5 |
0,049 |
0,041 |
|
4,0 |
0,038 |
0,030 |
|
6,0 |
0,018 |
0,018 |
|
8,0 |
0,010 |
0,0076 |
|
10,0 |
0,0065 |
0,0048 |
|
|
|
|
|
1,2 |
0,453 |
0,269 |
|
1,4 |
0,319 |
0,182 |
|
1,6 |
0,236 |
0,134 |
|
1,8 |
0,183 |
0,104 |
|
2,0 |
0,147 |
0,083 |
|
2,2 |
0,122 |
0,068 |
|
2,4 |
0,104 |
0,057 |
|
2,6 |
0,090 |
0,049 |
|
2,8 |
0,078 |
0,043 |
|
3,0 |
0,067 |
0,038 |
|
3,5 |
0,048 |
0,028 |
|
4,0 |
0,036 |
0,020 |
|
6,0 |
0,016 |
0,0087 |
|
8,0 |
0,0089 |
0,0049 |
|
10,0 |
0,0057 |
0,0031 |
Расчет на прочность брусьев большой
кривизны
Условие прочности для стержня малой кривизны, когда в его сечении действуют изгибающий момент и нормальная сила (рис. 7, г) имеет вид
,
(20)
где F — площадь сечения; W — момент сопротивления сечения.
Для стержня большой кривизны на основании (12) условие прочности будет
. (21)
При этом нужно рассматривать точки сечения, в
которых суммарные напряжения от изгиба и растяжения будут наибольшими (рис. 7, б, в, г). Для этих точек в формулу (21) следует подставлять 
над
и соответственно 
или 
.
Если брус большой кривизны изготовлен из
материала, для которого допускаемые напряжения на растяжение 
и сжатие 
различны (некоторые
чугуны, пластмассы и др.), то условия прочности должны выполняться для крайних
точек сечения, как в растянутой, так и в сжатой области.
Определение перемещений кривых
брусьев
Для определения перемещений в стержнях любой кривизны удобно пользоваться методом Мора
В стержнях малой кривизны можно пренебречь продольной деформацией и деформацией сдвига. Тогда в случае плоского изгиба можно пользоваться формулой Мора в виде
(22)
При плоском изгибе бруса большой кривизны
деформации элемента от действия усилий 
и 
тоже состоят из
удаления 
отрезка 
оси и относительного поворота 
сечений,
ограничивающих элемент (рис. 8, а, б).
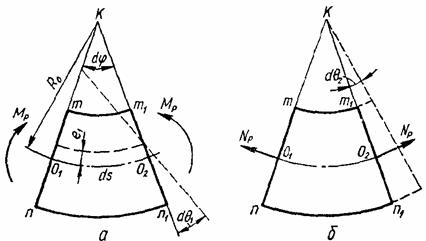
Рис.8
Взаимный угол поворота сечений 
, вызванный изгибающим моментом, можно определить из (11),
.
где 
.
Угол поворота сечений, вызванный осевыми силами вследствие неодинаковой длины волокон элемента (рис. 8, б), равен
Полный угол поворота
(23)
Удлинение элемента в результате действия осевых сил
Удлинение, вызванное поворотом сечения на
угол 
,
Полное удлинение осевого волокна
(24)
Подставляя (23) и (24) в формулу возможных перемещений, находим общую формулу для определения перемещений бруса большой кривизны
(25)
Обычно на практике пренебрегают влиянием поперечной силы, в результате чего последнее слагаемое в (25) не учитывается.
В таблице 3 даны значения интегралов, часто встречающихся при определении деформаций кривого бруса, а в таблице 4 приведены значения наибольших изгибающих моментов и соответствующих перемещений для наиболее распространенных видов кривых брусьев.
Таблица 3. Интегралы, часто встречающиеся при определении перемещений
в кривых брусьях
|
Вид интеграла |
Определенный интеграл в пределах от 0 до следующего значения угла |
|||
|
|
|
|
|
|
|
|
|
0,293 |
1 |
2 |
|
|
|
0,707 |
1 |
0 |
|
|
|
0,143 |
0,785 |
1,571 |
|
|
|
0,643 |
0,785 |
1,571 |
|
|
|
0,118 |
0,333 |
0 |
|
|
|
0,216 |
0,333 |
0,667 |
|
|
|
0,5 |
1 |
0 |
|
|
|
0,25 |
0,5 |
0 |
|
|
|
0,152 |
1 |
3,141 |
|
|
|
0,262 |
0,571 |
-2 |
|
|
|
0,933 |
0,868 |
2,47 |
|
|
|
0,226 |
0,368 |
2,47 |
Таблица 4. Наибольшие изгибающие моменты и перемещения в кривых брусьях
различного очертания
|
Вид кривого бруса |
Изгибающие моменты |
Перемещения |
|
|
|
Горизонтальное перемещение сечения
|
|
|
|
Горизонтальное перемещение сечения
|
|
|
|
Горизонтальное перемещение сечения
|
|
|
|
Сближение концевых сечений
|
Пример
2.
Рассмотрим стержень,
показанный на рис. 9. Определим максимальные нормальные
напряжения в криволинейной части стержня, если 
м, 
м, 
кН, 
кНм. Стержень имеет прямоугольное
поперечное сечение с высотой 
м, отношение 
. Найдем также горизонтальное перемещение левой подвижной
опоры.
Рис.9
Решение.
Прежде всего,
построим эпюры внутренних усилий в стержне. Сначала определим опорные реакции
обычным путем, составляя три уравнения равновесия. Найденные опорные реакции
показаны на рис. 10.
Рис.10
Для определения внутренних усилий рассечем
стержень на трех участках. На прямолинейной части фиксируем сечение координатой
х, на криволинейной части – углом 
(см. рис. 10). В
соответствии с методом сечений находим усилия, рассматривая все силы с одной
стороны от сечения:
участок 1: 
;
;
кН;
;
участок 2: 
;
;
;
;
участок 3: 
;
;
;
.
По этим выражениям строим эпюры N, Q и М. В криволинейной части стержня считаем величины усилий, задавая
значения 
(или 
) через определенные промежутки (например, через 30°).
Внесем результаты вычислений в таблицу 5.
Таблица 5
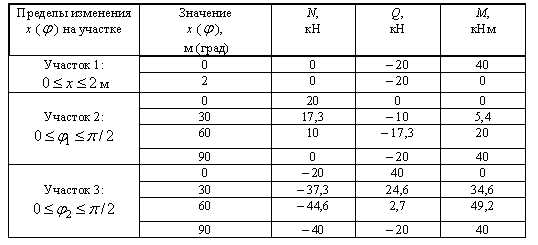
Отложим значения усилий в криволинейной части стержня в радиальном направлении, соединим ординаты плавными кривыми и получим эпюры N, Q и М (рис.11).
Рис.11
Эпюры штрихуем в радиальном направлении. Заметим, что так же, как и в прямолинейных стержнях, в сечении, где Q = 0, на эпюре М имеет место экстремум. Найдем экстремальное значение момента:
,
отсюда 
.
кНм.
В сечении 
действует так же
продольная сила N =
– 44,7 кН.
Построим эпюру нормальных напряжений,
определив значения напряжений в трех точках (a, b, c на рис. 12) опасного сечения
по формуле 
, добавив в нее напряжения от продольной силы. Так как
рассматриваемый криволинейный стержень является стержнем средней кривизны (
), то допустимо искать величину 
по приближенной
формуле 
м4;
м
м.
В точке a координата 
м и напряжение в этой точке
Аналогично в точке b 
м и
.
Наконец, в точке с, находящейся в центре тяжести сечения, напряжение
Эпюра напряжений построена на рис. 12.
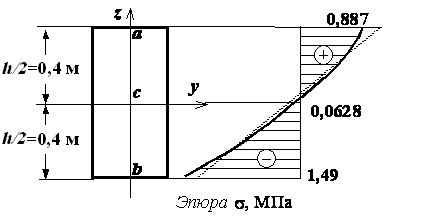
Рис.12. Эпюры напряжений в
опасном сечении:
_____ - по формуле для
криволинейных стержней
............ – по формуле для
прямолинейных стержней
Найдем напряжения в точках а и b по формуле для прямолинейных стержней
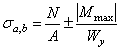
и сравним их с напряжениями, вычисленными по формуле для криволинейных стержней.
;
;
Разница между напряжениями, вычисленными по
разным формулам, составляет около 15%. Напомним, что в рассматриваемом стержне отношение
. Разница между напряжениями, вычисленными по разным
формулам, уменьшается с увеличением отношения 
. Для стержней малой кривизны (
) можно вычислять 
по теории
прямолинейных стержней.
Найдем теперь горизонтальное перемещение левой опоры. Для этого приложим в точке А горизонтальную единичную силу (рис. 13), найдем опорные реакции и запишем выражения для продольной силы и изгибающего момента, вызванных этой единичной силой, на каждом участке:
участок 1: ;
; 
;
участок 2: ;
; 
;
участок 3: ;
; 
.
Рис.13
При определении перемещений используем
формулу 
для прямолинейных стержней.
Подставим в нее выражения для продольной силы и изгибающего момента от заданной
нагрузки и от единичной силы и, принимая во внимание, что на прямолинейном
участке интеграл в рассматриваемом примере равен нулю и 
, получим
.
Используя известные значения определенных интегралов
; 
; 
; 
; 
,
найдем
.
Как легко выяснить, числитель первого слагаемого измеряется в кНм, а числитель второго – в кНм3. Найдем жесткости стержня при растяжении и изгибе:
кН;
кНсм2
и сосчитаем горизонтальное перемещение точки А:
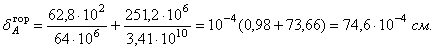
Первое слагаемое в сумме показывает вклад продольной силы в перемещение. Видно, что он незначителен.
В заключение найдем горизонтальное
перемещение точки А
по формуле для криволинейных стержней 
. Сосчитаем значение третьего интеграла в этой формуле:
Таким образом, по формуле для криволинейных стержней
Полученный результат показывает, что влияние кривизны стержня на перемещение меньше 3% и значительно меньше, чем влияние на напряжения. Поэтому для стержней малой и средней кривизны при определении перемещений можно использовать формулу Максвелла-Мора, относящуюся к прямолинейным стержням и учитывающую влияние на перемещения только изгибающего момента.
Пример
3. .
Для заданного бруса (рис. 14) необходимо:
1) Определить полное перемещение сечения А.
2) Определить вертикальное и горизонтальное перемещения сечения А.
3) Определить угол поворота сечения В.
4) Провести проверку найденных перемещений.
Дано: 
.
Рис.14
Решение.
Определим направление отсчета углов 
(рис. 14) для трех
участков, на которые разбиваем брус.
Перемещения в сечении К определяем при помощи интеграла Мора
,
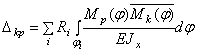где 
- радиус кривизны i-
ого участка; 
и 
- выражения
изгибающего момента для i- ого участка бруса от заданной нагрузки 
и единичной нагрузки,
приложенной в сечении К.
Для каждого участка составим аналитические
выражения изгибающего момента 
и единичных моментов 
, 
от вертикальных и
горизонтальных единичных сил, приложенных
в сечении А.
Рассмотрим
участок I (СА): 
Приложим в сечении А вертикальную и горизонтальную силы и покажем это на рис.15 и рис.16.
Рис.15
Рис.16
Из метода сечений на участке I следует, что 
Участок II (АВ): 
Участок III (ВD):
Построим эпюры моментов 
,
, 
(рис.17, 18, 19)
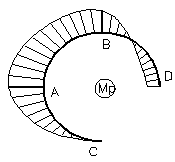
Рис. 17 Рис.
18 Рис. 19
Вычислим теперь вертикальное перемещение сечения А:
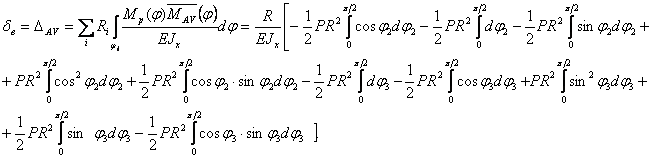
Интегралы
в этом выражении вычисляем при помощи таблицы интегралов. Получаем значение:
Знак минус говорит о том, что направление перемещения не совпадает с направлением единичной силы.
Определим теперь горизонтальное перемещение сечения А:
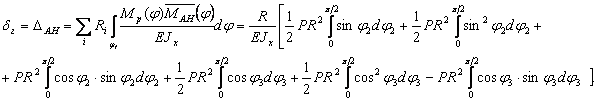
Используя найденные интегралы 
, вычисляем горизонтальное перемещение
2) Определим полное перемещение сечения А по формуле:
.
Подставляя найденные значения вертикального и горизонтального перемещений, получаем
.
3) Определим угол поворота сечения В (рис.20).
Для этого прикладываем в этом
сечении единичный момент и записываем по участкам аналитические выражения для изгибающего
момента 
:
Участок I (СА) :
Участок II (АB) :
Участок III (BD) :
Рис.20
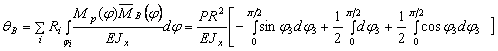
При помощи найденных интегралов 
находим величину 
4) Проведем проверку найденных перемещений.
Для этого составим аналитические выражения для моментов 
с противоположным
направлением отсчета углов 
(рис.21-23).
Определим при помощи уравнений статики
реакции в заделке:
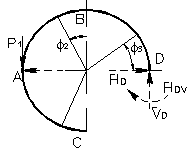
Рис. 21 Рис. 22
Рис. 23
а) 
б) 
в) 
г) 
Составим выражения изгибающих моментов для участков АВ и BD
Участок (АВ) :
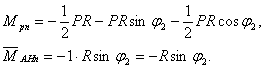
Участок (ВD)
Вычислим сначала вертикальное перемещение 
Таким образом, величина
найдена верно.
Найдем горизонтальное перемещение сечения А 
т.е. величина горизонтального перемещения найдена правильно.
Определим теперь угол поворота в сечении В:
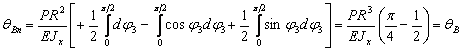
Таким образом, угол поворота совпадает с
найденным ранее значением, т.е. величина определена верно. В заключении построим эпюру 
(рис.24).
Рис. 24
Пример 4.
Для кривого стержня, показанного на рис.25, определить горизонтальное и вертикальное перемещение точки К.
Рис.25
Составляем уравнение изгибающего момента от внешних сил
Прикладываем единичную силу в горизонтальном направлении
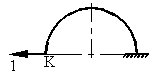
Рис.26
Составляем уравнение изгибающего момента от единичной силы
Определяем горизонтальное перемещение точки К
Прикладываем единичную силу в вертикальном направлении
Рис.27
Составляем уравнение изгибающего момента от единичной силы
Определяем вертикальное перемещение точки К
Ответ: 
, 
.
Пример 5.
Построить эпюры изгибающих моментов Мz, поперечных 
и нормальных N сил для трехшарнирной
круговой арки, показанной на рис. 28, а.
При расчете принять q = 3 т/м, F1 = F2 = 10 т, l = 24 м, f = 6 м.
Определить 
в прямоугольном поперечном
сечении арки. Размеры поперечного сечения принять 
.
Решение.
Определим опорные реакции VA, VB, для чего рассмотрим
откуда VB = 14,75 т;
откуда VA = 23,25 т.
Составим условие: 
тогда 
Горизонтальные опорные
реакции Н определяем из уравнения 
составляемого при
рассмотрении только правой части арки
откуда Н = 19,5 т.
Аналогичный результат получим, если рассмотреть только левую часть арки.
Найдем вертикальные опорные реакции RA, RB простой балки, показанной на рис. 28, б. Предположим, что на балку действует та же нагрузка, что и на арку. В этом случае найдем RA = VA , RB = VB.
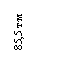
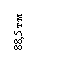
В общем виде
внутренние усилия в произвольном сечении 
трехшарнирной
арки выражаются через внутренние усилия 
соответствующего
сечения простой балки по формулам:
(26)
где – угол между
касательной к оси арки в точке х = const и горизонтальной линией х.
Таким образом, для использования формул (26) необходимо предварительно записать
аналитические выражения для изгибающих моментов поперечных сил для каждого участка
простой балки (рис. 28, б):
: 
По полученным формулам вычисляем для простой балки с шагом
1 м. Результаты заносим в таблицу 6.
По условию задачи арка очерчена по окружности, следовательно, ось арки имеет ординату
(27)
где радиус кривизны арки вычисляется по формуле
Для рассматриваемого случая формула (27) примет вид:
Находим значения у с шагом 1м, а результаты записываем в таблицу 6. Затем также с
шагом 1 м вычисляем значения 
, 
и 
по формулам:
(28)
И наконец, по формулам (26) находим значения
внутренних усилий, возникающих в арке. Например, в сечении х = 0 имеем у=0, 
= 0,8; = 0,6; Н = 19,5 т. Подставляя эти данные,
взятые из первой строки таблицы 6, в формулы (26) определяем:
Mz(x = 0) = 0 – 19,5·0 = 0;
N(x = 0) = – (23,25·0,8 + 19,5·0,6) = –30,3 т.
Полученные результаты записываем опять же в
первую строку таблицы 6. Затем повторяем все вычисления с шагом 
. При вычислении внутренних усилий необходимо помнить, что в
местах приложения сосредоточенных сил значения поперечных и нормальных N сил изменяются
скачкообразно.
Таблица 6
|
х м |
тм |
т |
у м |
|
|
|
Mz тм |
т |
N т |
|
0 1 2 3 4 5 6 |
0 21,75 40,5 56,25 69 78,75 85,5 |
23,25 20,25 17,25 14,25 11,25 8,25 5,25 |
0 1,2 2,1 3 3,69 4,27 4,75 |
1,33 1,08 0,9 0,75 0,63 0,53 0,44 |
0,6 0,68 0,74 0,8 0,85 0,88 0,92 |
0,8 0,73 0,67 0,6 0,53 0,47 0,4 |
0 –1,61 –2,02 –2,25 –2,93 –4,45 –7,08 |
–1,65 –0,53 –0,14 –0,3 –0,88 –1,8 –2,99 |
–30,3 –28,1 –26 –24,2 –22,5 –21,1 –20 |
|
6 7 8 9 10 11 12 |
85,5 90,75 96 101,2 106 111,7 117 |
5,25 |
4,75 5,14 5,46 5,7 5,87 5,97 6 |
0,44 0,35 0,28 0,2 0,13 0,07 0 |
0,92 0,94 0,96 0,98 0,99 0,998 1 |
0,4 0,33 0,27 0,2 0,13 0,07 0 |
–7,08 –9,52 –10,4 –9,84 –7,89 –4,6 0 |
–2,99 –1,55 –0,14 1,24 2,6 3,93 5,25 |
–20 –20,1 –20,2 –20,2 –20 –19,8 –9,5 |
|
12 13 14 15 16 17 18 |
117 112,2 107,5 102,7 98 93,25 88,5 |
–4,75 |
6 5,97 5,87 5,7 5,46 5,14 4,75 |
0 –0,07 –0,13 –0,2 –0,28 –0,35 –0,44 |
1 0,998 0,99 0,98 0,96 0,94 0,92 |
0 –0,07 –0,13 –0,2 –0,27 –0,33 –0,4 |
0 –4,1 –6,89 –8,34 –8,41 –7,02 –4,08 |
–4,75 –3,44 –2,11 –0,75 0,62 2,02 3,45 |
–19,5 –19,8 –20 –20,1 –20,1 –20 –19,8 |
|
18 19 20 21 22 23 24 |
88,5 73,75 59 44,25 29,5 14,75 0 |
–14,75 |
4,75 4,27 3,69 3 2,1 1,2 0 |
–0,44 –0,53 –0,63 –0,75 –0,9 –1,08 –1,33 |
0,92 0,88 0,85 0,8 0,74 0,68 0,6 |
–0,4 –0,47 –0,53 –0,6 –0,67 –0,73 –0,8 |
–4,08 –9,45 –12,9 –14,3 –13 –8,61 0 |
–5,72 –3,45 –0,21 –0,1 2 4,27 6,75 |
–23,77 –24,1 –24,4 –24,5 –24,4 –24,1 –23,5 |
Рассмотрим сечение х = 12 м (точка С на рис.
28, а). Величины и N в сечении х = 12
– 0 м, принадлежащим второму участку, приведены в таблице. Но сечение х = 12 + 0 м одновременно принадлежит и
третьему участку, поэтому определяем и N по формулам (26) при
условии, что 
берется в сечении х = 12 м третьего участка простой балки:
N(x = 12) = – (–4,75·0 + 19,5·1) = –19,5 т.
Аналогичные вычисления проводим для сечения х = 18 м, после чего приступаем к
построению эпюр Mz, , N для арки (рис.28, г).
Из рассмотрения эпюр внутренних усилий арки можно сделать вывод, что наиболее опасным будет поперечное сечение х = 21 м с
Mz,max = 14,3 т·м и N =
–24,5 т.
Учитывая, что h = 60 см, b =
20 см (рис. 29), из формулы 
определяем
Задачи для самостоятельного решения
Задача 1.
1) Построить эпюры изгибающих моментов М, поперечных Q и нормальных N сил для разрезанного кольца (рис. 30).
2) Построить эпюры изгибающих моментов М, поперечных Q и нормальных N сил для кривого стержня, показанного на рис. 31.
Ответ к рис.30:
MB =
MD =
rF, MC = 2rF, MA = ME = 0, NC = QD = F, QB = NA = –F, QC = NB = ND = 0.
Ответ к рис.31: MC = MA = 0, MB = rF, QCD = 0, QBC = –F, QA = 2F, NBD = 2F, NA = F.
Задача 2.
Построить эпюры изгибающих моментов М, поперечных Q и нормальных N сил для кривого стержня, показанного на рис.32.
Ответ: MC = MA = 0, MB = rF, MD = –rF,
ME = –2rF, QC
= QED = NB = F,
QA = –F, NA
= NC = NED = 0, ND = –F.
Задача
3.
Построить эпюры изгибающих моментов Mz, поперечных
и нормальных N сил для трехшарнирной параболической арки, показанной на
рис. 33. Ось параболической арки очерчена по кривой 
, где f = 6 м, l =
24 м. При расчете принять q = 3 т/м; F1 = F2 = 10 т, 
, а , вычисляются по
формулам Определить 
в прямоугольном
поперечном сечении арки. Размеры поперечного сечения принять 
У к а з а н и е. При решении задачи использовать методику, рассмотренную в примере 5.
Ответ: эпюры Mz, , N показаны на рис.
33; = –87,16 кг/см2 в сечении с х = 9 м.
Задача 4.
Построить эпюры изгибающих моментов Mz, поперечных
и нормальных N сил для
трехшарнирной эллиптической арки, показанной на рис. 34. Ось эллиптической арки
очерчена по кривой
, 
,
где f = 6 м, l =
24 м. При расчете принять q = 3 т/м; F1 = F2 = 10 т, а , вычисляются по
формулам Определить в прямоугольном
поперечном сечении арки. Размеры поперечного сечения принять 
У к а з а н и е. При решении задачи использовать методику, рассмотренную в примере 5.
Ответ: эпюры Mz,
, N показаны на рис.
34; = –313,44 кг/см2 в
сечении с х = 22 м.
Вопросы для самопроверки
- Какие элементы деталей машин и конструкций можно отнести к понятию «кривой брус»?
- Какая формула используется при расчете кривого бруса по нормальным напряжениям?
- Что происходит с положением нейтрального слоя при нагружении кривого бруса?
- Как определяется положение нейтрального слоя?
- По каким напряжениям ведется расчет кривых брусьев?
- Какие эпюры необходимо строить при расчете кривых брусьев?
-
Определение положения нейтральной линии в кривом брусе прямоугольного профиля.
Построение эпюры нормальных напряжений.
-
Правило знаков для внутренних силовых факторов в кривом брусе. Особенности
построения эпюр внутренних силовых факторов.
-
Какие точки поперечного сечения кривого бруса оказываются наиболее напряженными?
Почему?
-
Построение эпюр внутренних силовых факторов в кривом брусе (показать на
примере).
-
Определение напряжений в кривом брусе, условие прочности.
-
Определение перемещений в кривом брусе (показать на примере).
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
