Главная
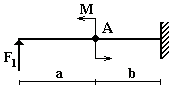
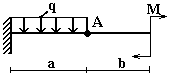
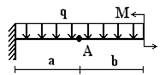
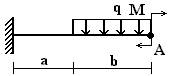
Задача 1. Определение прогибов в статически
определимых консольных балках
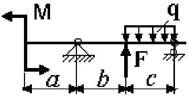
Для деревянной балки с размерами поперечного сечения
20х20 см (рис.1) требуется определить прогиб сечения А;
принять E=1∙104
МПа.
Данные взять из табл.1.
Таблица 1
|
Номер cтроки |
Схема по рис.1 |
F1, см2 |
а, м |
b, м |
М, кНм |
q, кН/м |
|
01 |
1 |
12 |
1 |
2 |
24 |
5 |
|
02 |
2 |
10 |
2 |
2 |
16 |
4 |
|
03 |
3 |
12 |
3 |
2 |
12 |
6 |
|
04 |
4 |
6 |
2 |
3 |
18 |
2 |
|
05 |
5 |
8 |
1 |
3 |
20 |
4 |
|
06 |
6 |
10 |
3 |
1 |
12 |
2 |
|
07 |
7 |
6 |
2 |
2 |
12 |
3 |
|
08 |
8 |
8 |
1 |
2 |
12 |
6 |
|
09 |
9 |
6 |
2 |
1 |
16 |
5 |
|
10 |
10 |
12 |
1 |
3 |
10 |
6 |
|
11 |
11 |
11 |
1 |
2 |
12 |
6 |
|
12 |
12 |
12 |
3 |
3 |
18 |
2 |
|
13 |
13 |
10 |
2 |
3 |
20 |
4 |
|
14 |
14 |
12 |
1 |
1 |
12 |
2 |
|
15 |
15 |
6 |
2 |
2 |
12 |
3 |
|
16 |
16 |
8 |
1 |
2 |
12 |
6 |
|
17 |
17 |
10 |
2 |
1 |
18 |
5 |
|
18 |
18 |
6 |
3 |
2 |
20 |
6 |
|
19 |
19 |
8 |
2 |
2 |
12 |
2 |
|
20 |
20 |
6 |
1 |
3 |
12 |
4 |
|
21 |
21 |
12 |
3 |
3 |
12 |
2 |
|
22 |
22 |
12 |
2 |
1 |
16 |
3 |
|
23 |
23 |
13 |
1 |
2 |
10 |
6 |
|
24 |
24 |
14 |
1 |
2 |
12 |
5 |
|
25 |
25 |
12 |
3 |
1 |
18 |
6 |
|
26 |
26 |
10 |
2 |
3 |
20 |
6 |
|
27 |
27 |
12 |
1 |
2 |
12 |
2 |
|
28 |
28 |
6 |
2 |
3 |
24 |
4 |
|
29 |
29 |
8 |
1 |
3 |
16 |
2 |
|
30 |
30 |
10 |
2 |
1 |
12 |
3 |
|
31 |
31 |
6 |
3 |
2 |
18 |
6 |
|
32 |
32 |
8 |
2 |
2 |
20 |
5 |
|
33 |
33 |
6 |
1 |
1 |
12 |
6 |
|
34 |
34 |
12 |
3 |
3 |
12 |
2 |
|
35 |
35 |
11 |
2 |
2 |
16 |
4 |
|
36 |
36 |
12 |
3 |
3 |
12 |
2 |
|
|
в |
б |
а |
г |
б |
а |
1 схема 2 схема 3
схема
4 схема 5 схема 6 схема
7 схема 8 схема 9 схема
10 схема 11 схема 12
схема
13 схема 14 схема 15 схема
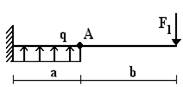
16 схема 17 схема 18 схема
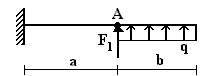
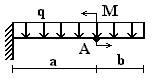
19 схема 20 схема 21 схема
22 схема 23 схема 24 схема
25 схема 26 схема 27 схема
28 схема 29 схема 30 схема
31 схема 32 схема 33 схема
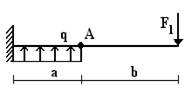
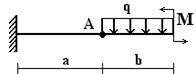
34 схема 35 схема 36 схема
Рис.1
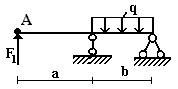
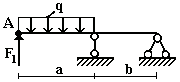
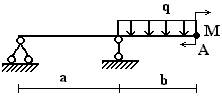
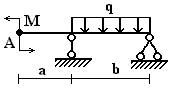
Задача 2. Определение прогибов и углов
поворота в статически определимых двухопорных балках
Для стальной балки из двутавра № 20
(рис.2) определить прогиб и угол поворота сечения А. Принять E=2∙105 МПа. Данные взять из табл. 2.
Таблица 2
|
Номер cтроки |
Номер схемы по рис.2 |
F1, см2 |
а, м |
b, м |
М, кНм |
q, кН/м |
|
01 |
1 |
12 |
1 |
2 |
24 |
5 |
|
02 |
2 |
10 |
2 |
2 |
16 |
4 |
|
03 |
3 |
12 |
3 |
2 |
12 |
6 |
|
04 |
4 |
6 |
2 |
3 |
18 |
2 |
|
05 |
5 |
8 |
1 |
3 |
20 |
4 |
|
06 |
6 |
10 |
3 |
1 |
12 |
2 |
|
07 |
7 |
6 |
2 |
2 |
12 |
3 |
|
08 |
8 |
8 |
1 |
2 |
12 |
6 |
|
09 |
9 |
6 |
2 |
1 |
16 |
5 |
|
10 |
10 |
12 |
1 |
3 |
10 |
6 |
|
11 |
11 |
11 |
1 |
2 |
12 |
6 |
|
12 |
12 |
12 |
3 |
3 |
18 |
2 |
|
13 |
13 |
10 |
2 |
3 |
20 |
4 |
|
14 |
14 |
12 |
1 |
1 |
12 |
2 |
|
15 |
15 |
6 |
2 |
2 |
12 |
3 |
|
16 |
16 |
8 |
1 |
2 |
12 |
6 |
|
17 |
17 |
10 |
2 |
1 |
18 |
5 |
|
18 |
18 |
6 |
3 |
2 |
20 |
6 |
|
19 |
19 |
8 |
2 |
2 |
12 |
2 |
|
20 |
20 |
6 |
1 |
3 |
12 |
4 |
|
21 |
21 |
12 |
3 |
3 |
12 |
2 |
|
22 |
22 |
12 |
2 |
1 |
16 |
3 |
|
23 |
23 |
13 |
1 |
2 |
10 |
6 |
|
24 |
24 |
14 |
1 |
2 |
12 |
5 |
|
25 |
25 |
12 |
3 |
1 |
18 |
6 |
|
26 |
26 |
10 |
2 |
3 |
20 |
6 |
|
27 |
27 |
12 |
1 |
2 |
12 |
2 |
|
28 |
28 |
6 |
2 |
3 |
24 |
4 |
|
29 |
29 |
8 |
1 |
3 |
16 |
2 |
|
30 |
30 |
10 |
2 |
1 |
12 |
3 |
|
31 |
31 |
6 |
3 |
2 |
18 |
6 |
|
32 |
32 |
8 |
2 |
2 |
20 |
5 |
|
33 |
33 |
6 |
1 |
1 |
12 |
6 |
|
34 |
34 |
12 |
3 |
3 |
12 |
2 |
|
35 |
35 |
11 |
2 |
2 |
16 |
4 |
|
36 |
36 |
12 |
3 |
3 |
12 |
2 |
|
|
б |
г |
а |
г |
в |
а |
1 схема 2 схема 3 схема
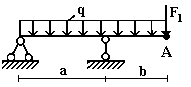
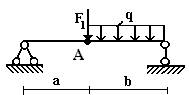
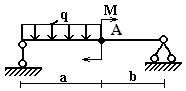
4 схема 5 схема 6 схема
7 схема 8 схема 9 схема
10 схема 11 схема 12 схема
13 схема 14 схема 15 схема
16 схема 17 схема
18 схема
19 схема 20 схема
21 схема
22 схема 23 схема 24 схема
25 схема 26 схема
27 схема
28 схема 29 схема
30 схема
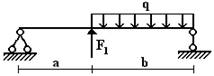
31 схема 32 схема
33 схема
34 схема 35 схема 36 схема
Рис.2
Задача 3. Определение прогибов и углов
поворота в статически определимых двухопорных балках
Для заданной стальной двутавровой балки требуется:
1. Определить опорные реакции.
2. Построить эпюры поперечных
сил и изгибающих моментов.
3. Из условия прочности подобрать двутавровое сечение балки.
4. В опасном сечении определить
прогиб y и угол поворота θ:
а) методом начальных параметров;
б) с применением
интеграла Мора;
в) способом
Верещагина.
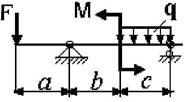
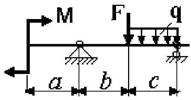
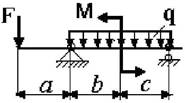
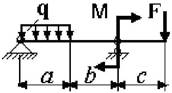
Примечание: Данные для решения задач взять в табл. 3 и на рис.3.
Таблица 3
|
Номер строки |
Схема по рис.3 |
Числовые данные вариантов |
|||||
|
а, м |
b, м |
с, м |
q, кН/м |
F, кН |
M, кНм |
||
|
01 |
1 |
1 |
1,5 |
2 |
2 |
3 |
5 |
|
02 |
2 |
1,2 |
1,6 |
1,8 |
2,5 |
2 |
6 |
|
03 |
3 |
1,4 |
1,8 |
1,6 |
3 |
4 |
8 |
|
04 |
4 |
1,6 |
2 |
1,4 |
2,8 |
5 |
4 |
|
05 |
5 |
1,8 |
1 |
1,2 |
2 |
2,5 |
7 |
|
06 |
6 |
2 |
1,2 |
1 |
4 |
3 |
3 |
|
07 |
7 |
2,2 |
1,4 |
1,8 |
3 |
2,5 |
5 |
|
08 |
8 |
2,4 |
1,6 |
2 |
2 |
2 |
2,5 |
|
09 |
9 |
2,6 |
1,8 |
1,6 |
3,5 |
3,5 |
4 |
|
10 |
10 |
2,8 |
2 |
1,4 |
4 |
3 |
6 |
|
11 |
11 |
3 |
2 |
2,8 |
2,5 |
1 |
2 |
|
12 |
12 |
2,9 |
2,1 |
2,6 |
4 |
2 |
4 |
|
13 |
13 |
2,8 |
2,2 |
2,4 |
3,5 |
3,5 |
3 |
|
14 |
14 |
2,7 |
2,3 |
2,2 |
4,5 |
2 |
2,5 |
|
15 |
15 |
2,6 |
2,4 |
2 |
3 |
2,5 |
2 |
|
16 |
16 |
2,5 |
2,5 |
1,8 |
3 |
2 |
3 |
|
17 |
17 |
2,4 |
2,6 |
1,6 |
2 |
4 |
4 |
|
18 |
18 |
2,3 |
2,7 |
1,4 |
5 |
3,5 |
3,5 |
|
19 |
19 |
2,2 |
2,8 |
1,2 |
4 |
3 |
5 |
|
20 |
20 |
2,1 |
2,9 |
1 |
2,5 |
2 |
3 |
|
21 |
21 |
2 |
2,6 |
3 |
3 |
1 |
5 |
|
22 |
22 |
1,8 |
2,8 |
2,8 |
2 |
1,5 |
4 |
|
23 |
23 |
1,6 |
3 |
2,6 |
1 |
1,5 |
6 |
|
24 |
24 |
1,4 |
3,2 |
2,4 |
1,5 |
2 |
3 |
|
25 |
25 |
1,2 |
3,4 |
2,5 |
2 |
1 |
1 |
|
26 |
26 |
1 |
3,6 |
2,2 |
6 |
1 |
2 |
|
27 |
27 |
1,5 |
3,8 |
2 |
5 |
2 |
1,5 |
|
28 |
28 |
2,2 |
2,4 |
3,2 |
4 |
2 |
1 |
|
29 |
29 |
2,4 |
2,2 |
3,4 |
5 |
1,5 |
1,5 |
|
30 |
30 |
2,6 |
2 |
3,6 |
6 |
3 |
2 |
|
|
в |
г |
б |
а |
в |
г |
б |
1 схема 2
схема
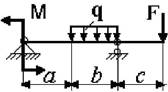
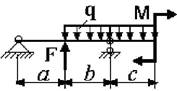
3 схема
4 схема
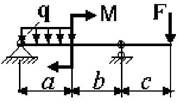
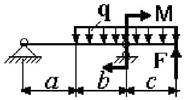
5 схема
6 схема
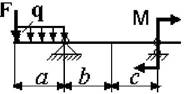
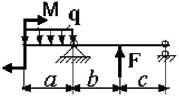
7 схема
8 схема
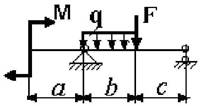
9 схема
10 схема
11 схема 12
схема
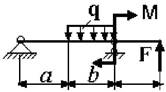
13 схема 14 схема
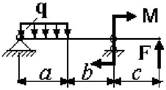
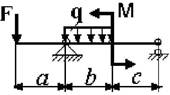
15 схема 16
схема
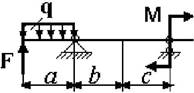
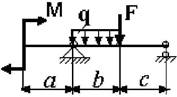
17 схема
18
схема
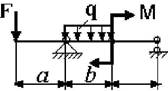
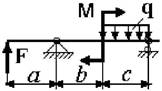
19 схема 20
схема
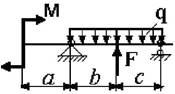
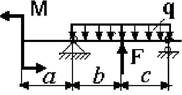
21 схема 22
схема
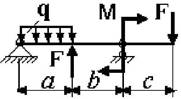
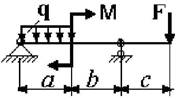
23 схема
24 схема
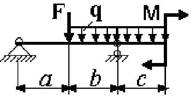
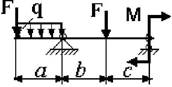
25 схема 26
схема
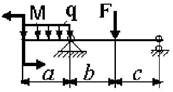
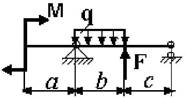
27 схема 28
схема
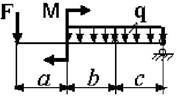
29 схема 30
схема
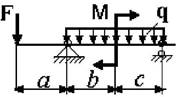
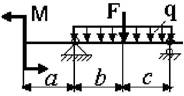
Рис. 3
Задача
4. Определение перемещений в статически определимых консольных балках
Задана
консольная балка постоянной жесткости (EIX = const), рис.4.
Требуется:
Определить по правилу Верещагина вертикальное перемещение
точки «В»
Данные
взять из табл. 4.
Таблица 4
|
№ строки |
Схема по рис.4 |
q, кН/м |
F, кН |
M, кНм |
l, м |
|
01 |
1 |
6 |
20 |
10 |
1,1 |
|
02 |
2 |
7 |
10 |
12 |
1,2 |
|
03 |
3 |
8 |
5 |
14 |
1,3 |
|
04 |
4 |
9 |
4 |
16 |
1,4 |
|
05 |
5 |
10 |
6 |
18 |
1,5 |
|
06 |
1 |
12 |
8 |
20 |
1,6 |
|
07 |
2 |
15 |
15 |
8 |
1,7 |
|
08 |
3 |
5 |
7 |
6 |
1,8 |
|
09 |
4 |
20 |
12 |
7 |
1,9 |
|
10 |
5 |
16 |
14 |
5 |
2,0 |
|
|
е |
а |
б |
в |
г |
1 схема
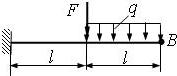
2 схема
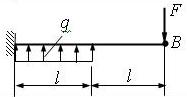
3 схема
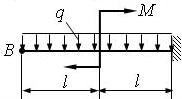
4 схема
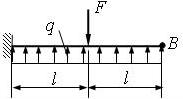
5 схема
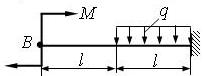
Рис. 4
Примеры выполнения
задач
Определение
перемещений методом Мора-Верещагина-Симпсона
Пример 1
Для балки изображенной на
рис.5,а проверить условие жесткости,
если vнорм
= l/300. Определить угол поворота
сечения над опорой А. Материал балки
сталь Ст 3, Е = 2∙105 МПа,
поперечное сечение двутавр № 30 по ГОСТ 8239-89 Ix=
7080 см4, распределенная нагрузка q = 30 кН/м.
Решение.
Загружаем балку заданной нагрузкой (рис. 5, а). Предварительно определив опорные реакции от заданной нагрузки,
строим грузовую эпюру изгибающих моментов Mf (рис.5, б).
Освобождаем балку от внешней нагрузки и прикладываем посредине пролета
вертикально направленную единичную силу (рис. 5, в). Определив опорные реакции, строим единичную эпюру изгибающих
моментов 
(рис. 5, г).
Прогиб посредине пролета по методу Мора будем вычислять с помощью правила
Симпсона
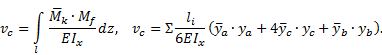
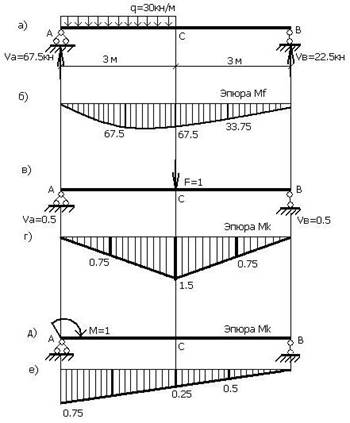
Рис.5. а) загружение внешней нагрузкой; б) грузовая эпюра изгибающих моментов;
в) загружение балки для определения прогиба в сечении «С»; г) эпюра изгибающих моментов от F = 1;
д) загружение балки для определения угла поворота сечения «А»; е)
эпюра изгибающих моментов от М = 1.
Для вычисления интеграла Мора с помощью правила Симпсона на каждом
участке эпюр Mf
, находим по три
ординаты (см. рис. 5, б, г).
Проверяем условие жесткости ∆с ≤ ∆норм.
Нормативный прогиб равен l/300 = 6/300 = 0,02 м. 0,0178 < 0,02.
Условие жесткости выполняется.
Определяем угол поворота сечения над опорой А. Над опорой, в сечении А
приложим единичный момент (рис. 5, д)
и построим единичную эпюру изгибающих моментов 
(рис. 5, е).
Угол поворота будем вычислять с помощью правила Симпсона
Разбиваем эпюру на два участка,
на каждом участке эпюры находим по три
ординаты (см. рис. 5, e).
Пример 2
Определить с помощью метода Мора прогиб и угол
поворота в сечении В для балки, изображенной на рис.
6,а, если жесткость поперечного
сечения балки равна EI =24000 кНм2.
Рис.6
Решение.
1. Изображаем грузовое состояние балки (рис.6,а), нагружая балку в сечении В сосредоточенной
силой, равной единице, и записываем
выражение для изгибающего момента в сечении x:
2. Изображаем первое единичное состояние балки (рис.6,б) и записываем выражение для единичного
изгибающего момента в сечении x:
3. Подставляем выражения (1) и (2) в формулу Мора 
и интегрируем:
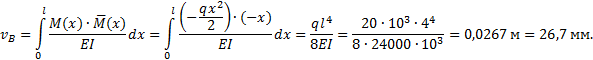
4. Изображаем второе единичное состояние (рис.6,в), нагружая балку в сечении В сосредоточенной парой сил, равной
единице, и записываем выражение для изгибающего момента в сечении x:
5. Подставляем выражения (1) и (3) в формулу Мора и интегрируем:
Пример 3
Используя метод
Мора-Симпсона, определить угол поворота в сечении В изображенной на рис.7,а балки, если жесткость поперечного
сечения балки EI =24000 кНм2.
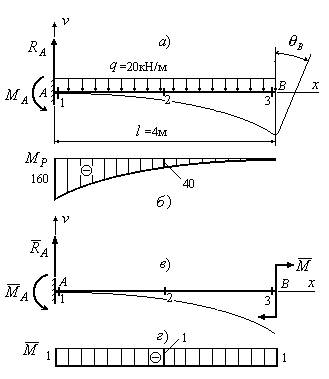
Рис.7
Решение.
1. Балка (рис.7,а) содержит один участок. Проставляем
характерные сечения и вычисляем в каждом
из них грузовые моменты. Значения моментов в характерных сечениях проставлены
на рис.7,б. Опорные реакции в данной
задаче можно не определять, изгибающие
моменты можно определить, производя вычисления справа.
2. Строим эпюру
грузовых изгибающих моментов MP.
3. Изображаем
единичное состояние балки, прикладывая в сечении В единичный момент 
(рис.7,в). Находим величины единичных
изгибающих моментов в характерных сечениях. Значения этих моментов проставлены
на рис.7,г.
4. Строим эпюру единичных изгибающих моментов
(рис.7,г).
5. Подставляя
найденные значения грузовых и единичных изгибающих моментов в формулу
Мора-Симпсона 
находим угол
поворота сечения В:
Определение
перемещений методом начальных параметров
В соответствии с этим методом сведение всех постоянных
интегрирования к двум – прогибу и углу поворота в начале координат – при любом
числе участков стало возможным при выполнении следующих условий:
1. Начало координат необходимо выбирать в крайней
левой (или правой) точке рассматриваемой балки и делать его общим для всех
участков балки.
2. Выражение для изгибающего момента M(x)
составлять, вычисляя моменты сил, расположенные по одну сторону от
рассматриваемого сечения со стороны начала координат.
3. При включении в уравнение внешнего сосредоточенного
момента M его следует умножать на множитель 
, равный единице, где 
- абсцисса точки, в которой приложен момент M.
4. В случае обрыва распределенной нагрузки ее
продлевают до рассматриваемого сечения, а для восстановления действительных
грузовых усилий вводят “компенсирующую” нагрузку обратного направления.
5. Интегрирование уравнений на всех участках следует
производить, не раскрывая скобок.
Рассмотрим балку (рис.8), нагруженную группой сил.
Начало координат поместим на левом конце балки в точке O и составим
уравнение изгибающих моментов для крайнего четвертого участка:
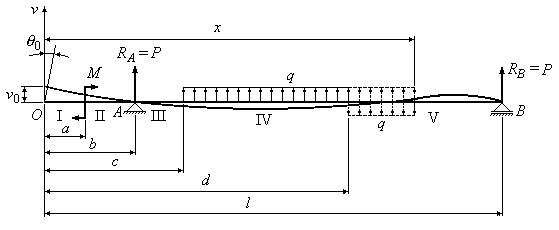
Рис.8
Исследуя рис.9 легко можно увидеть, что из уравнения (1)
изгибающий момент на IV участке получается путем вычеркивания членов,
появляющихся лишь на V участке:
Остальные члены, входящие в уравнение (2) остаются
такими же. Следует отметить, что коэффициенты 
входящие в уравнение изгибающих моментов, могут иметь
только положительные значения. Если окажется, что 
, то это означает, что соответствующая нагрузка
расположена справа от рассматриваемого сечения, если начало координат лежит
слева от сечения, или расположена слева от рассматриваемого
сечения, если начало координат лежит справа от сечения. В дальнейшем для вывода
окончательных выражений для перемещений будем считать, что начало координат расположено
на левом конце балки (рис.3).
Составим дифференциальное уравнение упругой линии для
участка V:
Интегрируя первый раз обе части равенства (3), не
раскрывая скобок, получим:
Интегрируем второй раз:
Дифференциальное уравнение на IV участке примет вид:
Проинтегрировав это уравнение дважды получим:
Вычислим теперь угол поворота сечения x=d, лежащего на стыке участков IV и V. Из условия плавного сопряжения участков получим:
Откуда: 
Принимая x=d и
подставляя в уравнения (18) и (15), из условия непрерывного сопряжения участков 
находим:
Выполнив аналогичные операции для остальных участков,
получим:
Определим геометрический смысл постоянных
интегрирования. Для этого найдем угол поворота и прогиб в начале координат при x=0. Это
сечение принадлежит первому участку. Составим уравнение углов поворота и прогибов
для первого участка, вычеркнув в уравнениях (14) и (15) слагаемые, учитывающие
нагрузки, приложенные на II – V участках:
Подставляя в эти уравнение x=0, получим:
Таким образом, произвольные постоянные C
и D равны соответственно углу
поворота и прогибу в начале координат 
,
которые принято называть геометрическими
начальными параметрами. Подставляя в уравнение (5)
вместо постоянных интегрирования C и D
равные им значения начальных параметров, получаем:
Если на балку действует несколько моментов и сил, а также несколько участков распределенной нагрузки,
уравнение для прогибов можно составить в следующем виде:
Уравнение (15) обычно называют универсальным уравнением упругой линии.
Продифференцировав уравнение (15), получим уравнение
углов поворота сечения:
Здесь и в формуле (25) приняты следующие обозначения: A
- тип внешнего силового
фактора (M,P,q); n - показатель степени, получаемый при интегрировании
дифференциального уравнения упругой линии; a - координата сечения, в котором приложена сосредоточенная
сила или момент, или координата сечения, к котором начинается действие
распределенной нагрузки. Соответствие величины показателя степени 
типу внешнего фактора
приведено в таблице 5.
Таблица
5
|
Тип внешней нагрузки A |
Показатель степени n |
|
Внешний момент M |
2 |
|
Сосредоточенная сила P |
3 |
|
Интенсивность
распределенной нагрузки q |
4 |
Знаки слагаемых в уравнения (15) и (16) определяются знаком изгибающего
момента, который вызывается соответствующим силовым фактором.
Характерной особенностью метода начальных параметров
является то, что для определения перемещения нет необходимости составлять и
интегрировать дифференциальное изогнутой оси балки. Достаточно составить универсальное
уравнение упругой линии (15), из условий на опорах найти начальные параметры и
снова воспользоваться универсальным уравнением, чтобы найти прогиб в
рассматриваемом сечении.
Пример 4
Определить прогиб посредине пролета балки, приведенной
на рис.9, и угол поворота сечения С на левом конце
балки с помощью метода начальных параметров. Материал балки - сталь с модулем упругости 
МПа. Балка
представляет собой двутавр № 20 с моментом инерции 
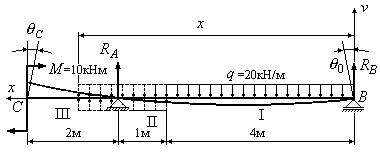
Рис.9
Решение.
1. Определим опорные реакции. Для этого составим два уравнения
равновесия:
Откуда
Откуда
2. Помещаем начало координат на правом конце балки в
точку В, ось
прогибов v направляем вверх, ось x - влево. Чем в данном случае определен выбор начала
координат? Если выбрать начало координат на левом конце балки в сечении С, то
предварительно придется искать оба начальных параметра, так как ни угол поворота
сечения С, ни прогиб в этом сечении
заранее неизвестны. Для их определения потребуется составлять систему из двух
уравнений и решать ее относительно двух неизвестных начальных параметров. Если
же выбрать начало координат на правом конце балки в сечении В, то находить придется лишь один
начальный параметр – угол поворота сечения В 
. Второй начальный параметр – прогиб в сечении В 
– искать не
нужно, так как он равен нулю из граничного условия на опоре В.
3. Разбиваем балку на участки (рис.9) и записываем
универсальное уравнение упругой линии (15) для последнего участка:
4. Из уравнения (а) определяем начальный параметр из условия, что
прогиб в сечении А
при x=5 м равен нулю:
Откуда
5. Определяем прогиб посредине пролета балки при x=2,5 м. Так
как сечение посредине балки принадлежит первому участку, вычеркиваем из
универсального уравнения все члены, принадлежащие второму и третьему участкам.
Получим:
Подставляем численные значения модуля упругости и
момента инерции в полученное выражение. Получаем:
Знак “-” означает, что направление прогиба не совпадает с направлением оси
прогибов v.
6. Определяем угол поворота сечения С. Для этого воспользуемся
выражением (16). Так как сечение С принадлежит
третьему участку, составим уравнение для угла поворота для этого участка:
Подставляем координату сечения С (x=7 м) в
уравнение (б). Получим:
После подстановки численного значения жесткости поперечного сечения
балки в выражение для угла поворота, имеем:
Знак “+” у угла поворота означает, что поворот сечения
происходит по часовой стрелке. Это верно, так как решение задача выполнялось в
левой системе координат.
Пример 5
Определить номер прокатного профиля из условия
жесткости для балки, изображенной на рис.10 с помощью метода начальных
параметров. Материал балки – сталь с модулем упругости МПа. Допускаемый
прогиб составляет 
, где l=4 м –
пролет балки. Допускаемое напряжения для материала
балки [σ]=160 МПа.
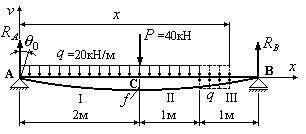
Рис.10
Решение.
1. Определяем опорные реакции. Для этого составим два
уравнения равновесия:
Решая уравнения (а) и (б) относительно реакций,
находим: 
кН, 
кН.
2. Начало координат выбираем на левом конце балки. Ось
прогибов v направляем вверх, ось 
- вправо.
3. Определяем начальные параметры. Из двух начальных
параметров прогиб в начале координат 
; угол поворота найдем,
приравняв нулю прогиб на опоре В при x=4 м:
Решая уравнение (в) относительно , находим:
4. Определяем прогиб посредине балки
в сечении С. Будем считать,
что максимальный прогиб f (стрела
прогиба) возникает посредине пролета. Сечение С принадлежит первому участку,
поэтому из универсального уравнения упругой линии, вычеркивая члены, не
принадлежащие первому участку, получим при x=2 м:
5. Находим требуемый момент инерции сечения из условия
жесткости:
Допускаемый прогиб 
Подставляя в
условие жесткости (д) модуль стрелы прогиба и величину допускаемого прогиба,
получаем:
Откуда
Из сортамента прокатной стали подбираем номер
прокатного двутавра. Таким двутавром
оказался двутавр
№ 40 с моментом инерции 
см4 и моментом сопротивления 
см3.
6. Выполняем проверку выбранного
двутавра на прочность. Максимальный изгибающий
момент, действующий в балке, равен 
кНм (расчет максимального изгибающего момента здесь не
приводится). Подставляем в условие прочности значения максимального изгибающего
момента 
и осевого
момента сопротивления 
и находим
максимальное напряжение, действующее в балке:
Этот напряжение оказалось меньше допускаемого [σ]=160 МПа.
Таким образом, окончательно принимаем двутавр №40, удовлетворяющий как
условию прочности, так и условию жесткости.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин Теория машин и механизмов
