Главная

Задача 1. Определение внутренних усилий и перемещений двухопорных балок, работающих на поперечный изгиб

Для балки, изображенной на рис.1, требуется:

1. простроить эпюры моментов и поперечных сил;

2. указать положение опасного сечения (сечение балки с максимальным моментом);

3. определить прогиб ∆y балки в точке приложения силы P.

Данные взять из табл.1.

Таблица 1

Номер cтроки	Схема по рис.1	P, кН	m, кНм	q, кН/м
01	1	3	20	12
02	2	6	20	28
03	3	1	20	12
04	4	3	10	16
05	5	6	10	24
06	6	9	24	20
07	7	8	30	8
08	8	21	30	32
09	9	7	40	36
10	10	18	40	36
11	11	7	10	24
12	12	12	18	2
13	13	11	20	12
14	14	6	20	12
15	15	13	10	24
16	16	21	10	24
17	17	16	10	24
18	18	5	20	12
19	19	21	40	4
20	20	17	20	12
21	21	16	10	16
22	22	6	40	4
23	23	14	30	32
24	24	2	30	32
25	25	2	40	4
26	26	20	21	20
27	27	16	30	8
28	28	18	20	12
29	29	14	22	20
30	30	10	30	8
31	31	4	20	12
32	32	16	30	8
33	33	15	10	16
34	34	4	10	16
35	35	12	40	36
36	36	9	40	4
	б	в	а	г

1 схема 2 схема

3 схема 4 схема

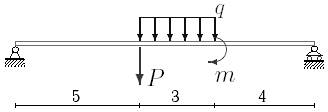
5 схема 6 схема

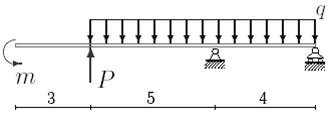
7 схема 8 схема

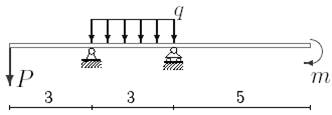
9 схема 10 схема

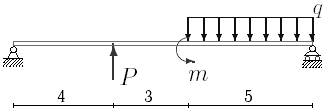
11 схема 12 схема

13 схема 14 схема

15 схема 16 схема

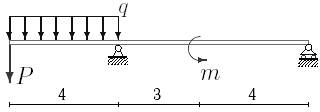
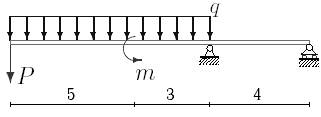
17 схема 18 схема

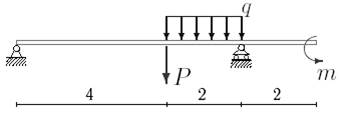
19 схема 20 схема

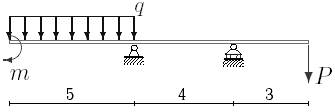
21 схема 22 схема

23 схема 24 схема

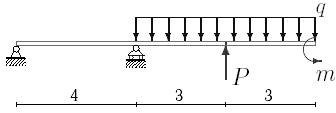
25 схема 26 схема

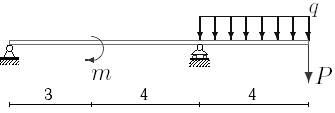
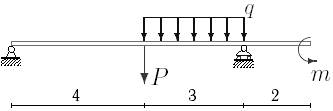
27 схема 28 схема

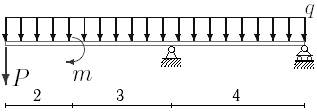
29 схема 30 схема

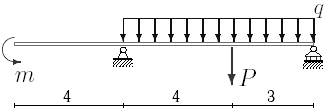
31 схема 32 схема

33 схема 34 схема

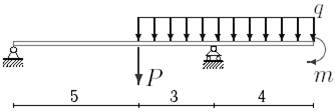
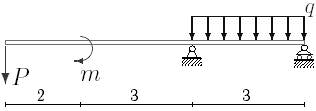
35 схема 36 схема

Рис.1

Задача 2. Определение внутренних усилий в балках при плоском поперечном изгибе

Исходные данные к задачам выбираются по табл. 2 и схемам на рис. 2.

1. Нарисуйте схему балки в масштабе в соответствии со своими данными. Отрицательные нагрузки покажите действующими в сторону, противоположную указанной на рисунке. На рисунке поставьте размеры балки и значения нагрузки в численном виде.

2. Определите опорные реакции.

3. Составьте выражения для поперечной силы Q и изгибающего момента М на каждом участке балки и вычислите значения Q и М на границах участков.

4. Постройте эпюры Q и М и проанализируйте результаты в соответствии с дифференциальными зависимостями между Q, M и q.

Таблица 2

Номер строки	l, м	q, кН/м	№ схемы на рис. 9	F0, кН	F1, кН	М0, кНм	М1, кНм
01	1	10	1	0	10	0	0
02	2	-10	2	0	0	20	0
03	3	20	3	0	0	60	0
04	2	-20	1	0	0	0	-60
05	1	30	2	-20	0	0	0
06	1	-30	3	0	0	0	-40
07	2	5	1	0	-20	0	0
08	3	-5	2	0	0	-40	0
09	4	40	3	0	0	-40	0
10	2	-40	1	0	0	0	40
	г	а	б	в	г	а	б

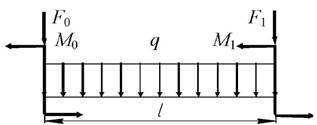
1 схема

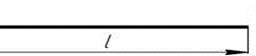
2 схема

3 схема

Рис. 2

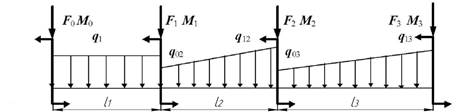
Задача 3. Определение внутренних усилий в балках при плоском поперечном изгибе

Исходные данные к задачам выбираются по табл. 3 и схемам на рис. 3.

1. Нарисуйте схему балки в масштабе в соответствии со своими данными. Отрицательные нагрузки покажите действующими в сторону, противоположную указанной на рисунке. На рисунке поставьте размеры балки и значения нагрузки в численном виде.

2. Определите опорные реакции.

3. Составьте выражения для поперечной силы Q и изгибающего момента М на каждом участке балки и вычислите значения Q и М на границах участков.

4. Постройте эпюры Q и М и проанализируйте результаты в соответствии с дифференциальными зависимостями между Q, M и q.

Таблица 3

Номер строки	Схема по рис. 3	F0, кH	F1, кH	F2, кH	l1, м	M0, кHм	M1, кHм	M2, кHм	l2, м	Интенсивность распределенной нагрузки, кH/м
										Вариант 1		Вариант 2
										q01=q11=q1	q02=q12=q2	q01	q11	q02	q12
01	1	0	20	0	2	10	0	0	1	40	0	40	0	-20	-20
02	2	0	0	30	3	0	-20	0	2	0	-40	10	10	0	-40
03	3	10	0	0	1	0	0	30	1	30	0	0	30	10	10
04	1	0	-20	0	4	-40	0	0	2	0	-30	-20	-20	30	0
05	2	0	0	-30	5	0	50	0	1	20	0	20	0	-10	-10
06	3	-10	0	0	1	0	0	-60	2	0	-20	20	20	0	-20
07	1	0	40	0	6	-50	0	0	1	10	0	0	-40	30	30
08	2	0	0	50	7	0	40	0	2	0	-10	-10	-10	-10	0
09	3	-20	0	0	1	0	0	-30	1	5	-5	0	5	-5	-5
10	1	0	-40	0	5	20	0	0	2	-10	10	-30	-30	0	30
	а	в	б	г	а	в	бг	а	в	б	г	а	в	б	г

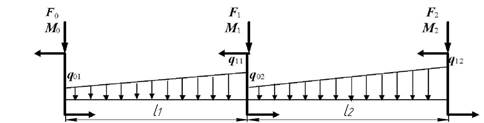
1 схема

2 схема

3 схема

Рис. 3

Задача 4. Определение внутренних усилий в балках при плоском поперечном изгибе

Исходные данные к задачам выбираются по табл. 4 и схемам на рис. 4.

1.Нарисуйте схему балки в масштабе в соответствии со своими данными. Отрицательные нагрузки покажите действующими в сторону, противоположную указанной на рисунке. На рисунке поставьте размеры балки и значения нагрузки в численном виде.

2.Определите опорные реакции.

3.Составьте выражения для поперечной силы Q и изгибающего момента М на каждом участке балки и вычислите значения Q и М на границах участков.

4.Постройте эпюры Q и М и проанализируйте результаты в соответствии с дифференциальными зависимостями между Q, M и q.

Таблица 4

Номер строки	F1, кH	F2, кH	M1, кHм	M2, кHм	q1, кH/м	Схема по рис. 4	F0, кH	F3, кH	M0, кHм	M3, кHм	l1, м	l2, м	l3, м	Интенсивность распределенной нагрузки, кH/м
														Вариант 1		Вариант 2
														q02=q12=q2	q03=q13=q3	q02	q12	q03	q13
01	20	0	0	0	5	1	0	10	0	0	1	1	1	0	30	0	0	0	30
02	0	0	20	0	-5	2	-30	0	0	0	0,5	0,5	0,5	10	0	10	0	0	0
03	-40	0	0	0	10	1	0	0	0	30	1	1	1	0	-30	0	0	-30	0
04	0	0	-60	0	-10	2	0	0	-50	0	1	0,5	0,5	-10	0	0	-10	0	0
05	0	0	0	-40	20	1	0	-30	0	0	2	1	1	0	20	0	0	20	0
06	0	-60	0	0	-20	2	50	0	0	0	0,5	0,5	0,5	20	0	-20	0	0	0
07	0	60	0	0	-5	1	0	0	0	-50	1	1	1	0	-20	0	0	0	-20
08	0	0	40	0	5	2	0	0	30	0	1	0,5	0,5	-20	0	0	-20	0	0
09	0	0	0	-60	-10	1	0	-40	0	0	2	1	1	0	10	0	0	0	10
10	0	0	-20	0	10	2	10	0	0	0	1	0,5	0,5	30	0	30	0	0	0
	а	г	в	б	а	г	в	б	а	г	в	б	а	г	в	б	а	г	в

1 схема

2 схема

Рис. 4

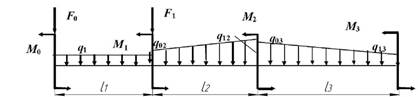
Задача 5. Определение внутренних усилий в балках при плоском поперечном изгибе

Исходные данные к задачам выбираются по табл. 5 и схемам на рис. 5.

1. Нарисуйте схему балки в масштабе в соответствии со своими данными. Отрицательные нагрузки покажите действующими в сторону, противоположную указанной на рисунке. На рисунке поставьте размеры балки и значения нагрузки в численном виде.

2. Определите опорные реакции.

3. Составьте выражения для поперечной силы Q и изгибающего момента М на каждом участке балки и вычислите значения Q и М на границах участков.

4. Постройте эпюры Q и М и проанализируйте результаты в соответствии с дифференциальными зависимостями между Q, M и q.

Таблица 5

Номер строки	l2, м	q1, кH/м	M0, кHм	Схема по рис. 5	F0, кH	F1, кH	М2, кНм	M1, кHм	l1, м	l3, м	M3, кHм	Интенсивность распределенной нагрузки, кH/м
												Вариант 1		Вариант 2
												q02=q12=q2	q03=q13=q3	q02	q12	q03	q13
01	4	0	60	1	0	10	0	0	3	4	0	0	10	0	0	0	10
02	5	20	0	2	0	0	0	-20	6	1	40	10	0	10	0	0	0
03	6	0	-60	3	10	0	0	0	1	3	0	0	-10	0	0	-10	0
04	7	-20	0	4	0	0	0	20	2	1	-50	-10	0	0	-10	0	0
05	8	0	-50	1	0	0	-20	0	5	2	0	0	-20	0	0	-20	0
06	7	-5	0	2	0	0	30	0	4	1	-30	20	0	0	20	0	0
07	6	0	50	3	0	0	40	0	2	6	0	0	20	0	0	0	20
08	5	10	0	4	-10	0	0	0	1	2	-40	-20	0	-20	0	0	0
09	4	0	-40	1	0	0	0	-40	4	4	0	0	-30	0	0	0	-30
10	3	-10	0	2	0	-20	0	0	3	2	50	30	0	30	0	0	0
	в	г	а	б	в	г	а	б	в	г	а	б	в	г	а	б	в

1 схема

2 схема

3 схема

4 схема

Рис. 5

Задача 6. Определение внутренних усилий в балках при плоском поперечном изгибе

Для трех заданных расчетных схем требуется:

1. разбить балку на участки, обозначив длину каждого из них;

2. при необходимости определить реакции опор;

3. используя уравнения равновесия, записать аналитические выражения для внутренних усилий Q и М в произвольном сечении каждого из участков;

4. построить эпюры внутренних усилий в выбранном масштабе;

5. проверить правильность построения эпюр, используя дифференциальные зависимости между М, Q и q.

Исходные данные к задачам выбираются по табл. 6 и схемам на рис. 6.

Таблица 6

Номер cтроки	Схема по рис.6	a, м	F, кН	М, кНм	q, кН/м
01	1	4,0	10	30	3
02	2	3,0	14	12	5
03	3	2,0	12	24	4
04	4	2,5	16	18	8
05	5	3,5	20	20	10
06	6	4,0	18	22	7
07	7	3,0	10	16	6
08	8	2,0	14	26	9
09	9	3,5	12	28	3
10	10	4,0	16	14	5
11	11	2,0	20	22	4
12	12	2,5	18	30	8
13	13	3,5	10	24	10
14	14	4,0	14	16	7
15	15	2,5	12	20	6
16	16	2,0	16	28	9
17	17	3,5	20	14	3
18	18	3,0	18	18	5
19	19	4,0	10	30	4
20	20	3,0	14	12	6
21	21	2,0	12	24	9
22	22	2,5	16	30	3
23	23	3,5	20	12	5
24	24	4,0	18	24	4
25	25	3,0	10	18	8
26	26	2,0	14	20	10
27	27	3,5	12	22	7
28	28	4,0	16	16	6
29	29	2,0	20	26	9
30	30	2,5	18	28	3
31	31	3,5	10	14	5
32	32	4,0	14	22	4
33	33	2,5	12	30	6
34	34	2,0	16	24	9
35	35	3,5	20	16	3
36	36	3,0	18	20	5
	б	а	в	а	г

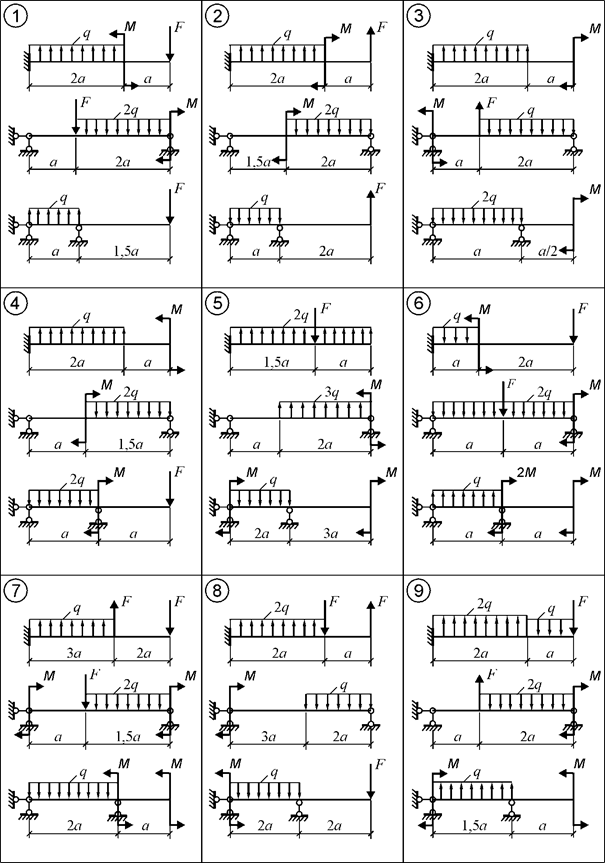
Рис. 6.

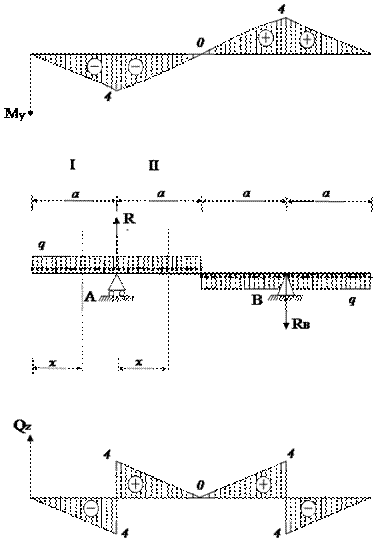
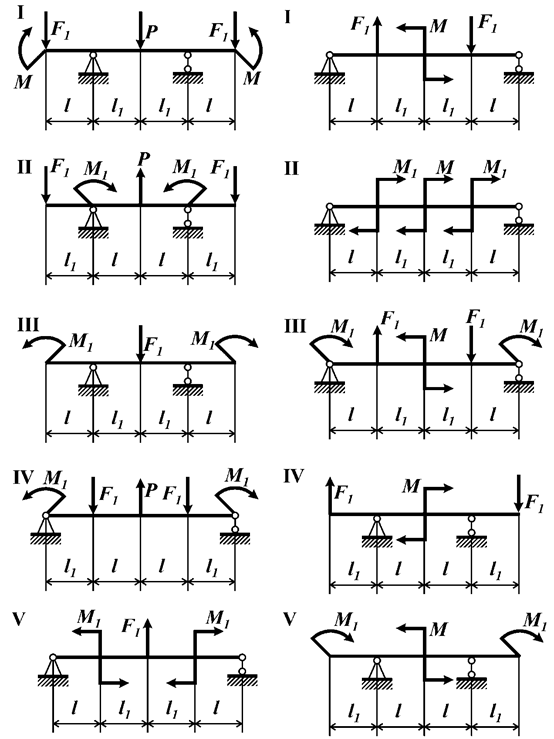
Задача 7. Определение внутренних усилий в симметричных балках при плоском поперечном изгибе

На симметричную балку (рис. 7) действуют симметричная (а) и кососимметричная (б) нагрузки.

Требуется построить эпюры поперечной силы и изгибающего момента.

Исходные данные к задачам выбираются по табл. 7 и схемам на рис. 7.

Таблица 7

Номер cтроки	Схема по рис.7	l1/l	M/Pl	M1/Pl	F1/P
01	I (рис.7,а)	2	2	3	2
02	II (рис.7,а)	1	3	2	1
03	III (рис.7,а)	2	2	1	3
04	IV (рис.7,а)	1	1	2	2
05	V (рис.7,а)	1	3	1	1
06	I (рис.7,б)	2	1	3	2
07	II (рис.7,б)	2	2	2	2
08	III (рис.7,б)	1	3	1	1
09	IV (рис.7,б)	1	1	2	1
10	V (рис.7,б)	2	1	2	2
11	I (рис.7,а)	2	2	3	2
12	II (рис.7,а)	1	3	2	1
13	III (рис.7,а)	2	2	1	3
14	IV (рис.7,а)	1	1	2	2
15	V (рис.7,а)	1	3	1	1
16	I (рис.7,б)	2	1	3	2
17	II (рис.7,б)	2	2	2	2
18	III (рис.7,б)	1	3	1	1
19	IV (рис.7,б)	1	1	2	1
20	V (рис.7,б)	2	1	2	2
21	I (рис.7,а)	2	2	3	2
22	II (рис.7,а)	1	3	2	1
23	III (рис.7,а)	2	2	1	3
24	IV (рис.7,а)	1	1	2	2
25	V (рис.7,а)	1	3	1	1
26	I (рис.7,б)	2	1	3	2
27	II (рис.7,б)	2	2	2	2
28	III (рис.7,б)	1	3	1	1
29	IV (рис.7,б)	1	1	2	1
30	V (рис.7,б)	2	1	2	2
31	I (рис.7,а)	2	2	3	2
32	II (рис.7,а)	1	3	2	1
33	III (рис.7,а)	2	2	1	3
34	IV (рис.7,а)	1	1	2	2
35	V (рис.7,а)	1	3	1	1
36	I (рис.7,б)	2	1	3	2
	б	а	в	а	г

а) б)

Рис.7

Задача 8. Определение внутренних усилий в консольных балках при плоском поперечном изгибе

Для консольной балки (рис. 8) построить эпюры поперечной силы и изгибающего момента.

Исходные данные к задачам выбираются по табл. 8 и схемам на рис. 8.

Таблица 8

Номер cтроки	Схема по рис.8	l1/l	l2/l	F/ql	M/ql^2	q1/q	q2/q
01	I	1,0	1,0	1,0	–1,0	2,0	3,0
02	II	2,0	1,0	–1,0	1,0	–1,0	–2,0
03	III	1,5	2,0	1,0	–2,0	2,0	1,0
04	IV	1,0	1,0	2,0	–2,0	–3,0	–2,0
05	V	2,0	1,0	–2,0	1,0	1,0	2,0
06	VI	1,0	2,0	2,0	–1,0	–3,0	–1,0
07	VII	1,5	1,0	–1,0	2,0	2,0	2,0
08	VIII	2,0	1,0	–2,0	1,0	–1,0	–2,0
09	IX	1,0	2,0	–1,0	3,0	2,0	1,0
10	X	2,0	1,0	–2,0	1,0	1,0	3,0
11	I	1,0	1,0	1,0	–1,0	2,0	3,0
12	II	2,0	1,0	–1,0	1,0	–1,0	–2,0
13	III	1,5	2,0	1,0	–2,0	2,0	1,0
14	IV	1,0	1,0	2,0	–2,0	–3,0	–2,0
15	V	2,0	1,0	–2,0	1,0	1,0	2,0
16	VI	1,0	2,0	2,0	–1,0	–3,0	–1,0
17	VII	1,5	1,0	–1,0	2,0	2,0	2,0
18	VIII	2,0	1,0	–2,0	1,0	–1,0	–2,0
19	IX	1,0	2,0	–1,0	3,0	2,0	1,0
20	X	2,0	1,0	–2,0	1,0	1,0	3,0
21	I	1,0	1,0	1,0	–1,0	2,0	3,0
22	II	2,0	1,0	–1,0	1,0	–1,0	–2,0
23	III	1,5	2,0	1,0	–2,0	2,0	1,0
24	IV	1,0	1,0	2,0	–2,0	–3,0	–2,0
25	V	2,0	1,0	–2,0	1,0	1,0	2,0
26	VI	1,0	2,0	2,0	–1,0	–3,0	–1,0
27	VII	1,5	1,0	–1,0	2,0	2,0	2,0
28	VIII	2,0	1,0	–2,0	1,0	–1,0	–2,0
29	IX	1,0	2,0	–1,0	3,0	2,0	1,0
30	X	2,0	1,0	–2,0	1,0	1,0	3,0
31	I	1,0	1,0	1,0	–1,0	2,0	3,0
32	II	2,0	1,0	–1,0	1,0	–1,0	–2,0
33	III	1,5	2,0	1,0	–2,0	2,0	1,0
34	IV	1,0	1,0	2,0	–2,0	–3,0	–2,0
35	V	2,0	1,0	–2,0	1,0	1,0	2,0
36	VI	1,0	2,0	2,0	–1,0	–3,0	–1,0
	г	а	в	а	б	г	в

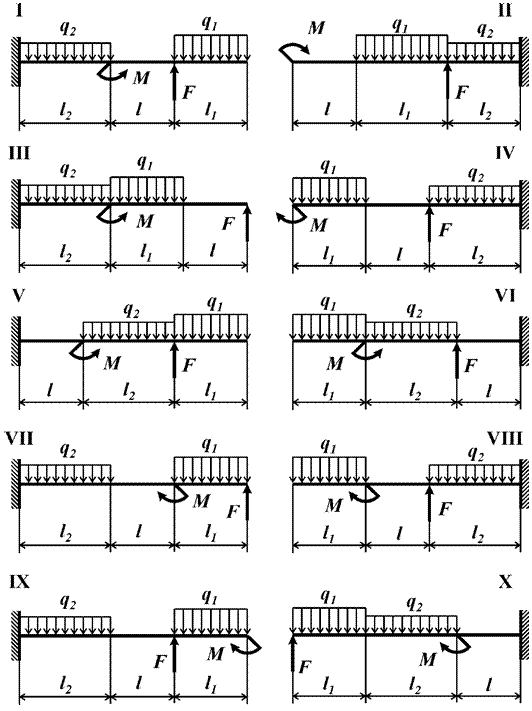
Рис.8

Задача 9. Определение внутренних усилий в шарнирно-опертых балках при плоском поперечном изгибе

Для шарнирно-опертой балки, изображенной на рис. 9, построить эпюры поперечной силы и изгибающего момента.

Исходные данные к задачам выбираются по табл. 9 и схемам на рис. 9.

Таблица 9

Номер cтроки	Схема по рис.9	l1/l	l2/l	F/ql	M/ql^2	q1/q
01	I	2	1	1	2,0	1
02	II	1	2	1	1,5	2
03	III	1	1	1	1,0	1
04	IV	2	1	2	1,0	2
05	V	1	2	2	1,0	1
06	VI	2	2	2	1,0	2
07	VII	1	1	1	2,0	1
08	VIII	1	2	1	1,0	2
09	IX	2	1	1	1,0	1
10	X	2	1	2	1,0	2
11	I	2	1	1	2,0	1
12	II	1	2	1	1,5	2
13	III	1	1	1	1,0	1
14	IV	2	1	2	1,0	2
15	V	1	2	2	1,0	1
16	VI	2	2	2	1,0	2
17	VII	1	1	1	2,0	1
18	VIII	1	2	1	1,0	2
19	IX	2	1	1	1,0	1
20	X	2	1	2	1,0	2
21	I	2	1	1	2,0	1
22	II	1	2	1	1,5	2
23	III	1	1	1	1,0	1
24	IV	2	1	2	1,0	2
25	V	1	2	2	1,0	1
26	VI	2	2	2	1,0	2
27	VII	1	1	1	2,0	1
28	VIII	1	2	1	1,0	2
29	IX	2	1	1	1,0	1
30	X	2	1	2	1,0	2
31	I	2	1	1	2,0	1
32	II	1	2	1	1,5	2
33	III	1	1	1	1,0	1
34	IV	2	1	2	1,0	2
35	V	1	2	2	1,0	1
36	VI	2	2	2	1,0	2
	в	а	г	а	в	г

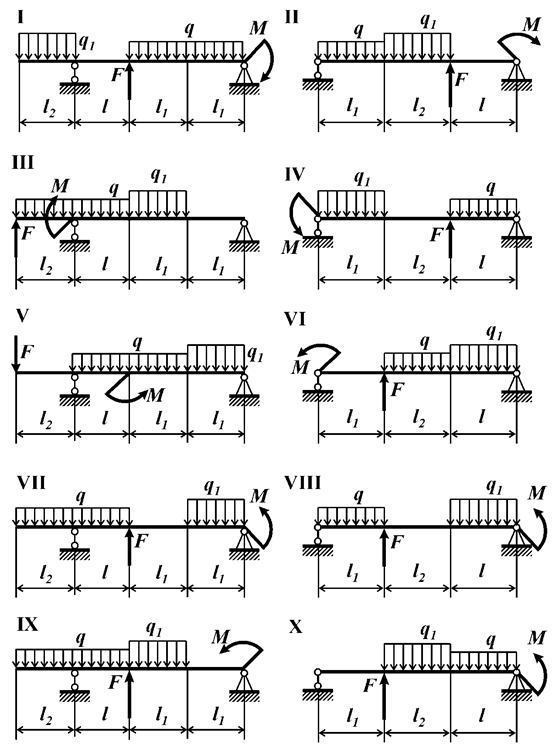
Рис.9

Задача 10. Определение внутренних усилий по эпюре изгибающего момента в балках при плоском поперечном изгибе

Известна эпюра изгибающего момента для балки (рис. 10).

Требуется построить эпюру поперечной силы и восстановить действующую на балку нагрузку.

Исходные данные к задачам выбираются по табл. 10 и схемам на рис. 10.

Таблица 10

Номер cтроки	Схема по рис.10	l1/l	l2/l	M1/ql^2	M2/ql^2	M3/ql^2	M4/ql^2
01	I	1,5	3,0	2	6	1	1
02	II	1,0	1,5	4	8	2	3
03	III	2,0	1,0	–2	0	1	5
04	IV	2,0	2,0	–8	4	2	–3
05	V	3,0	2,0	–2	6	1	1
06	VI	2,5	3,0	–4	8	2	–3
07	VII	1,0	2,5	–6	4	1	5
08	VIII	3,0	1,0	–8	–2	2	–1
09	IX	2,0	3,0	2	4	1	3
10	X	3,0	2,0	–2	2	2	1
11	I	1,5	3,0	2	6	1	1
12	II	1,0	1,5	4	8	2	3
13	III	2,0	1,0	–2	0	1	5
14	IV	2,0	2,0	–8	4	2	–3
15	V	3,0	2,0	–2	6	1	1
16	VI	2,5	3,0	–4	8	2	–3
17	VII	1,0	2,5	–6	4	1	5
18	VIII	3,0	1,0	–8	–2	2	–1
19	IX	2,0	3,0	2	4	1	3
20	X	3,0	2,0	–2	2	2	1
21	I	1,5	3,0	2	6	1	1
22	II	1,0	1,5	4	8	2	3
23	III	2,0	1,0	–2	0	1	5
24	IV	2,0	2,0	–8	4	2	–3
25	V	3,0	2,0	–2	6	1	1
26	VI	2,5	3,0	–4	8	2	–3
27	VII	1,0	2,5	–6	4	1	5
28	VIII	3,0	1,0	–8	–2	2	–1
29	IX	2,0	3,0	2	4	1	3
30	X	3,0	2,0	–2	2	2	1
31	I	1,5	3,0	2	6	1	1
32	II	1,0	1,5	4	8	2	3
33	III	2,0	1,0	–2	0	1	5
34	IV	2,0	2,0	–8	4	2	–3
35	V	3,0	2,0	–2	6	1	1
36	VI	2,5	3,0	–4	8	2	–3
	б	а	г	а	в	г	б

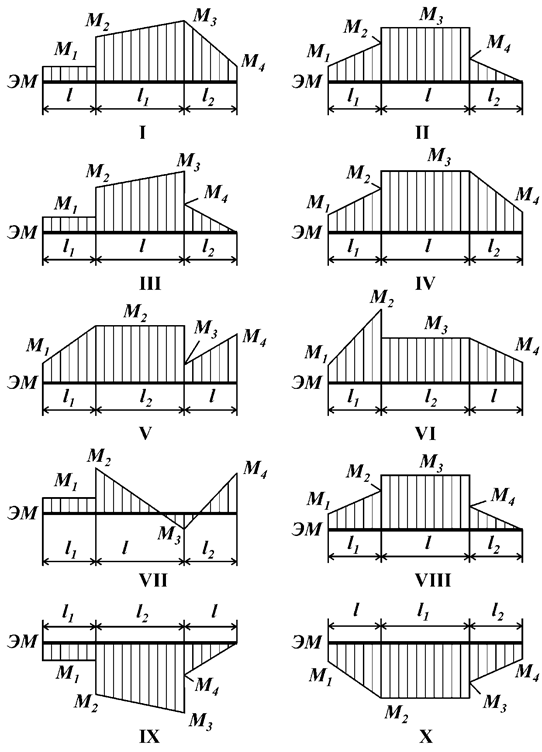
Рис.10

Примеры выполнения задач

Пример 1.

Балка длиной l защемлена левым концом и нагружена сосредоточенной силой F и моментом m=2Fl (рис. 11).

Требуется построить эпюры поперечных сил Q и изгибающих моментов М_из.

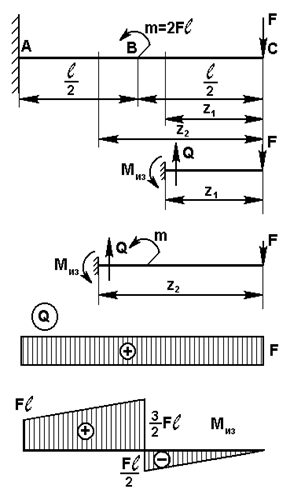
Рис.11

Решение.

В нашем случае на балку с правой стороны не наложено связей. Поэтому чтобы не определять опорные реакции, целесообразно рассматривать равновесие правой отсеченной части балка. Заданная балка имеет два участка нагружения. Границы участков-сечения, в которых приложены внешние силы:

1 участок – СВ,

2 участок – ВА.

Проводим произвольное сечение на участке 1 и рассмотрим равновесие правой отсеченной части длиною Z₁.

0≤Z₁≤l/2 (рис.11).

Из условия равновесия следует:

Q=F; М_из= -F∙Z₁ (1)

Поперечная сила положительна, т.к. внешняя сила F стремится повернуть отсеченную часть по часовой стрелке. Момент изгибающий считается отрицательным, т.к. он изгибает рассматриваемую часть балки выпуклостью вверх.

При составлении уравнений равновесия мысленно закрепляем место сечения, как это показано на рис.11; из уравнений (1) следует, что поперечная сила на I участке от Z₁ не зависит и является постоянной величиной. Положительную силу Q=F откладываем в масштабе вверх от осевой линии балки (рис.11), перпендикулярно к ней.

Изгибающий момент зависит от Z₁.

При Z₁=0 М_из=0

при Z₁=l/2 М_из= -Fl/2

Полученное значение (-Fl/2) откладываем вниз, т.е. эпюра М_из строится на сжатом волокне (рис.11).

Переходим ко второму участку (l/2≤Z₂≤l). Рассекаем участок II на произвольном расстоянии Z₂ от свободного правого торца балки (рис.11) и рассматриваем равновесие отсеченной части длиною Z₂ (рис.11). Изменение поперечной силы и изгибающего момента на основе условий равновесия можно выразить следующими уравнениями:

Q=F M_из= -FZ₂+2Fl

Величина и знак поперечной силы не изменились.

Эпюра поперечной силы представлена на (рис.11).

Величина изгибающего момента зависит от Z₂.

При Z₂= l/2 M_из=3Fl/2, при Z₂=l.

Изгибающий момент получился положительным, как в начале участка II, так и в конце его. На участке II балка изгибается выпуклостью вниз.

Откладываем в масштабе величины моментов вверх по осевой линии балки (т.е. эпюра строится на сжатом волокне). Эпюра М_из показана на (рис.11). Наибольший изгибающий момент возникает в сечении, где приложен внешний момент m и по абсолютной величине равен 3Fl/2.

Заметим, что на длине балки, где Q сохраняет постоянную величину, изгибающий момент М_из меняется линейно и представляется на эпюре наклонными прямыми. Из эпюр Q и М_из видно, что в сечении, где приложена внешняя поперечная сила, эпюра Q имеет скачок на величину этой силы, а эпюра М_из – излом. В сечении, где приложен внешний изгибающий момент, эпюра М_из имеет скачок на величину этого момента. На эпюре Q это не отражается. Из эпюры М_из видим, что max М_из=3Fl/2, следовательно, опасное сечение предельно приближено с левой стороны к т.В (рис.11).

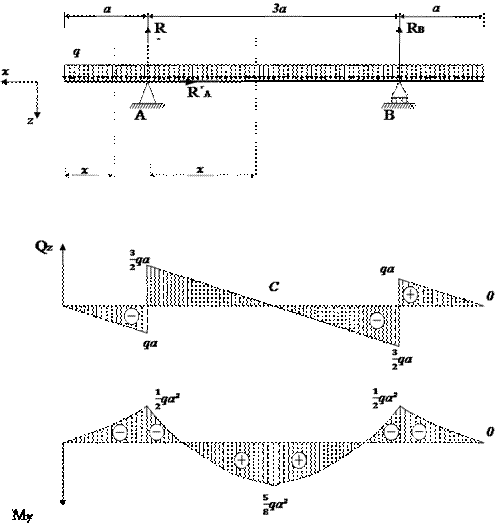
Пример 2.

Для балки изображенной на рис.12,а, построить эпюры поперечных сил и изгибающих моментов. На длине a балка нагружена равномерно распределенной нагрузкой с интенсивностью q (кН/см).

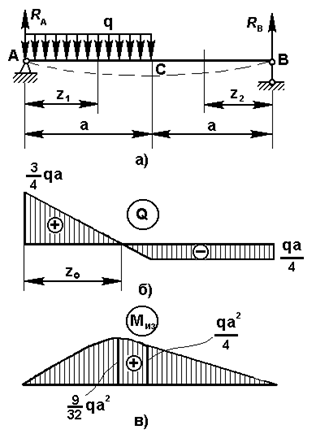
Рис.12

Решение.

На опоре А (шарнир неподвижный) возникнет вертикальная реакция R_a (горизонтальная реакция равна нулю), а на опоре В (подвижный шарнир) возникает вертикальная реакция R_в.

Определим вертикальные реакции опор, составляя уравнение моментов относительно опор А и В.

ΣM_A=0 qa²/2-R_B∙2a=0 R_B=qa/4

ΣM_B=0 R_A∙2a-qa∙3a/2=0 R_A=3qa/4

Проверим правильность определения реакции:

ΣY=0 R_A+R_B-qa=3qa/4+qa/4-qa=0

т.е. опорные реакции определены правильно.

Заданная балка имеет два участка нагружения:

I участок – АС.

II участок – СВ.

На первом участке 0≤Z₁≤a, в текущем сечении Z₁ (рис.12,а) из условия равновесия отсеченной части имеем

Q=R_A-qZ₁=3qa/4-qZ₁

При Z₁=0 Q=3qa/4.

При Z₁=a Q=-qa/4/

Эпюра Q имеет вид наклонной прямой, пересекающей ось Z (рис.12, б).

Уравнение изгибающих моментов на 1 участке балки:

Момент от реакции R_a изгибает балку на участке 1, выпуклостью вниз, поэтому изгибающий момент от реакции R_a вводится в уравнение со знаком плюс. Нагрузка qZ₁ изгибает балку выпуклостью вверх, поэтому момент от нее вводится в уравнение со знаком минус. Изгибающий момент изменяется по закону квадратной параболы.

Поэтому, необходимо выяснить имеет ли место экстремум. Между поперечной силой Q и изгибающим моментом существует дифференциальная зависимость на анализе которой мы остановимся далее

Как известно, функция имеет экстремум там, где производная равна нулю. Следовательно, чтобы определить при каком значении Z₁, изгибающий момент будет экстремальным, надо уравнение поперечной силы приравнять к нулю.

Q=3qa/4-qZ₁=0 Z₁=Z₀=3a/4

Так как поперечная сила меняет в данном сечении знак с плюса на минус, то изгибающий момент в этом сечении будет максимальным. Если Q меняет знак с минуса на плюс, то изгибающий момент в этом сечении будет минимальным.

Итак, изгибающий момент при Z₁=Z₀=3a/4, является максимальным.

Поэтому, строим параболу по трем точкам (рис.12,в)

При Z₁=0 М_из=0

При Z₁=Z₀=3a/4

При Z₁=a

Рассекаем второй участок на расстоянии Z₂ от опоры В (рис.12,а).

Из условия равновесия правой отсеченной части балки имеем:

При 0≤Z₂≤a величина Q=const,

изгибающий момент будет:

при Z₂=0 M_из=0,

при Z₂=a , т.е. M_ИЗ меняется по линейному закону.

Эпюра поперечных сил представлена на рис.12,б изгибающих моментов на рис.12,в. Примерный вид изогнутой оси балки предоставлен пунктиром на рис.12,а.

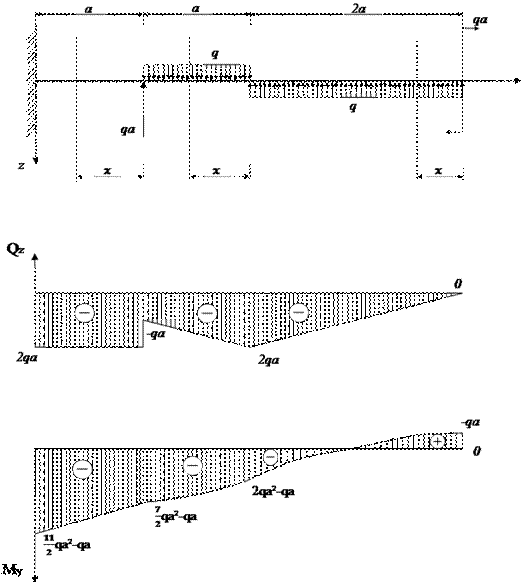
Пример 3.

Балка на двух опорах, имеющая пролет равный 2a и левую консоль длиною a, нагружена так, как показано на рис.13,а, где q (Кн/см) – погонная нагрузка. Опора А-шарнирно неподвижна, опора В – подвижный каток. Построить эпюры Q и М_из.

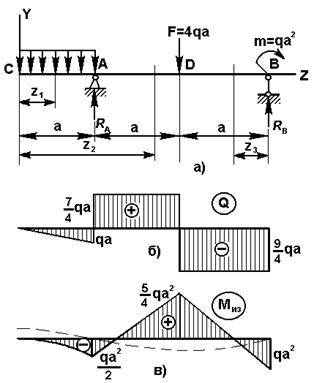
Рис.13

Решение.

Решение задачи следует начинать с определения реакций опор. Из условия равенства нулю суммы проекций всех сил на ось Z следует, что горизонтальная составляющая реакции на опоре А равна 0.

Для проверки используем уравнение

ΣY=0 R_A+R_B-qa-4qa=0

Уравнение равновесия удовлетворяются, следовательно, реакции вычислены правильно. Переходим к определению внутренних силовых факторов. Заданная балка имеет три участка нагружения:

1 участок – СА,

2 участок – АД,

3 участок – ДВ.

Рассечем 1 участок на расстояние Z₁ от левого торца балки (рис.13,а).

0≤Z₁≤a

Q = -qZ₁

,

При Z₁=0 Q=0 М_ИЗ=0

При Z₁=a Q= -qa М_ИЗ= -qa²/2.

Таким образом, на эпюре поперечных сил получается наклонная прямая, а на эпюре изгибающих моментов - парабола, вершина которой находится на левом конце балки рис.13,в.

На участке II (a≤ Z₂ ≤2a) для определения внутренних силовых факторов рассмотрим равновесие левой отсеченной части балки длиною Z₂. Из условия равновесия имеем:

Поперечная сила на этом участке постоянна.

При Z₂=a М_ИЗ= -qa²/2.

При Z₂=2a М_ИЗ= 5qa²/4.

На участке III (0≤ Z₃ ≤a)

Q=R_B

М_ИЗ= R_B∙Z₃ - qa².

Полная эпюра поперечных сил для всей балки имеет вид, представленный на рис.13,б. А на рис.13,в представлена полная эпюра изгибающих моментов и пунктиром показан примерный вид изогнутой оси балки рис.13,а.

Из эпюры видим, что наибольший изгибающий момент возникает в сечении под силой F и равен 5qa²/4. Это сечение будет самым опасным.

На эпюре М_из имеется скачок на опоре В, равный внешнему моменту, приложенному в данном сечении.

Пример 4.

Для трех заданных расчетных схем требуется:

1. разбить балку на участки, обозначив длину каждого из них;

2. при необходимости определить реакции опор;

3. используя уравнения равновесия, записать аналитические выражения для внутренних усилий Q и М в произвольном сечении каждого из участков;

4. построить эпюры внутренних усилий в выбранном масштабе;

5. проверить правильность построения эпюр, используя дифференциальные зависимости между М, Q и q.

Исходные данные к задачам выбираются по табл.11 и схемам на рис. 14.

Таблица 11

a, м	q, кН⁄м	F, кН	M, кНм
1	10	15	20

Рис. 14. Расчетные схемы балок

Задача по расчетной схеме а) рис.14

Рис. 15. Координаты сечений и схемы нагружения выделяемых частей балки

Построение эпюр внутренних усилий

Участок 1: 0 ≤ z₁ ≤ 2a.

Выражения для Q(z₁) и М(z₁), полученные из уравнений равновесия правой части балки (рис. 15):

Q(z₁) = - {- q(2a - z₁) + F};

М(z₁) = - {q(2a - z₁)∙ - F(2a - z₁ + a)}.

Для построения эпюр вычисляются значения Q(z₁) и М(z₁) в характерных точках участка 1.

Q(0) = 2q∙a - F = 2∙10∙1 - 15 = 5 кН.

Q(2a) = - F = - 15 кН.

М(0) = - q∙2a² + F∙3a = - 10∙2∙1² + 15∙3∙1 = 25 кНм.

М(a) = - q∙a²/2 + F∙2a = - 0,5∙10∙1² + 15∙2∙1 = 25 кНм.

М(2a) = F∙a = 15∙1 = 15 кНм.

В пределах участка знак поперечной силы изменяется, следовательно, М(z₁) имеет на участке точку экстремума. Координата точки Q(z₁) = 0: z₁ = 0,5a. Момент в точке экстремума:

М(0,5a) = - 0,5q(2a - 0,5a)² + F(3a - 0,5a) = - 0,5∙10∙(1,5∙1)² + 15∙(2,5∙1) = 26,25 кНм.

Участок 2: 0 ≤ z₂ ≤ a.

Выражения для Q(z₂) и М(z₂), полученные из уравнений равновесия правой части балки (см. рис. 15):

Q(z₂) = - { F } = const;

М(z₂) = - {- F(a - z₂)}.

Для построения эпюр вычисляются значения Q и М в характерных точках участка 2.

Q = const = - F = - 15 кН.

М(0)= F∙a = 15∙1 = 15 кНм.

М(a) = 0.

Эпюры Q и М, построенные по вычисленным значениям внутренних усилий в выбранных точках участков, изображены на рис. 16.

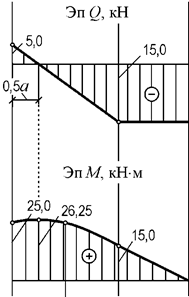
Рис. 16. Эпюры Q и M для расчетной схемы а) рис.14.

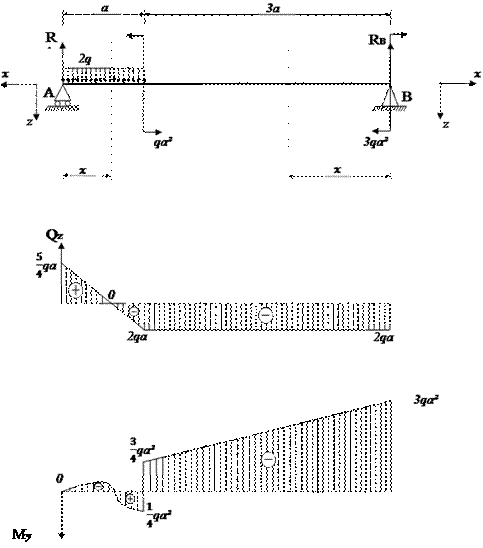
Задача по расчетной схеме б) рис.14

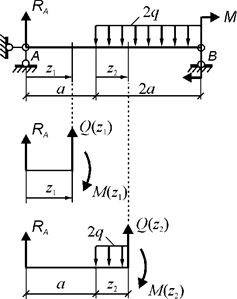
Рис. 17. Координаты сечений и схемы нагружения выделяемых частей балки

Определение реакции R_A (рис. 17)

ΣM_B = 0. R_A∙3a - 2q∙2a∙2a/2 + M = 0.

Отсюда

R_A = (4q∙a² - M) /3a= (4∙10∙1² - 20) = 6,67 кН.

Построение эпюр внутренних усилий

Участок 1: 0 ≤ z₁ ≤ a.

Выражения для Q(z₁) и М(z₁), полученные из уравнений равновесия левой части балки (см. рис. 17):

Q(z₁) = - { R_A };

М(z₁) = - { R_A ∙z₁ }.

Для построения эпюр вычисляются значения Q и М в характерных точках участка 1.

Q = const = - R_A = - 6,67 кН.

М(0) = 0.

М(a) = R_A∙a = 6,67∙1 = 6,67 кНм.

Участок 2: 0 ≤ z₂ ≤ 2a.

Выражения для Q(z₂) и М(z₂), полученные из уравнений равновесия левой части балки (см. рис. 17):

Q(z₂) = - {R_A - 2q∙z₂};

М(z₂) = - { R_A(a + z₂) - 2q∙z₂∙z₂/2}.

Для построения эпюр вычисляются значения Q и М в характерных точках участка 2.

Q(0) = - R_A = - 6,67 кН.

Q(2a) = - R_A + 2q∙2a = - 6,67 + 4∙10∙1 = 33,33 кН.

М(0) = - R_A ∙a = - 6,67∙1 = - 6,67 кНм.

М(a) = - R_A∙2a + q∙a² = - 6,67∙2∙1 + 10∙1² = - 3,33 кНм.

М(2a) = - R_A(a + 2a) + q(2a)² = - 6,67∙3∙1 + 10∙(2∙1)² = 20 кНм.

Так как в пределах участка знак поперечной силы изменяется, то М(z₂) имеет на участке точку экстремума. Координата точки экстремума: z₂=0,334a. Момент в точке экстремума:

М(0,334a) = - R_A(a + 0,334a) + q(0,334a)² = - 6,67∙1,334∙1 + 10∙(0,334∙1)² = - 7,78 кНм.

Эпюры Q и М, построенные по вычисленным значениям внутренних усилий в выбранных точках участков, изображены на рис. 18.

Рис. 18. Эпюры Q и M для расчетной схемы б) рис.14.

Задача по расчетной схеме в) рис.14

Рис. 19. Координаты сечений и схемы нагружения выделяемых частей балки

Определение реакции R_A (рис. 19)

ΣM_B = 0.

R_A∙1,5a - M + q∙1,5a∙1,5a/2 + F∙1,5a = 0.

Отсюда

R_A = (M - q∙1,5²a² - F∙1,5a) = (20 - ∙10∙1,5²∙1² - 15∙1,5∙1) = - 9,17 кН.

Построение эпюр внутренних усилий

Участок 1: 0 ≤ z₁ ≤ 1,5a.

Выражения для Q(z₁) и М(z₁), полученные из уравнений равновесия левой части балки (см. рис. 19):

Q(z₁) = - { R_A };

М(z₁) = - { R_A∙ z₁ - M}.

Для построения эпюр вычисляются значения Q и М в характерных точках участка 1.

Q = const = - R_A = 9,17 кН.

М(0) = M = 20 кНм.

М(1,5a) = - R_A∙1,5a + M = 9,17∙1,5∙1 + 20 = 33,75 кНм.

Участок 2: 0 ≤ z₂ ≤ 1,5a.

Выражения для Q(z₂) и М(z₂), полученные из уравнений равновесия правой части балки (см. рис. 19):

Q(z₂) = - {F + q(1,5a - z₂)};

М(z₂) = -{-F(1,5a - z₂) - q(1,5a - z₂)²}.

Для построения эпюр вычисляются значения Q и М в характерных точках участка 2.

Q(0) = - F - q∙1,5a = - 15 - 10∙1,5∙1 = - 30 кН.

Q(1,5a) = - F = - 15 кН.

М(0) = F∙1,5a + 0,5q(1,5a)² =15∙1,5∙1 + 0,5∙10∙1,5²∙1² = 33,75 кНм.

М(0,5a) = F∙a + 0,5q∙a² = 15∙1 + 0,5∙10∙1² = 20,0 кНм.

М(a) = F∙0,5a + 0,5q(0,5a)² = 15∙0,5∙1 + 0,5∙10∙0,5²∙1² = 8,75 кНм.

М(1,5a) = 0.

Эпюры Q и М, построенные по вычисленным значениям внутренних усилий в выбранных точках участков, изображены на рис. 20.

Рис. 20. Эпюры Q и M для расчетной схемы в) рис.14.

Пример 5.

Построить эпюры Q_y и M_x для консольной балки (рис. 21, а).

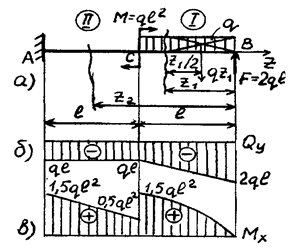
Рис.21

Решение.

Чтобы не определять реакции в опоре A, строим эпюры от правого конца балки в следующем порядке. Разобьем балку AB на участки I и II, в пределах которых законы изменения Q_y и M_x остаются постоянными. Границами участков являются: начало и конец балки, точки приложения внешних сосредоточенных сил (включая опорные реакции), начало и конец приложения распределенных сил q. Выберем начало координат на правом конце балки B и на основании формул и и правил знаков, составим выражения для Q_y и M_x в произвольных сечениях z для каждого участка. Участок I (0 ≤ z₁ ≤ l):

Q_y=-F+qz₁=-2ql+qz₁;

M_x=Fz₁-qz₁∙z₁/2=2qlz₁ -q/2;

здесь qz – равнодействующая распределенной нагрузки q в пределах отрезка длиной z; она приложена посредине этого отрезка и поэтому момент ее относительно сечения z₁ равен

При z₁ = 0; Q_y=-F=-2ql; M_x=0;

при z₁ =l; Q_y= -2ql+ql=-ql; M_x=2ql²-ql²/2=1,5ql².

Участок II (0 ≤ z₂ ≤ 2l): Q_y= -F+ql= -2ql+ql= -ql,

т.е. поперечная сила Q_y на участке II не зависит от z₂ (конец приложения нагрузки q совпал с началом этого участка.

M_x=Fz₂-ql(z₂-l/2)-M=2qlz₂-ql(z₂-l/2)-ql²;

при z₂ =l; M_x=2ql²-ql(l-l/2)-ql²=0,5ql²;

при z₂ = 2l; M_x=2ql∙2l-ql(2l-l/2)+ql²=1,5ql².

Выбрав масштаб, строим эпюры поперечных сил Q_y и изгибающих моментов M_x (рис. 21, б, в), а затем проверяем правильность их получения.

Пример 6.

Построить эпюры Q_y и M_x для двухопорной балки (рис. 22, а).

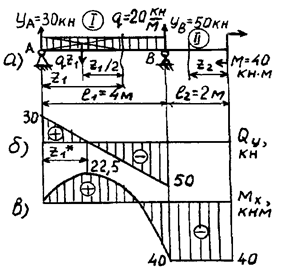
Рис.22

Решение:

Определяем опорные реакции:

Проверка: Σy=0; y_A-ql₁+y_B=0; 30 – 20∙4 + 50= 0.

Разбиваем балку на cиловые участки I и II; составляем выражения для Q_y и M_x:

Участок I (0 ≤ z₂ ≤ l₁=4 м):

при z₁ = 0; Q_y=y_a=30 кН;

M_x = 0; при z₁=4 м; Q_y = 30 –20∙4 = –50 кН;

M_x = 30∙4 – 20∙4²/2 = –40 кНм.

Построив эпюру Q_y видим, что она меняет знак c (+) на (–), т.е. на участке I на эпюре M_x необходимо определить экстремум. Согласно dM_x/dz=Q_y получим:

Тогда:

Участок II (0 ≤ z₂ ≤ l₂=2 м): Q_y = 0; M_x = -M = -40 кНм.

Эпюры Q_y и M_x показаны на рис. 22, б, в.

Пример 7.

Консоль, защемленная в сечении D, нагружена сосредоточенными силами Р₁ = 3 кН, Р₂ = 11 кН и парой сил, момент которой М = 8 кНм (рис.23).

Требуется:

1) найти значения поперечной силы и изгибающего момента в сечениях, примыкающих к границам участков;

2) по найденным значениям внутренних силовых факторов построить, соблюдая масштаб, эпюры Q_y(z) и M_x(z) и указать на них характерные ординаты с единицами измерения.

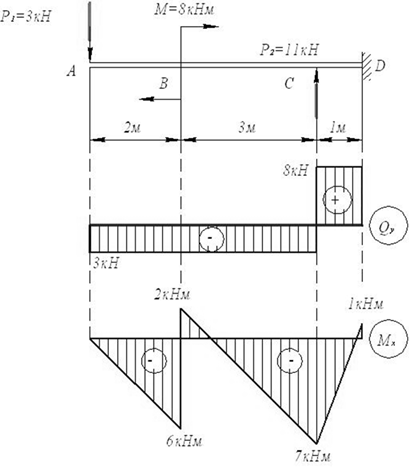
Рис.23

Решение.

Консоль состоит из трех участков АВ, ВС и СD.

Ни на одном из участков нет распределенной нагрузки. Значит, вдоль каждого из участков поперечная сила не меняет своего значения, а изгибающий момент меняется по линейному закону.

К сечению D приложена неизвестная реакция заделки, тогда как слева от любого сечения нагрузка известна. Поэтому будем находить поперечные силы и изгибающие моменты в граничных сечениях по нагрузке, приложенной к левой (отсеченной) части консоли.

Участок АВ:

Q_yA= -P₁= -3 кН; Q_yB= -3 кН.

M_xA= -P₁∙0= 0; M_xB= -3∙2= -6 кНм.

Участок ВС:

Q_yB= -3 кН; Q_yC= -3 кН.

M_xB= -3∙2+8 = 2 кНм; M_xС= -3∙5+8 = -7 кНм.

Участок СD:

Q_yС= -3+11=8 кН; Q_yD= 8 кН.

M_xC= -3∙5+8 = -7 кНм; M_xD= -3∙6+8+11∙1 = 1 кНм.

По результатам вычислений строим эпюры Q_y и M_x.

Заметим, что на участках АВ и ВС поперечная сила имеет равные значения. На этих участках эпюра изгибающего момента M_x представлена параллельными линиями.

На участке СD Q_y>0, здесь изгибающий момент возрастает.

В сечении С поперечная сила меняется скачкообразно от -3 кН до 8 кН, то есть на величину силы Р₂ = 11 кН.

В сечении В изгибающий момент меняется скачкообразно от -6 кНм до 2 кНм, то есть на величину момента М = 8 кНм.

Пример 8.

Балка АD нагружена распределенной нагрузкой интенсивностью q = 4 кН/м, сосредоточенной силой Р = 3 кН и парой сил, приложенной к сечению В (рис. 24). Поскольку момент пары сил полностью определяет ее действие на балку, то можно изобразить ее дуговой стрелкой, указав направление действия и численное значение момента.

Требуется:

1) определить реакции опор;

2) найти значения поперечной силы и изгибающего момента в сечениях, примыкающих к границам участков;

3) на участке с распределенной нагрузкой определить положение сечения, в котором поперечная сила равна нулю;

4) определить значение изгибающего момента в этом сечении;

5) по найденным значениям поперечной силы и изгибающего момента построить эпюры Q_y и M_x и указать на них характерные ординаты.

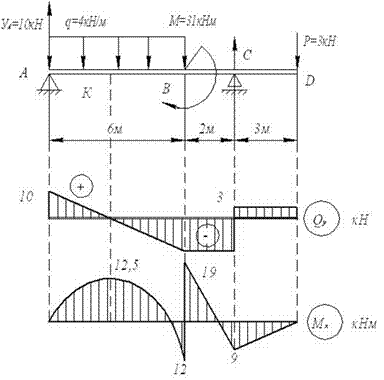
Рис.24

Решение.

Равнодействующая распределенной нагрузки

R= q∙AB=4∙6=24 кН.

Линия действия равнодействующей проходит через середину участка АВ и удалена от опоры А на 3 м и от опоры С – на 5 м.

Уравнения равновесия

Σm_A=0. Y_C∙(2+6) - P∙(3+2+6) – M - R∙3=0, или

8Y_C - 3∙11 – 31 - 24∙3 = 0.

Σm_C=0. -Y_A∙(2+6) + R∙5 – M - P∙3=0, или

-8Y_A +24∙5 – 31 -3∙3 = 0.

Решение уравнений

Y_A=10 кН, Y_C=17 кН.

Поперечные силы

На участке АВ поперечная сила меняется по линейному закону.

Q_yA=Y_A=10 кН. Q_yB=Y_A-q∙AB=10-4∙6= -14 кН.

На границе участков АВ и ВС нет сосредоточенной силы. Значит, вдоль всего участка ВС Q_y= -14 кН. При переходе через сечение С поперечная сила увеличится на величину силы Y_С. То есть на участке СD

Q_y= -14+17 = 3 кН.

Это значение поперечной силы можно найти и по нагрузке справа от сечения участка СD с учетом правила знаков.

Изгибающие моменты

Положение сечения К найдем из условия Q_yK = 0.

Эпюра М_х на участке АВ представляется параболой, проходящей через точки (0, 0), (2,5; 12,5) и (6, -12).

При переходе через сечение В изгибающий момент меняется скачкообразно и в сечении В участка ВС принимает значение

M_B= -12+31 = 19 кНм.

В сечении С изгибающий момент непрерывен, и его удобнее найти по нагрузке справа.

M_C= -P∙DC = -3∙3 = -9 кНм.

После построения эпюр Q_y и M_x следует проверить, соответствуют ли они друг другу с учетом закономерностей, отмеченных ранее. Так, на участках АК и СD Q_y>0 и изгибающий момент возрастает при обходе балки слева направо. На участках КВ и ВС Q_y<0 и изгибающий момент при таком же обходе балки убывает.

Пример 9.

На рисунке 25 изображена консольная балка, нагруженная сосредоточенной силой P=7 кН, парой сил, момент которой M=32 кНм, и равномерно распределенной нагрузкой интенсивностью q=4 кН/м.

Требуется:

1. Определить реакции опор.

2. Найти значения поперечной силы и изгибающего момента в сечениях, примыкающих к границам участков.

3. На участке с распределенной нагрузкой определить положение сечения, в котором поперечная сила равна нулю.

4. Определить значение изгибающего момента в этом сечении.

5. По найденным значениям поперечной силы и изгибающего момента построить в масштабе эпюры Q_y и M_x и указать на них характерные ординаты с единицами измерения.

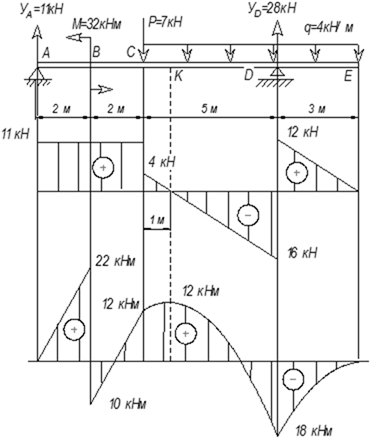
Рис. 25

Решение.

1. При построении уравнений равновесия необходимо мысленно заменить распределенную нагрузку ее равнодействующей. Она равна

R= q∙CE=4∙8=32 кН.

Линия действия равнодействующей проходит через середину отрезка СЕ. Она удалена от опоры А на 8 м и от опоры D – на 1 м.

Уравнения моментов:

Σm_A=0. Y_D∙9 - q∙8∙8 – P∙4+M = 0, или

Y_D∙9 - 4∙8∙8 – 7∙4+32 = 0.

Σm_D=0. -Y_A∙9 +M + P∙5+ q∙8∙1 = 0, или

-Y_A∙9 +32 + 7∙5+ 4∙8∙1 = 0.

Решение уравнений

Y_A=11 кН, Y_D=28 кН.

Проверка

ΣY=Y_A – P - q∙8 + Y_D = 11-7-4∙8+28=0.

2. На участках АВ и ВС нет распределенной нагрузки и нет сосредоточенных сил. Значит в пределах этих участков поперечная сила не меняет своего значения. По силам приложенным к балке слева от любого сечения участков АВ и ВС получаем

Q_y = Y_A = 11 кН.

К сечению С, которое разделяет участки ВС и СD, приложена сосредоточенная сила P = 7 кН, направленная вниз. Значит при переходе через сечение С поперечная сила уменьшается на величину силы Р.

При дальнейшем продвижении по участку СD поперечная сила меняется по линейному закону. В конечном сечении этого участка

или

То есть при переходе в пределах участка СD от сечения С к сечению D поперечная сила изменится на величину нагрузки, приложенной к этому участку.

При переходе через сечение D поперечная сила опять меняется скачкообразно

Значения поперечной силы в рассмотренных сечениях можно найти и по нагрузке, приложенной к балке справа от сечения. Так в конечном сечении Е поперечная сила равна нулю, а в сечении D участка ЕD поперечная сила равна равнодействующей распределенной нагрузки, приложенной к участку ED, то есть

При этом вычислении следует учесть, что нагрузка, приложенная справа от сечения, вызывает положительную поперечную силу, если она направления вниз.

3. Перейдем к определению изгибающих моментов.

В сечении, примыкающем к опорному сечению А, изгибающий момент равен нулю, так как плечо силы Y_A равно нулю. По мере удаления сечения от опоры А изгибающий момент возрастает по линейному закону и в сечении В участка АВ он равен

При переходе через сечение В изгибающий момент получает отрицательную добавку, равную моменту пары. Таким образом в сечении В участка ВС

Скачкообразное изменение изгибающего момента имеет место лишь в сечении В, где приложена внешняя пара сил. В остальных граничных сечениях изгибающий момент непрерывен. Значит в сечениях, принимающих к границам участков С и D слева и справа значения изгибающего момента будут одинаковы.

По нагрузке слева

M_C = Y_A∙AC - M= 11∙4 - 32 = 12 кНм;

По нагрузке справа

Изгибающий момент в конечном сечении Е равен нулю.

На участках СD и DE эпюра изгибающего момента представляется параболами.

Для построения параболы участка СD найдем положение сечения К этого участка, в котором поперечная сила равна нулю. Воспользуемся формулой Искомое сечение К удалено от сечения D на

а от сечения С на

По нагрузке справа

После построения эпюр Q_y и M_x по результатам вычислений следует проверить, соответствуют ли они друг другу.

Так на части балки с положительной поперечной силой изгибающий момент возрастает. На отрезке KD изгибающий момент убывает. На участках АВ и ВС с равными поперечными силами эпюры изгибающего момента представлены параллельными прямыми.

Пример 10.

Для статически определимой балки (рис.26) требуется:

1) Определить реакции опор;

2) Написать аналитические выражения для внутренних силовых факторов (поперечной силы Q и изгибающего момента M) для каждого участка балки в принятых локальных системах координат;

3) Построить эпюры Q и M;

4) Определить опасное сечение, где изгибающий момент имеет максимальное (по абсолютной величине) значение.

Дано:

Рис.26

Решение.

1. Отбросим опоры и заменим их влияние на балку опорными реакциями (рис.27).

2. Составим сумму моментов всех сил:

ΣM_A= -q∙a∙(a/2) - P∙a +q∙c∙(a+c/2) +R_B∙(a+c) =0

ΣM_B= -R_A∙(a+c) + P∙с +q∙a∙(c+a/2) - q∙c∙(c/2) = 0

3. Проверка реакций:

Составим сумму проекций всех сил на вертикальную ось Y:

ΣY=+R_A – P - q∙a + q∙c + R_B =0

ΣY=+15,4 – 28 - 20∙0,5 +20∙2 – 17,4 =0

0=0

4. Полученное тождество показывает, что реакции вычислены правильно.

5. Построим эпюры Q и M.

Балка имеет два участка. Используя метод сечений, составляем аналитические выражения для Q и M.

I участок

II участок

6. Из эпюры M следует (рис.27), что в опасном сечении балки M_max=7,57 кНм.

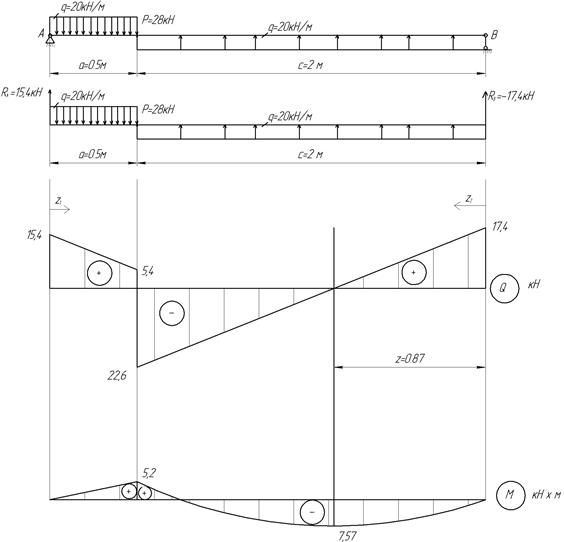
Рис.27

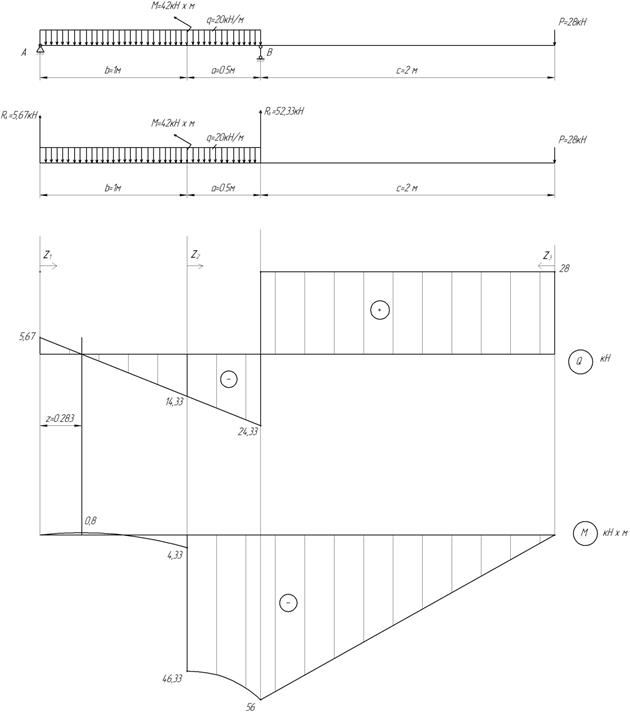
Пример 11.

Для статически определимой балки (рис.28) требуется:

1) Определить реакции опор;

2) Написать аналитические выражения для внутренних силовых факторов (поперечной силы Q и изгибающего момента M) для каждого участка балки в принятых локальных системах координат;

3) Построить эпюры Q и M;

4) Определить опасное сечение, где изгибающий момент имеет максимальное (по абсолютной величине) значение.

Дано:

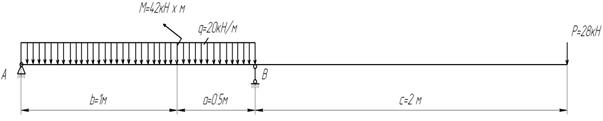
Рис.28

Решение.

1. Отбросим опоры и заменим их влияние на балку опорными реакциями (рис.29).

2. Составим сумму моментов всех сил:

ΣM_B=M - q∙(a+b)∙(b+a)/2 + R_B∙(a+b) - P∙(a+b+c) =0

ΣM_A= -RA∙(a+b) + M - P∙с + q∙(a+b)∙(b+a)/2 =0

3. Проверка реакций:

Составим сумму проекций всех сил на вертикальную ось Y:

ΣY=+R_A - q∙(a+b) +R_B – P=0

ΣY=+5,67 - 20∙1,5 + 52,33 - 28=0

0=0

4. Полученное тождество показывает, что реакции вычислены правильно.

5. Построим эпюры Q и M.

Балка имеет три участка. Используя метод сечений, составляем аналитические выражения для Q и M.

I участок

II участок

III участок

6. Из эпюры M (рис.29) следует, что в опасном сечении балки M_max=56 кНм.

Рис.29

Пример 12.

Для заданной консольной балки (рис.30) требуется построить эпюры поперечных сил и изгибающих моментов.

Рис.30

Решение.

1. При решении этой задачи нет необходимости определять опорные реакции в заделке. Определение поперечных сил Qz и изгибающих моментов M_y можно осуществлять сразу с помощью метода сечений, идя со свободного конца стержня. Разобьем стержень на три силовых участка.

2. Определяем поперечную силу и изгибающий момент на I участке. Проводим произвольное сечение в пределах участка. Считая мысленно отброшенной правую часть. В сечении, принадлежащем левой части, вводим систему координат xyz (ось x направлена от сечения в сторону мысленно отброшенной части). Координату сечения зададим от начала участка. На мысленно отброшенной части действует выделенная часть распределенной нагрузки q и сосредоточенный момент qa. Распределенная нагрузка на длине x имеет равнодействующую qx, за счет которой возникает отрицательная поперечная сила:

= -qx

при x = 0 = 0;

при x = 2а = -2a.

Зависимость поперечной силы от координаты сечения линейная.

Равномерно распределенная на длине x нагрузка имеет равнодействующую qx, линия действия которой проходит через центр тяжести прямоугольника со сторонами q и x, то есть на расстоянии x/2 от рассматриваемого сечения. Изгибающий момент в сечении под действием распределенной нагрузки численно равен сумме момента равнодействующей qx на плече x/2 (этот момент будет иметь знак “плюс”, так как распределенная нагрузка стремится изогнуть стержень выпуклостью в сторону направления оси z) и сосредоточенного момента (знак которого будет отрицательный, так как этот момент стремится изогнуть стержень выпуклостью в сторону, противоположную направлению оси z). Изгибающий момент:

= – qa

при x = 0 = -qa;

при x = 2а = 2qa² - qa.

Зависимость изгибающего момента от координаты сечения квадратичная, а на координате сосредоточенного момента qa будет скачок на эту величину.

3. Определяем внутренние силовые факторы на II участке. Для этого переводим сечение, которое провели на I участке, вместе с главными центральными осями на II участок. Считаем отброшенной правую часть. Ось x проводим вправо, задаем координату сечения справа от начала II участка. На отброшенной части действуют две распределенные силы q и сосредоточенный момент qa.

Определяем поперечную силу. Распределенная сила q на длине x имеет равнодействующую qx со знаком “плюс”, так как под действием силы мысленно отброшенная часть стремится повернуться по ходу часовой стрелки. Распределенная сила q на длине 2a имеет равнодействующую 2qa со знаком “минус”, поскольку она стремится повернуть мысленно отброшенную часть против хода часовой стрелки. В результате можно записать:

= -2qa + qx

при x = 0 = -2qa;

при x = а = -qa.

Изгибающий момент в сечении II участка возникает под действием двух распределенных сил q и сосредоточенного момента qa. Сосредоточенный момент qa дает отрицательный изгибающий момент как изложено выше. Распределенная сила q на длине 2a имеет равнодействующую 2qa, которая создает положительный изгибающий момент (она стремится изогнуть мысленно отброшенную часть выпуклостью в сторону оси z) на плече (a + x). За счет распределенной силы q на длине x имеющую равнодействующую qx возникает отрицательный изгибающий момент (сила стремится изогнуть мысленно отброшенную часть выпуклостью в сторону, противоположную оси z) на плече x. В результате получим:

= -qa + 2qa· (a+x) -

при x = 0 = 2qa² - qa;

при x = а = qa² - qa.

4. Аналогичным образом определяем поперечную силу и изгибающий момент на III участке:

= -2qa + qa – qa = -2qa;

= -qa + 2qa· (a+a+x) -qa∙ ( +x) +qa·x

при x = 0 = qa² - qa;

при x = а = qa² - qa.

По полученным значениям строим эпюры внутренних силовых факторов (рис.30).

Пример 13.

Для шарнирно-опертой статически определимой балки (рис.31) требуется построить эпюры поперечных сил и изгибающих моментов.

Рис.31

Решение.

1. Отбрасываем связи и заменяем их реактивными силами R_A, R´_A и R_B. Найти их можно с помощью уравнения равновесия:

= 0; R´_A = 0

= 0; R_A + R_B – 5qa = 0.

В данном примере нагрузка, действующая на стержень, является симметричной. В этом случае реакции опор всегда равны друг другу, то есть

R_A = R_B = 2,5qa

Кроме того, существует следующее правило: если нагрузка, действующая на стержень, является симметричной, то эпюра поперечных сил является кососимметричной, а эпюра изгибающих моментов – симметричной.

Поэтому достаточно вычислить значения и построить эпюры Q_z и M_y лишь для половины стержня, а для второй половины стержня достроить эпюры согласно вышеуказанному правилу.

2. В связи с этим выделяем два силовых участка. Используя правило знаков тоже, что и в предыдущей задаче находим поперечную силу и изгибающий момент на первом участке:

= -qx

при x = 0 = 0;

при x = а = -qa;

=

при x = 0 = 0;

при x = а = - .

3. Второй участок:

= -qa + R_A – qx

при x = 0 = -qa + 2,5qa = 1,5qa;

при x = 1,5а = -qa + 2,5qa -1,5qa = 0.

= -qa·(+x) + R_A·x -

при x = 0 = -qa·(+0) + R_A·0 - = - 0,5qa²;

при x = 1,5а = -qa·(+1,5a) + 2,5qa·1,5a - = qa².

4. По полученным результатам строим эпюры поперечных сил и изгибающих моментов (рис.31). При сосредоточенных силах реакций опор на эпюре Q_z мы видим скачки равные этом силе, а при сосредоточенных силах – наклонную прямую. На эпюре моментов при распределенной силе мы будем видеть прямую второго порядка. Точка С является экстремумом.

Пример 14.

Для шарнирно-опертой статически определимой балки (рис.32) с кососимметричной нагрузкой требуется построить эпюры поперечных сил и изгибающих моментов.

Рис.32

Решение.

1. Особенность этого стержня состоит в том, что нагрузка, приложенная к ней, является кососимметричной. Поэтому реакции R_A и R_B равны по модулю и противоположны по направлению.

Для нахождения R_A и R_B решим уравнение статики:

= 0; 3qa² - 2qa·( + 2a) – 2qa·( + 3a) + R_B·3a + 3qa² = 6qa² - 5qa² - 7qa² + R_B·3a = R_B·3a – 6qa² = 0.

Отсюда следует, что:

R_B = = 2qa где R_B = R_A = 2qa.

Аналогично предыдущей задачи нам достаточно вычислить значения и построить эпюры Q_z и M_y лишь для половины стержня, а для второй половины стержня достроить эпюры согласно правилу: если нагрузка, действующая на стержень, является кососимметричной, то эпюра поперечных сил является симметричной, а эпюра изгибающих моментов – кососимметричной.

2. В связи с этим выделяем три участка. Используя правило знаков тоже, что и в предыдущей задаче находим поперечную силу и изгибающий момент на первом участке:

= -2qx

при x = 0 = 0;

при x = а = -2qa;

= 3qa² -

при x = 0 = 3qa²;

при x = а = 3qa² - = 2qa².

3. Второй участок:

= -2qa -2qx + R_A

при x = 0 = -2qa -2q·0 + 2qa = 0;

при x = 1,5а = -2qa -2qa + 2qa = -2qa.

=3qa² -2qa·(+x) + R_A·x -

при x = 0 = 3qa² -2qa·(+0) + 2qa·0 - = 2qa²;

при x = а = 3qa² -2qa·(+a) + 2qa·a - = qa².

4. Третий участок:

= -4qa + R_A

при x = 0 = -4qa + 2qa = -2qa;

при x = 0,5а = -4qa + 2qa = -2qa.

=3qa² -4qa·(a +x) + R_A·(a+x)

при x = 0 = 3qa² -4qa·(a+0) + 2qa·(a+0) = qa²;

при x = а = 3qa² -4qa·(a+) + 2qa·(a+) = 0.

4. По полученным результатам строим эпюры поперечных сил и изгибающих моментов (рис.32). При сосредоточенных силах реакций опор на эпюре Q_z мы видим скачки равные этом силе, а при сосредоточенных силах – наклонную прямую. На эпюре моментов при распределенной силе мы будем видеть прямую второго порядка.

Пример 15.

Для шарнирно-опертой статически определимой балки (рис.33) требуется построить эпюры поперечных сил и изгибающих моментов.

Рис.33

Решение.

1. Нагрузка действующая на стержень, является произвольной. Стержень имеет два силовых участка. Определим реакции опор R_A и R_B воспользовавшись уравнением статики:

= 0; - + qa² - 3qa² + R_B·4a = R_B·4a - 3qa² = 0

тогда, R_B = qa.

= 0; - 3qa² + qa² 2qa·( + 3a) – R_A·4a = 0

-2qa² + 7qa² - R_A·4a = 0

R_A = qa.

Сделаем проверку правильности нахождения реакций R_A и R_B:

= 0; R_A -2qa + R_B = 0

qa – 2qa + qa = 0 (истинно).

2. Переходим к определению внутренних силовых факторов по участкам. Проведем сечение на первом участке и отбросим правую часть стержня:

= - R_B = qa.

= -3qa² + R_A·x

при x = 0 = -3qa² + qa ·0 = -3qa²;

при x = 3а = -3qa² + qa ·3a = - qa².

3. На втором участке отбросим левую часть стержня:

= R_A -2qx

при x = 0 = qa -2q·0 = qa;

при x = a = qa -2q·a = - qa.

=R_A·x -

при x = 0 = qa ·0 - = 0;

при x = а = qa ·a - = qa².

4. По полученным результатам строим эпюры поперечных сил и изгибающих моментов (рис.33). На границе I и II участка мы видим скачек сосредоточенного изгибающего момента, который равен согласно из условия задачи qa.

Пример 16.

Определить нагрузку в балке по приведенной эпюре изгибающих моментов (рис.34) и построить эпюру поперечных сил.

Рис.34

Решение.

1. Эпюра изгибающих моментов является кососимметричной, следовательно, нагрузка, действующая на стержень кососимметрична, а эпюра поперечных сил – симметрична.

Из эпюры M_y мы видим, что на стержень действует равномерно распределенная нагрузка (на всех трех участках), потому что линии эпюры являются второго порядка. Эпюра M_y имеет максимумы в сечении точек А и В от воздействия опорных сил R_A и R_B.

На основании проделанного исследования представим нагрузку, приложенную к стержню и определим значения q, R_A и R_B. На первом участке изгибающий момент представим как:

= -

при x = 0 = - = 0 кНм;

при x = 2 = - = -2q кНм.

так как M_y = 4 кНм, то q = M_y /2 = 2 кН/м.

2. Реакции опор R_A и R_B равны, но противоположны по направлению. Для их нахождения решим уравнения статики:

= 0; -2q·1 – 2q·1 + 4q·4 - R_B = 0

R_B = 4·q = 4·2 = 8 кН;

R_A = R_B = 8 кН.

Теперь определим поперечную силу Q_z:

= -qx

при x = 0 = -q·0 = 0;

при x = 2 = -q·2 = -2·2 = - 4 кН.

3. Так как нагрузка кососимметрична, то рассмотрим половину второго участка:

= - 2q·(1+x) + R_A·x -

при x = 0 = - 2·2·(1+0) + 8·0 – = -4 кНм;

при x = 2 = - 2·2·(1+2) + 8·2 – = 0 кНм.

= -2q + R_A - qx

при x = 0 = -2·2 + 8 - 2·0 = 4 кН;

при x = 2 = -2·2 + 8 - 2·2 = 0 кН.

Строим эпюру поперечных сил по полученным значениям для половины стержня, а вторую половину достраиваем симметрично первой (рис.34).

Онлайн-калькулятор "Подбор прямоугольного сечения балки при изгибе"

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00