Расчетно-графические работы

Главная

Задача 1. Расчет статически определимого вала, работающего на кручение.

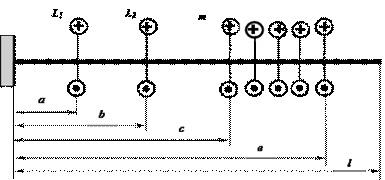
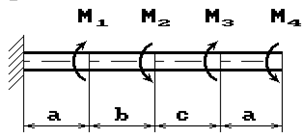
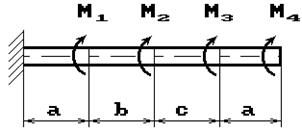
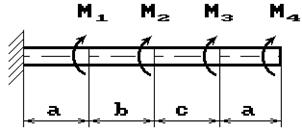
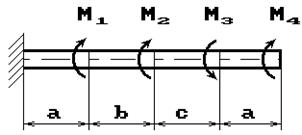
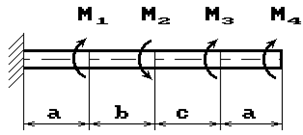
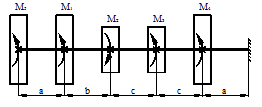
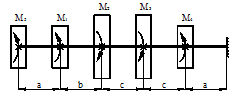
К стальному валу приложены скручивающие моменты: М₁, М₂, М₃, М_4,(рис.1). Требуется:

1) построить эпюру крутящих моментов;

2) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей, соответственно равной: 30, 35, 40,45, 50, 60, 70, 80, 90, 100 мм;

3) построить эпюру углов закручивания;

4) найти наибольший относительный угол закручивания.

Данные взять из табл.1.

Таблица 1

Номер строки	Схема по рис.1	Расстояние, м			Моменты, кНм		[τ], МПа
Номер строки	Схема по рис.1	а	b	с	М₁; М₃	М₂; М₄	[τ], МПа
01	1	1,1	1,1	1,1	2,1	1,1	35
02	2	1,2	1,2	1,2	2,2	1,2	40
03	3	1,3	1,3	1,3	2,3	1,3	45
04	4	1,4	1,4	1,4	2,4	1,4	50
05	5	1,5	1,5	1,5	2,5	1,5	55
06	6	1,6	1,6	1,6	1,6	0,6	60
07	7	1,7	1,7	1,7	1,7	0,7	65
08	8	1,8	1,8	1,8	1,8	0,8	70
09	9	1,9	1,9	1,9	1,9	0,9	75
10	10	2,0	2,0	2,0	2,0	1,0	80
11	11	1,6	1,3	1,6	2,3	1,2	35
12	12	1,7	1,4	1,7	2,4	1,3	40
13	13	1,8	1,5	1,8	2,5	1,4	45
14	14	1,9	1,6	1,9	1,6	1,5	50
15	15	2,0	1,7	2,0	1,7	0,6	55
16	16	1,3	1,8	1,1	1,8	0,7	60
17	17	1,4	1,1	1,2	1,9	0,8	65
18	18	1,5	1,2	1,3	1,6	0,9	70
19	19	1,6	1,3	1,4	1,7	1,1	60
20	20	1,7	1,4	1,5	1,8	1,2	65
21	21	1,9	1,5	1,9	1,9	1,3	70
22	22	2,0	1,6	2,0	2,0	1,4	75
23	23	1,6	1,7	1,6	2,3	1,5	80
24	24	1,7	1,6	1,7	2,4	0,6	35
25	25	1,8	1,7	1,8	2,5	0,7	40
26	26	1,9	1,8	1,9	1,6	0,8	45
27	27	2,0	1,9	1,1	1,8	0,9	50
28	28	1,3	2,0	1,2	1,9	1,0	55
29	29	1,1	1,3	1,3	2,0	1,2	35
30	30	1,2	1,4	1,4	2,3	1,3	40
31	31	1,3	1,5	1,5	2,4	1,4	45
32	32	1,4	1,4	1,6	2,5	1,5	50
33	33	1,5	1,5	1,7	1,6	0,6	55
34	34	1,6	1,6	1,8	1,7	0,7	60
35	35	1,7	1,7	1,9	1,8	0,8	65
36	36	1,8	1,6	1,6	2,3	0,9	45
	б	а	в	г	а	б	в

1 схема 2 схема

3 схема 4 схема

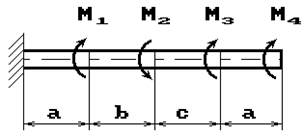
5 схема 6 схема

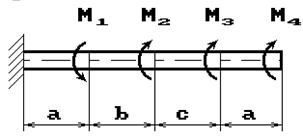
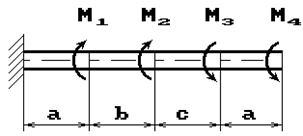
7 схема 8 схема

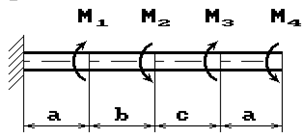
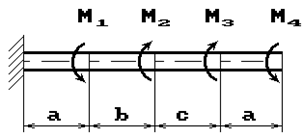
9 схема 10 схема

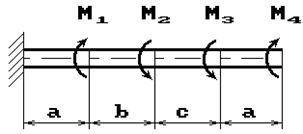
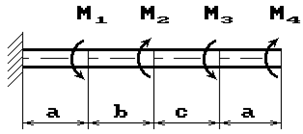
11 схема 12 схема

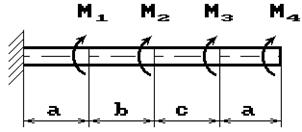
13 схема 14 схема

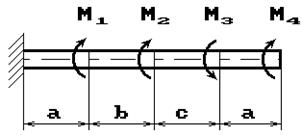
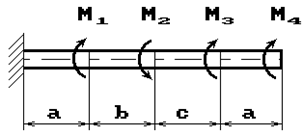
15 схема 16 схема

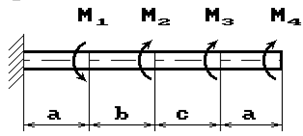
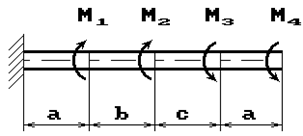
17 схема 18 схема

19 схема 20 схема

21 схема 22 схема

23 схема 24 схема

25 схема 26 схема

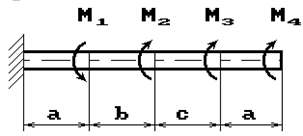
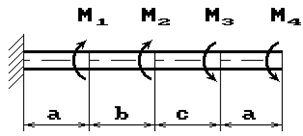
27 схема 28 схема

29 схема 30 схема

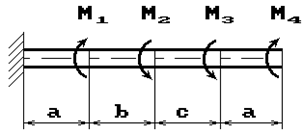
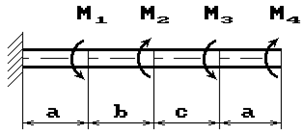
31 схема 32 схема

33 схема 34 схема

35 схема 36 схема

Рис. 1

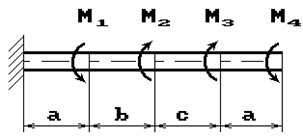
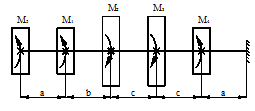
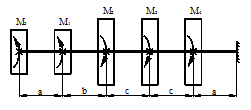
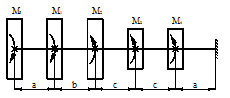
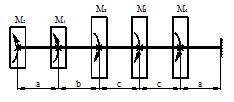
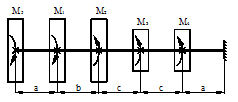
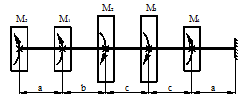
Задача 2. Подбор сечения статически определимого вала, работающего на кручение.

Для заданной расчетной схемы (рис.2) необходимо:

1) Вычертить расчетную схему вала в произвольном масштабе.

2) Построить эпюру крутящих моментов.

3) Из условия прочности определить размеры поперечного сечения вала, приняв сечение вала круглым, кольцевым, прямоугольным.

4) Построить эпюру углов закручивания для круглого вала, приняв жесткость сечения постоянной.

5) Сравнить веса валов.

Данные взять из табл.2.

Таблица 2

Номер cтроки	Схема по рис.2	а, м	b, м	с, м	М₁, Нм	М₂, Нм	М₃, Нм	М₄, Нм	М₅, Нм	ξ=d/D	h/b	[τ], МПа
01	1	0,2	0,7	0,5	100	500	800	400	600	0,4	1,1	50
02	2	0,3	0,6	0,6	200	600	700	300	500	0,5	1,2	60
03	3	0,4	0,5	0,4	300	700	600	800	300	0,6	1,3	70
04	4	0,5	0,4	0,3	400	800	500	700	200	0,7	1,4	80
05	5	0,6	0,3	0,5	500	900	400	600	700	0,8	1,5	90
06	6	0,7	0,2	0,8	600	1000	300	500	800	0,9	1,6	50
07	7	0,8	0,3	0,7	700	900	200	600	900	0,8	1,7	60
08	8	0,7	0,4	0,3	800	800	100	300	1000	0,7	1,8	70
09	9	0,6	0,5	0,4	900	700	1000	200	400	0,6	1,9	80
10	10	0,5	0,6	0,2	1000	100	900	300	100	0,5	2,0	90
11	11	0,3	0,6	0,6	300	600	700	800	500	0,5	1,2	60
12	12	0,4	0,5	0,4	400	700	600	700	300	0,6	1,3	70
13	13	0,5	0,4	0,3	500	800	500	600	200	0,7	1,4	80
14	14	0,6	0,3	0,5	600	900	400	500	700	0,8	1,5	90
15	15	0,7	0,2	0,8	700	1000	300	600	800	0,9	1,6	50
16	16	0,8	0,3	0,7	800	900	200	300	900	0,8	1,7	60
17	17	0,7	0,4	0,3	900	800	100	200	1000	0,7	1,8	70
18	18	0,6	0,5	0,4	1000	700	1000	300	400	0,6	1,9	80
19	19	0,5	0,7	0,5	100	600	900	800	600	0,5	2,0	90
20	20	0,5	0,6	0,6	200	700	500	700	500	0,6	1,8	60
21	21	0,6	0,5	0,4	300	800	400	600	300	0,7	1,9	70
22	22	0,7	0,4	0,3	400	900	300	500	200	0,8	2,0	80
23	23	0,8	0,3	0,5	500	1000	200	600	700	0,9	1,2	90
24	24	0,7	0,2	0,8	600	900	100	300	800	0,8	1,3	50
25	25	0,6	0,3	0,7	700	800	1000	200	900	0,7	1,4	60
26	26	0,5	0,4	0,3	800	700	900	300	1000	0,6	1,5	70
27	27	0,3	0,5	0,4	900	100	700	800	400	0,5	1,6	80
28	28	0,4	0,6	0,2	1000	600	600	700	100	0,5	1,7	90
29	29	0,5	0,6	0,6	300	700	500	600	500	0,6	1,8	60
30	30	0,6	0,5	0,4	400	800	400	500	300	0,7	1,9	70
31	31	0,7	0,4	0,3	500	900	300	600	200	0,8	2,0	80
32	32	0,8	0,3	0,5	600	1000	200	300	700	0,9	1,2	90
33	33	0,7	0,2	0,8	700	900	100	800	800	0,8	1,3	50
34	34	0,6	0,3	0,7	800	800	1000	700	900	0,8	1,4	50
35	35	0,5	0,4	0,3	900	700	700	600	500	0,9	1,5	60
36	36	0,3	0,5	0,4	300	900	600	500	300	0,8	1,6	70
	б	г	в	б	а	в	б	а	г	а	б	в

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

11 схема 12 схема

13 схема 14 схема

15 схема 16 схема

17 схема 18 схема

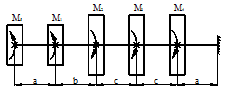
19 схема 20 схема

21 схема 22 схема

23 схема 24 схема

25 схема 26 схема

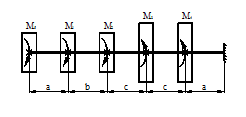
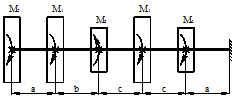
27 схема 28 схема

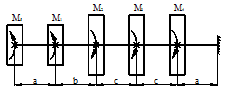
29 схема 30 схема

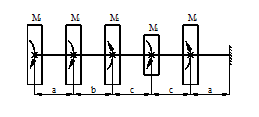
31 схема 32 схема

33 схема 34 схема

35 схема 36 схема

Рис.2

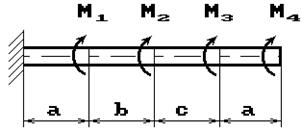
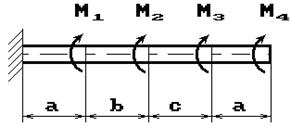
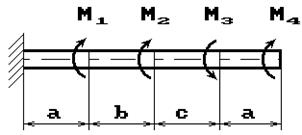
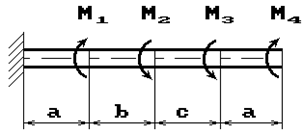
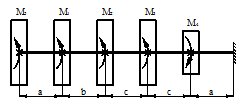
Задача 3. Подбор сечения статически определимого вала, работающего на кручение.

К стальному брусу круглого поперечного сечения приложены четыре крутящих момента M₁, M₂, M₃, X, три из которых известны.

Требуется:

1) установить, при каком значении момента Х угол поворота правого концевого сечения равен нулю;

2) при найденном значении Х построить эпюру крутящих моментов;

3) при заданном значении допускаемого напряжения [τ] определить диаметр вала из условия его прочности и округлить величину диаметра до ближайшей большей стандартной величины, равной 30, 35, 40, 45, 50, 60, 80, 90, 100 мм;

4) проверить, выполняется ли условие жесткости бруса при выбранном диаметре, если допускаемый угол закручивания [θ]= 1 град/м;

5) построить эпюру углов закручивания.

Для всех вариантов принять модуль сдвига для стали G=8∙10⁵ Мпа.

Числовые данные берутся из табл. 3, расчетные схемы – на рис. 3.

Таблица 3

Номер строки	Схема по рис. 3	Размер, м			Момент, кНм			[τ], МПа
Номер строки	Схема по рис. 3	а	в	с	M₁	M₂	M₃	[τ], МПа
01	1	0,8	0,4	1,0	2,0	1,6	1,0	35
02	2	0,6	0,5	0,5	1,8	1,7	1,2	40
03	3	0,4	0,7	0,7	1,7	0,9	0,7	50
04	4	0,6	0,4	0,6	1,5	0,8	1,5	45
05	5	0,5	0,8	0,4	1,3	2,0	1,4	60
06	6	0,7	1,0	0,8	1,0	1,7	2,0	40
07	7	1,0	0,7	1,0	1,6	1,5	1,6	35
08	8	0,4	0,6	0,5	1,4	1.6	1,8	70
09	9	0,7	0,4	0,6	1,5	0,8	0,9	80
10	10	0,5	0,5	0,4	0,9	1,0	1,5	60
	з	ж	а	б	в	г	д	е

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

Рис. 3

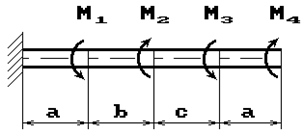
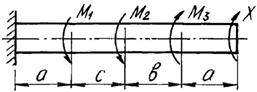
Задача 4. Расчет статически определимого вала, работающего на кручение. Определение допускаемой нагрузки.

На вал постоянного сечения насажены три шкива (рис.4). Из условия равновесия вала определить силу F₃ и построить эпюру крутящего момента.

Числовые данные берутся из табл. 4, расчетные схемы – на рис. 4.

Таблица 4

Номер cтроки	Схема по рис.4	r₁, м	r₂, м	r₃, м	F₁, кН	F₂, кН
01	I	0,20	0,05	0,10	40	50
02	II	0,10	0,20	0,15	10	20
03	III	0,15	0,10	0,20	30	10
04	IV	0,20	0,10	0,30	15	10
05	V	0,10	0,15	0,20	30	20
06	VI	0,30	0,10	0,15	40	10
07	VII	0,20	0,15	0,10	20	20
08	VIII	0,15	0,20	0,05	10	30
09	IX	0,05	0,15	0,20	20	10
10	X	0,10	0,20	0,15	30	30
11	I	0,20	0,05	0,10	40	50
12	II	0,10	0,20	0,15	10	20
13	III	0,15	0,10	0,20	30	10
14	IV	0,20	0,10	0,30	15	10
15	V	0,10	0,15	0,20	30	20
16	VI	0,30	0,10	0,15	40	10
17	VII	0,20	0,15	0,10	20	20
18	VIII	0,15	0,20	0,05	10	30
19	IX	0,05	0,15	0,20	20	10
20	X	0,10	0,20	0,15	30	30
21	I	0,20	0,05	0,10	40	50
22	II	0,10	0,20	0,15	10	20
23	III	0,15	0,10	0,20	30	10
24	IV	0,20	0,10	0,30	15	10
25	V	0,10	0,15	0,20	30	20
26	VI	0,30	0,10	0,15	40	10
27	VII	0,20	0,15	0,10	20	20
28	VIII	0,15	0,20	0,05	10	30
29	IX	0,05	0,15	0,20	20	10
30	X	0,10	0,20	0,15	30	30
31	I	0,20	0,05	0,10	40	50
32	II	0,10	0,20	0,15	10	20
33	III	0,15	0,10	0,20	30	10
34	IV	0,20	0,10	0,30	15	10
35	V	0,10	0,15	0,20	30	20
36	VI	0,30	0,10	0,15	40	10
	а	г	в	б	а	в

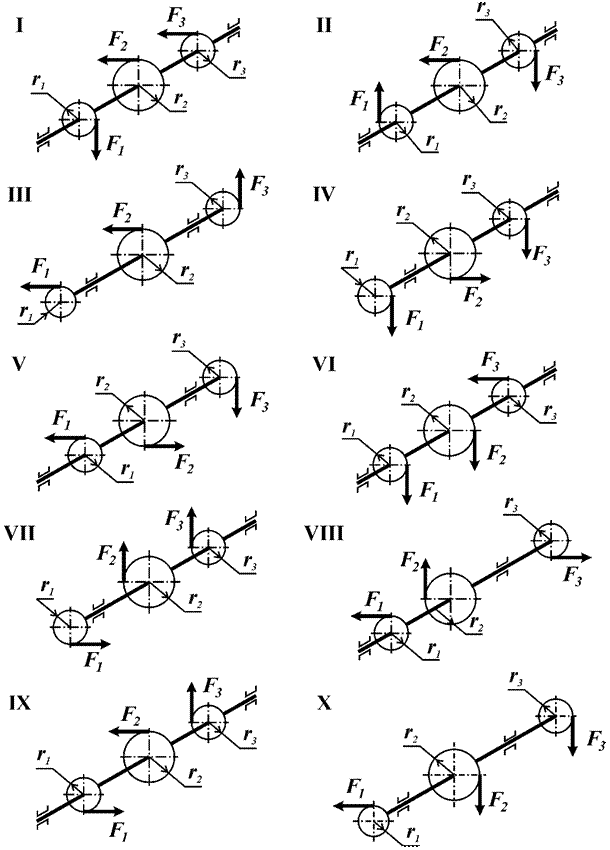
Рис.4

Задача 5. Расчет статически определимого вала, работающего на кручение. Построение эпюры M_k.

Вал (рис. 5) находится в равновесии под действием двух пар сил моментами M₁ и M₂ и двух равномерно распределенных по длине стержня моментов интенсивностью m₁ и m₂. Построить эпюру крутящего момента в долях ml.

Числовые данные берутся из табл. 5, расчетные схемы – на рис. 5.

Таблица 5

Номер cтроки	Схема по рис.5	l₁/l	l₂/l	m₁/m	m₂/m	M₁/ml	M₂/ml
01	I	1,0	1,5	1,0	1,0	–1,0	–2,0
02	II	2,0	1,0	2,5	–2,0	2,0	1,5
03	III	3,0	2,0	1,5	3,0	2,5	1,0
04	IV	1,5	3,0	2,0	–1,5	3,0	2,5
05	V	1,0	1,5	1,0	–2,5	–1,5	–1,0
06	VI	2,0	1,0	–1,5	–1,0	–1,5	1,0
07	VII	3,0	2,0	–2,5	2,0	2,0	–1,5
08	VIII	1,5	1,0	–1,0	–3,0	1,0	2,5
09	IX	1,0	2,0	–2,0	1,5	–2,5	–3,0
10	X	2,0	3,0	–1,0	2,5	1,5	–2,5
11	I	1,0	1,5	1,0	1,0	–1,0	–2,0
12	II	2,0	1,0	2,5	–2,0	2,0	1,5
13	III	3,0	2,0	1,5	3,0	2,5	1,0
14	IV	1,5	3,0	2,0	–1,5	3,0	2,5
15	V	1,0	1,5	1,0	–2,5	–1,5	–1,0
16	VI	2,0	1,0	–1,5	–1,0	–1,5	1,0
17	VII	3,0	2,0	–2,5	2,0	2,0	–1,5
18	VIII	1,5	1,0	–1,0	–3,0	1,0	2,5
19	IX	1,0	2,0	–2,0	1,5	–2,5	–3,0
20	X	2,0	3,0	–1,0	2,5	1,5	–2,5
21	I	1,0	1,5	1,0	1,0	–1,0	–2,0
22	II	2,0	1,0	2,5	–2,0	2,0	1,5
23	III	3,0	2,0	1,5	3,0	2,5	1,0
24	IV	1,5	3,0	2,0	–1,5	3,0	2,5
25	V	1,0	1,5	1,0	–2,5	–1,5	–1,0
26	VI	2,0	1,0	–1,5	–1,0	–1,5	1,0
27	VII	3,0	2,0	–2,5	2,0	2,0	–1,5
28	VIII	1,5	1,0	–1,0	–3,0	1,0	2,5
29	IX	1,0	2,0	–2,0	1,5	–2,5	–3,0
30	X	2,0	3,0	–1,0	2,5	1,5	–2,5
31	I	1,0	1,5	1,0	1,0	–1,0	–2,0
32	II	2,0	1,0	2,5	–2,0	2,0	1,5
33	III	3,0	2,0	1,5	3,0	2,5	1,0
34	IV	1,5	3,0	2,0	–1,5	3,0	2,5
35	V	1,0	1,5	1,0	–2,5	–1,5	–1,0
36	VI	2,0	1,0	–1,5	–1,0	–1,5	1,0
	г	а	в	б	а	в	б

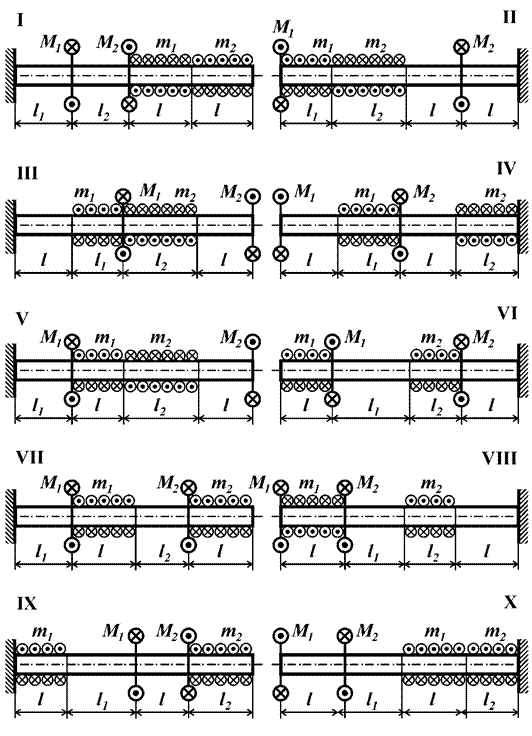
2пособие по сопромату задачи

Рис.5

Задача 6. Расчет статически определимого вала, работающего на кручение. Подбор сечения.

Для прямого стержня, нагруженного крутящими моментами по схеме, указанной на рис.6, необходимо:

1. Записать выражение крутящего момента M(z) и построить его график.

2. Подобрать из расчета на прочность по теории наибольших касательных напряжений диаметр круглого поперечного сечения.

3. Подобрать из расчета на прочность размеры кольцевого сечения при условии d=α∙D.

4. Сравнить веса выбранных стержней.

5. Найти величину и направление главных напряжений в опасной точке одного из стержней.

Числовые данные берутся из табл. 6, расчетная схема – на рис.6.

Рис.6. Схема нагружения и поперечное сечение

Таблица 6

Номер строки	l, м	a, м	b, м	c, м	e, м	L₁, кНм	L₂, кНм	m, кНм/м	α	[σ], МПа
1	0,4	0,2	0,4	0	0,3	1,2	- 1,7	4,0	0,8	103
2	0,5	0,4	0,2	0	0,5	1	- 1,5	3,7	0,5	109
3	0,4	0,4	0,2	0,1	0,3	1,5	- 1,9	4,6	0,6	119
4	0,6	0,4	0,6	0,1	0,2	1,5	1,8	- 4,0	0,8	120
5	0,8	0,5	0,7	0,2	0,8	1,2	2,4	3,6	0,7	122
6	0,8	0,3	0,6	0,2	0,8	- 2,6	- 1,1	5,4	0,8	134
7	0,6	0,4	0,6	0,1	0,5	1,5	- 2	3,4	0,8	114
8	0,8	0,3	0,1	0,5	0,8	- 2,5	1,5	3,9	0,6	142
9	0,5	0,3	0,5	0,1	0,2	- 1,2	1,4	3,9	0,6	113
10	0,4	0,2	0,4	0,1	0,2	- 1,4	1,2	3,7	0,9	120
11	0,8	0,3	0,7	0,1	0,5	- 1,5	-2,3	6,3	0,8	100
12	0,8	0,8	0,1	0,3	0,5	- 1,8	1,3	4,5	0,5	113
13	0,4	0,1	0,3	0,2	0,4	0,9	- 1,5	3,7	0,8	121
14	0,5	0,3	0,5	0,1	0,5	- 2,4	1,7	5,4	0,6	102
15	0,6	0,1	0,5	0,2	0,6	1	- 2,6	5,5	0,6	126
16	0,7	0,7	0,3	0,3	0,7	2,2	1,7	-6,4	0,5	117
17	0,4	0,3	0,1	0	0,4	- 1	2,2	5,5	0,6	151
18	0,6	0,6	0,1	0,2	0,4	1,5	- 2,9	5,3	0,6	161
19	0,5	0,3	0,5	0,1	0,4	1,5	1,8	3,7	0,6	164
20	0,5	0,4	0,3	0,1	0,5	- 2,1	1,4	5,7	0,5	124
21	0,4	0,4	0,2	0	0,3	- 0,6	- 0,3	5,2	0,7	122
22	0,8	0,2	0,8	0,3	0,8	1,5	2,5	-3,2	0,7	150
23	0,4	0,3	0,1	0,2	0,4	- 0,5	0,5	7,6	0,7	167
24	0,5	0,3	0,5	0	0,5	- 0,6	0,4	7,3	0,9	166
25	0,8	0,6	0,8	0	0,6	- 0,7	0,6	3,7	0,7	129
26	0,6	0,3	0,1	0,2	0,6	- 1	- 0,3	5,6	0,7	100
27	0,6	0,5	0,6	0,1	0,4	- 0,7	0,3	6,9	0,5	131
28	0,4	0,4	0,2	0	0,1	0,9	- 0,5	6,4	0,6	177
29	0,4	0,1	0,2	0	0,3	- 0,6	1,5	7,1	0,8	162
30	0,6	0,3	0,1	0	0,5	1,5	- 0,8	8,9	0,7	171
	в	г	а	б	а	г	в	б	а	г

Примеры выполнения задач

Пример 1

Для заданного бруса круглого сечения (рис. 7, а) требуется:

1) определить величину момента X, при котором угол поворота свободного конца бруса равен нулю,

2) построить эпюры крутящих моментов и углов закручивания,

3) подобрать диаметр сечения по условию прочности и произвести проверку бруса на жесткость.

Дано: а =0,8 м; в=1,0 м; с=0,4 м; M₁=2 кНм; M₂=0,9 кНм; M₂=1 кНм; [t]=40 МПа; G=8×10⁴МПа.

Рис.7. Брус, работающий на кручение:
а - расчетная схема; б - эпюра крутящих моментов;
в - эпюра углов закручивания

Решение.

1.Определение величины неизвестного крутящего момента Х.

Брус жестко заделан левым концом А, правый конец Е свободный. В сечениях В, С, и D приложены известные крутящие моменты. Для определения неизвестного момента Х используем условие равенства нулю угла поворота сечения Е.

Угол поворота сечения Е относительно сечения А определяется как сумма углов закручивания отдельных участков:

Крутящие моменты M_кр, входящие в выражение (1), определяются по приведенному выше правилу.

Вычисления начинаем с незакрепленного конца:

Используя выражения (2) и сокращая на GJ_ρ, приводим уравнение (1) к виду

(X-1,9)∙a+(X+0,1)∙b+(X+1,0)∙c+X∙a=0.

Подставляя значения a, b, c (рис.7, а) и решая это уравнение, получаем Х = 0,34 кНм.

Примечание: если значение Х получится со знаком минус, направление крутящего момента задано неправильно. В данном примере X положителен, следовательно, направление крутящего момента, показанное на рис.7, правильно.

2. Построение эпюры крутящих моментов.

Найденное значение Х = 0,34 кНм подставляем в выражения (2), вычисляя таким образом величину крутящего момента на каждом участке:

; ;

;

По найденным значениям М_кр строим эпюру крутящих моментов. Для этого рассматриваем последовательно участки ЕD, DC, CB и CA. Крутящие моменты, действующие на этих участках, уже вычислены.

Величина крутящего момента на каждом участке не зависит от положения сечения в пределах участка (крутящий момент постоянен), поэтому эпюра крутящих моментов ограничена отрезками прямых (рис.7,б). Построенная эпюра позволяет найти опасное сечение, т.е. такое, в котором действует максимальный (по модулю) крутящий момент.

В рассматриваемом примере опасными будут сечения в пределах участка АВ; расчетное значение крутящего момента

3. Подбор диаметра поперечного сечения бруса.

Используем условие прочности

Учитывая, что , выразим диаметр из условия прочности

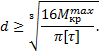
Подставляя и [τ]=40∙10⁶ Па, вычисляем диаметр поперечного сечения, округляя его до стандартной величины:

4. Проверка условия жесткости.

Условие жесткости записываем в форме:

По условию задачи [q]= 1 град/м. Переводя значение угла из градусной меры в радианную, получаем

Вычисляем выражение, стоящее в левой части условия жесткости, определив предварительно величину полярного момента инерции бруса:

Сравнение левой и правой частей условия жесткости показывает, что оно выполняется:

5. Построение эпюры углов закручивания.

Вычисляем углы закручивания по участкам, используя формулу :

Угол поворота каждого сечения равен сумме углов закручивания соответствующих участков бруса. Суммирование углов начинаем с незакрепленного конца А:

φ_A=0, так как сечение в заделке неподвижно;

φ_B=φ_AB= -0,01228;

φ_C=φ_AB+φ_BC= -0,01228+0,0043= -0,008;

φ_D=φ_AB+φ_BC+φ_CD= -0,01228+0,0043+0,0053= -0,0027;

φ_E=φ_AB+φ_BC+φ_CD+φ_DE= -0,01228+0,0043+0,0053+0,0027=0.

По вычисленным углам поворота сечений построена эпюра углов закручивания (рис. 7, в).

Равенство φ_E=0 является проверкой решения, так как неизвестный крутящий момент Х определялся из условия равенства нулю угла поворота свободного конца бруса.

Пример 2

К стальному валу приложены четыре сосредоточенных момента (рис. 8).

Дано: a=1,2 м, b=1,9 м, c=1,7 м, M₁=1,2 кНм, M₂=1,9 кНм, M₃=1,7 кНм, [τ]=40 Мпа. Для стали модуль поперечного сдвига равен G=80 Гпа.

Требуется:

1) построить эпюру крутящих моментов;

2) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его до ближайшей большей величины из нормального ряда чисел: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 125, 140, 160, 180, 200 мм;

3) найти наибольший относительный угол закручивания и проверить жесткость вала при [θ]=0,05 рад/м.

Рис. 8

Решение.

Крутящие моменты, возникающие в поперечных сечениях вала, определяются по внешним скручивающим моментам с помощью метода сечений (рис. 9):

участок № 1 (0≤z₁≤1,2 м), =-1,2 кНм;

участок № 2 (0≤z₂≤1,7 м), =-1,2+1,7=0,5 кНм;

участок № 3 (0≤z₃≤1,9 м), =-1,2+1,7+1,9=2,4 кНм;

участок № 4 (0≤z₄≤1,2 м), =-1,2+1,7+1,9-1,2=1,2 кНм.

Для удобства построения эпюр М_кр принимаем следующее правило знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части вала действующий на него момент представляется направленным по ходу часовой стрелки.

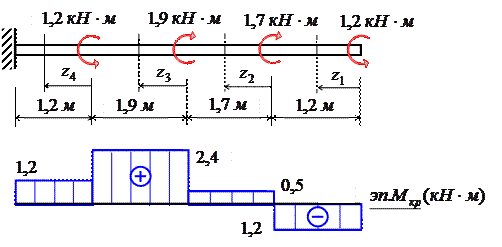
Рис. 9

Диаметр вала находим из условия прочности по касательным напряжениям

Принимаем d = 70 мм.

Крутильная жесткость поперечного сечения вала будет равна (полярный момент инерции для круглого сечения )

Наибольший относительный угол закручивания определяем по формуле

В нашем случае имеем θ_max<[θ], где [θ]=0,05. Таким образом, условие жесткости (θ_max≤[θ]) соблюдается.

Пример 3

К стальному валу приложены четыре сосредоточенных момента (рис. 10).

Дано: a= b= c=1,4 м, M₁=M₂=M₃=1,4 кНм, [τ]=50 Мпа. Для стали модуль поперечного сдвига равен G=8∙10⁴ МПа.

Требуется:

1) Установить, при каком значении момента угол поворота концевого сечения вала равен нулю.

2) Построить эпюру крутящих моментов.

3) Определить диаметр вала из условия прочности.

4) Построить эпюру углов закручивания.

5) Найти наибольший относительный угол закручивания.

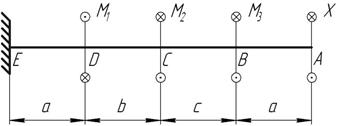
Рис.10

Решение.

1) Найдем, при каком значении момента угол поворота концевого сечения вала равен нулю

Получили значение момента , следовательно, нужно изменить направление действия момента.

2) Определи крутящие моменты на каждом участке вала

Участок АВ:

Участок BC:

Участок CD:

Участок DC:

По полученным результатам построим эпюру крутящих моментов (рис.11).

Рис.11. Эпюра

3) Определим диаметр вала

Условие прочности:

где – полярный момент сопротивления сечения вала, – наибольший по величине крутящий момент.

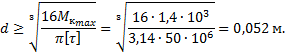
Примем

4) Определим углы закручивания поперечных сечений вала

По полученным результатам построим эпюру углов закручивания (рис.12).

Рис.12. Эпюра

5) Наибольший относительный угол закручивания

Пример 4

К статически неопределимому валу приложены четыре сосредоточенных момента (рис. 13).

Дано: М = 12 кНм; = 2,9 м; = 1,3 м; d = 0,25 м.

Требуется:

1) Раскрыть статическую неопределимость.

2) Построить эпюру крутящих моментов.

3) Вычислить максимальные напряжения в сечениях на каждом участке вала.

Рис.13

Решение.

Жесткость вала при кручении по всей его длине постоянна и равна GI_p. Для раскрытия статической неопределимости вала выберем основную систему, отбросив правую заделку и приложив вместо нее неизвестный пока момент X_B.

Составим уравнение деформаций, приравняв угол закручивания в сечении В от действия всех скручивающих моментов М, включая момент X_B, нулю. При составлении уравнения деформаций будем пользоваться принципом наложения, суммируя углы закручивания от действия каждого момента в отдельности:

Отсюда определим величину

Так как нагрузка действующая на вал симметрична, то момент в сечении А будет направлен в туже сторону и равен:

Теперь при известных крутящих моментах построим эпюру крутящих моментов (рис.14).

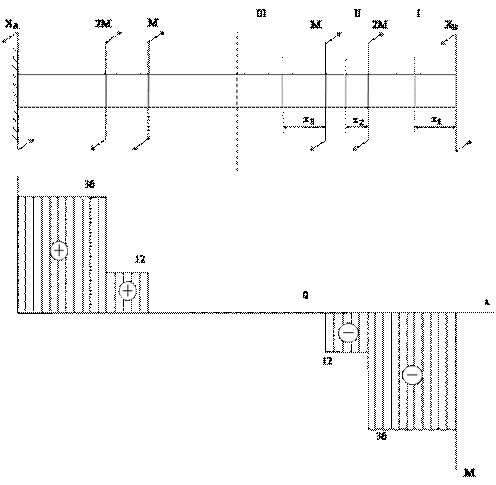
Рис.14

Вычислим максимальные напряжения в сечениях на каждом участке вала по формуле:

Пример 5

Для стержня постоянного сечения (рис. 15) требуется построить эпюру углов закручивания и из условия жесткости найти искомое значение диаметра стержня d. Материал стержня – сталь, G=80 Гпа.

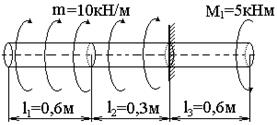
Рис.15

Решение.

1) Построение эпюры углов закручивания.

Разобьем стержень на участки AB и BC (рис.16).

Рис.16

В пределах каждого участка возьмем произвольные сечения z₁ и z₂ соответственно.

Из условия равновесия определим момент в заделке:

Участок AB (0z₁l₁+ l₂):

Участок BC (l₁+ l₂z₂l₁+ l₂+l₃):

Находим углы закручивания в долях 1/GI_p.

На участке АВ:

ввиду наличия заделки в точке В.

Функцией угла закручивания на участке АВ является парабола, вторая производная от которой отрицательна, следовательно, парабола выпуклая.

На участке ВС:

По полученным данным строим эпюру углов закручивания Эφ в долях от GI_p(рис. 16).

2) Расчет на жесткость.

По условию жесткости, максимальный угол поворота не должен превышать допускаемый []=0,001рад/м, то есть . Из эпюры углов поворота, построенной в долях от GI_p видно, что максимальный угол поворота находится в сечении А .

Полярный момент инерции сечения , откуда найдем диаметр стержня:

Примем (из ряда Ra40 по ГОСТ 6636-69) d=160 мм.

Окончательно рассчитывая углы поворота в каждом сечении, получаем рад/м; =0 рад/м; рад/м;

По полученным данным строим эпюру углов закручивания Э (рис.16).

Онлайн-калькулятор "Расчет прочности при кручении вала круглого сечения"

Расчет прочности при кручении вала круглого сечения

кНм - крутящий момент в сечении

см - диаметр сечения

МПа - допускаемые касательные напряжения, определяются исходя из материала и требований к конструкции, можно найти в справочниках

Касательные напряжения при кручении определяются по формуле

τ_{m a x} = \frac{M_{к р}}{W_{ρ}}

$\tau_{max} = \frac{ M_{кр} }{ W_{\rho} }$

Полярный момент сопротивления определяется так

W_{ρ} = \frac{π d^{3}}{16}

$W_{\rho} = \frac{\pi d^3}{16}$

Поэтому, условие прочности при кручении

τ_{m a x} = \frac{16 M_{к р}}{π d^{3}} <= [τ]

$\tau_{max} = \frac{16 M_{кр} }{ \pi d^3 } <=[\tau]$ где, если момент в Ньютонах на метр (Нм), а диаметр в см, напряжения получатся в Мегапаскалях (МПа).

Для нашего случая

τ_{m a x} = \frac{16 \cdot 70000}{π \cdot 12^{3}} = 206 М П а > [τ] = 80 М П а

$\tau_{max} = \frac{16 \cdot 70000 }{ \pi \cdot 12^3 } =206 МПа > [\tau]=80МПа$

Условие прочности не выполняется, необходимо увеличить сечение

Больше калькуляторов - на SOPROMAT.XYZ, кроме этого:

Расчет балок онлайн Расчет рам и ферм онлайн Растяжение-сжатие

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00