Главная

Задача 1. Определение напряжений и деформаций в криволинейном стержне

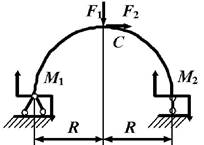
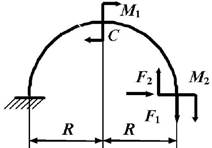
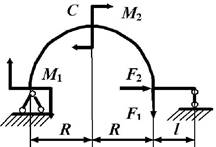
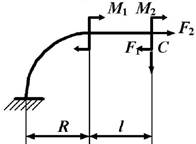
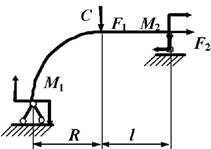
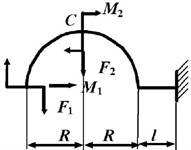
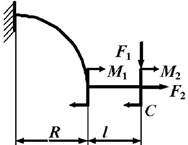
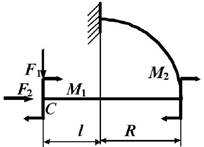
Исходные данные к задаче принимаются по табл. 1 и схемам на рис. 1.

1. Постройте эпюры внутренних усилий в стержне, вычисляя значения усилий для криволинейных участков через каждые 30^о, в начале и конце прямолинейного участка. Определите опасное сечение в криволинейной части стержня (сечение, где действует максимальный изгибающий момент).

2. Используя формулу для определения нормальных напряжений в криволинейных стержнях, найдите напряжения в крайних волокнах и в центре тяжести опасного сечения. При определении величины смещения нейтральной линии от центра тяжести при чистом изгибе стержней средней и малой кривизны (d/R = h/R < 0,5) допустимо использовать приближенную формулу z₀ = I_y / RA. Постройте эпюру нормальных напряжений в опасном сечении.

3. Вычислите напряжения в крайних волокнах опасного сечения по формуле теории прямолинейных стержней. Найдите процент расхождения в значениях максимальных растягивающих и сжимающих напряжений, полученных по теориям для криволинейных и прямолинейных стержней.

4. Определите вертикальное перемещение сечения C, используя приближенную формулу Максвелла - Мора для прямолинейных стержней.

5*. Оцените погрешность в определении перемещения при вычислении его по точной формуле Максвелла - Мора для криволинейных стержней по сравнению с вычислением по приближенной формуле.

Таблица 1

Номер строки	F1, кН	F2, кН	Схема на рис. 1,а	l, м	M1, кНм	M2, кНм	R, м	d/R (h/R)	Форма сечения на рис. 1,б	h/b	δ, мм
01	50	0	1	-	0	50	1,2	0,4	1	-	-
02	0	-50	2	-	-50	0	1,4	0,35	2	2	-
03	-60	0	3	1,6	0	60	1,6	0,3	3	-	10
04	0	60	4	1,4	-60	0	1,8	0,25	4	1	10
05	70	0	5	1,2	0	-70	2,0	0,2	1	-	-
06	0	-70	6	1,0	70	0	2,2	0,15	2	1	-
07	-80	0	7	0,8	0	90	2,4	0,25	3	-	20
08	0	80	8	0,6	-90	0	2,6	0,2	4	2	20
09	100	0	9	0,4	-100	0	2,8	0,15	1	-	-
10	0	-100	10	0,5	0	100	3,0	0,1	2	0,5	-
	а	в	г	б	а	в	г	б	а	в	г

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

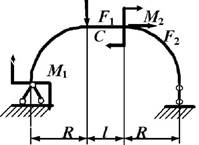
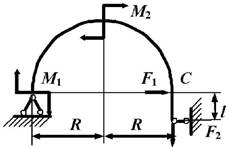
Рис.1,а

1 схема 2 схема 3 схема 4 схема

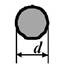
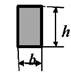
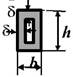
Рис. 1,б

Задача 2. Расчет криволинейной рамы с равномерно распределенной нагрузкой

Для каждого участка плоской криволинейной рамы записать закон изменения внутренних силовых факторов (в полярной системе координат) и построить соответствующие эпюры.

Исходные данные к задаче принимаются по табл. 2 и схемам на рис. 2.

Таблица 2

Номер строки	Схема на рис. 2	β	α, град
01	I	1	60
02	II	–1	45
03	III	1	90
04	IV	–1	120
05	V	1	90
06	I	–1	90
07	II	1	90
08	III	–1	60
09	IV	1	135
10	V	–1	60
	в	б	а

Рис.2

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00