Главная

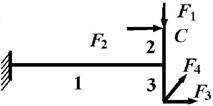
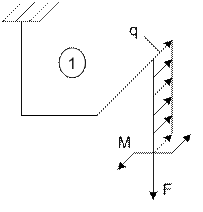
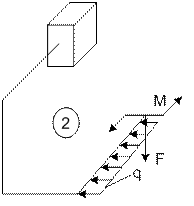
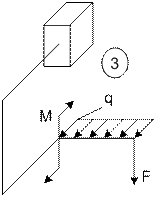
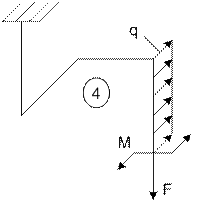
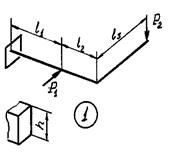
Задача 1. Расчет пространственного ломаного стержня

Исходные данные к задаче принимаются по табл. 1 и схемам на рис. 1.

1. Определите внутренние усилия (продольную и поперечные силы, изгибающие и крутящий моменты), действующие в сечениях стержня на различных участках. Постройте эпюры усилий.

2. Для стержня, примыкающего к заделке, обозначенного номером 1, определите положение опасного сечения.

3. Подберите размеры поперечного сечения из условия прочности. Дальнейший расчет проводится по двум вариантам: круглое и прямоугольное сечение:

- для круглого сечения предварительно подберите диаметр стержня, учитывая только действие изгиба и кручения, вычислив значение приведенного момента на основе соответствующей материалу стержня теории прочности;

- для прямоугольного сечения определите размеры его сторон при заданном соотношении h/b, учитывая в первом приближении только изгибающие моменты. Сечение должно быть расположено выгодным образом по отношению к силовым плоскостям.

4. Постройте эпюры нормальных и касательных напряжений в опасном сечении отдельно для каждого усилия, принимая во внимание все факторы. Для стержня круглого поперечного сечения допускается пренебречь действием поперечных сил.

5. Проверьте прочность стержня во всех опасных точках на основе соответствующей материалу теории прочности с учетом всех действующих усилий (кроме поперечной силы в случае круглого сечения). Если условие прочности не будет выполнено (либо сечение окажется неэкономичным), измените размеры сечения.

6*. Определите полное линейное и угловое перемещения сечения С, используя формулу Максвелла - Мора.

Таблица 1

Номер строки	ll, м	F1, кН	Схема по рис. 1	F4, кН	l2, м	h/b	F2, кН	F3, кН	l3, м	Материал
01	1,0	20	1	-10	0,5	1	20	0	0,6	Сталь
02	0,8	-10	2	20	0,4	2	0	10	0,5	Чугун
03	0,6	-20	3	-20	0,3	3	-30	0	0,4	Бронза
04	0,5	10	4	10	0,6	1	0	-20	0,3	Бронза
05	0,4	30	5	-30	0,7	2	-10	0	0,2	Чугун
06	0,3	-30	6	30	0,3	3	0	30	0,3	Бронза
07	0,6	5	7	-5	0,4	1	-20	0	0,4	Дюралюм.
08	0,7	-5	8	5	0,5	2	0	-10	0,5	Дюралюм.
09	0,9	40	9	-40	0,8	3	30	0	0,6	Сталь
10	1,0	-40	10	40	1,0	1	0	20	0,3	Сталь
	а	б	в	г	а	б	в	г	а	б

1 схема 2 схема

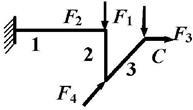
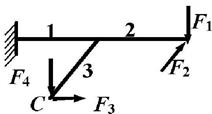
3 схема 4 схема

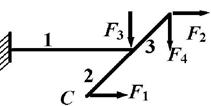
5 схема 6 схема

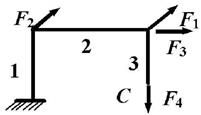
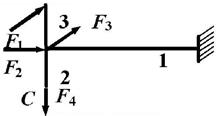
7 схема 8 схема

9 схема 10 схема

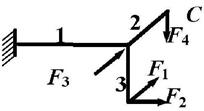
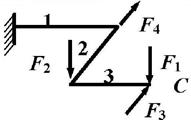
Рис.1

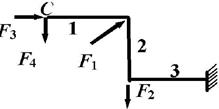
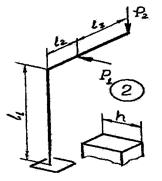
Задача 2. Расчет плоско-пространственной консольной рамы

Плоско-пространственная консольная рама нагружена сосредоточенными силами и парами сил.

Требуется: Построить эпюры внутренних силовых факторов.

Исходные данные к задаче принимаются по табл. 2 и схемам на рис. 2.

Таблица 2

Номер строки	Схема по рис.2	M/Pl	F1/P	F2/P	l1/l	l2/l	l3/l
01	I	1	3	2	2	1	1
02	II	1	2	2	1	1	2
03	III	1	1	0,5	2	1	2
04	IV	2	–3	1	1	1	2
05	V	2	2	2	2	2	1
06	VI	2	–1	1	1	2	1
07	VII	1	3	1,5	2	2	1
08	VIII	1	–2	1	1	1	2
09	IX	1	1	1	2	1	2
10	X	2	–1	2	1	1	2
11	I	1	3	1,5	2	1	1
12	II	1	2	1,5	1	1	2
13	III	1	1	2	2	1	2
14	IV	2	–3	1	1	1	2
15	V	2	2	1	2	2	1
16	VI	2	–1	2	1	2	1
17	VII	1	3	3	2	2	1
18	VIII	1	–2	1	1	1	2
19	IX	1	1	2	2	1	2
20	X	2	–1	2	1	1	2
21	I	1	3	2	2	1	1
22	II	1	2	2	1	1	2
23	III	1	1	4	2	1	2
24	IV	2	–3	1,4	1	1	2
25	V	2	2	4	2	2	1
26	VI	2	–1	2	1	2	1
27	VII	1	3	1,5	2	2	1
28	VIII	1	–2	1	1	1	2
29	IX	1	1	2	2	1	2
30	X	2	–1	1,5	1	1	2
	а	г	а	б	а	в	г

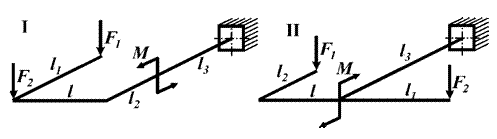
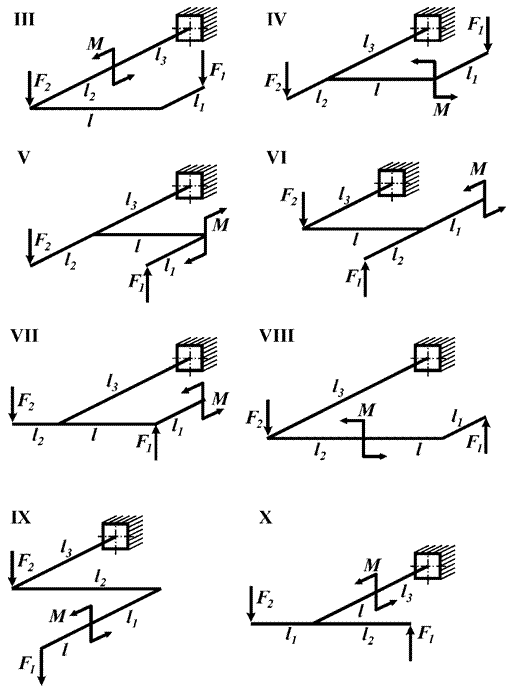
Рис.2

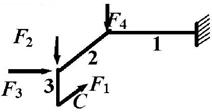
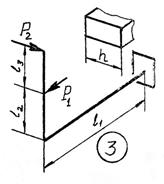
Задача 3. Расчет пространственной консольной рамы

Пространственная консольная рама нагружена сосредоточенными силами F₁ и F₂.

Требуется: Построить эпюры внутренних силовых факторов.

Исходные данные к задаче принимаются по табл. 3 и схемам на рис. 3.

Таблица 3

Номер строки	Схема по рис.3	F1/P	F2/P	l1/l	l2/l	l3/l
01	I	–1,0	1,0	0,5	1,0	1,0
02	II	1,5	2,0	1,5	2,0	2,0
03	III	–1,5	3,0	2,0	1,5	3,0
04	IV	2,0	2,0	1,5	1,5	3,0
05	V	–1,5	1,0	1,0	2,0	2,0
06	VI	1,0	–1,0	1,0	1,0	1,0
07	VII	1,0	–2,0	0,5	2,0	1,0
08	VIII	1,5	–3,0	1,5	1,5	2,0
09	IX	–2,0	–2,0	2,5	2,0	2,0
10	X	2,0	–1,0	2,0	1,0	3,0
11	I	–1,0	1,0	0,5	1,0	1,0
12	II	1,5	2,0	1,5	2,0	2,0
13	III	–1,5	3,0	2,0	1,5	3,0
14	IV	2,0	2,0	1,5	1,5	3,0
15	V	–1,5	1,0	1,0	2,0	2,0
16	VI	1,0	–1,0	1,0	1,0	1,0
17	VII	1,0	–2,0	0,5	2,0	1,0
18	VIII	1,5	–3,0	1,5	1,5	2,0
19	IX	–2,0	–2,0	2,5	2,0	2,0
20	X	2,0	–1,0	2,0	1,0	3,0
21	I	–1,0	1,0	0,5	1,0	1,0
22	II	1,5	2,0	1,5	2,0	2,0
23	III	–1,5	3,0	2,0	1,5	3,0
24	IV	2,0	2,0	1,5	1,5	3,0
25	V	–1,5	1,0	1,0	2,0	2,0
26	VI	1,0	–1,0	1,0	1,0	1,0
27	VII	1,0	–2,0	0,5	2,0	1,0
28	VIII	1,5	–3,0	1,5	1,5	2,0
29	IX	–2,0	–2,0	2,5	2,0	2,0
30	X	2,0	–1,0	2,0	1,0	3,0
	г	а	б	а	в	б

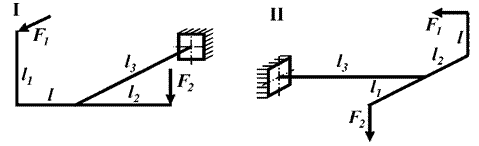
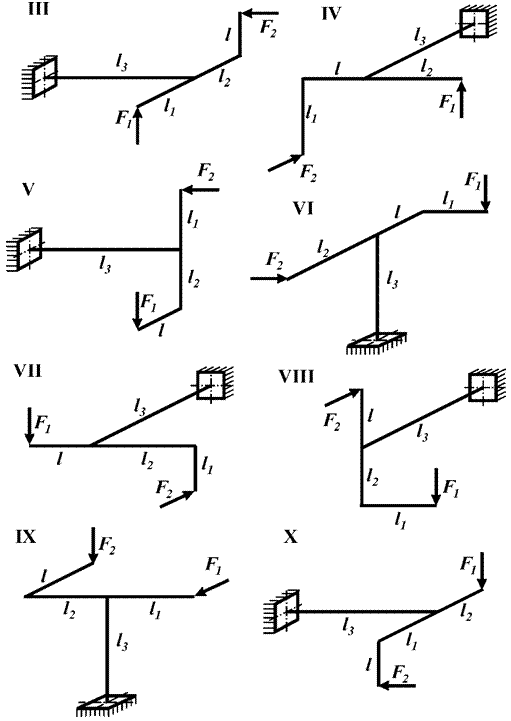
Рис.3

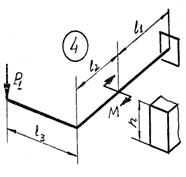
Задача 4. Расчет пространственной консольной рамы

Пространственная консольная рама нагружена сосредоточенными силами F₁, F₂ и F₃.

Требуется: Построить эпюры внутренних силовых факторов.

Исходные данные к задаче принимаются по табл. 4 и схемам на рис. 4.

Таблица 4

Номер строки	Схема по рис.4	F1/ql	F2/ql	F3/ql	l1/l	l2/l	l3/l
01	I	–2,0	1,0	–2,0	1,0	2,0	2,0
02	II	1,0	2,0	–1,0	2,0	1,0	3,0
03	III	2,0	3,0	1,0	1,5	2,0	1,0
04	IV	3,0	2,0	2,0	1,5	1,5	3,0
05	V	2,0	1,0	3,0	1,0	1,0	2,0
06	VI	1,0	–1,0	2,0	2,0	2,0	3,0
07	VII	–1,0	–2,0	1,0	2,5	1,5	1,0
08	VIII	–2,0	–3,0	–1,0	1,5	1,0	3,0
09	IX	–3,0	–2,0	–2,0	1,0	1,0	2,0
10	X	–2,0	–1,0	–3,0	2,0	2,0	3,0
11	I	–2,0	1,0	–2,0	1,0	2,0	2,0
12	II	1,0	2,0	–1,0	2,0	1,0	3,0
13	III	2,0	3,0	1,0	1,5	2,0	1,0
14	IV	3,0	2,0	2,0	1,5	1,5	3,0
15	V	2,0	1,0	3,0	1,0	1,0	2,0
16	VI	1,0	–1,0	2,0	2,0	2,0	3,0
17	VII	–1,0	–2,0	1,0	2,5	1,5	1,0
18	VIII	–2,0	–3,0	–1,0	1,5	1,0	3,0
19	IX	–3,0	–2,0	–2,0	1,0	1,0	2,0
20	X	–2,0	–1,0	–3,0	2,0	2,0	3,0
21	I	–2,0	1,0	–2,0	1,0	2,0	2,0
22	II	1,0	2,0	–1,0	2,0	1,0	3,0
23	III	2,0	3,0	1,0	1,5	2,0	1,0
24	IV	3,0	2,0	2,0	1,5	1,5	3,0
25	V	2,0	1,0	3,0	1,0	1,0	2,0
26	VI	1,0	–1,0	2,0	2,0	2,0	3,0
27	VII	–1,0	–2,0	1,0	2,5	1,5	1,0
28	VIII	–2,0	–3,0	–1,0	1,5	1,0	3,0
29	IX	–3,0	–2,0	–2,0	1,0	1,0	2,0
30	X	–2,0	–1,0	–3,0	2,0	2,0	3,0
	г	а	б	г	а	в	б

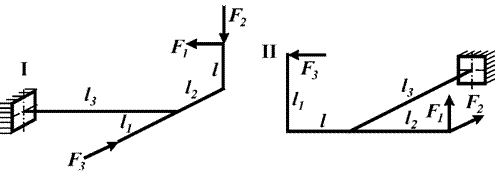
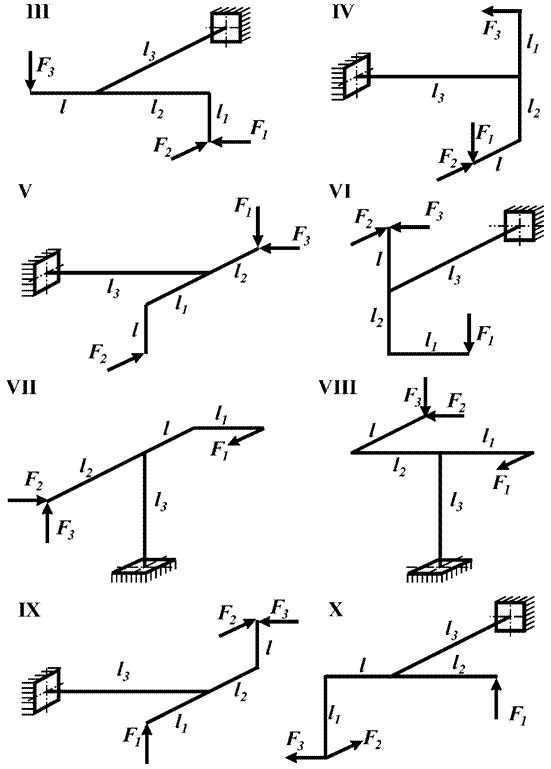
Рис.4

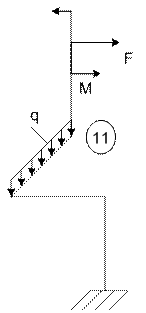
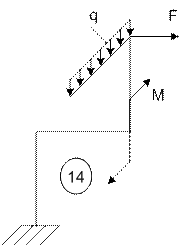
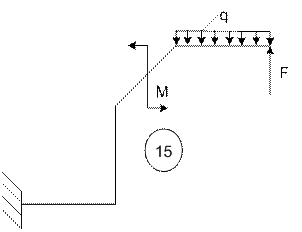
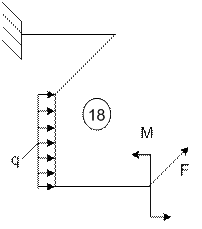
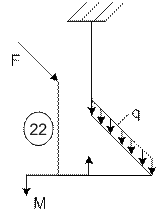
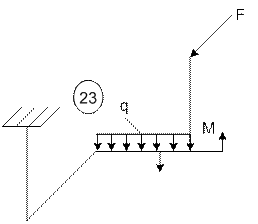
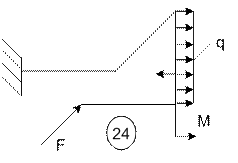
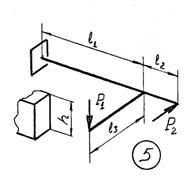
Задача 5. Расчет пространственного ломаного бруса переменного сечения

Исходные данные к задаче принимаются по табл. 5 и схемам на рис. 5.

1. Необходимо обозначить стержни, начиная от свободного конца;

2. Выбрать и построить плавающую систему координат;

3. Последовательно, от консоли к защемлению, выделить произвольные сечения с координатами привязки к началу участка;

4. Записать уравнения равновесия внутренних силовых факторов с учетом знаков;

5. Построить эпюры внутренних силовых факторов;

6. Произвести проверку правильности эпюр;

7. На третьем (круглого сечения) участке проанализировать загруженность сечений;

8. Произвести расчет круглого сечения с построением эпюр напряжений;

9. Проверить условия прочности круглого сечения;

10. Произвести анализ загруженности сечений четвертого (прямоугольного сечения) участка;

11. Подобрать сечение бруса из условия прочности, построить эпюры напряжений;

12. Проверить условия напряженного состояния прямоугольного сечения для характерных точек.

Таблица 5

Номер строки	Схема по рис. 5	q, кН/м	F, кН	M, кНм
01	1	5	8	4
02	2	6	6	5
03	3	4	5	6
04	4	3	9	3
05	5	5	8	5
06	6	7	6	4
07	7	6	7	3
08	8	5	9	4
09	9	6	6	5
10	10	4	8	5
11	11	7	7	4
12	12	5	8	9
13	13	4	7	8
14	14	5	6	7
15	15	3	5	8
16	16	4	4	6
17	17	5	7	9
18	18	7	6	5
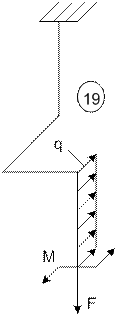
19	19	8	4	3
20	20	6	6	4
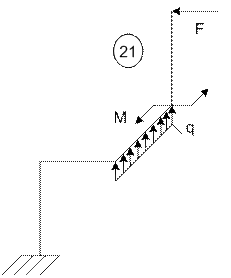
21	21	4	3	9
22	22	6	8	10
23	23	5	7	9
24	24	4	5	8
25	25	4	6	7
	в	г	а	в

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

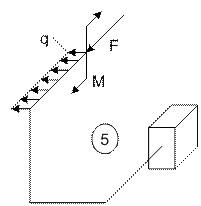
7 схема 8 схема

9 схема 10 схема

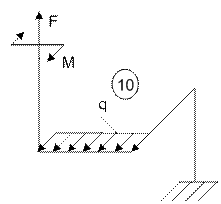
11 схема 12 схема

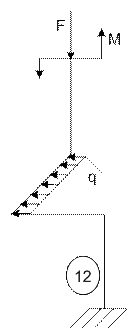
13 схема 14 схема

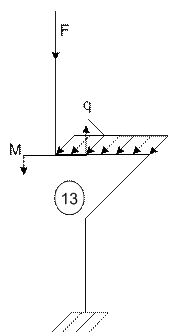
15 схема 16 схема

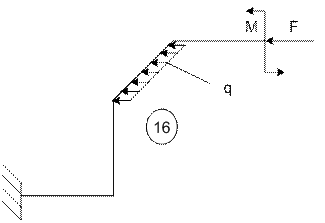
17 схема 18 схема

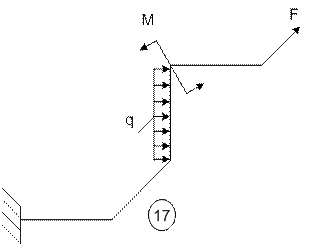
19 схема 20 схема

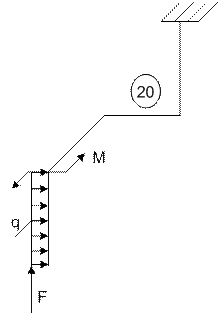
21 схема 22 схема

23 схема 24 схема

25 схема

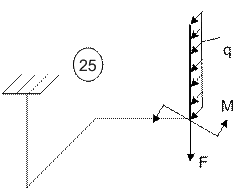
Рис.5

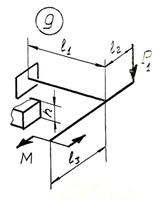
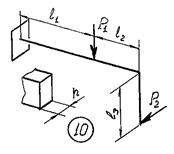
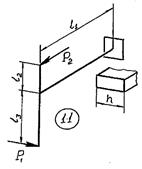
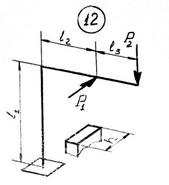
Задача 6. Расчет пространственного ломаного бруса

Для пространственного бруса требуется:

1. Построить эпюры изгибающих и крутящего момента.

2. По гипотезе наибольших касательных напряжений подобрать диаметр круглого бруса при допускаемом напряжении [𝜎].

3. Заменить круглое сечение бруса прямоугольным при заданном размере h стороны прямоугольного сечения.

Исходные данные к задаче принимаются по табл. 6 и схемам на рис. 6.

Таблица 6

Номер строки	Схема по рис.6	l1, м	l2, м	l3, м	P1, кН	P2, кН	М, кНм	[σ], МПа	h, см
01	1	2	1	2	3	1	0	160	8
02	4	3	1	2	1	0	4	120	8
03	7	1,5	1	0,5	2	3	0	120	9
04	10	2	2	1	2	0,5	0	120	8
05	13	2	1,5	2	0,5	0,5	0	120	6
06	3	3,5	1	1	1	0,5	0	160	6
07	5	3	1	1,5	2	1,5	0	160	10
08	8	4	2	1	1	4	0	160	10
09	11	2	0,5	1	1	4	0	120	10
10	15	2	3,5	2	2	2	0	120	14
11	2	4	0,5	1,5	2	2	0	160	16
12	6	2	0,5	1,5	2	0	8	120	12
13	9	1,5	1	2	2	0	6	100	12
14	12	1,5	1	1	2	3	0	120	9
15	14	1,5	0,5	1	1	0	2	120	8
16	2	3	2	2	1	1,5	0	100	10
17	6	4	1	3	1	0	1	120	6
18	7	3	1,5	1	4	3	0	160	15
19	11	2	3,5	2	1	1	0	120	7
20	14	3	1	2	2	0	8	120	16
21	1	4	4	2	1	0,25	0	100	6
22	5	3	1	2	2	3	0	120	10
23	9	3	2	4	1	0	3	100	12
24	12	4	0,5	1,4	1	1	0	160	8
25	13	4	3	4	1	1	0	120	6
26	3	7	2	2	0,5	0,25	0	120	8
27	4	2	1	1,5	2	0	6	100	14
28	8	2	0,5	1	0,5	2	0	120	5
29	10	2	1	2	6	2	0	160	16
30	15	2	1	1,5	1	4	0	120	5
	в	г	а	б	а	в	г	б	а

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

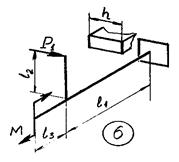
7 схема 8 схема

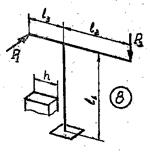
9 схема 10 схема

11 схема 12 схема

13 схема 14 схема

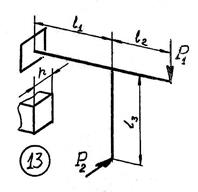
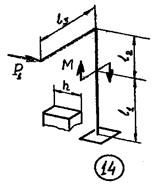
15 схема

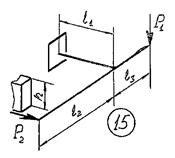
Рис.6

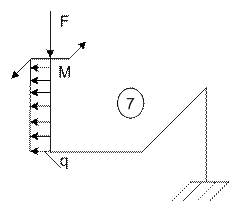
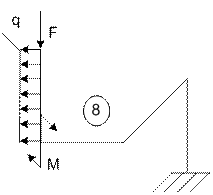
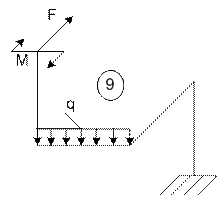
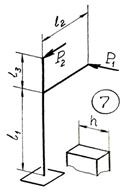
Примеры расчета пространственного ломаного бруса переменного сечения

Пример 1

На рис. 7 дана расчетная схема ломаного бруса (элемента коленчатого вала ДВС). Брус состоит из четырех участков, два из которых – третий и четвертый заданы круглым и прямоугольным сечениями, соответственно. Длина участков равна l. Силовое загружение включает сосредоточенную силу F, распределенную нагрузку q и момент M.

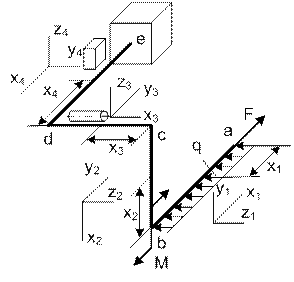
Рис. 7. Плавающая система координат

Решение.

Определяем плоскость, образованную двумя первыми стержнями (ab) и (bc). В данном примере – профильная плоскость. Вдоль стержня (ab) направляем ось X₁ к свободному концу; перпендикулярно к ней в профильной плоскости – ось Y₁; к плоскости X₁ – Y₁ восстанавливаем перпендикуляр – ось Z₁.

Примечание: ось Y₁ может быть направлена вверх или вниз; ось Z₁ может быть направлена вправо или влево.

1. Выбор и построение плавающей системы координат

1.1. Построение плавающей системы координат на остальных участках.

На участке bc система координат поворачивается относительно оси Z, перпендикулярной к плоскости, образованной стержнями ab и bc, следовательно, оси Z₁ и Z₂ имеют одинаковое направление, а ось X₂ направлена в сторону b. Поворачиваем "старую" систему до положения "новой" вокруг оси Z. При этом ось X₂ направлена вниз, ось Y₂ повернется из вертикального направления в горизонтальное от наблюдателя. Для третьего участка общим перпендикуляром к плоскости, образованной стержнями bc и cd, является ось Y. Для четвертого участка общий перпендикуляр к плоскости, образованной стержнями cd и de, – ось Z. Таким образом, вращая координатные системы вокруг общих перпендикуляров, получим остальные координатные системы.

На каждом участке выделяем отсеченные части (X₁ – X₄) с привязкой к началу рассматриваемого участка.

2. Уравнения равновесия отсеченных частей

Правила знаков сил и моментов

N –продольная сила – знак плюс при растяжении отсеченной части;

Q_y и Q_x – поперечные (перерезающие) силы определяются по направлению одноименных осей, вращение отсеченной части по часовой стрелке по направлению третьей координаты;

M_y и M_z – изгибающие моменты, действующие вокруг одноименных осей; знак плюс, если изгиб происходит в сторону третьей координаты;

T – крутящий момент, действующий вокруг оси X (в плоскости ZY); знак плюс определяется по правилу правого винта.

0≤Х₁≤l N₁=F; Q_y1=0; Q_z1=qx₁ (0; qa); M_y1=-qx₁²/2; M_z1=0; T₁=0.

0≤Х₂≤l N₁=0; Q_y2=F; Q_z2=ql; M_y2=-ql∙x₂²/2; M_z2=F∙x₂; T₂=-ql²/2.

0≤Х₃≤l N₃=-ql; Q_y3=F; Q_z3=0; M_y3=-ql²; M_z3=F∙x₃+ql²/2; T₃=Fl-M.

0≤Х₄≤l N₁=-F; Q_y4=-ql; Q_z4=0; M_y4=M-Fl; M_z4=Fl-ql(x₄-l/2); T₄=-ql².

3. Построение эпюр внутренних усилий N_x, Q_y, Q_z

Эпюра продольных сил N строится в плоскости XY с учетом знака, (см. рис. 8).

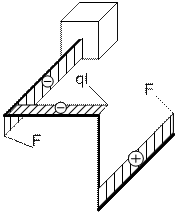
Рис. 8. Эпюра продольных сил N

Эпюры поперечных сил строятся в своих плоскостях со знаком, рис. 9 и рис. 10. Например, на первом участке эпюра Q_z1 имеет вид треугольника, построена в положительной полуплоскости X₁Z₁, рис. 10.

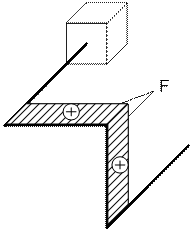
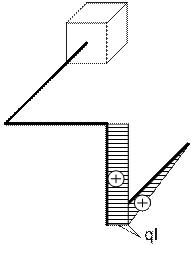
Рис. 9. Эпюра поперечных сил Q_y Рис.10. Эпюра поперечных сил Q_z

3.1. Проверка правильности построения эпюр сил

Главный вектор сил в узле равен нулю, если там отсутствует сосредоточенная сила. Необходимо определить попарно равенство ординат сил в узле.

Пример. Узел C: включает стержни bc и cd, табл. 7.

Таблица 7

Стержни	Эпюры
	Nx	Qy	Qz
bc	0	F	ql
cd	-ql	F	0

4. Построение эпюр моментов M_y, M_z, T

Эпюры изгибающих моментов M_y и M_z строятся на сжатых волокнах в плоскостях их действия, рис. 11 и рис. 12.

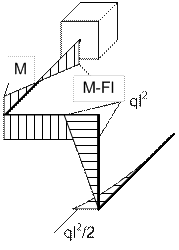
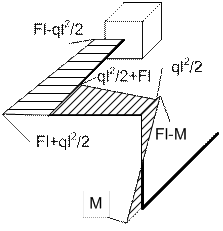
Рис.11. Эпюра изгибающего момента M_y Рис.12.Эпюра изгибающего момента M_z

Например: Уравнение равновесия M_z3=q∙l²/2+F∙x₄. Эпюра момента строится в горизонтальной плоскости в положительной полуплоскости (на сжатом волокне). При x₄=0; M_z4=q∙l²/2. При x₄=l; M_z4=q∙l²/2+F∙l.

Эпюра крутящего момента. Строится в плоскости ZY по правилу правого вращения отсеченной части стержня – положительное значение.

Например: Для третьего участка плоскость действия T(x₃) – Z₃Y₃ (профильная) наблюдается в виде прямой с указанием направления вращения. Для четвертого участка плоскость действия T(x₄) – Z₄Y₄ (фронтальная); в аксонометрии изображается в виде эллипса с указанием значения и направления вращения, рис. 13.

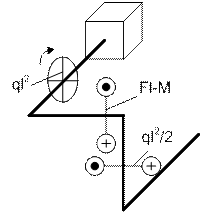
Рис. 13. Эпюра крутящего момента T

4.1. Проверка правильности построения эпюр моментов

Главный вектор момента в узле равен нулю, если там отсутствует сосредоточенный момент. Необходимо определить попарно равенство ординат моментов в узле.

Пример. Узел C: включает стержни bc и cd, табл. 8.

Таблица 8

Стержни	Эпюры
	My	Mz	T
bc	ql^2	Fl-M	ql^2/2
cd	ql^2	ql^2/2	Fl-M

5. Расчет на прочность круглого сечения

Ввиду линейности эпюр, проведем анализ загружения крайних сечений третьего стержня. Согласно табл. 9, сечения c и d одинаково загружены. Принимаем решение: произвести расчет по сечению c.

Примечание: касательные напряжения от поперечных сил Q_y и Q_z не учитываем ввиду их малости.

Таблица 9

Сечение	Эпюры
	N	My	Mz	T
c	-ql	ql^2	Fl-M	ql^2/2
d	-ql	ql^2	ql^2/2	Fl-M

Для этого развернем стержень cd вокруг Z₃, рис. 14.

Рис. 14. Расчет круглого сечения

5.1. Подбор диаметра круглого сечения

Считаем, что главным силовым фактором для круглого сечения является крутящий момент T=q∙l²/2

Условие прочности при действии момента T

Где W_x – полярный момент сопротивления; для круглого сечения W_x=π∙d³/16; [τ] – допускаемое напряжение для материала стержня; сталь 40Х – [τ]=80 МПа.

Из формулы (1) имеем

Округляем полученный результат в большую сторону с окончанием на "0" или "5" в мм.

5.2. Проверка напряженного состояния сечения С

5.2.1. Анализ по нормальным напряжениям

Проверка осуществляется с учетом нормальных напряжений, от действия силовых факторов N, M_y, M_z. Соответствующие напряжения определяют по зависимостям:

где A– площадь сечения; W_y, W_z – осевые моменты сопротивления относительно осей Y и Z, соответственно.

Для проверки строим эпюры напряжений

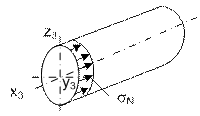
Рис. 15. Эпюра нормальных напряжений 𝛔_N

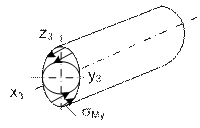
Рис. 16. Эпюра нормальных напряжений 𝛔_My

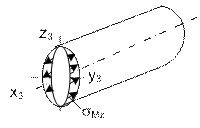
Рис. 17. Эпюра нормальных напряжений 𝛔_Mz

Эпюры показывают растяжение или сжатие волокон в соответствующих квадрантах.

Согласно рис. 15 – рис. 17 наиболее нагруженный квадрант – четвертый; в нем полное сжатие от действия трех факторов.

Напряженное состояние от указанных факторов считается одноосным, суммарное значение равно =σ_N+σ_My+σ_Mz. В данном примере σ_N имеет отрицательное значение, поэтому берем по модулю.

Условие первой проверки: ,

где [σ] – допускаемое нормальное напряжение, сталь 40Х [σ]=480 МПа.

В случае превышения допускаемого напряжения необходимо увеличивать диаметр стержня, добиваясь выполнения условия проверки.

5.2.2. Проверка по эквивалентным напряжениям

Условие второй проверки:

На рис.18 представлены эпюры касательных напряжений от T.

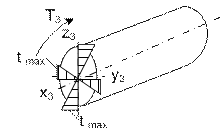
Рис.18. Эпюры касательных напряжений 𝛕

6. Расчет на прочность прямоугольного сечения

Анализ загруженности сечений четвертого стержня.

По табл. 10, определим, что сечение d загружено более. Произведем расчет по сечению d. На рис. 19 представлена расчетная схема прямоугольного стержня. Обозначим вершины граней сечения d цифрами 1– 4.

Таблица 10

Сечение	Эпюры
	N	My	Mz	T
d	-F	M-Fl	Fl+ql^2/2	-ql^2
e	-F	M-Fl	Fl-ql^2/2	-ql^2

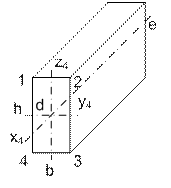
Рис. 19. Расчет прямоугольного сечения

6.1. Подбор параметров прямоугольного сечения

Для упрощения расчета принимаем соотношение сторон h/b=2. Основными силовыми факторами для прямоугольного стержня являются изгибающие моменты M_y и M_z.

Напряженное состояние от указанных факторов считается одноосным, суммарное значение равно =σ_My+σ_Mz. (1)

Запишем условие прочности и раскроем уравнение (1)

Где – осевой момент сопротивления (ось y₄); – осевой момент сопротивления (ось z₄). При соотношении h/b=2 и .

Из формулы (2) определим

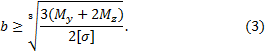
Округляем полученный результат в большую сторону с окончанием на "0" или "5" в мм.

6.2. Проверка напряженного состояния сечения d

6.2.1. Анализ по нормальным напряжениям

Первая проверка с учетом нормального напряжения от действия N. Соответствующие напряжения определяют по зависимостям:

где A– площадь сечения; W_y, W_z – осевые моменты сопротивления относительно осей Y и Z, соответственно.

Для проверки строим эпюры напряжений.

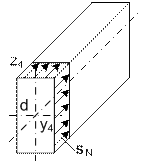
Рис. 20. Эпюра нормальных напряжений 𝛔_N

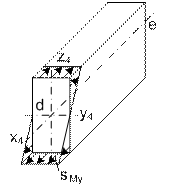
Рис. 21. Эпюра нормальных напряжений 𝛔_My

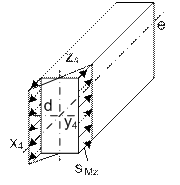
Рис. 22. Эпюра нормальных напряжений 𝛔_Mz

Согласно рис. 20–22 наиболее нагруженной точкой является точка 2.

Напряженное состояние от указанных факторов считается одноосным, суммарное значение равно =σ_N+σ_My+σ_Mz. В данном примере σ_N имеет отрицательное значение, поэтому берем по модулю.

Условие первой проверки: ,

где [σ] – допускаемое нормальное напряжение, сталь 40Х [σ]=480 МПа.

В случае превышения допускаемого напряжения необходимо увеличивать диаметр стержня, добиваясь выполнения условия проверки.

6.2.2. Проверка по эквивалентным напряжениям

Дополнительно проводят проверку напряженного состояния для точек 5 и 6.

На рис.23 представлена эпюра касательных напряжений от T.

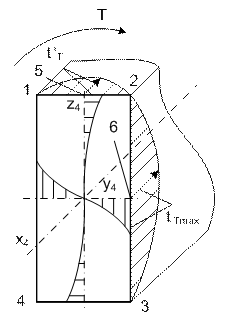
Рис.23. Эпюра касательных напряжений 𝛕

Условие проверки для точки 5:

Условие проверки для точки 6:

Касательные напряжения в призматических стержнях определяют по эмпирическим зависимостям и ,

Где β=0,493 при h/b=2; γ=0,795 при h/b=2.

7. Численный пример расчета на прочность

Рассмотрим прямоугольное сечение.

Исходные данные: q=5 кН/м; F=8 кН; M=6 кНм; l=0,5 м; [σ]=380 МПа.

По таблице 4 вычислим значения: N= -F= -8 кН; M_y=M-Fl=6-8∙0,5=2 кНм; M_z=Fl+ql²/2=8∙0,5+5∙0,5²/2=4,625 кНм; T=ql²=5∙0,5²=1,25 кНм.

Согласно формуле (3) определим

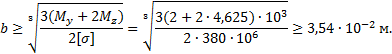
Переведем результат в мм и округлим в большую сторону: b=40 мм.

При этом площадь сечения A=2b²=2∙(40∙10^-3)²=3,2∙10^-3 м²;

моменты сопротивления

м³;

м³.

Условие первой проверки:

Вычислим напряжения от каждого силового фактора:

σ_N=N/A=-8∙10³/3,2∙10^-3=-2,5 МПа;

σ_My=M_y/W_y=2∙10³/42,66∙10^-6=46,8 МПа;

σ_Mz=M_z/W_z=4,625∙10³/21,33∙10^-6=216,8 Мпа.

Суммарное нормальное напряжение формируется с учетом знака σ_N. Необходимо определить наиболее напряженную точку сечения d. Анализ эпюр по рис. 20-22 дает точку 2 – все напряжения сжатия.

Вывод: первая проверка не выполняется – принимаем решение уменьшить сечение до b=35 мм.

Корректируем значения A=2b²=2∙(35∙10^-3)²=2,45∙10^-3 м^{2 ;}

м³;

м³.

Следовательно, новые значения

σ_N=N/A=-8∙10³/2,45∙10^-3=-3,26 МПа;

σ_My=M_y/W_y=2∙10³/25,58∙10^-6=69,98 МПа;

σ_Mz=M_z/W_z=4,625∙10³/14,29∙10^-6=329,87 Мпа.

Суммарное напряжение

Вывод: условие проверки выполняется.

Вторая проверка: Производится по эквивалентным напряжением с учетом касательных. При этом необходимо вычислить значения МПа;

МПа.

Согласно рис. 17 максимальное касательное напряжение в точке 6.

Проверка напряжения по формуле (6)

Мпа;

Дополнительная проверка точки 5, формула (5):

МПа.

Общий вывод: оставляем сечение b×h=0,035×0,070 м, полученное по условию первой проверки.

Пример 2

На рис. 24 изображена в аксонометрии ось ломаного стержня круглого поперечного сечения, расположенная в горизонтальной плоскости. Участки стержня образуют прямые углы.

Дано: α=0,9.

Требуется:

1) построить отдельно (в аксонометрии) эпюры изгибающих и крутящих моментов;

2) для каждого участка определить вид сопротивления и записать условие прочности (использовать четвертую гипотезу прочности).

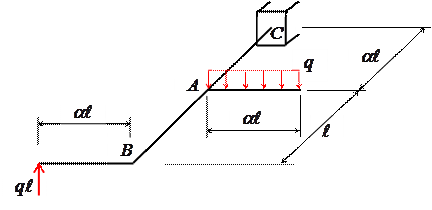
Рис. 24

Решение.

В пределах каждого участка (в нашем случае их четыре) проведем сечение на расстоянии z_i от начала участка (рис. 25). Запишем выражения внутренних силовых факторов, используя метод сечений.

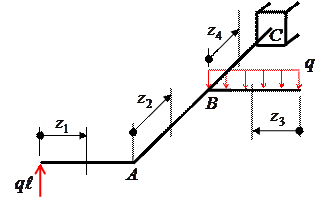
Рис. 25

Участок №1, 0≤z₁≤0,9l

M_u(z₁)=ql∙z₁,

M_u(0)=0,

M_u(0,9l)=0,9ql²,

M_кр(z₁)=0.

Участок №2, 0≤z₂≤l

M_u(z₂)=ql∙z₂,

M_u(0)=0,

M_u(l)=ql²,

M_кр(z₂)=0,9ql².

Участок №3, 0≤z₃≤0,9l

M_u(z₃)=-qz₃∙

M_u(0)=0,

M_u(0,9l)=-0,405ql²,

M_кр(z₃)=0.

Участок №4, 0≤z₄≤0,9l

M_u(z₄)=ql∙(l+z₄)-q∙0,9l∙z₄=0,1∙ql∙z₄+ql².

M_u(0)=ql²,

M_u(0,9l)=1,09ql²,

M_кр(z₄)=ql∙0,9l+0,9ql∙0,45l=1,305ql².

По полученным выражениям M_и и M_кр на каждом участке строим эпюры изгибающих и крутящих моментов (рис. 26).

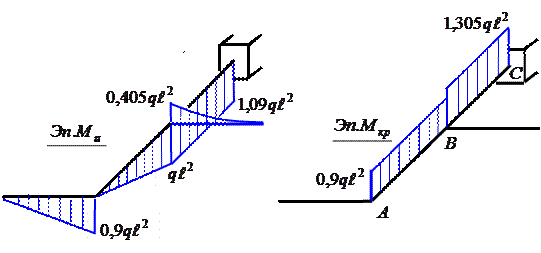
Рис. 26

Видно, что на первом и третьем участках ломаного стержня имеет место прямой поперечный изгиб. Условие прочности будет

σ_max≤[σ], где на первом участке =0,9ql², на третьем участке имеем =0,405ql².

На втором и четвертом участках ломаный стержень испытывает изгиб с кручением. Для опасных сечений, которые будут находиться соответственно в точках B (=ql²; =0,9ql²) и C (=1,09ql²; =1,305ql²), условие прочности по четвертой гипотезе прочности будет выглядеть следующим образом:

Пример 3

На рис.27 изображена пространственная рама, нагруженная двумя сосредоточенными силами.

Требуется: Полагая все участки рамы круглыми, определить требуемый диаметр сечения при допускаемом напряжении [σ]=160 Мпа. Затем заменить круглое сечение прямоугольным при заданном размере h стороны прямоугольного сечения.

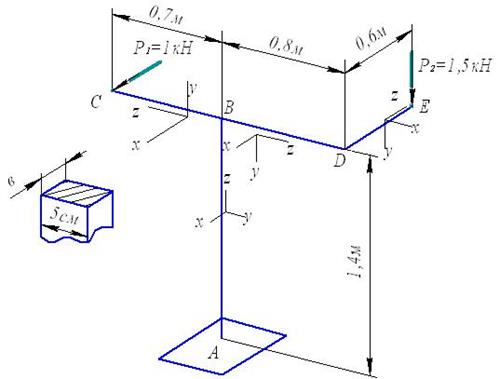
Рис.27

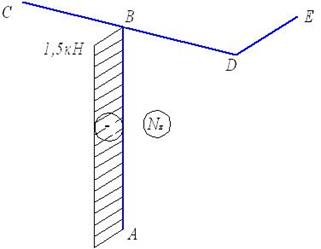
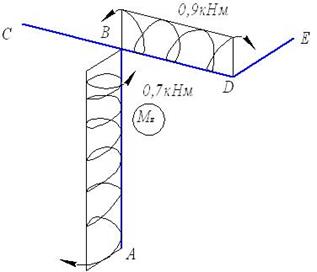
Рис.28. Эпюра продольной силы Рис.29. Эпюра крутящего момента

Решение.

Вводим скользящую систему координат. Ось z каждого стержня совпадает с его продольно осью и направлена к незакрепленной отсеченной части рамы. Оси х и у совмещены с главными центральными осями сечения стержня. Такая система для стержня АВ изображена сбоку, возле стержня, но следует помнить, что ось z ее совпадает с линией АВ.

Перемещаем начало координат системы от сечения А к сечению В и поворачиваем ее вокруг оси, перпендикулярной стержням АВ и ВD, то есть вокруг оси х, направив ось z к сечению D. Переход к стержню DE производится поворотом системы стержня BD вокруг оси у. Координатная система стержня ВС получена поворотом системы стержня АВ вокруг оси х так, чтобы ось z была направлена к сечению С.

Внутренние силовые факторы будем находить по нагрузке, приложенной к отсеченной незакрепленной части рамы, переходя от сечения Е к сечению D, затем к сечению В и к сечению А.

Продольные силы (рис. 28).

Стержни СВ, ВD, и DE продольными силами не нагружены. Стержень ВА сжат силой Р₂ = 1,5 кН. Именно эта сила параллельна продольной оси стержня ВА и приложена к верхней отсеченной части рамы. Здесь N_z = -P₂ = - 1,5 кН.

При определении крутящих и изгибающих моментов следует учесть, что момент силы относительно оси равен нулю, если сила пересекает ось или параллельна оси.

Значит, плечо силы не может измеряться расстоянием вдоль оси или вдоль силы.

Крутящий момент (рис. 29).

Отсеченная часть стержня СВ нагружена силой Р₁. Но она пересекает ось z. Значит, крутящий момент здесь равен нулю.

Так же нагружена силой Р₂ отсеченная часть стержня ЕD.

Стержень DB закручивается силой Р₂ с плечом ЕD. Крутящий момент здесь

M_z=P₂∙ED=1,5∙0,6=0,9 кНм.

В сечениях стержня ВА крутящий момент создается силой Р₁ с плечом СВ.

M_z=P₁∙CB=1∙0,7=0,7 кНм.

Сила Р₂ параллельна оси z стержня АВ и ее момент равен нулю.

Изгибающий момент М_х (рис. 30)

Сила Р₁, приложенная к отсеченной части стержня СВ, параллельна оси х. Значит, ее момент относительно оси х любого сечения этого стержня равен нулю.

Сила Р₂ вызывает в сечениях стержня ЕD изгибающий момент М_х, изгибая стержень ЕD в вертикальной плоскости. В сечении Е плечо силы Р₂ равно нулю, а в сечении D – 0,6 м.

M_XE=0, M_XD=P₂∙DE=1,5∙0,6=0,9 кНм.

При переходе к стержню DB меняется положение оси х. Значит, меняется и плечо силы Р₂. В сечении D оно равно нулю, а в сечении В – 0,8 м.

M_XD=0, M_XB=1,5∙0,8=1,2 кНм.

Сжатые слои стержней ED и DB расположены внизу.

При определении изгибающих моментов в сечениях стержня АВ следует учитывать уже обе силы – Р₁ и Р₂. Но ось х стержня АВ расположена так же, как и на участках СВ и DB. Значит, сила Р₁, как параллельная оси х, на величину изгибающего момента М_х не влияет. Плечо силы Р₂ при «движении» вдоль стержня ВА не меняется. Не меняется и изгибающий момент М_х.

M_XB=M_XA=P₂∙BD=1,5∙0,8=1,2 кНм.

Сжатые слои расположены справа.

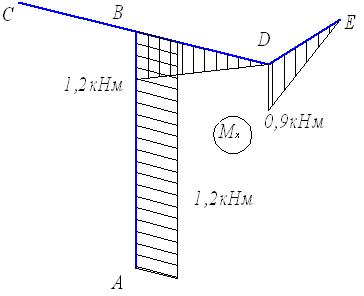
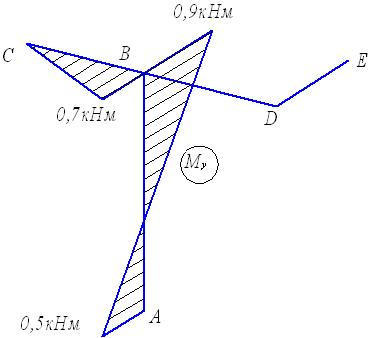
Рис.30. Эпюра М_x Рис.31. Эпюра М_y

Изгибающий момент М_у (рис. 31)

Сила Р₁, изгибая стержень СВ в плоскости xz, вызывает в сечениях стержня изгибающий момент М_у. В сечении С плечо ее равно нулю, в сечении В – 1 м.

M_yC=0, M_yB=0,7∙1=0,7 кНм.

Ось у стержней ED и DB параллельна силе Р₂. Значит, изгибающий момент в сечениях стержней ED и DB равен нулю.

При переходе к стержню ВА положение оси у меняется. Ось у сечения В пересекает линию действия силы Р₁. Значит, ее плечо равно нулю и в этом сечении изгибающий момент зависит лишь от силы Р₂.

M_yB=P₂∙ED=1,5∙0,6=0,9 кНм.

При вычислении изгибающего момента М_у в сечении А следует учесть, что плечо силы Р₂ такое же, как и в сечении В, и что моменты сил Р₁ и Р₂ имеют противоположные направления

M_yA=P₁∙AB- P₂∙ED =1∙1,4 - 1,5∙0,6=0,5 кНм.

Расчет круглого бруса АВ

По эпюрам заключаем, что опасным является сечение В. На рисунке 32 показаны внутренние силовые факторы в этом сечении и напряженное состояние в опасной точке.

Эквивалентный изгибающий момент

По условию прочности требуемый момент сопротивления

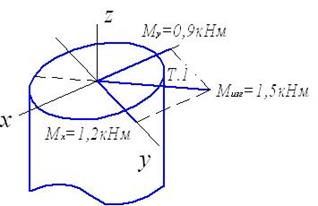
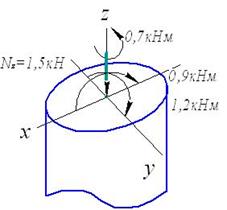
Рис.32. Круглое сечение

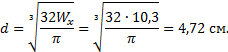
При таком расчете не учитывалась продольная сила N_z. Произведем проверку прочности с учетом продольной силы.

Изгибающий момент

Нормальное напряжение в точке 1

Касательное напряжение в точке 1

Эквивалентное напряжение по гипотезе Треска – Сен – Венана

Перегрузка составляет всего 0,6 %.

Расчет прямоугольного бруса АВ

Теперь заменим круглое сечение бруса АВ прямоугольным.

На рисунке 33 изображены внутренние силовые факторы в сечении В прямоугольного бруса и указан размер в, подлежащий определению.

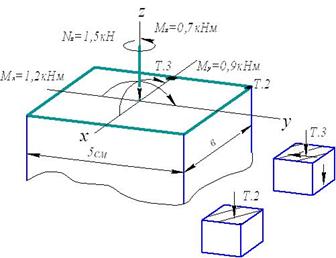
Рис.33. Прямоугольное сечение

Предварительный подбор сечения произведем с учетом лишь нормальных напряжений, принимающих наибольшее значение в угловой точке.

По условию прочности

Требуемое значение в = 3,66 см.

Теперь проверим прочность сечения в точке 3, где действует наибольшее касательное напряжение.

По отношению сторон и таблице кручения прямоугольного бруса найдем коэффициент α.

При линейной интерполяции

Момент сопротивления кручению

Нормальное напряжение в точке 3

Эквивалентное напряжение в точке 4

Условие прочности удовлетворяется.

Пример 4

На рисунке 34 изображена пространственная рама, нагруженная тремя сосредоточенными силами и парой сил, действующей в горизонтальной плоскости.

Требуется:

1. построить эпюры внутренних силовых факторов.

2. Брус СК рамы, изображенный на рис.34 имеет прямоугольное сечение. Остальные стержни рамы имеют круглое сечение одного диаметра. Размер стороны сечения бруса СК, перпендикулярный стержню ВСD, на 20% больше диаметра круглых стержней. Найти требуемый диаметр круглого стержня и второй размер сечения бруса СК.

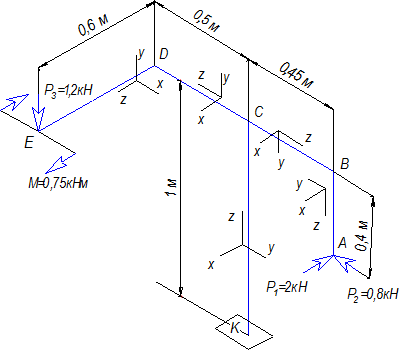
Рис. 34

Решение.

Для удобства построения эпюр целесообразно ввести скользящую систему координат. Ось z совпадает с продольной осью элемента рамы, оси x и y совмещены с главными центральными осями сечения стержня.

Сначала строим такую систему для стержня СК. Она изображена сбоку, возле стержня, но следует помнить, что ось z совпадает с линией КС. Доводим эту систему до сечения С и для перехода к участку СD поворачиваем ее так, чтобы ось z стала продольной для участка СD и была направлена к незакрепленной отсеченной части рамы, то есть влево. Поворот осуществляется вокруг оси, перпендикулярной стержням СК и СD, то есть вокруг оси x. Переход к стержню DE производится поворотом системы вокруг оси y, ибо эта ось перпендикулярна плоскости стержней СD и DE.

При переходе от стержня КС к стержню СВ ось z направляется вправо с поворотом координатной системы стержня КС вокруг оси x. Ось x сохраняется и при переходе к стержню ВА.

Продольные силы (рис.35).

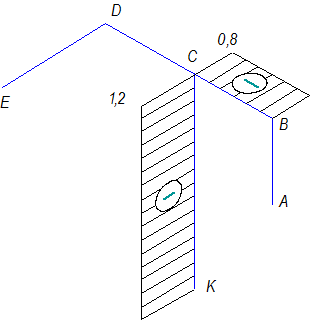
Рис.35. Эпюра продольных сил

Обходим раму от сечения А до сечения С. Участок АВ свободен от продольной нагрузки, ибо силы P₁ и P₂ перпендикулярны оси z этого участка. Участок ВС сжат силой P₂. Рассекая участки ЕD и DC замечаем, что приложенная к отсеченной свободной части сила P₃ перпендикулярна оси z. Значит продольная сила на этих участках равна нулю. Сила P₃ параллельна продольной оси участка СК. Она вызывает его сжатие. Эпюра продольной силы показана на рисунке.

Прежде чем приступить к вычислению крутящих и изгибающих моментов, заметим следующее:

1. Момент силы относительно оси равен нулю, если сила пересекает ось или ей параллельна. То есть если линия действия силы и ось расположены в одной плоскости.

2. Алгебраическая сумма моментов сил пары относительно оси, перпендикулярной плоскости действия пары, равна моменту пары.

3. Алгебраическая сумма моментов сил пары относительно оси параллельной плоскости действия пары равна нулю.

Крутящий момент (рис.36).

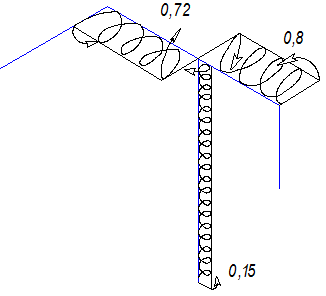
Рис. 36. Эпюра крутящих моментов

На основании первого замечания заключаем, что крутящий момент на участке АВ равен нулю (силы P₁ и P₂ пересекают ось z). На участке ЕD крутящий момент также равен нулю (сила P₃ пересекает ось z, плоскость пары параллельна оси z).

На участке ВС крутящий момент создается силой P₁. Плечо силы – АВ. Значит M_z=P₁∙AB=2∙0,40=0,8 кНм.

Участок CD закручивается силой P₃, момент которой равен M_z=P₃∙DE=1,2∙0,6=0,72 кНм.

На участке СК крутящий момент зависит от силы P₁ (плечо – ВС) и от пары M=0,75 кНм.

Продольная ось участка СК перпендикулярна плоскости действия пары М (замечание 2) и удалена от линии действия силы P₁ на расстояние СВ =0,45 м. Силы P₂ и P₃ не вызывают деформации кручения участка СК (сила P₂ пересекает ось z). Направления моментов пары М и силы P₁ противоположны. Значит M_z=P₁∙СB - M=2∙0,45 - 0,75=0,15 кНм.

Эпюра крутящего момента показана на рисунке 36. Здесь показаны и направления моментов, приложенных к граничным сечениям участков.

Изгибающий момент M_x (рис.37).

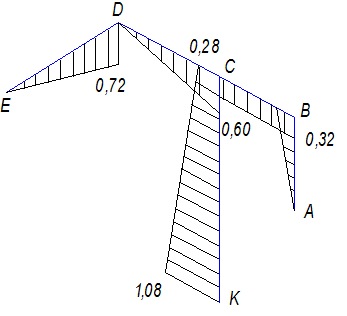
Рис. 37. Эпюра изгибающих моментов M_x

Если рассечь в любом месте стержень АВ или стержень ВС, то к отсеченной свободной части рамы будут приложены две силы - P₁ и P₂. Сила P₁ параллельна оси x стержней АВ и ВС. Значит на величину изгибающего момента M_x она не влияет. Сила P₂ перпендикулярна оси x. Она и создает момент M_x, который действует в вертикальной плоскости . В этой плоскости изображается эпюра M_x участка АВ. Плечо силы P₂ в сечении А равно нулю, а в сечении В равно АВ. Значит

M_xA=0, M_xB=P₂∙AB=0,8∙0,4=0,32 кНм.

Сжаты левые слои стержня.

При переходе к участку ВС направление оси x не меняется. Значит для момента M_x справедливо правило раствора циркуля. Так как плечо силы P₂ на этом участке рамы не меняется, то во всех сечениях стержня ВС M_x=0,32 кНм.

К отсеченной свободной части стержня ED приложены сила P₃ и пара сил, момент которой M=0,75 кНм. Плоскость действия пары проходит через оси x стержней ED и DC. Значит она не влияет на изгибающий момент M_x этих стержней. Момент M_x в сечениях стержней ED и DC вызывается силой P₃. Он действует в вертикальной плоскости и увеличивается от сечения Е к сечению D.

M_xE=0, M_xD=P₃∙ED=1,2∙0,6=0,72 кНм.

При переходе от стержня ED к стержню DC направление оси x не сохранилось. Значит правило раствора циркуля для момента M_x здесь не применимо. На участке DC плечо силы P₃ меняется от нуля (в сечении D) до 0,5 м (в сечении С).

M_xD=0, M_xC=P₃∙DE=1,2∙0,5=0,6 кНм.

На участке СК изгибающий момент M_x вызывается силами P₂ и P₃. Сила P₁ параллельна оси x этого участка, а пара сил М действует в плоскости xy. Значит на величину момента M_x участка СК сила P₁ и пара М не влияют.

Плечо силы P₃ остается неизменным для всех сечений стержня СК и равно 0,5 м. Значит момент M_x от силы P₃ равен

P₃∙CD=1,2∙0,5=0,6 кНм.

Этот момент вызывает сжатие левых слоев.

Плечо силы P₂ меняется с переходом от сечения С к сечению К. В сечении С плечо силы P₂ равно АВ.

M_xC=P₂∙AB=0,8∙0,4=0,32 кНм.

Направление этого момента совпадает с направлением хода часовой стрелки. Значит, действуя на стержень СК сверху, он вызывает сжатие правых слоев.

С учетом момента силы P₃ получим

M_xC=M_xC(P₃) - M_xC(P₂)=0,6 – 0,32 = 0,28 кНм.

Плечо силы P₂ в сечении К равно КС-АВ=1-0,4=0,6 м. Направление момента силы P₂ относительно оси x этого сечения совпадает с направлением момента силы P₃.

M_xK=M_xK(P₃) + M_xK(P₂)=0,6 + 0,8∙0,6 = 1,08 кНм.

Сжаты левые слои.

Изгибающий момент M_y (рис.38).

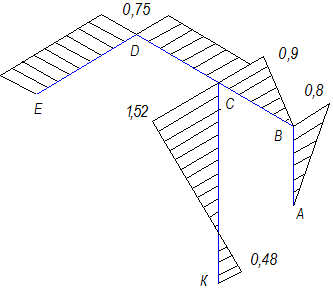
Рис. 38. Эпюра изгибающих моментов M_y

На участке АВ изгибающий момент M_y вызывается силой P₁. Плечо ее меняется вдоль этого участка от нуля до 0,4 метра. Значит

M_yA=0, M_yB=P₁∙AB=2∙0,4=0,8 кНм.

Этот момент действует в плоскости zx. В этой плоскости и изображена эпюра M_y.

При переходе к участку ВС направление оси y изменилось, следовательно правило раствора циркуля для момента M_y неприменимо.

Ось у любого сечения этого участка пересекает силу P₂. Значит момент M_y силы P₂ равен нулю. Момент M_y силы P₁ меняется вдоль стержня ВС, так как меняется ее плечо от нуля до 0,45 м. Таким образом,

M_yB=0, M_yC=P₁∙BC=2∙0,45=0,9 кНм.

Ось y участков ЕD и DC параллельна силе P₃. Значит сила P₃ на изгибающий момент M_y этих участков не влияет. По отмеченным выше свойствам пары сил изгибающий момент M_y на участках ED и DC равен моменту приложенной к сечению Е пары. То есть во всех сечениях этих участков.

M_y=M=0,75 кНм.

Изгибающий момент M_y в сечениях стержня СК вызывается силами P₁ и P₃ (сила P₂ и плоскость пары М параллельны оси y). Направления моментов силы P₁ (плечо АВ) и силы P₃ (плечо ЕD) относительно оси y сечения С совпадают. Значит

M_yC=P₁∙AB+P₃∙ED=2∙0,4+1,2∙0,6=1,52 кНм.

В сечении К изгибающий момент M_y равен разности моментов сил P₁ и P₃, ибо направление момента силы P₃, так же , как и плечо ее, осталось неизменными, а направление момента силы P₁ изменилось на противоположное. Плечо ее теперь равно 1-0,4=0,6 м.

M_yK=2∙0,6 - 1,2∙0,6=0,48 кНм.

Поскольку оси x и y взаимно перпендикулярны, то эпюры изгибающих моментов M_x и M_y на каждом участке рамы должны быть расположены во взаимно перпендикулярных плоскостях. Эпюра M_x - в плоскости yz, эпюра M_y - в плоскости xz.

Как видим, во многих сечениях стержней пространственной рамы одновременно не равны нулю несколько внутренних силовых факторов (M_x, M_y, M_z, N_z).

Продольная сила и изгибающие моменты вызывают в поперечном сечении нормальные напряжения, а крутящий момент – касательные. В результате материал бруса находится в сложном напряженном состоянии.

Для анализа сложного напряженного состояния необходимо найти напряжения от каждого внутреннего силового фактора.

Расчет цилиндрического стержня.

По эпюрам изгибающих моментов M_x и M_y (рис.37 и 38) видно, что наибольший изгибающий момент может быть в сечении D стержня ЕD, в сечении С стержня DC и в сечении С стержня BC.

Наибольшим оказался изгибающий момент в сечении D. Однако в этом сечении нет крутящего момента. В то время как в сечениях, примыкающих к узлу С, действуют крутящие моменты

Применяя гипотезу Треска-Сен-Венана найдем эквивалентные моменты в этих сечениях

Наиболее опасным оказалось сечение С стержня ВС.

На рисунке 39,а изображены внутренние силовые факторы в этом сечении, а на рисунке 39,б показан суммарный изгибающий момент M_изг и напряженное состояние в точке 1.

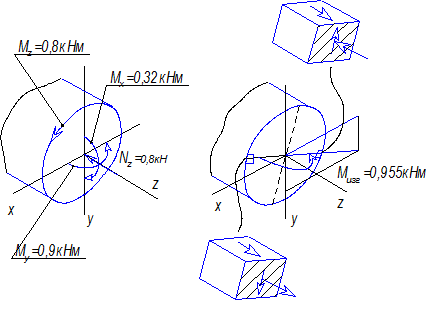
а) б)

Рис. 39

По условию прочности

требуемый момент сопротивления равен

Соответствующий диаметр стержня

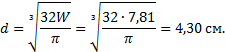
При таком определении требуемого диаметра не учтена продольная сила.

Наибольшее нормальное напряжение в этом сечении с учетом продольной силы

Видно, что напряжение, вызванное продольной силой, значительно меньше напряжения от изгибающего момента.

При касательном напряжении

Эквивалентное напряжение

При допускаемой пятипроцентной перегрузке условие прочности удовлетворяется.

Расчет прямоугольного бруса.

По условию задачи в=1,2d=1,2∙4,3=5,16 см.

Принимаем в=5,2 см.

По эпюрам изгибающих моментов M_x и M_y выясняем, что наиболее опасным может быть как сечение С, так и сечение К. На рисунках 40 и 41 показаны внутренние силовые факторы в этих сечениях.

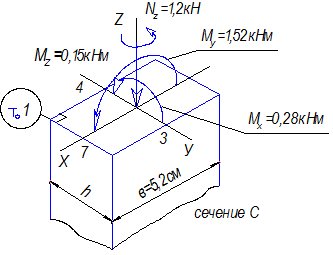
Рис.40

Поскольку продольная сила отрицательная, то нужно найти точки сечений, в которых действует наибольшее напряжение сжатия.

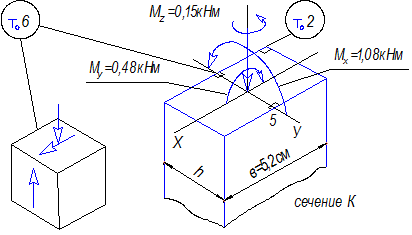
Рис. 41

Таковыми являются точка 1 сечения С и точка 2 сечения К.

По условию прочности

и формуле

составим уравнения

Решение уравнения (1) h=2,83 см.

Решение уравнения (2) h=3,15 см.

Принимаем большее значение h=3,15 см.

Теперь следует проверить прочность бруса в точках с наибольшим касательным напряжением. Таковыми являются точки 3, 4, 5 и 6. Касательное напряжение в этих точках имеют одинаковое значение

Здесь W_k=αbh².

По отношению

и таблице коэффициентов α и γ (см. раздел «Справочные данные») и формуле линейного интерполирования найдем

Момент сопротивления кручению

W_k=0,236∙5,2∙3,15²=12,2 см³.

Нормальное напряжение принимает большее по модулю значение в точке 6. Оно равно

На рисунке 41 изображено напряженное состояние в этой точке. Оно является упрощенным плоским. Эквивалентное напряжение для такого напряженного состояния по Треска-Сен-Венану определяется по формуле

Условие прочности удовлетворяется.

Изгибающий момент M_y в сечении С больше, чем изгибающий момент M_x сечения К. Так что нормальное напряжение в точке 7 может оказаться больше напряжения (3).

Найдем его.

Нормальное напряжение в точке 7 оказалось меньше напряжения в точке 6. Это объясняется большим значением момента сопротивления W_y. Ведь при его вычислении пришлось возводить в квадрат большую сторону сечения.

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00