Главная

Задача 1. Расчет сложных составных несимметричных поперечных сечений.

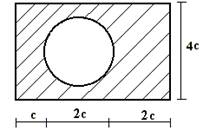
Для сечения, изображенного на рис.1 требуется:

1) вычертить сечение в масштабе и показать основные размеры в числах.

2) определить положение центра тяжести и указать положение главных центральных осей.

3) вычислить величину главных моментов инерции и моментов сопротивления сечения.

4) определить главные радиусы инерции сечения.

При расчете все необходимые данные следует взять из таблицы 1.

Таблица 1

Номер строки	Схема сечения по рис.1	с, м
01	1	0,1
02	2	0,15
03	3	0,2
04	4	0,25
05	5	0,3
06	6	0,1
07	7	0,15
08	8	0,2
09	9	0,25
10	10	0,3
11	11	0,2
12	12	0,25
13	13	0,3
14	14	0,1
15	15	0,15
16	16	0,1
17	17	0,15
18	18	0,2
19	19	0,25
20	20	0,3
21	21	0,1
22	22	0,15
23	23	0,2
24	24	0,25
25	25	0,3
26	26	0,2
27	27	0,25
28	28	0,3
29	29	0,25
30	30	0,3
31	31	0,1
32	32	0,15
33	33	0,2
34	34	0,25
35	35	0,3
36	36	0,2
	в	б

1 схема 2 схема 3 схема

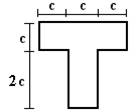
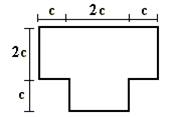
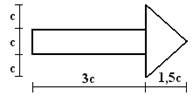
4 схема 5 схема 6 схема

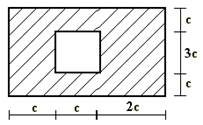
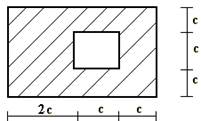
7 схема 8 схема 9 схема

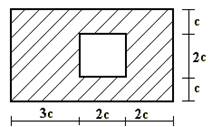
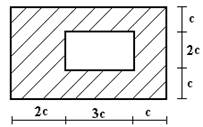
10 схема 11 схема 12 схема

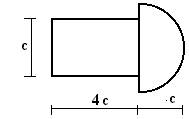
13 схема 14 схема 15 схема

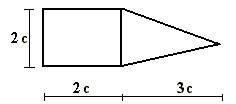
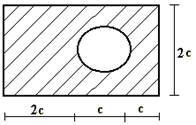
16 схема 17 схема 18 схема

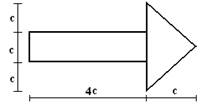
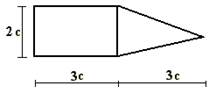
19 схема 20 схема 21 схема

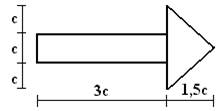
22 схема 23 схема 24 схема

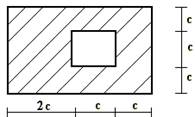
25 схема 26 схема 27 схема

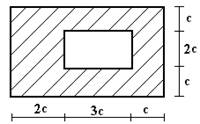
28 схема 29 схема 30 схема

31 схема 32 схема 33 схема

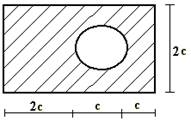
34 схема 35 схема 36 схема

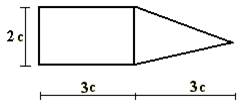
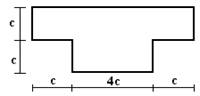
Рис.1

Задача 2. Расчет сложных составных несимметричных поперечных сечений из прокатных профилей.

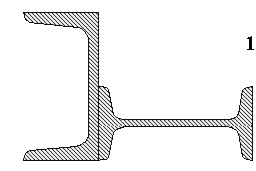
Для составного поперечного сечения (рис.2), состоящего из двутавра, швеллера, уголка, заданных в табл.2, требуется:

1) определить положение центра тяжести;

2) найти величину осевых и центробежных моментов инерции относительно центральных осей;

3) определить направление главных центральных осей;

4) найти величину моментов инерции относительно главных центральных осей;

5) вычертить сечений в масштабе 1:2 и указать на нем все размеры в числах и все оси.

При расчете все необходимые данные следует взять из таблицы 2 и сортамента.

Таблица 2

Номер строки	Схема сечения по рис.2	Швеллер №	Равнобокий уголок №	Двутавр №
01	1	14	8(8)	12
02	2	16	8(6)	14
03	3	18	9(8)	16
04	4	20	9(7)	18
05	5	22	9(6)	20а
06	6	24	10(8)	20
07	7	27	10(10)	22а
08	8	30	10(12)	22
09	9	33	12,5(10)	24а
10	10	36	12,5(12)	24
11	11	14	8(8)	12
12	12	16	8(6)	14
13	13	18	9(8)	16
14	14	20	9(7)	18
15	15	22	9(6)	20а
16	16	24	10(8)	20
17	17	27	10(10)	22а
18	18	30	10(12)	22
19	19	33	12,5(10)	24а
20	20	36	12,5(12)	24
21	21	14	8(8)	12
22	22	16	8(6)	14
23	23	18	9(8)	16
24	24	20	9(7)	18
25	25	22	9(6)	20а
26	26	24	10(8)	20
27	27	27	10(10)	22а
28	28	30	10(12)	22
29	29	33	12,5(10)	24а
30	30	36	12,5(12)	24
31	31	14	8(8)	18
32	32	16	8(6)	20а
33	33	18	9(8)	20
34	34	20	9(7)	22а
35	35	22	9(6)	22
36	36	24	10(8)	24а
	в	б	а	г

1 схема 2 схема 3 схема

4 схема 5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

11 схема 12 схема 13 схема

14 схема 15 схема 16 схема

17 схема 18 схема

19 схема 20 схема

21 схема 22 схема 23 схема

24 схема 25 схема 26 схема

27 схема 28 схема

29 схема 30 схема

31 схема 32 схема 33 схема

34 схема 35 схема 36 схема

Рис. 2

Задача 3. Расчет сложных составных несимметричных поперечных сечений из прокатных профилей.

Для заданных схем (рис.3) необходимо:

1) Вычертить поперечное сечение в строгом масштабе.

2) Определить положение центра тяжести.

3) Найти величины осевых моментов инерции относительно центральных осей.

4) Найти величину центробежного момента инерции относительно центральных осей.

5) Определить положение главных осей инерции.

6) Найти главные моменты инерции.

При расчете все необходимые данные следует взять из таблицы 3 и сортамента.

Таблица 3

Номер строки	Схема сечения по рис.3	Швеллер	Прямоугольник	Двутавр	Уголок равнополочный	Уголок неравнополочный
01	1	8	100х30	10	30x5	50x32x4
02	2	10	100х40	12	40x6	56x36x4
03	3	12	100х20	14	50x4	63x40x8
04	4	14	80х40	16	56x4	70x45x5
05	5	14а	80х60	18	63x6	80x50x6
06	6	16	80х100	20	70x8	90x56x6
07	7	16а	80х20	20а	80x8	100x63x6
08	8	18	60х40	22	90x9	90x56x8
09	9	18а	60х60	22а	75x9	140x90x10
10	10	20	60х40	27	100x10	160x100x12
11	11	14	100х20	14	40x6	56x36x4
12	12	16	80х40	16	50x4	63x40x8
13	13	18	80х60	18	56x4	70x45x5
14	14	10	80х100	20	63x6	80x50x6
15	15	12	80х20	20а	70x8	90x56x6
16	16	14	60х40	22	80x8	100x63x6
17	17	14а	100х20	22а	90x9	90x56x8
18	18	16	80х40	22	75x9	140x90x10
19	19	16а	80х60	24а	100x10	50x32x4
20	20	18	80х100	24	63x6	56x36x4
21	21	18а	80х20	20	70x8	63x40x8
22	22	20	80х40	20а	80x8	160x100x12
23	23	14	80х60	22	90x9	56x36x4
24	24	14а	80х100	22а	75x9	63x40x8
25	25	16	80х20	27	100x10	70x45x5
26	26	8	60х40	14	40x6	80x50x6
27	27	10	100х20	16	50x4	90x56x6
28	28	12	80х40	18	56x4	100x63x6
29	29	14	80х60	20	63x6	90x56x8
30	30	14а	80х100	20а	80x8	140x90x10
31	31	16	80х20	22	90x9	50x32x4
32	32	16а	100х20	22а	75x9	56x36x4
33	33	18	80х40	20	100x10	63x40x8
34	34	18а	80х60	22а	40x6	63x40x8
35	35	20	80х100	22	50x4	70x45x5
36	36	14	80х20	16	75x9	80x50x6
	а	б	в	г	а	б

1 схема 2 схема 3 схема 4 схема

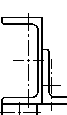
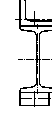
5 схема 6 схема 7 схема 8 схема

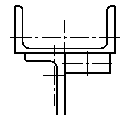
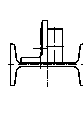
9 схема 10 схема 11 схема 12 схема

13 схема 14 схема 15 схема 16 схема

17 схема 18 схема 19 схема 20 схема

21 схема 22 схема 23 схема 24 схема

25 схема 26 схема 27 схема 28 схема

29 схема 30 схема 31 схема 32 схема

33 схема 34 схема 35 схема 36 схема

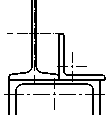
Рис.3

Задача 4. Расчет сложных составных несимметричных поперечных сечений из прокатных профилей.

Для несимметричных сечений (рис.4) при размерах, указанных в таблице 4, требуется:

1) определить положение центра тяжести;

2) вычислить осевые и центробежные моменты инерции относительно центральных осей;

3) определить положение главных центральных осей инерции и величины главных моментов инерции;

4) построить круг инерции и определить графически величины главных моментов инерции и направления главных центральных осей;

5) сравнить результаты аналитического и графического расчетов.

При расчете все необходимые данные для прокатных профилей следует взять из сортамента.

Таблица 4

Номер строки	Схема сечения по рис.4	Номер двутавра	Номер швеллера	Равнобокий уголок, мм	Неравнобокий уголок, мм	Лист, мм	а, см
01	1	10	10	80х80х6	100х63х8	160х10	5
02	2	12	12	90х90х6	110х70х8	160х12	6
03	3	14	14	90х90х8	125х80х7	180х10	8
04	4	16	16	100х100х8	125х80х8	180х12	10
05	5	18	18	100х100х12	125х80х10	200х10	12
06	6	20	20	110х110х7	140х90х8	200х12	4
07	7	22	22	110х110х8	140х90х10	200х16	16
08	8	24	24	125х125х8	160х100х10	220х12	15
09	9	27	27	125х125х10	180х110х10	220х14	18
10	10	30	30	140х140х12	180х110х12	240х16	20
11	11	33	33	160х160х12	200х125х14	240х20	7
12	12	36	36	160х160х16	200х125х16	300х16	9
13	13	40	36	200х200х16	250х160х12	350х16	11
14	14	45	40	220х220х16	250х160х16	400х20	14
15	15	10	10	110х110х7	100х63х8	180х12	8
16	16	12	12	110х110х8	110х70х8	200х10	10
17	17	14	14	125х125х8	125х80х7	200х12	12
18	18	16	16	125х125х10	125х80х8	200х16	4
19	19	18	18	140х140х12	125х80х10	220х12	16
20	20	20	20	160х160х12	125х80х8	220х14	15
21	21	22	22	160х160х16	125х80х10	240х16	18
22	22	24	24	200х200х16	140х90х8	240х20	20
23	23	27	27	220х220х16	140х90х10	300х16	7
24	24	30	10	80х80х6	160х100х10	160х10	9
25	25	33	12	90х90х6	180х110х10	160х12	5
26	26	36	14	90х90х8	180х110х12	180х10	6
27	27	40	16	100х100х8	200х125х14	180х12	8
28	28	45	18	100х100х12	200х125х16	200х10	10
29	29	33	20	110х110х7	250х160х12	200х12	12
30	30	36	22	110х110х8	250х160х16	200х16	4
31	31	40	24	125х125х8	100х63х8	220х12	16
32	32	45	27	125х125х10	110х70х8	220х14	15
33	33	10	30	140х140х12	125х80х7	240х16	18
34	34	12	33	160х160х12	180х110х10	180х12	10
35	35	14	36	160х160х16	180х110х12	200х10	16
36	36	16	36	125х125х8	200х125х14	200х12	12
	в	г	а	в	б	а	г

1 схема 2 схема 3 схема

4 схема 5 схема 6 схема

7 схема 8 схема 9 схема

10 схема 11 схема 12 схема

13схема 14 схема 15 схема

16 схема 17 схема 18 схема

19 схема 20 схема 21 схема

22 схема 23 схема 24 схема

25 схема 26 схема 27 схема

28 схема 29 схема 30 схема

31 схема 32 схема 33 схема

34 схема 35 схема 36 схема

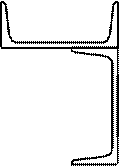
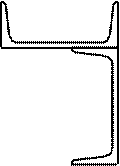
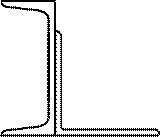
Рис.4

Задача 5. Расчет сложных составных симметричных поперечных сечений из прокатных профилей.

Для симметричных сечений (рис.5) при размерах, указанных в таблице 5, требуется:

1) Определить положение центра тяжести.

2) Найти величины осевых моментов инерции относительно центральных осей.

3) Найти величину центробежного момента инерции относительно центральных осей.

4) Определить положение главных центральных осей инерции.

5) Найти главные моменты инерции.

6) Построить круг инерции и определить графически величины главных моментов инерции и направления главных центральных осей.

7) Сравнить результаты аналитического и графического расчетов.

При расчете все необходимые данные для прокатных профилей следует взять из сортамента.

Таблица 5

Номер строки	Схема сечения по рис.5	Размеры прямоугольников и номера прокатных профилей
01	1	Прямоугольник 12х5 см^2 Двутавр № 10
02	2	Швеллер № 8 Двутавр № 12
03	3	Прямоугольник 10х5 см^2 Уголок равнобокий № 4
04	4	Прямоугольник 24х4 см^2 Швеллер № 16а
05	5	Прямоугольник 4х14 см^2 Уголок неравнобокий № 8/5
06	6	Швеллер № 24а Двутавр № 22
07	7	Двутавр № 20а Швеллер № 20
08	8	Швеллер № 24 Двутавр № 18
09	9	Швеллер № 5 Прямоугольник 2х10 см^2
10	10	Швеллер № 14а Прямоугольник 6х18 см^2
11	11	Двутавр № 14 Уголок равнобокий № 9
12	12	Швеллер № 12 Уголок равнобокий № 6,3
13	13	Швеллер № 18 Уголок равнобокий № 7,5
14	14	Прямоугольник 4х6 см^2 Уголок равнобокий № 9/5,6
15	15	Швеллер № 14 Уголок неравнобокий № 10/6,3
16	16	Прямоугольник 20х4 см^2 Уголок равнобокий № 8
17	17	Двутавр № 14 Уголок неравнобокий № 11/7
18	18	Прямоугольник 22х6 см^2 Двутавр № 16
19	19	Швеллер № 16 Уголок равнобокий № 7
20	20	Двутавр № 12 Швеллер № 16
21	21	Швеллер № 20 Уголок неравнобокий № 9/5,6
22	22	Двутавр № 20 Уголок неравнобокий № 16/10
23	23	Швеллер № 22 Уголок равнобокий № 10
24	24	Двутавр № 10 Уголок неравнобокий № 7/5,5
25	25	Швеллер № 18а Прямоугольник 8х22 см^2
26	26	Двутавр № 24 Прямоугольник 16х4 см^2
27	27	Двутавр № 18а Прямоугольник 6х26 см^2
28	28	Прямоугольник 20х6 см^2 Уголок неравнобокий № 12,5/8
29	29	Швеллер № 20 Уголок неравнобокий № 14/9
30	30	Прямоугольник 14х6 см^2 Швеллер № 10
31	31	Прямоугольник 4х14 см^2 Уголок неравнобокий № 8/5
32	32	Швеллер № 20 Двутавр № 18а
33	33	Швеллер № 10 Прямоугольник 2х10 см^2
34	34	Швеллер № 22 Прямоугольник 20х6 см^2
35	35	Швеллер № 18а Уголок равнобокий № 7,5
36	36	Прямоугольник 4х9 см^2 Уголок равнобокий № 9/5,6
	в	г

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

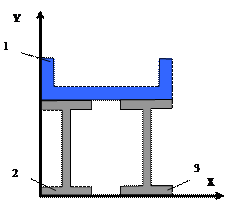
7 схема 8 схема

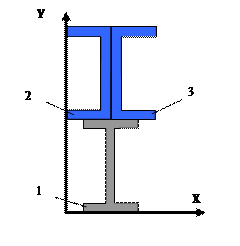
9 схема 10 схема

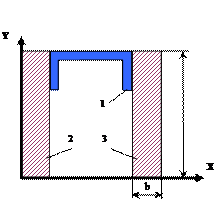
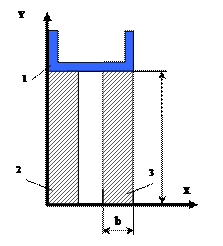
11 схема 12 схема

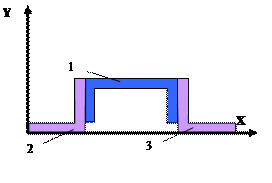
13 схема 14 схема

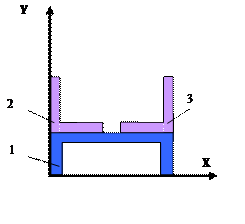
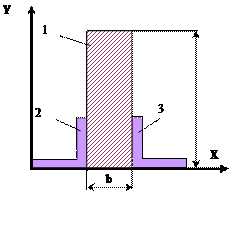
15 схема 16 схема

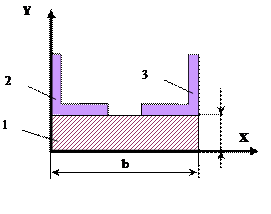
17 схема 18 схема

19 схема 20 схема

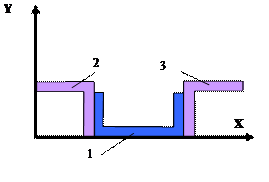
21 схема 22 схема

23 схема 24 схема

25 схема 26 схема

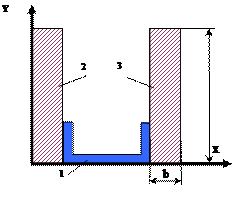
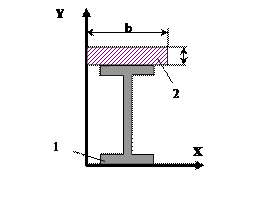
27 схема 28 схема

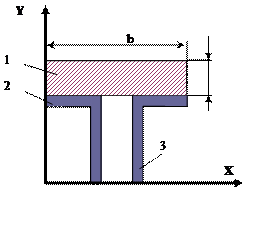
29 схема 30 схема

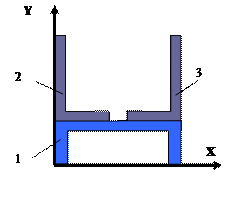
31 схема 32 схема

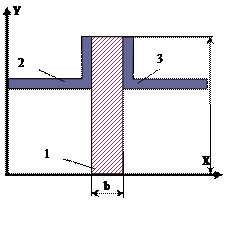
33 схема 34 схема

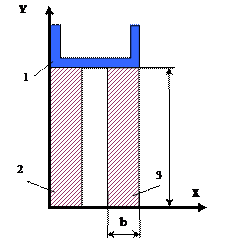
35 схема 36 схема

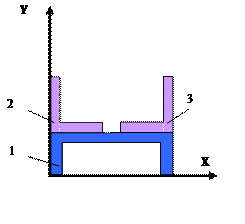
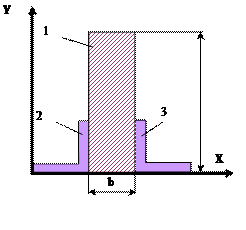
Рис.5

Задача 6. Расчет сложных составных несимметричных поперечных сечений из прокатных профилей.

Для несимметричных сечений (рис.6) при размерах, указанных в таблице 6, требуется:

1) Определить положение центра тяжести.

2) Найти величины осевых моментов инерции относительно центральных осей.

3) Найти величину центробежного момента инерции относительно центральных осей.

4) Определить положение главных центральных осей инерции.

5) Найти главные моменты инерции.

6) Построить круг инерции и определить графически величины главных моментов инерции и направления главных центральных осей.

7) Сравнить результаты аналитического и графического расчетов.

При расчете все необходимые данные для прокатных профилей следует взять из сортамента.

Таблица 6

Номер строки	Схема сечения по рис.6	Размеры прямоугольников и номера прокатных профилей
01	1	Уголок неравнобокий № 16/10 Швеллер № 22
02	2	Уголок равнобокий № 16 Прямоугольник 10х4 см^2
03	3	Швеллер № 22 Двутавр № 20
04	4	Двутавр № 18 Уголок неравнобокий № 18/11
05	5	Двутавр № 18 Швеллер № 18
06	6	Прямоугольник 4х5 см^2 Уголок неравнобокий № 5/3,2
07	7	Швеллер № 6,5 Уголок равнобокий № 3,2
08	8	Прямоугольник 4х5 см^2 Уголок неравнобокий № 5/3,2
09	9	Уголок неравнобокий № 14/9 Двутавр № 16
10	10	Уголок равнобокий № 7,5 Уголок неравнобокий № 10/6,3
11	11	Прямоугольник 20х4 см^2 Швеллер № 16
12	12	Прямоугольник 5х10 см^2 Двутавр № 10
13	13	Прямоугольник 12х4 см^2 Двутавр № 12
14	14	Двутавр № 12 Швеллер № 18
15	15	Уголок равнобокий № 10 Прямоугольник 6х10 см^2
16	16	Швеллер № 16а Двутавр № 14
17	17	Прямоугольник 4х12 см^2 Швеллер № 10
18	18	Уголок равнобокий № 14 Швеллер № 12
19	19	Уголок неравнобокий № 8/5 Прямоугольник 8х4 см^2
20	20	Уголок равнобокий № 7 Прямоугольник 8х6 см^2
21	21	Швеллер № 20 Прямоугольник 15х20 см^2
22	22	Прямоугольник 3х15 см^2 Швеллер № 12
23	23	Двутавр № 16 Уголок неравнобокий № 20/12,5
24	24	Швеллер № 5 Прямоугольник 6х3 см^2
25	25	Двутавр № 10 Уголок равнобокий № 18
26	26	Уголок равнобокий № 10 Швеллер № 10
27	27	Уголок неравнобокий № 11/7 Швеллер № 8
28	28	Швеллер № 16 Уголок равнобокий № 20
29	29	Прямоугольник 20х5 см^2 Двутавр № 22
30	30	Двутавр № 14 Уголок равнобокий № 8
31	31	Двутавр № 16 Уголок равнобокий № 10
32	32	Уголок равнобокий № 20 Швеллер № 16
33	33	Уголок неравнобокий № 20/12,5 Двутавр № 10
34	34	Уголок равнобокий № 7,5 Уголок неравнобокий № 11/7
35	35	Прямоугольник 20х4 см^2 Швеллер № 8
36	36	Прямоугольник 5х10 см^2 Двутавр № 14
	а	б

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

11 схема 12 схема

13 схема 14 схема

15 схема 16 схема

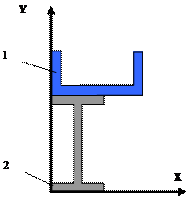
17 схема 18 схема

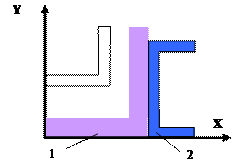
19 схема 20 схема

21 схема 22 схема

23 схема 24 схема

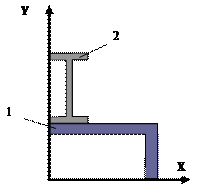
25 схема 26 схема

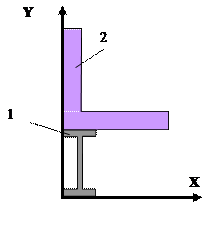
27 схема 28 схема

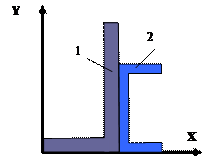
29 схема 30 схема

31 схема 32 схема

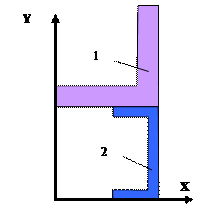
33 схема 34 схема

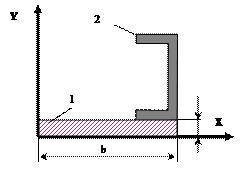
35 схема 36 схема

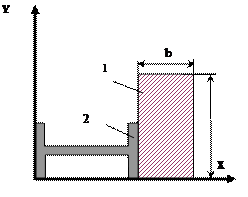
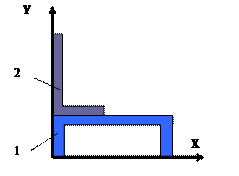
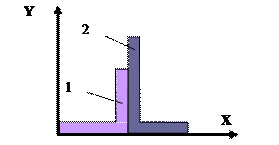
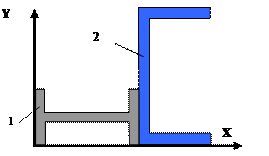
Рис.6

Задача 7. Расчет сложных составных несимметричных поперечных сечений из прокатных профилей.

Для несимметричных составных сечений (рис.7) при размерах, указанных в табл. 7, требуется:

1) Определить положение центра тяжести x_c и y_c.

2) Найти величины осевых моментов инерции относительно центральных осей J_x и J_y.

3) Найти величину центробежного момента инерции относительно центральных осей J_xy.

4) Определить положение главных центральных осей инерции (угол наклона главной оси инерции α_x).

5) Найти главные моменты инерции J_max и J_min.

6) Построить круг инерции и определить графически величины главных моментов инерции и направления главных центральных осей.

Ось x горизонтальная, направлена направо, ось y вертикальная, направлена вверх.

При расчете все необходимые данные для прокатных профилей следует взять из сортамента.

Таблица 7

Номер строки	Схема сечения по рис.7	Номера прокатных профилей
01	1	1- швеллер №10 2- двутавр №14
02	2	1- двутавр №22 2- уголок №125x125x10
03	3	1- швеллер №5 2- двутавр №24
04	4	1- швеллер №18 2- швеллер №20
05	5	1- швеллер №22 2- швеллер №30а
06	6	1- уголок №125x125x10 2- двутавр №33
07	7	1- двутавр №10 2- уголок №100x100x8
08	8	1- двутавр №22 2- двутавр №24
09	9	1- уголок №90x90x7 2- швеллер 24а
10	10	1- двутавр №18 2- швеллер №10
11	11	1- швеллер №16а 2- уголок №140x140x9
12	12	1- швеллер №12 2- швеллер №16а
13	13	1- двутавр №20 2- швеллер №10
14	14	1- швеллер №18а 2- швеллер №18
15	15	1- двутавр №18 2- швеллер №18а
16	16	1- двутавр №16 2- швеллер №30
17	17	1- уголок №100x100x8 2- уголок №160x160x12
18	18	1- швеллер №8 2- швеллер №10
19	19	1- двутавр №14 2- швеллер №20а
20	20	1- уголок №125x125x10 2- уголок №160x160x12
21	21	1- уголок №125x125x10 2- уголок №160x160x12
22	22	1- уголок №90x90x7 2- двутавр №33
23	23	1- уголок №100x100x8 2- швеллер 27
24	24	1- уголок №80x80x6 2- уголок №100x100x8
25	25	1- уголок №50x50x3 2- уголок №63x63x4
26	26	1- двутавр №16 2- швеллер №33
27	27	1- двутавр №24а 2- уголок №140x140x9
28	28	1- двутавр №27 2- уголок №63x63x4
29	29	1- двутавр №30 2- двутавр №40
30	30	1- швеллер №5 2- двутавр №30
31	31	1- двутавр №30 2- швеллер №18а
32	32	1- двутавр №10 2- уголок №90x90x7
33	33	1- швеллер №16 2- швеллер №20а
34	34	1- уголок №80x80x6 2- уголок №90x90x7
35	35	1- двутавр №24 2- уголок №90x90x7
36	36	1- швеллер №18 2- швеллер №20а
	б

1 схема 2 схема 3 схема

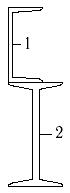
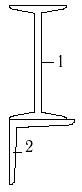
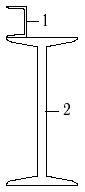
4 схема 5 схема 6 схема

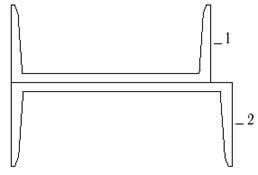
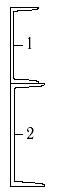
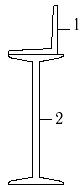
7 схема 8 схема 9 схема

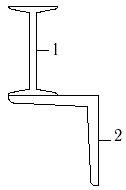
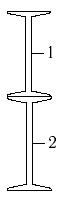
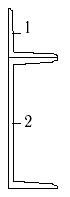
10 схема 11 схема 12 схема

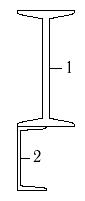
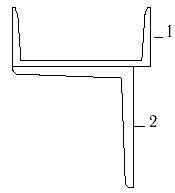
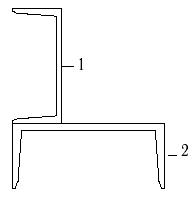
13 схема 14 схема 15 схема

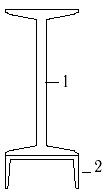
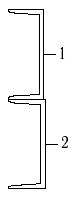
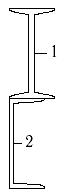
16 схема 17 схема 18 схема

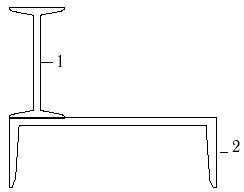
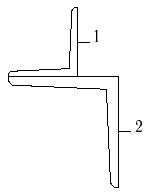
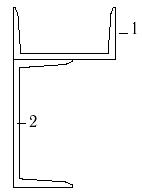
19 схема 20 схема 21 схема

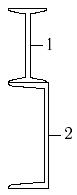
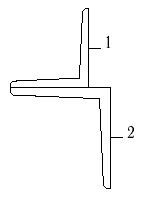
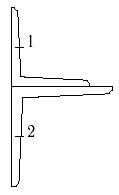
22 схема 23 схема 24 схема

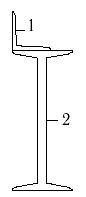
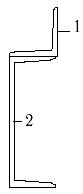
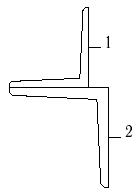
25 схема 26 схема 27 схема

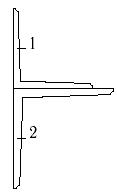
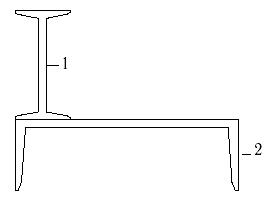
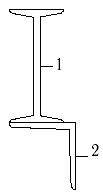
28 схема 29 схема 30 схема

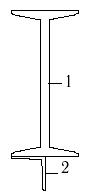
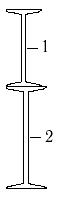
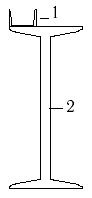
31 схема 32 схема 33 схема

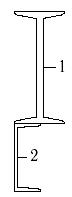
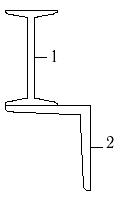
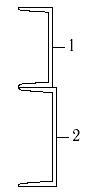
34 схема 35 схема 36 схема

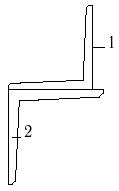
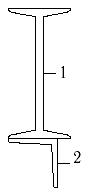
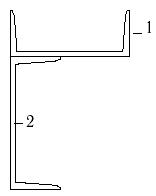
Рис.7

Задача 8. Расчет сложных составных несимметричных поперечных сечений из прокатных профилей.

Для составного несимметричного сечения, состоящего из листа и прокатных профилей, требуется:

1. Определить координаты центра тяжести сечения.

2. Вычислить центральные моменты инерции сечения.

3. Определить направление главных центральных осей инерции сечения.

4. Вычислить главные центральные моменты инерции сечения.

5. Выполнить проверку расчета.

Примечания:

1. При решении задачи сечение в плоскости чертежа не поворачивать.

2. Данные для решения задачи взять в табл. 8 и на рис 8.

3. Все чертежи выполнить согласно государственных стандартов с нанесением необходимых обозначений и размеров.

Таблица 8

Номер строки	Числовые значения вариантов
	Номер двутавра	Номер швеллера	Неравнобокий уголок, мм	Равнобокий уголок, мм	Пластина, мм
01	10	10	63x40x5	50x50x4	100x8
02	12	12	70x45x5	56x56x4	120x8
03	14	14	75x45x6	63x63x5	160x10
04	16	14 а	80x50x6	70x70x5	160x10
05	18	16	90x56x6	70x70x8	220x10
06	20	16 а	100x63x6	75x75x6	250x12
07	20 а	18	100x63x8	75x75x8	250x12
08	22	18 а	110x70x7	80x80x6	260x12
09	22 а	20	110x70x8	80x80x8	260x14
10	24	20 а	125x80x8	90x90x8	300x14
11	24 а	18	125x80x10	110x110x7	300x14
12	27	12	140x90x8	125x125x10	300x14
13	27 а	22 а	140x90x10	125x125x12	280x12
14	30	24	160x100x9	125x125x14	350x16
15	30 а	24 а	160x100x10	140x140x12	350x16
16	33	24	160x100x16	160x160x10	360x16
17	36	27	140x90x10	160x160x12	360x16
18	40	30	160x100x10	160x160x16	400x16
19	45	33	180x110x10	160x160x20	500x30
20	50	36	180x110x12	160x160x12	500x30
21	55	33	200x125x11	160x160x18	600x40
22	60	33	200x125x14	180x180x12	700x45
23	65	27	180x110x10	200x200x12	700x40
24	70	36	200x125x14	200x200x14	800x40
25	70 а	40	250x160x16	200x200x20	850x45
26	70 б	40	250x160x20	250x250x20	900x45
27	27	24	140x90x10	100x100x8	300x20
28	30	27	140x90x8	110x110x7	300x20
29	33	30	160x100x10	125x125x10	400x20
30	40	33	180x100x10	140x140x12	500x30
	в	г	а	б	в

1 схема 2 схема 3 схема 4 схема 5 схема

6 схема 7 схема 8 схема 9 схема 10 схема

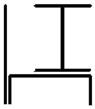
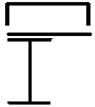
11 схема 12 схема 13 схема 14 схема 15 схема

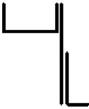
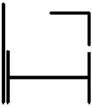
16 схема 17 схема 18 схема 19 схема 20 схема

21 схема 22 схема 23 схема 24 схема 25 схема

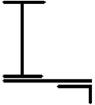
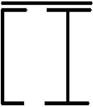
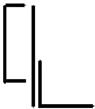
26 схема 27 схема 28 схема 29 схема 30 схема

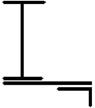
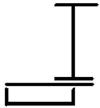
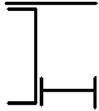
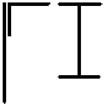
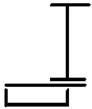
Рис. 8

Задача 9. Расчет сложных составных симметричных поперечных сечений из прокатных профилей.

Для двух заданных сечений, состоящих из нескольких элементов или имеющих вырезы, определить положение главных центральных осей инерции и вычислить величины моментов инерции относительно этих осей.

Первое сечение для расчета выбирается на рис. 9.1, второе – на рис. 9.2. Размеры элементов сечений и номера прокатных профилей берутся из таблицы 9. При расчете сечения, состоящего из прокатных профилей, уголок следует принимать в соответствии с заданными размерами; он может быть равнобоким или неравнобоким.

Таблица 9

Номер строки	Номер расчетной схемы (рис. 9.1, 9.2)	Размер а, см	Прокатный профиль
			полоса	швеллер	двутавр	уголок
01	1	10	160x10	10	12	75x75x8
02	2	20	180x10	12	14	75x50x6
03	3	12	180x6	14	10	90x90x6
04	4	14	200x10	14а	16	80x50x6
05	5	22	200x6	16	12	80x80x8
06	6	15	160x8	16а	18	70x45x5
07	7	18	210x8	14	14	75x75x6
08	8	16	220x10	12	16	80x50x6
09	9	20	220x8	14а	10	70x70x6
10	10	25	180x8	10	12	63x40x6
	з	ж	а	б	в	г

1 схема 2 схема

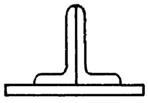
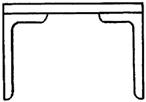
3 схема 4 схема

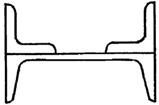
5 схема 6 схема

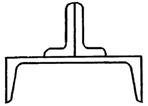
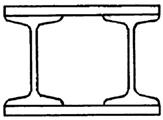
7 схема 8 схема

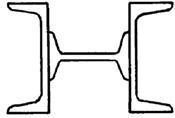
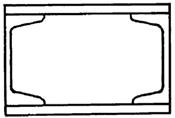
9 схема 10 схема

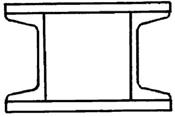
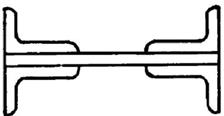
Рис. 9.1

1 схема 2 схема

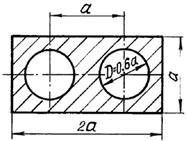
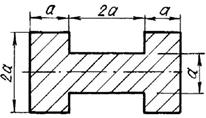
3 схема 4 схема

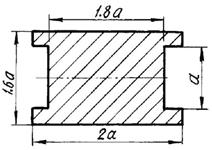
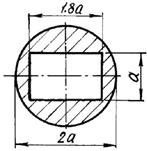
5 схема 6 схема

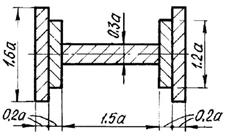
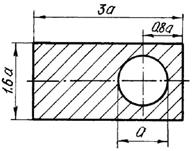
7 схема 8 схема

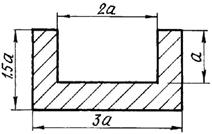
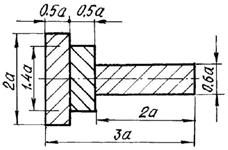
9 схема 10 схема

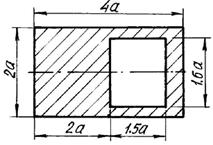
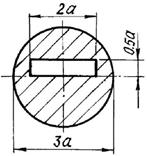
Рис. 9.2

Задача 10. Расчет сложных составных несимметричных поперечных сечений из прокатных профилей.

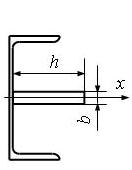
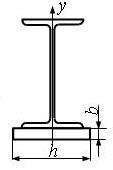
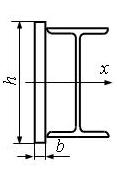
Задано сечение стального бруса, который состоит из листа и профильного проката – швеллера или двутавра. Одна ось (X или Y) является общей центральной осью составного сечения (рис. 10).

Требуется:

1. Привести геометрические характеристики простых составляющих сечения относительно их собственных центральных осей.

2. Вычертить сечение в масштабе с указанием основных размеров в числах и обозначением центральных осей простых составляющих сечения, параллельных вспомогательным осям.

3. Определить координаты центра тяжести всего сечения и построить на чертеже главные центральные оси, параллельные вспомогательным осям.

4. Выполнить проверку правильности выполнения третьего пункта путём вычисления статического момента всего сечения относительно общих центральных осей.

5. Определить значения главных центральных моментов инерции сечения.

6. Определить значения осевых моментов сопротивления (W_X, W_Y).

Данные взять из табл. 10 и рис.10.

Таблица 10

Номер строки	Схема по рис.10	Швеллер №	Двутавр №	Размеры сечения листа, см
				h	b
01 02 03 04 05 06 07 08 09 10	1 2 3 4 5 6 7 8 9 10	12 14 16 18 18^а 16^а 14^а 16 12 10	10 12 14 16 18 18^а 14 16 12 10	18 19 20 21 22 18 20 19 21 22	0,4 0,5 0,6 0,7 0,8 0,4 0,6 0,5 0,7 0,8
	е	в	е	д	г

1 схема 2 схема

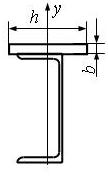
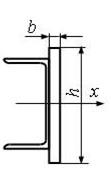
3 схема 4 схема

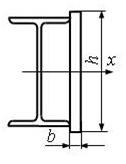
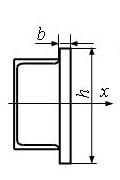
5 схема 6 схема

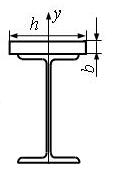
7 схема 8 схема

9 схема 10 схема

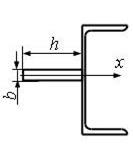
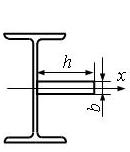
Рис. 10

Задача 11. Расчет сложных составных несимметричных поперечных сечений из прокатных профилей и фигур.

Для несимметричных сечений состоящих из двух фигур: поперечного сечения стандартного стального прокатного профиля и прямоугольника или треугольника (рис.11) при размерах указанных в таблице 11 требуется:

1) определить положение центра тяжести составной фигуры;

2) вычислить моменты инерции фигуры (осевые и центробежный) относительно произвольных центральных осей;

3) вычислить главные центральные моменты инерции;

4) определить положение главных центральных осей;

5) вычертить фигуру в масштабе, при этом показать все необходимые оси с указанием расстояний между ними, а также всех используемых размеров фигур, составляющих общую фигуру. Рисунок выполнить на отдельном листе формата А4.

При расчете все необходимые данные для прокатных профилей следует взять из сортамента.

Таблица 11

Номер строки	Схема по рис.11	Двутавр №	Швеллер №	Уголок неравнополочный		Уголок равнополочный		Размеры прямоугольника или треугольника
				Номер	Толщина полки	Номер	Толщина полки	h1	h2	d
1	1	14	22	9/5,6	6	11	8	b	0	0,5b
2	2	16	24	18/11	10	7	5	0,75b	0,25b	0,6b
3	3	18	27	12,5/8	10	8	7	0,5b	0,5b	0,7b
4	4	20	30	10/6,3	8	10	10	0,25b	0,75b	0,8b
5	5	22	14	20/12,5	12	12,5	10	0	b	0,9b
6	6	24	16	14/9	10	7,5	6	b	0	b
7	7	27	18	16/10	10	9	8	0,75b	0,25b	0,5b
8	8	30	20	9/5,6	6	11	8	0,5b	0,5b	0,6b
9	9	14	22	18/11	10	7	5	0,25b	0,75b	0,7b
10	10	16	24	12,5/8	10	8	7	0	b	0,8b
11	11	18	27	10/6,3	8	10	10	b	0	0,9b
12	12	20	30	20/12,5	12	12,5	10	0,75b	0,25b	b
13	13	22	14	14/9	10	7,5	6	0,5b	0,5b	0,5b
14	14	24	16	16/10	10	9	8	0,25b	0,75b	0,6b
15	15	27	18	9/5,6	6	11	8	0	b	0,7b
16	16	30	20	18/11	10	7	5	b	0	0,8b
17	17	14	22	12,5/8	10	8	7	0,75b	0,25b	0,9b
18	18	16	24	10/6,3	8	10	10	0,5b	0,5b	b
19	19	18	27	20/12,5	12	12,5	10	0,25b	0,75b	0,5b
20	20	20	30	14/9	10	7,5	6	0	b	0,6b
21	1	27	22	12,5/8	6	7,5	8	0,75b	0	0,5b
22	2	30	24	10/6,3	10	9	5	0,5b	0,25b	0,6b
23	3	14	27	20/12,5	10	11	7	0,25b	0,5b	0,7b
24	4	16	30	14/9	8	7	10	0	0,75b	0,8b
25	5	18	14	16/10	12	8	10	b	b	0,9b
26	6	20	16	9/5,6	10	10	6	0,75b	0	b
27	7	22	18	18/11	10	12,5	8	0,5b	0,25b	0,5b
28	8	24	20	12,5/8	6	7,5	8	0,25b	0,5b	0,6b
29	9	27	22	10/6,3	10	9	5	0	0,75b	0,7b
30	11	14	24	20/12,5	10	11	7	b	b	0,5b
31	12	16	27	14/9	8	7	10	0,75b	0	0,6b
32	13	18	30	16/10	12	8	10	0,5b	0,25b	0,7b
33	14	20	14	9/5,6	10	11	6	0,25b	0,5b	0,8b
34	15	22	16	14/9	8	7	5	b	0,75b	0,9b
35	16	24	18	16/10	12	8	7	0,75b	0,25b	b
36	17	27	22	9/5,6	10	10	10	0,5b	0,5b	0,5b
	б	в	а	г	б	в	а	г	б	в

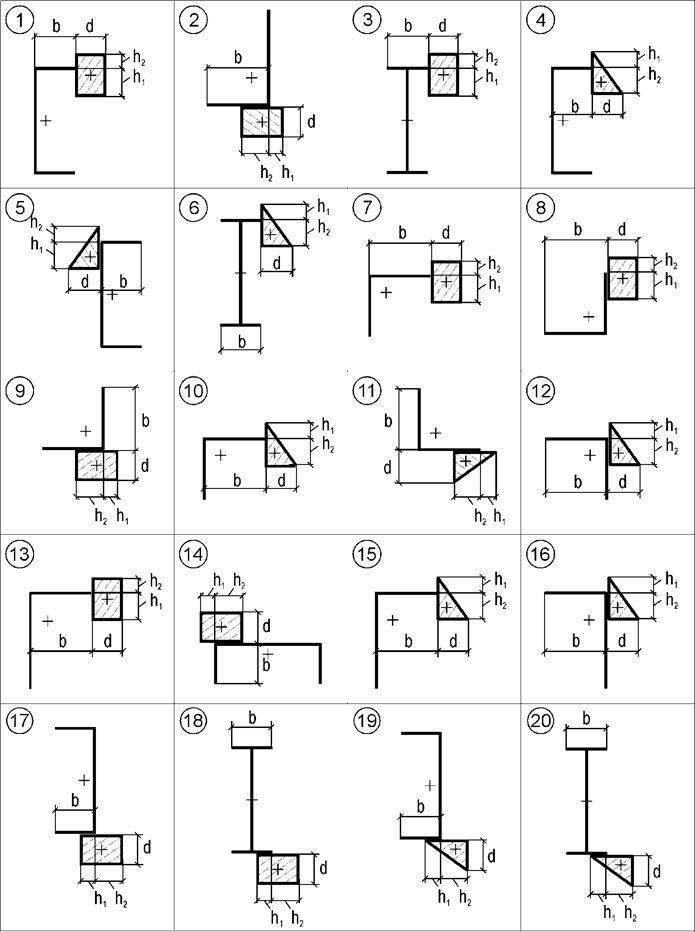
Рис.11

Задача 12. Расчет сложных симметричных поперечных сечений из фигур.

Для заданного сложного симметричного поперечного сечения требуется:

1. Начертить составную фигуру в масштабе 1:2 и указать на чертеже все размеры в буквенном и численном виде.

2. Ввести вспомогательную ось х_в и определить положение центра тяжести фигуры.

3. Определить главные моменты инерции фигуры.

Данные взять из табл. 12 и рис.12.

Таблица 12

Номер строки	Схема сечения по рис.12	a, м	b, м	c, м	d, м
01	1	0,12	0,21	0,15	0,32
02	2	0,15	0,25	0,21	0,1
03	3	0,2	0,3	0,25	0,15
04	4	0,25	0,1	0,3	0,1
05	5	0,3	0,15	0,1	0,15
06	6	0,1	0,2	0,15	0,2
07	7	0,15	0,25	0,2	0,25
08	8	0,2	0,33	0,25	0,3
09	9	0,25	0,11	0,3	0,12
10	10	0,3	0,15	0,2	0,15
11	1	0,2	0,2	0,25	0,2
12	2	0,25	0,25	0,32	0,25
13	3	0,3	0,32	0,25	0,3
14	4	0,11	0,29	0,31	0,2
15	5	0,15	0,25	0,1	0,25
16	6	0,18	0,3	0,15	0,3
17	7	0,15	0,1	0,2	0,25
18	8	0,2	0,15	0,25	0,32
19	9	0,25	0,12	0,34	0,1
20	10	0,31	0,15	0,2	0,15
21	1	0,16	0,26	0,15	0,2
22	2	0,15	0,1	0,24	0,25
23	3	0,22	0,15	0,25	0,3
24	4	0,25	0,21	0,34	0,22
25	5	0,35	0,25	0,14	0,35
26	6	0,2	0,31	0,15	0,14
27	7	0,25	0,1	0,2	0,15
28	8	0,34	0,15	0,25	0,17
29	9	0,25	0,25	0,31	0,15
30	10	0,32	0,25	0,28	0,21
31	1	0,12	0,25	0,25	0,25
32	2	0,15	0,33	0,32	0,31
33	3	0,2	0,1	0,25	0,1
34	4	0,25	0,15	0,3	0,15
35	5	0,31	0,14	0,11	0,2
36	6	0,21	0,15	0,15	0,25
	в	б	г	а	б

1 схема 2 схема

3 схема 4 схема

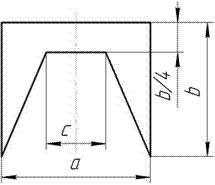
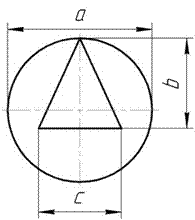
5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

Рис.12

Примеры выполнения задач

Пример 1

Плоская симметричная фигура (рис. 13) представлена трапецией с основаниями 12 см и 4 см с высотой 9 см. С центром на расстоянии 5 см от нижнего основания вырезан круг диаметром 6 см.

Требуется:

1. Найти центр тяжести фигуры.

2. Определить моменты инерции составной фигуры относительно центральных осей х_с и у_с.

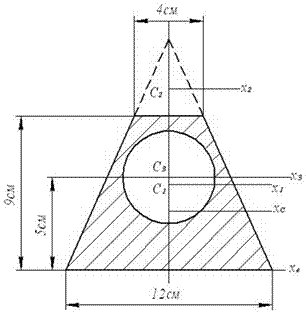
Рис.13

Решение.

Вводим вспомогательную ось х_В. Ординату у_с центра тяжести сечения найдем по формуле

Дополним трапецию треугольником с основанием 4 см, высота которого определяется пропорцией

Заданная фигура представляется совокупностью треугольника с основанием 12 см и высотой 13,5 см; круга и построенного треугольника с основанием 4 см и высотой h = 4,5 см.

Их площади и ординаты центров тяжести

Общая площадь фигуры

A=A₁-A₂-A₃=481-9-28,87=43,7 см².

Ордината центра тяжести составной фигуры

Оси х₁, х₂ и х₃ удалены от оси х_С на расстояния

Момент инерции составной фигуры относительно оси х_С в соответствии с формулами параллельного переноса

Ось симметрии у является главной центральной осью инерции. Момент инерции относительно оси у находится без использования формулы параллельного переноса оси.

Пример 2

В примере приняты схема, изображенная на рис. 14, и данные, представленные в табл. 14.

Рис.14. Схема фигуры

Таблица 14

Номер швеллера	Размеры прямоугольника
	h1	h2	d
18	0,75b	0,25b	0,7b

Решение.

Исходные данные фигур

Швеллер № 18 (см. раздел «Справочные данные»):

H = 18 см – высота швеллера;

b = 7 см – ширина полки;

А = 20,7 см² – площадь поперечного сечения;

J_max = 1090 см⁴ – наибольший момент инерции;

J_min = 86 см⁴ – наименьший момент инерции;

z₀ = 1,94 см – расстояние от наружной грани до центральной оси.

Прямоугольник:

h₁ = 0,75b = 0,75∙7 = 5,25 см;

h₂ = 0,25b = 0,25∙7 = 1,75 см;

d = 0,7b = 0,7∙7 = 4,9 см;

А = b∙0,7b = 7² ∙0,7 = 34,3 см².

Рисунок фигуры в масштабе

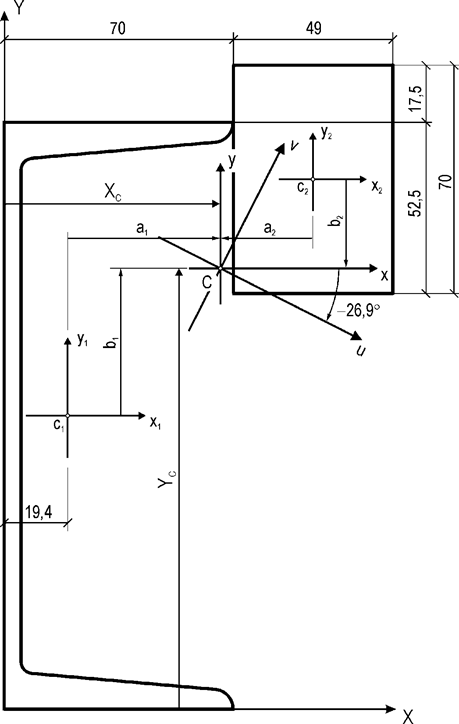
Рис. 15. Расчетные положения систем координатных осей составной фигуры

Примечание: оси, обозначения размеров или размеры наносятся на рисунок по мере выполнения расчетов.

1) Определение положения центра тяжести составной фигуры

(Далее индекс 1 относится к параметрам швеллера, а 2 – прямоугольника).

Определяются координаты центров тяжести отдельных фигур в выбранных осях X, Y (рис. 15):

X₁ = z₀ = 1,94 см;

Y₁ = H/2 = 18/2 = 9 см;

X₂ = b + d/2 = 7 + 4,9/2 = 9,45 см;

Y₂ = H – h₁ + b/2 = 18 – 5,25 + 7/2 = 16,25 см.

Вычисляются координаты центра тяжести всей фигуры:

Через центр тяжести (точка С) проводятся центральные оси х, у.

2) Определение моментов инерции фигуры относительно центральных осей х, у

Предварительно вычисляются расстояния от центральных осей отдельных фигур до центральных осей х, у (см. рис. 15):

а₁ = X_C - X₁ = 6,62 – 1,94 = 4,68 см;

b₁ = Y_C - Y₁ = 13,52 - 9 = 4,52 см;

а₂ = X_C - X₂ = 6,62 – 9,45 = -2,83 см;

b₂ = Y_C – Y₂ = 13,52 – 16,25 = -2,73 см.

Вычисляются моменты инерции фигуры относительно центральных осей х, у:

J_х = J_x1+ b₁²А₁ + J_x2+ b₂²А₂ =

= 1090 + 4,52²∙20,7 + 4,9∙7³/12 + (-2,73)²∙34,3 = 1908,6 см⁴;

J_у = J_y1+ а₁²А₁ + J_y1+ а₂²А₂ =

= 86 + 4,68² ∙20,7 + 7∙4,9³/12 + (-2,83)²∙34,3 = 882,7 см⁴;

J_ху = J_x1y1+ а₁b₁А₁ + J_x2y2+ а₂b₂А₂ =

= 0 + 4,68∙4,52∙20,7 + 0 + (-2,83)(-2,73)∙34,3= 702,9 см⁴.

3) Определение главных центральных моментов инерции фигуры

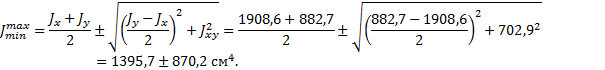
J_max = 2265,9 см⁴. J_min = 525,5 см⁴.

4) Определение положения главных центральных осей

α = -26,9^°.

Через центр тяжести фигуры проводятся главные центральные оси u, v (см. рис.15).

Таким образом,

J_u = J_max = 2265,9 см⁴,

J_v = J_min = 525,5 см⁴.

Пример 3

Рассмотрим сечение, имеющее две оси симметрии (рис. 16). Разбиваем это составное сечение на элементарные: I, II – прямоугольники, III - круг.

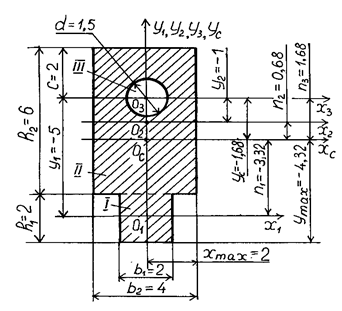
Рис.16

Решение.

1. Определение центра тяжести.

В качестве вспомогательных осей выбираем оси круга X₃, Y₃. В этом случае координата центра тяжести X_C= 0, т.к. центр тяжести сечения должен быть на оси симметрии Y₃.

На основании формулы получим:

где A₁=b_1∙h₁=2∙2 = 4 см²; A₂=b_2∙h₂=4∙6= 24 см²; A₃=πd²/4=3,14∙1,5²/4=1,76 см²;

Y₁=-5 см; Y₂=-1 см; Y₃=0.

Проводим центральные оси X_C, Y_C. Эти оси являются главными центральными осями сечения.

2. Определение главных центральных моментов инерции.

Для определения главных центральных моментов инерции применим формулы параллельного переноса

J_x=J_Xc+n²A,

J_y=J_yc+m²A,

J_xy=J_XcYc+nmA,

а также формулы:

И формулы

Получаем

где n₁= –3,32 см; n₂= 0,68 см; n₃= 1,68 см.

Так как оси Y₁, Y₂, Y₃, Y_C совпали, то главный центральный момент инерции всего сечения относительно оси Y_C определим как алгебраическую сумму осевых моментов составляющих сечений:

Пример 4

Задано сечение, составленное из прокатных профилей: швеллера № 16а и двух неравнобоких уголков 80×50×6 (рис. 17). Требуется вычислить главные центральные моменты инерции.

Рис. 17

Решение.

1. Из таблиц сортамента выписываются геометрические характеристики прокатных профилей, составляющих заданное сечение.

Швеллер №16а: размеры h =160 мм, b = 68 мм, площадь сечения F₁ =19,5 см²; осевые моменты инерции =823 см⁴, =78,8 см⁴, координата центра тяжести z₀=2 см.

Неравнобокий уголок 80×50×6: площадь сечения F₂ =7,55 см²; осевые моменты инерции =49 см⁴, =14,8 см⁴, координаты центра тяжести y₀=2,65 см, x₀=1,17 см..

Примечание. Если в состав сечения входит прямоугольник, то следует вычислить площадь и осевые моменты инерции

В соответствии с заданным вариантом сечения выполняется чертеж в масштабе 1:2 с указанием характерных размеров.

На чертеж наносятся центры тяжести швеллера C₁ и уголка C₂ и проводятся их собственные центральные оси y₁, z₁ и y₂, z₂ (см. рис. 17).

2. Определение положения центра тяжести заданного сечения.

Заданное сечение имеет одну ось симметрии, которая является главной центральной осью. Выбираем исходную систему координат: ось абсцисс y ^/ совмещаем c нижней границей сечения, а ось ординат Z - с осью симметрии. Координаты точек C₁ и C₂ легко определяются по чертежу.

Учитывая симметрию сечения, вычисляем ординату его центра тяжести по формуле

где F₁ - площадь швеллера, F₁=19,5 см²,

z_c1 - ордината точки C₁, z_c1 =6,8-2,0=4,8 см;

F₂ - площадь одного уголка, F₂ =7,55 см²;

Z_c2 - ордината точки – C₂, Z_c2 =y₀=2,65 см.

После подстановки числовых значений получаем

Откладывая найденное значение z_c=3,9 см на оси Z вверх от оси y^/, находим положение центра тяжести всего сечения C и проводим главные центральные оси Y , Z.

Примечание. Если фигура имеет две оси симметрии, центр тяжести лежит на их пересечении, то вычислений для определения его положения производить не нужно.

3. Вычисление главных центральных моментов инерции сечения относительно осей Y и Z .

Расстояния между осями определяются по чертежу:

а₁=6,8-3,9-2=0,90 см;

а₂=3,9-2,65=1,25 см;

b₁=0, так как оси Z и Z₁ совпадают;

b₂=8+1,17=9,17 см.

Главные центральные моменты инерции составного сечения J_Y и J_Z вычисляются по формулам

После подстановки числовых значений в эти формулы, получаем:

J_y=(78,8+0,9²∙19,5)+2∙(49+1,25²∙7,55)=216,2 см⁴;

J_z=(823)+2∙(14,8+9,17²∙7,55)=2122 см⁴.

Пример 5

Задано сечение (рис. 18). Размеры сечения заданы в сантиметрах. Требуется определить главные центральные моменты инерции этого сечения.

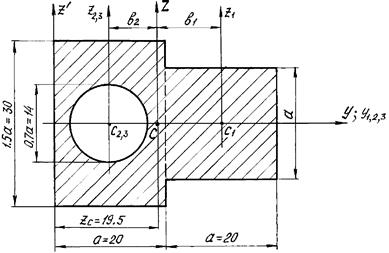
Рис. 18

Решение.

1. Заданное сечение вычерчивается в масштабе 1:2 и разбивается на простейшие фигуры: квадрат (1), прямоугольник (2) и круговое отверстие (3). На чертеже показываются центры тяжести составляющих фигур (точки C₁ и C_2,3) и проводятся их главные центральные оси y₁, z₁; y₂, z₂ и y₃, z₃ (см. рис. 18). Площади и моменты инерции составляющих фигур относительно их центральных осей вычисляются по известным формулам.

Для квадрата

F₁=a²=20²=400 см²;

Для прямоугольника

F₂=a∙1,5a=20∙1,5∙20=600 см²;

Для круга

2. Определение положения центра тяжести составного сечения.

Центр тяжести составной фигуры лежит на ее оси симметрии Y. Вспомогательная ось z’ совмещается с левой границей сечения. Координата центра тяжести всего сечения y_c в системе Yoz’ определяется по формуле:

По чертежу определяются абсциссы точек C₁ и C_2,3:

y_c1=1,5a=1,5∙20=30 см;

y_c2=y_c3=0,5a=0,5∙20=10 см.

Площадь круга подставляется в формулу (1) со знаком минус, так как площадь отверстия принято считать отрицательной величиной.

Подставляя числовые значения, получаем

Откладывая на оси Y отрезок ОС =19,5 см, находим точку С - центр тяжести составного сечения и проводим главную центральную ось Z, параллельную оси z^/ (см. рис.18).

3. Вычисление моментов инерции относительно главных центральных осей Y, Z.

Используем формулы

как и в предыдущем примере. Перед последним слагаемым в скобках ставится знак минус, так как моменты инерции отверстия считаются отрицательными:

Моменты инерции составляющих фигур относительно собственных главных центральных осей вычислены ранее. Оси y₁, y₂ и y₃ совпадают с главной центральной осью Y всей фигуры, поэтому расстояния между этими осями и осью Y равны нулю:

a₁=a₂=a₃=0.

По чертежу находим расстояние между осями Z и Z₁

b₁=a+0,5a-y_c=20+0,5∙20-19,5=10,5 см.

и расстояние между осями Z и Z₂

b₂=b₃=z_c-0,5a=19,5-0,5∙20=9,5 см.

Подставляя числовые значения в (2), вычисляем главные центральные моменты инерции составного сечения:

J_Y=13333+45000-1885=56448 см⁴;

J_z=(13333+400∙10,5²)+(20000+600∙9,5²)-(1885+154∙9,5²)=115800 см⁴.

Пример 6

Для заданного поперечного сечения (рис. 19), состоящего из двух стандартных профилей (швеллера и равнобокого уголка), требуется:

1) определить положение центра тяжести;

2) найти осевые и центробежный моменты инерции относительно центральных осей;

3) определить направление главных центральных осей (u и ν);

4) найти моменты инерции относительно главных центральных осей;

5) вычертить сечение и указать на нем все размеры в числах и все оси.

Дано: Сечение состоит из швеллера №20 и равнобокого уголка 125×125×12.

Рис. 19

Решение.

Из сортамента прокатной стали выписываем необходимые геометрические для швеллера №20 (ГОСТ 8240-86): A=23,4 см², h=20 см, b=7,6 см, z₀=2,07 см, I_x=1520 см⁴, I_y=113 см⁴; для уголка (ГОСТ 8509-86) имеем: A=28,9 см², b=12,5 см, z₀=3,53 см, I_x=422 см⁴, =670 см⁴, =174 см⁴.

Определяем координаты центра тяжести сечения относительно координат x₁ и y₂, представив его в виде двух простых фигур (рис. 18):

Здесь y_шв, y_уг и x_шв, x_уг - расстояния от центров тяжести простых фигур швеллера и уголка до вспомогательных осей x₁ и y₂.

Центр тяжести заданного сечения (точка C) должен лежать на прямой C₁C₂. Проводим через него центральные оси инерции x_c, y_c и определяем осевые и центробежный моменты инерции относительно этих осей по формулам для случая параллельного переноса осей:

Рис. 20

Здесь a₁=-y_c=-7,48 см, b₁=3,81 см, a₂=6,05 см, b₂=-x_c=-3,09 см - координаты центров тяжести швеллера и уголка в осях x_c, y_c.

Центробежный момент инерции сечения для уголка относительно осей x₂, y₂ можно определить по формуле:

Знак минус здесь поставлен, так как большая часть сечения уголка находится во второй и четвертой четвертях, где координаты имеют разные знаки. Центробежный момент инерции сечения для всего сечения:

Определяем угол наклона главных центральных осей:

Для нахождения оси max u ось x_c () поворачиваем против часовой стрелки (∠α>0) на α=21,3°.

Находим значения главных центральных моментов инерции:

I_max=4877 см⁴, I_min=583 см⁴.

Проверкой нам служит соблюдение равенства

4309+1151=4877+583;

5460=5460.

Пример 7

Для заданного поперечного сечения (рис. 21), состоящего из двух стандартных профилей (швеллера и равнобокого уголка), требуется:

1) Вычертить сечения в масштабе 1:2 и указать на нем все оси и размеры в числах.

2) Определить положение центра тяжести сечения.

3) Найти осевые и центробежный момент инерции относительно центральных осей.

4) Определить направление главных центральных осей.

5) Найти моменты инерции относительно главных осей.

Дано: Сечение состоит из швеллера №20 и равнобокого уголка 90×90×8.

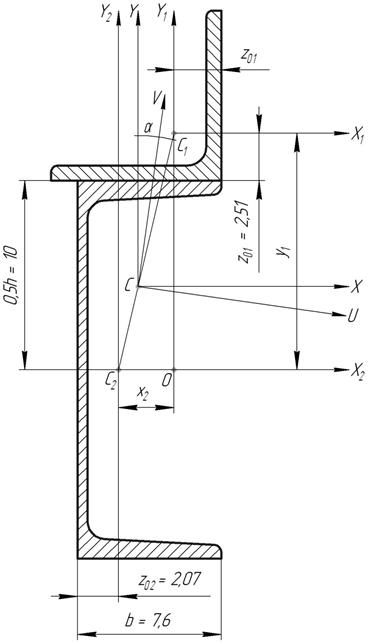
Рис.21

Решение.

1) Выбираем вспомогательные оси и выпишем все необходимые геометрические характеристики каждого профиля:

Уголок равнополочный (ГОСТ 8509 – 86):

Швеллер №20 (ГОСТ 8240 – 72):

2) Определим положение центра тяжести сечения в системе координат

3) Вычислим осевые и центробежный момент инерции сечения относительно центральных осей

4) Угол наклона главных центральных осей

Т.к. , то поворот выполняем по часовой стрелке.

5) Вычислим моменты инерции относительно главных центральных осей

Проверка:

Пример 8

Для заданного поперечного сечения (рис.22), состоящего из двух стандартных профилей (швеллера и неравнобокого уголка), требуется:

1) Определить положение центра тяжести несимметричного сечения, состоящего из стандартных профилей;

2) Определить положение главных центральных осей и вычислить значения главных центральных моментов инерции сечения.

Дано: Сечение состоит из швеллера №18а и неравнобокого уголка 14×9×0,8; а=37 мм.

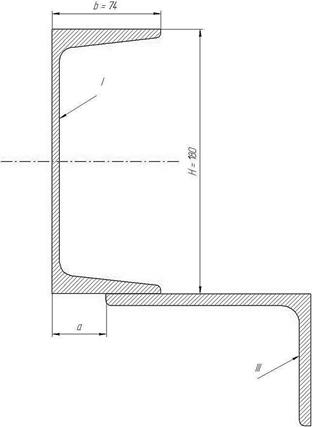
Рис.22

Решение.

По размерам, взятым из ГОСТ8240-72 и ГОСТ8510-72, вычерчиваем соответственно швеллер 18а и уголки .

1) Определим центр тяжести сечения:

Разобьем сечения на элементы I, III и обозначаем их центры тяжести (C₁ и C₂), через которые проводим соответственно параллельные центральные оси X₁ и Y₁, X₂ и Y₂ (рис.23). Вычислим расстояние между осями и указываем их на чертеже.

Площади сечений швеллера и уголка даны в таблицах ГОСТов:

Общая площадь сечения:

По рис.23 рассчитаем расстояние .

По условию АВ = a = 37 мм, ВС = 140 мм. Отсюда АС = АВ+ВС = 177 мм.

Из ГОСТ8240-72 и ГОСТ8510-72 найдем расстояния DE (оно равно 21,3 мм) и CF (оно равно 20,3 мм), HC (оно равно 44,9 мм).

Расстояние AJ = DE= 21,3 мм,

Расстояние от C₁ до C₂ по оси X- это расстояние (отрезок JH):

JH = AC – AJ – HC = 177 – 44,9 – 21,3 = 110,8 мм

Расстояние от C₁ до C₂ по оси Y- это расстояние (отрезок LM):

LM = AL + AM

AM = - CF = -20,3 мм; AL = -90 мм

LM = AL + AM = - 90 + (-20,3) = -110,3 мм

Находим положение центров тяжести сечения в системе координат C₁X₁Y₁:

Отмечаем центр тяжести на чертеже (т. С). Сделаем проверку. Проведем прямую С₁С₂. Точка С лежит на данной прямой, значит координаты найдены верно.

Через центр тяжести сечения проводим оси X₀ и Y₀ и указываем расстояние между осями X₁ и X₀ , Y₁ и Y₀.

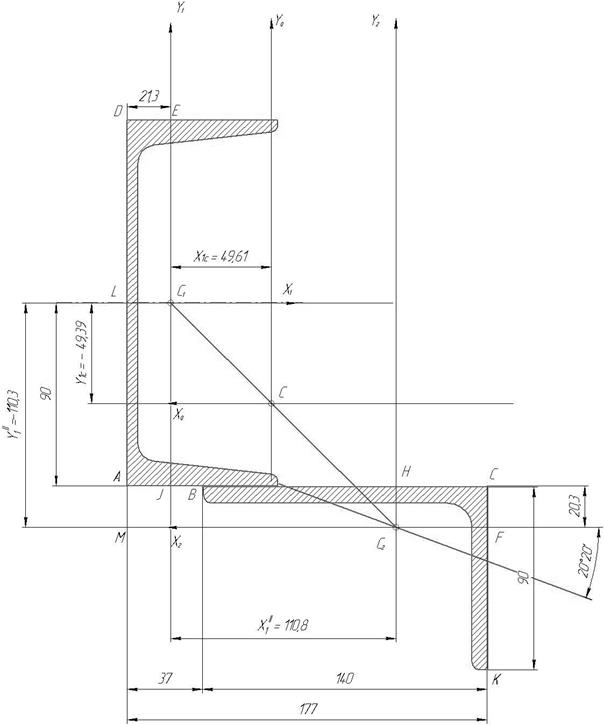
Размеры указаны в миллиметрах

Рис.23

2) Определение осевых и центробежного моментов инерции сечения (рис.24).

Выписываем из таблиц ГОСТов необходимые значения моментов инерции элементов сечения относительно указанных на чертеже осей:

Ось для уголка есть ось минимального момента инерции. Она наклонена к центральной оси, параллельной длинной полке под углом (по ГОСТу ) и пересекает обе полки уголка. В данном случае

Вторая главная центральная ось уголка (V₂) перпендикулярна оси . Для этой оси:

Центробежный момента инерции уголка относительно его центральных осей X₂ и Y₂:

Проверим полученное значение:

Значения равны, значит, центробежный момент инерции уголка найден правильно.

Для швеллера оси X₁ и Y₁ являются главными центральными, т.к. ось X₁ есть ось симметрии. Поэтому

Расстояние a₁ =

Расстояние a₂ =

Расстояние b₁ =

Расстояние b₂ =

Вычислим осевые и центробежный моменты инерции сечения относительно центральных осей X₀ и Y₀:

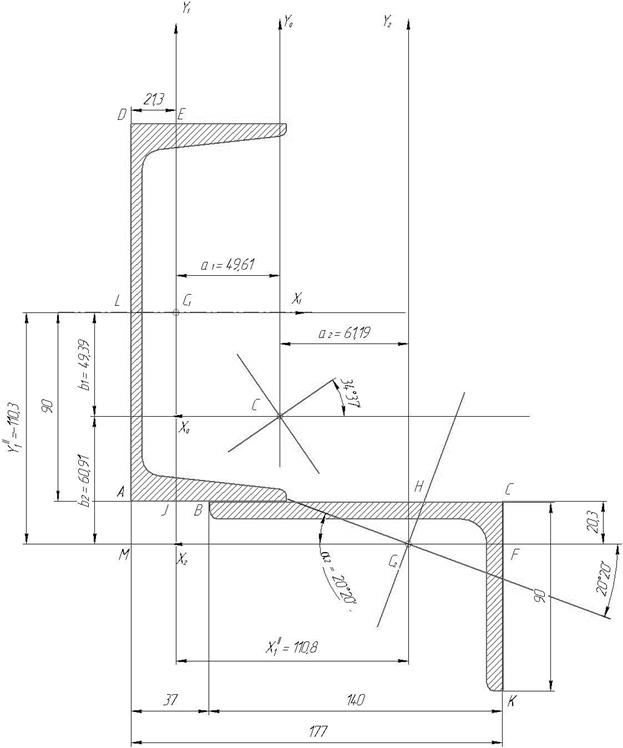
Размеры указаны в миллиметрах

Рис.24

3) Определение положения главных центральных осей и вычисление значения главных центральных моментов инерции сечения.

Следовательно:

Т.к. , оси X₀ и Y₀ для получения направлений главных центральных осей заданного сечения следует повернуть против хода часовой стрелки.

Вычислим значения главных центральных моментов инерции сечения:

Проверим правильность определения :

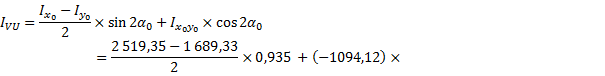
Главные центральные оси U (min) и V (max) проведены на чертеже сечения.

Онлайн-калькулятор "Расчет геометрических характеристик кольцевого сечения"

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00