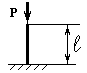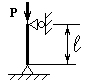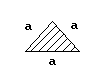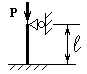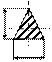Главная

Задача 1. Устойчивость сжатого стержня. Определение критической силы и подбор сечения

Стальной стержень длиной l сжимается силой Р. Требуется найти:

1. размеры поперечного сечения при допускаемом напряжении на сжатие [σ] =160 МПа (расчет производить последовательными приближениями, предварительно задаваясь величиной коэффициента φ=0,5);

2. величину критической силы и коэффициент запаса устойчивости.

Данные взять из табл. 1.

Таблица 1

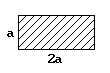
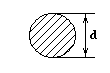
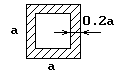
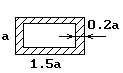
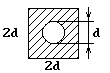
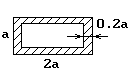
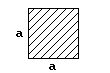
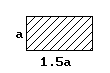
Номер строки	Вариант схемы формы сечения	Р кН	l м	Схема закрепления стержня	Форма сечения стержня
01 02	I II	100 200	2,1 2,2		I	II
03 04	III IV	300 400	2,3 2,4		III	IV
05 06	V VI	500 600	2,5 2,6		V	VI
07 08	VII VIII	700 800	2,7 2,8		VII	VIII
09 10	IX X	900 1000	2,9 3,0		IX	X
11 12	I III	300 400	2,3 2,5		I	II
13 14	III V	900 600	2,2 2,4		III	IV
15 16	V VII	500 900	2,5 2,8		V	VI
17 18	VII VIII	300 500	2,7 2,2		VII	VIII
19 20	IX X	100 1000	2,6 3,0		IX	X
21 22	I II	600 200	2,1 2,3		I	II
23 24	III IV	300 900	2,0 3,0		III	IV
25 26	V VI	400 600	2,2 2,5		V	VI
27 28	VII VIII	700 100	2,4 2,7		VII	VIII
29 30	IX X	200 1000	2,1 2,3		IX	X
31 32	IX X	800 600	2,7 2,9		IX	X
33 34	I II	100 300	2,1 3,0		I	II
35 36	III IV	700 200	2,1 2,7		III	IV
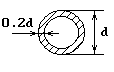
	б	а	в	г

Задача 2. Устойчивость сжатого стержня. Определение размеров поперечного сечения

Для стержня, нагруженного осевой сжимающей силой F, определить размеры поперечного сечения заданной по условию задачи формы и коэффициент запаса устойчивости К_у. Допускаемое напряжение σ задано в МПа, длина L - в м, сила F - в кН.

Данные взять из табл.2 и табл.3.

Таблица 2

Номер cтроки	Схема по табл.3	Строка с числовыми данными в схеме
01	1	1
02	2	2
03	3	3
04	4	4
05	5	1
06	6	2
07	7	3
08	8	4
09	9	1
10	10	2
11	11	3
12	12	4
13	13	1
14	14	2
15	15	3
16	16	4
17	17	1
18	18	2
19	19	3
20	20	4
21	21	1
22	22	2
23	23	3
24	24	4
25	25	1
26	26	2
27	27	3
28	28	4
29	29	1
30	30	2
31	31	3
32	32	4
33	33	1
34	34	2
35	35	3
36	36	4
	б	г

Таблица 3

1 схема F L		L	F	𝛔	2 схема F L		L	F	𝛔
	1	6	500	160		1	3	100	12
	2	5	400	160		2	3,5	150	12
	3	5,5	450	150		3	4	100	11
	4	4	300	150		4	3	200	11
	Сталь 3					H Дерево H
3 схема F L		L	F	𝛔	4 схема F L		L	F	𝛔
	1	5	400	150		1	3	100	10
	2	5,5	350	150		2	3,5	80	11
	3	4,5	300	160		3	3	60	12
	4	4	250	160		4	2,5	120	11
	Сталь 3					B Дерево H H/B=2
5 схема F L		L	F	𝛔	6 схема F L		L	F	𝛔
	1	4,5	200	150		1	3	80	11
	2	4	250	160		2	2,5	120	12
	3	3,5	150	160		3	3,5	80	10
	4	3	300	150		4	3	100	10
	Сталь 3					Дерево d
7 схема F L		L	F	𝛔	8 схема F L		L	F	𝛔
	1	5	150	80		1	6	400	160
	2	4,5	200	85		2	5,5	350	150
	3	4	250	80		3	5	300	150
	4	3,5	300	80		4	4	250	160
	H H1 Чугун H H1 H1/H=0,8					Сталь 3
9 схема F L		L	F	𝛔	10 схема F L		L	F	𝛔
	1	2,5	200	80		1	2,5	250	12
	2	3	150	85		2	2	200	11
	3	3,5	100	70		3	3	150	12
	4	4	100	75		4	3,5	100	11
	d Чугун D d/D=0,8					B Дерево H H/B=2
11 схема F L		L	F	𝛔	12 схема F L		L	F	𝛔
	1	5,5	300	160		1	2,5	360	11
	2	5	200	150		2	3	300	12
	3	4,5	200	160		3	3,5	250	11
	4	4	150	150		4	2,5	400	12
	Сталь 3					Дерево d
13 схема F L		L	F	𝛔	14 схема F L		L	F	𝛔
	1	4	300	160		1	2,5	350	11
	2	5	100	160		2	3	300	12
	3	3	150	150		3	3,5	250	11
	4	4	10	150		4	2,5	400	10
	Сталь 3					H Дерево H
15 схема F L		L	F	𝛔	16 схема F L		L	F	𝛔
	1	4,5	300	160		1	2,5	350	110
	2	4	10	160		2	3	300	120
	3	3,5	150	150		3	3,5	250	110
	4	3	200	150		4	2,5	400	110
	Сталь 3					Сталь 3 Iz=Iy
17 схема F L		L	F	𝛔	18 схема F L		L	F	𝛔
	1	4	10	11		1	4	10	10
	2	3,5	15	10		2	3,5	10	11
	3	3	20	12		3	3	15	12
	4	2,5	25	13		4	2,5	20	13
	H Дерево H					H Дерево H

19 схема F L		L	F	𝛔	20 схема F L		L	F	𝛔
	1	6	800	150		1	4	100	12
	2	5,5	700	150		2	3,5	120	11
	3	5	600	160		3	3	140	11
	4	4,4	500	160		4	2,5	160	12
	Сталь 3					Дерево d
21 схема F L		L	F	𝛔	22 схема F L		L	F	𝛔
	1	2,5	200	10		1	6	800	160
	2	3	150	11		2	5,5	600	150
	3	3,5	100	12		3	5	700	150
	4	3	120	13		4	4,5	400	150
	B Дерево H H/B=2					Сталь 3
23 схема F L		L	F	𝛔	24 схема F L		L	F	𝛔
	1	6	800	160		1	6	800	150
	2	5,5	700	150		2	5,5	700	160
	3	5	600	160		3	5	650	160
	4	4,5	500	150		4	4,5	600	150
	Сталь 3					Сталь 3
25 схема F L		L	F	𝛔	26 схема F L		L	F	𝛔
	1	4	450	160		1	4	300	160
	2	3,5	400	160		2	3,5	350	160
	3	3	300	160		3	3	600	150
	4	2,5	500	160		4	4,5	250	160
	Сталь 3					Сталь 3
27 схема F L		L	F	𝛔	28 схема F L		L	F	𝛔
	1	2,5	300	12		1	3,5	300	12
	2	3	250	11		2	3	350	13
	3	3	200	10		3	2,5	300	11
	4	3	150	11		4	3,5	350	12
	B Дерево H H/B=2					d
29 схема F L		L	F	𝛔	30 схема F L		L	F	𝛔
	1	4	300	150		1	3,5	200	12
	2	4,5	400	150		2	3	150	11
	3	3,5	500	160		3	2,5	150	10
	4	3	350	160		4	2	200	13
	Сталь 3					H Дерево H

31 схема F L		L	F	𝛔	32 схема F L		L	F	𝛔
	1	6	800	160		1	6	800	150
	2	5,5	500	140		2	5,5	700	160
	3	5	600	160		3	5	650	160
	4	4,5	700	150		4	4,5	600	150
	Сталь 3					Сталь 3
33 схема F L		L	F	𝛔	34 схема F L		L	F	𝛔
	1	4	10	12		1	4	10	13
	2	3,5	15	10		2	3,5	10	11
	3	3	20	11		3	3	15	12
	4	2,5	25	13		4	2,5	20	10
	H Дерево H					H Дерево H
35 схема F L		L	F	𝛔	36 схема F L		L	F	𝛔
	1	6	800	150		1	4	100	12
	2	5,5	700	150		2	3,5	120	11
	3	5	600	160		3	3	140	11
	4	4,4	500	160		4	2,5	160	12
	Сталь 3					Дерево d

Задача 3. Расчет сжатых стержней на устойчивость

Для стального стержня (рис.1, а, б) длиной l, сжимаемого силой F, требуется:

1. подобрать размеры поперечного сечения стержня из условия его устойчивости при допускаемом напряжении на сжатие [σ] =160 МПа (расчет проводить методом последовательных приближений по коэффициенту снижения допускаемых напряжений на сжатие);

2. найти величину критической силы и коэффициент запаса устойчивости n_у.

Числовые данные для расчета следует взять из табл. 4, расчетные схемы – на рис. 1, а, б.

Таблица 4

Номер строки	Схема по рис. 1, а, б	Сила F, кН	Длина стержня l, м
01	1	500	2,5
02	2	480	3,9
03	3	450	2,8
04	4	300	3,2
05	5	350	2,7
06	6	370	3,5
07	7	360	3,0
08	8	460	2,7
09	9	370	2,6
10	10	400	3,1
	з	ж	б

1 схема 2 схема

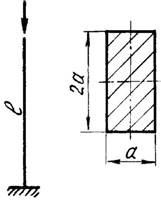
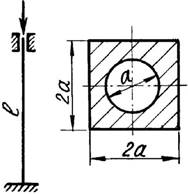
3 схема 4 схема

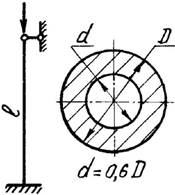
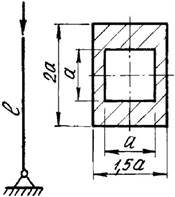
5 схема 6 схема

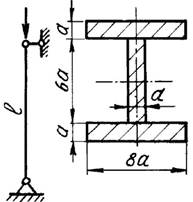
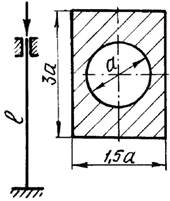
7 схема 8 схема

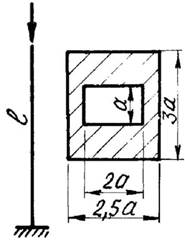
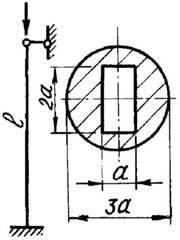
9 схема 10 схема

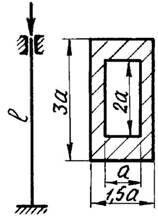
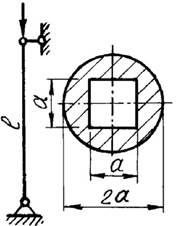
Рис. 1,а

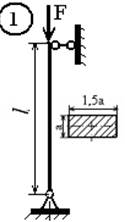
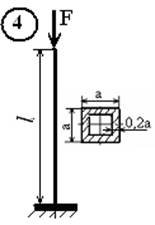
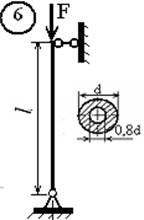
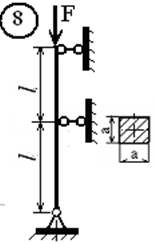
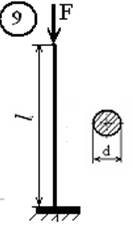
Рис.1,б

Задача 4. Расчет стальных стержней на устойчивость

Стальной стержень длиной l сжимается силой F (рис.2).

Требуется:

1. Найти размеры поперечного сечения стержня при расчетном сопротивлении стали R =160 МПа, пользуясь методом последовательных приближений.

2. Определить величину критической силы, если предельная гибкость равна λ_пред = 100.

3. Вычислить коэффициент запаса устойчивости.

Данные взять из табл. 5.

Таблица 5

Номер строки	Схема по рис. 2,а	Форма сечения по рис.2,б	F, кН	l, м
01	1	1	100	2,1
02	2	2	200	2,2
03	3	3	300	2,3
04	4	4	400	2,4
05	1	5	500	2,5
06	2	6	600	2,6
07	3	7	700	2,7
08	4	8	800	2,8
09	1	9	900	2,9
10	2	10	1000	3,0
	е	а	б	в

1 схема 2 схема 3 схема 4 схема

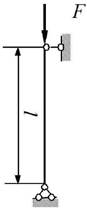
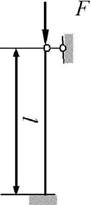
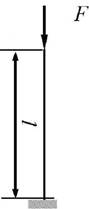
Рис.2,а

1 схема 2 схема 3 схема 4 схема 5 схема

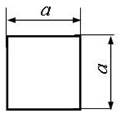
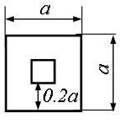
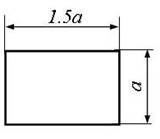
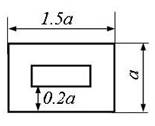
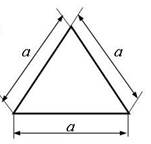
6 схема 7 схема 8 схема 9 схема 10 схема

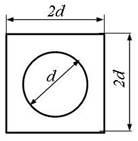
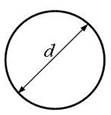
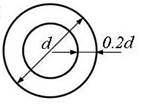
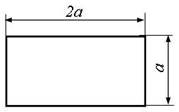
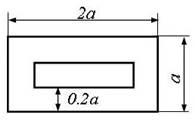
Рис. 2,б

Задача 5. Устойчивость сжатого стержня. Подбор поперечного сечения

Подобрать поперечное сечение сжатого стержня большой длины при допускаемом напряжении на сжатие [σ] =150 МПа. Вид закрепления стержня показан на рис.3.

Данные взять из табл.6.

Рис.3

Таблица 6

Номер cтроки	Схема по рис.3	F, кН	l, м	Форма поперечного сечения
01	I	50	6,5	Двутавр
02	II	60	6	Швеллер
03	III	70	5,5	Квадрат
04	IV	80	5	Окружность
05	I	90	4,5	Прямоугольник с соотношением сторон 1/2
06	II	100	4	Двутавр
07	III	110	3,5	Швеллер
08	IV	120	3	Квадрат
09	I	130	2,5	Окружность
10	II	140	2	Прямоугольник с соотношением сторон 1/2
11	III	60	6	Швеллер
12	IV	70	5,5	Квадрат
13	I	80	5	Окружность
14	II	90	4,5	Прямоугольник с соотношением сторон 1/2
15	III	100	4	Двутавр
16	IV	110	3,5	Швеллер
17	I	120	3	Двутавр
18	I	130	2,5	Швеллер
19	II	50	6,5	Квадрат
20	III	60	6	Окружность
21	IV	70	5,5	Прямоугольник с соотношением сторон 1/2
22	I	80	5	Двутавр
23	II	90	4,5	Швеллер
24	III	100	4	Квадрат
25	IV	110	3,5	Окружность
26	I	120	3	Прямоугольник с соотношением сторон 1/2
27	II	130	2,5	Швеллер
28	III	140	2	Квадрат
29	IV	60	6	Окружность
30	I	70	5,5	Прямоугольник с соотношением сторон 1/2
31	II	80	5	Двутавр
32	III	90	4,5	Швеллер
33	IV	100	4	Квадрат
34	I	110	3,5	Окружность
35	II	120	3	Прямоугольник с соотношением сторон 1/2
36	III	130	2,5	Швеллер
	а	в	б	г

Задача 6. Расчет стальной колонны на устойчивость и подбор сечения

Для стальной составной колонны с заданными нагрузкой P, длиной L и опорными закреплениями и типом поперечного сечения требуется:

1. Из условия устойчивости колонны подобрать номер прокатного профиля, принимая для стали Ст.3 допускаемое напряжение [σ] = 160 МПа.

2. Из условия устойчивости отдельных ветвей колонны определить необходимое количество соединительных планок и их размеры.

Согласно заданного варианта тип опорных закреплений взять на рис. 4.1, данные для расчета – из таблицы 7, тип поперечного сечения – на рис. 4.2.

Таблица 7

Номер строки	Схема сечения на рис. 4.2	Тип закрепления (рис.4.1)	L, м	C, x10^3, м	P, кН
01	1	1	3,0	2,0	400
02	2	2	2,5	1,2	330
03	3	3	2,8	2,0	300
04	4	4	3,3	2,6	500
05	5	3	2,8	2,0	350
06	6	1	2,4	3,0	380
07	7	4	2,5	4,0	250
08	8	2	2,0	2,0	590
09	9	3	1,7	1,4	280
10	10	1	1,8	3,5	530
11	11	2	2,6	4,2	380
12	12	4	3,1	3,6	330
13	13	3	2,2	2,8	350
14	14	1	3,2	3,0	520
15	15	2	2,0	2,0	480
16	16	3	1,4	3,2	360
17	17	4	2,7	1,4	420
18	18	4	3,4	3,0	390
19	19	1	2,8	4,0	370
20	20	2	3,0	2,8	400
21	21	4	3,2	1,4	410
22	22	3	2,8	1,5	450
23	23	2	2,5	4,0	490
24	24	3	2,9	2,2	340
25	25	1	2,3	1,8	320
26	26	2	2,2	3,0	380
27	27	4	2,1	2,0	400
28	28	2	2,7	3,4	480
29	29	4	3,3	3,2	450
30	30	1	3,6	2,6	430
	б	г	а	в	а

1 схема 2 схема 3 схема 4 схема

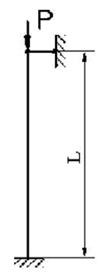
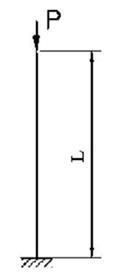
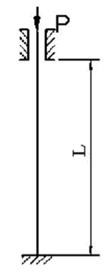
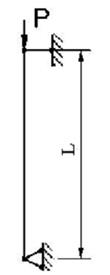
Рис. 4.1

1 схема 2 схема 3 схема 4 схема 5 схема

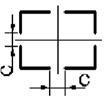
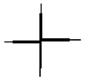
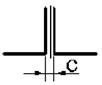
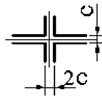
6 схема 7 схема 8 схема 9 схема 10 схема

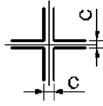
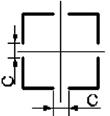
11 схема 12 схема 13 схема 14 схема 15 схема

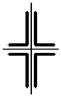
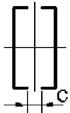
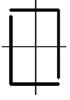
16 схема 17 схема 18 схема 19 схема 20 схема

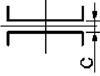
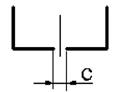
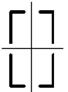
21 схема 22 схема 23 схема 24 схема 25 схема

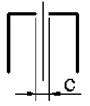
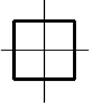
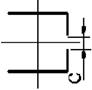
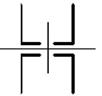
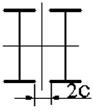
26 схема 27 схема 28 схема 29 схема 30 схема

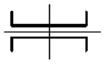
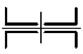
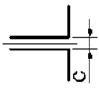
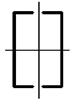
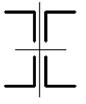
Рис. 4.2

Примеры выполнения задач

Пример 1

Стальной стержень длиной l =2,8 м заданной формы поперечного сечения сжимается силой Р = 411кН (рис.5).

Требуется:

1) подобрать размеры поперечного сечения стержня (расчет производить методом последовательных приближений по коэффициенту φ);

2) найти величину критической силы Р_кр и вычислить запас устойчивости стержня n_у. Материал стержня сталь Ст.3; допускаемое напряжение на сжатие [σ]_с=160 МПа.

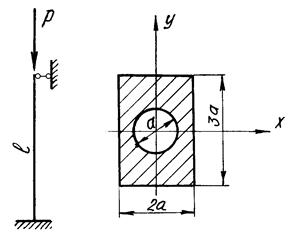
Рис. 5. Расчетная схема сжатого стержня и его поперечное сечение

Решение.

1. Определение геометрических характеристик сечения стержня через искомый размер сечения a:

Площадь сечения

Размер a

Главные центральные моменты инерции

Минимальный момент инерции

Минимальный радиус инерции

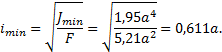
Для заданного варианта закрепления по табл. 8 выбирается коэффициент приведения длины μ = 0,7.

Гибкость стержня

2. Подбор поперечного сечения стержня.

Из условия устойчивости площадь поперечного сечения

Как указывалось выше, в условии устойчивости неизвестными величинами являются φ и F, которые можно найти методом последовательных приближений, для чего задается одна из неизвестных величин - φ.

Для первого приближения примем φ₁ = 0,5.

Тогда соответствующая площадь поперечного сечения стержня

Находим параметр а:

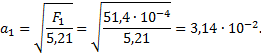
Проверяем, соответствует ли допускаемая нагрузка для подобранного сечения заданной силе.

Гибкость стержня при a₁ = 3,14∙10^-2 м

По табл. (см. раздел справочные данные) следует найти соответствующий коэффициент φ. Значения λ = 102 в таблице нет, поэтому искомое значения коэффициента j определяется линейной интерполяцией:

при λ = 100 𝜑₁₀₀ = 0,60;

при λ = 110 𝜑₁₁₀ = 0,5;

Соответствующая допускаемая сила

Расхождение между заданной силой и полученной

Подобранное сечение не удовлетворяет условию устойчивости, так как допускаемое расхождение между силами заданной и полученной расчетным путем не должно превышать 5%.

Вычисления повторяются еще раз.

Второе приближение: новое значение коэффициента j₂ определяется по выражению:

Все вычисления, выполненные при первом приближении, повторяются, но при новом значении φ = φ₂:

Расхождение между силами составляет менее 5%, что приемлемо. Тогда искомый размер a = a₂ = 3,02∙10^-2 м ≈ 3 см.

3. Определение критической силы.

Для подобранного сечения расчетная гибкость стержня

Предельная гибкость для стали марки Ст. 3 равна 100, поэтому критическую силу следует вычислять по формуле Эйлера, так как λ>λ_пр.

Минимальный момент инерции принятого сечения стержня

J_min = J_y = 1,95a⁴ = 1,95∙3⁴ = 158 см⁴.

Критическая сила

Запас устойчивости сжатого стержня:

Пример 2

Стальной стержень (сталь Ст.3) длиной l сжимается силой F.

Дано: F=1000 кН, l=2,4 м, схема закрепления концов стержня и форма сечения стержня показаны на рис. 6.

Требуется:

1) найти размеры поперечного сечения при допускаемом напряжении на простое сжатие [σ]=160 Мпа (расчет производить методом последовательных приближений, в первом приближении задавшись коэффициентом φ=0,5);

2) найти значение критической силы и коэффициента запаса устойчивости.

Рис. 6

Решение.

Расчет начинаем с вычисления всех необходимых геометрических характеристик поперечного сечения стойки, которые удобно выразить через площадь поперечного сечения A (b=h=2d):

Радиус инерции сечения относительно оси наименьшей жесткости:

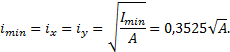
Гибкость стержня:

где μ - коэффициент приведения длины стержня, зависящий от условий закрепления стержня (табл.8)

Таблица 8. Коэффициенты приведения длины μ

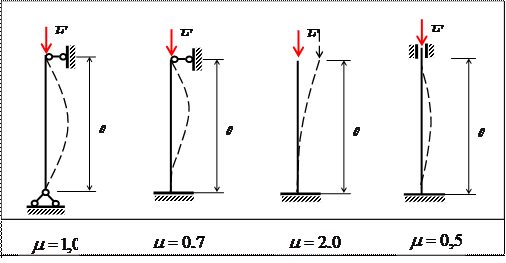
В условии устойчивости

неизвестны величины A и φ, где φ - коэффициент продольного изгиба.

Расчет производить методом последовательных приближений, в первом приближении задавшись коэффициентом φ=0,5:

тогда гибкость стержня

По таблице 9, используя линейную интерполяцию, находим

Таблица 9. Коэффициенты продольного изгиба φ для ст.3

λ	0	10	20	30	40	50	60	70	80	90	100
φ	1,00	0,99	0,96	0,94	0,92	0,89	0,86	0,81	0,75	0,69	0,60
λ	110	120	130	140	150	160	170	180	190	200
φ	0,52	0,45	0,40	0,36	0,32	0,29	0,26	0,23	0,21	0,19

Во втором приближении принимаем

В третьем приближении

В четвертом приближении

Полученное значение φ близко к принятому, поэтому проверим выполнение условия устойчивости:

Относительная погрешность между напряжениями составляет

это меньше одного процента, что допустимо. Принимая φ=0,763; получаем A=0,0082 м²;

Для материала стойки (сталь 3, E=200 Гпа, σ_пц=200 Мпа) значение предельной гибкости λ_пред будет равно

Поскольку в нашем случае гибкость стойки меньше предельной (λ=75<100), то величину критической силы определяем по формуле Ясинского (для ст.3 a=310 Мпа, b=1,14 Мпа):

F_кр=σ_кр∙A=(a-b∙λ)∙A=(310-1,14∙75)∙10⁶∙0,0082=1841 кН.

Стойка имеет коэффициент запаса устойчивости, равный

Пример 3

Стальной стержень (рис.7) сжимается силой .

Требуется:

1. Найти размеры поперечного сечения при допускаемом напряжении на простое сжатие Расчет производить последовательными приближениями.

2. Найти критическую силу и коэффициент запаса устойчивости.

Дано:

Рис.7

Решение.

1. Найдем размеры поперечного сечения

Площадь:

Минимальный осевой момент инерции:

Минимальный радиус инерции:

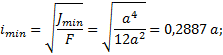
Гибкость стержня:

Здесь – коэффициент приведения длины стержня. Для рассматриваемого стержня

Размеры поперечного сечения стержня находим из расчетного уравнения:

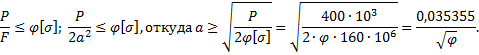
В первом приближении примем Вычислим и :

Для стали Ст3 при Значение коэффициента при гибкости найдем линейной интерполяцией:

Повторим расчет с новым значение коэффициента . Результаты вычислений на каждой итерации приведены в таблице 10.

Таблица 10

№ итерации	1	2	3	4	5
	0,0500	0,0679	0,0365	0,0355	0,0355
	166,28	30,67	8,86	8,39	8,38
	0,271	0,939	0,991	0,992	0,992

2. Найдем критическую силу и коэффициент запаса устойчивости

Поскольку гибкость стержня меньше предельного значения то критическую силу определим по формуле Ясинского:

Коэффициент запаса устойчивости:

Пример 4

Для показанного сечения стержня (стойки) (рис.8), составленного из четырех равнобоких уголков, требуется:

1. подобрать сечение из условия устойчивости на продольный изгиб при заданном коэффициенте запаса прочности n_т.

2. Определить расстояние между приваренными к профилям соединительными планками из условия равной гибкости всего стержня и участка профиля между планками.

Дано: Материал: сталь Ст3; предел текучести σ_т = 240 МПа; F = 0,68 МН; L = 4,4 м; n_т = 1,5.

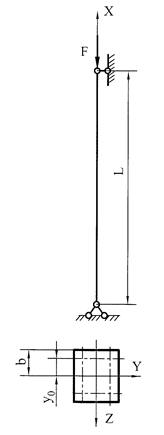
Рис.8. Схема стойки и форма сечения

Решение.

1.Выбор сечения

Расчет сечения ведем методом последовательных приближений

Шаг 1

Задаемся коэффициентом уменьшения допускаемого напряжения j₁ = 0,5.

Допускаемое напряжение

Площадь поперечного сечения стойки

Потребная площадь уголка

Подбираем уголок № 12,5х9 (рис.9).

А_уг = 22 см²; I_y = 327 см⁴; I_z' = 327 см⁴; y₀ = 3,4 см.

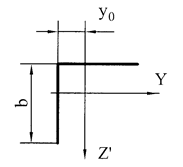
Рис.9

Минимальный момент инерции сечения стойки

I_{z min} = (I_z' + A_уг∙y₀²)∙4 = (327+22∙8,48²)∙4 = 7636 см⁴

Минимальный радиус инерции сечения стойки

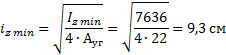
Гибкость стержня

где μ = 1 – коэффициент закрепления стойки.

По таблице (см.справочные данные) определяем коэффициент снижения допускаемого напряжения

Шаг 2

Коэффициент снижения допускаемого напряжения

Подбираем уголок № 11х7.

А_уг = 15,2 см²; I_y = 176 см⁴; I_z' = 176 см⁴; y₀ = 2,96 см; b = 110 мм

I_{z min} = (I_z' + A_уг∙y₀²)∙4 = (176 + 15,2∙8,04²)∙4 = 4634 см⁴

Шаг 3

Коэффициент снижения допускаемого напряжения

Подбираем уголок №10х7.

А_уг = 13,8 см²; I_y = 131 см⁴; I_z' = 131 см⁴; y₀ = 2,71 см; b = 100 мм

I_{z min} = (I_z' + A_уг∙y₀²)∙4 = (131 + 13,8∙7,29²)∙4 = 3457 см⁴

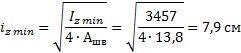
Шаг 4

Коэффициент снижения допускаемого напряжения

Подбираем уголок № 10х6,5.

А_уг = 12,8 см²; I_y = 122 см⁴; I_z' = 122 см⁴; y₀ = 2,68 см; b = 100 мм.

I_{z min} = (I_z' + A_уг∙y₀²)∙4 = (122 + 12,8∙7,32²)∙4 = 3231 см⁴

Проверка.

Напряжения в стойке

Отклонение напряжения от допускаемого

Перегруз 4,8% ≤ 5%

2.Определение расстояния между соединительными планками

Расстояние между соединительными планками определяем из условия равной гибкости одного уголка между планками и стойки.

λ_уг = λ = 55,7.

Гибкость уголка

где μ_уг = 1.

Из этого расстояние между планками

Так как Н = 4,4м, L= 4,4 м, то соединительных планок не требуется.

Пример 5

Подобрать сечение сжатого элемента стропильной фермы. Продольная сила в стержне N = 1200 кН. Сечение элемента фермы (рис.10) состоит из двух равнобоких уголков длиной 2 м, расположенных тавром и сваренных вместе через прокладку. Материал сталь, R = 240 МПа. Концы стержня оперты в узлах шарнирно.

Рис.10

Решение.

Из условия устойчивости определяем требуемую площадь поперечного сечения

Принимаем в первом приближении φ₁ = 0,5

Требуемая площадь сечения одного уголка А = 100/2 = 50 см². По ГОСТ 8509 – 86 уголок 160×160×16 мм имеет площадь 49,1 см². Тогда площадь сечения двух уголков 2×49,1 = 98,2см².

Как видно из рис.10 наименьший радиус инерции составного сечения будет относительно оси х, так как I_x < I_y. На основании выражения радиус инерции составного сечения относительно оси х равен радиусу инерции одного уголка относительно оси х. По сортаменту i_min = 4,89 см.

Определяем гибкость стержня, принимая для нашего случая закрепления концов стержня μ = 1

Используя таблицу коэффициентов φ (см.справочные данные), найденному значению гибкости λ соответствует коэффициент = 0,917.

При этом расчетное напряжение в стержне будет равно

Получилось очень большое недонапряжение, поэтому сечение необходимо уменьшить. Примем для второго приближения

Определяем необходимую площадь сечения

Подбираем два уголка 160×160×14 мм с А = 86,6 см². Наименьший радиус инерции для этого составного сечения i_min = 4,92 см.

Гибкость стержня

Этому значению гибкости по таблице коэффициентов j соответствует = 0,918.

Расчетное напряжение в этом случае составит

Опять получается значительное недонапряжение материала стержня фермы. Возьмем для третьего приближения значение коэффициента

Требуемая площадь сечения

Подбираем сечение из двух уголков125×125×12 мм, А = 57,8 см², i_min = 3,82см.

Определяем гибкость стержня из этих уголков:

Этому значению гибкости по таблице коэффициентов φ, соотвествует значение = 0,882.

Расчетное напряжение для этого случая

Недонапряжение составляет

Окончательно принимаем сечение стержня из двух равнобоких уголков 125×125×12 мм.

Пример 6

Для стойки (рис. 11) указанного сечения, одинаково закрепленной в плоскостях xy и xz потери устойчивости и сжатой центрально приложенной силой F требуется подобрать размеры поперечного сечения, c использованием коэффициента продольного изгиба. Материал - сталь Ст-3.

Дано: F =1000 кН; l =1,5 м; R= 220 МПа. Для стойки, имеющей защемляющую и шарнирную опоры, коэффициент приведенной длины μ = 0,7.

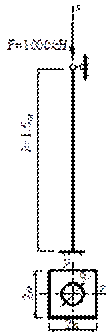
Рис.11

Решение.

Определим геометрические характеристики сечения:

радиусы инерции сечения

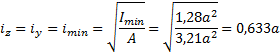
Гибкость стержня

Коэффициент продольного изгиба может принимать значения от нуля, до единицы. В первом приближении φ₁=0,5, тогда:

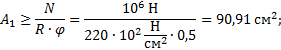
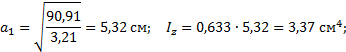
Используя таблицу коэффициентов φ (см.справочные данные), принимаем значения =0,935, которое существенно отличается от φ₁.

Во втором приближении коэффициент продольного изгиба принимаем как среднее арифметическое:

Повторяем расчет во втором, третьем и четвертом приближении (табл. 11)

Таблица 11

Приближение	φ	A, см^2	a, см	i, см	λ
1	0,5	90,9	5,32	3,37	31,2	0,935
2	0,718	63,3	4,44	2,81	59	0,82
3	0,77	59	4,3	2,71	61,2	0,816
4	0,79	5,57	4,16	2,63	63	0,805

Вычислим напряжения в четвертом приближении:

Перенапряжение составляет

Окончательно принимаем a = 4,2 см.

Пример 7

Стальной стержень длиной l = 2,5 м сжимается силой P = 170 кH (рис.12,а). Коэффициент приведения длины для данной схемы закрепления концов стержня μ=2/3. Стержень имеет квадратное поперечное сечение (рис.12,б).

Требуется:

1) найти размеры поперечного сечения при основном допускаемом напряжении на сжатие [σ]=160 МПа;

2) найти числовое значение критической силы и коэффициент запаса устойчивости.

Рис.12

Решение.

Найдём размеры поперечного сечения стержня, определив площадь поперечного сечения из расчёта сжатого стержня на устойчивость. Расчёт будем производить методом последовательных приближений (итераций), предварительно приняв значение коэффициента продольного изгиба φ=0,5 (гибкость стержня λ= 113):

Так как поперечное сечение представляет собой квадрат, то А=a², откуда

Примем сторону квадрата α=5 см, тогда А=25∙10^-4 м². Для квадратного сечения радиус инерции стержня:

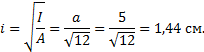
Гибкость стержня:

Вычисляем напряжение:

Окончательно принимаем размер поперечного сечения a=5 см.

Числовое значение критической силы найдём по формуле Эйлера:

Так как гибкость рассматриваемого стержня больше предельного значения гибкости для стального стержня (λ_пред=100).

E=2,1∙10⁸ кПа - модуль упругости материала стержня;

- осевой момент инерции квадратного поперечного сечения; тогда

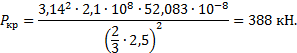
Коэффициент запаса устойчивости:

---

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00