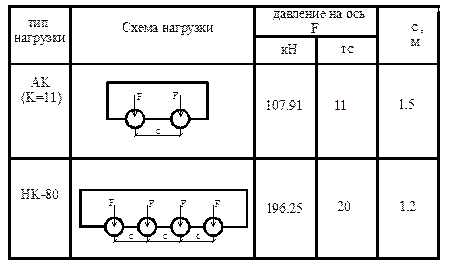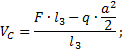Расчетно-графические работы

Главная

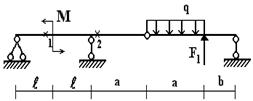
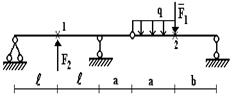
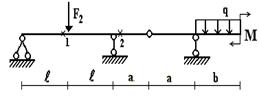
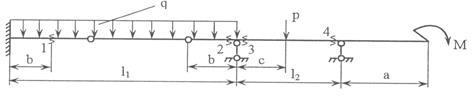
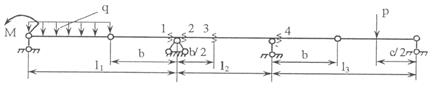
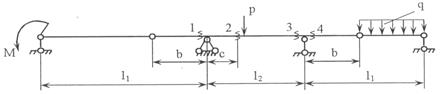
Задача 1. Расчет составных многопролетных балок, работающих на поперечный изгиб

Для балки, изображенной на рис.1, требуется:

1) простроить эпюры внутренних усилий;

2) указать положение опасного сечения.

3) для стальной балки из швеллера, подобрать номер прокатного профиля из условия прочности.

Данные взять из табл.1.

Таблица 1

Номер cтроки	Схема балки по рис.1	F₁, см²	а, м	b, м	М, кНм	q, кН/м
01	1	12	1	2	24	5
02	2	10	2	2	16	4
03	3	12	3	2	12	6
04	4	6	2	3	18	2
05	5	8	1	3	20	4
06	6	10	3	1	12	2
07	7	6	2	2	12	3
08	8	8	1	2	12	6
09	9	6	2	1	16	5
10	10	12	1	3	10	6
11	11	11	1	2	12	6
12	12	12	3	3	18	2
13	13	10	2	3	20	4
14	14	12	1	1	12	2
15	15	6	2	2	12	3
16	16	8	1	2	12	6
17	17	10	2	1	18	5
18	18	6	3	2	20	6
19	19	8	2	2	12	2
20	20	6	1	3	12	4
21	21	12	3	3	12	2
22	22	12	2	1	16	3
23	23	13	1	2	10	6
24	24	14	1	2	12	5
25	25	12	3	1	18	6
26	26	10	2	3	20	6
27	27	12	1	2	12	2
28	28	6	2	3	24	4
29	29	8	1	3	16	2
30	30	10	2	1	12	3
31	31	6	3	2	18	6
32	32	8	2	2	20	5
33	33	6	1	1	12	6
34	34	12	3	3	12	2
35	35	11	2	2	16	4
36	36	12	3	3	12	2
	г	г	а	б	б	в

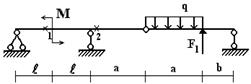
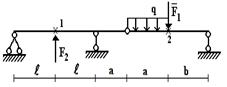
1 схема 2 схема

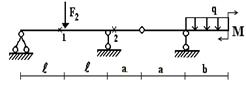
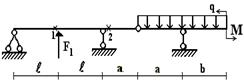
3 схема 4 схема

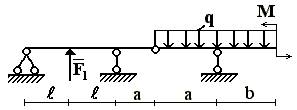
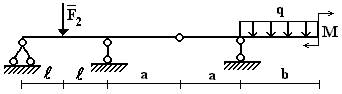
5 схема 6 схема

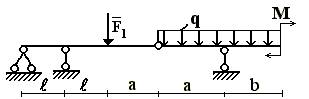
7 схема 8 схема

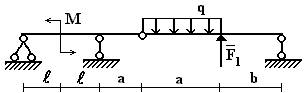
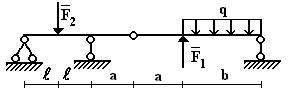
9 схема 10 схема

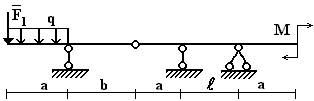
11 схема 12 схема

13 схема 14 схема

15 схема 16 схема

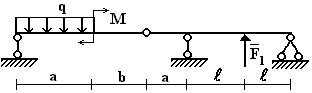
17 схема 18 схема

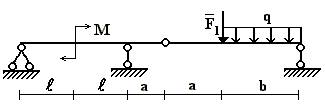
19 схема 20 схема

21 схема 22 схема

23 схема 24 схема

25 схема 26 схема

27 схема 28 схема

29 схема 30 схема

31 схема 32 схема

33 схема 34 схема

35 схема 36 схема

Рис.1

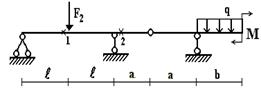
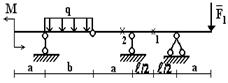
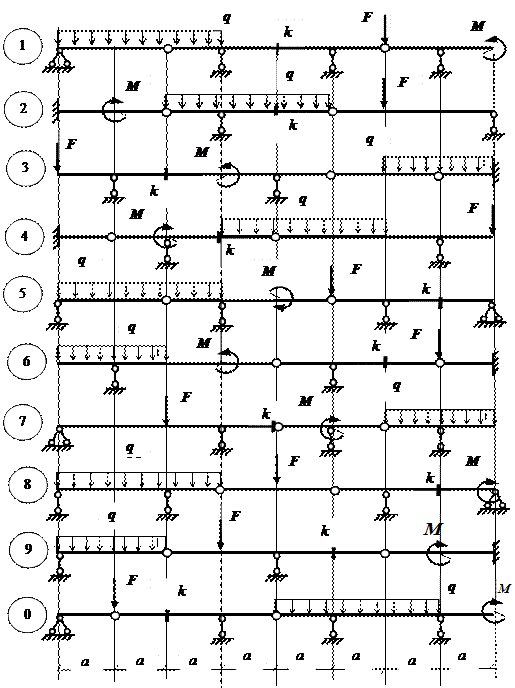
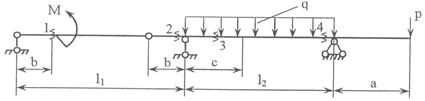
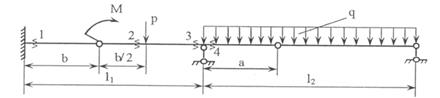
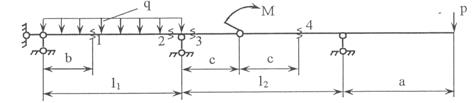
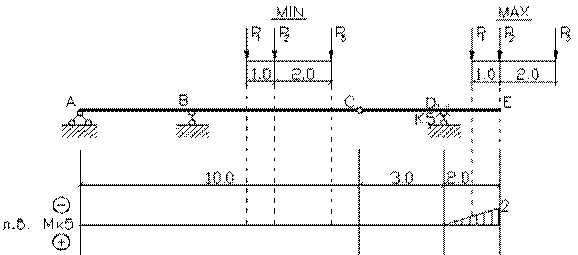
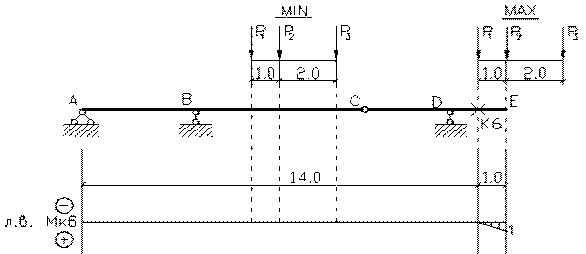
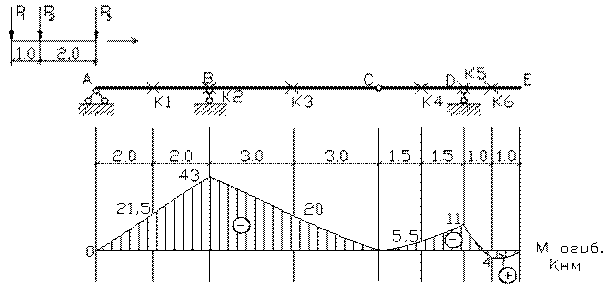
Задача 2. Расчет составных многопролетных балок, работающих на поперечный изгиб

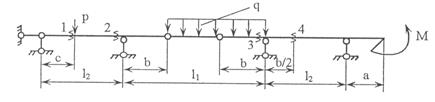
Для одной из многопролетных балок, изображенных на рис. 2 требуется:

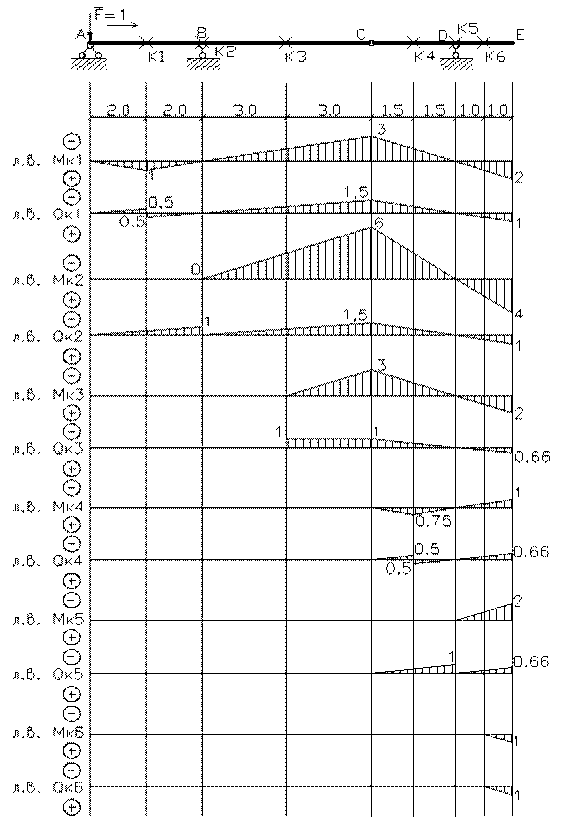
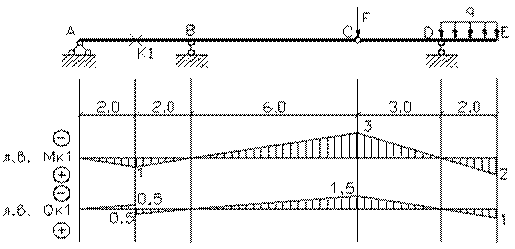
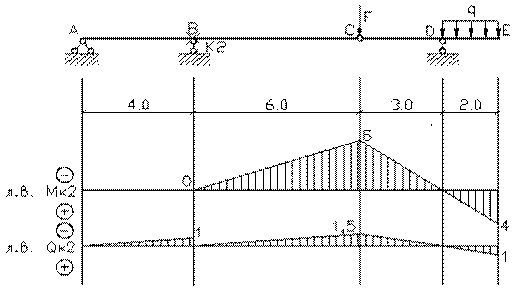
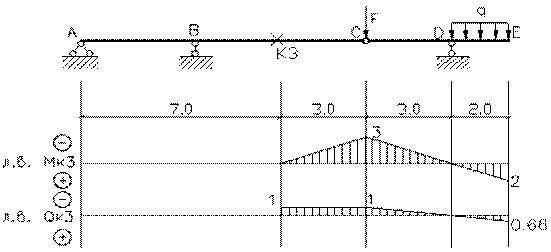
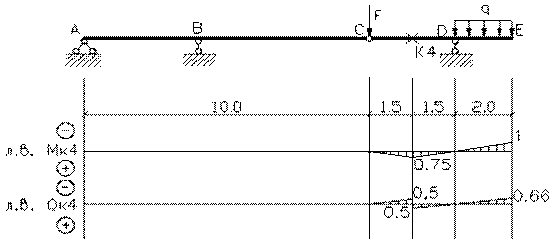
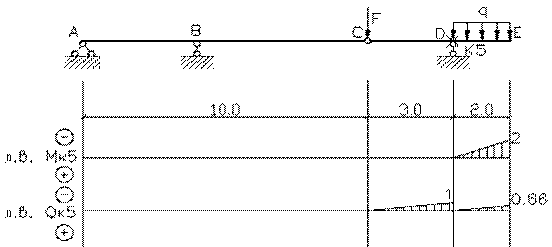
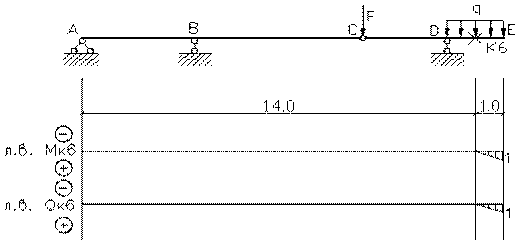
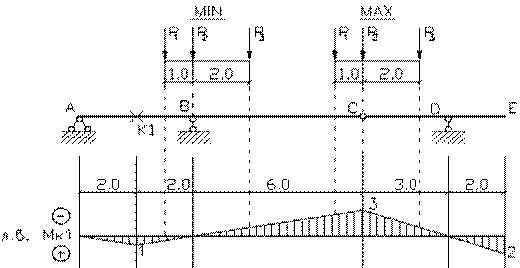
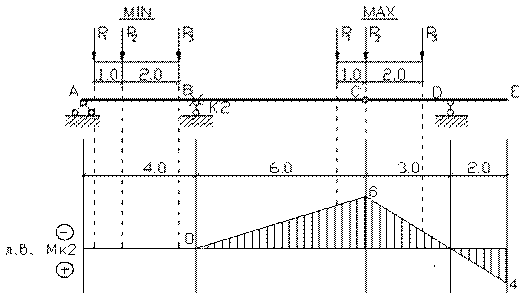
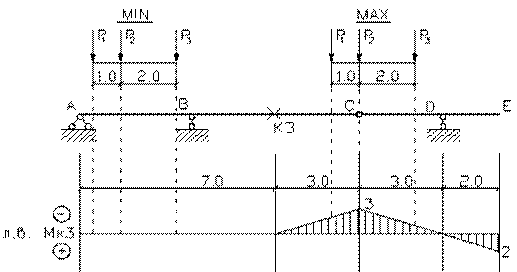
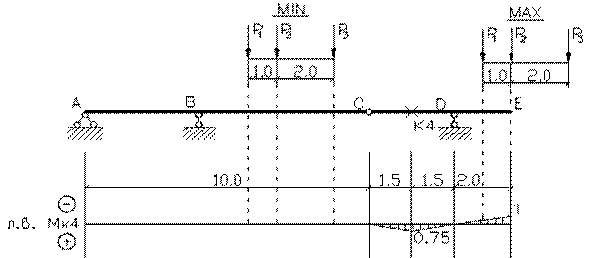
1) построить эпюры внутренних силовых факторов и линии влияния внутренних усилий в сечении k;

2) определить усилия в сечении k по линиям влияния от заданной нагрузки и сравнить их с усилиями на эпюрах;

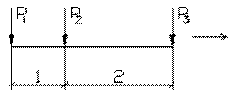
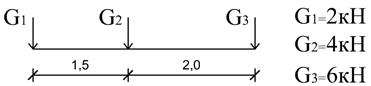
3) найти максимальное и минимальное значение изгибающего момента в сечении k от подвижной системы связанных грузов, показанной на рис.3.

Исходные данные для расчета принять из табл. 2.

Таблица 2

Номер строки	Схемы балки по рис. 2	l, м	M, кНм	F, кН	q, кН/м
01	1	2	6	4	2
02	2	3	5	5	1
03	3	4	4	3	3
04	4	2	6	6	4
05	5	2	8	7	2
06	6	4	10	2	1
07	7	3	7	8	3
08	8	5	10	3	2
09	9	1	9	4	1
10	10	2	8	7	4
11	11	4	7	8	5
12	12	3	6	3	2
13	13	2	5	6	4
14	14	5	2	5	3
15	15	3	5	2	5
16	16	4	6	8	1
17	17	3	7	5	4
18	18	1	8	3	2
19	19	2	9	4	5
20	20	5	10	8	3
21	21	3	4	9	1
22	22	2	5	2	3
23	23	4	8	3	2
24	24	2	7	5	4
25	25	1	6	7	5
26	1	5	4	6	2
27	2	5	2	5	3
28	3	3	5	2	5
29	4	4	6	8	1
30	5	3	7	5	4
31	6	1	8	3	2
32	7	2	9	4	5
33	8	5	10	8	3
34	9	3	4	9	1
35	10	2	5	2	3
	б	в	а	г	в

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

11 схема 12 схема

13 схема 14 схема

15 схема 16 схема

17 схема 18 схема

19 схема 20 схема

21 схема 22 схема

23 схема 24 схема

25 схема

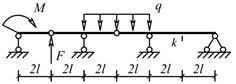
Рис.2

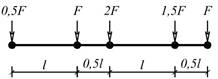
Рис.3

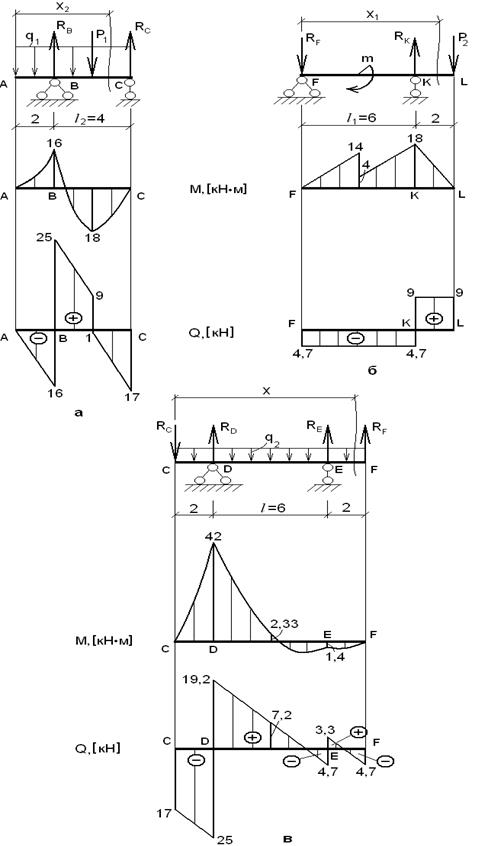
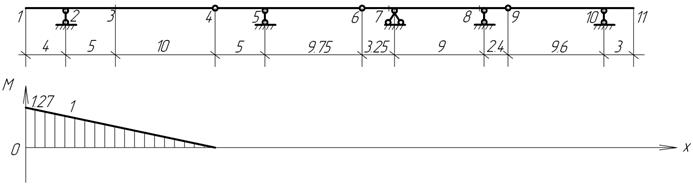
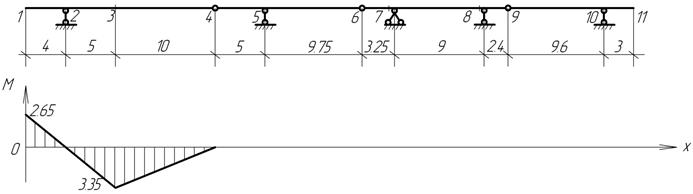
Пояснения к решению задачи

1) Стержневая система является статически определимой, если степень ее свободы W равна нулю и она геометрически неизменяемая. В геометрически неизменяемых системах перемещения от нагрузок являются следствием только деформаций ее элементов. Для многопролетных статически определимых балок анализ геометрической неизменяемости проще выполнять через построение т.н. «монтажно-поэтажной» схемы, показывающей последовательность монтажа отдельных балок. На каждом «этаже» такой схемы должно присутствовать три связи.

2) При определении реакций в связях многопролетной статически определимой балки целесообразно воспользоваться наиболее общим подходом, заключающимся в том, что любая многодисковая статически определимая система может быть представлена в виде набора отдельных дисков с действующими на них внешними нагрузками и реакциями связей, обеспечивающих им равновесие в составе системы. В теории статически определимых систем доказано, что число независимых уравнений статики в точности равно числу реакций в связях, включая и силы взаимодействия в шарнирах, которые на смежные диски прикладываются в соответствии с законом Ньютона «действие равно противодействию», т.е. равными и противоположно направленными.

Примечание. Сосредоточенные внешние силы, действующие на шарниры, можно приложить к любому из смежных дисков.

После построения эпюр внутренних силовых факторов в отдельных дисках они объединяются и образуют эпюры для многопролетной балки в целом.

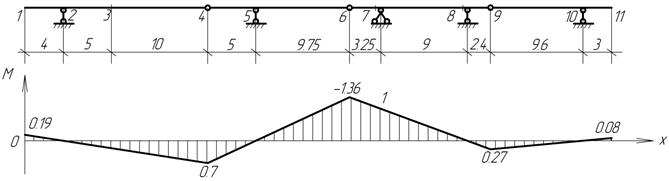
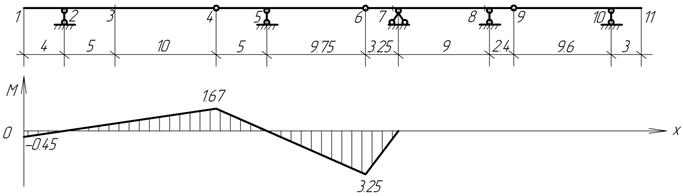
3) При построении линий влияния усилий в многопролетных балках проще всего воспользоваться статико-кинематическим методом. Поскольку линии влияния усилий в статически определимых системах имеют полигональный вид, то достаточно найти всего одну наиболее просто определяемую из условий равновесия ординату этой линии влияния. В примере определена ордината, когда единичный груз установлен над сечением k. При таком положении груза второстепенные балки не работают, их можно отбросить и из законов равновесия определить изгибающий момент и поперечную силу в сечении k основной балки.

4) Определение максимального и минимального значений усилия S от подвижной системы связанных между собой сосредоточенных грузов требует нахождения невыгодного загружения линии влияния этой системой грузов. В теории линий влияния доказано, что в при невыгодном загружении один из грузов (критический) должен находиться над одной из вершин (критической) линии влияния: над выпуклой, если отыскивается maxS, и вогнутой, если отыскивается minS (линия влияния при этом не должна быть перевернута). Условием, что груз и вершина действительно критические, является смена знака производной усилия при переходе грузом вершины: с «+» на «–», если отыскивается maxS, и с «–» на «+», если minS. Производная усилия определяется по формуле:

где F_i – сосредоточенный груз;

α_i - угол наклона линии влияния в месте приложения сосредоточенного груза F_i.

Задача нахождения критического груза и критической вершины решается перебором возможных вариантов. Определение maxS и minS осуществляется по формуле влияния

где F_i – сосредоточенный груз;

у_i– ординаты линии влияния усилия S под сосредоточенными грузами, установленными в положение невыгодного загружения.

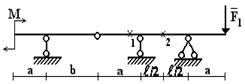
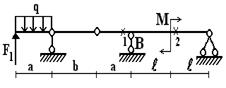
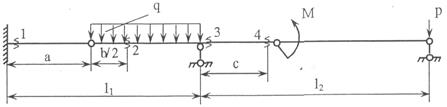
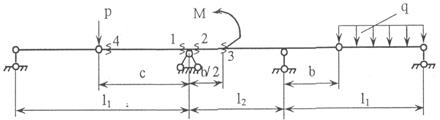
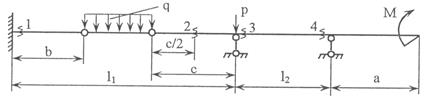
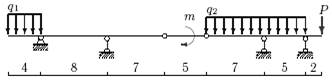
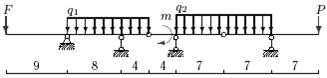
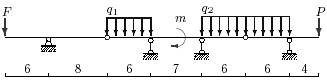
Задача 3. Расчет составных многопролетных балок, работающих на поперечный изгиб

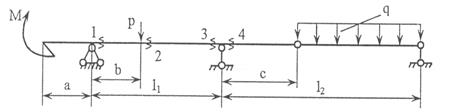
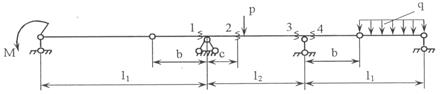
Для одной из многопролетных балок, изображенных на рис.4 требуется определить реакции опор.

Исходные данные для расчета принять из табл. 3.

Таблица 3

Номер cтроки	Схемы балки по рис.4	m, кНм	q₁, кН/м	q₂, кН/м	P, кН	F, кН
01	1	2	6	5	8	7
02	2	2	7	8	9	8
03	3	8	8	6	7	9
04	4	4	2	7	8	5
05	5	6	5	9	6	8
06	6	9	9	4	8	7
07	7	7	3	2	9	9
08	8	5	6	8	7	5
09	9	8	5	8	8	6
10	10	2	6	6	6	7
11	11	3	6	7	8	8
12	12	2	2	9	9	9
13	13	2	4	4	7	5
14	14	8	2	2	8	8
15	15	4	3	3	6	7
16	16	6	6	8	8	9
17	17	9	5	6	9	5
18	18	7	6	7	7	6
19	19	5	2	9	8	9
20	20	8	4	4	6	5
21	21	2	2	2	8	6
22	22	3	3	8	9	7
23	23	2	6	8	7	8
24	24	2	5	6	8	9
25	25	8	6	7	6	5
26	26	4	6	2	8	8
27	27	6	2	3	9	7
28	28	9	4	8	7	9
29	29	7	2	6	8	9
30	30	5	3	7	6	5
31	31	8	6	6	6	8
32	32	2	5	7	8	7
33	33	3	6	9	9	9
34	34	5	2	4	7	5
35	35	8	4	2	8	6
36	36	9	6	8	6	7
	б	г	в	а	б	а

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

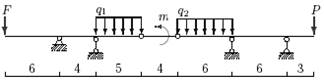
9 схема 10 схема

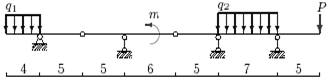
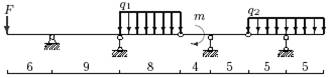
11 схема 12 схема

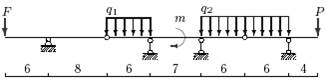
13 схема 14 схема

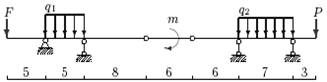
15 схема 16 схема

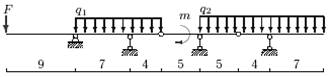
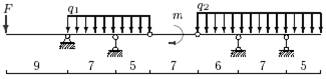
17 схема 18 схема

19 схема 20 схема

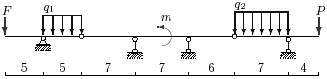
21 схема 22 схема

23 схема 24 схема

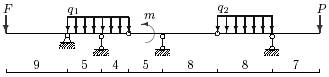
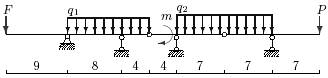
25 схема 26 схема

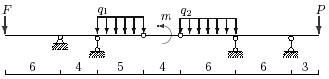
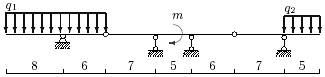
27 схема 28 схема

29 схема 30 схема

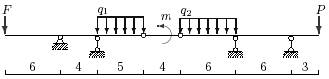
31 схема 32 схема

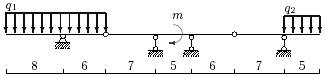
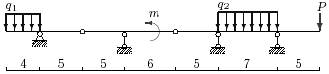
33 схема 34 схема

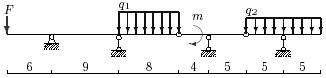
35 схема 36 схема

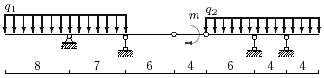
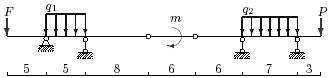
Рис.4

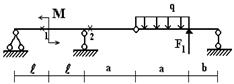
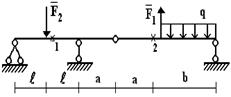
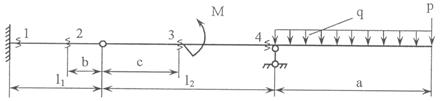
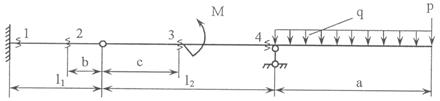
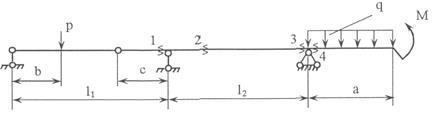
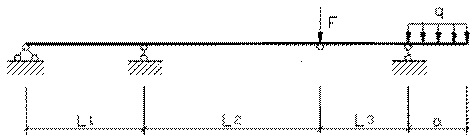
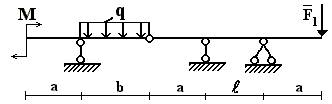
Задача 4. Расчет составных многопролетных балок, работающих на поперечный изгиб

Для составной балки, изображенной на рис.5 построить эпюры внутренних силовых факторов Q и M.

Исходные данные для расчета принять из табл. 4 и рис.4.

Таблица 4

Номер cтроки	Схема балки по рис.5	l₁/l	l₂/l	l₃/l	F₁/P	F₂/P	M/Pl
01	I	2	1	1	2	1	1
02	II	1	2	2	2	2	1
03	III	2	1	1	3	1	1
04	IV	1	2	2	3	2	1
05	V	1	2	1	1	1	2
06	VI	2	1	2	1	2	2
07	VII	2	1	2	2	2	1
08	VIII	1	2	1	3	1	1
09	IX	1	2	2	1	2	2
10	X	2	1	1	2	1	1
11	I	2	1	1	2	1	1
12	II	1	2	2	2	2	1
13	III	2	1	1	3	1	1
14	IV	1	2	2	3	2	1
15	V	1	2	1	1	1	2
16	VI	2	1	2	1	2	2
17	VII	2	1	2	2	2	1
18	VIII	1	2	1	3	1	1
19	IX	1	2	2	1	2	2
20	X	2	1	1	2	1	1
21	I	2	1	1	2	1	1
22	II	1	2	2	2	2	1
23	III	2	1	1	3	1	1
24	IV	1	2	2	3	2	1
25	V	1	2	1	1	1	2
26	VI	2	1	2	1	2	2
27	VII	2	1	2	2	2	1
28	VIII	1	2	1	3	1	1
29	IX	1	2	2	1	2	2
30	X	2	1	1	2	1	1
31	I	2	1	1	2	1	1
32	II	1	2	2	2	2	1
33	III	2	1	1	3	1	1
34	IV	1	2	2	3	2	1
35	V	1	2	1	1	1	2
36	VI	2	1	2	1	2	2
	а	г	б	а	в	б	г

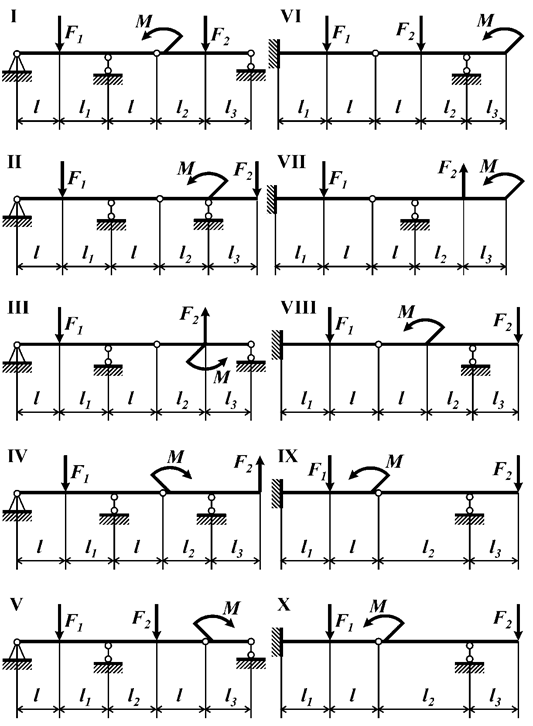
Рис.5

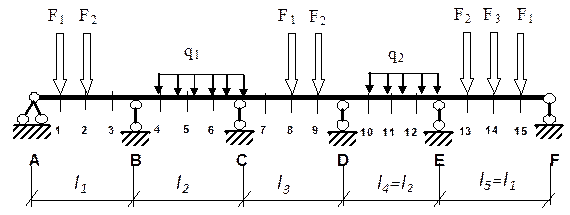
Задача 5. Расчет составных многопролетных балок, работающих на поперечный изгиб

Для балки, выбранной согласно варианту (рис.6), требуется:

1) построить эпюры изгибающих моментов M и поперечных сил Q от заданной внешней нагрузки аналитически;

2) построить линии влияния изгибающего момента M и поперечной силы Q во всех сечениях, показанных на рис. 6, а также линию влияния опорной реакции R (по выбору) от действия подвижной нагрузки;

3) определить по линиям влияния изгибающий момент M, поперечную силу Q и опорную реакцию R от заданной внешней нагрузки и сравнить их со значениями, полученными в пункте 1).

Исходные данные выбираются из табл.5.

Таблица 5

Номер cтроки	Схема балки по рис.6	а, м	q₁, кН/м	q₂, кН/м	P₁, кН	P₂, кН	M₁, кНм	M₂, кНм
01	1	0,8	1,2	0	0	3,2	2,0	0
02	2	1,5	0	2,2	3,0	0	0	1,5
03	3	1,9	2,0	0	0	4,0	2,2	0
04	4	1,4	0	1,0	2,5	0	0	2,8
05	5	2,1	1,8	0	0	8,0	2,7	0
06	6	1,3	0	0,8	6,0	0	0	3,0
07	7	2,2	3,0	0	0	5,0	2,4	0
08	8	2,0	0	1,4	2,8	0	0	2,6
09	9	1,2	1,5	0	0	3,3	2,5	0
10	10	1,0	0	2,5	7,0	0	0	1,1
11	11	0,9	1,4	0	0	2,6	1,7	0
12	12	1,6	0	1,5	3,6	0	0	1,1
13	13	1,7	1,6	0	0	2,2	1,8	0
14	14	1,8	0	1,8	2,8	0	0	1,2
15	15	1,1	2,2	0	0	2,4	1,9	0
16	16	1,9	0	2,0	5,5	0	1,3	0
17	17	1,5	2,4	0	0	3,3	2,9	0
18	18	1,4	0	1,9	4,5	0	0	1,4
19	19	2,0	1,7	0	0	3,5	2,6	0
20	20	2,1	0	1,3	3,0	0	0	1,6
21	21	2,2	3,0	0	0	5,0	2,4	0
22	22	2,0	0	1,4	2,8	0	0	2,6
23	23	1,2	1,5	0	0	3,3	2,5	0
24	24	1,0	0	2,5	7,0	0	0	1,1
25	25	0,9	1,4	0	0	2,6	1,7	0
26	26	1,5	0	2,2	3,0	0	0	1,5
27	27	1,9	2,0	0	0	4,0	2,2	0
28	28	1,4	0	1,0	2,5	0	0	2,8
29	29	2,1	1,8	0	0	8,0	2,7	0
30	30	1,3	0	0,8	6,0	0	0	3,0
31	31	2,2	3,0	0	0	5,0	2,4	0
32	32	2,0	0	1,4	2,8	0	0	2,6
33	33	1,2	1,5	0	0	3,3	2,5	0
34	34	1,0	0	2,5	7,0	0	0	1,1
35	35	1,4	0	1,9	4,5	0	0	1,4
36	36	2,0	1,7	0	0	3,5	2,6	0
	а	г	б	а	в	б	г	а

1 схема

2 схема

3 схема

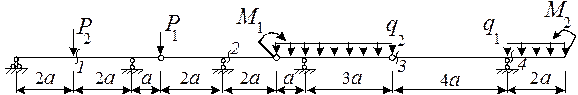
4 схема

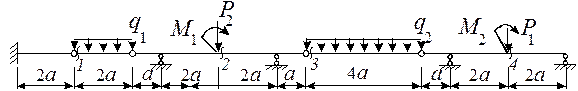
5 схема

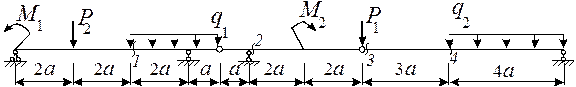
6 схема

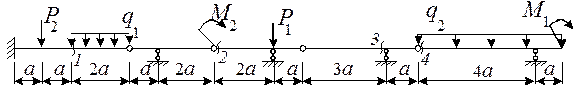
7 схема

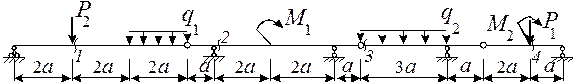
8 схема

9 схема

10 схема

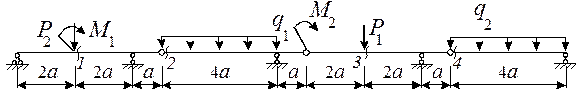
11 схема

12 схема

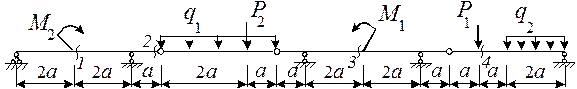
13 схема

14 схема

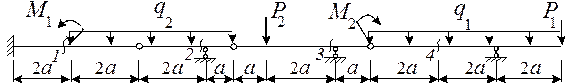
15 схема

16 схема

17 схема

18 схема

19 схема

20 схема

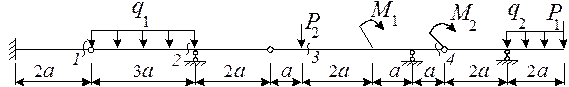
21 схема

22 схема

23 схема

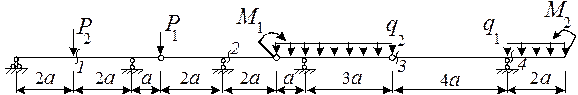
24 схема

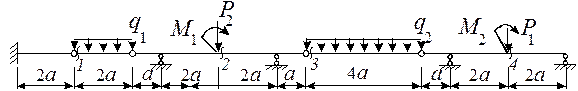
25 схема

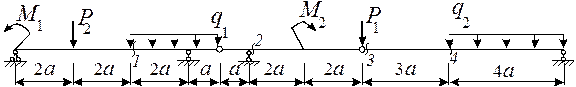
26 схема

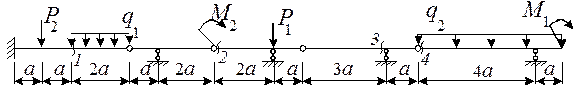
27 схема

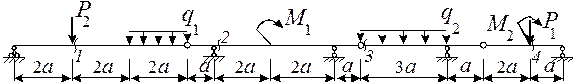
28 схема

29 схема

30 схема

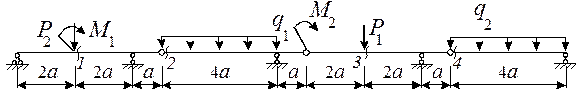
31 схема

32 схема

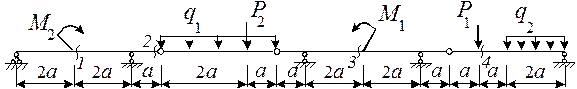
33 схема

34 схема

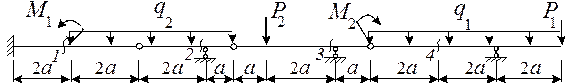
35 схема

36 схема

Рис.6

Пояснения к решению задачи

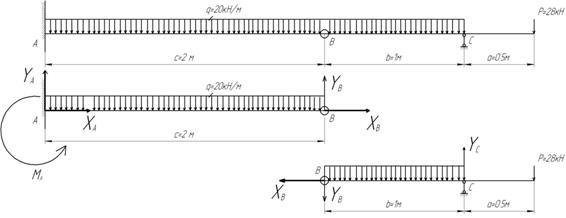
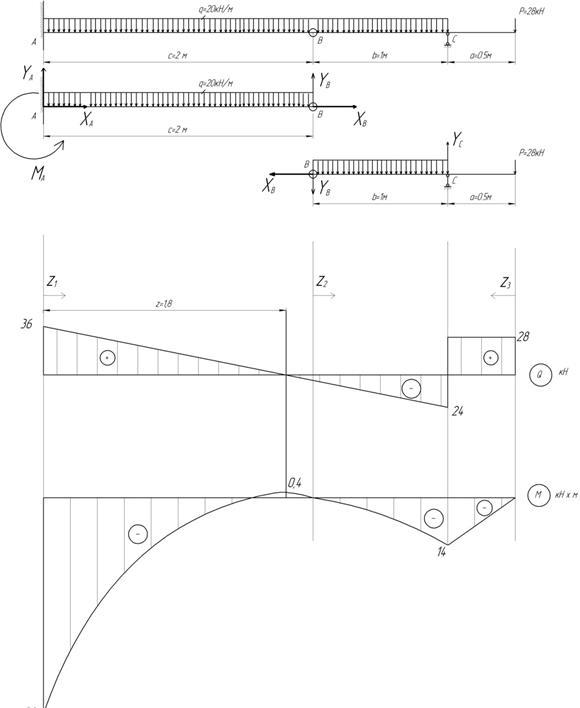
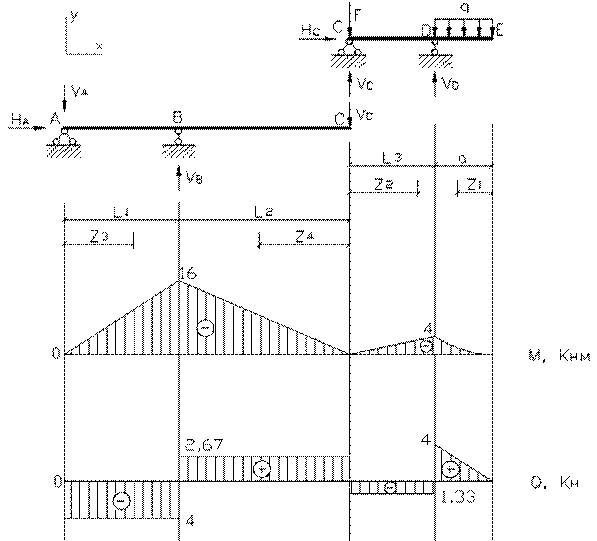
Для построения эпюр изгибающих моментов M и поперечных сил Q в многопролетных балках удобнее пользоваться схемой взаимодействия ("поэтажной" схемой), которую следует расположить непосредственно под схемой заданной балки. При построении "поэтажной" схемы нужно вначале выделить основные балки, что легко делается мысленным удалением шарниров, соединяющих балки между собой. Те балки, которые окажутся способными самостоятельно нести нагрузку (защемленные или имеющие две наземные опоры), будут основными. Вспомогательные балки имеют только одну опору или не имеют их вовсе. Недостающими опорами для них служат соединительные шарниры. После построения "поэтажной" схемы заданную балку можно рассматривать как ряд самостоятельных балок. Особенность задачи заключается в том, что для расчета нижележащих балок необходимо знать силы взаимодействия в шарнирах, являющихся опорными реакциями для вышележащих балок и нагрузкой для нижележащих. 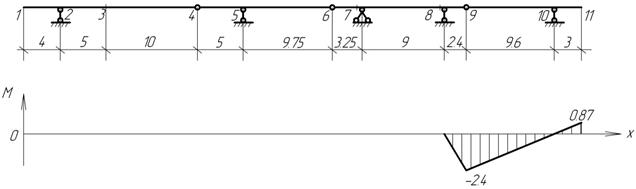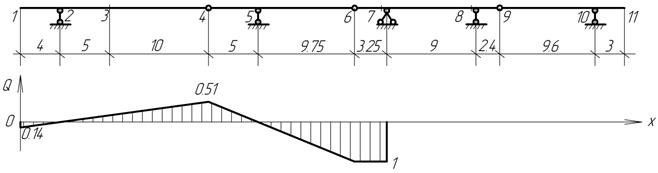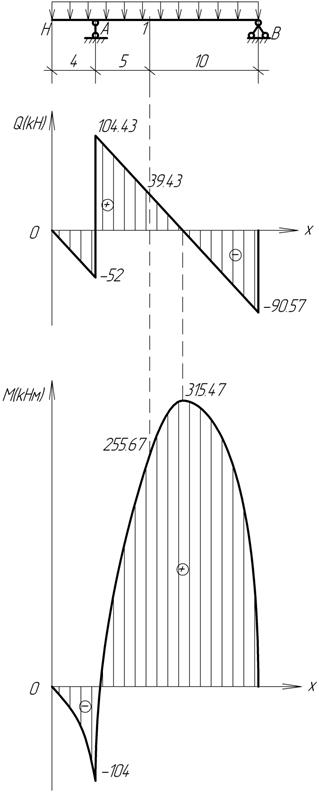Для расчета схемы каждой отдельной балки должны быть вычерчены отдельно, а эпюры изгибающих моментов M и поперечных сил Q можно строить на общей базе под "поэтажной" схемой. Ординаты эпюры моментов откладываются со стороны растянутых волокон (положительные вниз от оси). Знаков на эпюре моментов обычно не ставят, но обязательно надо проставлять значения характерных ординат с указанием размерности. При построении эпюры поперечных сил положительные ординаты откладываются вверх и на эпюрах обязательно проставляются знаки.

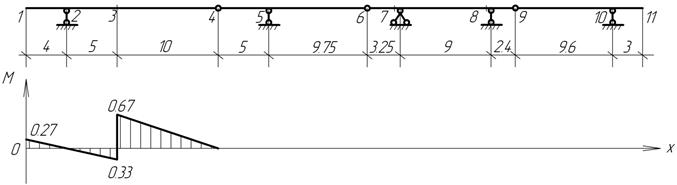
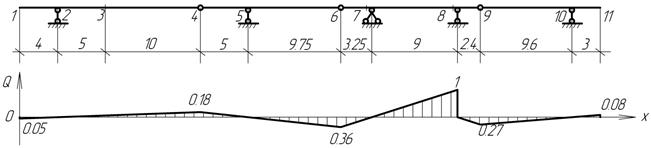
Линия влияния это график, изображающий закон изменения какого-либо фактора в сечении при передвижении по сооружению силы P=1. Для построения любой линии влияния усилия в данном месте сооружения применим следующий статический метод: поставив груз в произвольное положение, определяемое абсциссой x, и используя условия равновесия, даем аналитическое выражение данного усилия; затем представляем это выражение в графическом форме.

Необходимо вычертить "поэтажную" схему без заданной внешней нагрузки. В начале строится линия влияния искомого усилия в пределах той отдельной балки, к которой относится исследуемое сечение (или опора). Затем добавляется продолжение линии влияния, обусловленное взаимодействием отдельных балок.

Построенные линии влияния усилий можно использовать для отыскания их полных значений при действии на конструкцию сосредоточенных сил, распределенной нагрузки или внешнего момента. Величина S от действия сосредоточенных сил находится как сумма произведений сил на ординаты линии влияния, под ними расположенные. Величина S от равномерно распределенной нагрузки определяется произведением интенсивности нагрузки q на площадь, ограниченную линией влияния и осью абсцисс на участке действия нагрузки (площадь участка линии влияния). Величина S от действия внешнего момента равна произведению момента на тангенс угла наклона касательной к линии влияния в точке приложения этого момента (при возрастании ординат – знак плюс). При положительном моменте (по часовой стрелке) и убывании ординат нужно брать знак минус.

Задача 6. Расчет составных многопролетных балок, работающих на поперечный изгиб

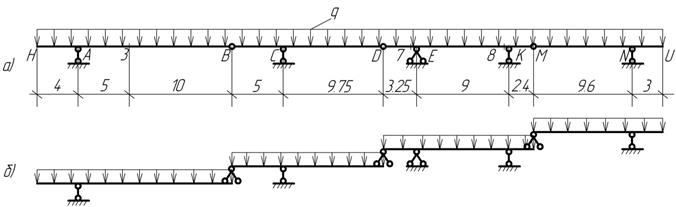
Для заданной балки с размерами и нагрузкой, определяемыми по табл. 6 и 7 и рис.7 и 8, требуется:

1) произвести кинематический анализ системы и построить поэтажную схему;

2) определить опорные реакции и построить эпюры М и Q;

3) рассчитать балку на ЭВМ и по результатам счета проверить правильность вычислений М и Q;

Таблица 6. Размеры балки

Номер cтроки	Схема балки по рис.7	l₃, м	l₂, м	l₁, м	К
01	1	5	7	7	0,3
02	9	6	8	6	0,2
03	8	6	9	8	0,7
04	7	8	6	6	0,5
05	4	8	6	9	0,8
06	5	9	8	7	0,45
07	6	10	9	6	0,35
08	3	9	10	8	0,7
09	2	6	7	6	0,5
10	6	5	8	9	0,3
11	1	6	9	6	0,2
12	2	6	6	8	0,7
13	3	8	6	8	0,5
14	4	8	8	6	0,8
15	5	9	9	7	0,45
16	6	10	10	6	0,35
17	7	5	6	8	0,5
18	8	6	7	6	0,8
19	9	6	8	9	0,45
20	5	8	9	6	0,35
21	1	8	9	8	0,7
22	2	9	10	8	0,5
23	3	10	6	6	0,3
24	4	9	7	7	0,2
25	5	6	8	6	0,7
26	6	5	9	8	0,5
27	7	6	6	6	0,3
28	8	6	6	9	0,2
29	9	8	8	6	0,7
30	4	8	9	8	0,5
31	1	9	10	8	0,8
32	2	10	6	6	0,45
33	3	9	7	7	0,35
34	4	6	8	6	0,7
35	5	5	9	8	0,5
36	6	6	6	6	0,3
	г	в	б	а	в

Таблица 7. Нагрузка на балку

Номер cтроки	Номер схемы загрузки по рис.8	М, кНм	P₂, кН	P₁, кН	q₁=q₂, кH/м
01	2	16	20	30	6,0
02	8	10	9	14	2,0
03	7	8	9	15	1,5
04	6	18	10	8	3,0
05	5	10	15	9	2,0
06	4	17	20	10	2,5
07	3	16	8	8	5,0
08	2	10	20	9	4,0
09	9	8	9	30	2,0
10	6	18	9	14	6,0
11	1	10	10	15	2,0
12	2	17	15	8	1,5
13	3	14	20	9	3,0
14	4	6	8	10	2,0
15	5	12	10	8	2,5
16	6	16	15	9	5,0
17	7	10	20	6	4,0
18	8	8	8	30	2,0
19	9	18	6	14	6,0
20	5	10	10	15	2,0
21	1	17	20	8	6,0
22	2	14	9	9	2,0
23	3	10	9	10	1,5
24	4	17	10	8	3,0
25	5	14	20	9	2,0
26	6	6	9	6	2,5
27	7	12	9	30	5,0
28	8	16	10	9	4,0
29	9	10	15	10	2,0
30	4	8	20	8	6,0
31	1	18	8	9	2,0
32	2	10	6	6	1,5
33	3	17	10	30	3,0
34	4	14	20	14	2,0
35	5	6	9	15	2,5
36	6	12	9	8	5,0
	а	в	б	г	б

Рис. 7 Рис. 8

Методические указания к задаче

Расчет статически определимой многопролетной балки можно произвести методом плоских сечений, с помощью линий влияния и с применением ЭВМ, для которых составляются программы, реализующие один из методов строительной механики.

Построение эпюр внутренних усилий многопролетной балки

1. При расчете многопролетных статически определимых балок целесообразно использовать схему взаимодействия элементов — поэтажную схему. Она позволяет свести расчет сложной балки к расчету простых балок с консолями. Для составления схемы взаимодействия в первую очередь необходимо выделить основные балки и опирающиеся на них второстепенные: основная балка рационально соединена тремя опорными стержнями, а второстепенная — менее чем тремя опорными стержнями с землей.

2. Произвести кинематический анализ многопролетной балки:

1) Определить ее число степеней свободы по формуле

W = 3D – 2Ш – С_оп,

где D — количество простых балок (дисков); Ш — число простых шарниров; С_оп — число опорных стержней.

При W = 0 балка статически определима и, возможно, геометрически неизменяема.

2) Проверить геометрическую неизменяемость многопролетной балки, положив в основу поэтажную схему.

Схема будет геометрически неизменяемой, если все основные балки соединены к земле, второстепенные — к земле и основным балкам с помощью трех опорных стержней, осевые линии которых не пересекаются в одной точке и не параллельны между собой.

3. Для каждой балки определяют опорные реакции и записывают уравнения внутренних усилий в сечении, находящемся на произвольном расстоянии X от левой опоры.

Верхние балки поэтажной схемы рассчитывают только на действие заданной нагрузки, а нижние балки — от давления, передаваемого через опоры верхних балок, и от заданной нагрузки.

После вычисления ординат внутренних усилий в характерных точках балки строят в выбранном масштабе эпюры М_х и Q_x по длине всей шарнирной балки.

Построение линий влияния многопролетной балки

1. Строят поэтажную схему.

2. Выбирают сечение или опору, для которых нужно построить ЛВ.

3. Если сечение или опора находятся на второстепенных балках АС и FL, то линии влияния в них строятся как для простых балок.

4. В пределах балки CF линии влияния строятся как для простой балки. Затем перемещают силу Р, равную 1, на второстепенную балку FL, а затем на такую же балку АС. На опорах С и F вводят местную систему координат — соответственно (X₁; Y₂) и (Х₂; Y₂) и определяют давление R_D и R_F как функции соответственно от X₁ и Х₂. Получают формулы исследуемых усилий в зависимости от R_D и R_F и по ним строят линии влияния.

Определение усилий по линиям влияния от заданной нагрузки

При действии на балку системы сил Р₁, Р₂ ... Р_n равномерно распределенных нагрузок q₁, q₂ ... q_n и моментов M₁, М₂ ... М_n полное усилие получим по принципу сложения действий сил:

S_K=ΣP_iy_i+Σq_i𝜔_i+ΣM_itg𝛼_i ,

где n - количество нагрузок P_i , q_i , M_i;

y_i - ордината линии влияния определяемого усилия под действием силы P_i;

𝜔_i - площадь участка линии влияния под нагрузкой q_i;

𝛼_i - угол наклона линии влияния в точке приложения момента M_i.

Задача 7. Расчет составных многопролетных балок, с построением линий влияния

Для одной из многопролетных балок, изображенных на рис.9 требуется:

1) построить эпюры внутренних силовых факторов;

2) построить линии влияния М₁; М₂; Q₁; R_B;

3) определить усилия М₁; М₂ по линиям влияния.

Исходные данные для расчета принять из табл. 8.

Таблица 8

Номер cтроки	Номер схемы по рис.9	F₁, кН	а, м	b, м	l, м	М, кНм	q, кН/м
01	1	12	1	2	2	24	5
02	2	10	2	2	3	16	4
03	3	12	3	2	4	12	6
04	4	6	2	3	2	18	2
05	5	8	1	3	5	20	4
06	6	10	3	1	6	12	2
07	7	6	2	2	3	12	3
08	8	8	1	2	2	12	6
09	9	6	2	1	4	16	5
10	10	12	1	3	3	10	6
11	11	11	1	2	5	12	6
12	12	12	3	3	1	18	2
13	13	10	2	3	2	20	4
14	14	12	1	1	4	12	2
15	15	6	2	2	5	12	3
16	16	8	1	2	3	12	6
17	17	10	2	1	2	18	5
18	18	6	3	2	5	20	6
19	19	8	2	2	3	12	2
20	20	6	1	3	2	12	4
21	21	12	3	3	1	12	2
22	22	12	2	1	3	16	3
23	23	13	1	2	4	10	6
24	24	14	1	2	5	12	5
25	25	12	3	1	3	18	6
26	26	10	2	3	2	20	6
27	27	12	1	2	1	12	2
28	28	6	2	3	3	24	4
29	29	8	1	3	5	16	2
30	30	10	2	1	4	12	3
31	31	6	3	2	2	18	6
32	32	8	2	2	1	20	5
33	33	6	1	1	3	12	6
34	34	12	3	3	6	12	2
35	35	11	2	2	4	16	4
36	36	8	3	2	4	24	6
	а	г	б	а	в	б	г

1 схема 2 схема

3 схема 4 схема

5 схема 6 схема

7 схема 8 схема

9 схема 10 схема

11 схема 12 схема

13 схема 14 схема

15 схема 16 схема

17 схема 18 схема

19 схема 20 схема

21 схема 22 схема

23 схема 24 схема

25 схема 26 схема

27 схема 28 схема

29 схема 30 схема

31 схема 32 схема

33 схема 34 схема

35 схема 36 схема

Рис.9

Задача 8. Расчет составных многопролетных балок, с построением линий влияния

Для балки, выбранной согласно варианту (рис. 10), требуется:

а) построить эпюры М и Q (аналитически);

б) построить линии влияния М и Q для заданного сечения, а также линию влияния одной опорной реакции R (по выбору студента);

в) определить по линиям влияния значения М, Q и R от заданной нагрузки;

г) определить прогиб и угол поворота заданного сечения балки.

Исходные данные выбираются в соответствии с шифром из табл. 9.

Таблица 9

Номер cтроки	Номер схемы по рис.10	а, м	q, кН/м	F, кН	M, кНм
01	1	3,2	1,2	10	18
02	2	3,8	2,0	12	20
03	3	4,2	1,8	16	24
04	4	4,6	2,4	24	10
05	5	4,8	2,6	22	12
06	6	4,5	1,4	20	8
07	7	3,4	1,5	15	14
08	8	2,8	1,6	18	22
09	9	3,0	2,0	14	25
10	0	2,6	2,5	25	16
11	1	4,6	1,8	10	18
12	2	4,8	2,4	12	20
13	3	4,5	2,6	16	24
14	4	3,4	1,4	24	10
15	5	2,8	1,5	22	12
16	6	3,0	1,6	20	8
17	7	2,6	2,0	15	14
18	8	4,6	2,5	18	22
19	9	4,5	1,8	10	25
20	0	3,4	2,4	12	16
21	1	2,8	2,6	16	18
22	2	3,0	1,2	24	20
23	3	2,6	2,0	22	24
24	4	4,6	1,8	20	10
25	5	4,8	2,4	15	10
26	6	4,5	2,6	18	12
27	7	3,4	1,4	10	8
28	8	2,8	1,5	12	14
29	9	3,0	1,6	16	22
30	0	2,6	1,2	24	25
31	1	4,6	2,0	22	16
32	2	4,5	1,8	20	24
33	3	3,4	2,4	15	16
34	4	2,8	2,6	18	14
35	5	3,0	1,4	10	8
36	6	2,6	1,5	12	10
	а	г	б	в	а

Рис. 10

Методические указания к решению задачи

Решению задачи должно предшествовать изучение тем: «Введение и основные понятия строительной механики», «Кинематический анализ сооружений», «Методы определения усилий от подвижной нагрузки», «Многопролетные статически определимые балки», а также повторение правил построения и проверки эпюр М и Q из курса сопротивления материалов.

Для построения эпюр М и Q удобнее пользоваться схемой взаимодействия («поэтажной» схемой), которую следует расположить непосредственно под схемой заданной балки. При построении «поэтажной» схемы нужно вначале выделить основные балки, что легко делается мысленным удалением шарниров, соединяющих балки между собой. Те балки, которые окажутся способными самостоятельно нести нагрузку (защемленные или имеющие две наземные опоры), будут основными. Вспомогательные балки имеют только одну наземную опору или не имеют их вовсе. Недостающими опорами для них служат соединительные шарниры.

После построения «поэтажной» схемы заданную балку можно рассматривать как ряд простых балок. Особенность задачи заключается в том, что для расчета нижележащих балок необходимо знать силы взаимодействия в шарнирах, которые являются опорными реакциями для вышележащих балок и нагрузкой для нижележащих. Для расчета схемы каждой отдельной балки должны быть вычерчены отдельно, а эпюры М и Q можно строить на общей базе под «поэтажной» схемой.

Ординаты эпюры моментов откладываются со стороны растянутых волокон (положительные вниз от оси). При построении эпюры поперечных сил положительные ординаты откладываются вверх и на эпюрах обязательно проставляются знаки.

Для построения линий влияния следует вычертить еще раз «поэтажную» схему, но уже без нагрузки. Обычно линии влияния строятся в два этапа. На первом этапе строится линия влияния искомого усилия в пределах той отдельной балки, к которой относится исследуемое сечение (или опора). На втором этапе добавляется продолжение линии влияния, обусловленное взаимодействием отдельных балок.

Все перемещения следует определять по формуле Мора с использованием правила Верещагина или Симпсона. Построение единичных эпюр моментов следует сопроводить расчетами. Грузовую и единичные эпюры изгибающих моментов при «умножении» рекомендуется делить на части таким образом, чтобы в пределах каждого участка «умножения» закон изменения изгибающего момента был постоянен.

Все расчеты должны сопровождаться необходимыми расчетными формулами, в общем и численном виде.

Задача 9. Расчет составных многопролетных балок на действие неподвижной нагрузки

Для балки, выбранной согласно варианту (рис. 11), требуется:

1. Произвести анализ геометрической неизменяемости заданной схемы балки. Для этой цели использовать выражение, представляющее собой необходимое условие геометрической неизменяемости,

Ш = С – 3.

где Ш – количество промежуточных шарниров; С – количество опорных связей, и выполнить анализ структуры взаимодействия отдельных дисков, построив поэтажную схему балки.

2. Составить схему взаимодействия отдельных дисков, расчленив заданную схему на главные и второстепенные балки, и определить реакции в связях от заданной нагрузки, составляя управления равновесия для каждого диска.

Порядок рассмотрения дисков – сверху вниз по поэтажной схеме.

3. Показать схему взаимодействия отдельных дисков с найденными реакциями в связях.

4. Произвести проверку правильности определения реакций в связях из условий равновесия всей расчетной схемы.

5. Построить эпюры поперечных сил и изгибающих моментов для отдельных дисков, объединив их для всей балки.

6. Произвести проверку построения эпюр усилий.

Исходные данные выбираются в соответствии с шифром из табл. 10.

Возможные места постановки шарниров отмечены сечениями 1-15 с шагом 0,25l , в каждом пролете (рис.11).

Таблица 10

Номер cтроки	Места постановки шарниров на рис.11	F₁, кН	F₂, кН	F₃, кН	q₁, кН/м	q₂, кН/м	l₁, м	l₂, м	l₃, м
01	3-6-10-13	36	0	72	0	9	12	16	18
02	4-6-9-12	0	72	54	12	0	16	24	18
03	3-5-11-13	72	0	96	0	12	32	18	24
04	5-7-9-11	0	36	96	24	0	24	16	32
05	4-7-9-12	84	0	72	0	24	12	24	32
06	3-7-9-12	0	84	84	15	0	24	12	18
07	3-5-10-12	42	0	96	0	18	16	18	32
08	3-7-9-13	0	96	72	18	0	16	32	12
09	4-7-10-12	96	0	84	0	15	32	24	12
10	4-6-9-13	0	54	96	12	0	12	18	32
11	3-6-10-13	36	0	72	0	9	12	16	18
12	4-6-9-12	0	72	54	12	0	16	24	18
13	3-5-11-13	72	0	96	0	12	32	18	24
14	5-7-9-11	0	36	96	24	0	24	16	32
15	4-7-9-12	84	0	72	0	24	12	24	32
16	3-7-9-12	0	84	84	15	0	24	12	18
17	3-5-10-12	42	0	96	0	18	16	18	32
18	3-7-9-13	0	96	72	18	0	16	32	12
19	4-7-10-12	96	0	84	0	15	32	24	12
20	4-6-9-13	0	54	96	12	0	12	18	32
21	3-6-10-13	36	0	72	0	9	12	16	18
22	4-6-9-12	0	72	54	12	0	16	24	18
23	3-5-11-13	72	0	96	0	12	32	18	24
24	5-7-9-11	0	36	96	24	0	24	16	32
25	4-7-9-12	84	0	72	0	24	12	24	32
26	3-7-9-12	0	84	84	15	0	24	12	18
27	3-5-10-12	42	0	96	0	18	16	18	32
28	3-7-9-13	0	96	72	18	0	16	32	12
29	4-7-10-12	96	0	84	0	15	32	24	12
30	4-6-9-13	0	54	96	12	0	12	18	32
31	3-6-10-13	36	0	72	0	9	12	16	18
32	4-6-9-12	0	72	54	12	0	16	24	18
33	3-5-11-13	72	0	96	0	12	32	18	24
34	5-7-9-11	0	36	96	24	0	24	16	32
35	4-7-9-12	84	0	72	0	24	12	24	32
36	3-7-9-12	0	84	84	15	0	24	12	18
	б	г	б	в	а	б	г	в	а

Рис.11

Задача 10. Расчет составных многопролетных балок на действие подвижной нагрузки

Для балки, выбранной согласно варианту (рис. 12), требуется:

1. Построить линию влияния одной из вертикальных опорных реакций основного диска шарнирно – консольной балки.

2. Определить величину опорной реакции от действия заданной неподвижной нагрузки по построенной линии влияния, используя формулу:

S = ΣF_iy_i + Σq_jω_j, (1)

где S – величина статического фактора, подлежащего определению (усилия, реакции); F_i – заданная сосредоточенная нагрузка; q_j – заданная равномерно распределенная нагрузка; y_i – ордината линии влияния под силой F_i; ω_j – площадь линии влияния под зоной действия нагрузки q_j.

Полученную по формуле (1) величину опорной реакции сравнить с результатом расчета в задаче 9.

3. Вычертить расчетную схему балки, выбрать один из основных дисков и на нём проставить сечения в пролёте через 0,25l, бесконечно близко слева и справа от опор и по концам консолей. Последовательно пронумеровать сечения слева направо.

4. Для каждого из отмеченных сечений построить линии влияния M и Q.

5. Для одного из сечений (по выбору студента) по построенным линиям влияния определить значения M и Q от заданной неподвижной нагрузки по формуле (1) и сравнить их с результатами расчета в задаче 9.

6. С помощью построенных в п. 4 линий влияния определить наибольшие по абсолютной величине положительные и отрицательные значения M и Q в отмеченных сечениях основного диска при действии подвижной нагрузки НК – 80 (табл.11) по формуле:

S = ΣG_iy_i , (2)

где S – величина статического фактора, подлежащего определению; G_i –величина подвижного груза; y_i– ординаты линии влияния под силами G_i при невыгоднейшей установке системы подвижных грузов.

Таблица 11. Основные показатели нормативных подвижных нагрузок

Примечание: При действии нагрузки АК равномерно распределенная нагрузка не учитывается.

При определении невыгоднейшего (расчетного) расположения подвижной нагрузки на ездовом поясе (на треугольном участке линии влияния) критический груз, устанавливаемый над наибольшей ординатой линии, может быть определен графо-аналитическим способом.

7. По результатам п. 6 построить огибающие эпюры M и Q для основного диска шарнирно – консольной балки.

Исходные данные выбираются в соответствии с шифром из табл. 12.

Возможные места постановки шарниров отмечены сечениями 1-15 с шагом 0,25l , в каждом пролете (рис.12).

Таблица 12

Номер cтроки	Места постановки шарниров на рис.12	F₁, кН	F₂, кН	F₃, кН	q₁, кН/м	q₂, кН/м	l₁, м	l₂, м	l₃, м
01	3-6-10-13	36	0	72	0	9	12	16	18
02	4-6-9-12	0	72	54	12	0	16	24	18
03	3-5-11-13	72	0	96	0	12	32	18	24
04	5-7-9-11	0	36	96	24	0	24	16	32
05	4-7-9-12	84	0	72	0	24	12	24	32
06	3-7-9-12	0	84	84	15	0	24	12	18
07	3-5-10-12	42	0	96	0	18	16	18	32
08	3-7-9-13	0	96	72	18	0	16	32	12
09	4-7-10-12	96	0	84	0	15	32	24	12
10	4-6-9-13	0	54	96	12	0	12	18	32
11	3-6-10-13	36	0	72	0	9	12	16	18
12	4-6-9-12	0	72	54	12	0	16	24	18
13	3-5-11-13	72	0	96	0	12	32	18	24
14	5-7-9-11	0	36	96	24	0	24	16	32
15	4-7-9-12	84	0	72	0	24	12	24	32
16	3-7-9-12	0	84	84	15	0	24	12	18
17	3-5-10-12	42	0	96	0	18	16	18	32
18	3-7-9-13	0	96	72	18	0	16	32	12
19	4-7-10-12	96	0	84	0	15	32	24	12
20	4-6-9-13	0	54	96	12	0	12	18	32
21	3-6-10-13	36	0	72	0	9	12	16	18
22	4-6-9-12	0	72	54	12	0	16	24	18
23	3-5-11-13	72	0	96	0	12	32	18	24
24	5-7-9-11	0	36	96	24	0	24	16	32
25	4-7-9-12	84	0	72	0	24	12	24	32
26	3-7-9-12	0	84	84	15	0	24	12	18
27	3-5-10-12	42	0	96	0	18	16	18	32
28	3-7-9-13	0	96	72	18	0	16	32	12
29	4-7-10-12	96	0	84	0	15	32	24	12
30	4-6-9-13	0	54	96	12	0	12	18	32
31	3-6-10-13	36	0	72	0	9	12	16	18
32	4-6-9-12	0	72	54	12	0	16	24	18
33	3-5-11-13	72	0	96	0	12	32	18	24
34	5-7-9-11	0	36	96	24	0	24	16	32
35	4-7-9-12	84	0	72	0	24	12	24	32
36	3-7-9-12	0	84	84	15	0	24	12	18
	б	г	б	в	а	б	г	в	а

Рис.12

Задача 11. Расчет многопролетных балок с построением линий влияния

Для балки, выбранной согласно варианту (рис. 12.2), требуется:

1) Провести кинематический анализ;

2) Построить эпюры изгибаемых моментов и поперечных сил (аналитически);

3) Построить линии влияния М и Q для заданного сечения, а также линию влияния одной опорной реакции (по выбору студента);

4) Определить по линиям влияния М, Q и R от заданной нагрузки и сравнить результаты пунктов 2 и 4;

5) Для заданного сечения определить наибольшие (по абсолютной величине) положительные или отрицательные значения М при действии заданной системы подвижных нагрузок;

6) Для заданного сечения определить наибольший и наименьший изгибающий момент от сочетания неподвижных и подвижных нагрузок.

Исходные данные выбираются в соответствии с шифром из табл. 13. Систему подвижных нагрузок принять следующей (рис.12.1):

Чертеж1-Model.png

Рис.12.1

Таблица 13

Номер cтроки	Номер схемы по рис.12.2	l₁, м	l₂, м	a, м	b, м	c, м	q, кН/м	P, кН	M, кНм
01	1	12	8	1,1	1,0	1,5	1,2	3	2,0
02	2	10	7	1,2	0,8	2,2	2,0	2,5	2,2
03	3	12	9	2,0	1,9	1,4	1,8	6	2,7
04	4	6	6	2,2	1,4	1,6	3,0	2,8	2,4
05	5	8	11	1,3	1,6	1,8	1,5	7	2,5
06	6	10	10	2,1	2,1	2,0	2,5	3,3	1,1
07	7	6	12	1,4	1,2	1,1	1,4	5	2,6
08	8	8	15	1,9	1,8	1,3	0,8	8	3,0
09	9	6	14	1,5	1,5	1,5	1,0	4	2,8
10	10	12	14	0,8	2,0	1,7	2,2	3,2	1,5
11	11	11	8	1,8	1,0	1,3	1,2	3	2,0
12	12	12	7	1,2	0,8	2,2	2,0	2,5	2,2
13	13	10	9	2,0	1,9	1,4	1,8	6	2,7
14	14	12	6	2,2	1,4	1,6	3,0	2,8	2,4
15	15	6	11	1,3	1,6	1,8	1,5	7	2,5
16	16	8	10	2,1	2,1	2,0	2,5	3,3	1,1
17	17	10	12	1,4	1,2	1,1	1,4	5	2,6
18	18	6	15	1,9	1,8	1,3	0,8	8	3,0
19	19	8	14	1,5	1,5	1,5	1,0	4	2,8
20	20	6	14	0,8	2,0	1,7	2,2	3,2	1,5
21	21	12	8	1,9	1,0	1,1	1,2	3	2,0
22	22	12	7	1,2	0,8	2,2	2,0	2,5	2,2
23	23	13	9	2,0	1,9	1,4	1,8	6	2,7
24	24	14	6	2,2	1,4	1,6	3,0	2,8	2,4
25	25	12	11	1,3	1,6	1,8	1,5	7	2,5
26	26	10	10	2,1	2,1	2,0	2,5	3,3	1,1
27	27	12	12	1,4	1,2	1,1	1,4	5	2,6
28	28	6	15	1,9	1,8	1,3	0,8	8	3,0
29	29	8	14	1,5	1,5	1,5	1,0	4	2,8
30	30	10	14	0,8	2,0	1,7	2,2	3,2	1,5
31	31	6	8	1,2	1,0	1,0	1,2	3	2,0
32	32	8	7	1,2	0,8	2,2	2,0	2,5	2,2
33	33	6	9	2,0	1,9	1,4	1,8	6	2,7
34	34	12	6	2,2	1,4	1,6	3,0	2,8	2,4
35	35	11	11	1,3	1,6	1,8	1,5	7	2,5
36	36	8	10	2,1	2,1	2,0	2,5	3,3	1,1
	а	г	б	а	в	б	г	а	б

1 схема

2 схема

3 схема

4 схема

5 схема

6 схема

7 схема

8 схема

9 схема

10 схема

11 схема

12 схема

13 схема

14 схема

15 схема

16 схема

17 схема

18 схема

19 схема

20 схема

21 схема

22 схема

23 схема

24 схема

25 схема

26 схема

27 схема

28 схема

29 схема

30 схема

31 схема

32 схема

33 схема

34 схема

35 схема

36 схема

Рис.12.2

Методические указания к решению задачи

Для построения эпюр М и Q удобнее пользоваться схемой взаимодействия («поэтажной» схемой), которую следует расположить под схемой заданной балки. При построении «поэтажной» схемы нужно вначале выделить основные балки, что легко делается мысленным удалением шарниров, соединяющих балки между собой.

Те балки, которые получают при этом подвижность (линейную или угловую), будут подвесными, а оставшиеся балки являются основными.

После построения «поэтажной» схемы заданную балку можно рассматривать как ряд простых балок. Расчёт следует начинать с подвесных балок. Для расчёта нижележащих балок необходимо знать силы взаимодействия в шарнирах.

Для построения линий влияния следует ещё раз вычертить «поэтажную» схему, но уже без нагрузки. Обычно линии влияния строятся в два этапа. На первом этапе строится линия влияния искомого усилия в пределах той отдельной балки, к которой относится исследуемое сечение (или опора). На втором этапе добавляется продолжение линии влияния, обусловленное взаимодействием отдельных балок.

Примеры расчета балки на подвижную и неподвижную нагрузку

Пример 1.

1. Рассмотрим балку (рис. 13, а).

Строим поэтажную схему (рис. 13, б) и определяем степень свободы балки:

W = 3D – 2Ш – С_оп= 3·3 – 2·3 – 6 = 0.

Главная балка CF прикреплена к земле тремя стержнями, осевые линии которых не пересекаются в одной точке и не параллельны между собой, значит, она геометрически неизменяема и статически определима (W=0). Балки AC и FL по приведенному признаку соединены с землей и главной балкой и поэтому являются геометрически неизменяемыми. Значит, в целом многопролетная балка статически определима и геометрически неизменяема.

2. Определяем опорные реакции, изгибающие моменты и поперечные силы в характерных сечениях балки.

Рис. 13

1) Для балки FL (рис. 14, б) определяем опорные реакции R_F и R_K из уравнений равновесия:

∑ M_K = 0: –R_F l₁ + m + 2P₂ = 0, откуда R_F = 4,7 кН,

∑ M_F = 0: –R_Kl₁ + m + P₂(l₁+ 2) = 0, откуда R_K = 13,7 кН.

Рис. 14

Проверяем правильность определения реакций: ∑ y = 0: –R_F + R_K – P₂ = 0. Реакции балки вычислены правильно.

Изгибающий момент и поперечная сила в сечении x₁ при изменении x₁ от 0 до 8 м вычисляются по формулам

M_x₁ = –R_F x₁ + m + R_K(x₁ – l₁);

Q_x₁ = –R_F + R_K;

При x₁ = 0 м: M_x₁ = 0 кНм, Q_x₁ = –R_F = –4,7 кН,

x₁ = 3 м: M_x₁ = –14 кНм, Q_x₁ = –R_F = –4,7 кН,

x^*₁ = 3 м: M^*_x₁ = –4 кНм, Q^*_x₁ = –R_F = –4,7 кН,

x₁ = 6 м: M_x₁ = –18 кНм, Q_x₁ = –R_F = –4,7 кН,

x^*₁ = 6 м: M^*_x₁= –18 кНм, Q^*_x₁= –R_F + R_K = 9 кН,

x₁ = 8 м: M_x₁ = 0 кНм, Q_x₁ = –R_F + R_K = 9 кН.

2) Проведем аналогичные расчеты для балки АС (см. рис. 13,а)

∑ M_C = 0: R_Bl₂ – P₁(l₂ – 2) – q₁(l₂ +2)²/2= 0, R_B = 41 кН.

∑ M_B = 0: –R_Cl₂ +P₁(l₂ - 2) – q₁·2² / 2 + q₁(l₂)² / 2 = 0, R_C = 17 кН.

Проверка реакций: ∑ y = 0: R_B + R_C – P₁ – q₁ · 6 = 0. Реакции вычислены правильно.

Изгибающий момент и поперечная сила в сечении х₂ при изменении х₂ от 0 до 6 м вычисляются по формулам

M_x₂ = R_B(x₂ – 2) – P₁(x₂ – 4) – q₁(x₂)² / 2;

Q_x₂ = –q x₂ + R_B – P₁;

При x₂ = 0 м: M_x₂ = 0 кНм, Q_x₂ = 0 кН,

x₂ = 2 м: M_x₂ = –16 кНм, Q_x₂ = 16 кН,

x^*₂ = 2 м: M^*_x₂ = –16 кНм, Q^*_x₂ = 25 кН,

x₂ = 4 м: M_x₂ = 18 кНм, Q_x₂ = 9 кН,

x^*₂ = 4 м: M^*_x₂= 18 кНм, Q^*_x₂ = –1 кН,

x₂ = 6 м: M_x₂ = 0 кНм, Q_x₂ = –17 кН.

3) Расчет главной балки CF. Загружаем ее в точках C и F давлением вышележащих балок R_D и R_E (реакциями с обратными знаками) (см. рис. 14, в) и вычисляем опорные реакции.

∑ M_E = 0: R_Dl – R_C ·8 – q₂ 8² / 2 + q₂ 2² / 2 – R_F · 2 = 0, откуда R_D = 44,2 кН.

∑ M_D = 0: –R_E l + q₂ ·8² / 2 – q₂ ·2² / 2 – R_F( l + 2) = 0, откуда R_E = 8,07 кН.

Проверяем правильность определения реакций.

∑ y = 0: R_E + R_D + R_F – q₂ · 10 –R_C = 0.

Реакции вычислены правильно.

Изгибающие моменты и поперечные силы в сечении х при изменении х от 0 до 10 м вычисляются по формулам

М_х₌–R_Cх –q₂х² / 2+ R_D(x₂ – 2)+ R_Е(x – 8);

Q_х= –R_C –q₂ х+ R_D+ R_Е.

При x = 0 м: M_x = 0 кНм, Q_x = –R_D = –17 кН,

x = 2 м: M_x = –42 кНм, Q_x = –25 кН,

x^* = 2 м: M^*_x = –42 кНм, Q^*_x = 19,2 кН,

x = 8 м: M_x = 13 кНм, Q_x = –4,7 кН,

x^* = 8 м: M^*_x = 13 кНм, Q^*_x = 3,3 кН,

x = 10 м: M_x = 0 кНм, Q_x = –4,7 кН.

По вычисленным значениям M и Q строятся эпюры внутренних усилий для каждой простой балки (см. рис. 14) и для многопролетной балки AL (см. рис. 13, в).

Пример 2.

Для составной многопролетной балки (рис.15) требуется построить эпюры внутренних усилий Q и M.

Дано:

Рис 5.jpg

Рис. 15

Решение.

1. Рассмотрим данную балку по частям. Первая часть – балка на отрезке AB, вторая – на отрезке BC. Отбросим опоры и заменим их влияние на балку опорными реакциями (рис.16).

Рис 6.jpg

Рис. 16

Составим сумму моментов всех сил для отрезка BC:

ΣX=0; X_B=0.

Проверка реакций:

Составим сумму проекций всех сил отрезка BC на вертикальную ось Y:

ΣY= -Y_B+Y_C-P-q∙b=0.

-4+52-28-20=0

0=0

Составим сумму моментов всех сил для отрезка AB:

ΣX=0; X_A+X_B=0 → X_A= -X_B=0.

Проверка реакций:

Составим сумму проекций всех сил отрезка AB на вертикальную ось Y:

ΣY= -Y_A+q∙c+Y_B=0.

36-20∙2+4=0

0=0

Проверка реакций всей балки:

Составим сумму проекций всех сил на вертикальную ось Y:

ΣY= Y_A-q∙(b+c)+Y_C-P=0.

36-20∙3+52-28=0

0=0

Полученное тождество показывает, что реакции вычислены правильно.

2. Построим эпюры Q и M (рис.17).

Балка имеет три участка. Используя метод сечений, составляем аналитические выражения для Q и M.

I участок

II участок

III участок

3. Из эпюр M следует, что в опасном сечении балки M_max=32 кНм.

Рис 7 - реакции и эпюры.jpg

Рис.17

Пример 3.

Пятиопорная шарнирная балка (рис. 18) состоит из четырех балок (дисков), соединенных тремя шарнирами, указанными на схемах балок. Балка загружена по всей длине расчетной равномерно распределенной нагрузкой q.

Требуется:

1. Вычертить в масштабе схему шарнирной балки, ее расчетную (поэтажную) схему, указать размеры в метрах.

2. Проверить геометрическую неизменяемость системы.

3. Построить восемь линий влияния:

а) линию влияния реакции крайней левой опоры;

б) линию влияния реакции средней опоры;

в) три линии влияния изгибающего момента и три линии влияния поперечной силы, возникающих в исследуемых сечениях (3, 7, 8).

Построение линий влияния следует сопровождать краткими пояснениями и необходимыми расчетными схемами.

4. Аналитически вычислить величину реакции крайней левой опоры, поперечной силы и изгибающего момента в исследуемом сечении первой балки, а также построить эпюры М и Q для этой балки.

Дано: l₁=20 м, l₂= 13 м, l₃=9 м, l₄=12 м, α=0,7, q=13 кH/м.

Рис. 18. а) схема шарнирной балки; б) расчетная схема.

Решение.

1. Вычертим схему шарнирной балки, а также расчетную схему (рис.18).

2. Проверим геометрическую неизменяемость системы.

Геометрическую неизменяемость системы определяется по формуле:

W=3 Д –2Ш –C₀; где W– число степеней свободы системы, Д – число дисков, Ш – число шарниров, C₀ – нулевое опорных стержней.

W=3∙4–2∙3–6=0, следовательно система геометрически неизменяема и статически определима.

3. Построение линий влияния.

а) Построим линию влияния реакции крайней левой опоры (рис.19).

Для этого рассмотрим первую балку слева.

Отбросим все внешние нагрузки и последовательно прикладываем единичную нагрузку в характерных сечениях.

Единичная сила приложена в сечении 1

∑M_b(F_i)=R_a∙15–1∙ (15+4)=0; R_a=(15+4)/15=1,27 кНм.

Единичная сила приложена в сечении 2

∑M_b(F_i)=R_a∙15–1∙15=0; R_a=15/15=1 кНм.

Единичная сила приложена в сечении 4

∑M_b(F_i)=R_a∙15=0; R_a=0.

33линия влияния для А

Рис. 19. Линия влияния для реакции R_a.

б) Построим линию влияния реакции средней опоры (сечение 7) (рис.20).

Отбросим все внешние нагрузки, последовательно прикладываем единичную нагрузку в характерных сечениях.

Рассмотрим третью балку

Единичная сила приложена в сечении 7, то в сечении 7 реакция средней опоры будет равна 1.

Единичная сила приложена в сечении 8, то в сечении 7 реакция средней опоры будет равна нулю. Далее распространяем линию влияния по правилу узловой нагрузки.

Определим значение ординаты реакции средней опоры, когда единичная сила находится в сечении 6 из подобия треугольников.

9/1=(9+3,25)/y; y=(9+3,25)∙1/9=1,36.

Единичная сила приложена в сечении 5, реакция опоры будет равна нулю.

Определим значение ординаты реакции средней опоры, когда единичная сила находится в сечении 4 из подобия треугольников.

9,75/1,36=5/y; y=5∙1,36/9,75=0,7.

Единичная сила приложена в сечении 2, то реакция опоры будет равна нулю.

Определим значение ординаты реакции средней опоры, когда единичная сила находится в сечении 1 из подобия треугольников.

15/0,7=4/y; y=4∙0,7/15=0,19.

Определим значение ординаты реакции средней опоры, когда единичная сила находится в сечении 9 из подобия треугольников.

9/1=2,4/y; y=2,4∙1/9=0,27.

Единичная сила приложена в сечении 10, то реакция опоры будет равна нулю.

Определим значение ординаты реакции средней опоры, когда единичная сила находится в сечении 11 из подобия треугольников.

9,6∙0,27=3/y; y=3∙0,27/9,6=0,08.

33линия влияния для рекции ср

Рис. 20. Линия влияния реакции средней опоры.

в) Построим линию влияния изгибающего момента сечения 3 (рис.21).

Для этого рассмотрим первую балку слева.

Отбросим все внешние нагрузки, последовательно прикладываем единичную нагрузку в характерных сечениях.

3.2.1 единичная сила приложена в сечении 1

∑M_b(F_i)=R_a∙15–1∙(15+4)=0; R_a=(15+4)/15=1,27 кН.

M(5)= R_a∙5–1∙(5+3,6)= 1,27∙5–1∙(5+4)= –2,65 кН;

3.2.2 единичная сила приложена в сечении 2

∑M_b(F_i)=R_a∙15–1∙15=0; R_a=15/15=1 кН.

M(5)= R_a∙5–1∙5= 1∙5–1∙5= 0;

3.2.3 единичная сила приложена в сечении 3

∑M_b(F_i)=R_a∙15–1∙10=0; R_a=10/15= 0,67 кН.

M(12,5)= R_a∙5= 0,67∙5= 3,35 кН;

3.2.4 единичная сила приложена в сечении 4

∑M_b(F_i)=R_a∙15=0; R_a=0.

M(5)= R_a∙5= 0;

33линия влияния для 3

Рис. 21. Линия влияния изгибающего момента для сечения 3.

г) Построим линию влияния изгибающего момента сечения 7 (рис.22).

Отбросим все внешние нагрузки, последовательно прикладываем единичную нагрузку в характерных сечениях.

Рассмотрим третью балку

Единичная сила приложена в сечении 6, тогда в сечении 7 будет действовать момент равный 1∙3,25=3,25 кНм

Единичная сила приложена в сечении 7, то в сечении 7 момент будет равен нулю.

Единичная сила приложена в сечении на участке от сечения 7 до 8, то момент в сечении 7 также будет равен нулю.

Единичная сила приложена в сечении 5, то то в сечении 7 момент будет равен нулю. Далее распространяем линию влияния по правилу узловой нагрузки.

Определим значение ординаты момента в сечении 7 когда единичная сила находится в сечении 4 из подобия треугольников.

9,75/5=3,25/y; y=3,25∙5/9,75=1,67.

Единичная сила приложена в сечении 2, то в сечении 7 момент будет равен нулю.

Определим значение ординаты момента в сечении 7 когда единичная сила находится в сечении 1 из подобия треугольников.

15/4=1,67/y; y=1,67∙4/15=1,67.

33линия влияния для сечения7

Рис. 22. Линия влияния изгибающего момента для сечения 7.

д) Построим линию влияния изгибающего момента сечения 8 (рис.23).

Отбросим все внешние нагрузки, последовательно прикладываем единичную нагрузку в характерных сечениях.

Рассмотрим третью балку

Если единичная сила приложена в сечении 8, то момент в этом сечении ноль.

Единичная сила приложена в сечении 9, то в сечении 8 момент будет равен –2,4∙1=–2,4 кНм.

Единичная сила приложена в сечении на участке от сечения 7 до 8, то момент в сечении 8 будет равен нулю.

Единичная сила приложена в сечении 10, то в сечении 8 момент будет равен нулю.

Далее распространяем линию влияния по правилу узловой нагрузки.

Определим значение ординаты момента в сечении 8 когда единичная сила находится в сечении 11 из подобия треугольников.

6,9/2,4=3/y; y=3∙2/6,9=0,87.

33линия влияния для 8

Рис. 23. Линия влияния изгибающего момента для сечения 8.

е) Построим линию влияния поперечной силы для сечения 3 (рис.24).

Для этого рассмотрим первую балку слева.

Отбросим все внешние нагрузки, последовательно прикладываем единичную нагрузку в характерных сечениях.

3.2.1 единичная сила приложена в сечении 1

∑M_b(F_i)=R_a∙15–1∙(15+4)=0; R_a=(15+4)/15=1.27 кН.

Q= R_a–1= 1,27–1= 0,27кН;

3.2.2 единичная сила приложена в сечении 2

∑M_b(F_i)=R_a∙15–1∙15=0; R_a=15/15=1 кН.

Q= R_a–1= 1–1= 0;

3.2.3 единичная сила приложена в сечении 3

∑M_b(F_i)=R_a∙15–1∙10=0; R_a=10/15= 0,67 кН.

Q= R_a= 0,67 кН;

3.2.4 единичная сила приложена в сечении 4

∑M_b(F_i)=R_a∙15=0; R_a=0.

M(5)= R_a∙5= 0;

33линия влияния для сечения3Q

Рис. 24. Линия влияния поперечной силы для сечения 3.

ж) Построим линию влияния поперечной силы сечения 7 (рис.25).

Отбросим все внешние нагрузки, последовательно прикладываем единичную нагрузку в характерных сечениях.

Рассмотрим третью балку.

Единичная сила приложена в сечении 6, тогда в сечении 7 будет действовать поперечная сила равная 1 кН.

Единичная сила приложена в сечении 7, то в сечении 7 поперечная сила будет равна 1 кН.

Единичная сила приложена в сечении на участке от сечения 7 до 8, то поперечная сила в сечении 7 будет равен нулю.

Единичная сила приложена в сечении 5, то в сечении 7 поперечная сила будет равен нулю.

Далее распространяем линию влияния по правилу узловой нагрузки.

Определим значение ординаты поперечной силы в сечении 7 когда единичная сила находится в сечении 4 из подобия треугольников.

9,75/1=5/y; y=5∙1/9,75=0,51.

Единичная сила приложена в сечении 2, то в сечении 7 поперечная сила будет равен нулю.

Определим значение ординаты поперечной силы в сечении 7 когда единичная сила находится в сечении 1 из подобия треугольников.

15/0,51=4/y; y=4∙0,51/15=0,14.

33линия влияния для сечения7Q

Рис. 25. Линия влияния поперечной силы для сечения 7.

з) Построим линию влияния изгибающего момента сечения 8 (рис.26).

Отбросим все внешние нагрузки, последовательно прикладываем единичную нагрузку в характерных сечениях.

Рассмотрим третью балку.

Единичная сила приложена в сечении 8, тогда в сечении 8 будет действовать поперечная сила равная 1кН.

Единичная сила приложена в сечении 7, то в сечении 8 поперечная сила будет ноль.

Далее распространяем линию влияния по правилу узловой нагрузки.

Определим значение ординаты поперечной силы в сечении 8 когда единичная сила находится в сечении 6 из подобия треугольников.

9/1=3,25/y; y=3,25∙1/9=0,36.

Единичная сила приложена в сечении 5, то в сечении 8 поперечная сила будет равен нулю.

Определим значение ординаты поперечной силы в сечении 8 когда единичная сила находится в сечении 4 из подобия треугольников.

9,75/0,36=5/y; y=5∙0,36/9,75=0,18.

Единичная сила приложена в сечении 2, то в сечении 7 поперечная сила будет равен нулю.

15/0,18=4/y; y=4∙0,18/15=0,05.

Если единичная сила приложена слева от опоры Е, то в сечении 8 поперечная сила будет равен нулю.

Определим значение ординаты поперечной силы в сечении 8 когда единичная сила находится в сечении 9.

∑M_К(F_i)=–R_Е∙9–1∙2,4=0; R_Е=–2,4/9=–0.27 кН.

Q= R_Е= –0,27= –0,27кН;

Единичная сила приложена в сечении 10, то в сечении 7 поперечная сила будет равен нулю.

Определим значение ординаты поперечной силы в сечении 7 когда единичная сила находится в сечении 11 из подобия треугольников.

9,6/0,27=3/y; y=3∙0,27/9,6=0,08.

33линия влияния для сечения8Q

Рис. 26. Линия влияния поперечной силы для сечения 8.

4. Построение эпюры М и Q для первой балки (рис.27).

4.1 Определение реакцию опоры А.

Для этого рассмотрим первую балку отдельно от всей системы. Для определения реакций опор составляем условие равновесия в виде суммы моментов всех сил относительно точек:

∑M_в(F_i)= –R_a ∙15+q∙(15+4)²/2=0;

∑M_h(F_i)= R_a ∙3,6–q∙(15+4)²/2– R_b ∙(15+4)=0;

R_a= [q∙(15+4)²/2]/15=[13∙(15+4)²/2]/15=156,43 кH;

R_b=( 156,43∙4–q∙(15+4)²/2)/(15+4)= –90,57 кH.

Проверка: ∑F_iy=R_a−q∙(15+4)– R_b=0; ∑F_iy=156,43−13∙(15+4)– 90.57=0.

4.2 Построение эпюр изгибающих моментов и поперечных сил.

На участке HА: x=0÷4;

Q(х)= −q∙x; Q(0)=−13∙0=0; Q(4)=−13∙4= –52 кH;

M(х)=− q∙x²/2 ; M(0)=0; M(4)= −13∙4²/2= –104 кHм;

На участке АС: x=0÷15;

Q(х)= −q∙ (4+x)+ R_a;

Q(0)=−13∙4+156,43= 104,43 кH;

Q(5)=−13∙(4+5)+156,43= 39,43 кH;

Q(15)=−13∙(4+15)+156,43= –90,57 кH;

M(х)= −q∙ (4+x)²/2+ R_a∙x ;

M(0)= −13∙4²/2+156,43∙0= –104 кHм;

M(5)= −13∙(4+5)²/2+156,43∙5= 255,67 кHм;

M(15)= −13∙(4+15)²/2+156,43∙15= 0;

На участке АB поперечная сила Q равна нулю, значит в этом сечении балки изгибающий момент достигает максимума (минимума) на данном участке.

Определим х₀ из уравнения Q(х₀)= −q∙4– q∙х₀+ R_a;

х₀=(–q∙4 + R_a)/q; х₀=(–13∙4+156,43)/13= 8,03 м;

тогда M(8,03)= −13∙(4+8.03)²/2+156,43∙8.03= 315,47 кHм.

эпюра

Рис. 27. Эпюры изгибающих моментов и поперечных сил.

Пример 4.

Пример построения линий влияния опорных реакций и внутренних усилий M_n, Q_n в сечении n многопролетной балки (рис. 28).

Решение.

На рис. 28, а приведена схема неподвижной нагрузки, необходимая для определения значений реакции и внутренних усилий с помощью линий влияния, а на рис. 28, б – схема движения единичной вертикальной силы Р, равной 1, по балке AL, от которой строятся линии влияния. Затем строим поэтажную схему (рис. 28, в).

Рис.28

1. Построение линий влияния опорных реакций R_D и R_E.

1) Ставится единичный груз P = 1 на балку CF. Начало системы координат (X, Y) принимается на опоре E. Абсцисса груза меняется в пределах –2 м < X < 8 м, а балки AC и FL мысленно отбрасываются

∑ M_E = 0: R_D l – Px = 0, откуда R_D = Px / l; (1)

∑ M_D = 0: –R_E l – P(l – x) = 0, откуда R_E = P(l – x) / l; (2)

При x = –2 м: R_D = –1/3, R_E = 4/3,

x = 0 м: R_D = 0, R_E = 1,

x = l м: R_D = 1, R_E = 0,

x = 8 м: R_D = 4/3, R_E = –1/3.

2) Единичный груз Р = 1 переносится на балку FL. Начало местной системы координат (X₁, Y₁) принимается на опоре K. Абсцисса груза меняется в пределах –2 м < x₁ < 6 м.

∑ M_K = 0: R_F l₁ – P x₁ = 0: R_F = P x₁ / l₁.

Выразим R_D и R_E через давление R_F. Для этого прикладываем давление R_F на балку CF в точке F, мысленно отбросив балки AC и FL.

∑ M_E = 0: R_D l + R_F · 2 = 0; R_D = –R_F · 2 / l = – (P x₁ / l₁) · 2/l;

∑ M_D = 0: –R_E l + R_F · 8 = 0; R_E = R_F · 8 / l = (P x₁ / l₁) · 8/l.

Итак, при движении P = 1 по участку FL реакции равны:

R_D= – (P x₁ / l₁) · 2/l; (3)

R_E = (P x₁ / l₁) · 8/l. (4)

При x₁ = –2 м: R_D = 1/9, R_E = –4/9,

x₁ = 0 м: R_D = 0, R_E = 0,

x₁ = l₁ м: R_D = –1/3, R_E = 4/3.

3) Переносим единичный груз P = 1 на балку AC. Начало местной системы координат (X₂, Y₂) примем на опоре С, абсциссу груза меняющейся в пределах 0 м < X₂ < 6 м.

Определяем реакцию R_C:

∑ M_B = 0: –R_C l₂ + P(l₂ – x₂) = 0, откуда R_C = P(l₂ – x₂) / l₂;

Выразим R_D и R_E через давление R_C. Для этого приложим R_C на балку CF в точке С, мысленно отбросим балки AC и FL.

∑M_E=0: R_D l – Rс·8=0; R_D=Rс·8/l=P((l₂ – x₂)/l₂) ·8/l;

∑M_D=0: –R_E l – R_C·2=0; R_E= –R_C·2/l=–P((l₂– x₂)/l₂) ·2/l;

Итак, при движении P=1 по участку AC реакции равны:

R_D= P ((l₂ – x₂)/l₂)·8/l; (5)

R_E= –P ((l₂ – x₂)/l₂)·2/l; (6)

При x₂=0 м: R_D= 4/3; R_E= –1/3;

x₂= l₂=4 м: R_D= 0; R_E=0;

x₂=6 м: R_D= –2/3; R_E=1/6.

По полученным ординатам строим ЛВ R_Dи R_E, (см. рис. 28, г, д).

2. Построение линии влияния M_n и Q_n в сечении n балки AL

1) Пусть единичная сила движется по балке CF левее сечения n, абсцисса меняется в пределах 3 м<x₂<8 м, а реакция R_E – по закону (2). Из равновесия части балки nF с меньшим количеством сил относительно сечения n получим

M_n=R_E b; (a)

Q_n= –R_E; (б)

Подставим значения R_E=P(l–x)/l из (2) в формулы (а) и (б), откуда получим:

M_n=bP(l-x)/l;

Q_n= –P(l–x)/l;

При x=3 м: M_n=1,5; Q_n= –0,5;

x=6 м: M_n=0; Q_n=0;

x=8 м: M_n= –1; Q_n= 1/3;

2) При движении единичной силы по балке АС абсцисса меняется в пределах 0<x₂<6м, а реакция R_E– по закону (6):

R_E=–P((l₂–x₂)/l₂) ·2/l;

Подставим значение R_E в формулы (а) и (б), получим:

M_n=R_E b=[–P((l₂–x₂)/l₂)) ·2/l]·b;

Q_n= –R_E= P((l₂–x₂)/l₂)) ·2/l;

При x₂=0 м: M_n= –1; Q_n=1/3;

x₂=l₂=4 м: M_n=0; Q_n=0;

x₂=6 м: M_n= 1/2; Q_n= –1/6;

3) Поставим единичную силу P=1 между сечением n и F балки CF, абсцисса будет меняться в этом случае в пределах –2 м<x<3 м, а реакция R_D– по закону(1): R_D=P·x/l.

Из равновесия левой части nC балки CF, ввиду того, что здесь меньше сил, получим для сечения n:

M_n=R_D a; (в)

Q_n=R_D; (г)

Подставим значение R_D в формулы (в) и (г), получим:

M_n=R_D a=(P x/l) ·a;

Q_n=P x/l;

При x= –2 м: M_n= –1; Q_n= –1/3;

x=0 м: M_n=0; Q_n=0;

x=b=3 м: M_n= 1,5; Q_n=0,5;

4) Переносим единичный груз на балку FL. Здесь: –2 м<x₁<6 м, а R_D определяется по формуле (3): R_D=– (P x₁/l₁) ·2/l;

Подставим значение R_D этого участка в формулы (в) и (г), получим:

M_n=R_D a=[–(P x₁/l₁) ·2/l] a;

Q_n=R_D= – (P x₁/l₁) ·2/l;

При x₁= –2 м: M_n=1/3; Q_n=1/9;

x₁=0 м: M_n=0; Q_n=0;

x₁=l₁=6 м: M_n= –1; Q_n= –1/3;

По полученным значениям ординат строим линию влияния изгибающего момента M_n и поперечной силы Q_n в сечении n балки (см. рис. 28, е, ж).

3. Определение реакции R_D, изгибающего момента M_nи поперечной силы Q_n в сечении n балки AL от заданной нагрузки, показанной на рис. 28, а.

1. Вычисление величины опорной реакции R_D,

R_D=P₁y₁+P₂y₂+q₁ω₁+q₂ω₂+m tgα;

По рис. 28, г определяем ординаты под силами P₁ и P₂ на ЛВ R_D:

y₁=2/3; y₂=1/9;

ω₁=(–2/3)·2·1/2+(4/3)·4·1/2=2 м² – площадь ЛВ R_D под распределенной нагрузкой q₁;

ω₂=(4/3)·8·1/2–(1/3)·2·1/2=5 м² – площадь ЛВ R_D под распределенной нагрузкой q₂;

tgα=(1/3)·1/6=1/18 – тангенс угла наклона ЛВ R_Dв точке приложения сосредоточенного момента m.

R_D=10·2/3+9·1/9+8·2+4·5+10·1/18=44,2 кН.

2. Вычисление изгибающего момента M_n в сечении n.

M_n=P₁ y₁+P₂ y₂+q₁ ω₁+q₂ ω₂+m tgα.

По рис. 28, е определяем ординаты под силами P₁ и P₂ на ЛВ M_n:

y₁= –1/2; y₂=1/3;

ω₁=1/2·2·1/2–1·4·1/2= –1,5 м²– площадь ЛВ M_nпод распределенной нагрузкой q₁;

ω₂= –1·2·1/2+1,5·3·1/2–1·2·1/2=2,5 м²– площадь ЛВ M_n под распределенной нагрузкой q₂;

tgα=1/6 – тангенс угла наклона ЛВ M_n в точке приложения сосредоточенного момента m.

M_n=10·(–1/2)+9·1/3+8·(–1,5)+4·2,5+10·1/6= –2,33 кН.

3. Вычисление поперечной силы Q_n в сечении n.

Q_n=P₁ y₁+P₂ y₂+q₁ ω₁+q₂ ω₂+m tgα.

По рис. 28, ж определяем:

y₁= –1/2; y₂=1/3;

ω₁=(–1/6)·2·1/2+(1/3)·4·1/2=1/2 м²– площадь ЛВ Q_nпод распределенной нагрузкой q₁;

ω₂=1/3·2·1/2–0,5·3·1/2+0,5·3·1/2–1/3·2·1/2=0 м²– площадь ЛВ Q_n под распределенной нагрузкой q₂;

tgα=1/3·1/6=1/18 – тангенс угла наклона ЛВ Q_n в точке приложения сосредоточенного момента m.

Q_n=10·1/6+9·1/9+8·1/2+4·0+10·1/18=7,2 кН.

Из вычислений видно, что результаты усилий по методу плоских сечений и линиям влияний практически совпадают.

Пример 5.

Для составной многопролетной балки (рис.29) требуется:

1. Построить эпюры M и Q.

2. Построить линии влияния M и Q для шести сечений.

3. Загрузить линии влияния заданной неподвижной нагрузкой.

4. Построить огибающую эпюру моментов от заданной подвижной нагрузки.

Дано: q=2∙10³ Н/м, F=4∙10³ Н, a=2 м, l₁=4 м, l₂=6 м, l₃=3 м.

Рис.29. Расчетная схема составной балки

Решение.

1. Построение эпюр M, Q (рис.30).

Рис. 30. Расчетная схема балки и эпюры M и Q

Рассмотрим равновесие диска CDE. Определим неизвестные реакции опор V_C, V_D, H_C по следующим формулам равновесия:

ΣF_Y=0; ΣM_C=0; ΣM_D=0; ΣF_X=0;

Так как на диск не действуют силы по оси x, то реакция H_C=0;

ΣM_C=0;

ΣM_D=0;

По условию ΣF_Y=0 проверим правильность определения реакций:

V_C+ V_D-F-qa=0;

2670+5330-4000-2000∙2=0;

Сумма проекций всех сил на ось Y равна нулю, следовательно, реакции определены правильно.

Составим функции M, Q и N по длине диска. Он имеет два силовых участка – CD и DE.

Участок DE 0≤z₁≤2 м;

Участок CD 0≤z₂≤3 м;

Рассмотрим равновесие диска ABC. Определим неизвестные реакции опор V_A, V_B, H_A по следующим формулам равновесия:

ΣF_Y=0; ΣM_A=0; ΣM_B=0; ΣF_X=0;

Так как на диск не действуют силы по оси x, то реакция H_A=0;

ΣM_A=0;

ΣM_B=0;

По условию ΣF_Y=0 проверим правильность определения реакций:

-V_A+ V_B- V_C=0;

-4000+6670-2670=0;

Сумма проекций всех сил на ось Y равна нулю, следовательно, реакции определены правильно.

Составим функции M, Q и N по длине диска. Он имеет два силовых участка – AB и BC.

Участок AB 0≤z₃≤4 м;

Участок BC 0≤z₄≤6 м;

По полученным данным строим эпюры M и Q (рис. 30).

2. Построение линий влияния M и Q

Построим линии влияния моментов и поперечных сил в пяти сечениях: К₁_,К₂, К₃, К_4, К₅ и К₆. Для этого рассмотрим балку под действием подвижной единичной сосредоточенной силы (рис.31).

Рис. 31. Линии влияния в сечениях К1-К6

3. Загружение линий влияния заданной неподвижной нагрузкой

Для определения усилий загружаем линии влияния и находим величину усилий по формуле:

Загружаем линии влияния сечения К1 заданной неподвижной нагрузкой (рис.32):

Рис. 32. Балка, загруженная заданной неподвижной нагрузкой и линии влияния сечения К1

Загружаем линии влияния сечения К2 заданной неподвижной нагрузкой (рис.33):

Рис. 33. Балка, загруженная заданной неподвижной нагрузкой и линии влияния сечения К2

Загружаем линии влияния сечения К3 заданной неподвижной нагрузкой (рис.34):

Рис. 34. Балка, загруженная заданной неподвижной нагрузкой и линии влияния сечения К3

Загружаем линии влияния сечения К4 заданной неподвижной нагрузкой (рис.35):

Рис. 35. Балка, загруженная заданной неподвижной нагрузкой и линии влияния сечения К4

Загружаем линии влияния сечения К5 заданной неподвижной нагрузкой (рис.36):

Рис. 36. Балка, загруженная заданной неподвижной нагрузкой и линии влияния сечения К5

Загружаем линии влияния сечения К6 заданной неподвижной нагрузкой (рис.37):

Рис. 37. Балка, загруженная заданной неподвижной нагрузкой и линии влияния сечения К6

Вывод: значения внутренних усилий, в сечениях К1-К6 вычисленные методом сечений, совпадают со значениями, полученными при загружении линий влияния этих сечений.

4. Построение огибающей эпюры моментов от заданной подвижной нагрузки.

Расчетные данные: P₁=3∙10³ Н, P₂=4∙10³ Н, P₃=2∙10³ Н, l₁=1 м, l₂=2 м,

Рис. 38. Схема подвижной нагрузки

Располагаем подвижную нагрузку так, чтобы в одном случае она создавала в сечении максимальный, а в другом минимальный изгибающий момент.

Загружаем линию влияния сечения К1 заданной подвижной нагрузкой (рис.39):

Рис. 39. Балка, загруженная заданной подвижной нагрузкой и линия влияния сечения К1

M_MIN₍_K₁₎₌4∙0+3∙0,5-2∙1=-1,5 кНм;

M_MAX₍_K_1)=-4∙3-2∙1-3∙2,5=-21,5 кНм;

Загружаем линию влияния сечения К2 заданной подвижной нагрузкой (рис.40):

Рис. 40. Балка, загруженная заданной подвижной нагрузкой и линия влияния сечения К2

M_MIN₍_K₂₎₌4∙0+3∙0+2∙0=0 кНм;

M_MAX₍_K_2)=-4∙6-2∙2-3∙5=-43 кНм;

Загружаем линию влияния сечения К3 заданной подвижной нагрузкой (рис.41):

Рис. 41. Балка, загруженная заданной подвижной нагрузкой и линия влияния сечения К3

M_MIN₍_K₃₎₌4∙0+3∙0-2∙0=0 кНм;

M_MAX₍_K_3)=-4∙3-2∙1-3∙2=-20 кНм;

Загружаем линию влияния сечения К4 заданной подвижной нагрузкой (рис.42):

Рис. 42. Балка, загруженная заданной подвижной нагрузкой и линия влияния сечения К4

M_MIN₍_K₄₎₌4∙0+3∙0-2∙0=0;

M_MAX₍_K_4)=-4∙1-3∙0,5=-5,5 кНм;

Загружаем линию влияния сечения К5 заданной подвижной нагрузкой (рис.43):

Рис. 43. Балка, загруженная заданной подвижной нагрузкой и линия влияния сечения К5

M_MIN₍_K₅₎₌4∙0+3∙0+2∙0=0;

M_MAX₍_K_5)=-4∙2-3∙1=-11 кНм;

Загружаем линию влияния сечения К6 заданной подвижной нагрузкой (рис.44):

Рис. 44. Балка, загруженная заданной подвижной нагрузкой и линия влияния сечения К6

M_MIN₍_K₆₎₌4∙0+3∙0-2∙0=0;

M_MAX₍_K_6)=-4∙1=4 кНм;

Сечение	M_min	M_max
К1	-1,5	-21,5
К2	-43	0
К3	-20	0
К4	-5,5	0
К5	-11	0
К6	4	0

По полученным данным строим огибающую эпюру M (рис. 45).

Рис. 45. Огибающая эпюра моментов

email: KarimovI@rambler.ru

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Строительная механика

Прикладная механика Детали машин Теория машин и механизмов

00:00:00